An Improved Fading Factor-Based Adaptive Robust Filtering Algorithm for SINS/GNSS Integration with Dynamic Disturbance Suppression
Abstract
1. Introduction
2. Methods
2.1. Research Design Framework
- Problem-driven: In complex dynamic environments (such as urban canyons, marine high-vibration scenarios), the SINS/GNSS integrated navigation system faces the following core challenges: (1) Model structure mismatch: The traditional EKF uses first-order Taylor expansion linearization. When encountering high-frequency vibrations, the second-order truncation error accumulates, resulting in a non-positive state estimation covariance matrix, causing the risk of filtering divergence. (2) Dissimilation of noise characteristics: GNSS observation noise exhibits pulse characteristics due to multipath effects and occlusion; the colored noise generated by IMU in the vibration environment breaks through the classical Gaussian white noise hypothesis, which leads to the inaccurate estimation of the noise model by the system and affects the filtering effect.
- Theoretical modeling: Based on the SINS/GNSS loosely coupled model, the 15-dimensional error state vector and the 6-dimensional observation vector are defined and the state equation and measurement equation are constructed.
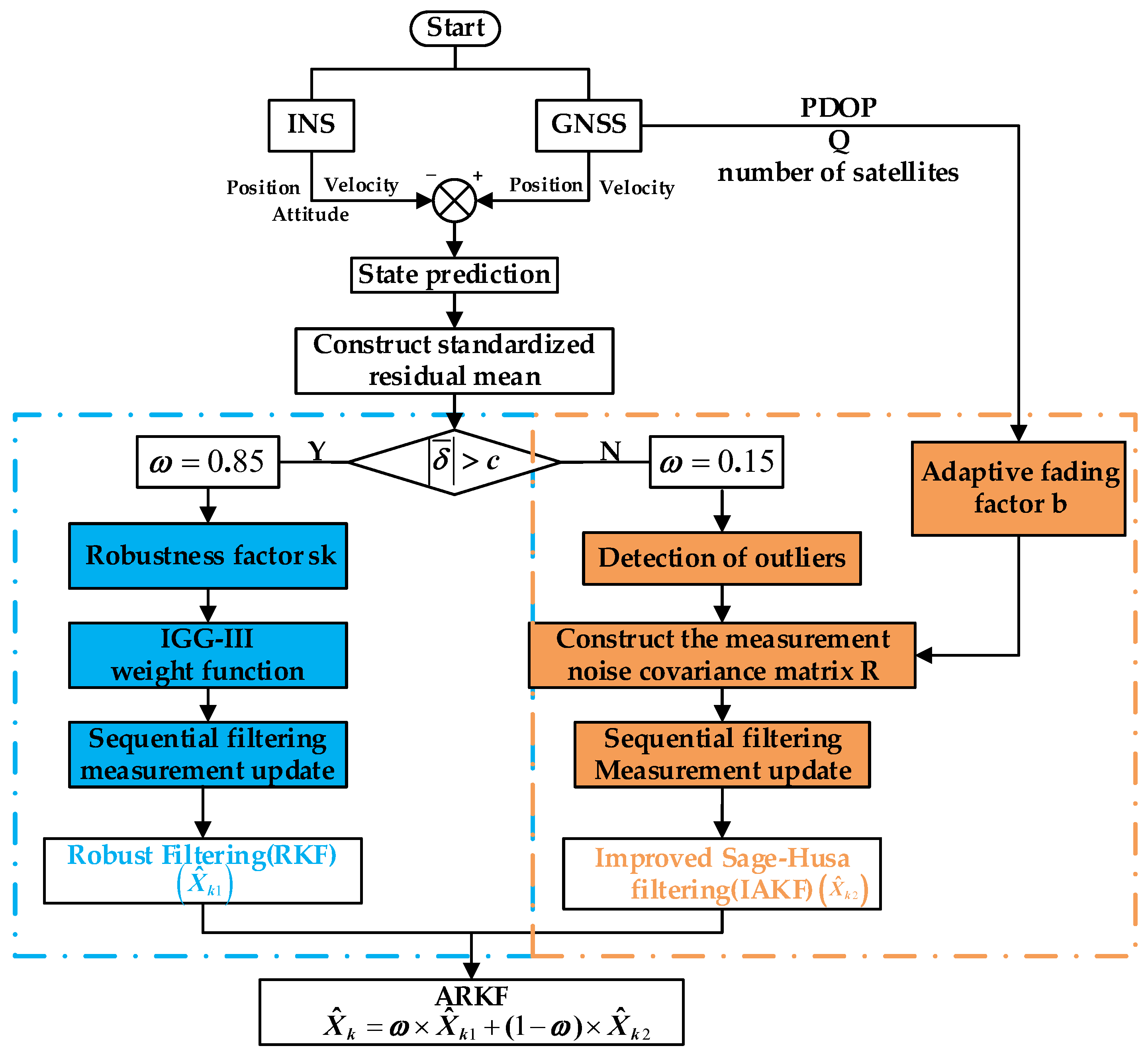
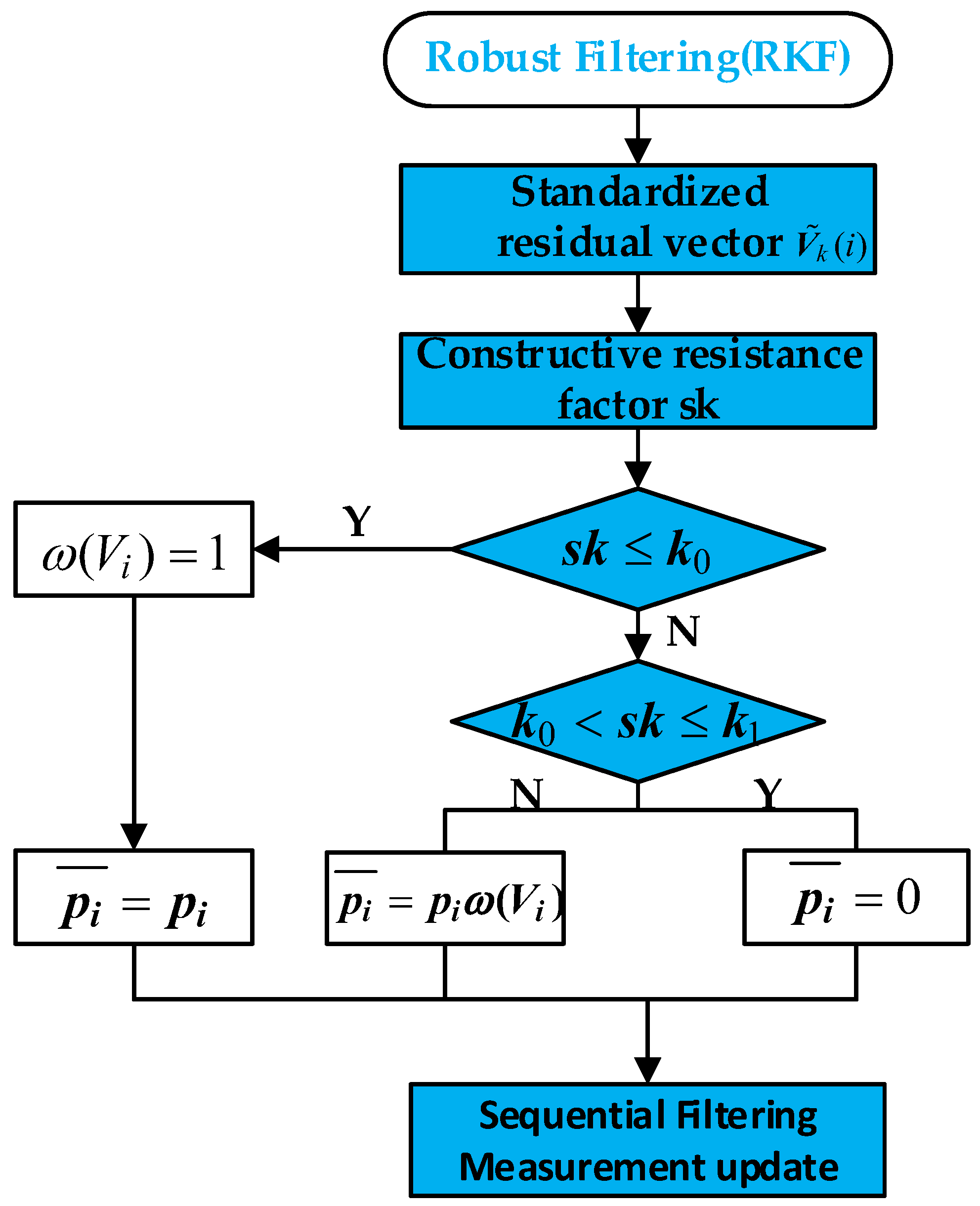
- Algorithm design: The dynamic fading factor is constructed by multi-source information fusion, and the sequential filtering is used to update the measurement to avoid the negative determination of the measurement noise covariance matrix. At the same time, the standardized residual and IGG-III weight function are combined to suppress the influence of abnormal observation on state update, and the two-factor robust mechanism is realized.
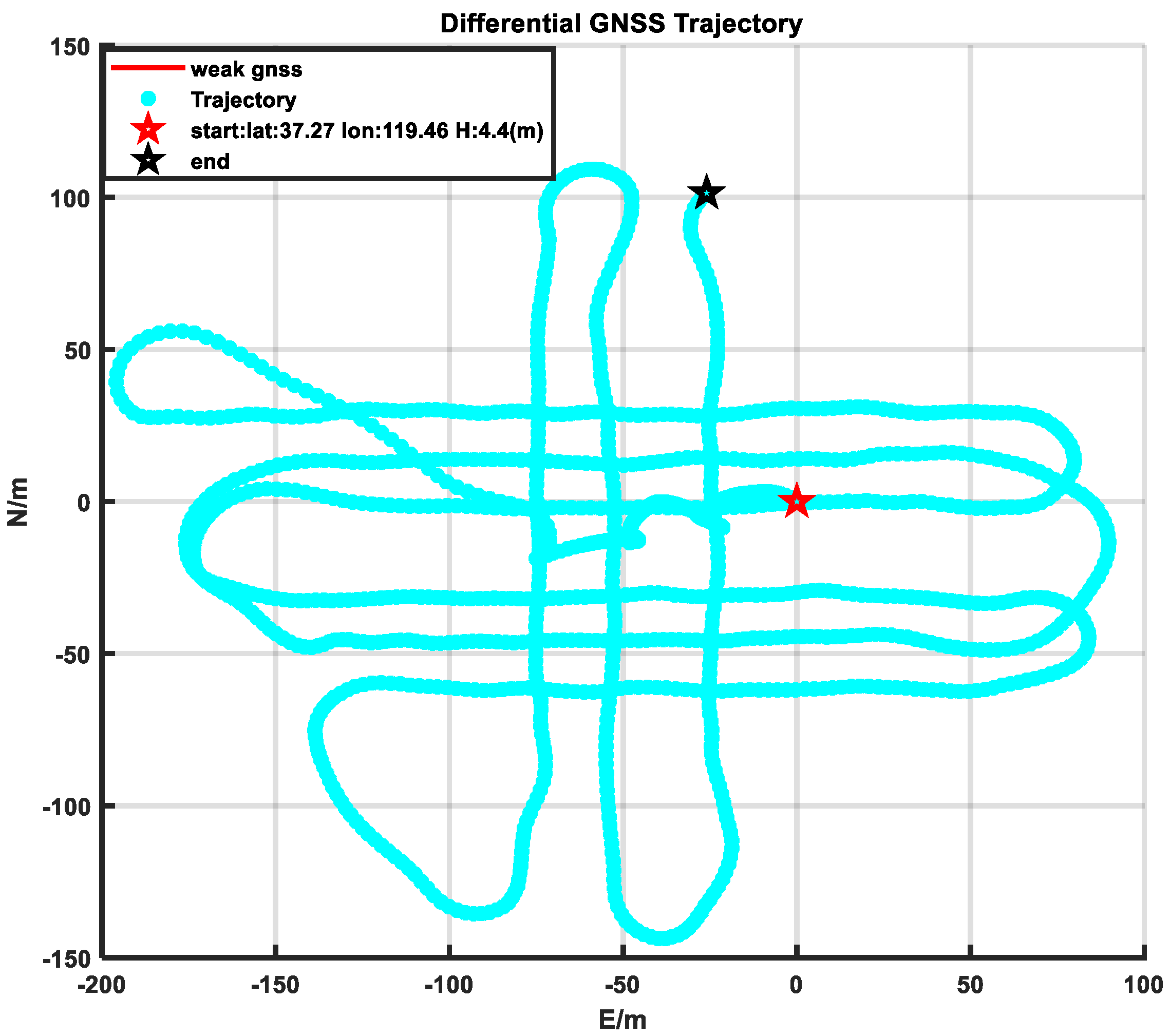
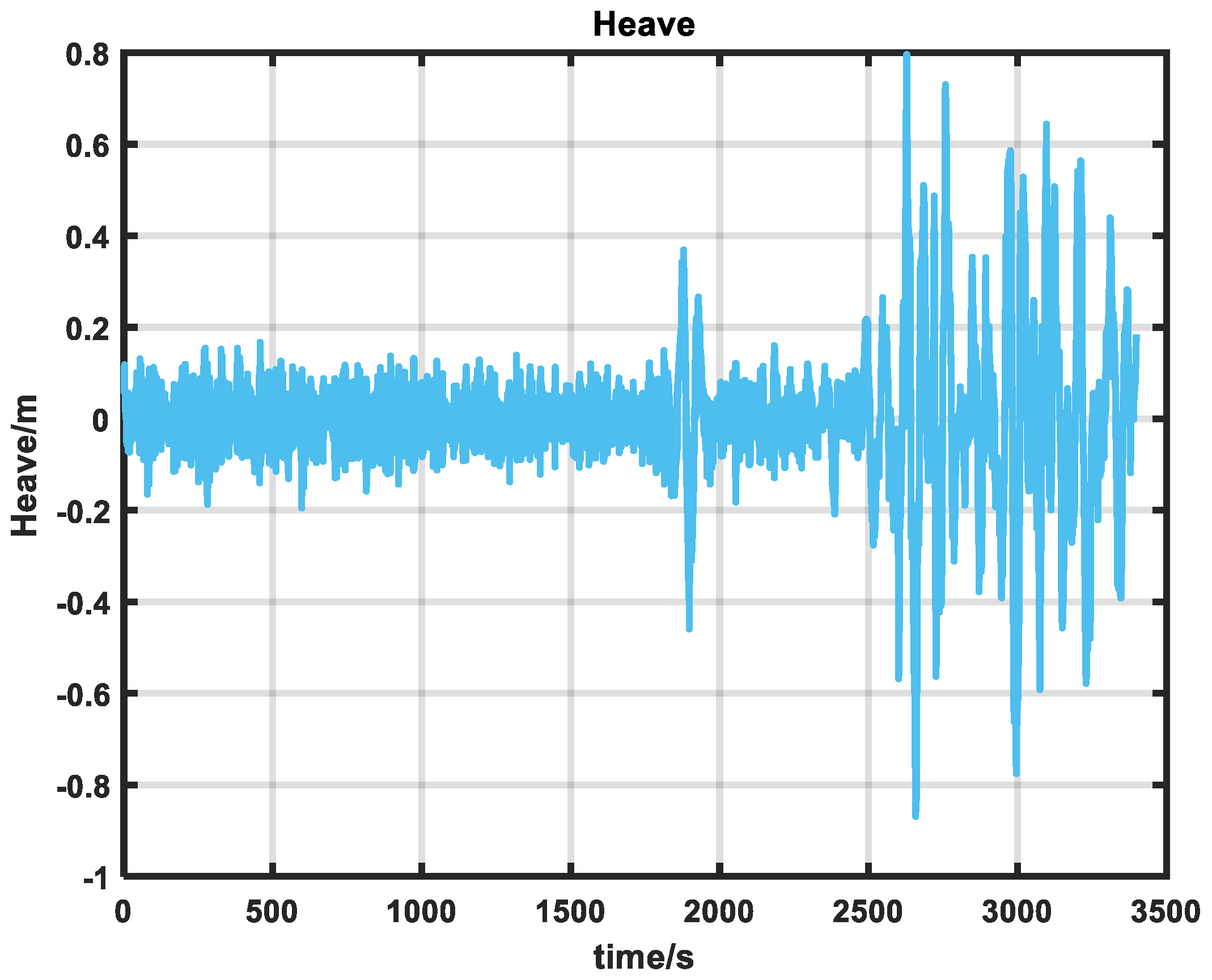
- Experimental verification: In order to verify the performance of the algorithm, a set of vehicle-mounted experiments was designed. The experimental time was about 20 min. Due to the high-rise occlusion, the data had a GNSS signal of about 200 s. A set of ship-borne experiments, three-level sea conditions, were designed, and the experiment lasted about 1 h. After the 2000s, the heave of the ship was significantly increased due to the wind and waves. The emergence of these abnormal conditions increases the uncertainty of navigation and can better verify the stability of the algorithm in a disturbed environment.
2.2. Combined SINS/GNSS Navigation Models
2.3. SINS/GNSS Adaptive Robust Filtering Algorithm Based on Improved Fading Factor (ARKF)
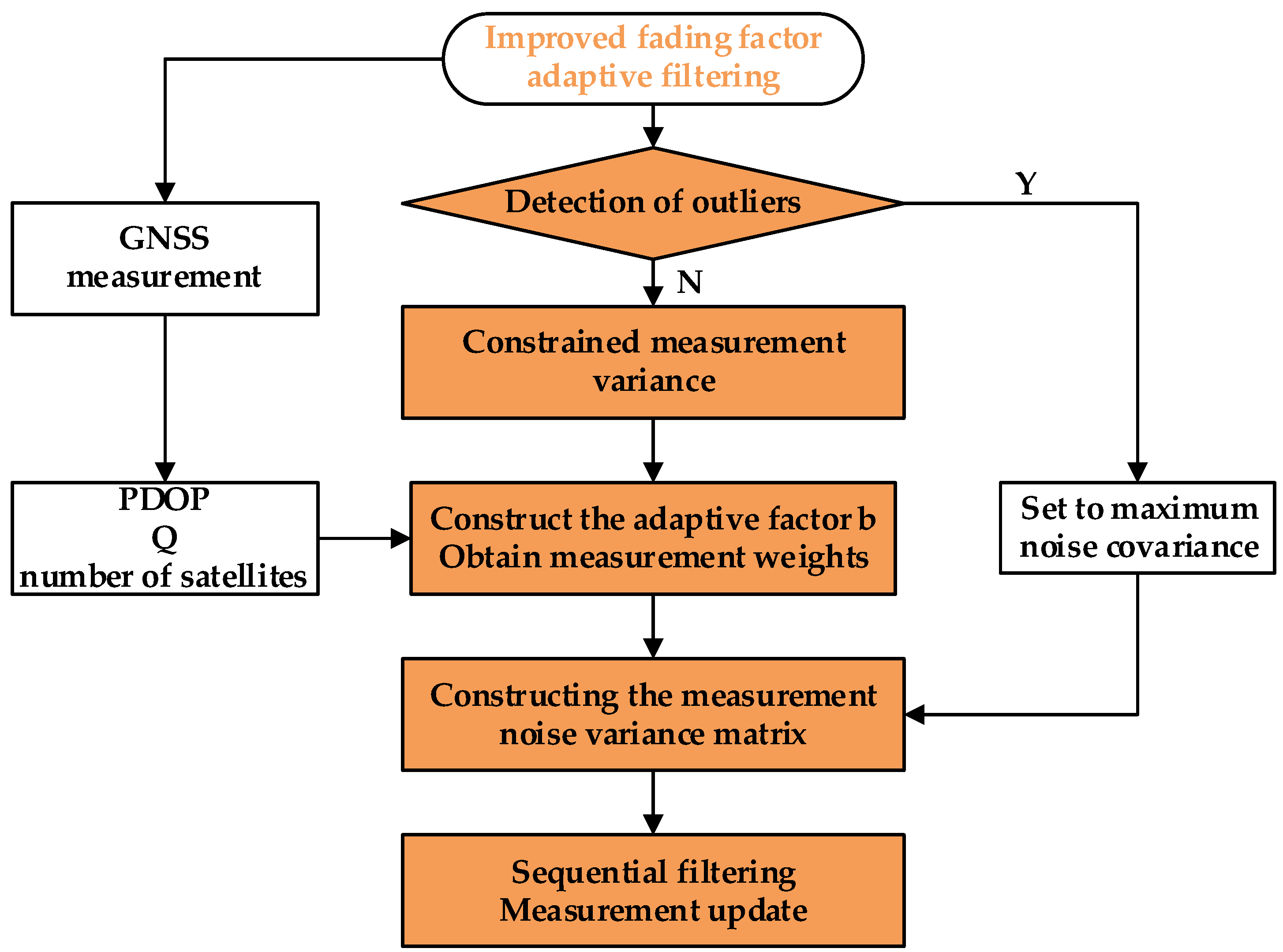
2.4. Improved Fading Factor Adaptive Filtering Algorithm (IAKF)
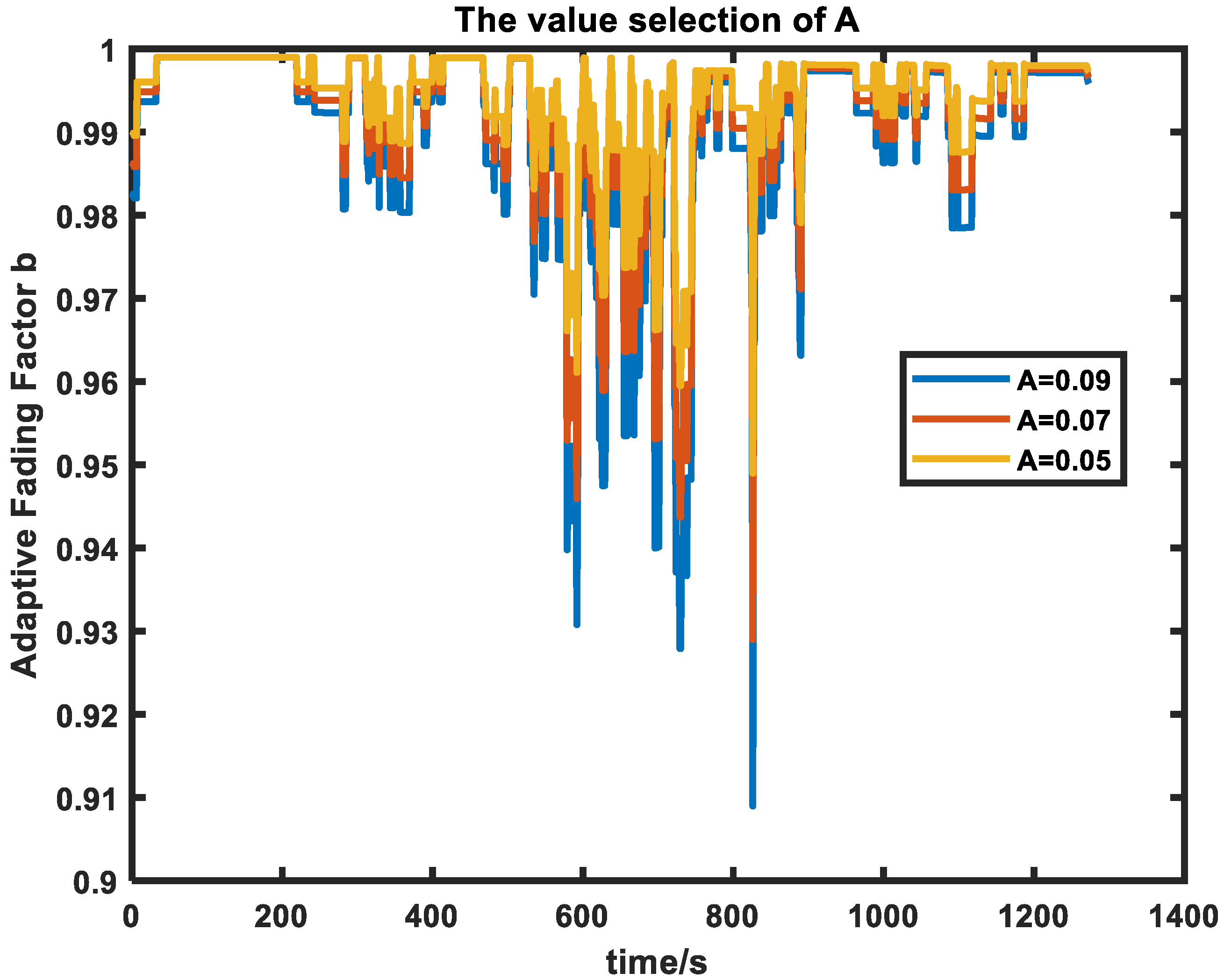
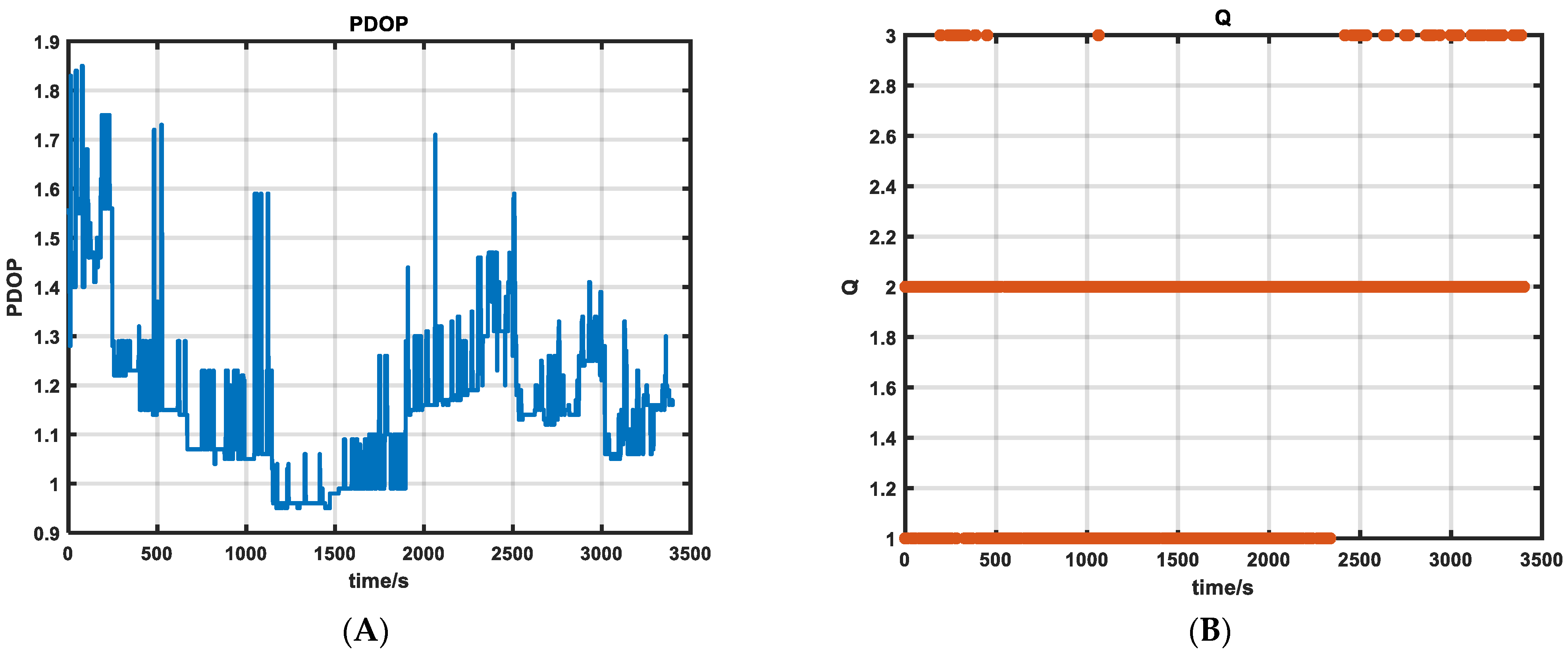
- Satellite geometric precision factor (PDOP): it directly reflects the influence of satellite geometric distribution on positioning accuracy [27], and its weight is set to 0.4.
- Satellite solution factor (Q): used to quantify the quality of GNSS solution. Table 1 shows the relationship between Q value and 3D positioning accuracy. The Q value directly reflects the error range of GNSS positioning. Its weight is also set to 0.4.
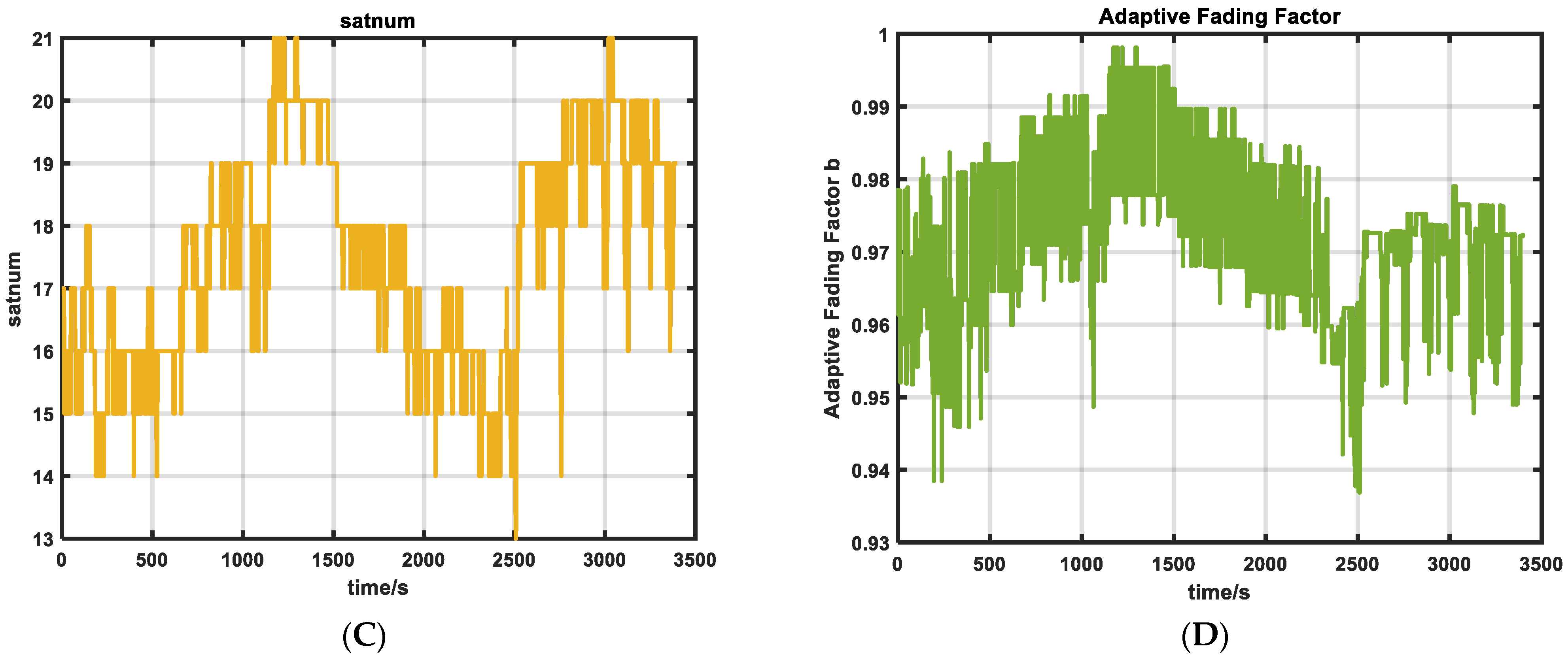
- The number of effective satellite observations (Satnum): The number of effective satellite observations does not directly reflect the advantages and disadvantages of GNSS positioning solutions, but it can reflect the redundancy of GNSS positioning. Therefore, this paper sets its weight to 0.2.
- When the GNSS observations are reliable, when the satellite geometry is well distributed and the number of effective satellite observations is sufficient, the PDOP value and Q value are usually low, and the system can obtain high-quality positioning results [31]. In this case, the fading factor b will increase, the confidence of the filter to the observation data will increase, and the system believes that the measurement data are more reliable. The update of the measurement noise covariance matrix will become more stable, and the filter will give greater weight when processing the observation data, so that the estimation results are more dependent on the observation data.
- When the GNSS observations are unreliable, when the satellite geometric distribution is poor and the number of effective satellite observations is insufficient, the PDOP value and Q value will increase, and the system will face higher uncertainty and positioning error. In this case, the quality of the observation data is poor, and there may be a large measurement error or noise, which will lead to a decrease in the trust of the filter to the observation data [31]. As the fading factor decreases, the update of the measurement noise covariance matrix becomes more conservative, the trust of the filter to the measurement data decreases, and the system depends more on the inertial navigation system (SINS). This dynamic adjustment can effectively avoid the estimation error caused by measurement noise or abnormal data.
2.5. Robust Filtering (RKF)
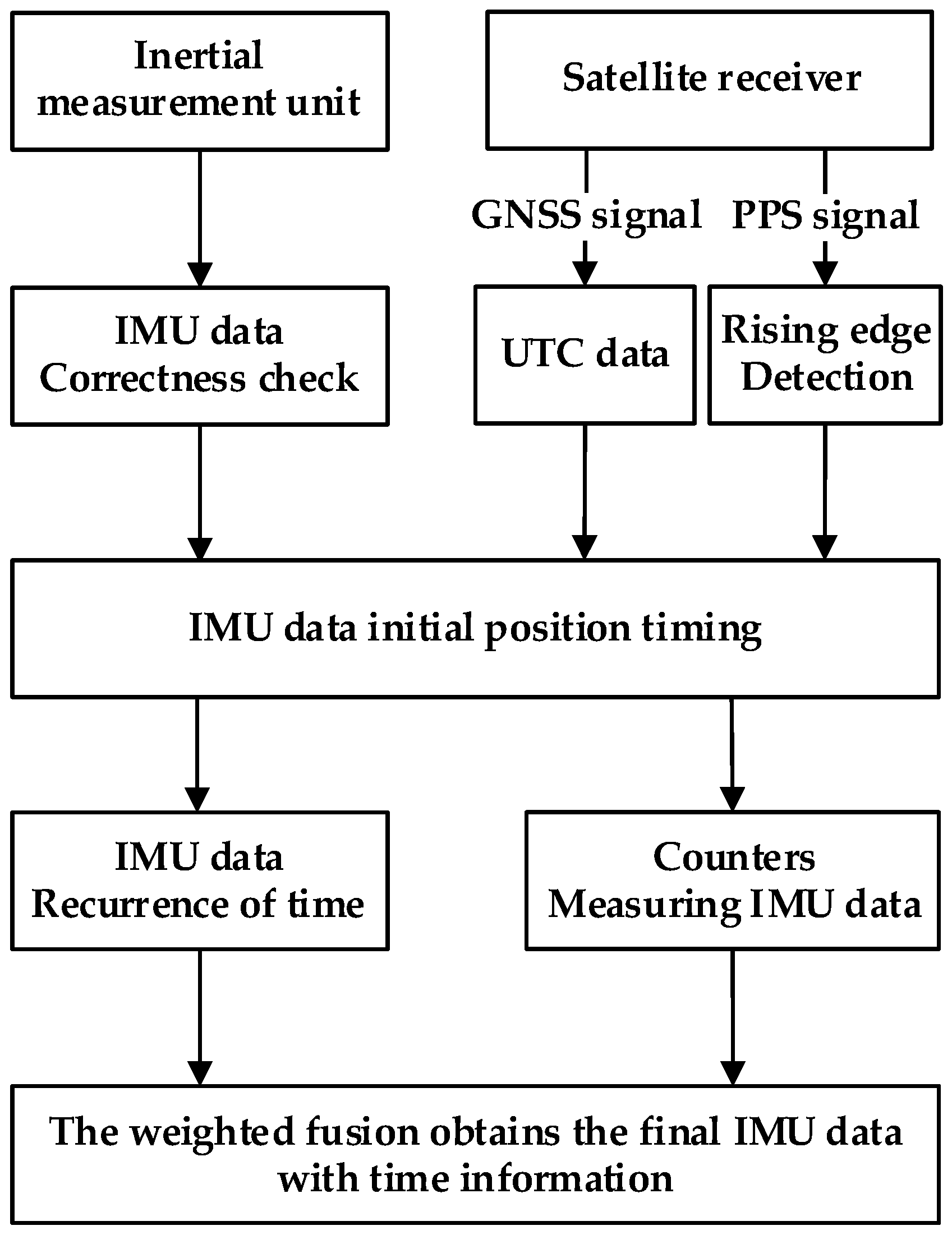
2.6. Data Collection and Processing Analysis Strategy
3. Experimental Demonstration and Analysis of Results
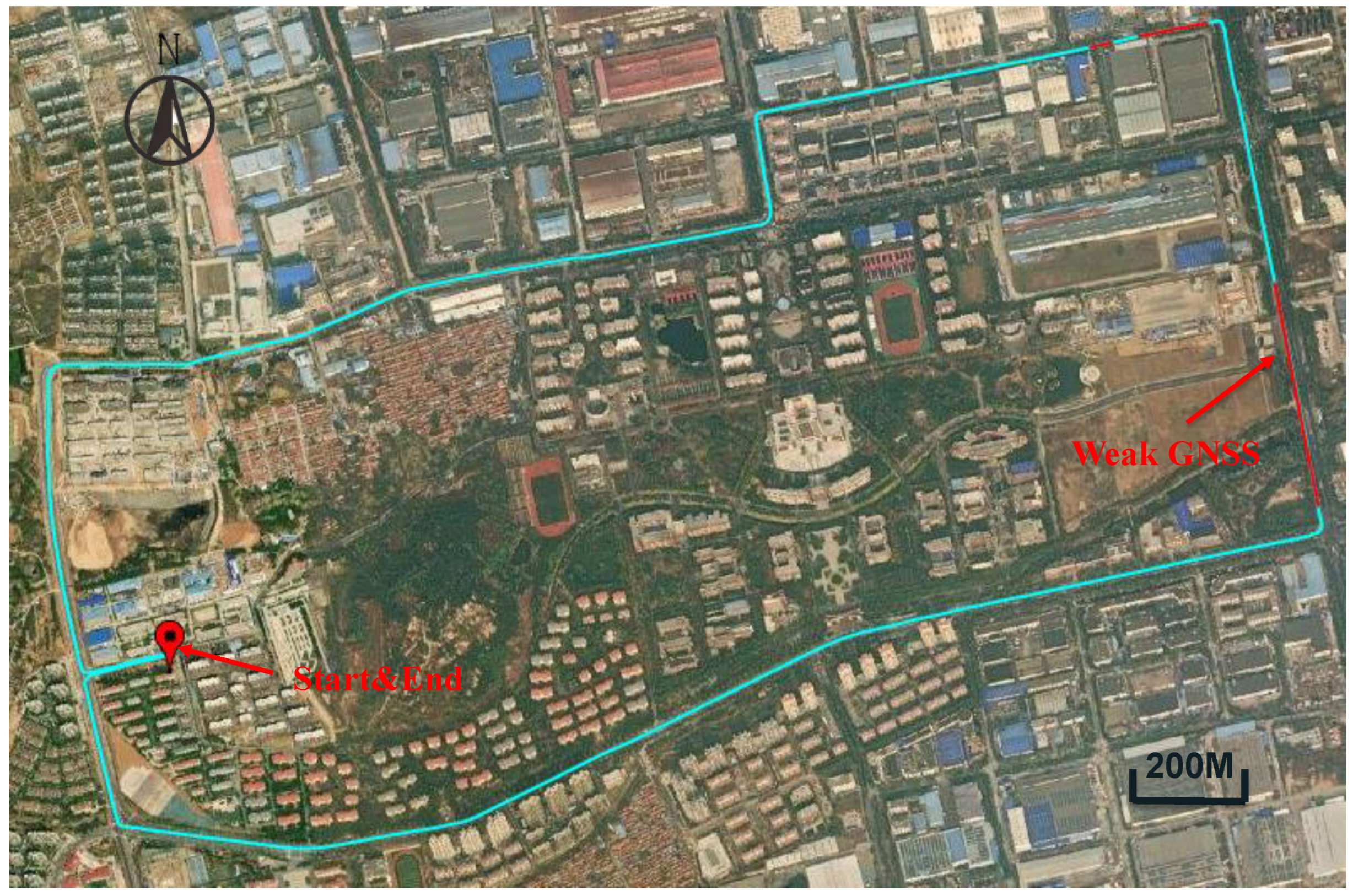
3.1. Experimental Environment
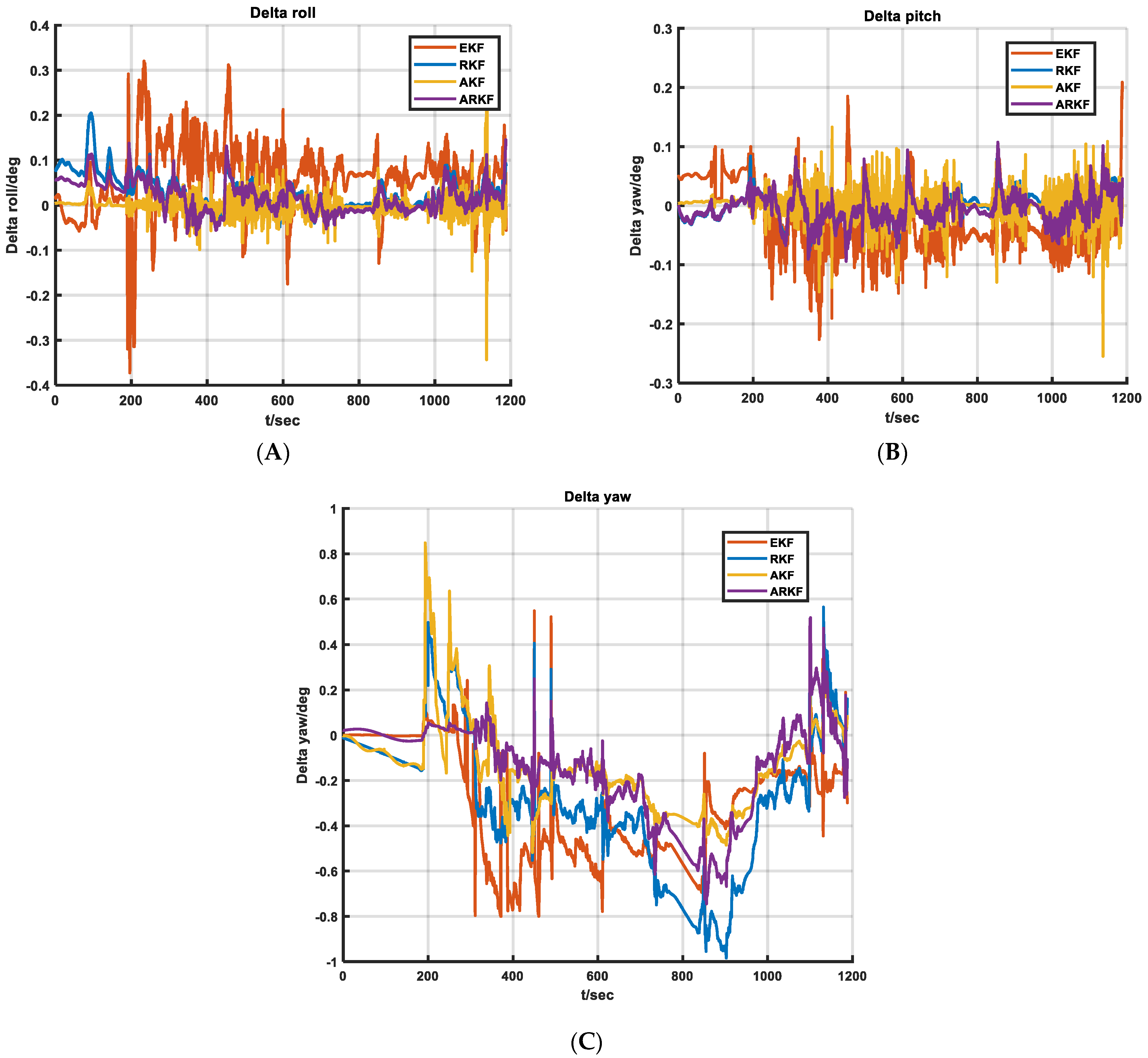
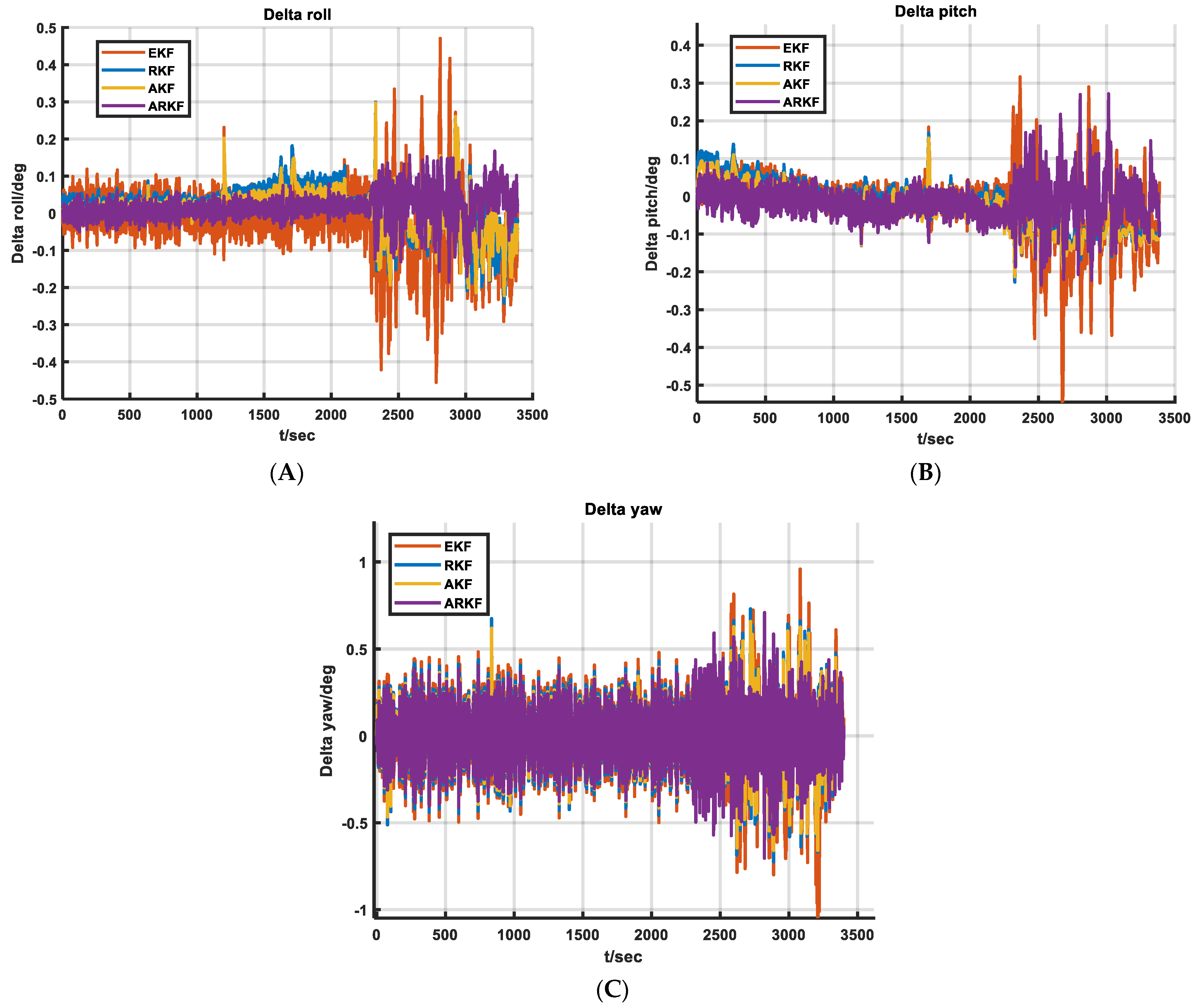
3.2. In-Vehicle Experiments
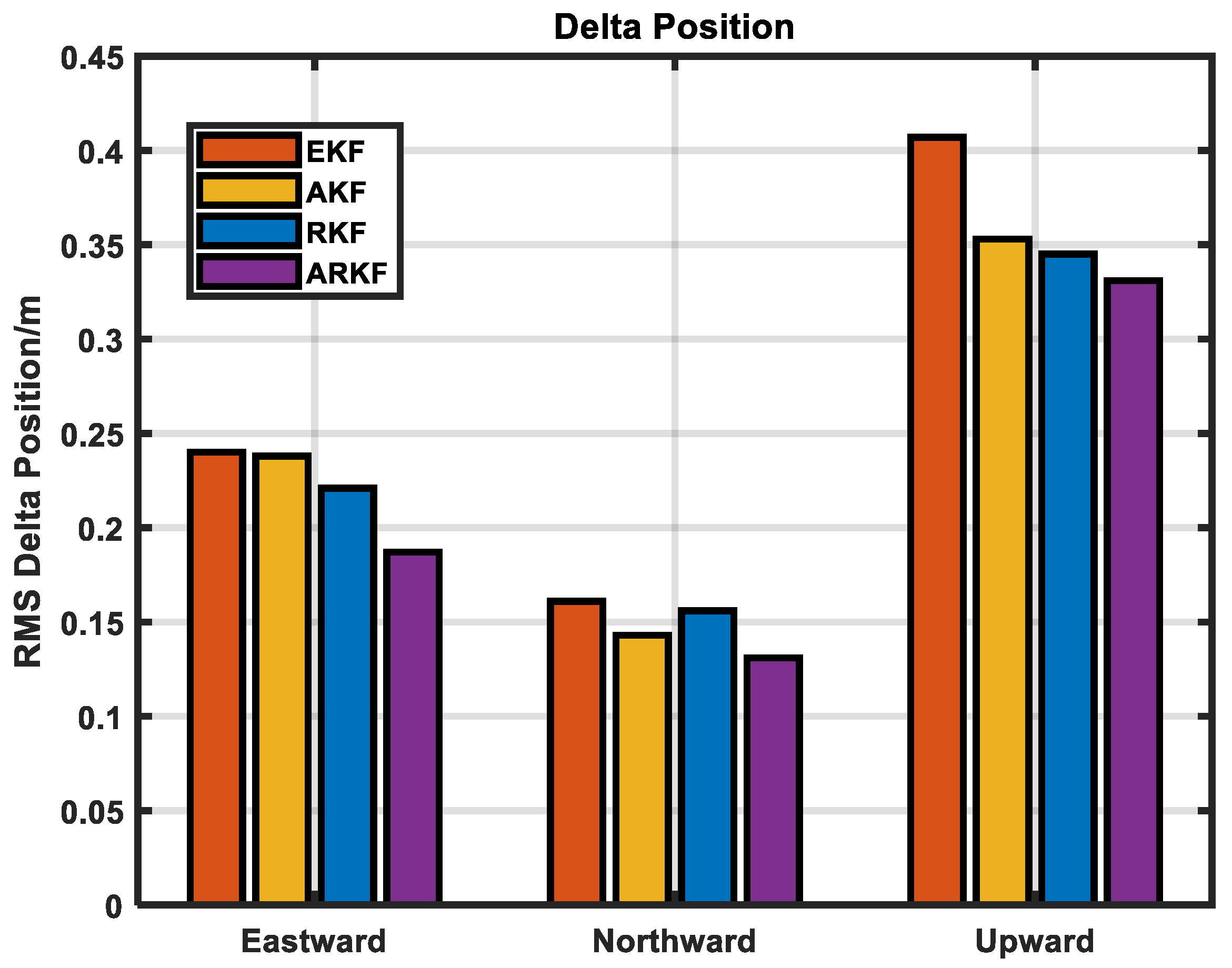
3.3. Shipboard Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Xiao, G.; Nie, Z.; Ferreira, V.; Casula, G. High-Precision and High-Reliability Positioning, Navigation, and Timing: Opportunities and Challenges. Remote Sens. 2024, 16, 4403. [Google Scholar] [CrossRef]
- Yang, Y.; Yao, Z.; Mao, Y.; Xu, T.; Wang, D. Resilient satellite-based PNT system design and key technologies. Sci. China Earth Sci. 2025, 68, 669–682. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Guo, Y.; Zhang, J.; Razzaqi, A.A. A novel adaptive filter for cooperative localization under time-varying delay and non-Gaussian noise. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Delamer, J.-A.; Watanabe, Y.; Chanel, C.P. Safe path planning for UAV urban operation under GNSS signal occlusion risk. Robot. Auton. Syst. 2021, 142, 103800. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, Z.; Chen, Y.; Yuan, Y.; Yalikun, Y.; Shang, C. Emerging MEMS sensors for ocean physics: Principles, materials, and applications. Appl. Phys. Rev. 2024, 11, 021320. [Google Scholar] [CrossRef]
- Yang, Y.; Cui, X. Adaptively robust filter with multi adaptive factors. Surv. Rev. 2008, 40, 260–270. [Google Scholar] [CrossRef]
- Song, S.; Wu, J. Motion State Estimation of Target Vehicle under Unknown Time-Varying Noises Based on Improved Square-Root Cubature Kalman Filter. Sensors 2020, 20, 2620. [Google Scholar] [CrossRef]
- Ma, C.; Pan, S.; Gao, W.; Wang, H.; Liu, L. Variational Bayesian-based robust adaptive filtering for GNSS/INS tightly coupled positioning in urban environments. Measurement 2023, 223, 113668. [Google Scholar] [CrossRef]
- Xiong, J.; Cheong, J.W.; Xiong, Z.; Dempster, A.G.; Tian, S.; Wang, R. Adaptive hybrid robust filter for multi-sensor relative navigation system. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11026–11040. [Google Scholar] [CrossRef]
- Narasimhappa, M.; Mahindrakar, A.D.; Guizilini, V.C.; Terra, M.H.; Sabat, S.L. MEMS-based IMU drift minimization: Sage Husa adaptive robust Kalman filtering. IEEE Sens. J. 2019, 20, 250–260. [Google Scholar] [CrossRef]
- Zou, T.; Zeng, W.; Yang, W.; Ong, M.C.; Wang, Y.; Situ, W. An adaptive robust cubature Kalman filter based on Sage-Husa estimator for improving ship heave measurement accuracy. IEEE Sens. J. 2023, 23, 10089–10099. [Google Scholar] [CrossRef]
- Petrus, P. Robust Huber adaptive filter. IEEE Trans. Signal Process. 1999, 47, 1129–1133. [Google Scholar] [CrossRef]
- Mao, Y.; Sun, R.; Wang, J.; Cheng, Q.; Kiong, L.C.; Ochieng, W.Y. New time-differenced carrier phase approach to GNSS/INS integration. GPS Solut. 2022, 26, 122. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, L.; Wang, X. Loosely coupled GNSS/INS integration based on factor graph and aided by ARIMA model. IEEE Sens. J. 2021, 21, 24379–24387. [Google Scholar] [CrossRef]
- Zhang, Q.; Dai, Y.; Zhang, T.; Guo, C.; Niu, X. Road Semantic-Enhanced Land Vehicle Integrated Navigation in GNSS Denied Environments. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20889–20899. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, S.; Li, H.; Li, Z. Performance evaluation of the filters with adaptive factor and fading factor for GNSS/INS integrated systems. GPS Solut. 2021, 25, 130. [Google Scholar] [CrossRef]
- Song, J.; Li, J.; Wei, X.; Hu, C.; Zhang, Z.; Zhao, L.; Jiao, Y. Improved multiple-model adaptive estimation method for integrated navigation with time-varying noise. Sensors 2022, 22, 5976. [Google Scholar] [CrossRef]
- Yan, G.; Weng, J. Integrated Inertial Navigation Algorithms and Principles of Integrated Navigation; Northwestern Polytechnical University: Xi’an, China, 2019; ISBN 978-7-5612-6547-5. [Google Scholar]
- Liu, Y.; Wang, L.; Hu, L.; Cui, H.; Wang, S. Analysis of the Influence of Attitude Error on Underwater Positioning and Its High-Precision Realization Algorithm. Remote Sens. 2022, 14, 3878. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, X. Adaptive robust Kalman filtering for precise point positioning. Meas. Sci. Technol. 2024, 25, 105011. [Google Scholar] [CrossRef]
- Yin, Z.; Yang, J.; Ma, Y.; Wang, S.; Chai, D.; Cui, H. A Robust Adaptive Extended Kalman Filter Based on an Improved Measurement Noise Covariance Matrix for the Monitoring and Isolation of Abnormal Disturbances in GNSS/INS Vehicle Navigation. Remote Sens. 2023, 15, 4125. [Google Scholar] [CrossRef]
- Jiang, Y.; Pan, S.; Meng, Q.; Zhang, M.; Ma, C.; Yu, H.; Gao, W. Multiple faults detection algorithm based on REKF for GNSS/INS integrated navigation. In Proceedings of the International Conference on Guidance, Navigation and Control, Harbin, China, 5–7 August 2022; Springer Nature Singapore: Singapore, 2022; pp. 886–894. [Google Scholar] [CrossRef]
- Liu, J.; Pu, J.; Sun, L.; He, Z. An approach to robust INS/UWB integrated positioning for autonomous indoor mobile robots. Sensors 2019, 19, 950. [Google Scholar] [CrossRef] [PubMed]
- Chhabra, A.; Venepally, J.R.; Kim, D. Measurement noise covariance-adapting Kalman filters for varying sensor noise situations. Sensors 2021, 21, 8304. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Zhang, S.; Wang, X.; Wang, H.; Yang, H. Kalman Filter with Adaptive Covariance Estimation for Carrier Tracking under Weak Signals and Dynamic Conditions. Electronics 2024, 13, 1288. [Google Scholar] [CrossRef]
- Li, H.; Medina, D.; Vilà-Valls, J.; Closas, P. Robust variational-based Kalman filter for outlier rejection with correlated measurements. IEEE Trans. Signal Process. 2020, 69, 357–369. [Google Scholar] [CrossRef]
- Biswas, S.K.; Qiao, L.; Dempster, A.G. Effect of PDOP on performance of Kalman Filters for GNSS-based space vehicle position estimation. GPS Solut. 2017, 21, 1379–1387. [Google Scholar] [CrossRef]
- Wang, Z.; Song, S.; Jiao, W.; Wei, W.; Zhou, W.; Jiao, G.; Liu, J. A unified PDOP evaluation method for multi-GNSS with optimization grid model and temporal–spatial resolution. GPS Solut. 2024, 28, 36. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, J.; Bo, Y.; Chen, Y.; Jiang, C.; Jia, J.; Duan, Z.; Karjalainen, M.; Hyyppä, J. Pedestrian Smartphone Navigation Based on Weighted Graph Factor Optimization Utilizing GPS/BDS Multi-Constellation. Remote Sens. 2023, 15, 2506. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, Y.; Liu, Q. Advancements in Buoy Wave Data Processing through the Application of the Sage–Husa Adaptive Kalman Filtering Algorithm. Sensors 2023, 23, 7298. [Google Scholar] [CrossRef]
- Rahemi, N.; Mosavi, M.R.; Martín, D. A new variance-covariance matrix for improving positioning accuracy in high-speed GPS receivers. Sensors 2021, 21, 7324. [Google Scholar] [CrossRef]
- Wang, D.; Dong, Y.; Li, Z.; Li, Q.; Wu, J. Constrained MEMS-based GNSS/INS tightly coupled system with robust Kalman filter for accurate land vehicular navigation. IEEE Trans. Instrum. Meas. 2019, 69, 5138–5148. [Google Scholar] [CrossRef]
- Knight, N.L.; Wang, J. A comparison of outlier detection procedures and robust estimation methods in GPS positioning. J. Navig. 2009, 62, 699–709. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Zhang, L.; Li, Q.; Wu, J. Tightly coupled GNSS/INS integration with robust sequential Kalman filter for accurate vehicular navigation. Sensors 2020, 20, 561. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Rizos, C.; Lee, H.K.; Lee, H.K. A GPS-slaved time synchronization system for hybrid navigation. GPS Solut. 2006, 10, 207–217. [Google Scholar] [CrossRef]
- Chai, D.; Sang, W.; Chen, G.; Ning, Y.; Xing, J.; Yu, M.; Wang, S. A novel method of ambiguity resolution and cycle slip processing for single-frequency GNSS/INS tightly coupled integration system. Adv. Space Res. 2022, 69, 359–375. [Google Scholar] [CrossRef]
- Instructions for the Software (Inertial Explorer 8.70) Used as the Reference Truth Value in the Comparative Experiment. Available online: https://hexagondownloads.blob.core.windows.net/public/Novatel/assets/Documents/Waypoint/Downloads/GrafNav-GrafNet-User-Manual-870/GrafNav-GrafNet-User-Manual-870.pdf (accessed on 1 April 2025).




| Q | Description | 3D Accuracy (m) |
|---|---|---|
| 1 | Fixed integer | 0.00–015 |
| 2 | Converged float or noisy fixed integer | 0.05–0.40 |
| 3 | Converging float | 0.20–1.00 |
| 4 | Converging float | 0.50–2.00 |
| 5 | DGPS | 1.00–5.00 |
| Performance Parameters | HG4930 | |
|---|---|---|
| gyros | ±400 | |
| 0.35 | ||
| 0.05 | ||
| accelerometer | ±20 | |
| 0.05 | ||
| 0.05 |
| ERROR | EKF | AKF | RKF | ARKF | |
|---|---|---|---|---|---|
| Velocity (m/s) | Eastward | 0.191 | 0.068 | 0.024 | 0.011 |
| Northward | 0.215 | 0.075 | 0.015 | 0.012 | |
| Upward | 0.078 | 0.040 | 0.054 | 0.055 | |
| Attitude (deg) | Roll | 0.098 | 0.125 | 0.049 | 0.038 |
| Pitch | 0.054 | 0.131 | 0.022 | 0.026 | |
| Heading | 0.715 | 0.308 | 0.575 | 0.313 | |
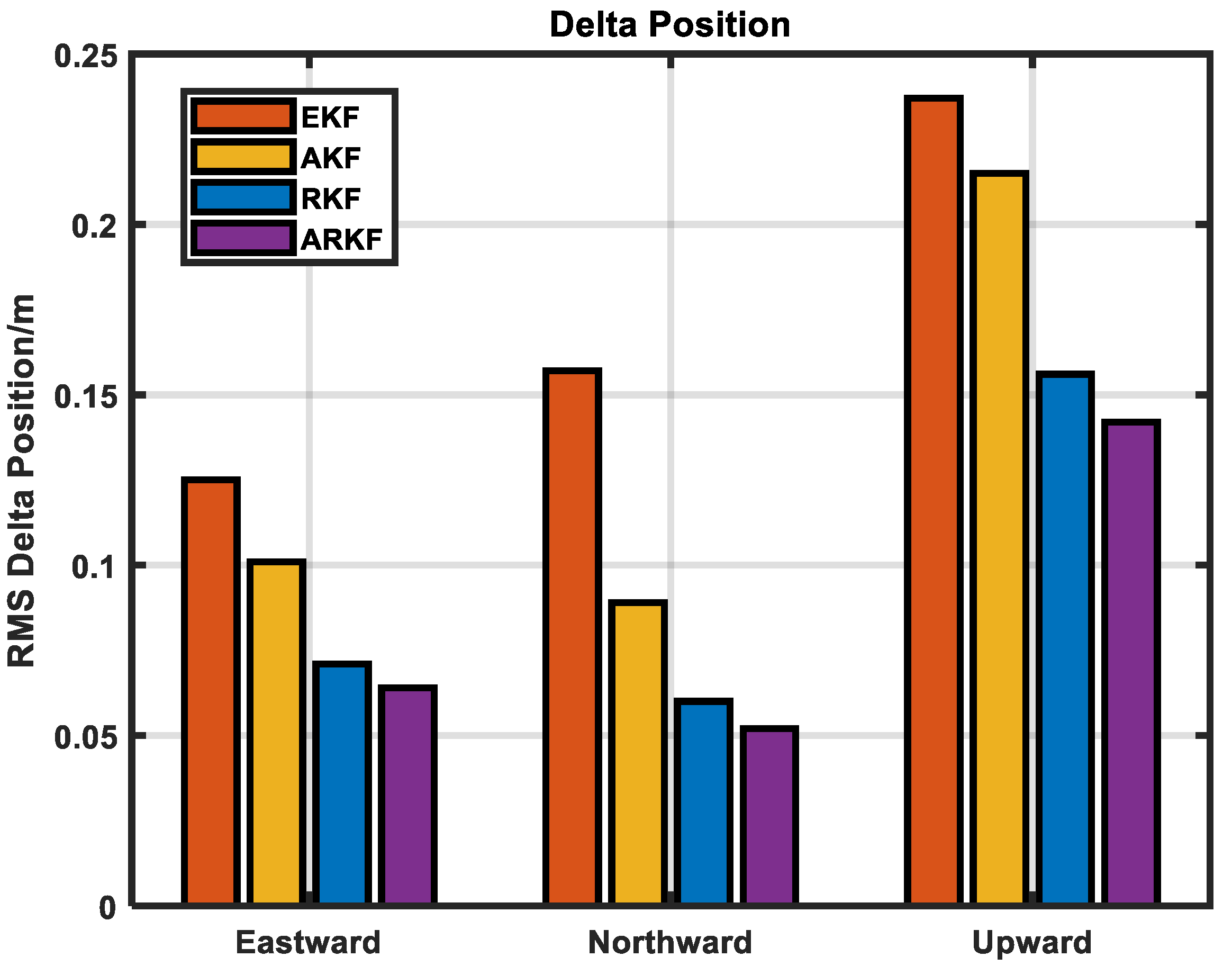
| Position (m) | Eastward | 0.125 | 0.101 | 0.071 | 0.064 |
| Northward | 0.157 | 0.089 | 0.060 | 0.052 | |
| Upward | 0.237 | 0.215 | 0.156 | 0.142 | |
| Improved accuracy (%) | 47.12% | 35.26% | 9.58% | ||
| ERROR | EKF | AKF | RKF | ARKF | |
|---|---|---|---|---|---|
| Velocity (m/s) | Eastward | 0.101 | 0.091 | 0.084 | 0.080 |
| Northward | 0.112 | 0.094 | 0.086 | 0.071 | |
| Upward | 0.254 | 0.216 | 0.209 | 0.173 | |
| Attitude (deg) | Roll | 0.181 | 0.140 | 0.151 | 0.107 |
| Pitch | 0.204 | 0.163 | 0.141 | 0.128 | |
| Heading | 0.355 | 0.279 | 0.321 | 0.223 | |
| Position (m) | Eastward | 0.240 | 0.238 | 0.221 | 0.187 |
| Northward | 0.161 | 0.143 | 0.156 | 0.134 | |
| Upward | 0.407 | 0.353 | 0.345 | 0.331 | |
| Improved accuracy (%) | 19.44% | 10.47% | 8.28% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Liu, Y.; Liu, S.; Wang, S.; Yang, L. An Improved Fading Factor-Based Adaptive Robust Filtering Algorithm for SINS/GNSS Integration with Dynamic Disturbance Suppression. Remote Sens. 2025, 17, 1449. https://doi.org/10.3390/rs17081449
Chen Z, Liu Y, Liu S, Wang S, Yang L. An Improved Fading Factor-Based Adaptive Robust Filtering Algorithm for SINS/GNSS Integration with Dynamic Disturbance Suppression. Remote Sensing. 2025; 17(8):1449. https://doi.org/10.3390/rs17081449
Chicago/Turabian StyleChen, Zhaohao, Yixu Liu, Shangguo Liu, Shengli Wang, and Lei Yang. 2025. "An Improved Fading Factor-Based Adaptive Robust Filtering Algorithm for SINS/GNSS Integration with Dynamic Disturbance Suppression" Remote Sensing 17, no. 8: 1449. https://doi.org/10.3390/rs17081449
APA StyleChen, Z., Liu, Y., Liu, S., Wang, S., & Yang, L. (2025). An Improved Fading Factor-Based Adaptive Robust Filtering Algorithm for SINS/GNSS Integration with Dynamic Disturbance Suppression. Remote Sensing, 17(8), 1449. https://doi.org/10.3390/rs17081449





