Detecting the Distribution of Callery Pear (Pyrus calleryana) in an Urban U.S. Landscape Using High Spatial Resolution Satellite Imagery and Machine Learning
Abstract
:1. Introduction
2. Materials and Method
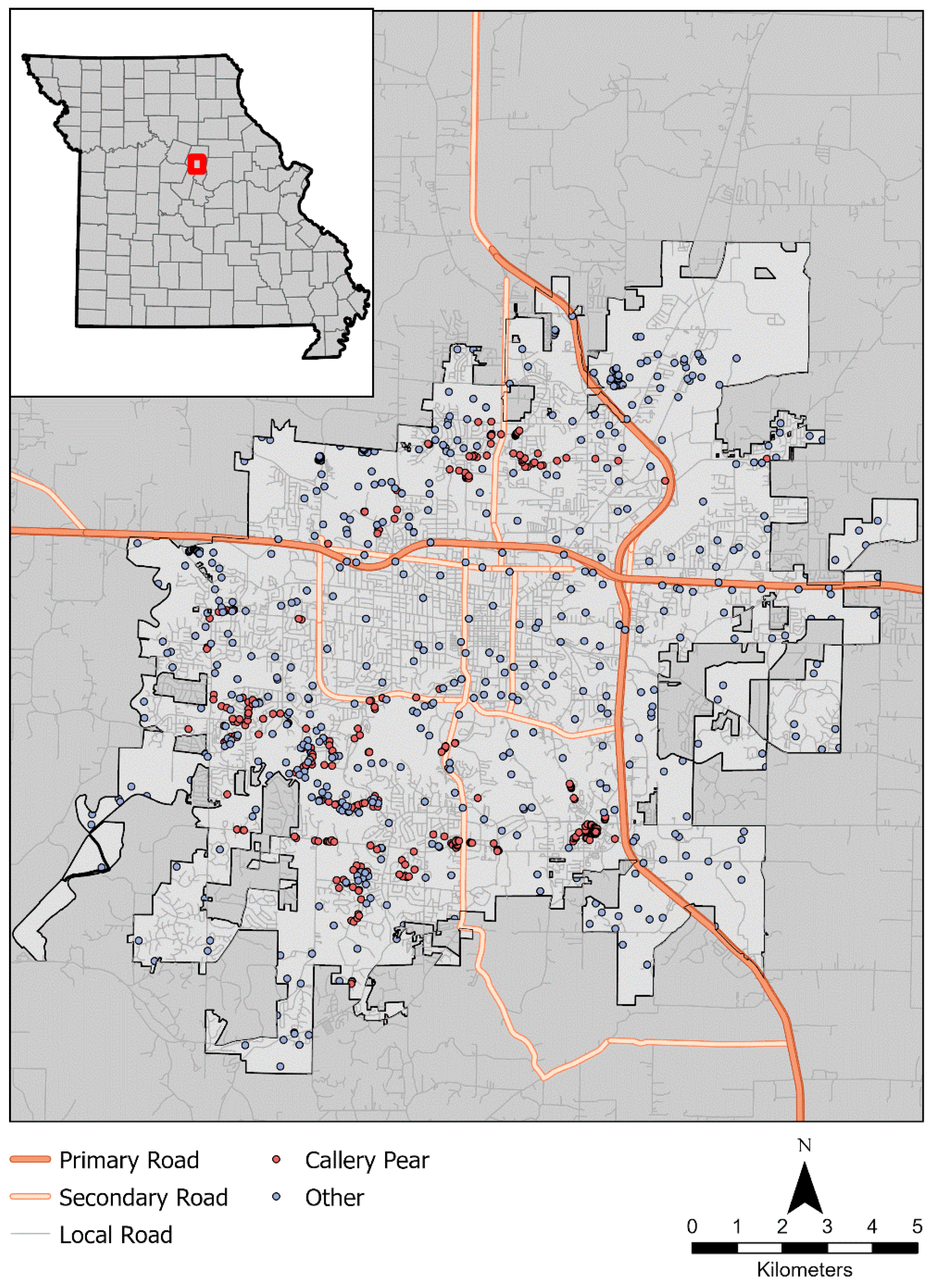
2.1. Study Area
2.2. Field Sampling and Training Data
2.3. Planetscope Data
2.4. Machine Learning
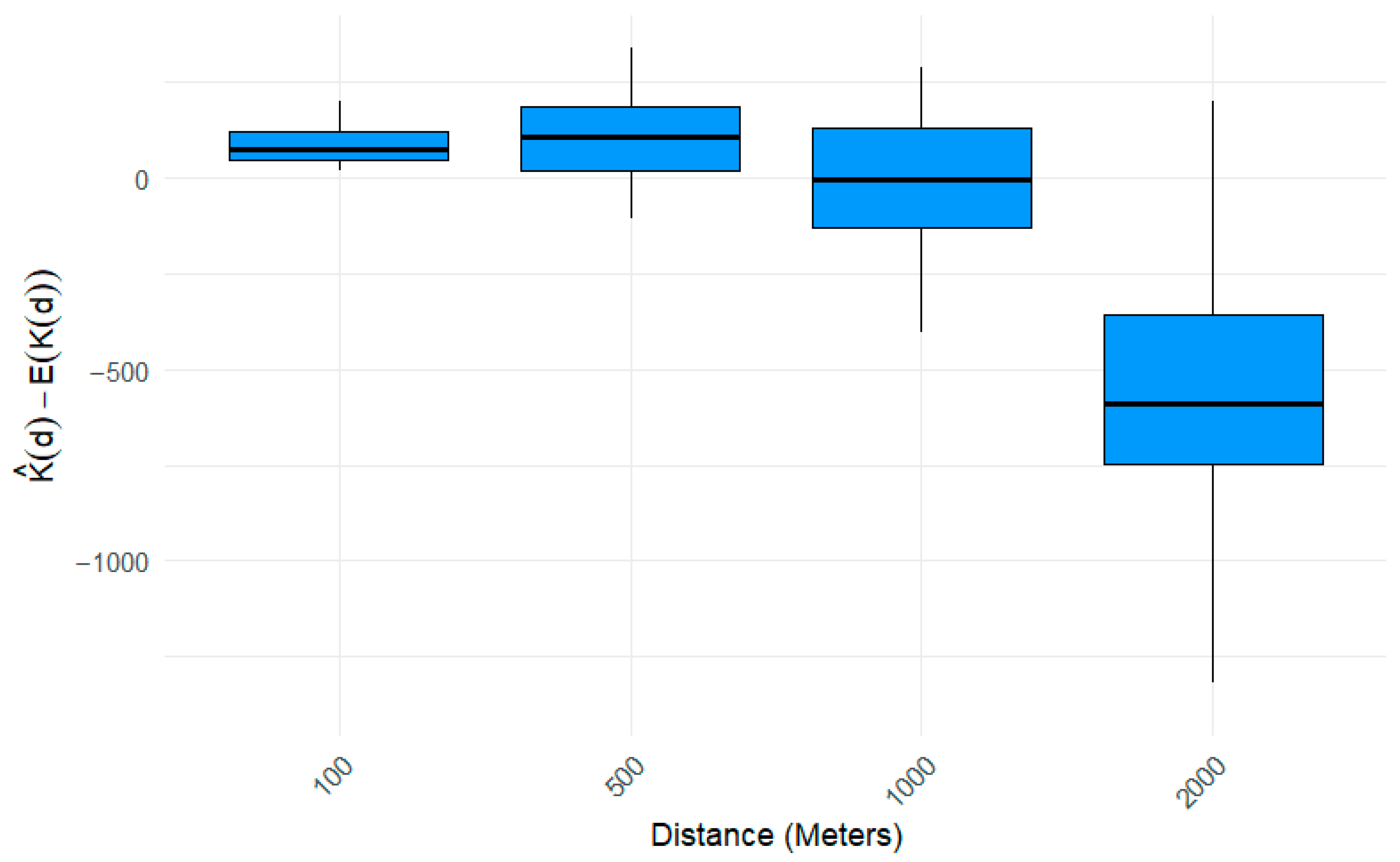
2.5. Spatial Pattern Analysis
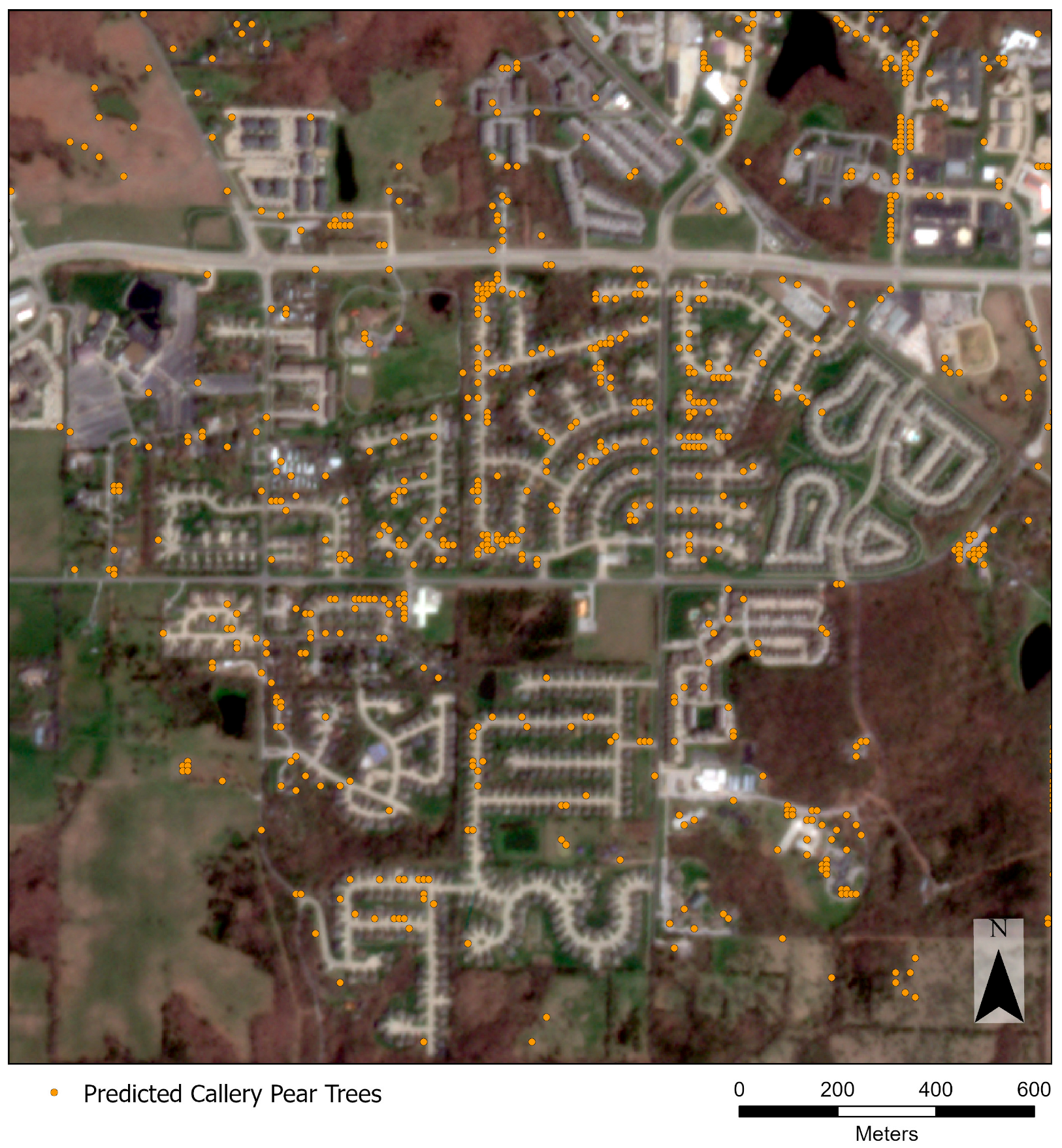
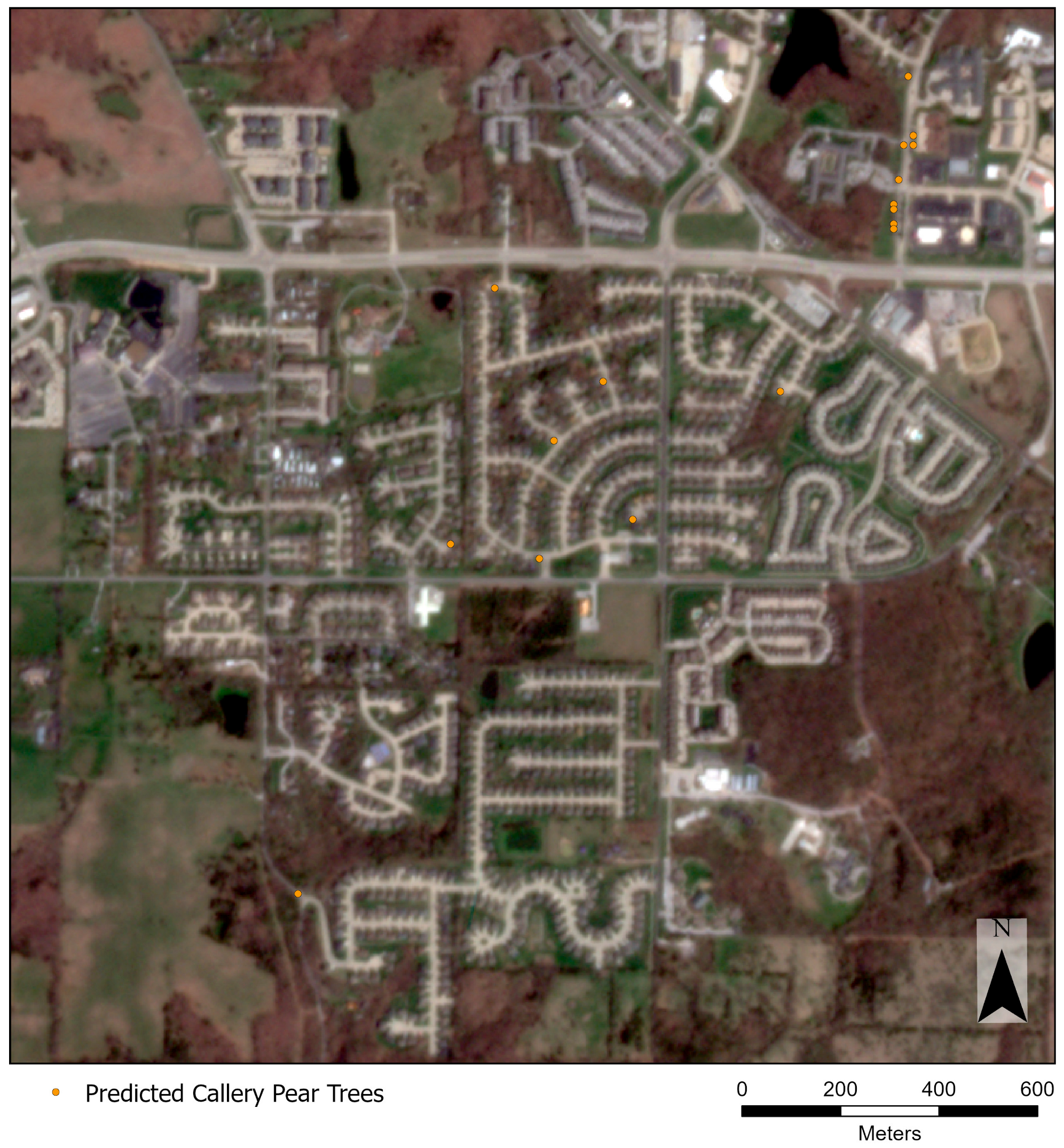
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Culley, T.M.; Hardiman, N.A. The Beginning of a New Invasive Plant: A History of the Ornamental Callery Pear in the United States. BioScience 2007, 57, 956–964. [Google Scholar] [CrossRef]
- Culley, T.M.; Hardiman, N.A.; Hawks, J. The role of horticulture in plant invasions: How grafting in cultivars of Callery pear (Pyrus calleryana) can facilitate spread into natural areas. Biol. Invasions 2011, 13, 739–746. [Google Scholar] [CrossRef]
- Vincent, M.A. On the Spread and Current Distribution of Pyrus calleryana in the United States. Castanea 2005, 70, 20–31. [Google Scholar] [CrossRef]
- Fertakos, M.E.; Bradley, B.A. Propagule pressure from historic U.S. plant sales explains establishment but not invasion. Ecol. Lett. 2024, 27, e14494. [Google Scholar] [CrossRef]
- Rejmánek, M. Invasive plants: Approaches and predictions. Austral Ecol. 2000, 25, 497–506. [Google Scholar] [CrossRef]
- Januchowski-Hartley, S.R.; Visconti, P.; Pressey, R.L. A systematic approach for prioritizing multiple management actions for invasive species. Biol. Invasions 2011, 13, 1241–1253. [Google Scholar] [CrossRef]
- Pile Knapp, L.; Coyle, D.; Dey, D.; Fraser, J.; Hutchinson, T.; Jenkins, M.; Kern, C.; Knapp, B.; Maddox, D.; Pinchot, C.; et al. Invasive plant management in eastern North American Forests: A systematic review. For. Ecol. Manag. 2023, 550, 121517. [Google Scholar] [CrossRef]
- Haley, A.L.; Lemieux, T.A.; Piczak, M.L.; Karau, S.; D’addario, A.; Irvine, R.L.; Beaudoin, C.; Bennett, J.R.; Cooke, S.J. On the effectiveness of public awareness campaigns for the management of invasive species. Environ. Conserv. 2023, 50, 202–211. [Google Scholar] [CrossRef]
- Thapa, B.; Darling, L.; Choi, D.; Ardohain, C.; Firoze, A.; Aliaga, D.; Hardiman, B.; Fei, S. Application of multi-temporal satellite imagery for urban tree species identification. Urban For. Urban Green. 2024, 98, 128409. [Google Scholar] [CrossRef]
- Joshi, C.; De Leeuw, J.; van Duren, I.C. Remote sensing and GIS applications for mapping and spatial modelling of invasive species. In Proceedings of the XXth ISPRS Congress: Geo-Imagery Bridging Continents, Istanbul, Turkey, 12–23 July 2004; Volume 35. [Google Scholar]
- Papp, L.; van Leeuwen, B.; Szilassi, P.; Tobak, Z.; Szatmári, J.; Árvai, M.; Mészáros, J.; Pásztor, L. Monitoring Invasive Plant Species Using Hyperspectral Remote Sensing Data. Land 2021, 10, 29. [Google Scholar] [CrossRef]
- Resasco, J.; Hale, A.N.; Henry, M.C.; Gorchov, D.L. Detecting an invasive shrub in a deciduous forest understory using late-fall Landsat sensor imagery. Int. J. Remote Sens. 2007, 28, 3739–3745. [Google Scholar] [CrossRef]
- Robinson, T.P.; Wardell-Johnson, G.W.; Pracilio, G.; Brown, C.; Corner, R.; van Klinken, R.D. Testing the discrimination and detection limits of WorldView-2 imagery on a challenging invasive plant target. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 23–30. [Google Scholar] [CrossRef]
- Kattenborn, T.; Lopatin, J.; Förster, M.; Braun, A.C.; Fassnacht, F.E. UAV data as alternative to field sampling to map woody invasive species based on combined Sentinel-1 and Sentinel-2 data. Remote Sens. Environ. 2019, 227, 61–73. [Google Scholar] [CrossRef]
- Lake, T.A.; Briscoe Runquist, R.D.; Moeller, D.A. Deep learning detects invasive plant species across complex landscapes using Worldview-2 and Planetscope satellite imagery. Remote Sens. Ecol. Conserv. 2022, 8, 875–889. [Google Scholar] [CrossRef]
- Nininahazwe, F.; Théau, J.; Marc Antoine, G.; Varin, M. Mapping invasive alien plant species with very high spatial resolution and multi-date satellite imagery using object-based and machine learning techniques: A comparative study. GIScience Remote Sens. 2023, 60, 2190203. [Google Scholar] [CrossRef]
- Bradley, B.A. Remote detection of invasive plants: A review of spectral, textural and phenological approaches. Biol. Invasions 2014, 16, 1411–1425. [Google Scholar] [CrossRef]
- Fang, F.; McNeil, B.; Warner, T.; Maxwell, A.; Dahle, G.; Eutsler, E.; Li, J. Discriminating tree species at different taxonomic levels using multi-temporal WorldView-3 imagery in Washington D.C., USA. Remote Sens. Environ. 2020, 246, 111811. [Google Scholar] [CrossRef]
- Martin, F.M.; Müllerová, J.; Borgniet, L.; Dommanget, F.; Breton, V.; Evette, A. Using single- and multi-date UAV and satellite imagery to accurately monitor invasive knotweed species. Remote Sens. 2018, 10, 1662. [Google Scholar] [CrossRef]
- Ardohain, C.; Wingren, C.; Thapa, B.; Fei, S. Invasive species identification from high-resolution 4-band multispectral imagery. Biol. Invasions 2024, 26, 3603–3619. [Google Scholar] [CrossRef]
- U.S. Census Bureau. Annual Estimates of the Resident Population: April 1, 2022 to July 1, 2023. 2023. Available online: https://www.census.gov/programs-surveys/popest.html (accessed on 11 November 2024).
- Dewitz, J. National Land Cover Database (NLCD) 2021 Products: U.S. Geological Survey Data Release. 2021. Available online: https://www.mrlc.gov (accessed on 8 August 2024).
- U.S. Census Bureau. TIGER/Line Shapefiles: Places. 2021. Available online: https://www.census.gov/geographies/mapping-files/time-series/geo/tiger-line-file.html (accessed on 8 August 2024).
- Esri. “Imagery” [Basemap]. Scale Not Given. “World Imagery”. 15 December 2023. Available online: https://www.arcgis.com/home/item.html?id=10df2279f9684e4a9f6a7f08febac2a9 (accessed on 23 September 2024).
- Planet Labs. PlanetScope Overview[Webpage]. Available online: https://developers.planet.com/docs/data/planetscope/scope (accessed on 11 November 2024).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. Available online: https://CRAN.R-project.org/package=randomForest (accessed on 8 October 2024).
- Esri. (n.d.). How Multi-Distance Spatial Cluster Analysis (Ripley’s K-Function) Works. ArcGIS Pro. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-statistics/h-how-multi-distance-spatial-cluster-analysis-ripl.htm (accessed on 11 November 2024).
- U.S. Census Bureau. American Community Survey 5-Year Estimates, 2018–2022. U.S. Department of Commerce. 2023. Available online: https://www.census.gov/programs-surveys/acs (accessed on 11 November 2024).
- Key, T.; Warner, T.A.; Mcgraw, J.B.; Fajvan, M.A. A Comparison of Multispectral and Multitemporal Information in High Spatial Resolution Imagery for Classification of Individual Tree Species in a Temperate Hardwood Forest. Remote Sens. Environ. 2001, 75, 100–112. [Google Scholar] [CrossRef]
- Singh, K.K.; Chen, Y.H.; Smart, L.; Gray, J.; Meentemeyer, R.K. Intra-annual phenology for detecting understory plant invasion in urban forests. ISPRS J. Photogramm. Remote Sens. 2018, 142, 151–161. [Google Scholar] [CrossRef]

| Spectral Vegetation Indices | Calculation |
|---|---|
| Normalized Difference Vegetation Index | (NIR − R)/(NIR + R) |
| Green Normalized Difference Vegetation Index | (NIR − G)/(NIR + G) |
| Green–Red Ratio | (G − R)/(G + R) |
| Green–Yellow Ratio | (G − Y)/(G + Y) |
| Modified Soil-Adjusted Vegetation Index | |
| Transformed Chlorophyll Absorption in Reflectance Index | |
| Visible Atmospherically Resistant Index | (G − R)/(G + R − B) |
| Scene ‘Whiteness’ | R + G + B |
| Texture Indices | Calculation |
|---|---|
| Gray-Level Co-Occurrence Matrix–Mean | |
| Gray-Level Co-Occurrence Matrix–Variance | |
| Gray-Level Co-Occurrence Matrix–Homogeneity | |
| Gray-Level Co-Occurrence Matrix–Entropy |
| Callery Pear | Other | Class Error | |
|---|---|---|---|
| Callery pear | 208 | 92 | 30.6% |
| Other | 0 | 600 | 0.0% |
| Variable | d | Correlation Coefficient (r) | Model Type | Adjusted R2 |
|---|---|---|---|---|
| Median Household Income | 100 | 0.397 * | Linear Regression | 0.1313 * |
| 500 | 0.499 * | 0.2252 ** | ||
| 1000 | 0.566 ** | 0.2989 *** | ||
| 2000 | 0.640 *** | 0.3907 *** | ||
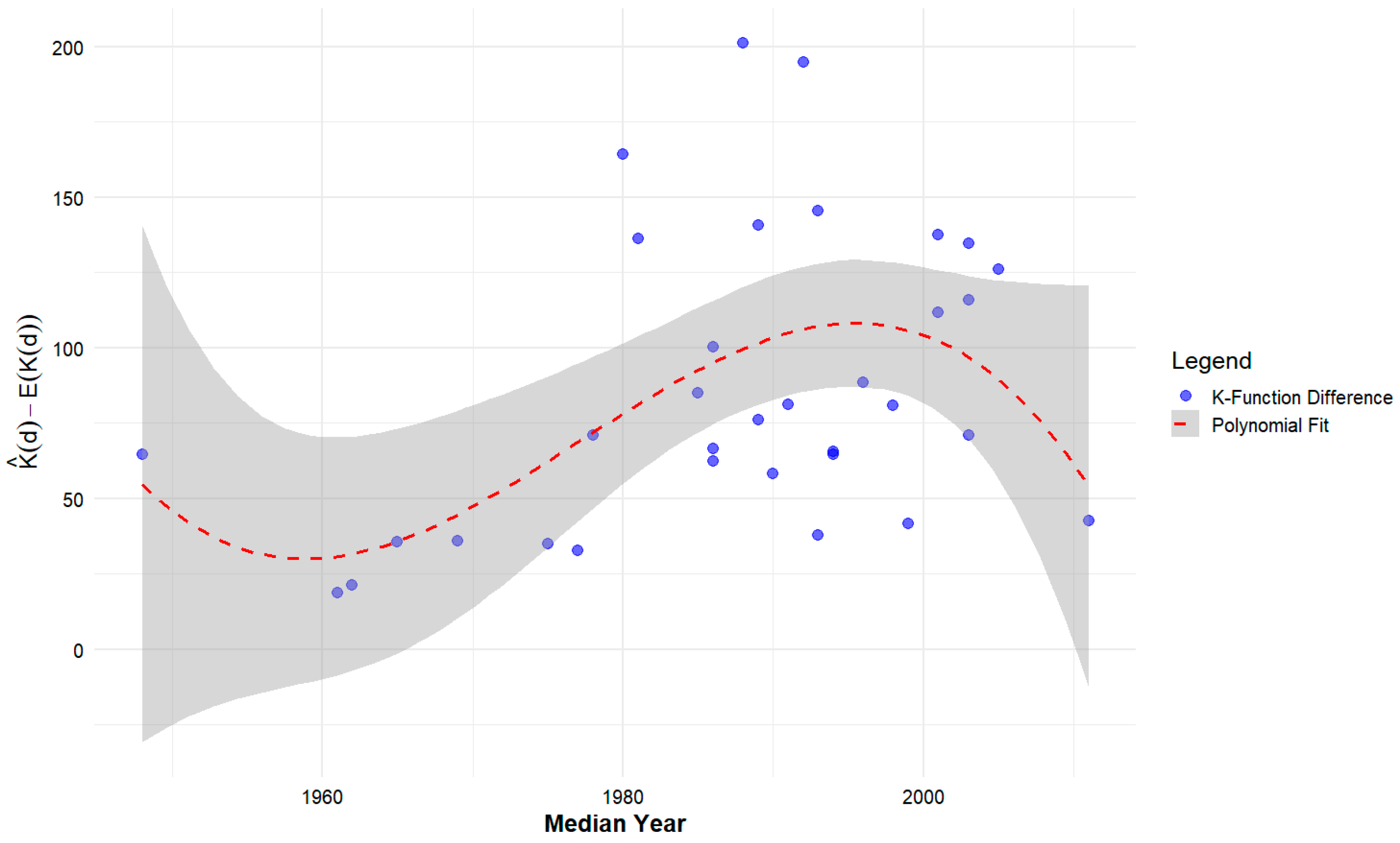
| Median Year Built | 100 | 0.364 * | Polynomial Regression (third degree) | 0.1758 * |
| 500 | 0.324 | 0.2542 ** | ||
| 1000 | 0.387 * | 0.3113 ** | ||
| 2000 | 0.399 * | 0.2878 ** | ||
| Median Value | 100 | 0.3773 * | Linear Regression | 0.1156 * |
| 500 | 0.5449 ** | 0.2749 *** | ||
| 1000 | 0.5680 ** | 0.3014 *** | ||
| 2000 | 0.6010 ** | 0.3411 *** | ||
| Population Density | 100 | −0.5597 ** | Linear Regression | 0.2919 *** |
| 500 | −0.727 *** | 0.5148 *** | ||
| 1000 | −0.778 *** | 0.5926 *** | ||
| 2000 | −0.785 *** | 0.604 *** | ||
| Combined | 100 | Linear Regression | 0.3344 ** | |
| 500 | 0.5497 *** | |||
| 1000 | 0.6746 *** | |||
| 2000 | 0.7182 *** |
| Cutoff | Callery Pear | Other | Class Error | |
|---|---|---|---|---|
| Callery pear | 0.75 | 264 | 36 | 12.0% |
| Other | 0.75 | 0 | 600 | 0.0% |
| Callery pear | 0.95 | 92 | 208 | 69.3% |
| Other | 0.95 | 0 | 600 | 0.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krohn, J.; He, H.; Matisziw, T.C.; Pile Knapp, L.S.; Fraser, J.S.; Sunde, M. Detecting the Distribution of Callery Pear (Pyrus calleryana) in an Urban U.S. Landscape Using High Spatial Resolution Satellite Imagery and Machine Learning. Remote Sens. 2025, 17, 1453. https://doi.org/10.3390/rs17081453
Krohn J, He H, Matisziw TC, Pile Knapp LS, Fraser JS, Sunde M. Detecting the Distribution of Callery Pear (Pyrus calleryana) in an Urban U.S. Landscape Using High Spatial Resolution Satellite Imagery and Machine Learning. Remote Sensing. 2025; 17(8):1453. https://doi.org/10.3390/rs17081453
Chicago/Turabian StyleKrohn, Justin, Hong He, Timothy C. Matisziw, Lauren S. Pile Knapp, Jacob S. Fraser, and Michael Sunde. 2025. "Detecting the Distribution of Callery Pear (Pyrus calleryana) in an Urban U.S. Landscape Using High Spatial Resolution Satellite Imagery and Machine Learning" Remote Sensing 17, no. 8: 1453. https://doi.org/10.3390/rs17081453
APA StyleKrohn, J., He, H., Matisziw, T. C., Pile Knapp, L. S., Fraser, J. S., & Sunde, M. (2025). Detecting the Distribution of Callery Pear (Pyrus calleryana) in an Urban U.S. Landscape Using High Spatial Resolution Satellite Imagery and Machine Learning. Remote Sensing, 17(8), 1453. https://doi.org/10.3390/rs17081453






