Temporal and Spatial Prediction of Column Dust Optical Depth Trend on Mars Based on Deep Learning
Abstract
1. Introduction
2. Data and Study Areas
2.1. The Data of CDOD
2.2. Study Areas
3. Time-Series Prediction
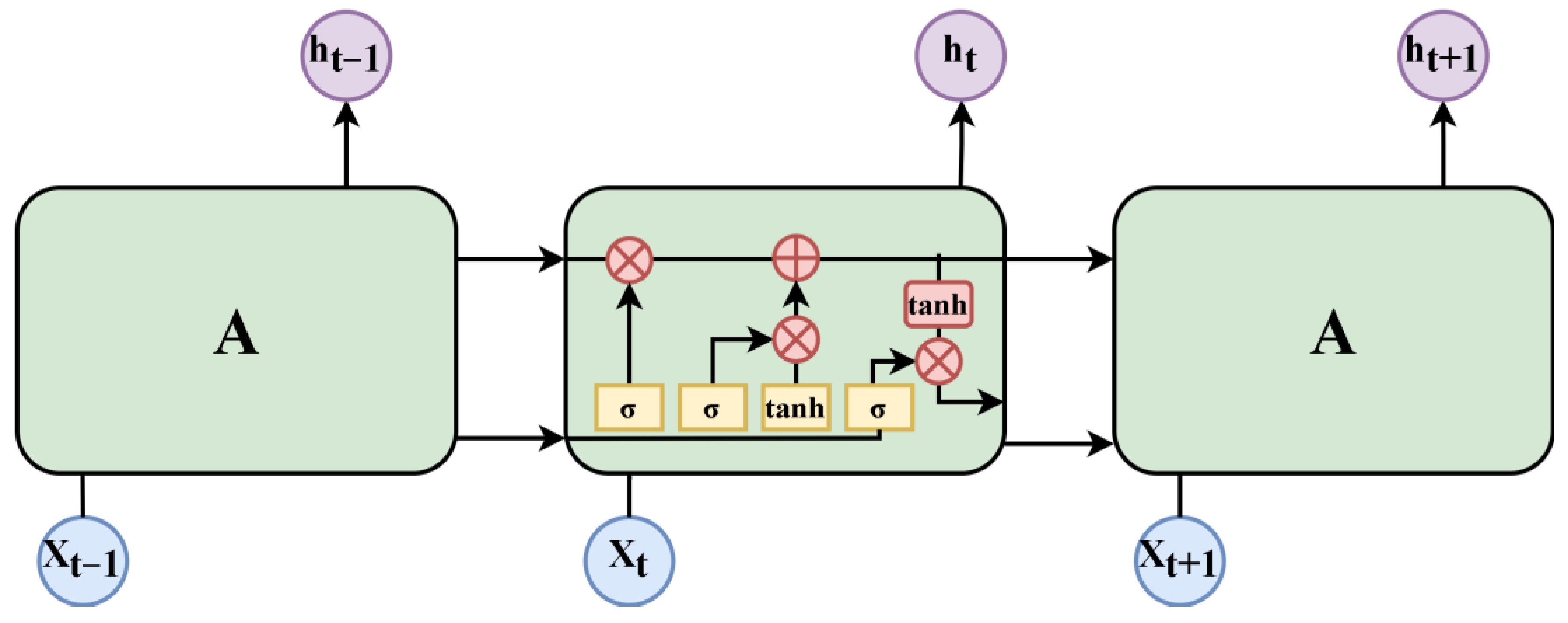
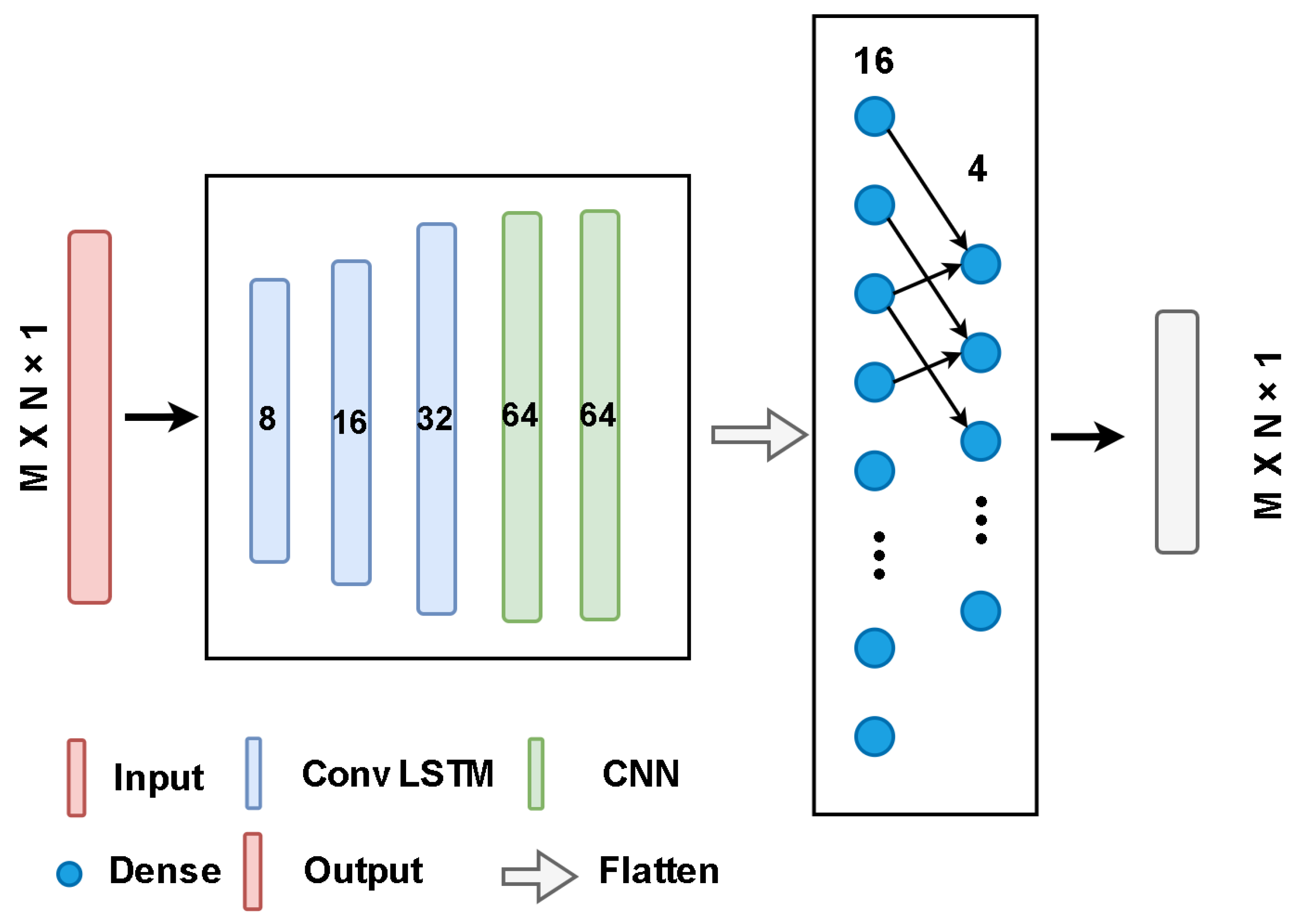
3.1. Model
3.2. Data Preparation
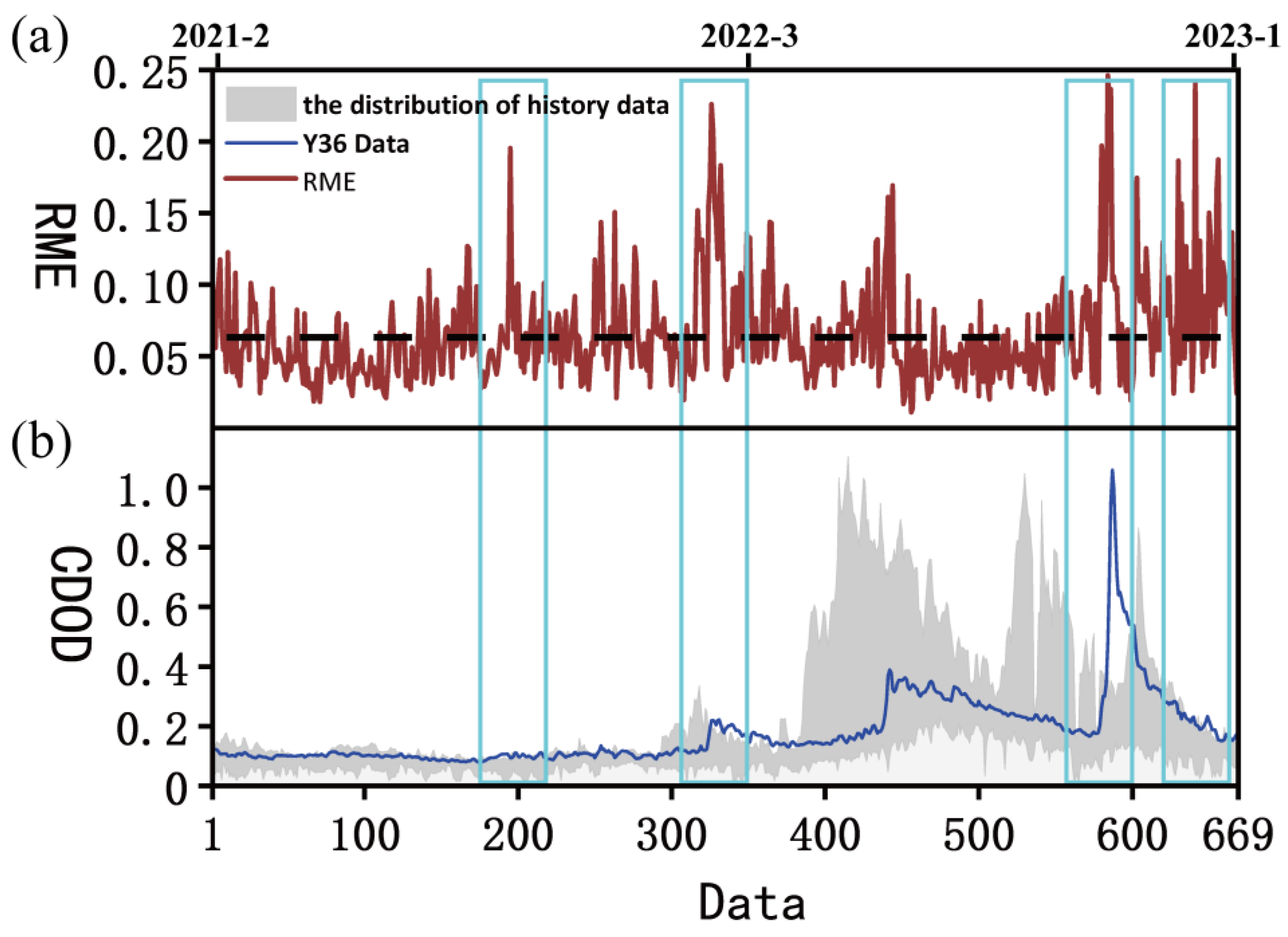
3.2.1. Data Processing
- (1)
- Stationarity test: A stationary time series is one whose mean and variance do not change over time. We use the Augmented Dickey–Fuller test to examine the stationarity of the CDOD series [31]. If the test result is a non-stationary time series, first-order difference is applied to transform it into a stationary series.
- (2)
- Pure randomness stationarity test: Even a stationary time series may exhibit strong randomness, which can evidently affect prediction accuracy. Therefore, the Ljung–Box test is used to verify the pure randomness of the obtained stationary time series, ensuring its non-randomness [31].
- (3)
- Data normalization: Due to the significant fluctuations in CDOD data caused by global dust storms, the prediction accuracy of the network could be greatly affected. Thus, Min-Max normalization is applied to the processed data, mapping the CDOD values to a range between 0 and 1.
3.2.2. Training Set
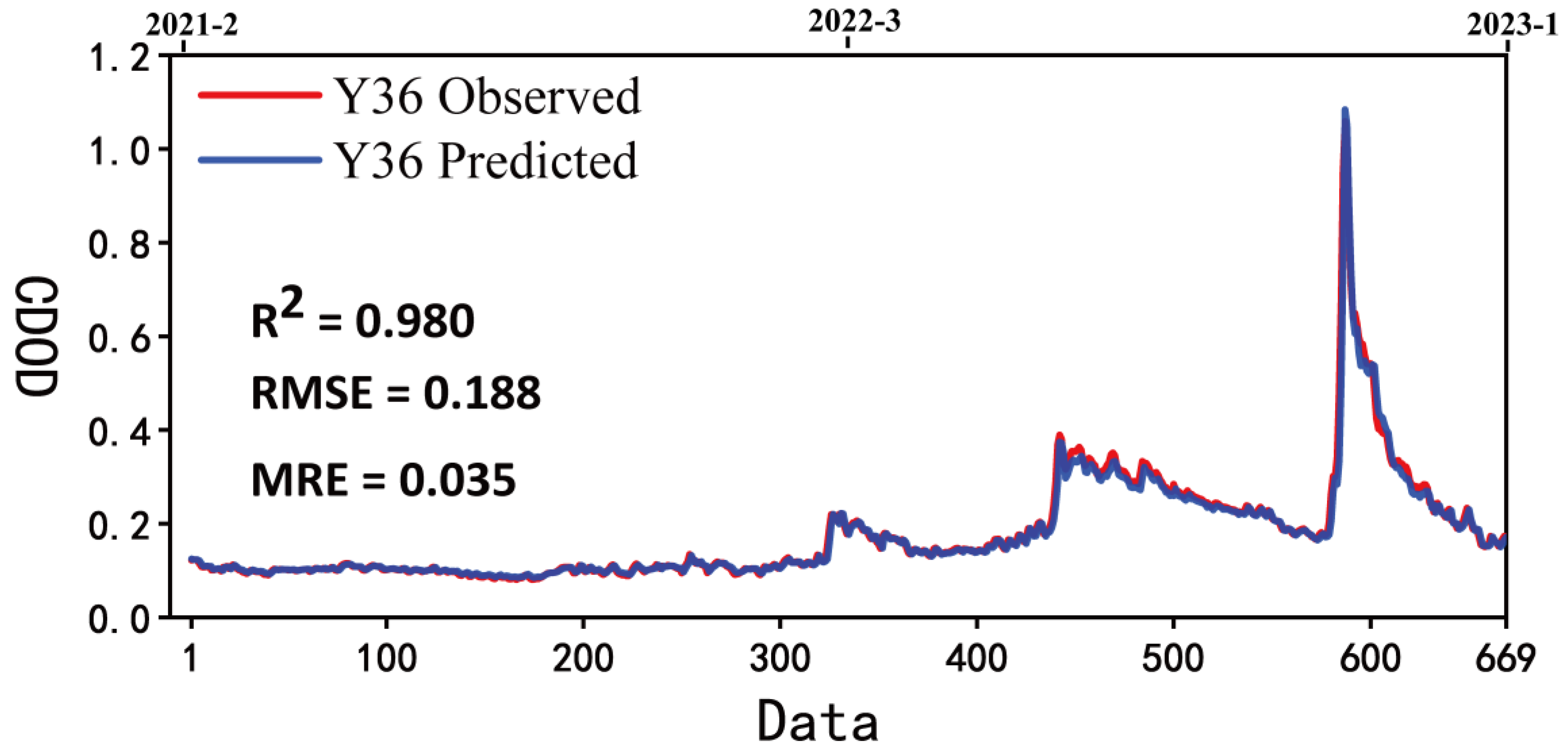
3.3. Model Training and Evaluation
3.3.1. Model Training
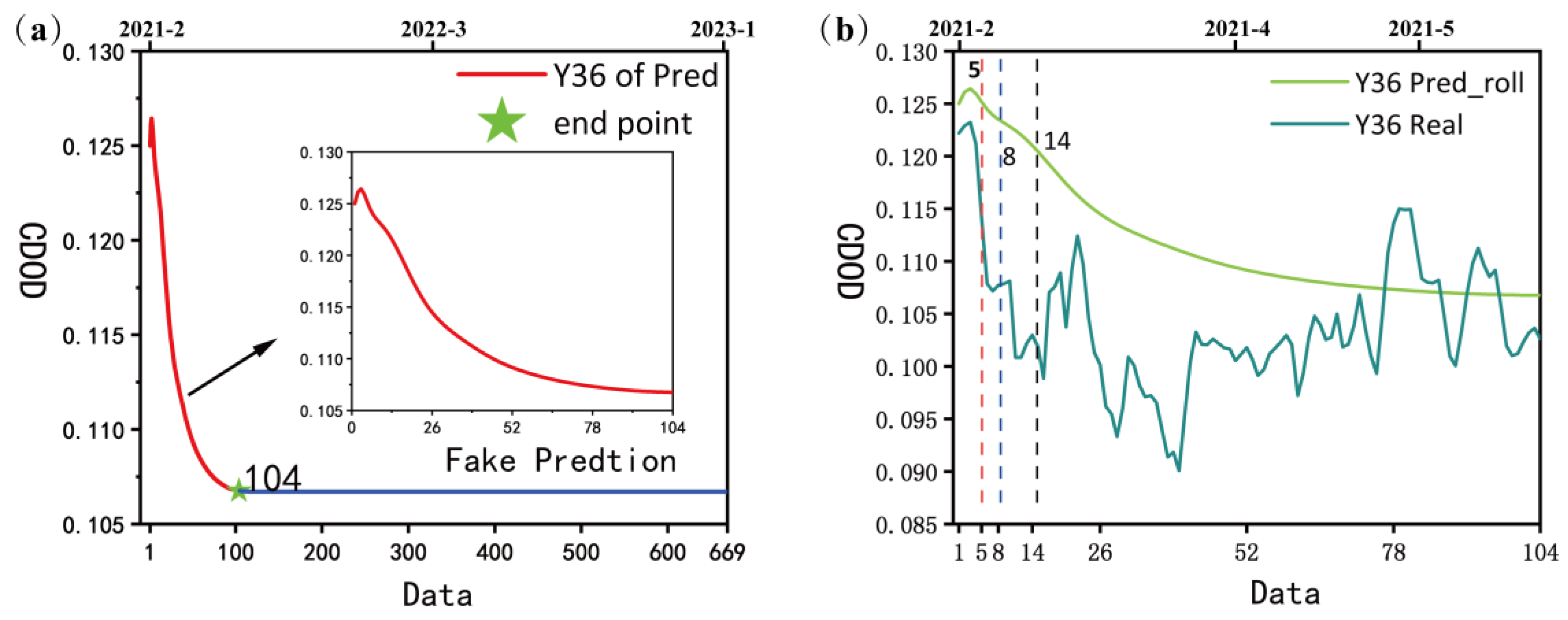
3.3.2. Evaluation Strategy for Rolling Forecast
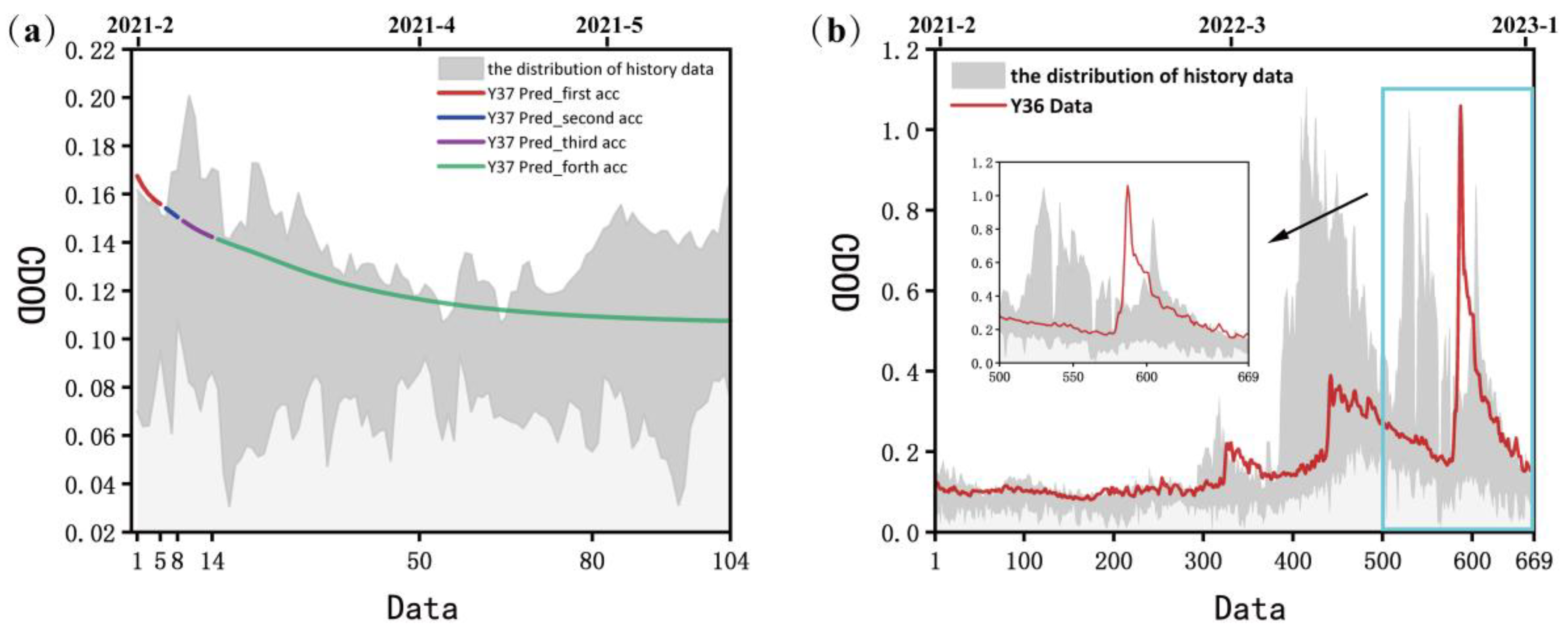
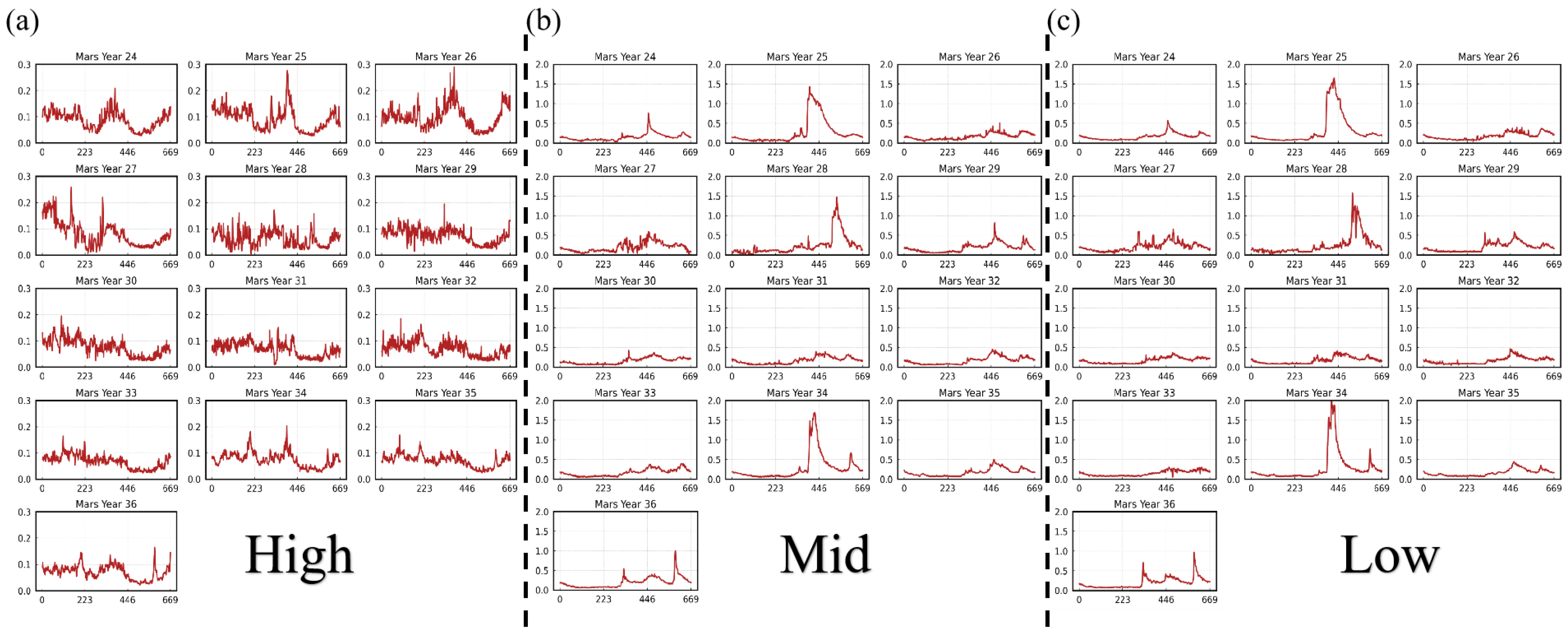
3.3.3. Evaluation Across Different Regions
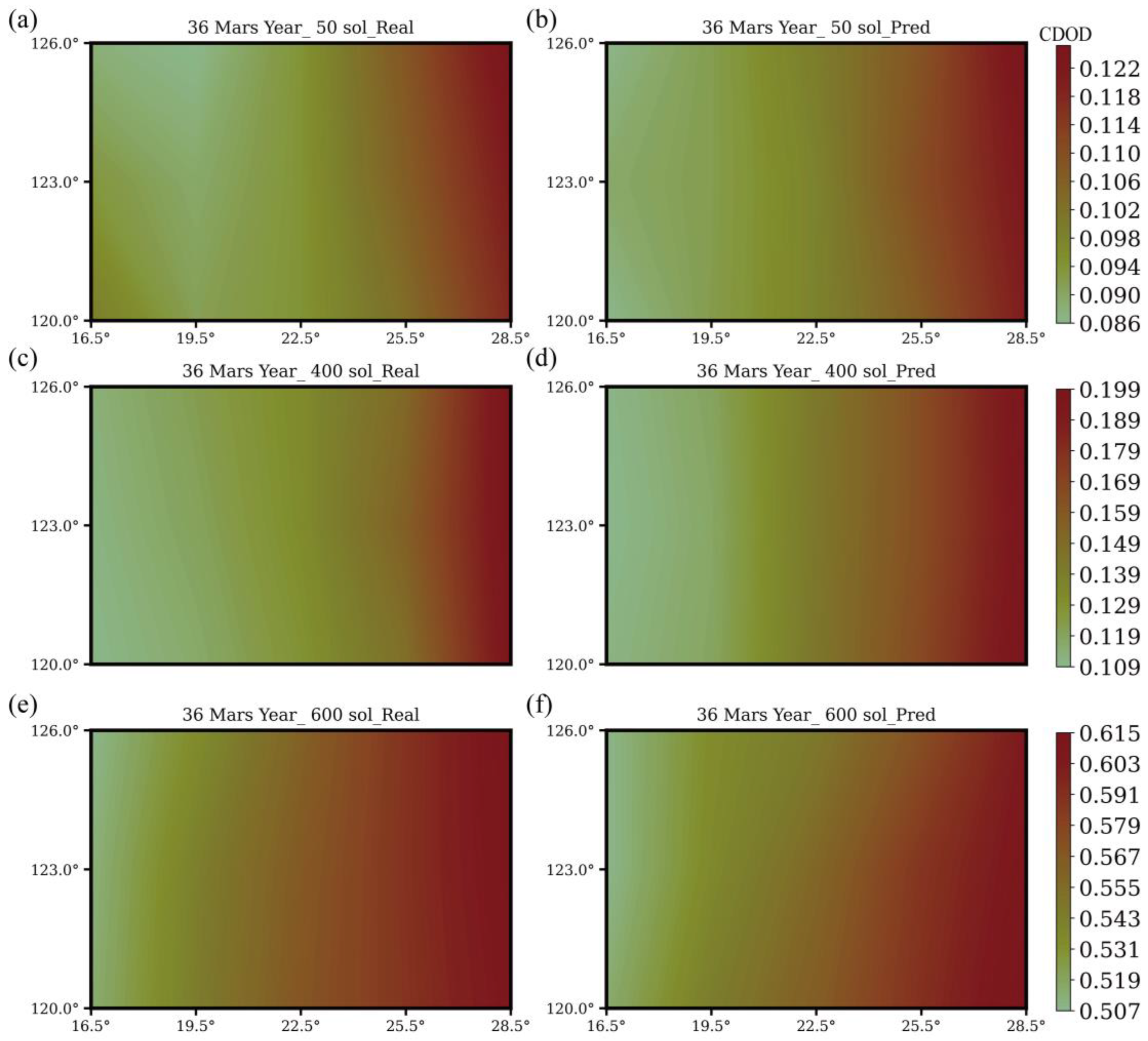
4. Spatial Distribution Prediction
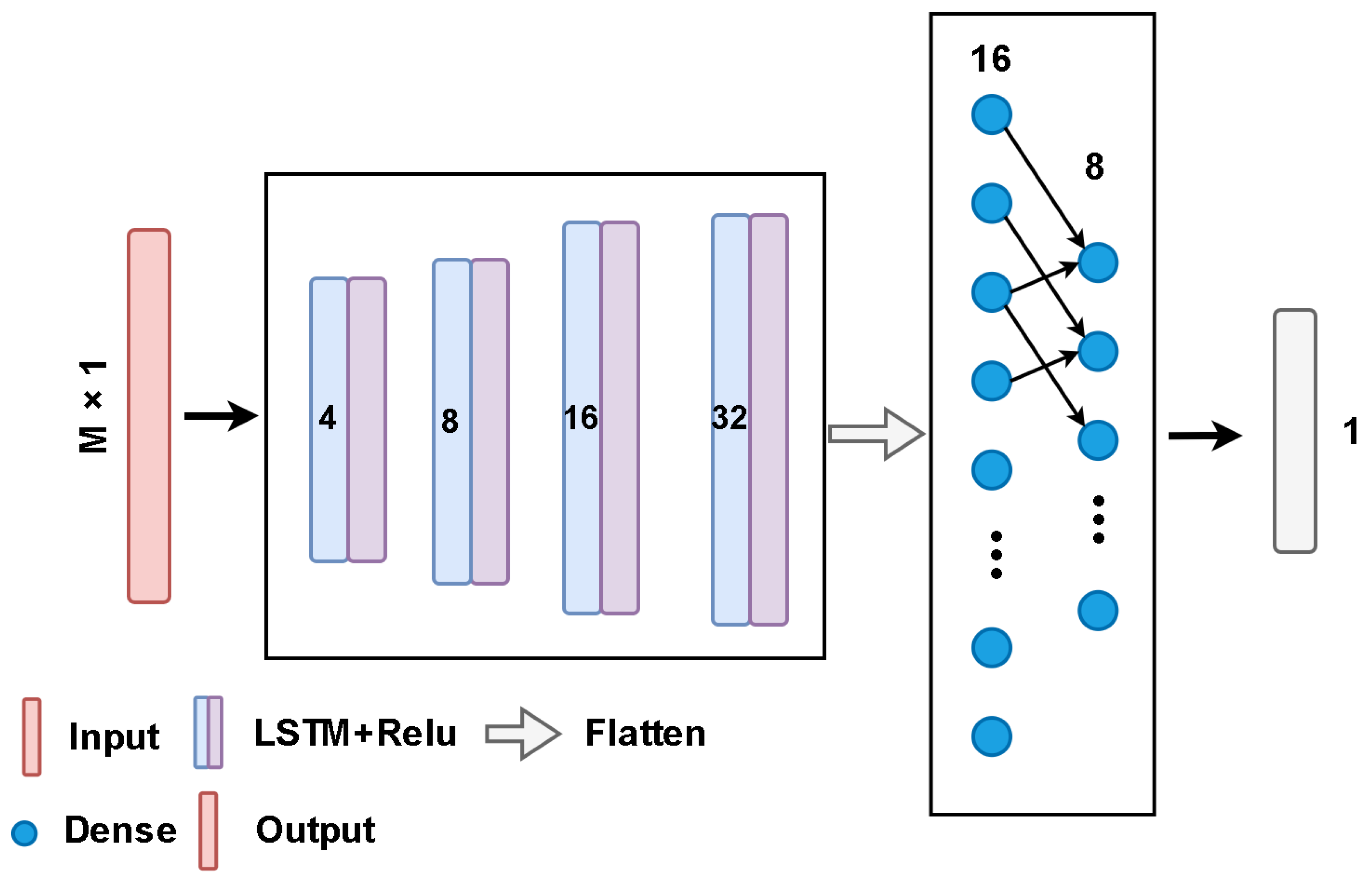
4.1. Model
4.2. Model Training and Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yiğit, E. Coupling and interactions across the Martian whole atmosphere system. Nat. Geosci. 2023, 16, 123–132. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Y.; Fan, K.; He, F.; Rong, Z.; Zhou, X.; Tan, N. The impact of dust storms on Mars surface rovers: Review and prospect. Chin. Sci. Bull. 2022, 68, 368–379. (In Chinese) [Google Scholar] [CrossRef]
- Cantor, B.A.; James, P.B.; Caplinger, M.; Wolff, M.J. Martian dust storms: 1999 Mars Orbiter Camera observations. J. Geophys. Res. Planets 2001, 106, 23653–23687. [Google Scholar] [CrossRef]
- Kass, D.M.; Kleinböhl, A.; McCleese, D.J.; Schofield, J.T.; Smith, M.D. Interannual similarity in the Martian atmosphere during the dust storm season. Geophys. Res. Lett. 2016, 43, 6111–6118. [Google Scholar] [CrossRef]
- Wang, H.; Richardson, M.I. The origin, evolution, and trajectory of large dust storms on Mars during Mars years 24–30 (1999–2011). Icarus 2015, 251, 112–127. [Google Scholar] [CrossRef]
- Montabone, L.; Spiga, A.; Kass, D.M.; Kleinböhl, A.; Forget, F.; Millour, E. Martian Year 34 Column Dust Climatology from Mars Climate Sounder Observations: Reconstructed Maps and Model Simulations. J. Geophys. Res. Planets 2020, 125, e2019JE006111. [Google Scholar] [CrossRef]
- He, F.; Wei, Y.; Rong, Z.; Ren, Z.; Yan, L.; Tan, N.; Wang, Y.; Fan, K.; Zhou, X.; Gao, J. Monitoring methods for Martian dust storms. Chin. Sci. Bull. 2023, 68, 2046–2057. [Google Scholar] [CrossRef]
- Guha, B.K.; Gebhardt, C.; Young, R.M.B.; Wolff, M.J.; Montabone, L. Seasonal and diurnal variations of duststorms in Martian year 36 based on the EMM-EXI database. J. Geophys. Res. Planets 2024, 129, e2023JE008156. [Google Scholar] [CrossRef]
- Rong, Z.; Wei, Y.; He, F.; Gao, J.; Fan, K.; Wang, Y.; Klinger, L.; Yan, L.; Ren, Z.; Zhou, X.; et al. The orbit schemes to monitor Martian dust storms: Benefits to China’s future Mars missions. Chin. Sci. Bull. 2023, 68, 716–728. [Google Scholar] [CrossRef]
- Gichu, R.; Ogohara, K. Segmentation of dust storm areas on Mars images using principal component analysis and neural network. Prog. Earth Planet. Sci. 2019, 6, 19. [Google Scholar] [CrossRef]
- Ogohara, K.; Gichu, R. Automated segmentation of textured dust storms on mars remote sensing images using an encoder-decoder type convolutional neural network. Comput. Geosci. 2022, 160, 105043. [Google Scholar] [CrossRef]
- Pla-García, J.; Rafkin, S.C.R.; Martinez, G.M.; Vicente-Retortillo, Á.; Newman, C.E.; Savijärvi, H.; de la Torre, M.; Rodriguez-Manfredi, J.A.; Gómez, F.; Molina, A.; et al. Meteorological Predictions for Mars 2020 Perseverance Rover Landing Site at Jezero Crater. Space Sci. Rev. 2020, 216, 148. [Google Scholar] [CrossRef] [PubMed]
- Newman, C.E.; de la Torre Juárez, M.; Pla-García, J.; Wilson, R.J.; Lewis, S.R.; Neary, L.; Kahre, M.A.; Forget, F.; Spiga, A.; Richardson, M.I.; et al. Multi-model Meteorological and Aeolian Predictions for Mars 2020 and the Jezero Crater Region. Space Sci. Rev. 2021, 217, 20. [Google Scholar] [CrossRef] [PubMed]
- Montabone, L.; Forget, F. On forecasting dust storms on Mars. In Proceedings of the 48th International Conference on Environmental Systems, Albuquerque, NM, USA, 8–12 July 2018. [Google Scholar]
- Wei, Y.; He, F.; Fan, K.; Rong, Z.; Wang, Y. Preliminary predictions of the dust storm activity at the landing site of China’s Zhurong Mars rover in 2022. Chin. Sci. Bull. 2022, 67, 1938–1944. [Google Scholar] [CrossRef]
- Cheng, K.; Su, M.; Xue, Y.; Qiu, D.; Li, G. Instantaneous inversion of transient electromagnetic data using machine learning. Acta Geophys. 2024, 72, 3407–34016. [Google Scholar] [CrossRef]
- Hao, Z.; Liu, S.; Zhang, Y.; Ying, C.; Feng, Y.; Su, H.; Zhu, J. Physics-Informed Machine Learning: A Survey on Problems, Methods and Applications. arXiv 2022, arXiv:2211.08064. [Google Scholar]
- Lv, P.; Xue, G.; Chen, W.; Song, W. Application of the transfer learning method in multisource geophysical data fusion. J. Geophys. Eng. 2023, 20, 361–375. [Google Scholar] [CrossRef]
- Deng, F.; Hu, J.; Wang, X.; Yu, S.; Zhang, B.; Li, S.; Li, X. Magnetotelluric Deep Learning Forward Modeling and Its Application in Inversion. Remote Sens. 2023, 15, 3667. [Google Scholar] [CrossRef]
- Bellutta, D. The Fog of War: A Machine Learning Approach to Forecasting Weather on Mars. arXiv 2017, arXiv:1706.08915. [Google Scholar]
- Eltahan, M.; Moharm, K.; Daoud, N. Sensitivity of different optimization solvers in LSTM algorithm for temperature forecast over Mars at Jezero Crater landing site. In Proceedings of the 2020 21st International Arab Conference on Information Technology (ACIT), Giza, Egypt, 28–30 November 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Priyadarshini, I.; Puri, V. Mars weather data analysis using machine learning techniques. Earth Sci. Inform. 2021, 14, 1885–1898. [Google Scholar] [CrossRef]
- Alshehhi, R.; Gebhardt, C. Detection of Martian dust storms using mask regional convolutional neural networks. Prog. Earth Planet. Sci. 2022, 9, 4. [Google Scholar] [CrossRef]
- Al-Saad, M.; Aburaed, N.; al Mansoori, S.; Mansoor, W.; Al-Ahmad, H. A Study on Deep Learning Approaches for Mars Weather Forecasting. In Proceedings of the 2022 5th International Conference on Signal Processing and Information Security, ICSPIS 2022, Dubai, United Arab Emirates, 7–8 December 2022. [Google Scholar] [CrossRef]
- He, Z.; Zhang, J.; Sheng, Z.; Tang, M. Deep learning-based 12-hour global dust distribution forecasting on Martian. Rev. Geophys. Planet. Phys. 2024, 55, 479–492. [Google Scholar] [CrossRef]
- Clancy, R.T.; Wolff, M.J.; Whitney, B.A.; Cantor, B.A.; Smith, M.D.; McConnochie, T.H. Extension of atmospheric dust loading to high altitudes during the 2001 Mars dust storm: MGS TES limb observations. Icarus 2010, 207, 98–109. [Google Scholar] [CrossRef]
- Montabone, L.; Forget, F.; Millour, E.; Wilson, R.J.; Lewis, S.R.; Cantor, B.; Kass, D.; Kleinböhl, A.; Lemmon, M.T.; Smith, M.D.; et al. Eight-year climatology of dust optical depth on Mars. Icarus 2015, 251, 65–95. [Google Scholar] [CrossRef]
- Forget, F.; Montabone, L. Atmospheric Dust on Mars: A Review. In Proceedings of the 47th International Conference on Environmental Systems, Rome, Italy, 16–20 July 2017. [Google Scholar]
- Song, X.; Liu, Y.; Xue, L.; Wang, J.; Zhang, J.; Wang, J.; Jiang, L.; Cheng, Z. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model. J. Pet. Sci. Eng. 2020, 186, 106682. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Liu, H.; Lei, D.; Yuan, J.; Yuan, G.; Cui, C.; Wang, Y.; Xue, W. Ionospheric TEC Prediction in China Based on the Multiple-Attention LSTM Model. Atmosphere 2022, 13, 1939. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 1, 802–810. [Google Scholar]
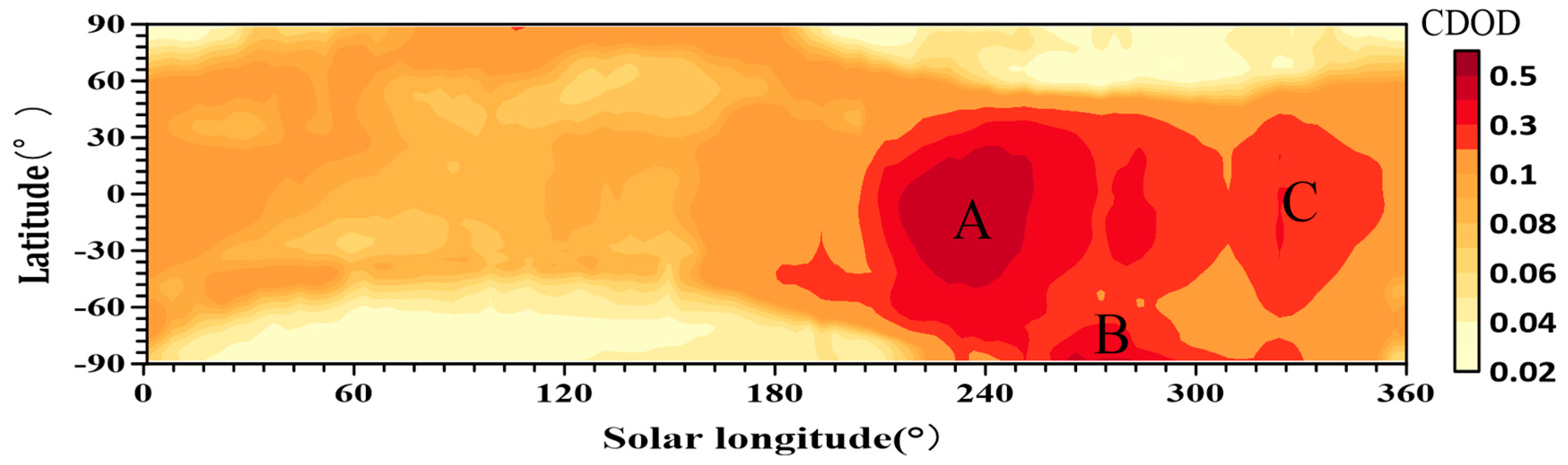
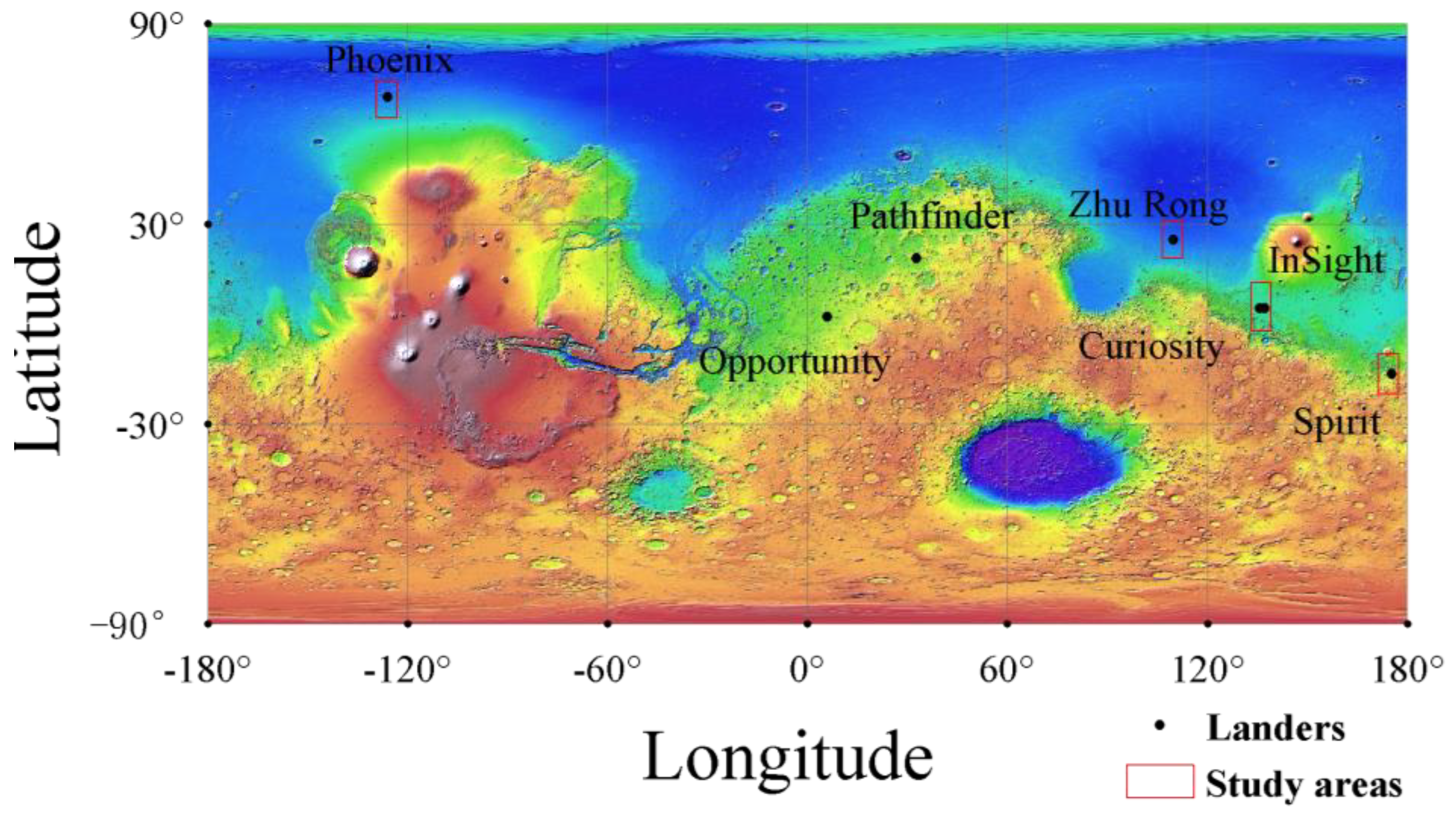


| Latitude Range | Longitude Range | Probe | |
|---|---|---|---|
| Equatorial region | 7.5°S~7.5°N | 132°E~138°E | Curiosity, InSight |
| South tropical region | 10.5°S~22.5°S | 171°E~177°E | Spirit |
| North tropical region | 16.5°N~28.5°N | 120°E~126°E | Zhurong |
| High latitude region | 58.5°N~70.5°N | 231°E~237°E | Phoenix |
| Accuracy | R2 | RMSE | MRE | |
|---|---|---|---|---|
| Sols | ||||
| 1 | 0.980 | 0.188 | 0.035 | |
| 5 | 0.788 | 0.299 | 0.081 | |
| 10 | 0.292 | 0.351 | 0.111 | |
| 20 | 0.027 | 0.599 | 0.249 | |
| R2 | RMSE | RME | |
|---|---|---|---|
| Equatorial | 0.971 | 0.212 | 0.045 |
| Tropics | 0.981 | 0.206 | 0.042 |
| High latitude | 0.910 | 0.278 | 0.077 |
| Equatorial | Tropics | High Latitude | |
|---|---|---|---|
| max_sols | 97 | 79 | 106 |
| first_acc | 1~18 | 1~9 | 1 |
| second_acc | 19~97 | 10~18 | 2 |
| third_acc | -- | 19~28 | 3 |
| forth_acc | -- | 29~79 | 4~106 |
| Time Series/Spatial Distribution | RMSE | RME |
|---|---|---|
| Equatorial | 0.212/0.315 | 0.045/0.072 |
| Tropics | 0.206/0.297 | 0.042/0.080 |
| High latitude | 0.278/0.428 | 0.077/0.125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Li, Z.; Yu, T.; Xia, C. Temporal and Spatial Prediction of Column Dust Optical Depth Trend on Mars Based on Deep Learning. Remote Sens. 2025, 17, 1472. https://doi.org/10.3390/rs17081472
Yan X, Li Z, Yu T, Xia C. Temporal and Spatial Prediction of Column Dust Optical Depth Trend on Mars Based on Deep Learning. Remote Sensing. 2025; 17(8):1472. https://doi.org/10.3390/rs17081472
Chicago/Turabian StyleYan, Xiangxiang, Ziteng Li, Tao Yu, and Chunliang Xia. 2025. "Temporal and Spatial Prediction of Column Dust Optical Depth Trend on Mars Based on Deep Learning" Remote Sensing 17, no. 8: 1472. https://doi.org/10.3390/rs17081472
APA StyleYan, X., Li, Z., Yu, T., & Xia, C. (2025). Temporal and Spatial Prediction of Column Dust Optical Depth Trend on Mars Based on Deep Learning. Remote Sensing, 17(8), 1472. https://doi.org/10.3390/rs17081472





