Use of Tropospheric Delay in GNSS-Based Climate Monitoring—A Review
Abstract
:1. Introduction
2. GNSS Tropospheric Products
2.1. Zenith Troposheric Delay Components: ZTD, ZHD, and ZWD
2.2. IWV/PWV: Estimation and Applications
3. GNSS-Based Climate Monitoring
3.1. Climate Trends from GNSS
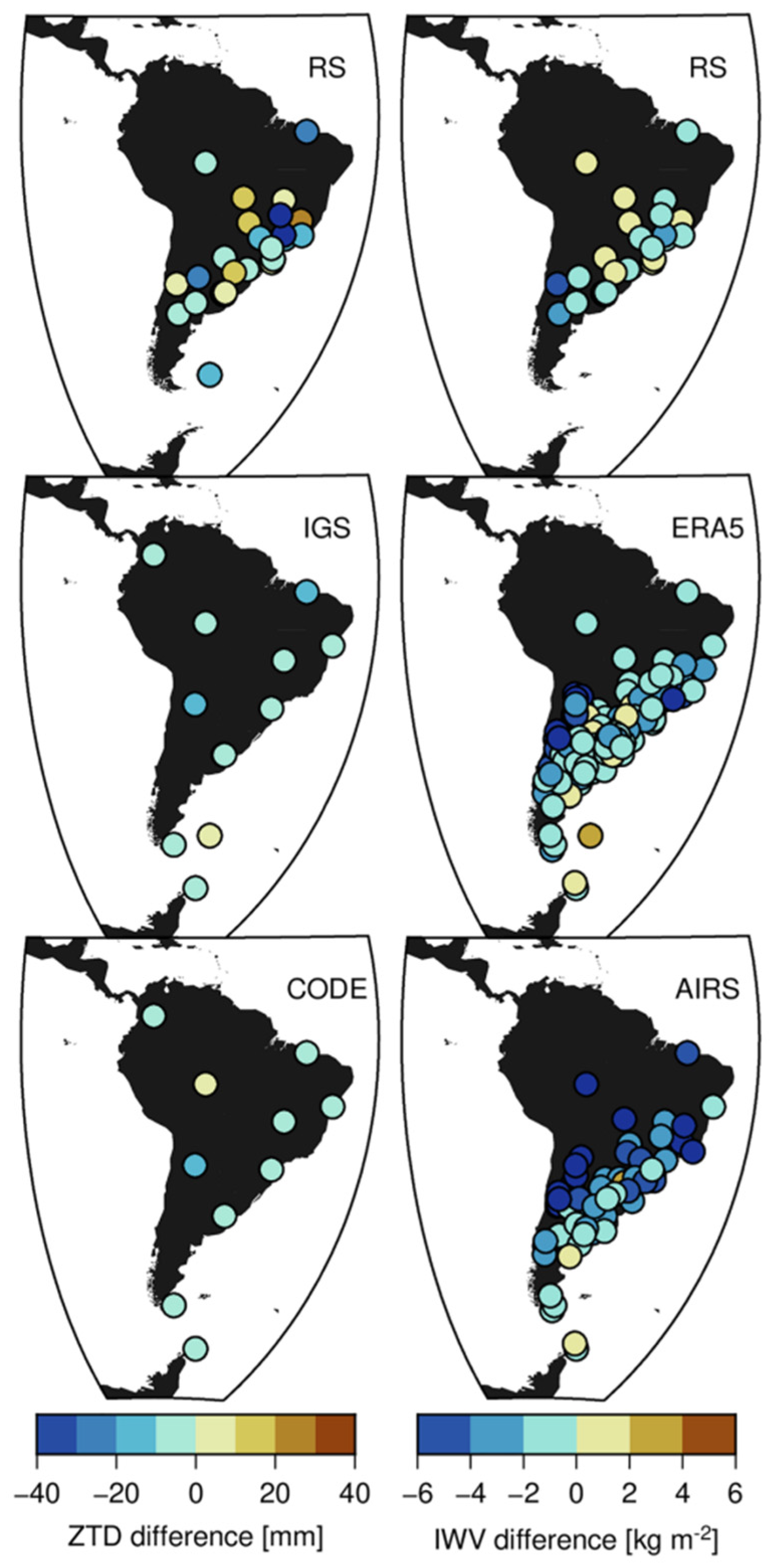
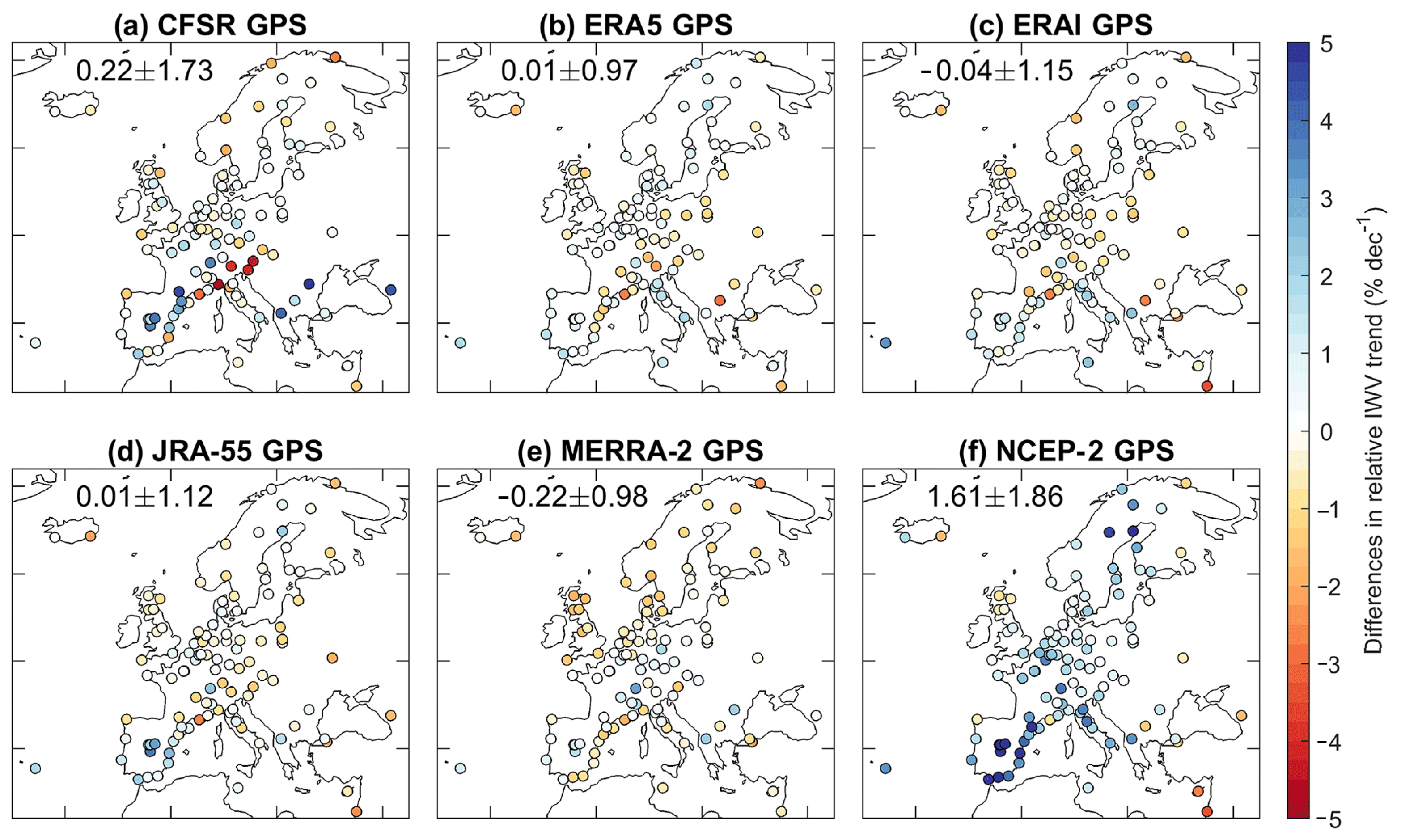
3.2. Integrating GNSS-Derived Water Vapor with Reanalysis Data for Climate Monitoring
3.3. Extreme Weather Events
3.4. AI and Machine Learning
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Speight, J.G. Natural Water Remediation; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 9780128038109. [Google Scholar]
- Holton, J.; Hakim, G. An Introduction to Dynamic Meteorology; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 9780123848666. [Google Scholar]
- Colman, R.A. Climate Radiative Feedbacks and Adjustments at the Earth’s Surface. J. Geophys. Res. Atmos. 2015, 120, 3173–3182. [Google Scholar] [CrossRef]
- Patel, V.K.; Kuttippurath, J. Increase in Tropospheric Water Vapor Amplifies Global Warming and Climate Change. Ocean-Land-Atmos. Res. 2023, 2, 15. [Google Scholar] [CrossRef]
- Peixóto, J.P.; Oort, A.H. The Atmospheric Branch of the Hydrological Cycle and Climate. In Variations in the Global Water Budget; Springer: Dordrecht, The Netherlands, 1983; pp. 5–65. [Google Scholar]
- Acker, J.; Williams, R.; Chiu, L.; Ardanuy, P.; Miller, S.; Schueler, C.; Vachon, P.W.; Manore, M. Remote Sensing from Satellites. In Encyclopedia of Physical Science and Technology; Elsevier: Amsterdam, The Netherlands, 2003; pp. 161–202. [Google Scholar]
- Rasmussen, R.; Khalil, M. The Behavior of Trace Gases in the Troposphere. Sci. Total Environ. 1986, 48, 169–186. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust Responses of the Hydrological Cycle to Global Warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Dai, A. Recent Climatology, Variability, and Trends in Global Surface Humidity. J. Clim. 2006, 19, 3589–3606. [Google Scholar] [CrossRef]
- Bony, S.; Stevens, B.; Frierson, D.M.W.; Jakob, C.; Kageyama, M.; Pincus, R.; Shepherd, T.G.; Sherwood, S.C.; Siebesma, A.P.; Sobel, A.H.; et al. Clouds, Circulation and Climate Sensitivity. Nat. Geosci. 2015, 8, 261–268. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Amiri-Simkooei, A. Function-Based Troposphere Tomography Technique for Optimal Downscaling of Precipitation. Remote Sens. 2022, 14, 2548. [Google Scholar] [CrossRef]
- Gauss, M.; Myhre, G.; Pitari, G.; Prather, M.J.; Isaksen, I.S.A.; Berntsen, T.K.; Brasseur, G.P.; Dentener, F.J.; Derwent, R.G.; Hauglustaine, D.A.; et al. Radiative Forcing in the 21st Century Due to Ozone Changes in the Troposphere and the Lower Stratosphere. J. Geophys. Res. Atmos. 2003, 108, 2624. [Google Scholar] [CrossRef]
- Jeevanjee, N.; Romps, D.M. Mean Precipitation Change from a Deepening Troposphere. Proc. Natl. Acad. Sci. USA 2018, 115, 11465–11470. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, L.; Liu, D.; Han, T.; Bao, R. Circulation Patterns in the Middle and Upper Troposphere and Their Relationships with Summer Precipitation in the Jianghuai River Basin. Int. J. Climatol. 2024, 44, 887–901. [Google Scholar] [CrossRef]
- Pincus, R.; Beljaars, A.; Buehler, S.A.; Kirchengast, G.; Ladstaedter, F.; Whitaker, J.S. The Representation of Tropospheric Water Vapor Over Low-Latitude Oceans in (Re-)Analysis: Errors, Impacts, and the Ability to Exploit Current and Prospective Observations. Surv. Geophys. 2017, 38, 1399–1423. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Roca, R.; Weckwerth, T.M.; Andronova, N.G. Tropospheric Water Vapor, Convection, and Climate. Rev. Geophys. 2010, 48, RG2001. [Google Scholar] [CrossRef]
- Jin, X.; Liu, X.; Guo, J.; Zhou, M.; Wu, K. A Novel All-Weather Method to Determine Deflection of the Vertical by Combining 3D Laser Tracking Free-Fall and Multi-GNSS Baselines. Remote Sens. 2022, 14, 4156. [Google Scholar] [CrossRef]
- Nehrir, A.R.; Kiemle, C.; Lebsock, M.D.; Kirchengast, G.; Buehler, S.A.; Löhnert, U.; Liu, C.-L.; Hargrave, P.C.; Barrera-Verdejo, M.; Winker, D.M. Emerging Technologies and Synergies for Airborne and Space-Based Measurements of Water Vapor Profiles. Surv. Geophys. 2017, 38, 1445–1482. [Google Scholar] [CrossRef] [PubMed]
- Antuña-Marrero, J.C.; Román, R.; Cachorro, V.E.; Mateos, D.; Toledano, C.; Calle, A.; Antuña-Sánchez, J.C.; Vaquero-Martínez, J.; Antón, M.; de Frutos Baraja, Á.M. Integrated Water Vapor over the Arctic: Comparison between Radiosondes and Sun Photometer Observations. Atmos. Res. 2022, 270, 106059. [Google Scholar] [CrossRef]
- Li, L.; Gao, Y.; Xu, S.; Lu, H.; He, Q.; Yu, H. The New Improved ZHD and Weighted Mean Temperature Models Based on GNSS and Radiosonde Data Using GPT3 and Fourier Function. Atmosphere 2022, 13, 1648. [Google Scholar] [CrossRef]
- Feng, P.; Li, F.; Yan, J.; Zhang, F.; Barriot, J.P. Assessment of the Accuracy of the Saastamoinen Model and Vmf1/Vmf3 Mapping Functions with Respect to Ray-Tracing from Radiosonde Data in the Framework of Gnss Meteorology. Remote Sens. 2020, 12, 3337. [Google Scholar] [CrossRef]
- Xia, P.; Cai, C.; Liu, Z. GNSS Troposphere Tomography Based on Two-Step Reconstructions Using GPS Observations and COSMIC Profiles. Ann. Geophys. 2013, 31, 1805–1815. [Google Scholar] [CrossRef]
- Li, X.; Zus, F.; Lu, C.; Dick, G.; Ning, T.; Ge, M.; Wickert, J.; Schuh, H. Retrieving of Atmospheric Parameters from Multi-GNSS in Real Time: Validation with Water Vapor Radiometer and Numerical Weather Model. J. Geophys. Res. 2015, 120, 7189–7204. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Costa, M.J.; Bortoli, D.; Navas-Guzmán, F.; Alados-Arboledas, L. Microwave Radiometer, Sun-Photometer and GNSS Multi-Comparison of Integrated Water Vapor in Southwestern Europe. Atmos. Res. 2023, 287, 106698. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Ortiz de Galisteo, J.P.; Cachorro, V.E.; Álvarez-Zapatero, P.; Román, R.; Loyola, D.; Costa, M.J.; Wang, H.; Abad, G.G.; et al. Inter-Comparison of Integrated Water Vapor from Satellite Instruments Using Reference GPS Data at the Iberian Peninsula. Remote Sens. Environ. 2018, 204, 729–740. [Google Scholar] [CrossRef]
- Xie, Y.; Li, Z.; Hou, W.; Guang, J.; Ma, Y.; Wang, Y.; Wang, S.; Yang, D. Validation of FY-3D MERSI-2 Precipitable Water Vapor (PWV) Datasets Using Ground-Based PWV Data from AERONET. Remote Sens. 2021, 13, 3246. [Google Scholar] [CrossRef]
- Chan, K.L.; Valks, P.; Heue, K.-P.; Lutz, R.; Hedelt, P.; Loyola, D.; Pinardi, G.; Van Roozendael, M.; Hendrick, F.; Wagner, T.; et al. Global Ozone Monitoring Experiment-2 (GOME-2) Daily and Monthly Level-3 Products of Atmospheric Trace Gas Columns. Earth Syst. Sci. Data 2023, 15, 1831–1870. [Google Scholar] [CrossRef]
- Guerova, G.; Simeonov, T. GNSS Monitoring of the Troposphere (GNSS-M). In Global Navigation Satellite System Monitoring of the Atmosphere; Elsevier: Amsterdam, The Netherlands, 2022; pp. 41–63. [Google Scholar]
- Vaquero-Martínez, J.; Antón, M. Review on the Role of Gnss Meteorology in Monitoring Water Vapor for Atmospheric Physics. Remote Sens. 2021, 13, 2287. [Google Scholar] [CrossRef]
- Ning, T.; Wang, J.; Elgered, G.; Dick, G.; Wickert, J.; Bradke, M.; Sommer, M.; Querel, R.; Smale, D. The Uncertainty of the Atmospheric Integrated Water Vapour Estimated from GNSS Observations. Atmos. Meas. Tech. 2016, 9, 79–92. [Google Scholar] [CrossRef]
- Li, L.; Zhang, K.; Wu, S.; Li, H.; Wang, X.; Hu, A.; Li, W.; Fu, E.; Zhang, M.; Shen, Z. An Improved Method for Rainfall Forecast Based on GNSS-PWV. Remote Sens. 2022, 14, 4280. [Google Scholar] [CrossRef]
- Bosser, P.; Bock, O. IWV Retrieval from Ground GNSS Receivers during NAWDEX. Adv. Geosci. 2021, 55, 13–22. [Google Scholar] [CrossRef]
- Tralli, D.M.; Lichten, S.M. Stochastic Estimation of Tropospheric Path Delays in Global Positioning System Geodetic Measurements. Bull. Géodésique 1990, 64, 127–159. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Picquenard, A. Tropospheric Propagation. In Radio Wave Propagation; Macmillan Education: London, UK, 1974; pp. 13–53. [Google Scholar]
- Hobiger, T.; Jakowski, N. Atmospheric Signal Propagation. In Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Cham, Switzerland, 2017; pp. 165–193. [Google Scholar]
- Stoew, B.; Elgered, G. Characterization of Atmospheric Parameters Using a Ground Based GPS Network in North Europe. J. Meteorol. Soc. Jpn. Ser. II 2004, 82, 587–596. [Google Scholar] [CrossRef]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Marut, G.; Hadas, T.; Kaplon, J.; Trzcina, E.; Rohm, W. Monitoring the Water Vapor Content at High Spatio-Temporal Resolution Using a Network of Low-Cost Multi-GNSS Receivers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5804614. [Google Scholar] [CrossRef]
- Baldysz, Z.; Nykiel, G.; Figurski, M.; Araszkiewicz, A. Assessment of the Impact of GNSS Processing Strategies on the Long-Term Parameters of 20 Years IWV Time Series. Remote Sens. 2018, 10, 496. [Google Scholar] [CrossRef]
- Hordyniec, P.; Bosy, J.; Rohm, W. Assessment of Errors in Precipitable Water Data Derived from Global Navigation Satellite System Observations. J. Atmos. Sol.-Terr. Phys. 2015, 129, 69–77. [Google Scholar] [CrossRef]
- Benvenuto, L.; Dabove, P.; Ferrando, I.; Sguerso, D. Preliminary Results on Tropospheric Ztd Estimation by Smartphone. Remote Sens. 2021, 13, 4567. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, H.; Xia, P. Exploration and Analysis of the Factors Influencing GNSS PWV for Nowcasting Applications. Adv. Space Res. 2021, 67, 3960–3978. [Google Scholar] [CrossRef]
- Sapucci, L.F.; Machado, L.A.T.; de Souza, E.M.; Campos, T.B. Global Positioning System Precipitable Water Vapour (GPS-PWV) Jumps before Intense Rain Events: A Potential Application to Nowcasting. Meteorol. Appl. 2019, 26, 49–63. [Google Scholar] [CrossRef]
- Shi, J.; Li, X.; Li, L.; Ouyang, C.; Xu, C. An Efficient Deep Learning-Based Troposphere ZTD Dataset Generation Method for Massive GNSS CORS Stations. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5801311. [Google Scholar] [CrossRef]
- Gendt, G.; Dick, G.; Reigber, C.; Tomassini, M.; Liu, Y.; Ramatschi, M. Near Real Time GPS Water Vapor Monitoring for Numerical Weather Prediction in Germany. J. Meteorol. Soc. Jpn. 2004, 82, 361–370. [Google Scholar] [CrossRef]
- Rohm, W.; Yuan, Y.; Biadeglgne, B.; Zhang, K.; Marshall, J. Le Ground-Based GNSS ZTD/IWV Estimation System for Numerical Weather Prediction in Challenging Weather Conditions. Atmos. Res. 2014, 138, 414–426. [Google Scholar] [CrossRef]
- Trzcina, E.; Rohm, W. Estimation of 3D Wet Refractivity by Tomography, Combining GNSS and NWP Data: First Results from Assimilation of Wet Refractivity into NWP. Q. J. R. Meteorol. Soc. 2019, 145, 1034–1051. [Google Scholar] [CrossRef]
- Makama, E.K.; Lim, H.S. Variability and Trend in Integrated Water Vapour from ERA-Interim and IGRA2 Observations over Peninsular Malaysia. Atmosphere 2020, 11, 1012. [Google Scholar] [CrossRef]
- Parracho, A.C.; Bock, O.; Bastin, S. Global IWV Trends and Variability in Atmospheric Reanalyses and GPS Observations. Atmos. Chem. Phys. 2018, 18, 16213–16237. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Yao, Y. A Global Model for Estimating Tropospheric Delay and Weighted Mean Temperature Developed with Atmospheric Reanalysis Data from 1979 to 2017. Remote Sens. 2019, 11, 1893. [Google Scholar] [CrossRef]
- Jadala, N.B.; Sridhar, M.; Dutta, G.; Yousuf, M.; Reddy, Y.K. Integrated Water Vapor during Active and Break Spells of Monsoon and Its Relationship with Temperature, Precipitation and Precipitation Efficiency over a Tropical Site. Geod. Geodyn. 2022, 13, 238–246. [Google Scholar] [CrossRef]
- Guo, L.; Huang, L.; Li, J.; Liu, L.; Huang, L.; Fu, B.; Xie, S.; He, H.; Ren, C. A Comprehensive Evaluation of Key Tropospheric Parameters from Era5 and Merra-2 Reanalysis Products Using Radiosonde Data and Gnss Measurements. Remote Sens. 2021, 13, 8. [Google Scholar] [CrossRef]
- Huang, L.; Wang, X.; Xiong, S.; Li, J.; Liu, L.; Mo, Z.; Fu, B.; He, H. High-Precision GNSS PWV Retrieval Using Dense GNSS Sites and in-Situ Meteorological Observations for the Evaluation of MERRA-2 and ERA5 Reanalysis Products over China. Atmos. Res. 2022, 276, 106247. [Google Scholar] [CrossRef]
- Yuan, P.; Van Malderen, R.; Yin, X.; Vogelmann, H.; Jiang, W.; Awange, J.; Heck, B.; Kutterer, H. Characterisations of Europe’s Integrated Water Vapour and Assessments of Atmospheric Reanalyses Using More than 2 Decades of Ground-Based GPS. Atmos. Chem. Phys. 2023, 23, 3517–3541. [Google Scholar] [CrossRef]
- Bosy, J.; Kaplon, J.; Rohm, W.; Sierny, J.; Hadas, T. Near Real-Time Estimation of Water Vapour in the Troposphere Using Ground GNSS and the Meteorological Data. Ann. Geophys. 2012, 30, 1379–1391. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, J.; Chen, M.; Shi, J.; Zhou, L. Quantitative Assessment of Meteorological and Tropospheric Zenith Hydrostatic Delay Models. Adv. Space Res. 2016, 58, 1033–1043. [Google Scholar] [CrossRef]
- Wilgan, K.; Hurter, F.; Geiger, A.; Rohm, W.; Bosy, J. Tropospheric Refractivity and Zenith Path Delays from Least-Squares Collocation of Meteorological and GNSS Data. J. Geod. 2017, 91, 117–134. [Google Scholar] [CrossRef]
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-Technique Validation of Tropospheric Slant Total Delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]
- Hadas, T.; Kaplon, J.; Bosy, J.; Sierny, J.; Wilgan, K. Near-Real-Time Regional Troposphere Models for the GNSS Precise Point Positioning Technique. Meas. Sci. Technol. 2013, 24, 055003. [Google Scholar] [CrossRef]
- Fernandes, M.J.; Pires, N.; Lázaro, C.; Nunes, A.L. Tropospheric Delays from GNSS for Application in Coastal Altimetry. Adv. Space Res. 2013, 51, 1352–1368. [Google Scholar] [CrossRef]
- Rohm, W.; Zhang, K.; Bosy, J. Limited Constraint, Robust Kalman Filtering for GNSS Troposphere Tomography. Atmos. Meas. Tech. 2014, 7, 1475–1486. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Ding, W.; Teferle, F.N.; Kazmierski, K.; Laurichesse, D.; Yuan, Y. An Evaluation of Real-Time Troposphere Estimation Based on GNSS Precise Point Positioning. J. Geophys. Res. 2017, 122, 2779–2790. [Google Scholar] [CrossRef]
- Lu, C.; Chen, X.; Liu, G.; Dick, G.; Wickert, J.; Jiang, X.; Zheng, K.; Schuh, H. Real-Time Tropospheric Delays Retrieved from Multi-GNSS Observations and IGS Real-Time Product Streams. Remote Sens. 2017, 9, 1317. [Google Scholar] [CrossRef]
- Mendez Astudillo, J.; Lau, L.; Tang, Y.-T.; Moore, T. Analysing the Zenith Tropospheric Delay Estimates in On-Line Precise Point Positioning (PPP) Services and PPP Software Packages. Sensors 2018, 18, 580. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Li, Z. Real-Time Precise Point Positioning-Based Zenith Tropospheric Delay for Precipitation Forecasting. Sci. Rep. 2018, 8, 7939. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Cheng, J.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Real-Time Tropospheric Delay Retrieval from Multi-GNSS PPP Ambiguity Resolution: Validation with Final Troposphere Products and a Numerical Weather Model. Remote Sens. 2018, 10, 481. [Google Scholar] [CrossRef]
- Tunalı, E.; Özlüdemir, M.T. GNSS PPP with Different Troposphere Models during Severe Weather Conditions. GPS Solut. 2019, 23, 82. [Google Scholar] [CrossRef]
- Hadas, T.; Hobiger, T.; Hordyniec, P. Considering Different Recent Advancements in GNSS on Real-Time Zenith Troposphere Estimates. GPS Solut. 2020, 24, 99. [Google Scholar] [CrossRef]
- Wilgan, K.; Dick, G.; Zus, F.; Wickert, J. Towards Operational Multi-GNSS Tropospheric Products at GFZ Potsdam. Atmos. Meas. Tech. 2022, 15, 21–39. [Google Scholar] [CrossRef]
- Zhao, Q.; Su, J.; Xu, C.; Yao, Y.; Zhang, X.; Wu, J. High-Precision ZTD Model of Altitude-Related Correction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 609–621. [Google Scholar] [CrossRef]
- Xia, P.; Tong, M.; Ye, S.; Qian, J.; Fangxin, H. Establishing a High-Precision Real-Time ZTD Model of China with GPS and ERA5 Historical Data and Its Application in PPP. GPS Solut. 2023, 27, 2. [Google Scholar] [CrossRef]
- Trzcina, E.; Rohm, W.; Smolak, K. Parameterisation of the GNSS Troposphere Tomography Domain with Optimisation of the Nodes’ Distribution. J. Geod. 2023, 97, 2. [Google Scholar] [CrossRef]
- Barba, P.; Ramírez-Zelaya, J.; Jiménez, V.; Rosado, B.; Jaramillo, E.; Moreno, M.; Berrocoso, M. Tropospheric and Ionospheric Modeling Using GNSS Time Series in Volcanic Eruptions (La Palma, 2021). Eng. Proc. 2023, 39, 9047. [Google Scholar] [CrossRef]
- Douša, J.; Václavovic, P.; Zhao, L.; Kačmařík, M. New Adaptable All-in-One Strategy for Estimating Advanced Tropospheric Parameters and Using Real-Time Orbits and Clocks. Remote Sens. 2018, 10, 232. [Google Scholar] [CrossRef]
- Lu, C.; Zhong, Y.; Wu, Z.; Zheng, Y.; Wang, Q. A Tropospheric Delay Model to Integrate ERA5 and GNSS Reference Network for Mountainous Areas: Application to Precise Point Positioning. GPS Solut. 2023, 27, 81. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, W.; Li, Z.; Du, Z.; Yang, P.; Yao, W.; Yao, Y. A High-Precision ZTD Interpolation Method Considering Large Area and Height Differences. GPS Solut. 2024, 28, 4. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L. Climate Applications of a Global, 2-Hourly Atmospheric Precipitable Water Dataset Derived from IGS Tropospheric Products. J. Geod. 2009, 83, 209–217. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, K.; Rohm, W.; Choy, S.; Norman, R.; Wang, C.S. Real-Time Retrieval of Precipitable Water Vapor from GPS Precise Point Positioning. J. Geophys. Res. Atmos. 2014, 119, 10044–10057. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Guo, J.; Gao, Y. Real-Time GPS Precise Point Positioning-Based Precipitable Water Vapor Estimation for Rainfall Monitoring and Forecasting. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3452–3459. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Xu, Y.; Tang, L.; Yang, N.; Zhang, G. GNSS Real-Time ZTD/PWV Retrieval Based on PPP with Broadcast Ephemerides. Atmosphere 2024, 15, 1030. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, K.; Wu, S.; Wan, M.; Lin, Y. Retrieving Precipitable Water Vapor from Real-Time Precise Point Positioning Using VMF1/VMF3 Forecasting Products. Remote Sens. 2021, 13, 3245. [Google Scholar] [CrossRef]
- Aragón Paz, J.M.; Mendoza, L.P.O.; Fernández, L.I. Near-Real-Time GNSS Tropospheric IWV Monitoring System for South America. GPS Solut. 2023, 27, 93. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S. GPS-PWV Based Improved Long-Term Rainfall Prediction Algorithm for Tropical Regions. Remote Sens. 2019, 11, 2643. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Bock, Y.; Liang, H.; Dong, D.; Fang, P. Dynamic Mapping of the Movement of Landfalling Atmospheric Rivers Over Southern California with GPS Data. Geophys. Res. Lett. 2019, 46, 3551–3559. [Google Scholar] [CrossRef]
- Kim, H.D.; Kim, K.-H. Analysis of Rip Current Characteristics Using Dye Tracking Method. Atmosphere 2021, 12, 719. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Li, Q.; Yang, J.; Li, L.; Wang, T. Impact of Different Microphysics and Cumulus Parameterizations in WRF for Heavy Rainfall Simulations in the Central Segment of the Tianshan Mountains, China. Atmos. Res. 2020, 244, 105052. [Google Scholar] [CrossRef]
- Jadala, N.B.; Sridhar, M.; Dashora, N.; Dutta, G. Annual, Seasonal and Diurnal Variations of Integrated Water Vapor Using GPS Observations over Hyderabad, a Tropical Station. Adv. Space Res. 2020, 65, 529–540. [Google Scholar] [CrossRef]
- Negusini, M.; Petkov, B.H.; Tornatore, V.; Barindelli, S.; Martelli, L.; Sarti, P.; Tomasi, C. Water Vapour Assessment Using GNSS and Radiosondes over Polar Regions and Estimation of Climatological Trends from Long-Term Time Series Analysis. Remote Sens. 2021, 13, 4871. [Google Scholar] [CrossRef]
- Ning, T.; Elgered, G. Trends in the Atmospheric Water Vapour Estimated from GPS Data for Different Elevation Cutoff Angles. Atmos. Meas. Tech. Discuss. 2018, preprint. [Google Scholar]
- Yadav, R.; Giri, R.K.; Puviarasan, N.; Bhan, S.C. Annual, Seasonal, Monthly & Diurnal IPWV Analysis and Precipitation Forecasting over the Indian Subcontinent Based on Monthly Thresholds of Ground-Based GNSS-IPWV. Adv. Space Res. 2022, 70, 3122–3136. [Google Scholar] [CrossRef]
- Ding, J.; Chen, J. Assessment of Empirical Troposphere Model GPT3 Based on NGL’s Global Troposphere Products. Sensors 2020, 20, 3631. [Google Scholar] [CrossRef]
- Bosser, P.; Bock, O.; Flamant, C.; Bony, S.; Speich, S. Integrated Water Vapour Content Retrievals from Ship-Borne GNSS Receivers during Eurec4a. Earth Syst. Sci. Data 2021, 13, 1499–1517. [Google Scholar] [CrossRef]
- Chen, B.; Yu, W.; Wang, W.; Zhang, Z.; Dai, W. A Global Assessment of Precipitable Water Vapor Derived From GNSS Zenith Tropospheric Delays With ERA5, NCEP FNL, and NCEP GFS Products. Earth Space Sci. 2021, 8, e2021EA001796. [Google Scholar] [CrossRef]
- Li, S.; Xu, T.; Jiang, N.; Yang, H.; Wang, S.; Zhang, Z. Regional Zenith Tropospheric Delay Modeling Based on Least Squares Support Vector Machine Using Gnss and Era5 Data. Remote Sens. 2021, 13, 1004. [Google Scholar] [CrossRef]
- Kannemadugu, H.B.S.; Ranganathan, K.; Gharai, B.; MVR, S. GNSS-GPS Derived Integrated Water Vapor and Performance Assessment of ERA-5 Data over India. J. Atmos. Sol.-Terr. Phys. 2022, 227, 105807. [Google Scholar] [CrossRef]
- Xia, P.; Peng, W.; Yuan, P.; Ye, S. Monitoring Urban Heat Island Intensity Based on GNSS Tomography Technique. J. Geod. 2024, 98, 1. [Google Scholar] [CrossRef]
- Zhao, L.; Cui, M.; Song, J. An Improved Strategy for Real-Time Troposphere Estimation and Its Application in the Severe Weather Event Monitoring. Atmosphere 2022, 14, 46. [Google Scholar] [CrossRef]
- Hordyniec, P.; Kaplon, J.; Rohm, W.; Kryza, M. Residuals of Tropospheric Delays from GNSS Data and Ray-Tracing as a Potential Indicator of Rain and Clouds. Remote Sens. 2018, 10, 1917. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Qiu, C.; Zhang, S.; Zhang, J.; Xie, M.; Li, L. Development of an Improved Model for Prediction of Short-Term Heavy Precipitation Based on Gnss-Derived Pwv. Remote Sens. 2020, 12, 4101. [Google Scholar] [CrossRef]
- Hanna, N.; Trzcina, E.; Möller, G.; Rohm, W.; Weber, R. Assimilation of GNSS Tomography Products into the Weather Research and Forecasting Model Using Radio Occultation Data Assimilation Operator. Atmos. Meas. Tech. 2019, 12, 4829–4848. [Google Scholar] [CrossRef]
- Chang, C.-C.; Yang, S.-C. Impact of Assimilating Formosat-7/COSMIC-II GNSS Radio Occultation Data on Heavy Rainfall Prediction in Taiwan. Terr. Atmos. Ocean. Sci. 2022, 33, 7. [Google Scholar] [CrossRef]
- He, Q.; Zhang, K.; Wu, S.; Zhao, Q.; Wang, X.; Shen, Z.; Li, L.; Wan, M.; Liu, X. Real-Time GNSS-Derived PWV for Typhoon Characterizations: A Case Study for Super Typhoon Mangkhut in Hong Kong. Remote Sens. 2019, 12, 104. [Google Scholar] [CrossRef]
- Lian, D.; He, Q.; Li, L.; Zhang, K.; Fu, E.; Li, G.; Wang, R.; Gao, B.; Song, K. A Novel Method for Monitoring Tropical Cyclones’ Movement Using GNSS Zenith Tropospheric Delay. Remote Sens. 2023, 15, 3247. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Moeller, G.; Qi, M.; Ding, N. An Adaptive-Degree Layered Function-Based Method to GNSS Tropospheric Tomography. GPS Solut. 2023, 27, 67. [Google Scholar] [CrossRef]
- Zhang, W.; Moller, G.; Zheng, N.; Zhang, S.; Qi, M.; Wang, M. A New Multi-Resolution GNSS Tomography Method Based on Atmospheric Water Vapor Distributions. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4102314. [Google Scholar] [CrossRef]
- Selbesoglu, M.O. Prediction of Tropospheric Wet Delay by an Artificial Neural Network Model Based on Meteorological and GNSS Data. Eng. Sci. Technol. Int. J. 2020, 23, 967–972. [Google Scholar] [CrossRef]
- Yang, P.; Zhao, Q.; Li, Z.; Yao, W.; Yao, Y. High Temporal Resolution Global PWV Dataset of 2005–2016 by Using a Neural Network Approach to Determine the Mean Temperature of the Atmosphere. Adv. Space Res. 2021, 67, 3087–3097. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Rohm, W.; Kryza, M.; Smolak, K. Machine Learning-Based Wet Refractivity Prediction Through GNSS Troposphere Tomography for Ensemble Troposphere Conditions Forecasting. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4106118. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Rohm, W.; Hadas, T.; Bosy, J. Machine Learning-Based Tropospheric Delay Prediction for Real-Time Precise Point Positioning under Extreme Weather Conditions. GPS Solut. 2025, 29, 36. [Google Scholar] [CrossRef]
- Łoś, M.; Smolak, K.; Guerova, G.; Rohm, W. GNSS-Based Machine Learning Storm Nowcasting. Remote Sens. 2020, 12, 2536. [Google Scholar] [CrossRef]
- Bisht, D.S.; Rao, T.N.; Rao, N.R.; Chandrakanth, S.V.; Sharma, A. Prediction of Integrated Water Vapor Using a Machine Learning Technique. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1006705. [Google Scholar] [CrossRef]
- Ghaffari Razin, M.R.; Voosoghi, B. Modeling of Precipitable Water Vapor from GPS Observations Using Machine Learning and Tomography Methods. Adv. Space Res. 2022, 69, 2671–2681. [Google Scholar] [CrossRef]
- Aichinger-Rosenberger, M.; Brockmann, E.; Crocetti, L.; Soja, B.; Moeller, G. Machine Learning-Based Prediction of Alpine Foehn Events Using GNSS Troposphere Products: First Results for Altdorf, Switzerland. Atmos. Meas. Tech. 2022, 15, 5821–5839. [Google Scholar] [CrossRef]
- Shamshiri, R.; Motagh, M.; Nahavandchi, H.; Haghshenas Haghighi, M.; Hoseini, M. Improving Tropospheric Corrections on Large-Scale Sentinel-1 Interferograms Using a Machine Learning Approach for Integration with GNSS-Derived Zenith Total Delay (ZTD). Remote Sens. Environ. 2020, 239, 111608. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Nico, G. Neural Network Approach to Forecast Hourly Intense Rainfall Using GNSS Precipitable Water Vapor and Meteorological Sensors. Remote Sens. 2019, 11, 966. [Google Scholar] [CrossRef]
- Liu, C.; Yao, Y.; Xu, C. Conventional and Neural Network-Based Water Vapor Density Model for GNSS Troposphere Tomography. GPS Solut. 2022, 26, 4. [Google Scholar] [CrossRef]
- Selbesoglu, M.O. Spatial Interpolation of GNSS Troposphere Wet Delay by a Newly Designed Artificial Neural Network Model. Appl. Sci. 2019, 9, 4688. [Google Scholar] [CrossRef]
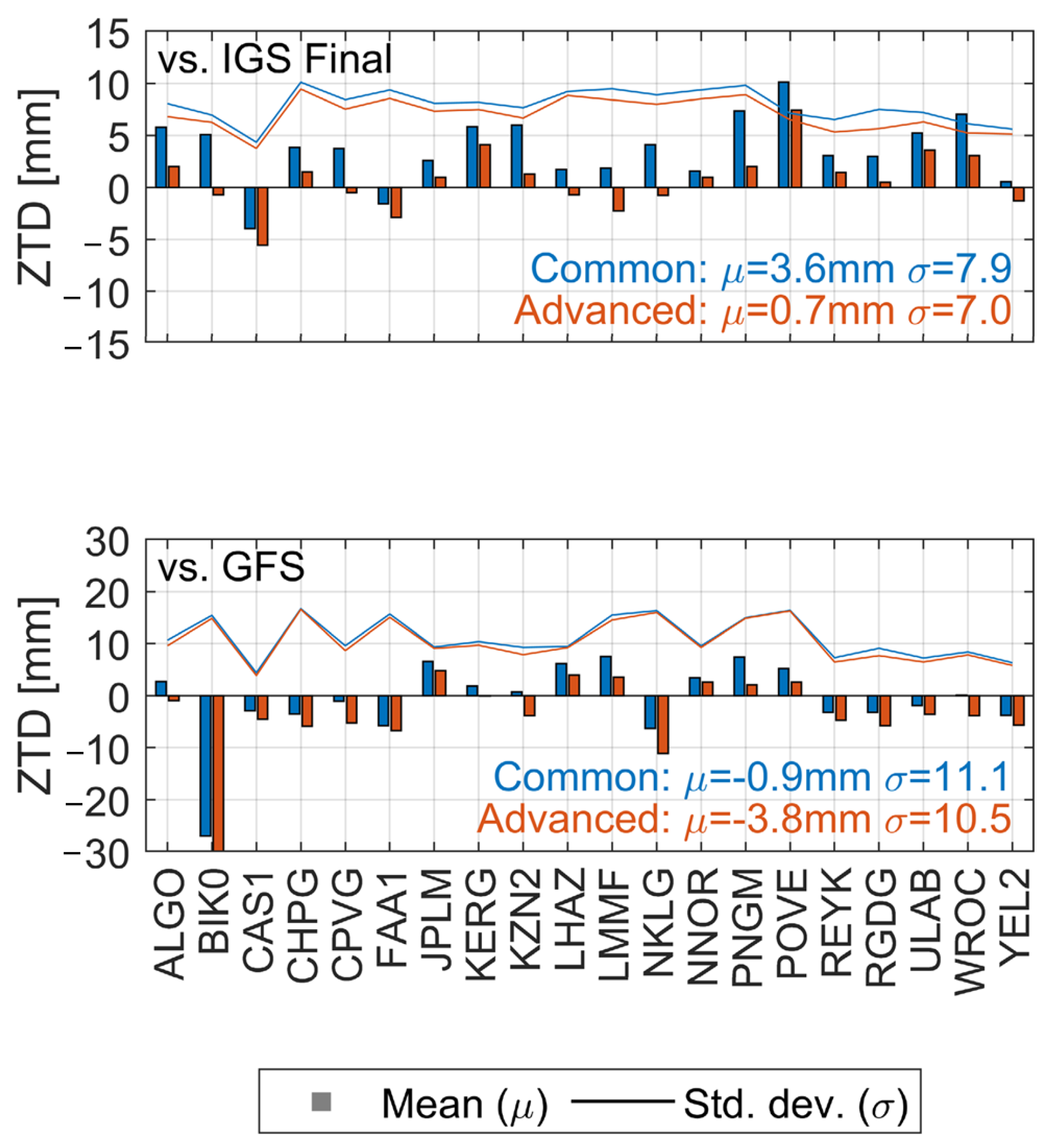
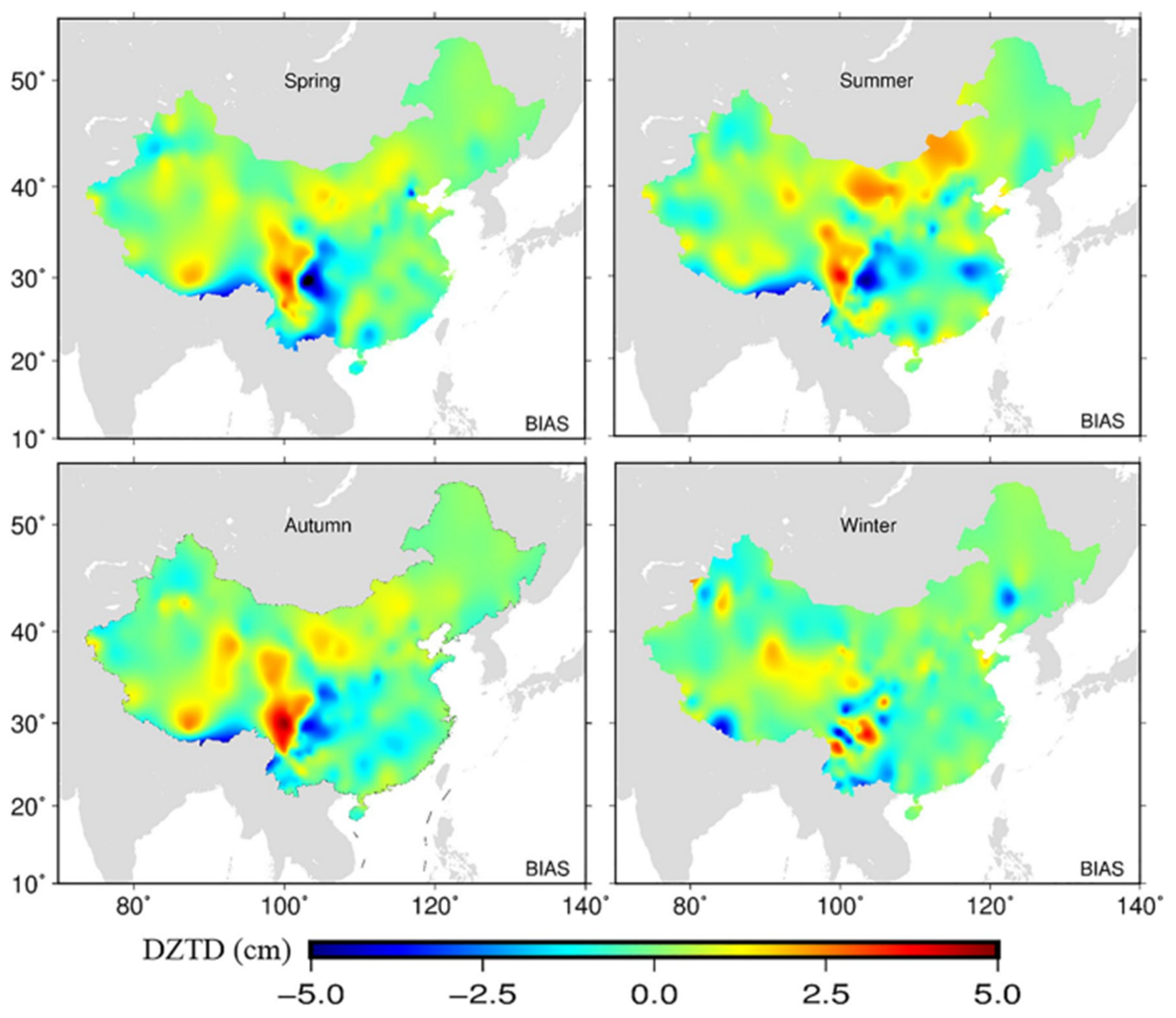
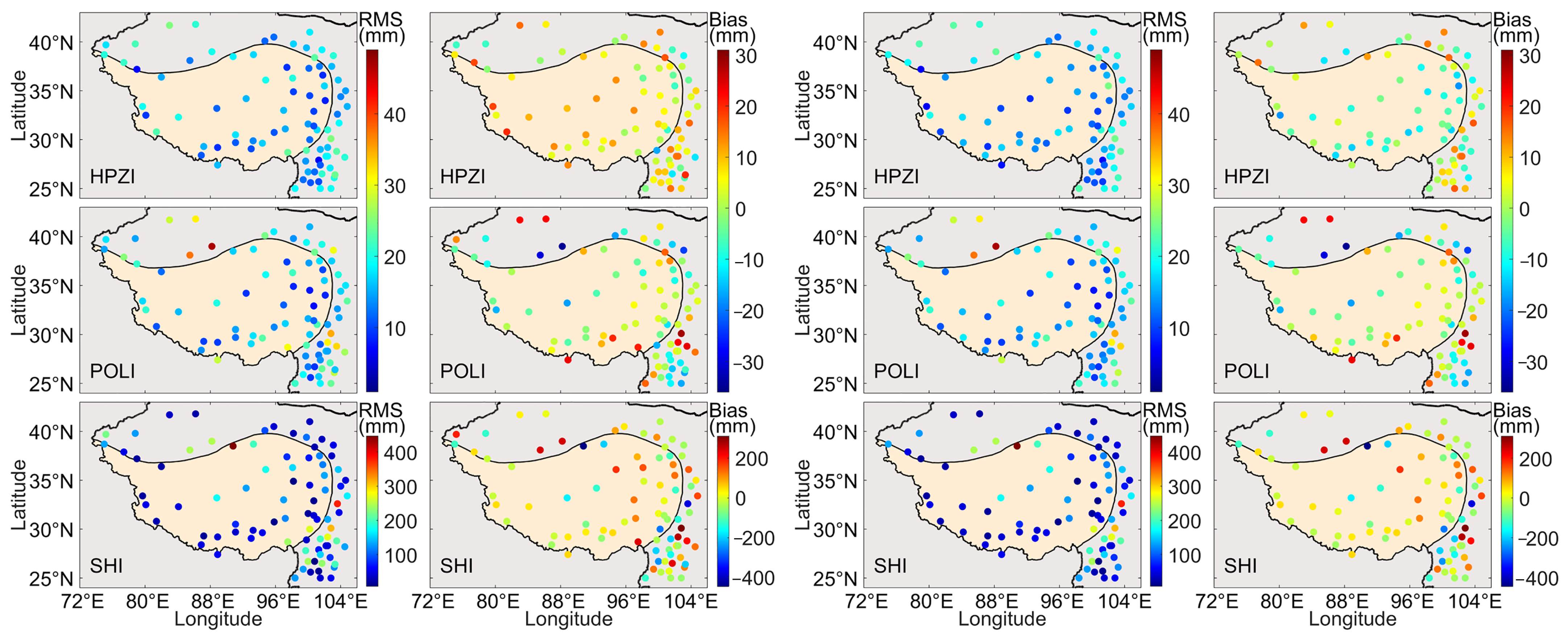
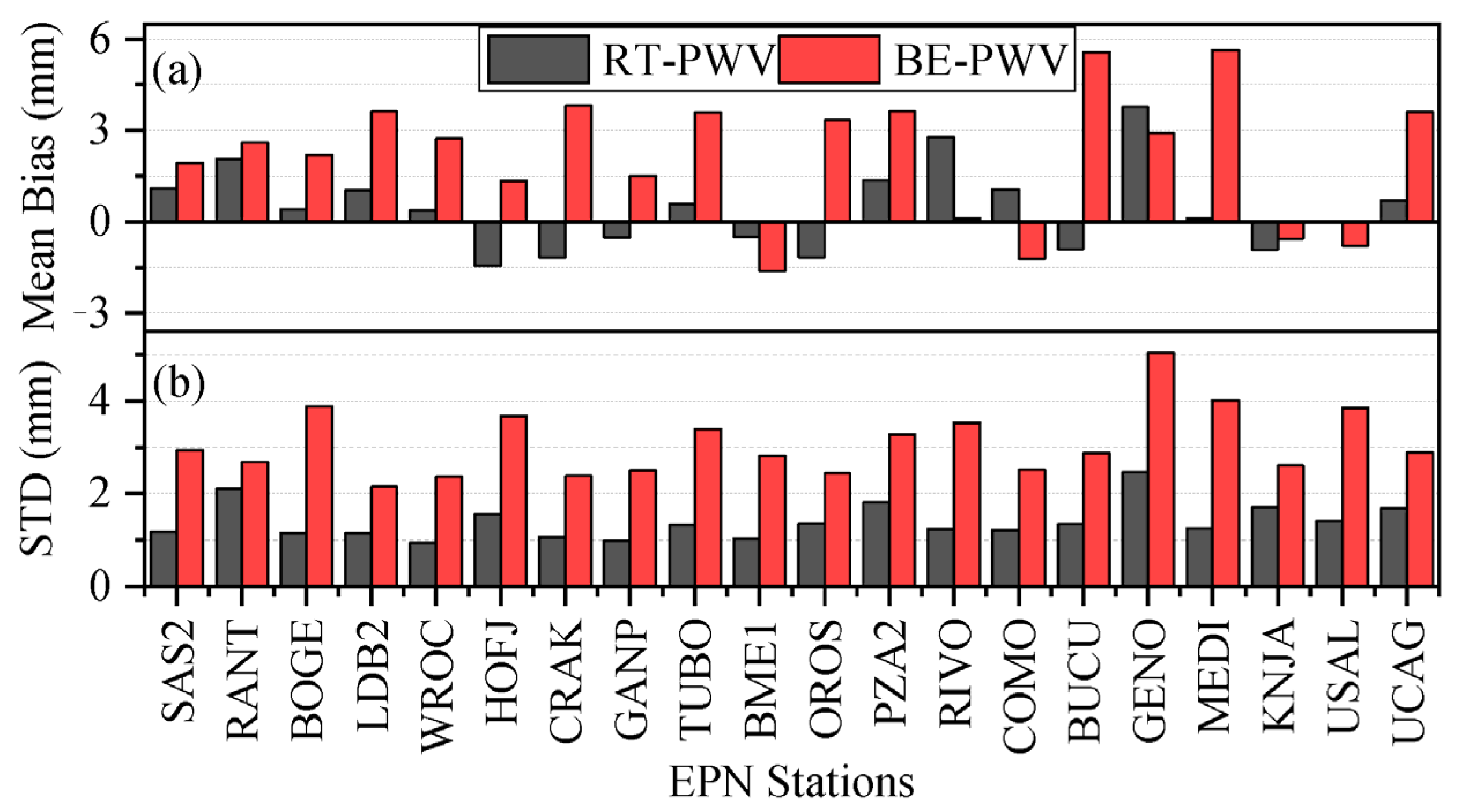
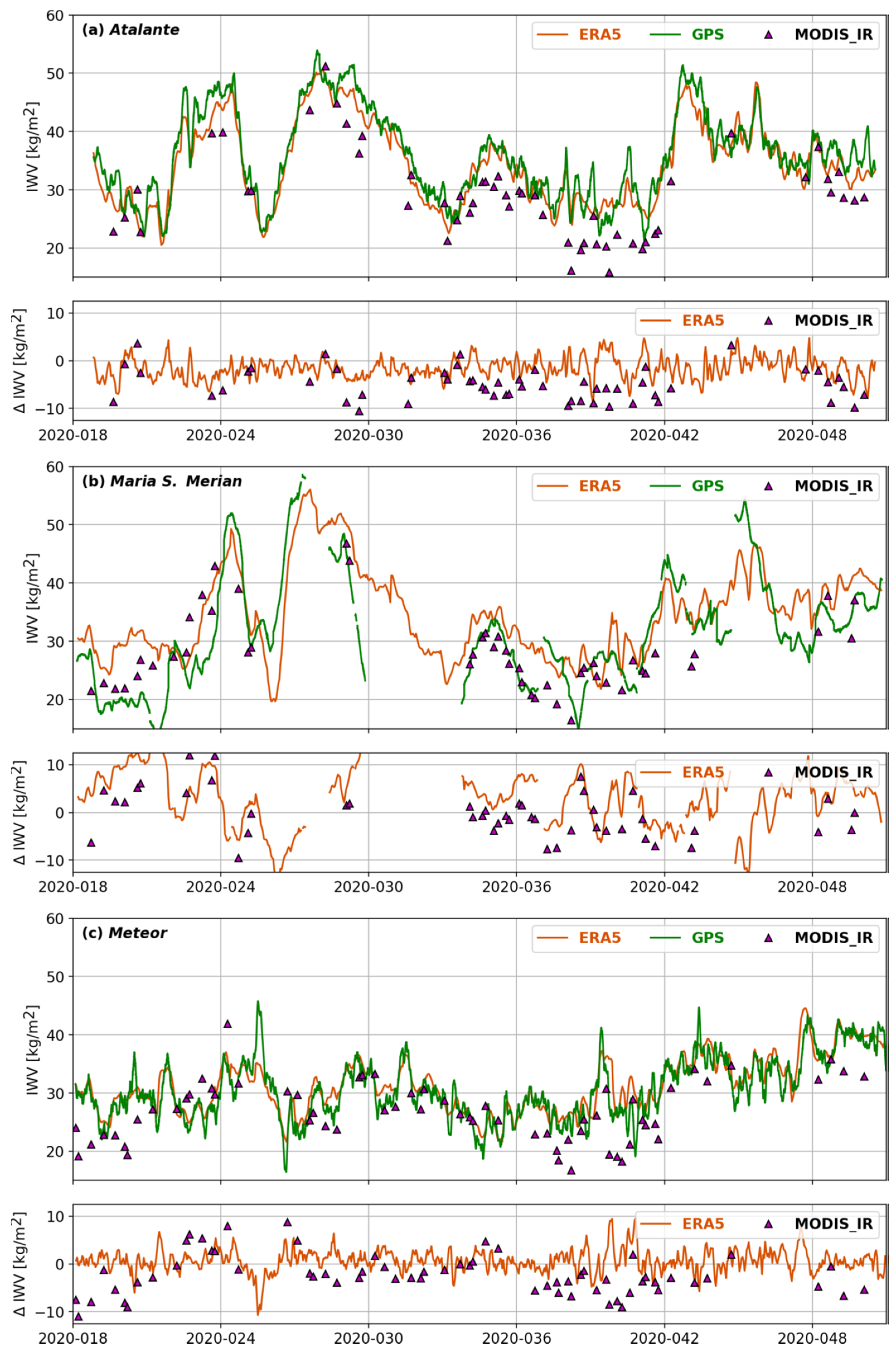
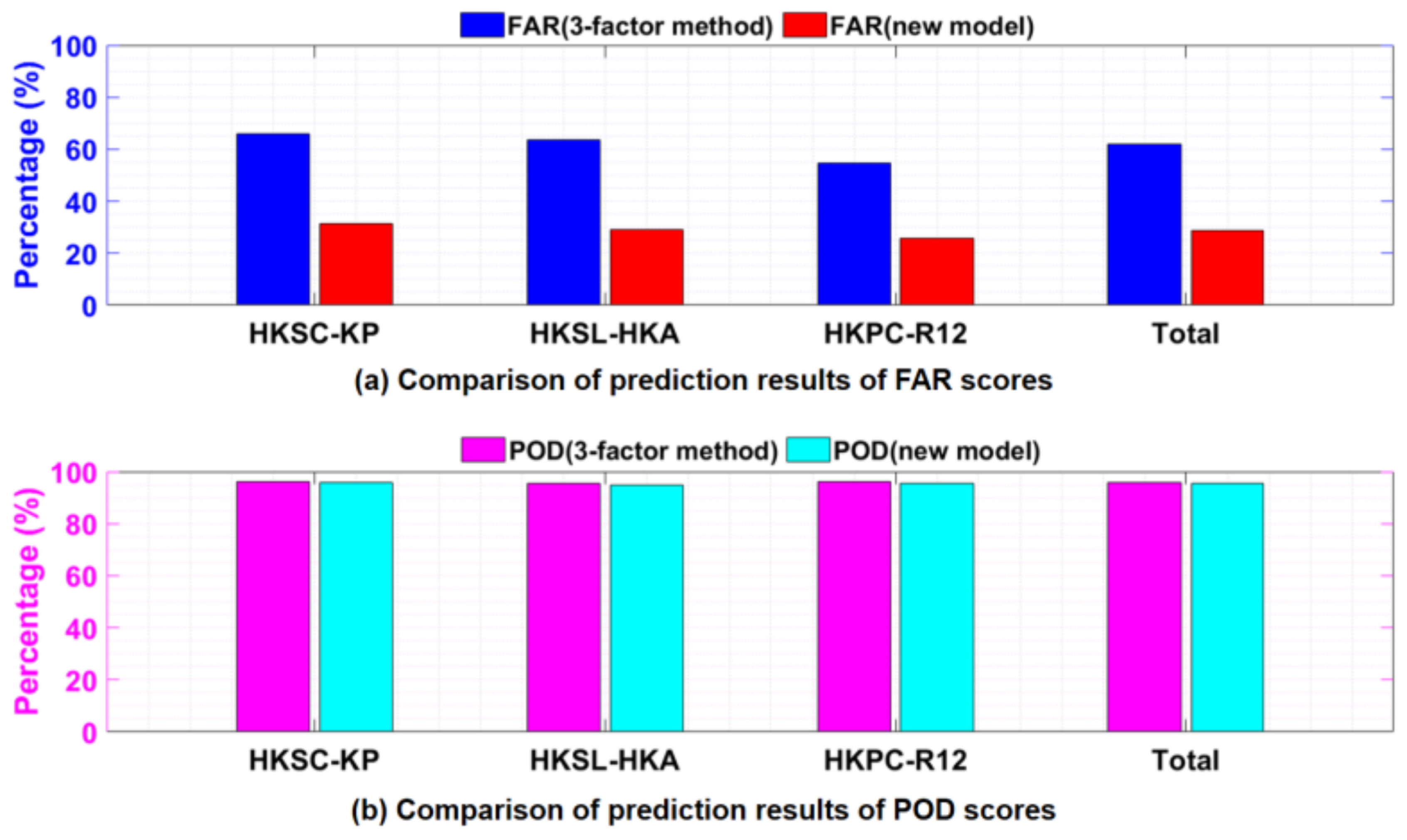

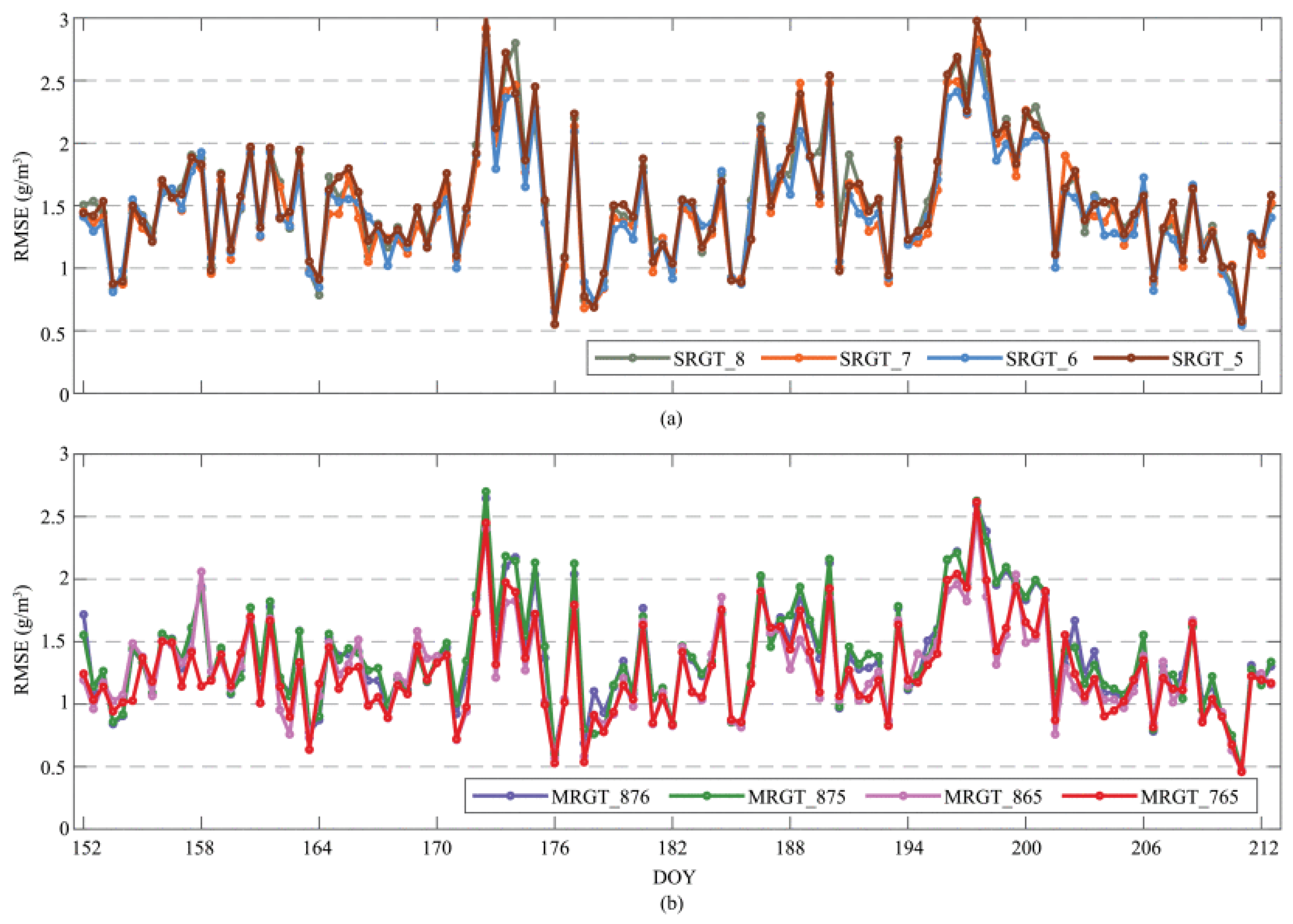


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maciejewska, A. Use of Tropospheric Delay in GNSS-Based Climate Monitoring—A Review. Remote Sens. 2025, 17, 1501. https://doi.org/10.3390/rs17091501
Maciejewska A. Use of Tropospheric Delay in GNSS-Based Climate Monitoring—A Review. Remote Sensing. 2025; 17(9):1501. https://doi.org/10.3390/rs17091501
Chicago/Turabian StyleMaciejewska, Aleksandra. 2025. "Use of Tropospheric Delay in GNSS-Based Climate Monitoring—A Review" Remote Sensing 17, no. 9: 1501. https://doi.org/10.3390/rs17091501
APA StyleMaciejewska, A. (2025). Use of Tropospheric Delay in GNSS-Based Climate Monitoring—A Review. Remote Sensing, 17(9), 1501. https://doi.org/10.3390/rs17091501





