Next Article in Journal
Rule-Based Multi-Task Deep Learning for Highly Efficient Rice Lodging Segmentation
Previous Article in Journal
Geographic Object-Oriented Analysis of UAV Multispectral Images for Tree Distribution Mapping in Mangroves
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 9
10.3390/rs17091504
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Optimizing Unmanned Aerial Vehicle LiDAR Data Collection in Cotton Through Flight Settings and Data Processing

by
Anish Bhattarai
1,
Gonzalo J. Scarpin
1,2,
Amrinder Jakhar
1,
Wesley Porter
3,
Lavesta C. Hand
3,
John L. Snider
3 and
Leonardo M. Bastos
1,*
1
Department of Crop and Soil Sciences, University of Georgia, Miller Plant Sciences Building, 120 Carlton Street, Athens, GA 30602, USA
2
Instituto Nacional de Tecnología Agropecuaria (INTA), Estación Experimental de Reconquista, Ruta Nacional N.° 11, km 773, Reconquista 3560, Santa Fe, Argentina
3
Department of Crop and Soil Sciences, University of Georgia, 2282 Rainwater Rd., Tifton, GA 31793, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(9), 1504; https://doi.org/10.3390/rs17091504
Submission received: 28 February 2025 / Revised: 14 April 2025 / Accepted: 18 April 2025 / Published: 24 April 2025
(This article belongs to the Special Issue Precision Agriculture and Crop Monitoring Based on Remote Sensing Methods)
Browse Figures
Versions Notes

Abstract

:
Light Detection and Ranging (LiDAR) technology can be used to assess canopy height in cotton (Gossypium hirsutum L.), but standardized data acquisition and processing guidelines are lacking. Accurate canopy height estimation is crucial in cotton for optimizing growth regulator application and maximizing yield. The main goal of this study was to determine the optimal unmanned aerial vehicle flight settings—altitude and speed—and assess specific processing parameters’ impact on data accuracy, processing time, and file size. Nine flight settings comprising three altitudes (12.2 m, 24.4 m, and 48.8 m) and three speeds (4.8 km/h, 9.6 km/h, and 14.4 km/h) were tested. LiDAR data were processed using DJI Terra software (v. 4.1.0), where two user-defined processing steps were examined: point-cloud thinning via grid size sub-sampling (0, 10, 20, 30, 40, and 50 cm) and slope classification (flat, gentle, and steep). The optimal flight altitude was 24.4 m, with no effect of flight speed. Grid sub-sampling up to 20 cm produced balanced accuracy, processing time, and file size. The choice of slope category had no significant effect on LiDAR-derived canopy height. These findings contribute to the development of standardized LiDAR data acquisition and processing guidelines for cotton to support crop management decision.

1. Introduction

Cotton (Gossypium hirsutum L.) is one of the most significant fiber crops globally. The U.S. produced around 14.4 million bales of cotton in the year 2023/24, ranking forth globally in cotton production after India, China, and Brazil [1]. Within the U.S., Texas (30%), Georgia (16%), and Arkansas (9%) are the largest cotton producing states, responsible for 55% of cotton lint production in the U.S. and 12% of world production [2].
Cotton is a perennial plant that is cultivated as an annual crop. This is achieved by using management techniques such as plant growth regulators, which help control growth rate and plant height, preventing the crop from expending too much energy on vegetative growth and directing it towards reproductive growth [3,4]. Balancing vegetative and reproductive sinks is important in cotton to optimize fiber yield and quality [5].
Different metrics exist to determine cotton growth rates and serve as a decision-making tools for deciding the timing and rate of synthetic plant growth regulator applications [6]. The most commonly used metrics are the height-to-node ratio (HNR) (ratio between plant height and total number of nodes) and length of the upper five internodes [7]. HNR values below growth-stage-specific thresholds indicate sub-optimal growth rates, whereas values above the threshold indicate excessive growth rates that need to be controlled using exogenously applied plant growth regulators like mepiquat chloride. For example, during the early bloom stage, if the HNR exceeds 6.4 cm/node, it is recommended to apply mepiquat chloride at a rate ranging from 0.5 to 2 L/ha at a standard concentration of 4.2% w/v [8]. The rate of application is determined based on multiple factors, including the cotton variety, the plant growth stage, the current rate of vegetative growth and weather conditions [8,9].
Traditionally, plant height is determined by visiting the field and collecting manual height measurements on plants across multiple areas in the field. This approach is time- and labor-intensive, and as cotton plants grow and form dense canopies, walking a field can potentially damage the crop. For large-scale commercial farming, such manual methods are impractical for achieving the required precision and speed in decision making. Additionally, capturing height variation accurately across large fields remains one of the biggest constraints, as it directly impacts yield estimation, canopy structure analysis, and variable rate input applications.
To overcome this issue, different technologies have been developed to create estimated continuous maps of plant height, including the unmanned aerial vehicle (UAV) imagery-based canopy height model (difference of the height at the top of the plant canopy and the elevation of the bare ground) [10,11]; tractor-mounted LiDAR (Light Detection and Ranging) [12]; and UAV-based LiDAR systems. The latter has emerged as a solution to bridge the gap between ground-based platforms, known for their high accuracy but low efficiency, and UAV imagery-based platforms, which offer extensive coverage but limited detail [13]. LiDAR directly measures crop height by emitting laser pulses, making it more accurate than UAV-mounted passive spectral imaging, which relies on ambient light and requires additional processing [14]. Height estimation from spectral data depends on photogrammetry techniques like structure-from-motion (SfM), which reconstructs 3D models based on overlapping images [15]. This approach requires ideal lighting, minimal occlusion, and accurate tie points, with additional steps to separate crop height from ground elevation. Errors in shadowed areas, vegetation movement, or point matching can reduce accuracy, making LiDAR the more reliable option for precise height measurements, especially in dense or complex canopies [16].
LiDAR application in row crops such as maize started around the mid-2010s, when it was used for evaluating crop structure [17] and predicting yield potential [18]. Studies on the use of UAV-mounted LiDAR to estimate plant height in cotton are scant [19]. This is a limitation especially because different flight settings like altitude and speed, and data processing steps like point cloud classification, grid size for height extraction and canopy modeling, can contribute to the accuracy of LiDAR-based height estimates, yet no studies exist that provide best-practice recommendations for the cotton crop.
For example, adjusting the point cloud density—the number of laser returns per square meter—is key [20] to generate accurate LiDAR-based height estimates. Achieving a high point cloud density enhances measurement accuracy but requires a UAV to fly at lower altitudes, slower speeds, or with greater overlap between flight paths, all of which extend flight time and increase the cost and complexity of data collection and data processing. A high point cloud density poses a challenge as it generates larger data files [21], which demand significant storage capacity and increase computing power requirements and/or processing times. Therefore, identifying flight characteristics and data processing steps that optimize crop height estimation accuracy while minimizing flight time and data storage and processing requirements is of utmost importance.
Another key processing step with LiDAR data is grid-based sub-sampling, where the raw LiDAR point cloud data are selectively thinned based on the highest-height point within each predefined grid cell [22]. By identifying a grid cell size that balances data retention and reduction, one can minimize file size, reduce computational requirements, and improve processing speed, all of which contribute to more efficient and cost-effective UAV-based LiDAR applications [20,23]. The decision on the size of the grid cell to be utilized at this step is left to the user, and no best-practice recommendations exist when using LiDAR in row crops in general, or cotton in specific.
Another important step when processing LiDAR data in DJI Terra (DJI, China), a LiDAR mapping and analysis software developed by DJI, is selecting the appropriate field slope type for the initial classification of point clouds. This choice helps the software distinguish between ground and non-ground points based on terrain variation. The classification process is influenced by the field slope characteristics, as variations in topography affect the differentiation between ground and non-ground points [24]. Like grid cell size selection, the decision on the slope choice is left to the user, and no best-practice recommendations exist.
The overall aim of this study was to establish best-practice guidelines for UAV LiDAR flight settings and data processing to ensure high-quality data acquisition for accurate cotton canopy height estimation. The first objective of this study was to determine and select the optimal UAV flight settings—altitude and speed—that provide the most accurate LiDAR-derived crop height estimates. Based on the best flight settings identified in the first objective, the second and third objectives focused on evaluating the impact of two user-dependent data processing steps on crop height estimation. Specifically, the second objective assessed how defining different grid cell sizes for sub-sampling point clouds affects crop height accuracy, processing time, and file size. The third objective examined the effect of selecting the field slope type on the accuracy of crop height estimation.

2. Materials and Methods

2.1. Experimental Site Description

This experiment was conducted in two different irrigated fields in Georgia, USA near Midville (32.875761, −82.222197) and Watkinsville (33.870858, −83.452716) for the year 2024. The field in Midville had a flat terrain predominately characterized by Tifton soil series and the Dothan soil series (fine-loamy, kaolinitic, thermic plinthic kandiudults), which are both deep, well-drained, and have a fine-loamy texture [25]. The field in Watkinsville has a somewhat flat terrain characterized by Cecil sandy loam soil with 2% to 6% slope [25]. Cotton was planted at a row spacing of 91 cm and seeding rate of 90,000 seeds/ha. The varieties planted were NexGen 3195 Bollgard® 3 XtendFlex® in Watkinsville and Dyna-Gro 3799 Bollgard® 3 XtendFlex® in Midville, and were selected according to local recommendations. Planting occurred on 26th of June in Midville and 2nd of July in Watkinsville.
Each trial was implemented as a nitrogen (N) fertilizer side-dress rate study, with N rate treatments of 0 + 0, 112 + 0, 40 + 26, 40 + 60, 40 + 94, and 40 + 128 kg/ha, denoted as preplant + side-dress application rates. The experiment followed a randomized complete block design with four blocks. In brief, all plots, except for the control (0 + 0) and the 112 + 0 treatment, received a baseline application of 40 kg N/ha at planting, applied using a tractor-mounted boom sprayer. The fertilizer source for the application was urea ammonium nitrate (UAN) 28% N, which is a liquid fertilizer. At the blooming crop stage (approximately 49–52 days after planting), side-dress N fertilizer treatments were applied with a variable rate applicator. For this manuscript, the treatment design of N rates was utilized only to generate variability in crop height, and therefore further statistical analysis did not incorporate N rate as an explanatory variable.

2.2. Aerial LiDAR Data Collection and Pre-Processing

The workflow for data acquisition, pre-processing, and analysis consisted of four main steps: (i) field characterization, (ii) data acquisition with different flight settings, (iii) data processing, and (iv) validation (Figure 1). Field characterization in relation to slope is an important initial step used to define processing settings in the DJI Terra (DJI, Shenzen, China) v. 4.1.0 software. DJI Terra provides the user with the option of identifying the field as flat (1–4 degrees slope), gentle (4–7 degrees slope), or steep (8–12 degrees slope) as one of the first steps in the processing pipeline. To conduct field characterization in our study, elevation data were retrieved for each field from the Google Earth Engine data catalogue of USGS 3 DEP 1 m National Map using the geemap library [26] in Python 3.9. Then, the elevation raster was imported into R software v. 2024.12.0 (R development team, 2024), where the terra package [27] v. 1.8-42 was used to calculate the slope of the field. The field was then classified into one of flat (1–4 degrees), gentle (4–7 degrees), or steep (8–12 degrees) slope to match the options provided by DJI Terra.
Data acquisition was conducted on August 10th in Midville (76 days after planting) and August 27th in Watkinsville (86 days after planting) in 2024. Cotton typically reaches its first flower at 50–60 days after planting, with peak bloom occurring 20–30 days later [28]. This period is critical for assessing management practices like plant growth regulator (PGR) application, making accurate crop height data essential for informed decision making. First, 10 plants from each of 28 plots had their height measured manually using a measuring tape, for a total of 280 plants measured in each field. On the same day, a DJI Matrice 350 (DJI, Shenzhen, China) UAV mounted with a Zenmuse L2 (DJI, Shenzhen, China) LiDAR sensor was used to collect the sensor data from the field from each combination of three different flight altitudes (12.2, 24.4, 48.8 m) and three different flight speeds (4.8, 9.6, 14.4 km/h), resulting in a total of nine unique flight settings per location. Each combination of flight altitude and speed was flown once per location, totaling 18 flights across the two locations. Flight altitudes of 12.2, 24.4, and 48.8 m and speeds of 4.8, 9.6, and 14.4 kmph were selected to balance data quality and operational efficiency in UAV LiDAR surveys. Lower altitudes (12.2 m) increase point density and detail, ideal for precise canopy measurements, while higher altitudes (48.8 m) enable faster, broader coverage with an acceptable resolution for field-scale assessment [29,30,31]. Similarly, slower speeds (4.8 kmph) improve point cloud density and accuracy by allowing for more LiDAR pulses per unit area, whereas faster speeds (14.4 kmph) prioritize survey efficiency at the cost of reduced detail [32]. For speed selection, 4.8 km/h was the default setting in the DJI flight planner application. To assess its impact on data acquisition and quality, additional speeds were chosen at double (9.6 km/h) and triple (14.4 km/h) the default value. Higher speeds were chosen to allow for a comparative analysis of speed’s influence on data accuracy and efficiency.
The Zenmuse L2 integrates the Livox LiDAR module, a high-precision inertial moment unit (IMU), a mapping camera, and three-axis gimbals. The IMU includes a three-axis accelerometer, a three-axis angular velocity and a barometric altimeter, which is used to measure attitude. All the flights were conducted at a frontal overlap of 80% and side overlap of 10%. The scanner pulse repetition rate was set at 240 kHz, and the scanner angle to 90 degrees. The UAV was connected with a D-RTK 2 high precision GNSS mobile station (DJI, Shenzhen, China) that supports four global satellite navigation systems, BeiDou, GPS, Galileo, GLONASS, and 11-frequency satellite reception, providing real-time differential corrections to facilitate the aircraft in centimeter-level precision positioning and help to get the precise geolocation of each of the cloud points from the LiDAR.
Data were processed on a desktop computer with AMD Ryzen Threadripper PRO 5975WX 32, core 3.6 GHz processor, 128 GB RAM. The movements of the UAV were corrected using the DJI Terra software (DJI, Shenzhen, China) which combines the GNSS correction, and the movement data recorded by the IMU, with a manufacture-reported precision of ~4 cm for all flights. Data processing involved the steps of point cloud classification, DTM generation, normalization, DSM generation, canopy modeling, rasterization, and metric extraction using different software.
To produce a geo-referenced point cloud, the flight path and raw point cloud data were combined in DJI Terra software (DJI, Shenzhen, China). After uploading the data into the software, the user can initiate the subsampling method using a grid-based approach to systematically reduce point cloud density. This method involved partitioning the area into predefined grid sizes (00 cm or no sub-sampling, 10 cm, 20 cm, 30 cm, 40 cm, and 50 cm) and retaining only the highest point within each grid cell. The point clouds were also classified in the software as ground and non-ground points using a field slope-based approach. Previous studies have employed algorithms such as the cloth simulation filter [33] and progressive morphological filter [34], as well as software platforms including CloudCompare 2.10 [32] and ArcGIS 10.4.1 (ESRI, Redlands, CA, USA) [35] to perform this task. In this study, point cloud ground classification was conducted using DJI Terra software as it has been specifically developed by DJI to ensure seamless integration with their hardware systems, such as the Zenmuse L2 LiDAR sensor. In DJI Terra, at this stage, the user is required to select the field slope classification. For the fields in this study, the correct classification was “flat” based on open-source elevation data obtained pre-flight at the field characterization step. Because an improper selection of field slope can potentially impact the quality of the processed data, the impact of the slope type parameter selected during ground point classification in DJI Terra was evaluated by processing the LiDAR data using all the available slope settings: ‘Flat’, ‘Gentle’, and ‘Steep’. These settings represent varying terrain slope conditions and influence how the software identifies and classifies ground points within the LiDAR dataset. The final co-registered and geo-referenced point cloud datasets were stored in LAS format (Figure 1).
The LAS file exported from DJI Terra was then further processed in R using the lidR package [36] v. 2.0.0 in five sub-steps: (i) digital terrain model generation; (ii) height normalization, (iii) noise filtering, (iv) digital surface model generation, and (v) canopy height model generation. The first sub-step in processing the LiDAR data in R involved creating a DTM from the LAS file obtained from DJI Terra. This was achieved using the triangular irregular network (TIN) [37] method, which leverages ground point data to model the DTM. TIN was selected as the triangulation method due to being straightforward and computationally efficient, as it does not require complex adjustments or additional parameters compared to other methods [24].
The second sub-step in processing was the height normalization which was performed based on the DTM generated on the previous sub-step. In this process, the terrain height values in the DTM were set as a baseline (considered zero). Also, any points that were within 6 cm height from the ground were considered as ground so to smooth out small bumps on the field, and the remaining points above this threshold were regarded as representing heights above the terrain, effectively isolating the plant heights. A similar approach was adopted by other studies [38,39], where a ground offset of 5 to 10 cm was applied to account for ground surface roughness. The third sub-step in processing was noise filtering which was implemented to improve data quality by flagging and filtering out noisy points in the point cloud. A noisy point was considered as any point that fell below the DTM (indicating negative heights). This filtering step ensured that only relevant data points were retained for accurate canopy height measurements.
The fourth sub-step in processing was to generate a digital surface model (DSM) using a TIN and incorporating all points from the LiDAR point cloud, including those at higher elevations such as crop canopies, trees, or structures. Unlike a DTM, which uses only the lowest points to represent the bare ground, a DSM captures the highest elevation at each location. The TIN for a DSM is formed by connecting these points into an irregular mesh, creating a 3D representation of the entire surface, including all objects above the ground. Finally, the fifth sub-step in processing was to generate the canopy height model (CHM) which was calculated by subtracting the DSM and the DTM which is a commonly used method for canopy height estimation [34,40]. The CHM represents the canopy height, providing a measure of plant height above ground level. The resulting CHM was then rasterized to facilitate further spatial analysis.
To match the CHM with the manual measurements of plant height, the rasterized CHM was intersected with the bounding boxes around 10 marked plants per plot. The mean height for these 10 plants was calculated for both LiDAR and manual measurements. These averages were then compared using regression analysis.

2.3. Data Analysis and Validation

To assess the impact of flight altitude and speed, data from both locations were analyzed together to account for the potential site-specific variations as our objective was to determine the optimal flight setting for quality data retrieval. A regression model was used to examine the relationship between LiDAR-derived height and manual height measurements, with location incorporated as a random effect. However, for evaluating the optimal grid sub-sampling method, the data from each location were analyzed separately. This separate analysis was necessary because the two locations differed in field size, which directly influenced the amount of LiDAR data collected and the overall processing time. To assess grid sub-sampling performance, three metrics were evaluated: (i) file size (smaller file sizes improve storage efficiency), (ii) processing time (faster processing reduces computational burden), and (iii) height prediction quality (to ensure the subsampled data retained sufficient accuracy). To evaluate height prediction quality, a regression analysis comparing the LiDAR-derived heights obtained through different grid sub-sampling methods against manually measured height was conducted. The coefficient of determination (R2, higher is better), root mean square error (RMSE, lower is better), and mean absolute error (MAE, lower is better) were used as the evaluation metrics. Furthermore, the intercept and slope of the equation were tested using the linearHypothesis function from the car package [41] v. 3.1.3 for significant differences from 0 and 1, respectively, with a significance level of 0.05.
Moreover, to evaluate the effect of the slope choice (flat, gentle and steep) for point cloud classification in DJI Terra software to derive the LiDAR height, the difference between manual and LiDAR-derived height was explained as a function of slope type, location, and their interaction as fixed effects, while the block nested within location was treated as random effect. Similarly, to further extend our understanding of the slope choice for point cloud classification the data from both locations were analyzed together. A regression model was used to examine the relationship between LiDAR-derived height and manual height measurements, with location incorporated as a random effect to account for variability between sites.

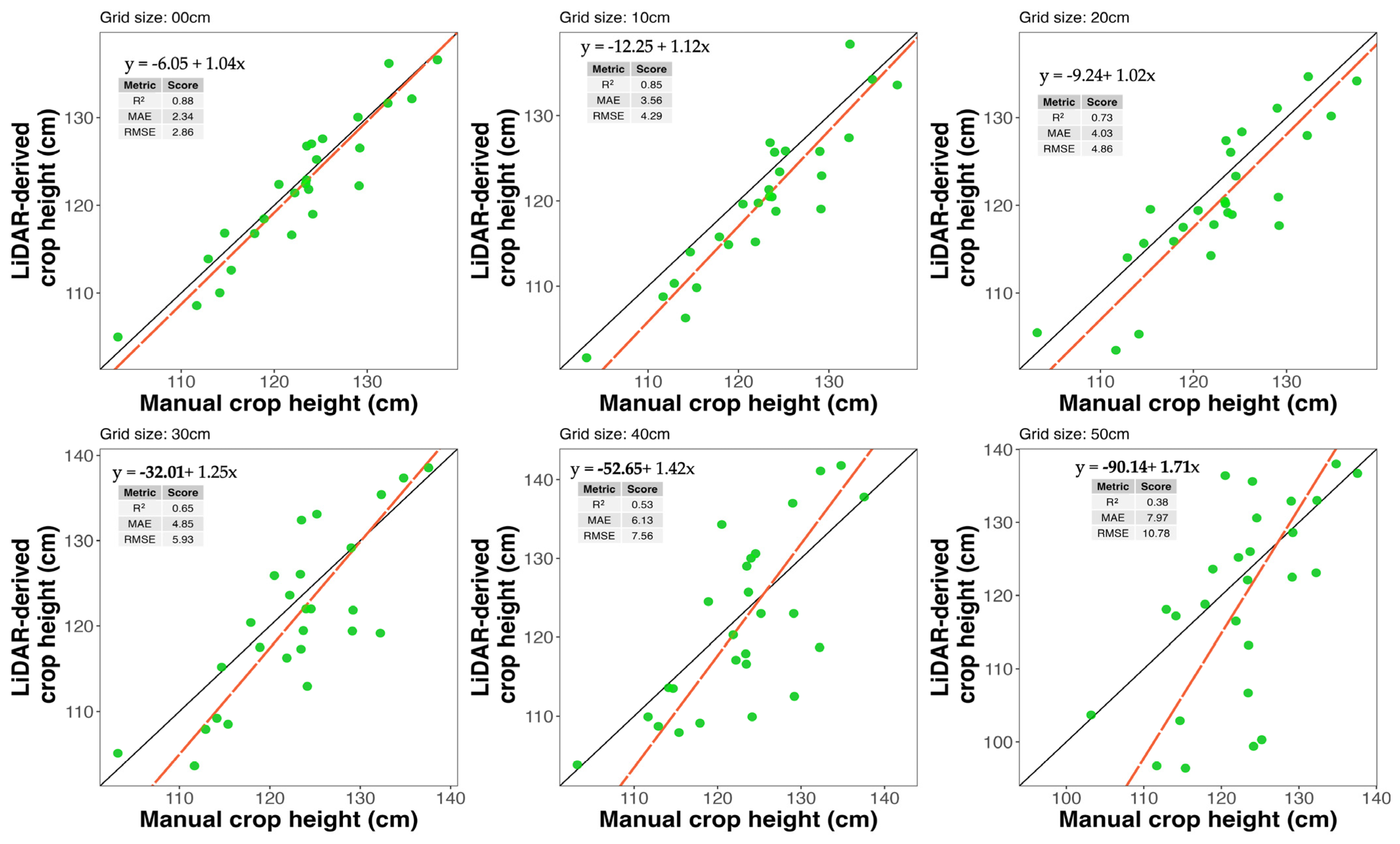
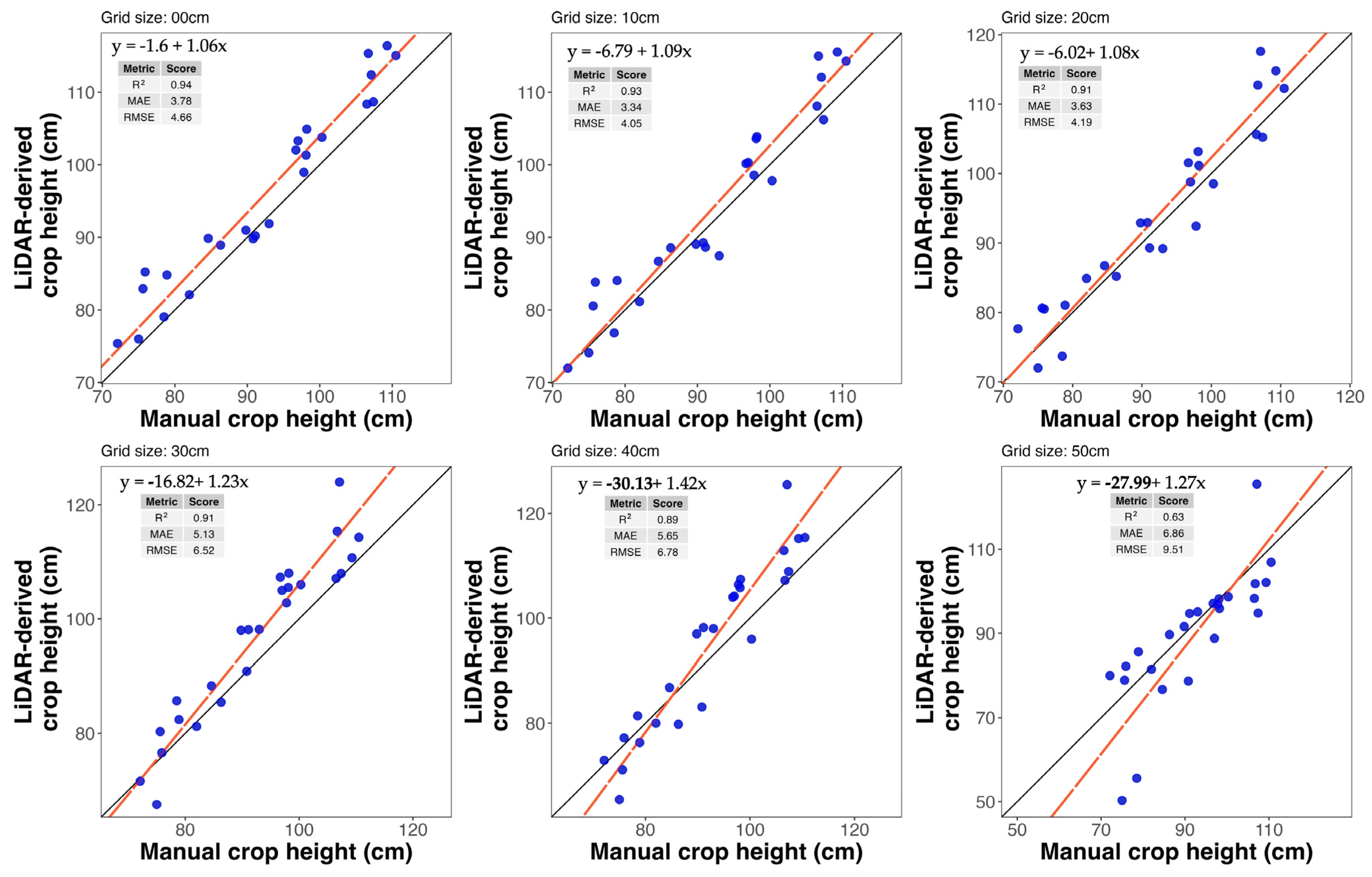
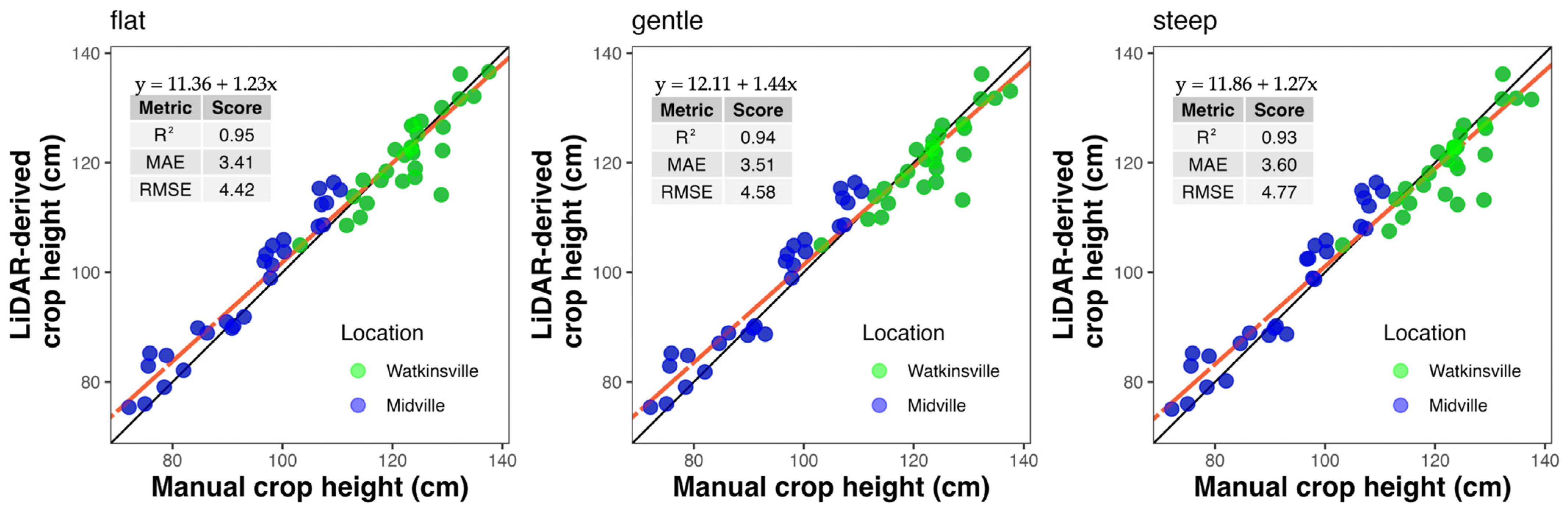
3. Results

The relationship between manual height measurements and LiDAR-derived height measurements for each combination of flight altitude and speed was analyzed combining the data from both locations (Figure 2). Among the tested settings, the UAV flight at a speed of 14.5 km/h and an altitude of 24.4 m had the best performance, achieving the highest R2 value (0.97) and the lowest RMSE (3.65 cm) and MAE (3.09 cm). At higher altitudes (48.8 m), the accuracy decreased significantly as evidenced by slightly lower R2 values (0.86–0.87), and increased RMSE (10.18–11.71 cm) and MAE (8.87–9.62 cm) values, indicating a weaker correlation between manual and LiDAR-derived height. In contrast, at the moderate altitude of 24.4 m, increasing speed improved accuracy, with the highest R2 (0.97) and the lowest RMSE (3.65 cm) and MAE (3.09 cm) achieved at 14.5 km/h. However, at higher altitudes, faster speeds lead to reduced accuracy evidenced by increased RMSE. Overall, optimal accuracy is achieved at moderate altitudes (24.4 m) with higher flight speeds, while higher altitude compromised measurement precision, particularly at faster speeds. The intercept and slope were significantly different from 0 and 1, respectively, only for the highest flight altitude (48.8 m) at all three speed settings (Figure 2).
Using the results above, data from the UAV flight setting that optimized plant height prediction (i.e., flight altitude of 28.8 m and flight speed of 14.4 km/h) were selected and used in the downstream analysis of sub-sampling grid size for each location separately. For Watkinsville, as the grid sub-sampling size increased from 0 cm to 50 cm, there was a significant reduction in processing time and file size, demonstrating that larger grid sub-sampling improves computational efficiency and reduces storage requirements (Table 1). Point cloud density decreased drastically by 99.6%, from 5834 points/m2 at 0 cm to just 21 points/m2 at 50 cm. Total processing time followed a similar trend, reduced by 55.8% from 206 s at 0 cm to 91 s at 50 cm. File size decreased significantly, declining by 99.5% from 812 MB at 0 cm to just 4 MB at 50 cm (Table 1).
An increase in sub-sampling grid size and concurrent decreases in processing time and file size concur in lower quality of LiDAR data by reducing the point cloud density (Table 1). In Watkinsville, the greatest agreement between manual height and LiDAR-derived height was obtained at no sub-sampling (i.e., sub-sampling grid size of 0 cm, R2 = 0.88, RMSE = 2.86, MAE = 2.34 cm), with a 10 cm sub-sampling grid size producing acceptable agreement (R2 = 0.85, RMSE = 4.29 cm, MAE = 3.56 cm, Figure 3). With the coarsest sub-sampling grid size, fit metrics were significantly compromised (R2 = 0.38, RMSE = 10.78 cm, MAE = 7.97 cm). Both the intercept and slope were significantly different from 0 and 1, respectively, for the coarsest sub-sampling grid size (50 cm). Only the intercept showed a significant difference from 0 for the 30 cm and 40 cm sub-sampling grid sizes. In contrast, neither the intercept nor the slope differed significantly from 0 and 1, respectively, for grid sizes smaller than 30 cm (Figure 3).
For Midville, as the grid sub-sampling size increased from 0 cm to 50 cm, there was a significant decline in all parameters, demonstrating the efficiency of larger grid sub-sampling (Table 2). As grid sub-sampling size increased from 0 cm to 50 cm, point cloud density decreased significantly, dropping by approximately 99.7% from 2637 points/m2 to 9 points/m2. Similarly, total processing time reduced by 57.4% from 183 s to 78 s, with benchmarking time in DJI Terra and R showing reductions of 47.2% and 80.4%, respectively. Additionally, file size decreased 99.6% from 718 MB to just 3 MB (Table 2).
In Midville, the greatest agreement between manual height and LiDAR-derived height was obtained at no sub-sampling (i.e., sub-sampling grid size of 0 cm, R2 = 0.94, RMSE = 4.66 cm, MAE = 3.78 cm), with an up to 20 cm sub-sampling grid size still producing acceptable agreement (R2 = 0.91, RMSE = 4.19 cm, Figure 4). With the coarsest sub-sampling grid size, fit metrics were significantly compromised (R2 = 0.63, RMSE = 9.51 cm, MAE = 6.86 cm). Only the intercept showed a significant difference from 0 for coarsest and 40 cm sub-sampling grid sizes. In contrast, neither the intercept nor the slope differed significantly from 0 and 1, respectively, for grid sizes smaller than 40 cm (Figure 4).
Slope choice during the processing of the point clouds had no significant effect on the mean difference between manual and LiDAR-derived heights across two locations. The mean difference between manual and LiDAR-derived heights were −1.1 cm, −0.57 cm, and −0.24 cm for flat, gentle, and steep, respectively.
Similarly, the tested slope choices (flat, gentle and steep) in DJI Terra software for point cloud classification showed similar performance across both locations when compared to manually measured heights, as reflected by comparable R2 (0.93–0.95), RMSE (4.42–4.77 cm) and MAE (3.41–3.6 cm, Figure 5). The intercept and slope were not significantly different from 0 and 1, respectively, for any of the three slope choices (Figure 5).

4. Discussion

In this study, the effect of UAV flight parameters and data processing steps on cotton plant height estimation accuracy was investigated. This research establishes a framework for developing optimized flight plans and data processing protocols aimed at improving the accuracy, efficiency, and scalability of LiDAR-derived information. This work is unique and fills an important methodological gap in using UAV LiDAR for row crop height estimation. In specific, this research can serve as a foundational framework for selecting flight settings during the peak bloom stage of cotton that balance data quality with practical considerations, such as minimizing processing time and maintaining manageable file sizes. Additionally, it holds particular significance for cotton, where management practices like PGR application rely on accurate plant height measurements to optimize production [42]. Various studies have found that the application of PGR produced more flowers [4], reduced the spatial yield variability within a field [43], controlled excessive vegetative growth [44,45], and, in some cases, increased cotton yield [46,47,48]. Additionally, the application of PGR has been shown to enhance cotton fiber quality by promoting earlier maturation of the cotton plant. In this context, [49] reported that delayed harvesting negatively affects the cotton fiber quality. Moreover, UAV-based LiDAR data can support variable rate application of PGR which has shown to reduce the PGR application rates ranging from 10 to 53% and PGR cost by 17% when compared to fixed-rate applications [50].
In this study, a UAV-mounted LiDAR sensor at different flight settings was tested as it often provides better height estimation compared to multispectral imagery or SfM technology. A study on wheat [51] reported that the multispectral imagery under-estimated the height and was less accurate compared to the LiDAR estimated height. Similarly, several studies reported that the correlation between digitally derived canopy height and ground measurements was found to range from 0.5 to 0.87 [52,53], which is low compared to the correlation obtained from LiDAR, ranging from 0.8 to 0.97 [12,54].
Our results showed that varying UAV flight speed had a minimal impact on the accuracy of plant height assessment compared to changes in flight altitude. This aligns with previous studies that have highlighted the significant influence of altitude on point cloud density and the subsequent accuracy of vegetation structure measurements [21,30]. Lower flight altitudes generally produce denser point clouds, which enhance measurement precision but may introduce more noise due to increased overlap and redundant data capture. Studies like [55] on forest canopy and [54] maize and soybean suggested that it is not necessary to have high LiDAR point cloud density to achieve the desired estimation precision of vegetation parameters. Conversely, higher altitudes result in sparser point clouds, potentially reducing measurement accuracy [31,33,56]. A study conducted in maize and soybeans [54] found that when a UAV-mounted LiDAR was flown at the height of 150 m above ground level, a weak correlation of R2 (0.64 and 0.4, respectively, for each crop) was found. For instance, [57] demonstrated that a flight altitude of 85 m provided more accurate tree height estimations compared to 145 m, while ensuring sufficient coverage and sensor safety in complex terrains. These findings suggest that lower flight altitudes improve height estimation accuracy, likely due to higher point cloud density. However, there is a difference in LiDAR application between tree canopies and row crops such as cotton, stemming from their distinct structural characteristics. Unlike trees, which have loose and varied canopies, cotton canopies have dense, uniform foliage that heavily obscures the ground. This dense foliage complicates the accurate estimation of DTM, as also noted by [53,58,59]. In our study, lower flight altitudes were more effective in capturing detailed ground information under dense cotton canopies, demonstrating the importance of tailoring flight parameters to the specific structural characteristics of the vegetation being analyzed. [12] reported that a LiDAR sensor mounted on a tractor achieved a root mean square error (RMSE) of 6.5 cm in field-based cotton height measurements. In comparison, our study demonstrated that under optimal UAV flight settings, an RMSE of 3.65 cm could be achieved, indicating a higher level of accuracy. Furthermore, while both approaches provide valuable canopy height estimations, UAV-based LiDAR offers a significantly more efficient and rapid data acquisition method.
Our study further demonstrated the value of optimizing data processing techniques for LiDAR datasets. For instance, sub-sampling the point cloud to a grid size of up to 20 cm (86–90% reduction in point cloud density from the original data) maintained sufficient accuracy for height measurements while significantly reduced file size. This aligns with recent advancements in point cloud processing, such as shape-aware down-sampling techniques, which have been shown to preserve structural integrity while eliminating unnecessary data points, thereby improving the overall quality of the dataset [60]. Furthermore, reducing the point cloud density by 25% still resulted in accurate LiDAR-derived crop height estimations, maintaining an R2 of 0.96 with the actual measured crop height [61]. Also, reducing the point cloud density to approximately 7.32 points/m2 maintained a strong correlation between LiDAR-derived and manually measured canopy heights, with R2 values ranging from 0.65 to 0.75. However, when the point cloud density was further reduced to 0.074 points/m2, the accuracy declined significantly, with R2 dropping to 0.3 [30]. This suggests that while some level of point cloud thinning is feasible without substantial accuracy loss, excessive reduction in point density compromises the reliability of canopy height estimations. The reduction in point cloud density also translated to smaller file sizes and shorter processing times, enhancing the practicality of working with LiDAR datasets in resource-limited environments. Larger file sizes tend to slow down analysis and increase computational overhead, which can be a significant bottleneck for large-scale studies.
Our study revealed that varying slope parameters during the classification of LiDAR point clouds into ground and non-ground points had no significant effect on the classification accuracy. This finding suggests that the underlying algorithms utilized by DJI Terra are robust and effectively handled variations in user-defined slope settings during the data processing workflow.

5. Conclusions

This study provided key recommendations for UAV LiDAR flight settings and data processing steps for cotton height estimation and serves as an initial step for new users of this technology. UAV flight speed had no significant effect on the accuracy of LiDAR data acquisition, whereas flight altitude significantly influenced data quality. As flight altitude increased, point cloud density decreased, which led to a gradual loss of structural integrity in the captured vegetation data, thereby affecting the accuracy of canopy height estimation. For any optimal flight height, to address challenges associated with longer data processing times and larger file sizes, sub-sampling the point cloud up to 20 cm grid size provided an effective balance between data reduction and information retention. Additionally, our findings indicate that the slope choices during point cloud classification did not affect the accuracy of LiDAR-derived measurements, further highlighting the effectiveness of DJI Terra’s automated classification algorithm in ensuring reliable data outputs.
Although this work represents an important step in proposing recommendations for UAV-based LiDAR use in cotton, some limitations and gaps remain. The major limitation of this research was its focus on a single crop, cotton, which restricts the generalizability of findings to other crops with different canopy structures and growth patterns. Also, this study focused on a single growth stage when the canopy was fully developed and provided maximum coverage. While these results are highly relevant for critical cotton growth stages such as flowering and boll development—key periods for evaluating plant height for management practices—they may not be as applicable to the early growth stages when canopy cover is minimal. Early-stage flights would likely exhibit different LiDAR responses, including greater ground visibility and less point cloud interference from overlapping leaves. Moreover, other influential flight factors such as flight overlap, scan angles, and UAV trajectory planning were not addressed. Flight overlaps and scan angles, for example, play a critical role in ensuring data completeness and accuracy, particularly in terrains or fields with uneven surfaces [62].
Future studies should include UAV flights on various crops with differing canopy structures, such as maize, wheat, and soybean. Additionally, flights at different growth stages should be further tested to improve generalizability across the growing season. Research on varying flight overlap, scan angles, and UAV trajectories could further elucidate other aspects of flight settings to optimize data collection for different crops and field conditions, and merit attention in future studies.

Author Contributions

Conceptualization, A.B. and L.M.B.; Methodology, A.B. and L.M.B.; Software, A.B.; Validation, A.B.; Formal analysis, A.B.; Investigation, A.B. and L.M.B.; Resources, L.M.B.; Data curation, A.B.; Writing—original draft, A.B. and J.L.S.; Writing—review & editing, G.J.S., A.J., W.P., L.C.H. and L.M.B.; Visualization, A.B.; Supervision, L.M.B.; Project administration, L.M.B.; Funding acquisition, L.M.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the Institute of Integrative Precision Agriculture at the University of Georgia, and Deere & Company.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Meyer, L. Cotton and Wool Outlook: October 2024. 2024. Available online: https://ers.usda.gov/sites/default/files/_laserfiche/outlooks/110207/CWS-24j.pdf?v=42812 (accessed on 20 February 2025).
  2. USDA. Cotton Explorer International Production Assessment Division, United States Department of Agriculture. 2024. Available online: https://ipad.fas.usda.gov/cropexplorer/cropview/commodityView.aspx?cropid=2631000 (accessed on 18 February 2025).
  3. Cothren, J.T.; Oosterhuis, D.M. Use of Growth Regulators in Cotton Production. In Physiology of Cotton; Stewart, J.M., Oosterhuis, D.M., Heitholt, J.J., Mauney, J.R., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 289–303. [Google Scholar] [CrossRef]
  4. Pettigrew, W.T. Effects of Different Seeding Rates and Plant Growth Regulators on Early-planted Cotton. J. Cotton Sci. 2005, 9, 189–198. [Google Scholar]
  5. Bradow, J.M.; Davidonis, G.H. Quantitation of Fiber Quality and the Cotton Production-Processing Interface: A Physiologist’s Perspective. J. Cotton Sci. 2000, 4, 34–64. [Google Scholar]
  6. Oosterhuis, D.M. Growth and Development of a Cotton Plant. In Nitrogen Nutrition of Cotton: Practical Issues; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1990; pp. 1–24. [Google Scholar] [CrossRef]
  7. Kerby, T.A.; Plant, R.E.; Horrocks, R.D. Height-to-Node Ratio as an Index of Early Season Cotton Growth. J. Prod. Agric. 1997, 10, 80–83. [Google Scholar] [CrossRef]
  8. Hand, L.C.; Snider, J.; Roberts, P. Cotton Growth Monitoring and PGR Management; Circular 1244; University of Georgia: Athens, GA, USA, 2022. [Google Scholar]
  9. Byrd, S. Plant Growth Regulators in Cotton; PSS-2189; Oklahoma Cooperative Extensive Service: Oklahoma City, OK, USA, 2019. [Google Scholar]
  10. Kawamura, K.; Asai, H.; Yasuda, T.; Khanthavong, P.; Soisouvanh, P.; Phongchanmixay, S. Field phenotyping of plant height in an upland rice field in Laos using low-cost small unmanned aerial vehicles (UAVs). Plant Prod. Sci. 2020, 23, 452–465. [Google Scholar] [CrossRef]
  11. Lu, W.; Okayama, T.; Komatsuzaki, M. Rice Height Monitoring between Different Estimation Models Using UAV Photogrammetry and Multispectral Technology. Remote Sens. 2022, 14, 78. [Google Scholar] [CrossRef]
  12. Sun, S.; Li, C.; Paterson, A.H.; Jiang, Y.; Xu, R.; Robertson, J.S.; Snider, J.L.; Chee, P.W. In-field High Throughput Phenotyping and Cotton Plant Growth Analysis Using LiDAR. Front. Plant Sci. 2018, 9, 16. [Google Scholar] [CrossRef] [PubMed]
  13. Watanabe, K.; Guo, W.; Arai, K.; Takanashi, H.; Kajiya-Kanegae, H.; Kobayashi, M.; Yano, K.; Tokunaga, T.; Fujiwara, T.; Tsutsumi, N.; et al. High-Throughput Phenotyping of Sorghum Plant Height Using an Unmanned Aerial Vehicle and Its Application to Genomic Prediction Modeling. Front. Plant Sci. 2017, 8, 421. [Google Scholar] [CrossRef]
  14. Amann, M.-C.; Bosch, T.M.; Lescure, M.; Myllylae, R.A.; Rioux, M. Laser ranging: A critical review of unusual techniques for distance measurement. Opt. Eng. 2001, 40, 10–19. [Google Scholar] [CrossRef]
  15. Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
  16. Tao, W.; Lei, Y.; Mooney, P. Dense point cloud extraction from UAV captured images in forest area. In Proceedings of the 2011 IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services, Fuzhou, China, 29 June–1 July 2011; pp. 389–392. [Google Scholar] [CrossRef]
  17. Garrido, M.; Paraforos, D.S.; Reiser, D.; Vázquez Arellano, M.; Griepentrog, H.W.; Valero, C. 3D Maize Plant Reconstruction Based on Georeferenced Overlapping LiDAR Point Clouds. Remote Sens. 2015, 7, 17077–17096. [Google Scholar] [CrossRef]
  18. Anderson, S.L.; Murray, S.C.; Malambo, L.; Ratcliff, C.; Popescu, S.; Cope, D.; Chang, A.; Jung, J.; Thomasson, J.A. Prediction of Maize Grain Yield before Maturity Using Improved Temporal Height Estimates of Unmanned Aerial Systems. Plant Phenome J. 2019, 2, 190004. [Google Scholar] [CrossRef]
  19. Xu, W.; Yang, W.; Wu, J.; Chen, P.; Lan, Y.; Zhang, L. Canopy Laser Interception Compensation Mechanism—UAV LiDAR Precise Monitoring Method for Cotton Height. Agronomy 2023, 13, 2584. [Google Scholar] [CrossRef]
  20. Peng, X.; Zhao, A.; Chen, Y.; Chen, Q.; Liu, H. Tree Height Measurements in Degraded Tropical Forests Based on UAV-LiDAR Data of Different Point Cloud Densities: A Case Study on Dacrydium pierrei in China. Forests 2021, 12, 328. [Google Scholar] [CrossRef]
  21. Singh, K.K.; Chen, G.; McCarter, J.B.; Meentemeyer, R.K. Effects of LiDAR point density and landscape context on estimates of urban forest biomass. ISPRS J. Photogramm. Remote Sens. 2015, 101, 310–322. [Google Scholar] [CrossRef]
  22. Jakubowski, M.K.; Guo, Q.; Kelly, M. Tradeoffs between lidar pulse density and forest measurement accuracy. Remote Sens. Environ. 2013, 130, 245–253. [Google Scholar] [CrossRef]
  23. Béjar-Martos, J.A.; Rueda-Ruiz, A.J.; Ogayar-Anguita, C.J.; Segura-Sánchez, R.J.; López-Ruiz, A. Strategies for the Storage of Large LiDAR Datasets—A Performance Comparison. Remote Sens. 2022, 14, 2623. [Google Scholar] [CrossRef]
  24. Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne LIDAR data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
  25. Soil Survey Staff. Soil Survey Geographic Database (SSURGO)|Natural Resources Conservation Service. 2025. Available online: https://www.nrcs.usda.gov/resources/data-and-reports/soil-survey-geographic-database-ssurgo (accessed on 10 February 2025).
  26. Wu, Q. geemap: A Python package for interactive mapping with Google Earth Engine. J. Open Source Softw. 2020, 5, 2305. [Google Scholar] [CrossRef]
  27. Hijmans, R.J.; Barbosa, M.; Bivand, R.; Brown, A.; Chirico, M.; Cordano, E.; Dyba, K.; Pebesma, E.; Rowlingson, B.; Sumner, M.D. terra: Spatial Data Analysis (Version 1.8-15) [Computer software]. 2025. Available online: https://cran.rproject.org/web/packages/terra/index.html (accessed on 10 February 2025).
  28. Mauney, J.R.; Stewart, J.M. Cotton Physiology. 1986. Available online: https://www.cotton.org/foundation/reference-books/cotton-physiology/upload/COTTON-PHYSIOLOGY.pdf (accessed on 10 February 2025).
  29. Kuželka, K.; Slavík, M.; Surový, P. Very High Density Point Clouds from UAV Laser Scanning for Automatic Tree Stem Detection and Direct Diameter Measurement. Remote Sens. 2020, 12, 1236. [Google Scholar] [CrossRef]
  30. Luo, S.; Chen, J.M.; Wang, C.; Xi, X.; Zeng, H.; Peng, D.; Li, D. Effects of LiDAR point density, sampling size and height threshold on estimation accuracy of crop biophysical parameters. Opt. Express 2016, 24, 11578–11593. [Google Scholar] [CrossRef]
  31. Boucher, P.B.; Hockridge, E.G.; Singh, J.; Davies, A.B. Flying high: Sampling savanna vegetation with UAV-lidar. Methods Ecol. Evol. 2023, 14, 1668–1686. [Google Scholar] [CrossRef]
  32. Brede, B.; Calders, K.; Lau, A.; Raumonen, P.; Bartholomeus, H.M.; Herold, M.; Kooistra, L. Non-destructive tree volume estimation through quantitative structure modelling: Comparing UAV laser scanning with terrestrial LIDAR. Remote Sens. Environ. 2019, 233, 111355. [Google Scholar] [CrossRef]
  33. Zhang, Q.; Hu, M.; Zhou, Y.; Wan, B.; Jiang, L.; Zhang, Q.; Wang, D. Effects of UAV-LiDAR and Photogrammetric Point Density on Tea Plucking Area Identification. Remote Sens. 2022, 14, 1505. [Google Scholar] [CrossRef]
  34. Navarro, A.; Young, M.; Allan, B.; Carnell, P.; Macreadie, P.; Ierodiaconou, D. The application of Unmanned Aerial Vehicles (UAVs) to estimate above-ground biomass of mangrove ecosystems. Remote Sens. Environ. 2020, 242, 111747. [Google Scholar] [CrossRef]
  35. Moudrý, V.; Gdulová, K.; Fogl, M.; Klápště, P.; Urban, R.; Komárek, J.; Moudrá, L.; Štroner, M.; Barták, V.; Solský, M. Comparison of leaf-off and leaf-on combined UAV imagery and airborne LiDAR for assessment of a post-mining site terrain and vegetation structure: Prospects for monitoring hazards and restoration success. Appl. Geogr. 2019, 104, 32–41. [Google Scholar] [CrossRef]
  36. Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. lidR: An R package for analysis of Airborne Laser Scanning (ALS) data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
  37. Chang, Y.; Habib, A.; Lee, D.; Yom, J. Automatic classification of lidar data into ground and non-ground points. Int. Arch. Photogramm. Remote Sens. 2008, 37, 463–468. [Google Scholar]
  38. Jimenez-Berni, J.A.; Deery, D.M.; Rozas-Larraondo, P.; Condon, A.G.; Rebetzke, G.J.; James, R.A.; Bovill, W.D.; Furbank, R.T.; Sirault, X.R.R. High Throughput Determination of Plant Height, Ground Cover, and Above-Ground Biomass in Wheat with LiDAR. Front. Plant Sci. 2018, 9, 237. [Google Scholar] [CrossRef]
  39. Walter, J.D.C.; Edwards, J.; McDonald, G.; Kuchel, H. Estimating Biomass and Canopy Height With LiDAR for Field Crop Breeding. Front. Plant Sci. 2019, 10, 1145. [Google Scholar] [CrossRef]
  40. Alexander, C.; Korstjens, A.H.; Hill, R.A. Influence of micro-topography and crown characteristics on tree height estimations in tropical forests based on LiDAR canopy height models. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 105–113. [Google Scholar] [CrossRef]
  41. Fox, J.; Weisberg, S. An R Companion to Applied Regression, 3rd ed.; Sage: Washington, DC, USA, 2019; Available online: https://us.sagepub.com/en-us/nam/an-r-companion-to-applied-regression/book246125#resources (accessed on 20 January 2025).
  42. Hand, L.C.; Stanley, C.; Jenna, V.; Glen, H.; Bob, K.; Liu, Y. 2024 Georgia Cotton Production Guide. UGA Extension Cotton Team 2360 Rainwater Road Tifton, GA 31793. 2024. Available online: https://secure.caes.uga.edu/extension/publications/files/pdf/AP%20124-4_2.PDF (accessed on 10 February 2025).
  43. Vaz, C.M.P.; Franchini, J.C.; Speranza, E.A.; Inamasu, R.Y.; De CJorge, L.A.; Rabello, L.M.; De ONLopes, I.; Das Chagas, S.; De Souza, J.L.R.; De Souza, M.; et al. Zonal Application of Plant Growth Regulator in Cotton to Reduce Variability and Increase Yield in a Highly Variable Field. J. Cotton Sci. 2023, 23, 60–73. [Google Scholar] [CrossRef]
  44. Fang, S.; Gao, K.; Hu, W.; Wang, S.; Chen, B.; Zhou, Z. Foliar and seed application of plant growth regulators affects cotton yield by altering leaf physiology and floral bud carbohydrate accumulation. Field Crops Res. 2019, 231, 105–114. [Google Scholar] [CrossRef]
  45. Samples, C.; Dodds, D.M.; Catchot, A.L.; Golden, B.R.; Gore, J.; Varco, J.J. Determining optimum plant growth regulator application rates in response to fruiting structure and flower bud removal. J. Cotton Sci. 2015, 19, 359–367. [Google Scholar] [CrossRef]
  46. Leal, A.J.F.; Piati, G.L.; Leite, R.C.; Zanella, M.S.; Osorio, C.R.W.S.; Lima, S.F. Nitrogen and mepiquat chloride can affect fiber quality and cotton yield. Revista Brasileira de Engenharia Agrícola e Ambiental 2020, 24, 238–243. [Google Scholar] [CrossRef]
  47. Tung, S.A.; Huang, Y.; Hafeez, A.; Ali, S.; Liu, A.; Chattha, M.S.; Ahmad, S.; Yang, G. Morpho-physiological Effects and Molecular Mode of Action of Mepiquat Chloride Application in Cotton: A Review. J. Soil Sci. Plant Nutr. 2020, 20, 2073–2086. [Google Scholar] [CrossRef]
  48. Sawana, Z.M.; Hafez, S.A.; Alkassas, A.R. Nitrogen, potassium and plant growth retardant effects on oil content and quality of cotton seed. Grasas y Aceites 2007, 58, 243–251. [Google Scholar] [CrossRef]
  49. Scarpin, G.J.; Cereijo, A.E.; Dileo, P.N.; Winkler, H.H.M.; Muchut, R.J.; Lorenzini, F.G.; Roeschlin, R.A.; Paytas, M. Delayed harvest time affects strength and color parameters in cotton fibers. Agron. J. 2023, 115, 583–594. [Google Scholar] [CrossRef]
  50. Trevisan, R.G.; Vilanova Júnior, N.S.; Eitelwein, M.T.; Molin, J.P. Management of Plant Growth Regulators in Cotton Using Active Crop Canopy Sensors. Agriculture 2018, 8, 101. [Google Scholar] [CrossRef]
  51. Madec, S.; Baret, F.; De Solan, B.; Thomas, S.; Dutartre, D.; Jezequel, S.; Hemmerlé, M.; Colombeau, G.; Comar, A. High-throughput phenotyping of plant height: Comparing unmanned aerial vehicles and ground LiDAR estimates. Front. Plant Sci. 2017, 8, 2002. [Google Scholar] [CrossRef]
  52. Wang, H.; Singh, K.; Poudel, H.; Ravichandran, P.; Natarajan, M.; Eisenreich, B. Estimation of Crop Height and Digital Biomass from UAV-Based Multispectral Imagery. In Proceedings of the 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Athens, Greece, 31 October–2 November 2023; pp. 1–4. [Google Scholar] [CrossRef]
  53. Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
  54. Luo, S.; Liu, W.; Zhang, Y.; Wang, C.; Xi, X.; Nie, S.; Ma, D.; Lin, Y.; Zhou, G. Maize and soybean heights estimation from unmanned aerial vehicle (UAV) LiDAR data. Comput. Electron. Agric. 2021, 182, 106005. [Google Scholar] [CrossRef]
  55. Roussel, J.-R.; Caspersen, J.; Béland, M.; Thomas, S.; Achim, A. Removing bias from LiDAR-based estimates of canopy height: Accounting for the effects of pulse density and footprint size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
  56. Storch, M.; Jarmer, T.; Adam, M.; De Lange, N. Systematic Approach for Remote Sensing of Historical Conflict Landscapes with UAV-Based Laserscanning. Sensors 2021, 22, 217. [Google Scholar] [CrossRef]
  57. Maguya, A.S.; Junttila, V.; Kauranne, T. Adaptive algorithm for large scale dtm interpolation from lidar data for forestry applications in steep forested terrain. ISPRS J. Photogramm. Remote Sens. 2013, 85, 74–83. [Google Scholar] [CrossRef]
  58. Tsoulias, N.; Paraforos, D.S.; Fountas, S.; Zude-Sasse, M. Estimating Canopy Parameters Based on the Stem Position in Apple Trees Using a 2D LiDAR. Agronomy 2019, 9, 740. [Google Scholar] [CrossRef]
  59. Stereńczak, K.; Ciesielski, M.; Balazy, R.; Zawiła-Niedźwiecki, T. Comparison of various algorithms for DTM interpolation from LIDAR data in dense mountain forests. Eur. J. Remote Sens. 2016, 49, 599–621. [Google Scholar] [CrossRef]
  60. Li, D.; Zhou, Z.; Wei, Y. Unsupervised shape-aware SOM down-sampling for plant point clouds. ISPRS J. Photogramm. Remote Sens. 2024, 211, 172–207. [Google Scholar] [CrossRef]
  61. Hämmerle, M.; Höfle, B. Effects of Reduced Terrestrial LiDAR Point Density on High-Resolution Grain Crop Surface Models in Precision Agriculture. Sensors 2014, 14, 24212–24230. [Google Scholar] [CrossRef]
  62. Ding, Q.; Chen, W.; King, B.; Liu, Y.; Liu, G. Combination of overlap-driven adjustment and Phong model for LiDAR intensity correction. ISPRS J. Photogramm. Remote Sens. 2013, 75, 40–47. [Google Scholar] [CrossRef]
Remotesensing 17 01504 g001
Figure 1. LiDAR-based crop height estimation workflow including step 1: field characterization (elevation and slope); step 2: data acquisition (varying flight settings and manual plant height measurements); step 3: data processing (canopy modeling and metric extraction); and step 4: validation (regression between LiDAR plant height estimate and ground truth plant height).
Figure 1. LiDAR-based crop height estimation workflow including step 1: field characterization (elevation and slope); step 2: data acquisition (varying flight settings and manual plant height measurements); step 3: data processing (canopy modeling and metric extraction); and step 4: validation (regression between LiDAR plant height estimate and ground truth plant height).
Remotesensing 17 01504 g001
Remotesensing 17 01504 g002
Figure 2. Scatterplots of manual measured plant height (cm) and LiDAR-derived plant height (cm) where points represent heights from two locations: Watkinsville (green) and Midville (blue). Each panel represents data from one unmanned aerial vehicle (UAV) flight altitude and speed combination. The solid black line represents the 1:1 line. The red line represents the regression line, with its equation shown inside each panel. The bolded intercept and slope values indicate a significant difference from 0 and 1, respectively, at p < 0.05; non-bold values are not significantly different. R2 is the coefficient of determination. R2 is the coefficient of determination. MAE is the mean absolute error. RMSE is the root mean squared error.
Figure 2. Scatterplots of manual measured plant height (cm) and LiDAR-derived plant height (cm) where points represent heights from two locations: Watkinsville (green) and Midville (blue). Each panel represents data from one unmanned aerial vehicle (UAV) flight altitude and speed combination. The solid black line represents the 1:1 line. The red line represents the regression line, with its equation shown inside each panel. The bolded intercept and slope values indicate a significant difference from 0 and 1, respectively, at p < 0.05; non-bold values are not significantly different. R2 is the coefficient of determination. R2 is the coefficient of determination. MAE is the mean absolute error. RMSE is the root mean squared error.
Remotesensing 17 01504 g002
Remotesensing 17 01504 g003
Figure 3. Scatterplots of manual height and LiDAR-derived height in Watkinsville, GA. Each panel represents data from different sub-sampling grid sizes in Watkinsville. The title on left top of each graph shows the grid size used for sub-sampling. The solid black line represents the 1:1 line. The red line represents the regression line, with its equation showed inside each panel. The bolded intercept and slope values indicate a significant difference from 0 and 1, respectively, at p < 0.05; non-bold values are not significantly different. R2 is the coefficient of determination. MAE is the mean absolute error. RMSE is the root mean squared error. Grid size: 00cm denotes the original resolution layer, meaning the data is in its full detail with no subsampling performed.
Figure 3. Scatterplots of manual height and LiDAR-derived height in Watkinsville, GA. Each panel represents data from different sub-sampling grid sizes in Watkinsville. The title on left top of each graph shows the grid size used for sub-sampling. The solid black line represents the 1:1 line. The red line represents the regression line, with its equation showed inside each panel. The bolded intercept and slope values indicate a significant difference from 0 and 1, respectively, at p < 0.05; non-bold values are not significantly different. R2 is the coefficient of determination. MAE is the mean absolute error. RMSE is the root mean squared error. Grid size: 00cm denotes the original resolution layer, meaning the data is in its full detail with no subsampling performed.
Remotesensing 17 01504 g003
Remotesensing 17 01504 g004
Figure 4. Scatterplots of manual height and LiDAR-derived height in Midville, GA. Each panel represents data from different sub-sampling grid sizes in Midville. The title on left top of each graph shows the grid size used for sub-sampling. The solid black line represents the 1:1 line. The red line represents the regression line, with its equation showed inside each panel. The bolded intercept and slope values indicate a significant difference from 0 and 1, respectively, at p < 0.05; non-bold values are not significantly different. R2 is the coefficient of determination. MAE is the mean absolute error. RMSE is the root mean squared error. Grid size: 00cm denotes the original resolution layer, meaning the data is in its full detail with no subsampling performed.
Figure 4. Scatterplots of manual height and LiDAR-derived height in Midville, GA. Each panel represents data from different sub-sampling grid sizes in Midville. The title on left top of each graph shows the grid size used for sub-sampling. The solid black line represents the 1:1 line. The red line represents the regression line, with its equation showed inside each panel. The bolded intercept and slope values indicate a significant difference from 0 and 1, respectively, at p < 0.05; non-bold values are not significantly different. R2 is the coefficient of determination. MAE is the mean absolute error. RMSE is the root mean squared error. Grid size: 00cm denotes the original resolution layer, meaning the data is in its full detail with no subsampling performed.
Remotesensing 17 01504 g004
Remotesensing 17 01504 g005
Figure 5. Scatterplots of manual height and LiDAR-derived height. Each panel represents data from different slope choices for point cloud classification for two locations, Watkinsville (green) and Midville (blue). The title on left top of each graph shows the slope choice made. Solid black line represents the 1:1 line. Red line represents the regression line, with its equation showed inside each panel. The bolded intercept and slope values indicate a significant difference from 0 and 1, respectively, at p < 0.05; non-bold values are not significantly different. MAE is the mean absolute error. RMSE is the root mean squared error.
Figure 5. Scatterplots of manual height and LiDAR-derived height. Each panel represents data from different slope choices for point cloud classification for two locations, Watkinsville (green) and Midville (blue). The title on left top of each graph shows the slope choice made. Solid black line represents the 1:1 line. Red line represents the regression line, with its equation showed inside each panel. The bolded intercept and slope values indicate a significant difference from 0 and 1, respectively, at p < 0.05; non-bold values are not significantly different. MAE is the mean absolute error. RMSE is the root mean squared error.
Remotesensing 17 01504 g005
Table 1. Effect of grid sub-sampling size on LiDAR point cloud density, processing time and file size with data obtained from Watkinsville.
Table 1. Effect of grid sub-sampling size on LiDAR point cloud density, processing time and file size with data obtained from Watkinsville.
Grid Sub-Sampling
(cm)		Point Cloud Density
(points/m2)		Benchmarking Time
DJI Terra
(3D LiDAR Point Cloud Modeling)
(s)		Benchmarking
Time R
(Elevation Modeling)
(s)		Total Time for Processing
(s)		File Size (mb)
0583414363206812
1053910155156149
20110833712035
3041822110313
40208019996
50217714914
Table 2. Effect of grid sub-sampling size on LiDAR point cloud density, processing time, and file size with data obtained from Midville.
Table 2. Effect of grid sub-sampling size on LiDAR point cloud density, processing time, and file size with data obtained from Midville.
Grid Sub-Sampling
(cm)		Point Cloud Density
(points/m2)		Benchmarking Time
DJI Terra
(3D LiDAR Point Cloud Modeling)
(s)		Benchmarking
Time R
(Elevation Modeling)
(s)		Total Time for Processing
(s)		File Size (mb)
0263712756183718
10362774011799
208770269624
30347017879
40176713805
5096711783
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bhattarai, A.; Scarpin, G.J.; Jakhar, A.; Porter, W.; Hand, L.C.; Snider, J.L.; Bastos, L.M. Optimizing Unmanned Aerial Vehicle LiDAR Data Collection in Cotton Through Flight Settings and Data Processing. Remote Sens. 2025, 17, 1504. https://doi.org/10.3390/rs17091504

AMA Style

Bhattarai A, Scarpin GJ, Jakhar A, Porter W, Hand LC, Snider JL, Bastos LM. Optimizing Unmanned Aerial Vehicle LiDAR Data Collection in Cotton Through Flight Settings and Data Processing. Remote Sensing. 2025; 17(9):1504. https://doi.org/10.3390/rs17091504

Chicago/Turabian Style

Bhattarai, Anish, Gonzalo J. Scarpin, Amrinder Jakhar, Wesley Porter, Lavesta C. Hand, John L. Snider, and Leonardo M. Bastos. 2025. "Optimizing Unmanned Aerial Vehicle LiDAR Data Collection in Cotton Through Flight Settings and Data Processing" Remote Sensing 17, no. 9: 1504. https://doi.org/10.3390/rs17091504

APA Style

Bhattarai, A., Scarpin, G. J., Jakhar, A., Porter, W., Hand, L. C., Snider, J. L., & Bastos, L. M. (2025). Optimizing Unmanned Aerial Vehicle LiDAR Data Collection in Cotton Through Flight Settings and Data Processing. Remote Sensing, 17(9), 1504. https://doi.org/10.3390/rs17091504

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop