Multi-Year Global Oscillations in GNSS Deformation and Surface Loading Contributions
Abstract
1. Introduction
2. Materials and Methods
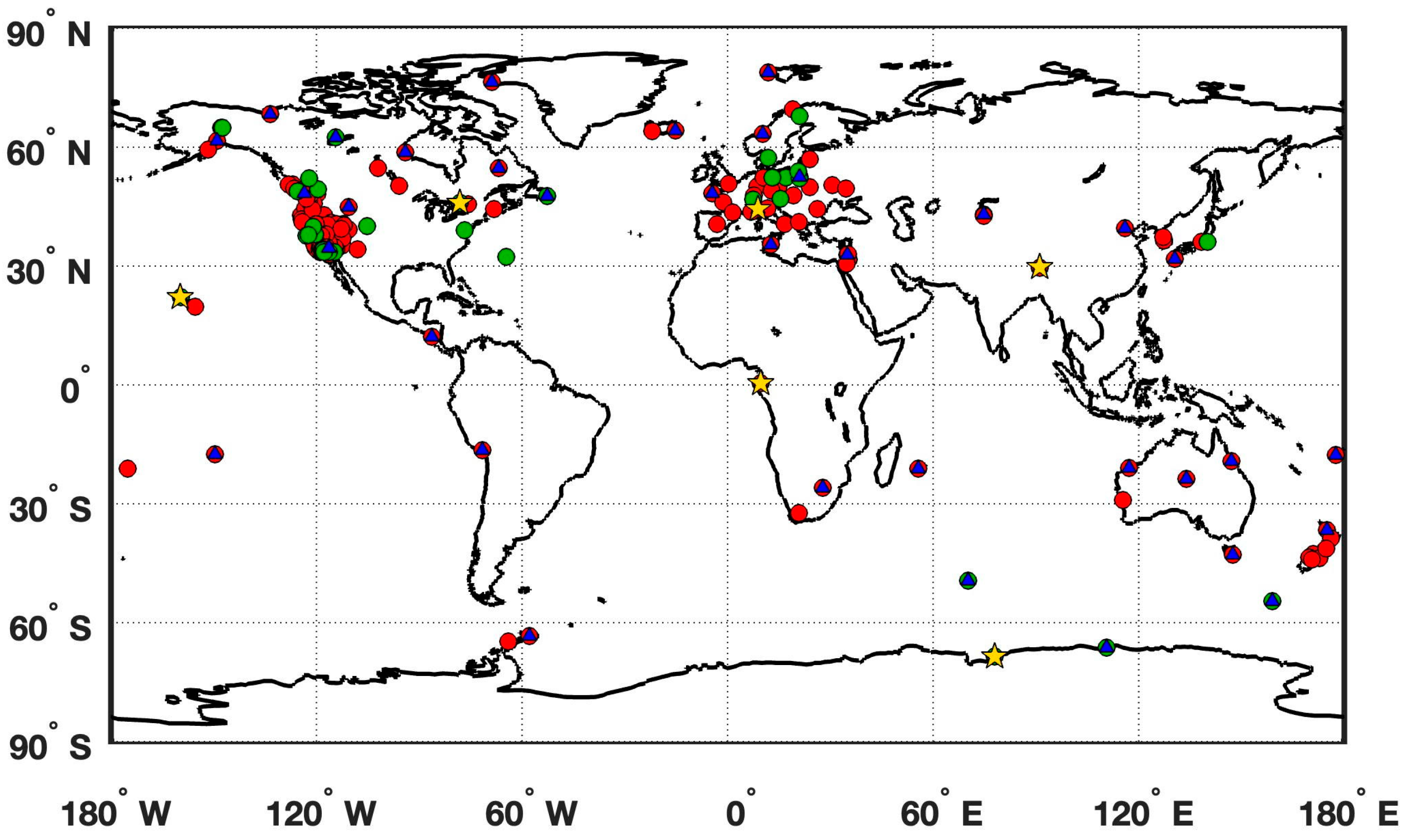
2.1. GPS Data
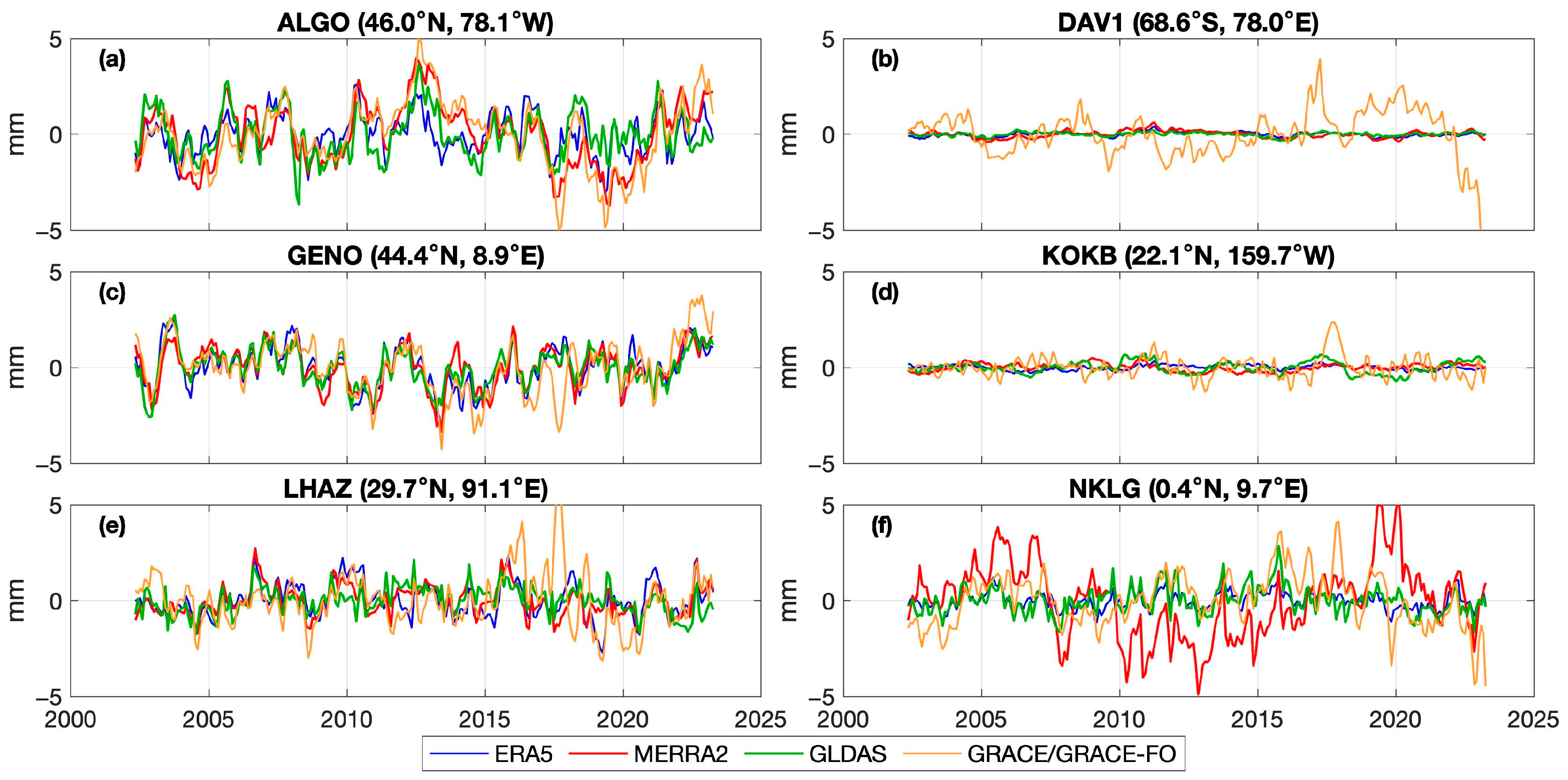
2.2. Loading Data
2.3. Methods
3. Results
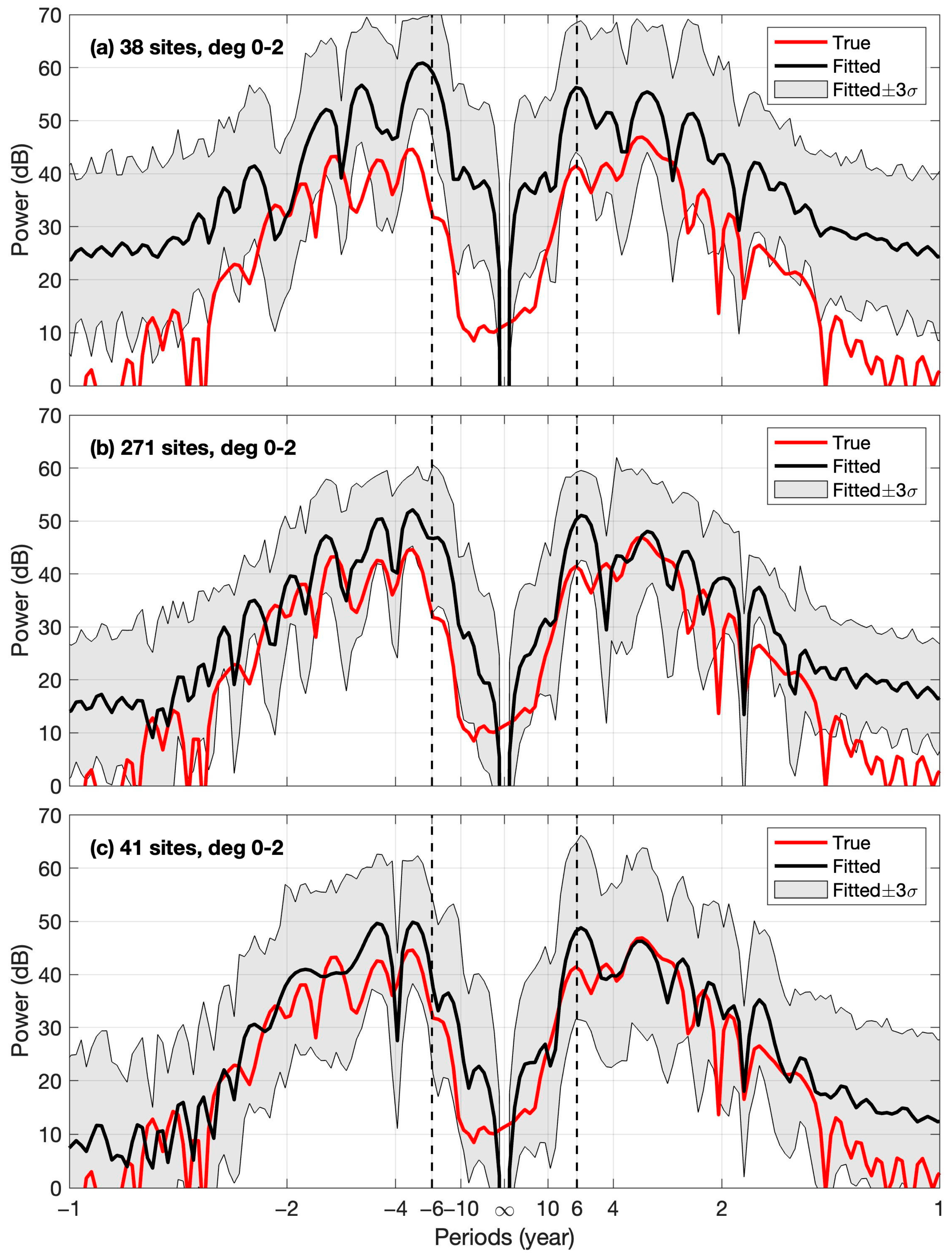
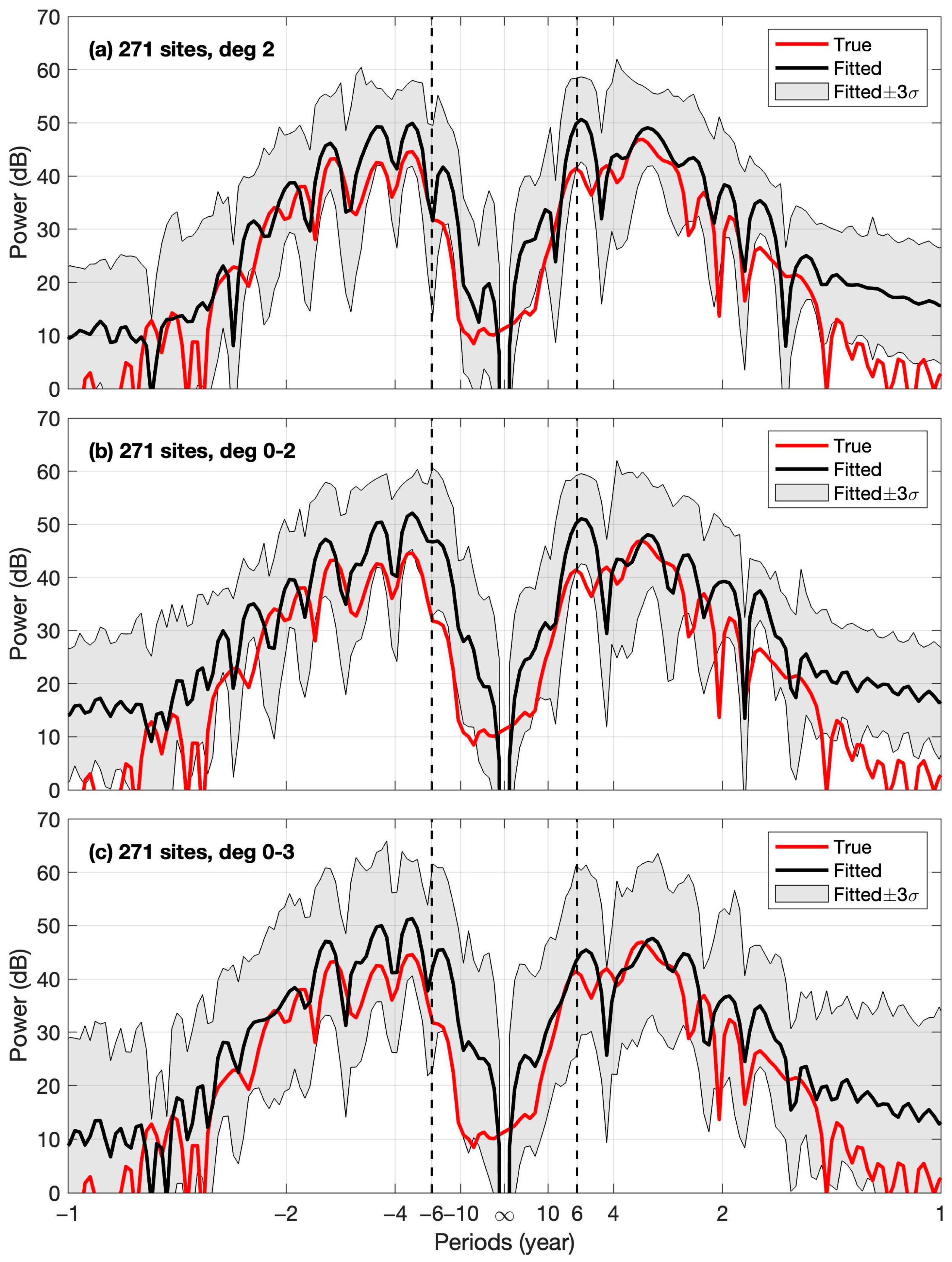
3.1. Synthetic Tests of SH Coefficient Estimation
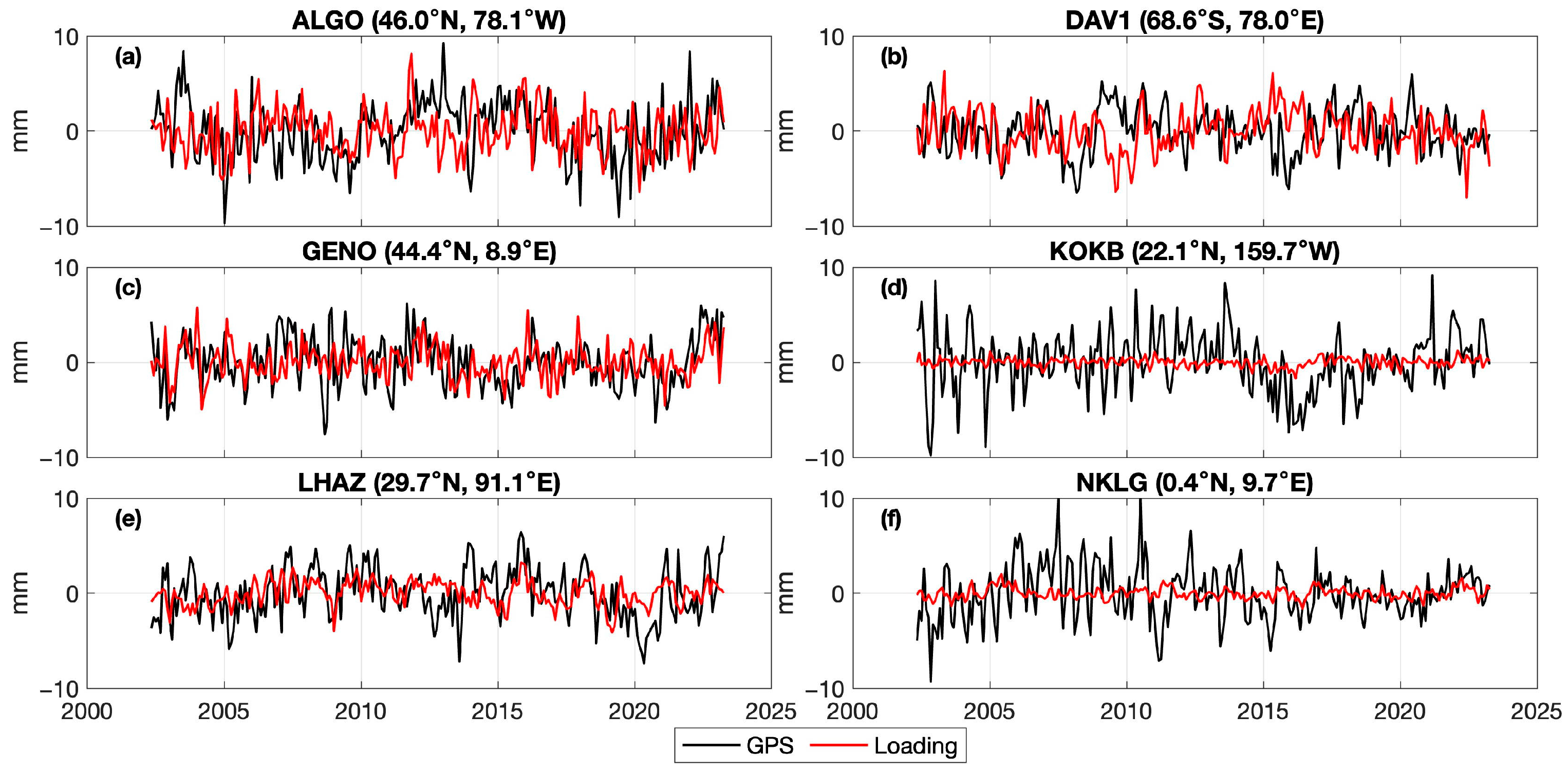
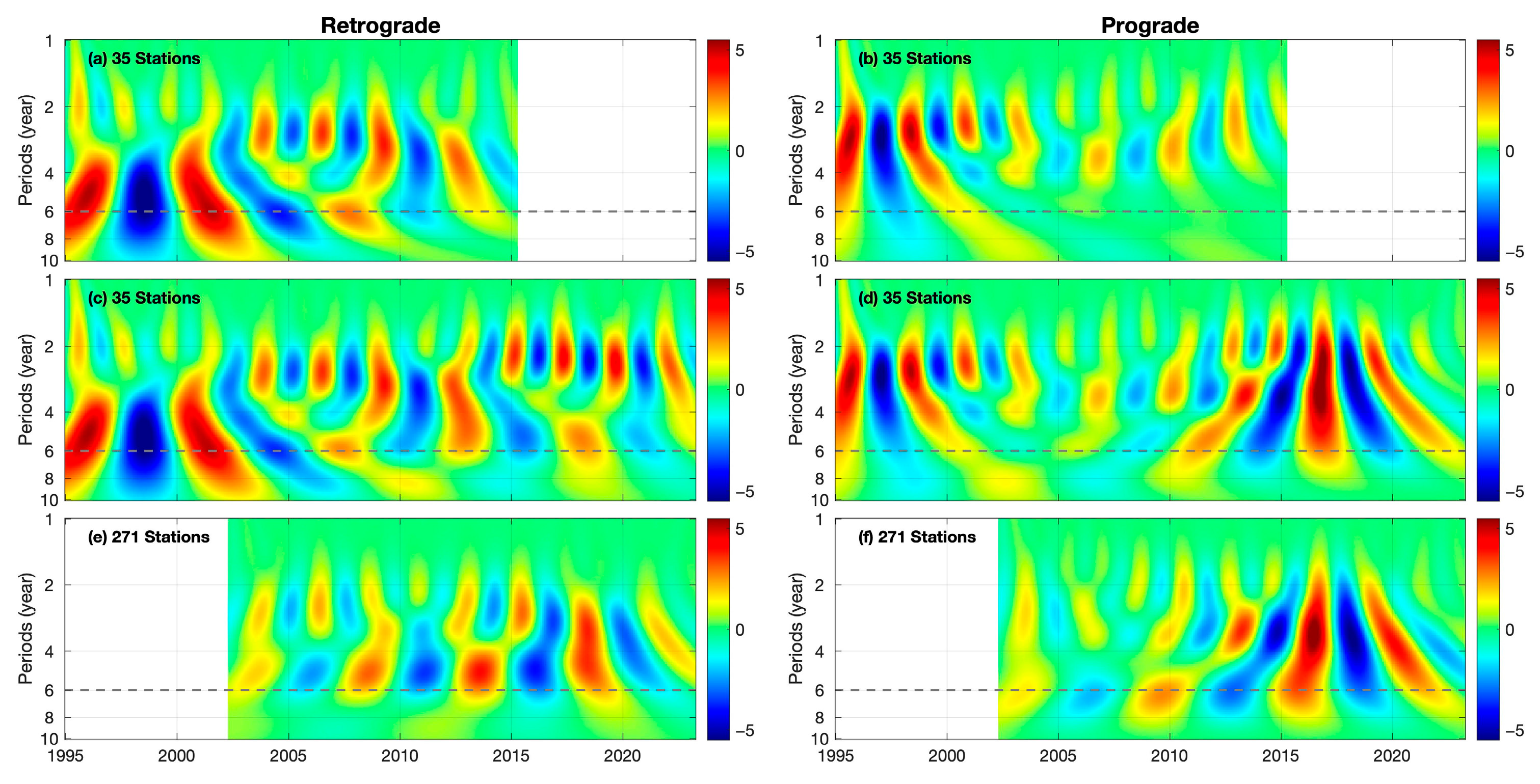
3.2. SYO Signals in GPS Observations
3.2.1. Spectral Analysis
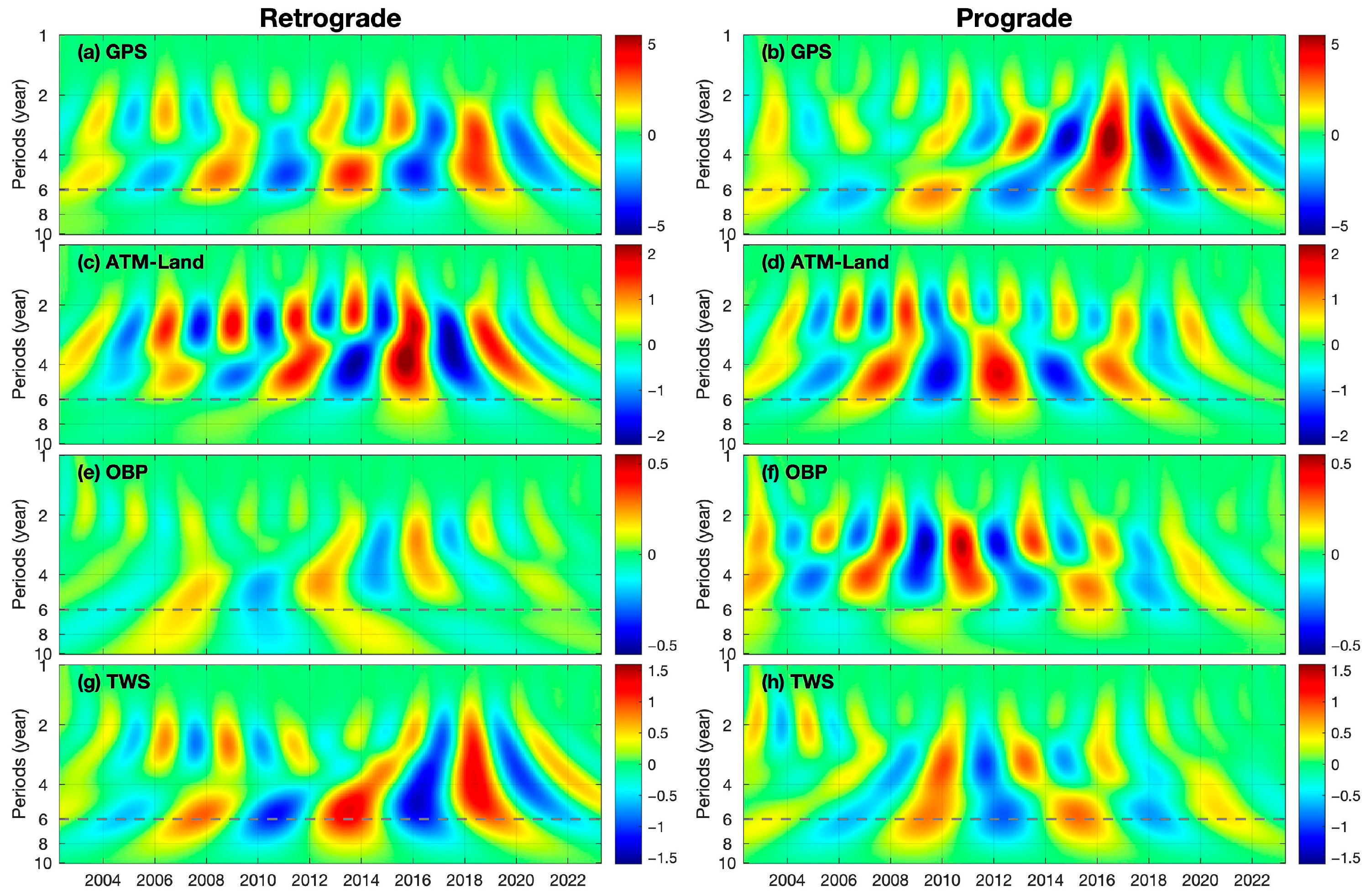
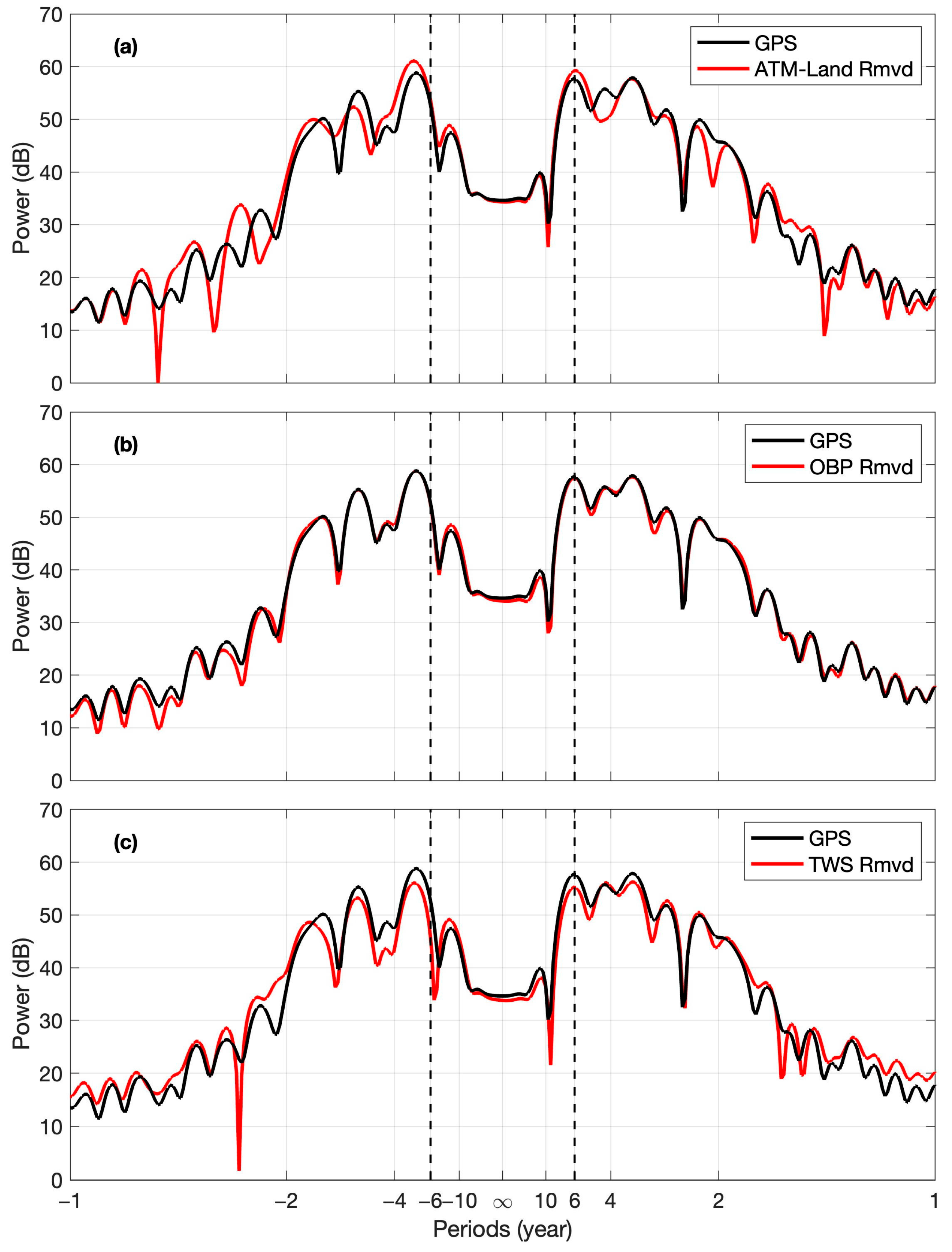
3.2.2. Surface Loading Effects
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Discrete Fourier Transform |
| ECCO | Circulation and Climate of the Ocean |
| EOST | School and Observatory of Earth Sciences |
| ERA5 | European Centre for Medium-Range Weather Forecasts Reanalysis 5 |
| EWT | Equivalent water thickness |
| GIA | Glacial isostatic adjustment |
| GLDAS | Global Land Data Assimilation System |
| GNSS | Global Navigation Satellite Systems |
| GPS | Global Positioning System |
| GRACE | Gravity Recovery and Climate Experiment |
| GRACE-FO | GRACE Follow-On |
| IB | Inverted barometer |
| JPL | Jet Propulsion Laboratory |
| LOD | Length of day |
| LSQ | Least square fit |
| MERRA | Modern-Era Retrospective analysis for Research and Applications |
| MICG | Mantle-Inner-Core Gravitational coupling |
| OBP | Ocean bottom pressures |
| SH | Spherical harmonic |
| SYO | 6-year oscillation |
| TWS | Terrestrial water storage |
| UTCSR | University of Texas at Austin Center for Space Research |
References
- Abarca Del Rio, R.; Gambis, D.; Salstein, D.A. Interannual Signals in Length of Day and Atmospheric Angular Momentum. Ann. Geophys. 2000, 18, 347–364. [Google Scholar] [CrossRef]
- Djurović, D.; Pâquet, P. The Common Oscillations of Solar Activity, the Geomagnetic Field, and the Earth’s Rotation. Sol. Phys. 1996, 167, 427–439. [Google Scholar] [CrossRef]
- Vondrák, J. The Rotation of the Earth between 1955.5 and 1976.5. Stud. Geophys. Geod. 1977, 21, 107–117. [Google Scholar] [CrossRef]
- Chen, J.; Wilson, C.R.; Kuang, W.; Chao, B.F. Interannual Oscillations in Earth Rotation. JGR Solid Earth 2019, 124, 13404–13414. [Google Scholar] [CrossRef]
- Silva, L.; Jackson, L.; Mound, J. Assessing the Importance and Expression of the 6 Year Geomagnetic Oscillation. J. Geophys. Res. 2012, 117, B10101. [Google Scholar] [CrossRef]
- Chao, B.F.; Yu, Y. Variation of the Equatorial Moments of Inertia Associated with a 6-Year Westward Rotary Motion in the Earth. Earth Planet. Sci. Lett. 2020, 542, 116316. [Google Scholar] [CrossRef]
- Dumberry, M. Gravity Variations Induced by Core Flows. Geophys. J. Int. 2010, 180, 635–650. [Google Scholar] [CrossRef]
- Ding, H.; Chao, B.F. A 6-Year Westward Rotary Motion in the Earth: Detection and Possible MICG Coupling Mechanism. Earth Planet. Sci. Lett. 2018, 495, 50–55. [Google Scholar] [CrossRef]
- Watkins, A.; Fu, Y.; Gross, R. Earth’s Subdecadal Angular Momentum Balance from Deformation and Rotation Data. Sci. Rep. 2018, 8, 13761. [Google Scholar] [CrossRef]
- Meyer, P.G.; Kantz, H. A Simple Decomposition of European Temperature Variability Capturing the Variance from Days to a Decade. Clim. Dyn. 2019, 53, 6909–6917. [Google Scholar] [CrossRef]
- Moreira, L.; Cazenave, A.; Palanisamy, H. Influence of Interannual Variability in Estimating the Rate and Acceleration of Present-Day Global Mean Sea Level. Glob. Planet. Change 2021, 199, 103450. [Google Scholar] [CrossRef]
- Pfeffer, J.; Cazenave, A.; Rosat, S.; Moreira, L.; Mandea, M.; Dehant, V.; Coupry, B. A 6-Year Cycle in the Earth System. Glob. Planet. Change 2023, 229, 104245. [Google Scholar] [CrossRef]
- Cazenave, A.; Pfeffer, J.; Mandea, M.; Dehant, V.; Gillet, N. Why is the Earth System Oscillating at a 6-Year Period? Surv. Geophys. 2025, 1–26. [Google Scholar] [CrossRef]
- Chao, B.F. Dynamics of Axial Torsional Libration under the Mantle-inner Core Gravitational Interaction. JGR Solid Earth 2017, 122, 560–571. [Google Scholar] [CrossRef]
- Gillet, N.; Jault, D.; Canet, E.; Fournier, A. Fast Torsional Waves and Strong Magnetic Field within the Earth’s Core. Nature 2010, 465, 74–77. [Google Scholar] [CrossRef]
- Gross, R.S. Earth Rotation Variations—Long Period. In Treatise on Geophysics; Elsevier: Amsterdam, The Netherlands, 2007; Volume 3, ISBN 978-0-444-52748-6. [Google Scholar]
- Mound, J.E.; Buffett, B.A. Interannual Oscillations in Length of Day: Implications for the Structure of the Mantle and Core. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Gillet, N.; Dumberry, M.; Rosat, S. The Limited Contribution from Outer Core Dynamics to Global Deformations at the Earth’s Surface. Geophys. J. Int. 2020, 224, 216–229. [Google Scholar] [CrossRef]
- Pan, Y.; Jiang, W.; Ding, H.; Shum, C.K.; Jiao, J.; Xiao, Y.; Wu, Q. Interannual Variability of Vertical Land Motion over High Mountain Central Asia from GPS and GRACE/GRACE-FO Observations. GPS Solut. 2023, 27, 168. [Google Scholar] [CrossRef]
- Cazenave, A.; Pfeffer, J.; Mandea, M.; Dehant, V. ESD Ideas: A 6-Year Oscillation in the Whole Earth System? Earth Syst. Dynam. 2023, 14, 733–735. [Google Scholar] [CrossRef]
- Rosat, S.; Gillet, N.; Boy, J.-P.; Couhert, A.; Dumberry, M. Interannual Variations of Degree 2 from Geodetic Observations and Surface Processes. Geophys. J. Int. 2021, 225, 200–221. [Google Scholar] [CrossRef]
- Dumberry, M.; Mandea, M. Gravity Variations and Ground Deformations Resulting from Core Dynamics. Surv. Geophys. 2022, 43, 5–39. [Google Scholar] [CrossRef] [PubMed]
- Lecomte, H.; Rosat, S.; Mandea, M.; Boy, J.; Pfeffer, J. Uncertainty of Low-Degree Space Gravimetry Observations: Surface Processes Versus Earth’s Core Signal. JGR Solid Earth 2023, 128, e2023JB026503. [Google Scholar] [CrossRef]
- Argus, D.F.; Landerer, F.W.; Wiese, D.N.; Martens, H.R.; Fu, Y.; Famiglietti, J.S.; Thomas, B.F.; Farr, T.G.; Moore, A.W.; Watkins, M.M. Sustained Water Loss in California’s Mountain Ranges During Severe Drought from 2012 to 2015 Inferred from GPS. J. Geophys. Res. Solid Earth 2017, 122, 10559–10585. [Google Scholar] [CrossRef]
- Heflin, M.; Donnellan, A.; Parker, J.; Lyzenga, G.; Moore, A.; Ludwig, L.G.; Rundle, J.; Wang, J.; Pierce, M. Automated Estimation and Tools to Extract Positions, Velocities, Breaks, and Seasonal Terms from Daily GNSS Measurements: Illuminating Nonlinear Salton Trough Deformation. Earth Space Sci. 2020, 7, e2019EA000644. [Google Scholar] [CrossRef]
- Gegout, P.; Boy, J.-P.; Hinderer, J.; Ferhat, G. Modeling and Observation of Loading Contribution to Time-Variable GPS Sites Positions. In Gravity, Geoid and Earth Observation: IAG Commission 2: Gravity Field, Chania, Crete, Greece, 23–27 June 2008; Mertikas, S.P., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 135, pp. 651–659. [Google Scholar]
- Mémin, A.; Boy, J.-P.; Santamaría-Gómez, A. Correcting GPS Measurements for Non-Tidal Loading. GPS Solut. 2020, 24, 45. [Google Scholar] [CrossRef]
- Save, H. CSR GRACE and GRACE-FO RL06 Mascon Solutions V02; The University of Texas at Austin: Austin, TX, USA, 2020. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-Resolution CSR GRACE RL05 Mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by Surface Loads. Rev. Geophys. Space Phys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Han, D.; Wahr, J. The Viscoelastic Relaxation of a Realistically Stratified Earth, and a Further Analysis of Postglacial Rebound. Geophys. J. Int. 1995, 120, 287–311. [Google Scholar] [CrossRef]
- Chao, B.F.; Naito, I. Wavelet Analysis Provides a New Tool for Studying Earth’s Rotation. EoS Trans. 1995, 76, 161–165. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Giard, D. Wave Propagation and Sampling Theory—Part II: Sampling Theory and Complex Waves. Geophysics 1982, 47, 222–236. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, R.; Ding, H.; Xu, X.; Zheng, G.; Shen, W.; Xiao, Y.; Li, S. Common Mode Component and Its Potential Effect on GPS-Inferred Three-Dimensional Crustal Deformations in the Eastern Tibetan Plateau. Remote Sens. 2019, 11, 1975. [Google Scholar] [CrossRef]
- Premoli, A.; Tavella, P. A Revisited Three-Cornered Hat Method for Estimating Frequency Standard Instability. IEEE Trans. Instrum. Meas. 1993, 42, 7–13. [Google Scholar] [CrossRef]
- Wang, S.Y.; Li, J.; Chen, J.; Hu, X. Uncertainty Assessments of Load Deformation from Different GPS Time Series Products, GRACE Estimates and Model Predictions: A Case Study over Europe. Remote Sens. 2021, 13, 2765. [Google Scholar] [CrossRef]
- Rekier, J.; Chao, B.F.; Chen, J.; Dehant, V.; Rosat, S.; Zhu, P. Earth’s Rotation: Observations and Relation to Deep Interior. Surv. Geophys. 2022, 43, 149–175. [Google Scholar] [CrossRef]


| Retrograde | Prograde | |
|---|---|---|
| GPS | 341 | 218 |
| ATM-Land | 146 | 11 |
| OBP | 328 | 186 |
| TWS | 318 | 205 |
| ERA5 | MERRA-2 | GLDAS | GRACE/GRACE-FO | |
|---|---|---|---|---|
| Prograde | 24% | 51% | 57% | 56% |
| Retrograde | 32% | 49% | 67% | 93% |
| ERA5 | MERRA-2 | GLDAS | GRACE/GRACE-FO | |
|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wilson, C.R.; Chen, J.; Fu, Y.; Kuang, W.; Seo, K.-W. Multi-Year Global Oscillations in GNSS Deformation and Surface Loading Contributions. Remote Sens. 2025, 17, 1509. https://doi.org/10.3390/rs17091509
Wang S, Wilson CR, Chen J, Fu Y, Kuang W, Seo K-W. Multi-Year Global Oscillations in GNSS Deformation and Surface Loading Contributions. Remote Sensing. 2025; 17(9):1509. https://doi.org/10.3390/rs17091509
Chicago/Turabian StyleWang, Songyun, Clark R. Wilson, Jianli Chen, Yuning Fu, Weijia Kuang, and Ki-Weon Seo. 2025. "Multi-Year Global Oscillations in GNSS Deformation and Surface Loading Contributions" Remote Sensing 17, no. 9: 1509. https://doi.org/10.3390/rs17091509
APA StyleWang, S., Wilson, C. R., Chen, J., Fu, Y., Kuang, W., & Seo, K.-W. (2025). Multi-Year Global Oscillations in GNSS Deformation and Surface Loading Contributions. Remote Sensing, 17(9), 1509. https://doi.org/10.3390/rs17091509






