Evaluation of Daytime Evaporative Fraction from MODIS TOA Radiances Using FLUXNET Observations
Abstract
:1. Introduction
2. Materials and Methodology
2.1. Remote Sensing Data
2.2. FLUXNET Observations
2.3. Methodology
2.4. Algorithm Evaluation
3. Results and Discussion
3.1. Energy Imbalance of Flux Tower Measurements
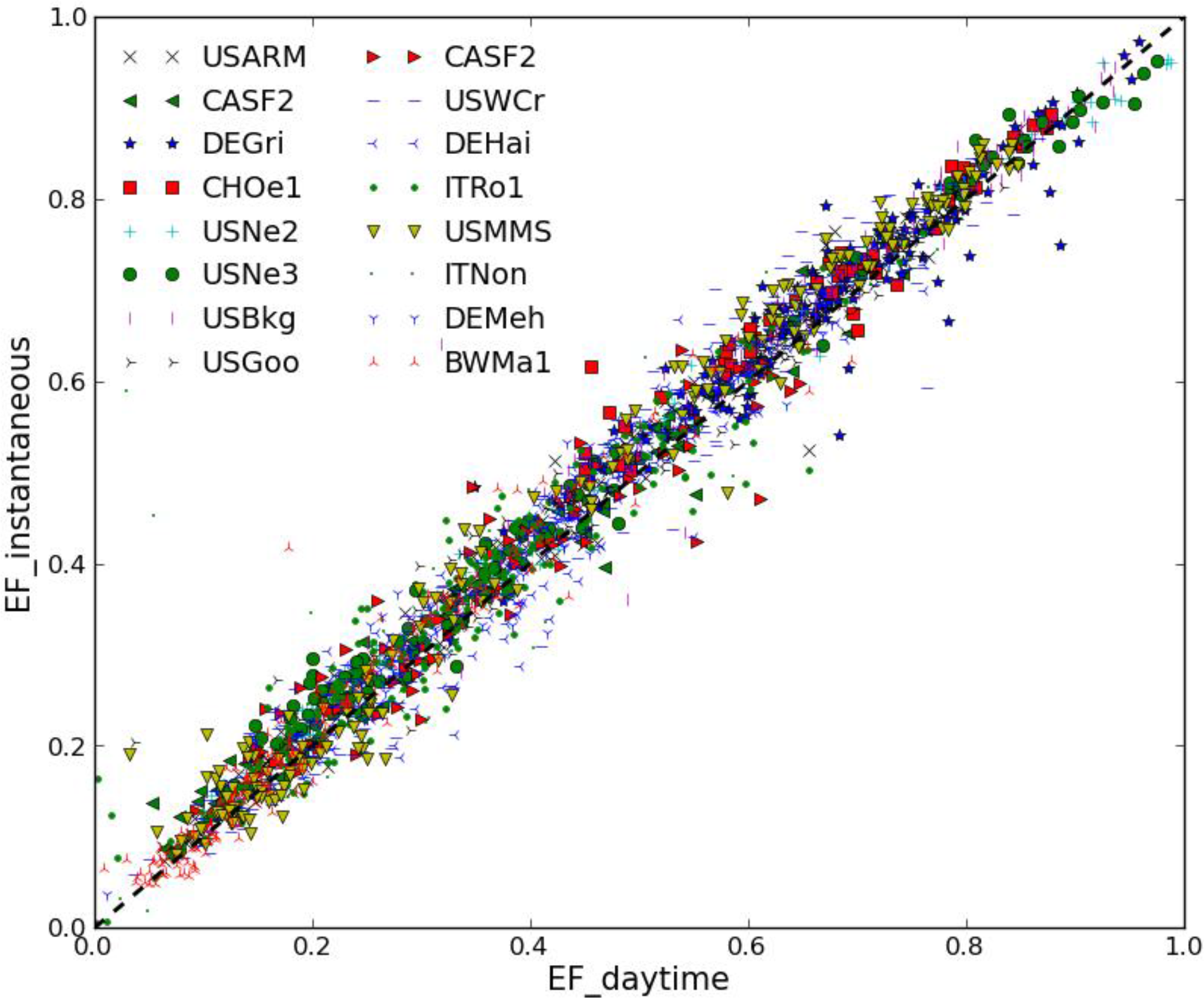
3.2. Can Near Noon Instantaneous EF Represent Daytime EF?
3.3. Evaluation of Daytime EF from MODIS TOA Radiances
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar]
- Sellers, P.; Dickinson, R.; Randall, D.; Betts, A.; Hall, F.; Berry, J.; Collatz, G.; Denning, A.; Mooney, H.; Nobre, C. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar]
- Lettau, H. Evapotranspiration climatonomy. Mon. Weather Rev 1969, 97, 691–699. [Google Scholar]
- Rodriguez-Iturbe, I. Ecohydrology: A hydrologic perspective of climate-soil-vegetation dynamics. Water Resour. Res 2000, 36, 3–9. [Google Scholar]
- Farahani, H.J.; Howell, T.A.; Shuttleworth, W.J.; Bausch, W.C. Evapotranspiration: Progress in measurement and modeling in agriculture. Trans. ASABE 2007, 50, 1627–1638. [Google Scholar]
- Kalma, J.; McVicar, T.; McCabe, M. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys 2008, 29, 421–469. [Google Scholar]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys 2012, 50, RG2005. [Google Scholar]
- Bateni, S.M.; Entekhabi, D.; Castelli, F. Mapping evaporation and estimation of surface control of evaporation using remotely sensed land surface temperature from a constellation of satellites. Water Resour. Res 2013, 49, 950–968. [Google Scholar]
- Caparrini, F.; Castelli, F.; Entekhabi, D. Mapping of land-atmosphere heat fluxes and surface parameters with remote sensing data. Bound.-Layer Meteorol 2003, 107, 605–633. [Google Scholar]
- Wang, K.; Li, Z.; Cribb, M. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: A new method to determine the priestley–taylor parameter. Remote Sens. Environ 2006, 102, 293–305. [Google Scholar]
- Caparrini, F.; Castelli, F.; Entekhabi, D. Estimation of surface turbulent fluxes through assimilation of radiometric surface temperature sequences. J. Hydrometeorol 2004, 5, 145–159. [Google Scholar]
- Gómez, M.; Olioso, A.; Sobrino, J.A.; Jacob, F. Retrieval of evapotranspiration over the alpilles/reseda experimental site using airborne polder sensor and a thermal camera. Remote Sens. Environ 2005, 96, 399–408. [Google Scholar]
- Nishida, K.; Nemani, R.R.; Running, S.W.; Glassy, J.M. An operational remote sensing algorithm of land surface evaporation. J. Geophys. Res.: Atmos 2003, 108, 4270–4283. [Google Scholar]
- Jiang, L.; Islam, S. Estimation of surface evaporation map over southern great plains using remote sensing data. Water Resour. Res 2001, 37, 329–340. [Google Scholar]
- Nemani, R.R.; Running, S.W. Estimation of regional surface resistance to evapotranspiration from NDVI and thermal-IR AVHRR data. J. Appl. Meteorol 1989, 28, 276–284. [Google Scholar]
- Price, J. Using spatial context in satellite data to infer regional scale evapotranspiration. IEEE Trans. Geosci. Remote Sens 1990, 28, 940–948. [Google Scholar]
- Batra, N.; Islam, S.; Venturini, V.; Bisht, G.; Jiang, L. Estimation and comparison of evapotranspiration from MODIS and AVHRR sensors for clear sky days over the southern great plains. Remote Sens. Environ 2006, 103, 1–15. [Google Scholar]
- Long, D.; Singh, V.P. A modified surface energy balance algorithm for land (m-sebal) based on a trapezoidal framework. Water Resour. Res 2012, 48, W02528. [Google Scholar]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration—Applied to msg-seviri data in the senegal river basin. Remote Sens. Environ 2008, 112, 1242–1255. [Google Scholar]
- Margulis, S.A.; Kim, J.; Hogue, T. A comparison of the triangle retrieval and variational data assimilation methods for surface turbulent flux estimation. J. Hydrometeorol 2005, 6, 1063–1072. [Google Scholar]
- Lambin, E.F.; Ehrlich, D. The surface temperature-vegetation index space for land cover and land-cover change analysis. Int. J. Remote Sens 1996, 17, 463–487. [Google Scholar]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ 2002, 79, 213–224. [Google Scholar]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Petropoulos, G.; Carlson, T.; Wooster, M.; Islam, S. A review of TS/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr 2009, 33, 224–250. [Google Scholar]
- Tang, R.; Li, Z.-L.; Chen, K.-S. Validating MODIS-derived land surface evapotranspiration with in situ measurements at two ameriflux sites in a semiarid region. J. Geophys. Res.: Atmos 2011, 116, D04106. [Google Scholar]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ 2013, 131, 14–37. [Google Scholar]
- Vermote, E.F.; El Saleous, N.; Justice, C.O.; Kaufman, Y.J.; Privette, J.L.; Remer, L.; Roger, J.C.; Tanré, D. Atmospheric correction of visible to middle-infrared EOS-MODIS data over land surfaces: Background, operational algorithm and validation. J. Geophys. Res.: Atmos 1997, 102, 17131–17141. [Google Scholar]
- Peng, J.; Liu, Y.; Zhao, X.; Loew, A. Estimation of evapotranspiration from MODIS TOA radiances in the Poyang lake basin, China. Hydrol. Earth Syst. Sci 2013, 17, 1431–1444. [Google Scholar]
- Venturini, V.; Bisht, G.; Islam, S.; Jiang, L. Comparison of evaporative fractions estimated from AVHRR and MODIS sensors over south Florida. Remote Sens. Environ 2004, 93, 77–86. [Google Scholar]
- Peng, J.; Liu, Y. Estimation of evaporative fraction from top-of-atmosphere radiance. IAHS-AISH Publ 2011, 343, 47–52. [Google Scholar]
- Jiang, L.; Islam, S. An intercomparison of regional latent heat flux estimation using remote sensing data. Int. J. Remote Sens 2003, 24, 2221–2236. [Google Scholar]
- Long, D.; Singh, V.P. A two-source trapezoid model for evapotranspiration (TTME) from satellite imagery. Remote Sens. Environ 2012, 121, 370–388. [Google Scholar]
- Peng, J.; Liu, Y.; Loew, A. Uncertainties in estimating normalized difference temperature index from TOA radiances. IEEE Trans. Geosci. Remote Sens 2013, 51, 2487–2497. [Google Scholar]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 fluxnet sites. Remote Sens. Environ 2008, 112, 901–919. [Google Scholar]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ 2011, 115, 801–823. [Google Scholar]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; DeFries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The moderate resolution imaging spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens 1998, 36, 1228–1249. [Google Scholar]
- Aubinet, M.; Grelle, A.; Ibrom, A.; Rannik, Ü.; Moncrieff, J.; Foken, T.; Kowalski, A.S.; Martin, P.H.; Berbigier, P.; Bernhofer, C.; et al. Estimates of the Annual Net Carbon and Water Exchange of Forests: The Euroflux Methodology. In Advances in Ecological Research; Fitter, A.H., Raffaelli, D.G., Eds.; Academic Press: Waltham, MA, USA, 1999; pp. 113–175. [Google Scholar]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. Fluxnet: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities. Bull. Am. Meteorol. Soc 2001, 82, 2415–2434. [Google Scholar]
- Fischer, M.L.; Billesbach, D.P.; Berry, J.A.; Riley, W.J.; Torn, M.S. Spatiotemporal variations in growing season exchanges of CO2, H2O, and sensible heat in agricultural fields of the southern great plains. Earth Interact 2007, 11, 1–21. [Google Scholar]
- Amiro, B.D.; Barr, A.G.; Black, T.A.; Iwashita, H.; Kljun, N.; McCaughey, J.H.; Morgenstern, K.; Murayama, S.; Nesic, Z.; Orchansky, A.L.; et al. Carbon, energy and water fluxes at mature and disturbed forest sites, Saskatchewan, Canada. Agric. For. Meteorol 2006, 136, 237–251. [Google Scholar]
- Gilmanov, T.G.; Soussana, J.F.; Aires, L.; Allard, V.; Ammann, C.; Balzarolo, M.; Barcza, Z.; Bernhofer, C.; Campbell, C.L.; Cernusca, A.; et al. Partitioning european grassland net ecosystem CO2 exchange into gross primary productivity and ecosystem respiration using light response function analysis. Agric. Ecosyst. Environ 2007, 121, 93–120. [Google Scholar]
- Ammann, C.; Flechard, C.R.; Leifeld, J.; Neftel, A.; Fuhrer, J. The carbon budget of newly established temperate grassland depends on management intensity. Agric. Ecosyst. Environ 2007, 121, 5–20. [Google Scholar]
- Verma, S.B.; Dobermann, A.; Cassman, K.G.; Walters, D.T.; Knops, J.M.; Arkebauer, T.J.; Suyker, A.E.; Burba, G.G.; Amos, B.; Yang, H.; et al. Annual carbon dioxide exchange in irrigated and rainfed maize-based agroecosystems. Agric. For. Meteorol 2005, 131, 77–96. [Google Scholar]
- Gilmanov, T.G.; Tieszen, L.L.; Wylie, B.K.; Flanagan, L.B.; Frank, A.B.; Haferkamp, M.R.; Meyers, T.P.; Morgan, J.A. Integration of CO2 flux and remotely-sensed data for primary production and ecosystem respiration analyses in the northern great plains: Potential for quantitative spatial extrapolation. Glob. Ecol. Biogeogr 2005, 14, 271–292. [Google Scholar]
- Bolstad, P.V.; Davis, K.J.; Martin, J.; Cook, B.D.; Wang, W. Component and whole-system respiration fluxes in northern deciduous forests. Tree Physiol 2004, 24, 493–504. [Google Scholar]
- Cook, B.D.; Davis, K.J.; Wang, W.; Desai, A.; Berger, B.W.; Teclaw, R.M.; Martin, J.G.; Bolstad, P.V.; Bakwin, P.S.; Yi, C.; et al. Carbon exchange and venting anomalies in an upland deciduous forest in Northern Wisconsin, USA. Agric. For. Meteorol 2004, 126, 271–295. [Google Scholar]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol 2005, 11, 1424–1439. [Google Scholar]
- Rey, A.; Pegoraro, E.; Tedeschi, V.; de Parri, I.; Jarvis, P.G.; Valentini, R. Annual variation in soil respiration and its components in a coppice oak forest in Central Italy. Glob. Chang. Biol 2002, 8, 851–866. [Google Scholar]
- Curtis, P.S.; Hanson, P.J.; Bolstad, P.; Barford, C.; Randolph, J.C.; Schmid, H.P.; Wilson, K.B. Biometric and eddy-covariance based estimates of annual carbon storage in five eastern north American deciduous forests. Agric. For. Meteorol 2002, 113, 3–19. [Google Scholar]
- Reichstein, M.; Rey, A.; Freibauer, A.; Tenhunen, J.; Valentini, R.; Banza, J.; Casals, P.; Cheng, Y.; Grünzweig, J.M.; Irvine, J.; et al. Modeling temporal and large-scale spatial variability of soil respiration from soil water availability, temperature and vegetation productivity indices. Glob. Biogeochem. Cycles 2003, 17, 1104–1118. [Google Scholar]
- Wang, T.; Ciais, P.; Piao, S.; Ottlé, C.; Brender, P.; Maignan, F.; Arain, A.; Cescatti, A.; Gianelle, D.; Gough, C. Controls on winter ecosystem respiration in temperate and boreal ecosystems. Biogeosciences 2011, 8, 2009–2025. [Google Scholar]
- Veenendaal, E.M.; Kolle, O.; Lloyd, J. Seasonal variation in energy fluxes and carbon dioxide exchange for a broad-leaved semi-arid savanna (mopane woodland) in southern Africa. Glob. Chang. Biol 2004, 10, 318–328. [Google Scholar]
- Foken, T.; Aubinet, M.; Finnigan, J.J.; Leclerc, M.Y.; Mauder, M.; Pawu, K.T. Results of a panel discussion about the energy balance closure correction for trace gases. Bull. Am. Meteorol. Soc 2011, 92, ES13–ES18. [Google Scholar]
- Twine, T.E.; Kustas, W.; Norman, J.; Cook, D.; Houser, P.; Meyers, T.; Prueger, J.; Starks, P.; Wesely, M. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol 2000, 103, 279–300. [Google Scholar]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C. Energy balance closure at fluxnet sites. Agric. For. Meteorol 2002, 113, 223–243. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Li, F.; Prueger, J.H.; Mecikalski, J.R. Effects of vegetation clumping on two–source model estimates of surface energy fluxes from an agricultural landscape during smacex. J. Hydrometeorol 2005, 6, 892–909. [Google Scholar]
- Barr, A.G.; van der Kamp, G.; Black, T.A.; McCaughey, J.H.; Nesic, Z. Energy balance closure at the berms flux towers in relation to the water balance of the white gull creek watershed 1999–2009. Agric. For. Meteorol 2012, 153, 3–13. [Google Scholar]
- Nagler, P.L.; Scott, R.L.; Westenburg, C.; Cleverly, J.R.; Glenn, E.P.; Huete, A.R. Evapotranspiration on western U.S. Rivers estimated using the enhanced vegetation index from modis and data from eddy covariance and bowen ratio flux towers. Remote Sens. Environ 2005, 97, 337–351. [Google Scholar]
- Wilson, K.B.; Baldocchi, D.; Falge, E.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Dolman, H.; Field, C.; Goldstein, A.; Granier, A.; et al. Diurnal centroid of ecosystem energy and carbon fluxes at fluxnet sites. J. Geophys. Res.: Atmos 2003, 108, 4664–4676. [Google Scholar]
- Brutsaert, W.; Sugita, M. Application of self-preservation in the diurnal evolution of the surface energy budget to determine daily evaporation. J. Geophys. Res.: Atmos 1992, 97, 18377–18382. [Google Scholar]
- Crago, R.D.; Brutsaert, W. A comparison of several evaporation equations. Water Resour. Res 1992, 28, 951–954. [Google Scholar]
- Choi, M.; Kustas, W.P.; Anderson, M.C.; Allen, R.G.; Li, F.; Kjaersgaard, J.H. An intercomparison of three remote sensing-based surface energy balance algorithms over a corn and soybean production region (Iowa, U.S.) during smacex. Agric. For. Meteorol 2009, 149, 2082–2097. [Google Scholar]
- Eichinger, W.E.; Parlange, M.B.; Stricker, H. On the concept of equilibrium evaporation and the value of the priestley-taylor coefficient. Water Resour. Res 1996, 32, 161–164. [Google Scholar]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc 1982, 63, 1309–1313. [Google Scholar]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl 2008, 18, 1351–1367. [Google Scholar]
- Crago, R.D. Conservation and variability of the evaporative fraction during the daytime. J. Hydrol 1996, 180, 173–194. [Google Scholar]
- Peng, J.; Borsche, M.; Liu, Y.; Loew, A. How representative are instantaneous evaporative fraction measurements of daytime fluxes? Hydrol. Earth Syst. Sci 2013, 17, 3913–3919. [Google Scholar]
- Jiang, L.; Islam, S.; Guo, W.; Singh Jutla, A.; Senarath, S.U.S.; Ramsay, B.H.; Eltahir, E. A satellite-based daily actual evapotranspiration estimation algorithm over South Florida. Glob. Planet. Chang 2009, 67, 62–77. [Google Scholar]
- Jiang, L.; Islam, S.; Carlson, T.N. Uncertainties in latent heat flux measurement and estimation: Implications for using a simplified approach with remote sensing data. Can. J. Remote Sens 2004, 30, 769–787. [Google Scholar]
- Iwasaki, H.; Saito, H.; Kuwao, K.; Maximov, T.C.; Hasegawa, S. Forest decline caused by high soil water conditions in a permafrost region. Hydrol. Earth Syst. Sci 2010, 14, 301–307. [Google Scholar]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar]
- Kustas, W.P.; Li, F.; Jackson, T.J.; Prueger, J.H.; MacPherson, J.I.; Wolde, M. Effects of remote sensing pixel resolution on modeled energy flux variability of croplands in Iowa. Remote Sens. Environ 2004, 92, 535–547. [Google Scholar]
- McCabe, M.F.; Wood, E.F. Scale influences on the remote estimation of evapotranspiration using multiple satellite sensors. Remote Sens. Environ 2006, 105, 271–285. [Google Scholar]




| Site | Location | Biome Type | Latitude | Longitude | Elev (m) | Years | Sample Days | Reference |
|---|---|---|---|---|---|---|---|---|
| USARM | United States | Grasslands | 36.6058 | −97.4888 | 314 | 2003–2006 | 105 | [39] |
| CASF2 | Canada | Grasslands | 54.2539 | −105.878 | 520 | 2003–2005 | 81 | [40] |
| DEGri | Germany | Grasslands | 50.9495 | 13.5125 | 385 | 2004–2009 | 175 | [41] |
| CHOe1 | Switzerland | Grasslands | 47.2856 | 7.7321 | 450 | 2002–2003 | 54 | [42] |
| USNe2 | United States | Croplands | 41.1649 | −96.4701 | 362 | 2001–2005 | 112 | [43] |
| USNe3 | United States | Croplands | 41.1797 | −96.4396 | 363 | 2001–2005 | 115 | [43] |
| USBkg | United States | Croplands | 44.3453 | −96.8362 | 510 | 2004–2006 | 130 | [44] |
| USGoo | United States | Cropland/Natural Vegetation Mosaic | 34.2547 | −89.8735 | 87 | 2002–2006 | 252 | [45] |
| CASF3 | Canada | Closed Shrublands | 54.0916 | −106.005 | 540 | 2003–2005 | 81 | [40] |
| USWCr | United States | Deciduous Broadleaf Forest | 45.8059 | −90.0799 | 520 | 2000–2006 | 297 | [46] |
| DEHai | Germany | Deciduous Broadleaf Forest | 51.0793 | 10.452 | 430 | 2003–2007 | 142 | [47] |
| ITRo1 | Italy | Deciduous Broadleaf Forest | 42.4081 | 11.93 | 235 | 2000–2006 | 251 | [48] |
| USMMS | United States | Mixed Forest | 39.3231 | −86.4131 | 275 | 2000–2005 | 189 | [49] |
| ITNon | Italy | Mixed Forest | 44.6898 | 11.0887 | 25 | 2001–2003 | 106 | [50] |
| DEMeh | Germany | Mixed Forest | 51.2753 | 10.6555 | 286 | 2003–2006 | 110 | [51] |
| BWMa1 | Botswana | Savannas | −19.917 | 23.5603 | 950 | 2000–2001 | 211 | [52] |
| Site | BIAS | MAD | RMSD | Relative Error(%) | R |
|---|---|---|---|---|---|
| USARM | −0.019 | 0.029 | 0.036 | −5.33 | 0.990 |
| CASF2 | −0.016 | 0.025 | 0.032 | −4.28 | 0.989 |
| DEGri | −0.019 | 0.032 | 0.041 | −2.82 | 0.961 |
| CHOe1 | −0.033 | 0.036 | 0.045 | −4.63 | 0.973 |
| USNe2 | −0.020 | 0.027 | 0.032 | −4.33 | 0.996 |
| USNe3 | −0.024 | 0.030 | 0.035 | −5.47 | 0.995 |
| USBkg | −0.027 | 0.034 | 0.048 | −4.01 | 0.978 |
| USGoo | −0.018 | 0.023 | 0.031 | −3.25 | 0.991 |
| CASF3 | −0.011 | 0.033 | 0.046 | −2.89 | 0.952 |
| USWCr | −0.017 | 0.032 | 0.042 | −3.78 | 0.988 |
| DEHai | −0.013 | 0.033 | 0.041 | −3.14 | 0.964 |
| ITRo1 | −0.017 | 0.032 | 0.042 | −4.85 | 0.968 |
| USMMS | −0.021 | 0.032 | 0.042 | −4.71 | 0.991 |
| ITNon | −0.035 | 0.050 | 0.084 | −7.19 | 0.931 |
| DEMeh | −0.021 | 0.029 | 0.036 | −4.47 | 0.985 |
| BWMa1 | −0.016 | 0.025 | 0.035 | −6.33 | 0.980 |
| All sites | −0.020 | 0.031 | 0.042 | −4.47 | 0.977 |
| Site | Biome Type | BIAS | MAD | RMSD | R |
|---|---|---|---|---|---|
| USARM | Grasslands | 0.004 | 0.129 | 0.153 | 0.741 |
| CASF2 | Grasslands | 0.077 | 0.160 | 0.190 | 0.524 |
| DEGri | Grasslands | −0.035 | 0.141 | 0.182 | 0.382 |
| CHOe1 | Grasslands | −0.013 | 0.080 | 0.103 | 0.714 |
| USNe2 | Croplands | 0.011 | 0.150 | 0.177 | 0.787 |
| USNe3 | Croplands | −0.003 | 0.115 | 0.140 | 0.846 |
| USBkg | Croplands | −0.080 | 0.133 | 0.160 | 0.790 |
| USGoo | Cropland/Natural Vegetation Mosaic | 0.007 | 0.133 | 0.166 | 0.786 |
| CASF3 | Closed Shrublands | 0.020 | 0.143 | 0.172 | 0.369 |
| USWCr | Deciduous Broadleaf Forest | 0.028 | 0.142 | 0.172 | 0.702 |
| DEHai | Deciduous Broadleaf Forest | 0.120 | 0.184 | 0.224 | 0.400 |
| ITRo1 | Deciduous Broadleaf Forest | −0.052 | 0.161 | 0.202 | 0.365 |
| USMMS | Mixed Forest | −0.024 | 0.132 | 0.167 | 0.780 |
| ITNon | Mixed Forest | −0.002 | 0.145 | 0.173 | 0.725 |
| DEMeh | Mixed Forest | 0.033 | 0.118 | 0.142 | 0.807 |
| BWMa1 | Savannas | 0.194 | 0.289 | 0.327 | −0.280 |
| All sites | 0.018 | 0.147 | 0.178 | 0.590 |
| Reference | Sensor Used | BIAS (Mean Value) | RMSD (Mean Value) | R (Mean Value) |
|---|---|---|---|---|
| [13] | MODIS | −0.130–0.100 (0.010) | 0.110–0.280 (0.170) | 0.100–0.900 (0.710) |
| [29] | MODIS, AVHRR | −0.069–0.088 (0.009) | 0.081–0.188 (0.130) | 0.442–0.768 (0.580) |
| [10] | MODIS | −0.182–0.131 (−0.018) | 0.077–0.244 (0.157) | −0.634–0.89 (0.437) |
| [19] | MSG SEVIRI | −0.040–0.120 (0.060) | 0.130–0.190 (0.160) | 0.350–0.640 (0.510) |
| [68] | AVHRR | −0.038–0.154 (0.049) | 0.119–0.242 (0.158) | −0.868–0.037 (−0.414) |
| [25] | MODIS | −0.039–0.067 (0.057) | 0.100–0.125 (0.112) | 0.338–0.648 (0.496) |
| This study | MODIS | −0.08–0.12 (0.018) | 0.103–0.224 (0.178) | −0.280–0.846 (0.590) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Peng, J.; Loew, A. Evaluation of Daytime Evaporative Fraction from MODIS TOA Radiances Using FLUXNET Observations. Remote Sens. 2014, 6, 5959-5975. https://doi.org/10.3390/rs6075959
Peng J, Loew A. Evaluation of Daytime Evaporative Fraction from MODIS TOA Radiances Using FLUXNET Observations. Remote Sensing. 2014; 6(7):5959-5975. https://doi.org/10.3390/rs6075959
Chicago/Turabian StylePeng, Jian, and Alexander Loew. 2014. "Evaluation of Daytime Evaporative Fraction from MODIS TOA Radiances Using FLUXNET Observations" Remote Sensing 6, no. 7: 5959-5975. https://doi.org/10.3390/rs6075959
APA StylePeng, J., & Loew, A. (2014). Evaluation of Daytime Evaporative Fraction from MODIS TOA Radiances Using FLUXNET Observations. Remote Sensing, 6(7), 5959-5975. https://doi.org/10.3390/rs6075959






