Classification of Ultra-High Resolution Orthophotos Combined with DSM Using a Dual Morphological Top Hat Profile
Abstract
:1. Introduction
1.1. Background
1.2. Related Works in Classification Using Spatial Information
1.3. Related Works in Classification and Data Interpretation Using Height Information
1.4. The Proposed Spatial Feature and Object-Based Classification
- (1)
- There are rarely studies addressing the classification problem in ultra-high resolution detail, mainly due to the high spectral ambiguity and large perspective distortion. We incorporate 3D information to improve the traditional land cover classification problem and investigate its accuracy potential in ultra-high resolution data.
- (2)
- 2D spatial features are used to enhance the classification results. We aim to develop an effective and computationally-efficient spatial feature that can be applied to the 3D information, for achieving higher accuracy than traditional spatial features.
- (3)
- The existing research works lack quantitative evaluation on the major spatial features and their performance on the 3D information. We aim to provide such comparative studies in the course of the presentation of our novel 3D spatial feature.
2. Methods
2.1. Dual Morphological Top-Hat Profiles with Adaptive Scale Estimation
2.1.1. Morphological Profiles
2.1.2. Morphological Top-Hat Profiles
- Top-hat by reconstruction:
- Top-hat by erosion:

2.1.3. Adaptive Scale Estimation

2.2. Spectral- and Height-Assisted Segmentation for Object-Based Classification
2.2.1. Height-Assisted Synergic Mean-Shift Segmentation

2.2.2. Classification Combining the Spectral and DMTHP Features

3. Experimental Results
3.1. Experimental Setup
| Experiment 1 | Experiment 2 | ||
|---|---|---|---|
| Training sample for each class | Building | 51 | 101 |
| Road | 72 | 103 | |
| Tree | 51 | 101 | |
| Car | 53 | 110 | |
| Grass | 52 | 103 | |
| Ground | 53 | / | |
| Shadow | 53 | / | |
| Water | / | 118 | |
| Total training samples | 385 | 636 | |
| Total test samples | 10,312 | 32,947 | |
| Total segments | 41,465 | 46,867 | |
| Percentage (%) | 0.93 | 1.35 | |
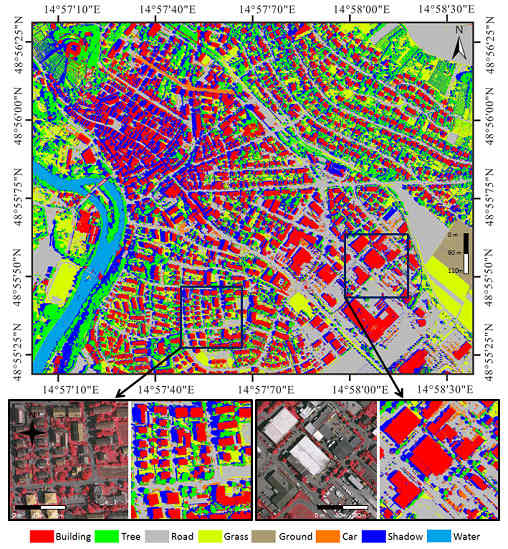
3.2. Experiment with Test Dataset 1

| Building | Road | Tree | Car | Grass | Ground | Shadow | CV | OA | |
|---|---|---|---|---|---|---|---|---|---|
| (P) | 94.77 | 95.97 | 96.22 | 83.04 | 99.33 | 72.20 | 99.23 | 88.49 | 93.98 |
| (U) | 98.66 | 75.87 | 98.37 | 98.88 | 96.90 | 93.15 | 85.81 |
3.3. Experiment with Test Dataset 2

| Building | Road | Tree | Car | Grass | Water | CV | OA | |
|---|---|---|---|---|---|---|---|---|
| (P) | 96.03 | 96.30 | 90.33 | 83.04 | 79.63 | 91.95 | 89.15 | 94.48 |
| (U) | 89.26 | 85.71 | 97.59 | 89.86 | 90.91 | 99.99 |
3.4. Test Dataset 3

4. Validations and Discussions
4.1. Comparative Studies and Validations


| % | PCA | PCA + DMP | PCA + Height | PCA + nDSM | PCA + DMTHP (Regular) | PCA + DMTHP (Adaptive) | |
|---|---|---|---|---|---|---|---|
| Building | (P) | 60.74 | 76.98 | 77.36 | 89.53 | 92.19 | 94.77 |
| (U) | 88.18 | 95.48 | 95.21 | 95.15 | 96.17 | 98.66 | |
| Road | (P) | 89.28 | 96.29 | 67.25 | 96.62 | 96.29 | 95.97 |
| (U) | 78.99 | 76.24 | 72.21 | 75.56 | 76.06 | 75.87 | |
| Tree | (P) | 70.04 | 88.36 | 84.67 | 90.41 | 94.00 | 96.22 |
| (U) | 81.38 | 96.90 | 84.68 | 96.25 | 97.99 | 98.37 | |
| Car | (P) | 64.87 | 73.41 | 69.08 | 70.03 | 78.57 | 83.04 |
| (U) | 93.19 | 94.73 | 96.71 | 95.77 | 98.85 | 98.88 | |
| Grass | (P) | 83.43 | 99.03 | 84.22 | 97.34 | 99.16 | 99.33 |
| (U) | 75.92 | 91.42 | 84.00 | 91.55 | 96.35 | 96.90 | |
| Ground | (P) | 90.19 | 72.22 | 80.35 | 72.18 | 72.22 | 72.20 |
| (U) | 70.37 | 76.80 | 61.66 | 87.76 | 93.26 | 93.15 | |
| Shadow | (P) | 92.35 | 99.37 | 98.09 | 98.22 | 99.40 | 99.23 |
| (U) | 74.27 | 79.83 | 79.35 | 80.23 | 81.61 | 85.81 | |
| CV | 71.58 | 85.08 | 80.49 | 81.94 | 87.62 | 88.49 | |
| OA | 71.50 | 83.61 | 80.29 | 89.98 | 92.27 | 93.98 | |
| % | PCA | DMP | PCA + Height | PCA + nDSM | PCA + DMTHP (regular) | PCA + DMTHP (adaptive) | |
|---|---|---|---|---|---|---|---|
| Building | (P) | 47.96 | 93.60 | 91.32 | 90.29 | 89.68 | 96.03 |
| (U) | 58.90 | 87.23 | 83.46 | 81.15 | 85.42 | 89.26 | |
| Road | (P) | 77.65 | 95.82 | 94.19 | 94.43 | 95.60 | 96.30 |
| (U) | 62.44 | 79.17 | 83.22 | 85.55 | 79.25 | 85.71 | |
| Tree | (P) | 61.37 | 91.06 | 84.78 | 89.10 | 88.15 | 90.33 |
| (U) | 89.25 | 87.27 | 82.71 | 96.68 | 97.86 | 97.59 | |
| Car | (P) | 73.40 | 76.20 | 70.44 | 71.22 | 79.32 | 79.63 |
| (U) | 68.58 | 88.07 | 82.41 | 82.93 | 92.31 | 89.86 | |
| Grass | (P) | 93.43 | 86.30 | 81.25 | 96.95 | 96.96 | 97.21 |
| (U) | 71.73 | 90.29 | 82.51 | 89.22 | 90.19 | 90.91 | |
| Water | (P) | 90.96 | 90.88 | 90.97 | 91.66 | 90.88 | 91.95 |
| (U) | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | 99.99 | |
| CV | 63.85 | 86.60 | 83.87 | 85.51 | 86.41 | 89.15 | |
| OA | 63.93 | 92.40 | 88.87 | 91.53 | 91.70 | 94.48 | |
4.2. Uncertainties, Errors, Accuracies and Performance
| Time (s) | Experiment 1 | Experiment 2 | ||||
|---|---|---|---|---|---|---|
| DMP | DMTHP (Regular) | DMTHP (Adaptive) | DMP | DMTHP (Regular) | DMTHP (Adaptive) | |
| Segmentation | 471.20 | 468.54 | 468.54 | 821.51 | 821.25 | 821.25 |
| Feature Extraction | 396.08 | 260.57 | 71.87 | 551.48 | 360.83 | 457.37 |
| Training | 1.31 | 7.44 | 0.68 | 2.38 | 1.18 | 0.76 |
| Classification | 1.28 | 2.03 | 0.81 | 1.44 | 1.15 | 1.12 |
| Total | 869.87 | 738.59 | 541.96 | 1376.81 | 1184.41 | 1280.50 |
5. Conclusions
- (1)
- We have presented a novel feature DMTHP with adaptive scale selection to address large-scale variation of urban objects in the UHR data, as well as reduced the computational load and feature dimensionality, which have obtained the optimal classification accuracy in comparison with existing features (2%–10% enhancement to the well-known DMP feature and other height features).
- (2)
- We have demonstrated that in the best case, the proposed method has improved the classification accuracy to 94%, as compared to 64% using only spectral information. This is important to draw the attention of the land cover mappers to consider the use of the height information for land cover classification tasks.
- (3)
- A complete quantitative analysis of different UHR data with a 9-cm and a 5-cm GSD has been performed, with comparative studies on some of the existing height features. This provides valid insights for researchers working on 3D spatial features.
- (4)
- We have performed a qualitative experiment with 20,000 × 20,000 pixels, which has shown that the proposed method can be used in a large-scale dataset to obtain very detailed land cover information.
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Tucker, C.J.; Townshend, J.R.; Goff, T.E. African land-cover classification using satellite data. Science 1985, 227, 369–375. [Google Scholar] [CrossRef] [PubMed]
- De Fries, R.; Hansen, M.; Townshend, J.; Sohlberg, R. Global land cover classifications at 8 km spatial resolution: The use of training data derived from Landsat imagery in decision tree classifiers. Int. J. Remote Sens. 1998, 19, 3141–3168. [Google Scholar] [CrossRef]
- Collins, J.B.; Woodcock, C.E. An assessment of several linear change detection techniques for mapping forest mortality using multitemporal Landsat TM data. Remote Sens. Environ. 1996, 56, 66–77. [Google Scholar] [CrossRef]
- Yuan, F.; Sawaya, K.E.; Loeffelholz, B.C.; Bauer, M.E. Land cover classification and change analysis of the twin cities (Minnesota) metropolitan area by multitemporal Landsat remote sensing. Remote Sens. Environ. 2005, 98, 317–328. [Google Scholar] [CrossRef]
- Dell’Acqua, F.; Gamba, P.; Ferrari, A.; Palmason, J.; Benediktsson, J.; Arnason, K. Exploiting spectral and spatial information in hyperspectral urban data with high resolution. IEEE Geosci. Remote Sens. Lett. 2004, 1, 322–326. [Google Scholar] [CrossRef]
- Pacifici, F.; Chini, M.; Emery, W.J. A neural network approach using multi-scale textural metrics from very high-resolution panchromatic imagery for urban land-use classification. Remote Sens. Environ. 2009, 113, 1276–1292. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. An SVM ensemble approach combining spectral, structural, and semantic features for the classification of high-resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 257–272. [Google Scholar] [CrossRef]
- Qin, R. An object-based hierarchical method for change detection using unmanned aerial vehicle images. Remote Sens. 2014, 6, 7911–7932. [Google Scholar] [CrossRef]
- Qin, R.; Grün, A.; Huang, X. UAV project—Building a reality-based 3D model. Coordinates 2013, 9, 18–26. [Google Scholar]
- Mylonas, S.K.; Stavrakoudis, D.G.; Theocharis, J.B.; Mastorocostas, P. Classification of remotely sensed images using the genesis fuzzy segmentation algorithm. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5352–5376. [Google Scholar] [CrossRef]
- Tuia, D.; Ratle, F.; Pozdnoukhov, A.; Camps-Valls, G. Multisource composite kernels for urban-image classification. IEEE Geosci. Remote Sens. Lett. 2010, 7, 88–92. [Google Scholar] [CrossRef]
- Hester, D.B.; Cakir, H.I.; Nelson, S.A.; Khorram, S. Per-pixel classification of high spatial resolution satellite imagery for urban land-cover mapping. Photogramm. Eng. Remote Sens. 2008, 74, 463–471. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, X.; Huang, B.; Li, P. A pixel shape index coupled with spectral information for classification of high spatial resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2950–2961. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Shackelford, A.K.; Davis, C.H. A hierarchical fuzzy classification approach for high-resolution multispectral data over urban areas. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1920–1932. [Google Scholar] [CrossRef]
- Yoo, H.Y.; Lee, K.; Kwon, B.-D. Quantitative indices based on 3D discrete wavelet transform for urban complexity estimation using remotely sensed imagery. Int. J. Remote Sens. 2009, 30, 6219–6239. [Google Scholar] [CrossRef]
- Pesaresi, M.; Benediktsson, J.A. A new approach for the morphological segmentation of high-resolution satellite imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 309–320. [Google Scholar] [CrossRef]
- Zhang, Y. Optimisation of building detection in satellite images by combining multispectral classification and texture filtering. ISPRS J. Photogramm. Remote Sens. 1999, 54, 50–60. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. A multiscale urban complexity index based on 3D wavelet transform for spectral–spatial feature extraction and classification: An evaluation on the 8-channel worldview-2 imagery. Int. J. Remote Sens. 2012, 33, 2641–2656. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Qin, R. A mean shift vector-based shape feature for classification of high spatial resolution remotely sensed imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1974–1985. [Google Scholar] [CrossRef]
- Vincent, L. Morphological grayscale reconstruction in image analysis: Applications and efficient algorithms. IEEE Trans. Image Process. 1993, 2, 176–201. [Google Scholar] [CrossRef] [PubMed]
- Benediktsson, J.A.; Pesaresi, M.; Amason, K. Classification and feature extraction for remote sensing images from urban areas based on morphological transformations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1940–1949. [Google Scholar] [CrossRef]
- Walter, V. Object-based classification of remote sensing data for change detection. ISPRS J. Photogramm. Remote Sens. 2004, 58, 225–238. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Gong, W. Information fusion of aerial images and LIDAR data in urban areas: Vector-stacking, re-classification and post-processing approaches. Int. J. Remote Sens. 2011, 32, 69–84. [Google Scholar] [CrossRef]
- Chaabouni-Chouayakh, H.; Reinartz, P. Towards automatic 3D change detection inside urban areas by combining height and shape information. Photogram. Fernerkund. Geoinf. 2011, 2011, 205–217. [Google Scholar] [CrossRef]
- Qin, R. Change detection on LOD 2 building models with very high resolution spaceborne stereo imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 179–192. [Google Scholar] [CrossRef]
- Qin, R.; Gruen, A. 3D change detection at street level using mobile laser scanning point clouds and terrestrial images. ISPRS J. Photogramm. Remote Sens. 2014, 90, 23–35. [Google Scholar] [CrossRef]
- Qin, R.; Huang, X.; Gruen, A.; Schmitt, G. Object-based 3-D building change detection on multitemporal stereo images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 5, 2125–2137. [Google Scholar] [CrossRef]
- Qin, R.; Tian, J.; Reinartz, P. Spatiotemporal inferences for use in building detection using series of very-high-resolution space-borne stereo images. Int. J. Remote Sens. 2015. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, Q.; Jia, X.; Benediktsson, J.A. A novel MKL model of integrating LIDAR data and MSI for urban area classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5312–5326. [Google Scholar]
- Cramer, M. The DGPF-test on digital airborne camera evaluation overview and test design. Photogram.-Fernerkund.-Geoinf. 2010, 2010, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Tuia, D.; Pacifici, F.; Kanevski, M.; Emery, W.J. Classification of very high spatial resolution imagery using mathematical morphology and support vector machines. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3866–3879. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. A multidirectional and multiscale morphological index for automatic building extraction from multispectral Geoeye-1 imagery. Photogramm. Eng. Remote Sens. 2011, 77, 721–732. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. Morphological building/shadow index for building extraction from high-resolution imagery over urban areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 161–172. [Google Scholar] [CrossRef]
- Qin, R.; Fang, W. A hierarchical building detection method for very high resolution remotely sensed images combined with dsm using graph cut optimization. Photogramm. Eng. Remote Sens. 2014, 80, 37–48. [Google Scholar] [CrossRef]
- Christoudias, C.M.; Georgescu, B.; Meer, P. Synergism in low level vision. In Proceedings of the 16th International Conference on Pattern Recognition, Quebec, ON, Canada, 11–15 August 2002; IEEE: Quebec, ON, Canada, 2002; pp. 150–155. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 6, 679–698. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gruen, A.; Huang, X.; Qin, R.; Du, T.; Fang, W.; Boavida, J.; Oliveira, A. Joint processing of UAV imagery and terrestrial mobile mapping system data for very high resolution city modeling. ISPRS J. Photogramm. Remote Sens. 2013, 1, 175–182. [Google Scholar] [CrossRef]
- Hirschmüller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Wenzel, K.; Rothermel, M.; Fritsch, D. Sure–the IFP software for dense image matching. Photogramm. Week 2013, 13, 59–70. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Qin, R.; Huang, X.; Fang, Y.; Liu, L. Classification of Ultra-High Resolution Orthophotos Combined with DSM Using a Dual Morphological Top Hat Profile. Remote Sens. 2015, 7, 16422-16440. https://doi.org/10.3390/rs71215840
Zhang Q, Qin R, Huang X, Fang Y, Liu L. Classification of Ultra-High Resolution Orthophotos Combined with DSM Using a Dual Morphological Top Hat Profile. Remote Sensing. 2015; 7(12):16422-16440. https://doi.org/10.3390/rs71215840
Chicago/Turabian StyleZhang, Qian, Rongjun Qin, Xin Huang, Yong Fang, and Liang Liu. 2015. "Classification of Ultra-High Resolution Orthophotos Combined with DSM Using a Dual Morphological Top Hat Profile" Remote Sensing 7, no. 12: 16422-16440. https://doi.org/10.3390/rs71215840
APA StyleZhang, Q., Qin, R., Huang, X., Fang, Y., & Liu, L. (2015). Classification of Ultra-High Resolution Orthophotos Combined with DSM Using a Dual Morphological Top Hat Profile. Remote Sensing, 7(12), 16422-16440. https://doi.org/10.3390/rs71215840