Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data
Abstract
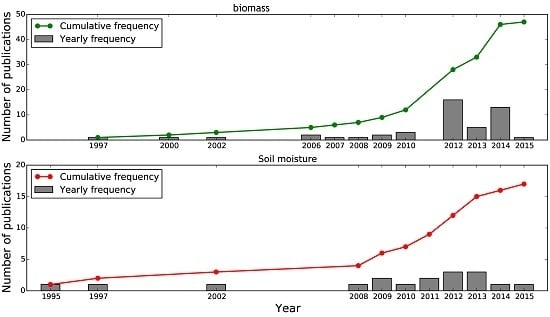
:1. Introduction

2. Retrieval Approaches: Concepts and Challenges
2.1. Limitations and Challenges
- The complexity and non-linearity that often characterize the relationship between remote sensing measurements and target variables [10]: On the one hand, geo-/bio-physical variables may affect the electromagnetic properties of a target differently along their range of variability, potentially leading to signal saturation and other nonlinear effects [11]. On the other hand, electromagnetic radiation usually shows a non-uniform sensitivity to the different physical phenomena depending, for instance, on the wavelength of the signal or the acquisition geometry [12,13,14].
- The ill-posed nature of the retrieval problem: The total electromagnetic response of a target is typically the result of multiple contributions, each one determined by a different structural, chemical or physical characteristic [15]. This aspect determines the so-called variable equifinality issue, or parameter ambiguity, i.e., the phenomenon whereby similar electromagnetic responses can be associated with different geo-/bio-physical variable configurations [16,17].
- The image formation process at the sensor level: Remote sensing sensors provide a quantized representation of the investigated scene in the spatial domain. The electromagnetic energy measured within an elementary resolution cell is the result of the presence of multiple objects on the ground with slightly (or sometimes strongly) different characteristics. This behavior is the origin of a mixed contribution at the sensor level. Even by increasing the spatial resolution, this mixing phenomenon cannot be completely canceled, as it remains in pixels representing the boundaries between objects [18]. Moreover, the response corresponding to a pixel can also be affected by radiation components coming from the surrounding of the investigated area [19].
- The influence of external disturbing factors: The remote sensing acquisition system is not ideal, but affected by disturbing factors, such as the noise and non-linearity at the sensor level and the presence of the atmosphere. Even if these issues can be determined and corrected to some extent with the help of calibration and atmospheric correction procedures, they may still corrupt the signal measured at the sensor level and, thus, introduce further ambiguity and complexity in the retrieval process [20,21].
2.2. Retrieval Problem
2.3. Classical Parameter Retrieval Methodologies
2.4. Machine Learning Methodologies
3. Retrieval of Essential Variables: Biomass
| Biome | Coverage (%) [42] | Carbon Stocks (Mg/ha) [43] | ||
|---|---|---|---|---|
| Above Ground | Soil | Total | ||
| Grasslands/Herbaceous | 31.5 | 21 | 160 | 181 |
| Forests | 27.7 | 97 | 113 | 210 |
| Croplands | 12.6 | 2 | 80 | 82 |
- Utilization of satellite-driven parameters (i.e., vegetation indices, textural features, backscatter) for the development of regression-based retrieval models,
- Machine learning algorithms and
- Simulation or biophysical models (data assimilation)
3.1. Grassland Biomass Retrieval
3.2. Croplands Biomass Retrieval
| Reference | Sensor | Crop/Parameter | Model/Method | Performance |
|---|---|---|---|---|
| [57] | UAV | Wheat and rapeseed crops; green area index | Radiative transfer inversion model | |
| [55] | Test-bed, X-band spectrometer | Spinach; biomass, LAI, average plant height, soil moisture content | ANN | Performance analysis of different transfer functions |
| [59] | Field spectrometry | Winter wheat; LAI | Data assimilation; Kalman filter; Crop Environment REsource Synthesis (CERES) wheat crop model | |
| [60] | Field spectrometry | Rice; LAI, green leaf chlorophyll density (GLCD) | Support Vector Machines (SVM) | units, mg m |
| [58] | Field spectrometry (Hyperspectral) | Sugar beet (detection of plant diseases) | SVM (classification) | 84.05%–92.35% |
| [56] | Aerial hyperspectral | Corn; biomass, yield, plant height, nitrogen, chlorophyll, leaf greenness | SVM | |
| [54,55] | Aerial (color infrared) | Mapping Ridolfia segetum infestations in sunflower crop | Evolutionary Product-Unit Neural Networks (EPUNNs), SVM, Logistic Regression (LR), Logistic Regression using Initial covariates and Product Units (LRIPU), logistic model trees (LMT) | LRIPU: |
| [61] | Aerial photographs | Sunflower yield mapping | EPUNN, Sparse Multinomial Logistic Regression (SMLR) | SMLR: ; EPUNN: |
| [56] | Airborne (Hyperspectral) | Corn; weed, nitrogen stress | ANN, SVM | SVM: ; ANN: |
| [62] | L-/X-band field radiometer | Wheat; plant water content (PWC), soil moisture content (SMC) | ANN | , |
| Reference | Sensor | Crop/Parameter | ML Classifier | Performance |
|---|---|---|---|---|
| [63] | Landsat-5 TM and -7 ETM+ | Discriminating various crop types | SVM | |
| [64] | TerraSAR-X, RADARSAT-2 | Corn, soybeans | Decision tree classification (DTC) | |
| [65] | Hyperion satellite hyperspectral sensor | Soybeans | Optimally-pruned extreme learning machines (OP-ELM), SVM, 1-NN, C 4.5 | OP-ELM () produced the best results |
| [66] | RapidEye | Different crop types | SVM, random forest (RF) | |
| [67] | Hyperion (hyperspectral), QuickBird | Land cover types, including permanent crops | SVM, object-based classification (OBC) | SVM: ; OBC: |
| [68] | Landsat TM | Land cover (14 classes) | RF, classification tree (CT) | Crops (, ) |
| [69] | Hyperion (hyperspectral) | Land cover/use (10 classes) | SVM, ANN | SVM: ; ANN: |
| [70] | SPOT-5 | Corn, cotton, grain sorghum, sugarcane | SVM | 84.3%–94.0% |
| [71] | ALOS | Paddy rice mapping | SVM | |
| [72] | MODIS, AVHRR | Land cover mapping (25 classes) | DTC, Gaussian adaptive resonance theory (ART), fuzzy ART neural network (ARTNN), maximum likelihood classification (MLC) | MLC: 495–53%; DT: ; Gaussian ART: ; fuzzy ARTNN: |
3.3. Forest Biomass Retrieval
| Reference | Sensor | Parameter(s) | ML algorithm | Performance |
|---|---|---|---|---|
| [102] | ALOS PALSAR | Biomass | Bagging stochastic gradient boosting (BagSGB) | |
| [103] | QuickBird | Height, biomass, volume | Support vector regression (SVR) | |
| [104] | TerraSAR-X | Stem volume (v), basal area (a), height (h), diameter (d) | Random forest | RMSE (%): v = 34, a = 29, h = 14, d = 19.7 |
| [105] | WorldView-2 | Biomass | Random forest (RF), regression | RF: RMSE = 12.9%, regression: RMSE = 15.9% |
| [106] | Landsat | Above-ground woody biomass | RF | |
| [107] | SPOT-5, LiDAR | Above-ground biomass | RF | |
| [108] | ASTER | Volume (v), basal area (a), stems (s) | k-NN, SVR, RF | RF: , , ; SVR: , , ; k-NN: , |
| [79] | Landsat-7 | Biomass | SVM | SVM = 84.62%; regressive analysis = 82.93% |
| [109] | Landsat time series | Forest biomass dynamics | Reduced major axis, gradient nearest neighbor, RF | RF: , |
4. Retrieval of Essential Variables: Soil Moisture
- Empirical approaches
- Approaches based on theoretical electromagnetic models
- Machine learning approaches.
4.1. Machine Learning Methodologies for Soil Moisture Retrieval
- ANN:
- Fuzzy logic:
- Multivariate statistics:
- ANN: , and ;
- RVM: , and ;
- SVM: , and ;
- GLM: , and .
| Reference | Sensor | Parameter | Model/Method | Performance |
|---|---|---|---|---|
| [119] | POLARimetric SCATterometer (POLARSCAT) (airborne) | Soil moisture | Integral equation model (IEM) + multilayer perceptron basis function | m/m |
| [121] | ENVISAT ASAR/RADARSAT-2/ Optical data for vegetation correction | Soil moisture | IEM + multilayer perceptron (MLP) | m/m < < 0.06 m/m based on different input configurations |
| [123] | Ground-based scatterometer data | Soil moisture/leaf area index/biomass | Back-propagation learning algorithm (BPNN) | m/m |
| [122] | RADARSAT-2 | Soil moisture/surface roughness | IEM + MLP | m/m without prior information, m/m with prior information |
| [124] | Advanced Microwave Scanning Radiometer-EOS (AMSR-E) | Soil moisture | BPNN | m/m |
| [127] | RADARSAT-2 | Soil moisture | Support vector regression (SVR) | m/m |
| [128] | TRMM + AVHRR | Soil moisture | SVM | m/m |
| [129] | SMOS | Soil moisture downscaling | SVR, relevance vector machine (RVM), ANN | ANN: m/m, SVR and RVM: m/m |
| [130] | Synthetic data | Soil moisture downscaling | Self-regularized regressive model (SRRM) | m/m |
| [132] | Ground data (soil moisture and meteorological time series) | Soil moisture forecast | SVM | m/m ( m/m with only meteorological data, 0.076–0.086 m/m with only soil moisture data) |
| [133] | AirSAR data (SMEX02) | Soil moisture | SVM, RVM | SVM: m/m RVM: m/m |
| [122] | Multispectral sensor on UAV | Soil moisture | ANN | m/m |
5. Conclusions
| Algorithms | Examples | Advantages | Disadvantages |
|---|---|---|---|
| Regression | Linear, power, logistic regression | The principal advantage of empirical modeling is its simplicity, availability, interpretability and acceptance among the scientific community. | In a nonlinear dynamic environment, the data from chaotic systems do not correspond to the strong assumptions of a linear model. These models do not have a physical basis and are mostly used for site-specific analysis or model development. |
| Machine learning | Often much more accurate than human-crafted rules, as they are data driven. Automatic method to search for hypotheses explaining data. Flexible and can be applied to any learning task. Rich interplay between theory and practice, with improved results as datasets increase. | Data-driven methods need many labeled data, requiring extensive ground truth datasets. Typically require some programming knowledge. | |
| Decision tree | Conditional decision trees, C5.0, decision stump | Simple to understand and to interpret. Trees can be visualized. Requires little data preparation. Fast and able to handle both numerical and categorical data. | Decision-tree learners can create over-complex trees that do not generalize the data well, and trees can be biased if some classes dominate. |
| Bayesian | Bayesian network, naive, Gaussian naive and multinomial naive Bayes | Provide good results with small samples size. Past information about the parameter can be used for future analysis. It provides a natural and theoretically solid mechanism to combine prior information and data. | It is difficult to select prior, and posterior distributions are heavily influenced by the priors. The models with a large number of parameters are computationally high in cost. |
| Artificial neural network | Perceptron, back-propagation, radial basis function network | Artificial neural networks have the power to retrieve the complex, dynamic and non-linear patterns from the data. Being one of the oldest machine learning methods, they are well studied and are easy to implement as many libraries and software tools are available. | Artificial neural networks are “black boxes”, and the user has no role/control, except providing the input data. With large datasets, the process gets slow. Back-propagation networks tend to be slower to train than other types of networks and sometimes require thousands of epochs. |
| Deep learning | Deep belief networks, convolutional neural networks | Capable of processing the complex input data and learning tasks. It is capable of “learning features” from the data at each level. | Deep learning is not an easy to use method, but packages (Torch7 and Theano + Pylearn2) are available for users for different applications. |
| Ensemble | Random forest, bagging, gradient boosting | The basic idea is to train a set of experts and to allow them to vote. | This provides an improved estimation accuracy. It is difficult to understand an ensemble of classifiers. |
| Support vectors | Support vector machines, support vector regression | It has a regularization parameter and uses the kernel trick. SVM is defined by a convex optimization problem, and it is an approximation to a bound on the test error rate. | Kernel models are sensitive to over-fitting. From a practical perspective, it gives poor results if the number of features is much greater than the number of samples. |
- The development of retrieval methodologies that can fully exploit the high temporal frequency of new generation and upcoming satellite remote sensing systems to improve the temporal consistency and accuracy of the estimation process. Moreover, the combined use of multiple frequency (C-, X- and L-band) can further improve the retrieval process, but being in its infancy, this needs further development.
- The study of automatic methods for the adaptation of the retrieval system to different domains (e.g., several study areas with slightly different topographic and phenological conditions) [136].
- Generalization of the proposed methods and systems to the retrieval of different geo-/bio-physical variables from a new generation of satellite remote sensing imagery.
Author Contributions
Conflicts of Interest
References
- Eisfelder, C.; Kuenzer, C.; Dech, S. Derivation of biomass information for semi-arid areas using remote-sensing data. Int. J. Remote Sens. 2012, 33, 2937–2984. [Google Scholar] [CrossRef]
- Global Terrestrial Observing System. Assessment of the Status of the Development of the Standards for the Terrestrial Essential Climate Variables; Global Terrestrial Observing System: Viterbo, Italy, 2015. [Google Scholar]
- UNEP-WCMC. Carbon in Drylands: Desertification, Climate Change and Carbon Finance. A UNEP-UNDP-UNCCD Technical Note. In Proceedings of the Seventh Session of the Committee for the Review of the Implementation of the Convention (CRIC 7), Istanbul, Turkey, 3–14 November 2008.
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Toan, T.L.; Quegan, S. BIOMASS Biomass Monitoring Mission for Carbon Assessment; CESBIO: Toulouse, France, 2015. [Google Scholar]
- Malhi, Y.; Meir, P.; Brown, S. Forests, carbon and global climate. Philos. Trans. R. Soc. Lond. A 2002, 360, 1567–1591. [Google Scholar] [CrossRef] [PubMed]
- Vatsavai, R.R.; Ganguly, A.; Chandola, V.; Stefanidis, A.; Klasky, S.; Shekhar, S. Spatiotemporal data mining in the era of big spatial data: Algorithms and applications. In Proceedings of the 1st ACM SIGSPATIAL International Workshop on Analytics for Big Geospatial Data, Redondo Beach, CA, USA, 6 November 2012; pp. 1–10.
- Schanda, E. Physical Fundamentals of Remote Sensing; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, Volume I: Fundamentals and Radiometry; Artech House Publishers: Norwood, MA, USA, 1986. [Google Scholar]
- Twomey, S. Introduction to the Mathematics of Inversion in Remote Sensing and Indirect Measurements; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive, Volume II: Radar Remote Sensing and Surface Scattering and Emission Theory; Artech House Publishers: Norwood, MA, USA, 1986. [Google Scholar]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Jackson, T.J.; Schmugge, T.J. Vegetation effects on the microwave emission of soils. Remote Sens. Environ. 1991, 36, 203–212. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modeling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef] [Green Version]
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing, 3rd ed.; Academic Press: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Borengasser, M.; Hungate, W.S.; Watkins, R. Hyperspectral Remote Sensing: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Chen, H.S. Remote Sensing Calibration Systems: An Introduction; A Deepak Pub: Hampton, VA, USA, 1997. [Google Scholar]
- Hadjimitsis, D.G.; Clayton, C.R.I.; Hope, V.S. An assessment of the effectiveness of atmospheric correction algorithms through the remote sensing of some reservoirs. Int. J. Remote Sens. 2004, 25, 3651–3674. [Google Scholar] [CrossRef]
- Colombo, R.; Bellingeri, D.; Fasolini, D.; Marino, C.M. Retrieval of leaf area index in different vegetation types using high resolution satellite data. Remote Sens. Environ. 2003, 86, 120–131. [Google Scholar] [CrossRef]
- Heiskanen, J. Estimating aboveground tree biomass and leaf area index in a mountain birch forest using ASTER satellite data. Int. J. Remote Sens. 2006, 27, 1135–1158. [Google Scholar] [CrossRef]
- Teodoro, A.; Veloso-Gomes, F.; Goncalves, H. Retrieving TSM Concentration From Multispectral Satellite Data by Multiple Regression and Artificial Neural Networks. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1342–1350. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res.: Oceans 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for LAI mapping in poplar plantations. Remote Sens. Environ. 2004, 92, 195–206. [Google Scholar] [CrossRef]
- Fung, A.; Li, Z.; Chen, K. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Karam, M.; Fung, A.; Lang, R.; Chauhan, N. A microwave scattering model for layered vegetation. IEEE Trans. Geosci. Remote Sens. 1992, 30, 767–784. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K. A three-dimensional radar backscatter model of forest canopies. IEEE Trans. Geosci. Remote Sens. 1995, 33, 372–382. [Google Scholar]
- Jacquemoud, S. Comparison of four radiative transfer models to simulate plant canopies reflectance direct and inverse mode. Remote Sens. Environ. 2000, 74, 471–481. [Google Scholar] [CrossRef]
- Turner, D.P.; Ollinger, S.V.; Kimball, J.S. Integrating remote sensing and ecosystem process models for landscape- to regional-scale analysis of the carbon cycle. BioScience 2004, 54, 573–584. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C. Inversion of a forest reflectance model to estimate structural canopy variables from hyperspectral remote sensing data. Remote Sens. Environ. 2006, 100, 281–294. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Paloscia, S.; Pampaloni, P.; Pettinato, S.; Santi, E. A comparison of algorithms for retrieving soil moisture from ENVISAT/ASAR images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3274–3284. [Google Scholar] [CrossRef]
- Song, K.; Zhou, X.; Fan, Y. Empirically adopted IEM for retrieval of soil moisture from radar backscattering coefficients. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1662–1672. [Google Scholar] [CrossRef]
- Beale, R.; Jackson, T. Neural Computing—An Introduction; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Notarnicola, C.; Angiulli, M.; Posa, F. Soil moisture retrieval from remotely sensed data: Neural network approach versus Bayesian method. IEEE Trans. Geosci. Remote Sens. 2008, 46, 547–557. [Google Scholar] [CrossRef]
- Del Frate, F.; Ferrazzoli, P.; Schiavon, G. Retrieving soil moisture and agricultural variables by microwave radiometry using neural networks. Remote Sens. Environ. 2003, 84, 174–183. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S. Automatic parameter optimization for support vector regression for land and sea surface temperature estimation from remote sensing data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 909–921. [Google Scholar] [CrossRef]
- Latham, J.; Cumani, R.; Rosati, I.; Bloise, M. Global Land Cover SHARE (GLC-SHARE): Database Beta-Release Version 1.0-2014; Technical Report; FAO: Rome, Italy, 2014. [Google Scholar]
- Franzluebbers, A.J. Soil organic carbon in managed pastures of the southeastern United States of America. In Grassland Carbon Sequestration: Management, Policy and Economics; Integrated Crop Management Vol. 11–2010; FAO: Rome, Italy, 2010; Volume 11, pp. 163–175. [Google Scholar]
- Chuvieco, E. Satellite observation of biomass burning. In Earth Observation of Global Change; Chuvieco, E., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 2008; pp. 109–142. [Google Scholar]
- Gordon, R.C. Range Vegetation Type Mapping and Above-Ground Green Biomass Estimates Using Multispectral Imagery. Master’s Thesis, Department of Geology, University of Wyoming, Laramie, WY, USA, 1974. [Google Scholar]
- Clevers, J.; Van Der Heijden, G.; Verzakov, S.; Schaepman, M. Estimating grassland biomass using SVM band shaving of hyperspectral data. Photogramm. Eng. Remote Sens. 2007, 73, 1141. [Google Scholar] [CrossRef]
- Xie, Y.; Sha, Z.; Yu, M.; Bai, Y.; Zhang, L. A comparison of two models with Landsat data for estimating above ground grassland biomass in Inner Mongolia, China. Ecol. Model. 2009, 220, 1810–1818. [Google Scholar] [CrossRef]
- Yang, X.; Xu, B.; Yunxiang, J.; Jinya, L.; Zhu, X. On grass yield remote sensing estimation models of China’s northern farming-pastoral ecotone. In Advances in Computational Environment Science; Lee, G., Ed.; Number 142 in Advances in Intelligent and Soft Computing; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2012; pp. 281–291. [Google Scholar]
- Ali, I.; Cawkwell, F.; Green, S.; Dwyer, E. Application of statistical and machine learning modelds for grassland yield estimation based on a hyper- temporal satellite remote sensing time series. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2014), Quebec City, QC, Canada, 13–18 July 2014; pp. 5060–5063.
- Rajesh, S.; Arivazhagan, S.; Moses, K.P.; Abisekaraj, R. ANFIS based land cover/land use mapping of LISS IV imagery using optimized wavelet packet features. J. Indian Soc. Remote Sens. 2014, 42, 267–277. [Google Scholar] [CrossRef]
- Karimi, G.; Sedaghat, S.B.; Banitalebi, R. Designing and modeling of ultra low voltage and ultra low power LNA using ANN and ANFIS for Bluetooth applications. Neurocomputing 2013, 120, 504–508. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, L.N.; Ji, X. Prediction of concrete compressive strength: Research on hybrid models genetic based algorithms and ANFIS. Adv. Eng. Softw. 2014, 67, 156–163. [Google Scholar] [CrossRef]
- Schellberg, J.; Hill, M.J.; Gerhards, R.; Rothmund, M.; Braun, M. Precision agriculture on grassland: Applications, perspectives and constraints. Eur. J. Agron. 2008, 29, 59–71. [Google Scholar] [CrossRef]
- Moran, M.S.; Inoue, Y.; Barnes, E.M. Opportunities and limitations for image-based remote sensing in precision crop management. Remote Sens. Environ. 1997, 61, 319–346. [Google Scholar] [CrossRef]
- Prasad, R.; Pandey, A.; Singh, K.P.; Singh, V.P.; Mishra, R.K.; Singh, D. Retrieval of spinach crop parameters by microwave remote sensing with back propagation artificial neural networks: A comparison of different transfer functions. Adv. Space Res. 2012, 50, 363–370. [Google Scholar] [CrossRef]
- Karimi, Y.; Prasher, S.O.; Patel, R.M.; Kim, S.H. Application of support vector machine technology for weed and nitrogen stress detection in corn. Comput. Electr. Agric. 2006, 51, 99–109. [Google Scholar] [CrossRef]
- Verger, A.; Vigneau, N.; Chéron, C.; Gilliot, J.M.; Comar, A.; Baret, F. Green area index from an unmanned aerial system over wheat and rapeseed crops. Remote Sens. Environ. 2014, 152, 654–664. [Google Scholar] [CrossRef]
- Rumpf, T.; Mahlein, A.K.; Steiner, U.; Oerke, E.C.; Dehne, H.W.; Plümer, L. Early detection and classification of plant diseases with Support Vector Machines based on hyperspectral reflectance. Comput. Electr. Agric. 2010, 74, 91–99. [Google Scholar] [CrossRef]
- Li, R.; Li, C.J.; Dong, Y.Y.; Liu, F.; Wang, J.H.; Yang, X.D.; Pan, Y.C. Assimilation of remote sensing and crop model for LAI estimation based on ensemble Kaiman Filter. Agric. Sci. China 2011, 10, 1595–1602. [Google Scholar] [CrossRef]
- Yang, X.; Huang, J.; Wu, Y.; Wang, J.; Wang, P.; Wang, X.; Huete, A.R. Estimating biophysical parameters of rice with remote sensing data using support vector machines. Sci. China Life Sci. 2011, 54, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, P.A.; López-Granados, F.; Peẽa Barragán, J.M.; Jurado-Expósito, M.; Gómez-Casero, M.T.; Hervás-Martínez, C. Mapping sunflower yield as affected by Ridolfia segetum patches and elevation by applying evolutionary product unit neural networks to remote sensed data. Comput. Electr. Agric. 2008, 60, 122–132. [Google Scholar] [CrossRef]
- Liu, S.F.; Liou, Y.A.; Wang, W.J.; Wigneron, J.P.; Lee, J.B. Retrieval of crop biomass and soil moisture from measured 1.4 and 10.65 GHz brightness temperatures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1260–1268. [Google Scholar]
- Zheng, B.; Myint, S.W.; Thenkabail, P.S.; Aggarwal, R.M. A support vector machine to identify irrigated crop types using time-series Landsat NDVI data. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 103–112. [Google Scholar] [CrossRef]
- McNairn, H.; Kross, A.; Lapen, D.; Caves, R.; Shang, J. Early season monitoring of corn and soybeans with TerraSAR-X and RADARSAT-2. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 252–259. [Google Scholar] [CrossRef]
- Moreno, R.; Corona, F.; Lendasse, A.; Graña, M.; Galvão, L.S. Extreme learning machines for soybean classification in remote sensing hyperspectral images. Neurocomputing 2014, 128, 207–216. [Google Scholar] [CrossRef]
- Löw, F.; Michel, U.; Dech, S.; Conrad, C. Impact of feature selection on the accuracy and spatial uncertainty of per-field crop classification using Support Vector Machines. ISPRS J. Photogramm. Remote Sens. 2013, 85, 102–119. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Kalaitzidis, C.; Prasad Vadrevu, K. Support vector machines and object-based classification for obtaining land-use/cover cartography from Hyperion hyperspectral imagery. Comput. Geosci. 2012, 41, 99–107. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Arvanitis, K.; Sigrimis, N. Hyperion hyperspectral imagery analysis combined with machine learning classifiers for land use/cover mapping. Exp. Syst. Appl. 2012, 39, 3800–3809. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Murden, D. Evaluating high resolution SPOT 5 satellite imagery for crop identification. Comput. Electr. Agric. 2011, 75, 347–354. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.; Wu, J.; Qi, J.; Salas, W.A. Mapping paddy rice with multitemporal ALOS/PALSAR imagery in southeast China. Int. J. Remote Sens. 2009, 30, 6301–6315. [Google Scholar] [CrossRef]
- Muchoney, D.; Borak, J.; Chi, H.; Friedl, M.; Gopal, S.; Hodges, J.; Morrow, N.; Strahler, A. Application of the MODIS global supervised classification model to vegetation and land cover mapping of Central America. Int. J. Remote Sens. 2000, 21, 1115–1138. [Google Scholar] [CrossRef]
- Schulthess, U.; Timsina, J.; Herrera, J.M.; McDonald, A. Mapping field-scale yield gaps for maize: An example from Bangladesh. Field Crops Res. 2013, 143, 151–156. [Google Scholar] [CrossRef]
- Kogan, F.; Kussul, N.; Adamenko, T.; Skakun, S.; Kravchenko, O.; Kryvobok, O.; Shelestov, A.; Kolotii, A.; Kussul, O.; Lavrenyuk, A. Winter wheat yield forecasting in Ukraine based on Earth observation, meteorological data and biophysical models. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 192–203. [Google Scholar] [CrossRef]
- Jia, M.; Tong, L.; Chen, Y.; Wang, Y.; Zhang, Y. Rice biomass retrieval from multitemporal ground-based scatterometer data and RADARSAT-2 images using neural networks. J. Appl. Remote Sens. 2013, 7, 073509. [Google Scholar] [CrossRef]
- Johnson, D.M. An assessment of pre- and within-season remotely sensed variables for forecasting corn and soybean yields in the United States. Remote Sens. Environ. 2014, 141, 116–128. [Google Scholar] [CrossRef]
- Tapia-Silva, F.O.; Itzerott, S.; Foerster, S.; Kuhlmann, B.; Kreibich, H. Estimation of flood losses to agricultural crops using remote sensing. Phys. Chem. Earth, Parts A/B/C 2011, 36, 253–265. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Ahmed, F.B.; Ismail, R. Random forest regression and spectral band selection for estimating sugarcane leaf nitrogen concentration using EO-1 Hyperion hyperspectral data. Int. J. Remote Sens. 2012, 34, 712–728. [Google Scholar] [CrossRef]
- Li, D.; Chen, Y. Computer and Computing Technologies in Agriculture V: 5th IFIP TC 5/SIG 5.1 Conference, CCTA 2011, Beijing, China, October 29-31, 2011, Proceedings, Part II; Li, D., Chen, Y., Eds.; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.; Tignor, M.; Miller, H. (Eds.) IPCC, 2007: Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007.
- Koch, B. Status and future of laser scanning, synthetic aperture radar and hyperspectral remote sensing data for forest biomass assessment. ISPRS J. Photogramm. Remote Sens. 2010, 65, 581–590. [Google Scholar] [CrossRef]
- Chave, J.; Condit, R.; Lao, S.; Caspersen, J.P.; Foster, R.B.; Hubbell, S.P. Spatial and temporal variation of biomass in a tropical forest: Results from a large census plot in Panama. J. Ecol. 2003, 91, 240–252. [Google Scholar] [CrossRef]
- Wijaya, A.; Gloaguen, R. Fusion of ALOS Palsar and Landsat ETM data for land cover classification and biomass modeling using non-linear methods. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2009), Cape Town, South Africa, 12–17 July 2009; Vol. 3, pp. 581–584.
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping U.S. forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.; Shi, X.; Wang, S. Monitoring mangrove forest changes using remote sensing and GIS data with decision-tree learning. Wetlands 2008, 28, 336–346. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Houghton, R.A.; Dos Santos Alvalá, R.C.; Soares, J.V.; Yu, Y. Distribution of aboveground live biomass in the Amazon basin. Glob. Change Biol. 2007, 13, 816–837. [Google Scholar] [CrossRef]
- Magdon, P.; Fischer, C.; Fuchs, H.; Kleinn, C. Translating criteria of international forest definitions into remote sensing image analysis. Remote Sens. Environ. 2014, 149, 252–262. [Google Scholar] [CrossRef]
- Frazier, R.J.; Coops, N.C.; Wulder, M.A.; Kennedy, R. Characterization of aboveground biomass in an unmanaged boreal forest using Landsat temporal segmentation metrics. ISPRS J. Photogramm. Remote Sens. 2014, 92, 137–146. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest biomass estimation from airborne LiDAR data using machine learning approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Li, M.; Im, J.; Quackenbush, L.; Liu, T. Forest biomass and carbon stock quantification using airborne LiDAR data: A case study over huntington wildlife forest in the Adirondack Park. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3143–3156. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Meng, X.; Pang, Y.; Agca, M. Characterizing forest canopy structure with LiDAR composite metrics and machine learning. Remote Sens. Environ. 2011, 115, 1978–1996. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne LiDAR. J. Geophys. Res.: Biogeosci. 2011, 116, 1–12. [Google Scholar] [CrossRef]
- Del Frate, F.; Solimini, D. On neural network algorithms for retrieving forest biomass from SAR data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 24–34. [Google Scholar] [CrossRef]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing Performance of L- and P-band Polarimetric Interferometric SAR Data in Estimating Boreal Forest Above-Ground Biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- Tanase, M.A.; Panciera, R.; Lowell, K.; Tian, S.; Hacker, J.M.; Walker, J.P. Airborne multi-temporal L-band polarimetric SAR data for biomass estimation in semi-arid forests. Remote Sens. Environ. 2014, 145, 93–104. [Google Scholar] [CrossRef]
- Güneralp, İ.; Filippi, A.M.; Randall, J. Estimation of floodplain aboveground biomass using multispectral remote sensing and nonparametric modeling. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 119–126. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Elhadi, A.; Ismail, R. Intra-and-Inter species biomass prediction in a plantation forest: Testing the utility of high spatial resolution spaceborne multispectral RapidEye sensor and advanced machine learning algorithms. Sensors 2014, 14, 15348–15370. [Google Scholar] [CrossRef] [PubMed]
- Carreiras, J.M.B.; Melo, J.B.; Vasconcelos, M.J. Estimating the above-ground biomass in miombo savanna woodlands (Mozambique, East Africa) using L-band synthetic aperture radar data. Remote Sens. 2013, 5, 1524–1548. [Google Scholar] [CrossRef]
- Joibary, S.S. Forest attributes estimation using aerial laser scanner and TM data. For. Syst. 2013, 22, 484–496. [Google Scholar]
- Zhang, Y.; Liang, S.; Sun, G. Forest biomass mapping of northeastern China using GLAS and MODIS data. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 140–152. [Google Scholar] [CrossRef]
- Jachowski, N.R.A.; Quak, M.S.Y.; Friess, D.A.; Duangnamon, D.; Webb, E.L.; Ziegler, A.D. Mangrove biomass estimation in Southwest Thailand using machine learning. Appl. Geogr. 2013, 45, 311–321. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Vasconcelos, M.J.; Lucas, R.M. Understanding the relationship between aboveground biomass and ALOS PALSAR data in the forests of Guinea-Bissau (West Africa). Remote Sens. Environ. 2012, 121, 426–442. [Google Scholar] [CrossRef]
- Chen, G.; Hay, G.J.; St-Onge, B. A GEOBIA framework to estimate forest parameters from LiDAR transects, Quickbird imagery and machine learning: A case study in Quebec, Canada. Int. J. Appl. Earth Obs. Geoinf. 2012, 15, 28–37. [Google Scholar] [CrossRef]
- Karjalainen, M.; Kankare, V.; Vastaranta, M.; Holopainen, M.; Hyyppä, J. Prediction of plot-level forest variables using TerraSAR-X stereo SAR data. Remote Sens. Environ. 2012, 117, 338–347. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Avitabile, V.; Baccini, A.; Friedl, M.A.; Schmullius, C. Capabilities and limitations of Landsat and land cover data for aboveground woody biomass estimation of Uganda. Remote Sens. Environ. 2012, 117, 366–380. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Z.; Zhang, X.; Chen, E.X.; Bai, L.; Tian, X.; He, Q.; Feng, Q.; Li, W. Optimal Support Vector Machines for forest above-ground biomass estimation from multisource remote sensing data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2012), Munich, Germany, 22–27 July 2012; pp. 6388–6391.
- Shataee, S.; Kalbi, S.; Fallah, A.; Pelz, D. Forest attribute imputation using machine-learning methods and ASTER data: Comparison of k-NN, SVR and random forest regression algorithms. Int. J. Remote Sens. 2012, 33, 6254–6280. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; D’Odorico, P.; Porporato, A.; Ridolfi, L. On the spatial and temporal links between vegetation, climate, and soil moisture. Water Resour. Res. 1999, 35, 3709–3722. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Heathman, G.C.; Starks, P.J.; Ahuja, L.R.; Jackson, T.J. Assimilation of surface soil moisture to estimate profile soil water content. J. Hydrol. 2003, 279, 1–17. [Google Scholar] [CrossRef]
- Wang, J.R. The dielectric properties of soil-water mixtures at microwave frequencies. Radio Sci. 1980, 15, 977–985. [Google Scholar] [CrossRef]
- Luckman, A. The effects of topography on mechanisms of radar backscatter from coniferous forest and upland pasture. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1830–1834. [Google Scholar] [CrossRef]
- Pasolli, L.; Notarnicola, C.; Bertoldi, G.; Bruzzone, L.; Remelgado, R.; Greifeneder, F.; Niedrist, G.; Della Chiesa, S.; Tappeiner, U.; Zebisch, M. Estimation of soil moisture in mountain areas using SVR technique applied to multiscale active radar images at C-band. IEEE J. Select. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 262–283. [Google Scholar] [CrossRef]
- Barrett, B.W.; Dwyer, E.; Whelan, P. Soil moisture retrieval from active spaceborne microwave observations: An evaluation of current techniques. Remote Sens. 2009, 1, 210–242. [Google Scholar] [CrossRef]
- Notarnicola, C.; Casarano, D.; Posa, F.; Refice, A.; Satalino, G. Stima di parametri geofisici a partire da dati SAR polarimetrici multifrequenza. In Proceedings of the Atti del VII Convegno Nazionale dell’Associazione Italiana di Telerilevamento (AIT), Chieri, Italy, 17–20 October 1995; pp. 443–448.
- Dawson, M.; Fung, A.; Manry, M. A robust statistical-based estimator for soil moisture retrieval from radar measurements. IEEE Trans. Geosci. Remote Sens. 1997, 35, 57–67. [Google Scholar] [CrossRef]
- Satalino, G.; Mattia, F.; Davidson, M.; le Toan, T.; Pasquariello, G.; Borgeaud, M. On current limits of soil moisture retrieval from ERS-SAR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2438–2447. [Google Scholar] [CrossRef]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar]
- Baghdadi, N.; Cresson, R.; el Hajj, M.; Ludwig, R.; la Jeunesse, I. Estimation of soil parameters over bare agriculture areas from C-band polarimetric SAR data using neural networks. Hydrol. Earth Syst. Sci. 2012, 16, 1607–1621. [Google Scholar] [CrossRef] [Green Version]
- Prasad, R.; Kumar, R.; Singh, D. A radial basis function approach to retrieve soil moistrure and crop variables from Xband scatterometer ovservations. Prog. Electromagn. Res. B 2009, 12, 201–217. [Google Scholar] [CrossRef]
- Xie, X.M.; Xu, J.W.; Zhao, J.F.; Liu, S.; Wang, P. Soil moisture inversion using AMSR-E remote sensing data: An artificial neural network approach. Appl. Mech. Mater. 2014, 501–504, 2073–2076. [Google Scholar] [CrossRef]
- Lakhankar, T.; Ghedira, H.; Temimi, M.; Sengupta, M.; Khanbilvardi, R.; Blake, R. Non-Parametric methods for soil moisture retrieval from satellite remote sensing data. Remote Sens. 2009, 1, 3–21. [Google Scholar] [CrossRef] [Green Version]
- Pasolli, L.; Notarnicola, C.; Bruzzone, L. Estimating soil moisture with the support vector regression technique. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1080–1084. [Google Scholar] [CrossRef]
- Pasolli, L.; Notarnicola, C.; Bruzzone, L.; Bertoldi, G.; Chiesa, S.D.; Niedrist, G.; Tappeiner, U.; Zebisch, M. Polarimetric RADARSAT-2 imagery for soil moisture retrieval in alpine areas. Can. J. Remote Sens. 2011, 37, 535–547. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar]
- Srivastava, P.K.; Han, D.; Ramirez, M.R.; Islam, T. Machine learning techniques for downscaling SMOS satellite soil moisture using MODIS land surface temperature for hydrological application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Judge, J.; Rangarajan, A.; Ranka, S. Disaggregation of remotely sensed soil moisture in heterogeneous landscapes using holistic structure based models. IEEE Trans. Image Rocess. 2015. submitted. [Google Scholar]
- Kerr, Y.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.; et al. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Gill, M.K.; Asefa, T.; Kemblowski, M.W.; McKee, M. Soil moisture prediction using support vector machines. J. Am. Water Resour. Assoc. 2006, 42, 1033–1046. [Google Scholar] [CrossRef]
- Zaman, B.; McKee, M.; Neale, C.M.U. Fusion of remotely sensed data for soil moisture estimation using relevance vector and support vector machines. Int. J. Remote Sens. 2012, 33, 6516–6552. [Google Scholar] [CrossRef]
- Wagner, W.; Noll, J.; Borgeaud, M.; Rott, H. Monitoring soil moisture over the Canadian Prairies with the ERS scatterometer. IEEE Trans. Geosci. Remote Sens. 1999, 37, 206–216. [Google Scholar] [CrossRef]
- Gruber, A.; Paloscia, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Smolander, T.; Pulliainen, J.; Mittelbach, H.; Dorigo, W.; Wagner, W. Performance inter-comparison of soil moisture retrieval models for the MetOp-A ASCAT instrument. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2014), Quebec City, QC, Canada, 13–18 July 2014; pp. 2455–2458.
- Demir, B.; Bruzzone, L. A multiple criteria active learning method for support vector regression. Pattern Recognit. 2014, 47, 2558–2567. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data. Remote Sens. 2015, 7, 16398-16421. https://doi.org/10.3390/rs71215841
Ali I, Greifeneder F, Stamenkovic J, Neumann M, Notarnicola C. Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data. Remote Sensing. 2015; 7(12):16398-16421. https://doi.org/10.3390/rs71215841
Chicago/Turabian StyleAli, Iftikhar, Felix Greifeneder, Jelena Stamenkovic, Maxim Neumann, and Claudia Notarnicola. 2015. "Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data" Remote Sensing 7, no. 12: 16398-16421. https://doi.org/10.3390/rs71215841
APA StyleAli, I., Greifeneder, F., Stamenkovic, J., Neumann, M., & Notarnicola, C. (2015). Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data. Remote Sensing, 7(12), 16398-16421. https://doi.org/10.3390/rs71215841