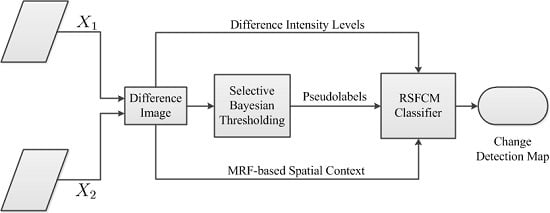
2.2.1. FCM Algorithm
The purpose of the difference image analysis is to discriminate changed regions from unchanged regions. This process belongs to the field of image segmentation. As mentioned in
Section 1, changed and unchanged classes in the difference image are not clearly defined, and an ambiguous region exists between these two classes. Therefore, we attempt to solve the change detection problem using fuzzy clustering, because fuzzy set theory [
31] provides useful concepts and tools to deal with imprecise information [
32]. In fuzzy clustering, difference image patterns are assigned neither to the changed nor the unchanged group but to both groups with certain membership degrees. In particular, the present work applies the properly designed RSFCM to difference image analysis, which is a variation of the standard FCM. The RSFCM description begins with a brief summary of FCM.
FCM was first introduced by Dunn [
33] and was later improved by Bezdek [
34]. It is an iterative clustering method that attempts to partition a finite collection of
N data points into a set of
C fuzzy clusters by minimizing the weighting within the group sum of the squared error objective function [
25]
with the following constraints:
where
is the dataset to be grouped;
C is the cluster number;
U is the fuzzy partition matrix (membership functions), such that
ukn indicates the membership grade of
yn in the
kth cluster;
m is the weighting exponent in each fuzzy membership;
V is the set of the prototypes
vk associated with clusters; and
is the squared distance measure (Euclidean norm) between pattern
yn and cluster center
vk.
The computation of the cluster centers and membership functions is performed as follows:
The fuzzy partition matrix
U is generally normalized, with its elements falling within [0, 1], and
U and
V are iteratively updated to approach an optimum solution. The iterative process ends when
is achieved, where
and
are the partition matrix in the
rth and (
r − 1)th iteration, respectively, and
is a small positive threshold predefined manually. More details of FCM can be referenced in [
34]. The dataset to be clustered in our problem is the difference image, which is divided into two groups: changed and unchanged. Therefore,
and
C = 2.
The FCM algorithm provides an appropriate tool to cluster the overlapping changed and unchanged clusters. Nevertheless, given no information on pseudolabels and spatial context, the conventional FCM only uses the difference intensity levels of the difference image pixels. We attempt to integrate these two types of valuable information into FCM to enhance the performance in change detection results, which is more difficult than when only spatial information is incorporated. Strategies to exploit labeling knowledge and information on the mutual influences among image pixels are presented in
Section 2.2.2 and
Section 2.2.3, respectively.
2.2.2. Strategy for Exploiting Labeling Knowledge
Several techniques have been proposed to enhance FCM performance with the help of partial supervision [
29,
30,
35,
36,
37]. Bensaid and Bezdek [
35] used labeled patterns as seeds to initialize the clusters’ centers. However, the potential of labeled data points has not been fully realized because they have only been used for initializing the cluster prototypes. To fully utilize this potential, labeled patterns are given more weight than the unlabeled ones in [
36] when the cluster centers are calculated. Nevertheless, this approach assumes that the labeled patterns all have a correct label; the reassignment of patterns is conducted only for unlabeled patterns. This manner is inappropriate for our condition because the label set
Yl, which is obtained automatically, can have noisy elements (error labels). Semi-supervised clustering algorithms based on a modified FCM objective function were discussed in [
29,
30,
37]. These algorithms do not only fully exploit the labeled data points but are also suitable for conditions in which data is neither completely nor perfectly labeled.
Inspired by [
30], we propose the approach for incorporating partial supervision into the process of analyzing the difference image, in which the problem of clustering labeled and unlabeled data is explicitly expressed as an augmented objective function. The main idea of this strategy is to use the labeled patterns (the nearly certain patterns) to guide the process of segmenting the difference image to obtain a more accurate membership. The augmented objective function consists of two components. The former is namely the FCM objective function, and it concerns unsupervised clustering. The latter retains the relationship between the pseudolabels and clusters generated by the first component.
The following is the detailed description of the proposed technique for exploiting the pseudolabels. The augmented objective function adopted assumes the following form:
The parameter α is a scaling factor that helps establish a sound balance between the unsupervised and supervised components. Furthermore, the terms are the optimal membership degrees for the labelled data points, which are derived from the labeling information contained in the set Yl. The matrix in Equation (11) helps to optimize the membership for the difference image pixels to the changed and unchanged classes using labeling information () in contrast to ukn. The second (supervised) term is minimized when the value of ukn becomes close to that of . Therefore, the membership value ukn is constrained to approach the corresponding . Ideally, both ukn and should have the same value.
Using Equation (11), both the hidden and the visible structures of the difference image can be captured. The first term attempts to discover the hidden data structure, whereas the second term considers the visible data structure reflected by the available labels (pseudolabels). The matrix
is the main part of the second component. The terms
are iteratively computed as follows:
where the superscript
r refers to consecutive iterations and
is a
binary matrix used to arrange labeling information, so that
if pattern
yn belongs to the
kth class and 0 otherwise. The vector
is two valued and specifies whether the data point
n is labeled (
i.e.,
if
yn is a labeled pattern and 0 otherwise). Moreover, the parameter
η in Equation (12) is a positive learning rate that controls the process of updating the membership grades of
. By substituting Equation (13) into Equation (12), the learning rule Equation (12) is transformed into the following:
Equation (14) optimizes the amount
by exploiting the learning rate η and computed difference.
is initialized by
U(°
), which is obtained by applying the standard FCM to the difference image. The iterative process of computing
terminates when
is reached, where
is a small positive threshold. The resulting matrix
is used to compute the second term in Equation (11), the difference between
U and
. The process of computing
is the same process of minimizing
.
After obtaining the matrix
, an iterative semi-supervised algorithm for minimizing Equation (11) can be derived by evaluating cluster centers and membership matrices that satisfy a zero gradient condition. For simplicity, the weighting exponent
m in Equation (11) is set to 2 in this work. The calculation formulas of the cluster centers and membership functions are as follows [
30]:
Thus far, the utilization of labeling information (the pseudolabels) is accomplished by the terms
in Equations (15) and (16), and a semisupervised FCM algorithm (SFCM) is presented. However, similar to the conventional FCM, SFCM is also sensitive to noise and outliers because it does not consider information on spatial context. Moreover, the SFCM performance can be affected to a certain extent by the noisy (error) labels contained in the set
Yl. Local spatial information is introduced into SFCM, as presented in
Section 2.2.3, to enhance the robustness of SFCM to noise pixels and error labels.
2.2.3. Strategy for Utilizing Information on Spatial Context
This section proposes a technique for incorporating information on spatial context in SFCM, by which the RSFCM clustering algorithm is developed. The developed technique does not improve the SFCM by modifying its objective function as in [
21,
25]. Instead, it focuses on the modification of the membership in each iteration process. The aim of the modification is to discourage unlikely or undesirable configurations in the SFCM membership functions, such as a high membership value immediately surrounded by low values of the same class (
Figure 3a).
A Markov random field (MRF) provides an opportune tool to introduce information on the mutual influences among image pixels in a powerful and formal manner, and it has been widely used for the change detection problem [
7,
12,
26,
38,
39]. We call a random field an MRF if and only if some property of each site (pixel) is related only to the neighborhood ones and has no relationship with the other ones in a field (an image) [
39]. Thus, the complexity of utilizing the spatial contextual information can be largely simplified by passing from a global model to a model of the local image properties (
i.e., adopting the MRF method). An important issue of MRF model is the energy function, by which the abstract MRF expression is converted into a computable expression.
The SFCM algorithm is improved in this work based on the MRF-based spatial context, which is incorporated into the SFCM membership by adding a new spatial energy term. We then use to denote the data points of the difference image, where (i, j) represents the pixel coordinates.
First, we present the conventional local MRF energy function because it has a basic relationship with the proposed scheme for the utilization of spatial context. The local energy function for pixel
takes on the following form [
12,
38,
40]:
where
is the spectral energy function from the observed image, and
is the spatial energy term that describes information on the mutual influences among neighboring pixels. Introducing the concept of the spatial neighborhood system is necessary to determine the spatial energy term, and the most commonly used second-order neighborhood system (
Figure 3b) is adopted. The second-order neighborhood system for pixel (
i,
j) is denoted by
N(
i,
j). The spatial energy term can then be defined as follows [
12,
38]:
The parameter β is a constant used to tune the influence of information on spatial context, and
and
(
) denote the class labels for the pixel (
i,
j) and its neighborhood, respectively. Furthermore,
is an indicator function that is applied to count the number of neighborhood pixels that belong to the same class of
, which is defined as follows:
On the basis of the MRF energy Equation (17), we propose the approach to improve the membership of SFCM. After calculating it in each iteration process, the SFCM membership is modified by adding a novel fuzzy spatial term. The modified membership takes on the following form:
The term is the membership grade for the pixel (i, j) to class k computed by Equation (16), and is the additional spatial term defined as follows.
The spatial information contained within the neighborhood centered at pixel (
i,
j) can be effectively used with Equation (18). However, Equation (18) is defined following classical set theory and uses the hard indicator function
. Therefore, it is inappropriate for defining the spatial term
as the SFCM algorithm belongs to the family of fuzzy clustering, in which the pixels are assigned not to any one class but to all the classes with certain membership grades. Additionally, we change the influence of the pixels within the local window flexibly based on their spatial distances to reflect the damping extent of the neighborhood pixels with the spatial distance from the center pixel. Thus, to determine the degree of influence of the neighboring pixels for the center pixel, a fuzzy spatial information measure is defined based on the membership degree and distance as follows:
where
is the membership degree for
to cluster
k computed by Equation (16),
is the spatial Euclidean distance (
Figure 3c) between pixel (
i,
j) and its neighborhood
, and parameter β is used to control the influence of spatial information on the change detection process. Generally, different β-values can be considered. Here, we simply set the value of β to 1 as both
and
are the membership of SFCM calculated by Equation (16).
In expression Equation (21), we adopt the membership
to replace the hard indicator function
to describe the influence of neighboring pixels on the central pixel. The inverse distance
is used, as the closer the neighbors from the center (
i,
j) are, the more influence they exert on the result and
vice versa. With the proposed fuzzy spatial term Equation (21), unlikely or undesirable configurations in the membership functions can be discouraged. For instance, if the central pixel is corrupted by noise while its neighboring pixels are homogeneous,
i.e., not corrupted by noise (
Figure 3a), the undesirable membership grade of the noisy (central) pixel will converge to similar neighboring pixel membership degrees because of the addition of the fuzzy spatial term Equation (21).
Eventually, we achieve a robust semi-supervised FCM algorithm called RSFCM, of which the main steps are presented in tabular form (Algorithm 1). In RSFCM, difference intensity levels and labeling information are used to estimate the membership, which is then modified by information about spatial context (as shown in Steps 3a–d of Algorithm 1). In the stage of estimating membership functions, the supervised (second) term of Equation (11) constrains the membership value ukn to approach the optimal and enables the nearly certain change patterns to have a greater membership of the change class (see Step 3b), by which the change information is enhanced; in the stage of modifying the membership, the fuzzy spatial term Equation (21) discourages the undesirable configurations of membership functions caused by noise or error labels (see Step 3d), by which membership functions become spatially smooth. Therefore, RSFCM provides noise-immunity and preserves more detailed change information.
Notably, in the proposed RSFCM algorithm, the weighting exponent m is set to the value of 2 (see Equations (15) and (16)). In addition, the modified membership grades computed by Equation (20) are normalized in each iteration process, with their elements falling in [0,1].
| Algorithm 1 Main steps of the RSFCM clustering algorithm |
- 1:
The standard FCM is applied to the difference image to produce an initial partition matrix U(°). - 2:
The matrix is derived with labeling knowledge. is initialized with U(°) and r = 1 is set. Repeat is computed using Equation (14). Until where is a small positive threshold. - 3:
Membership functions U are computed using intensity levels, and spatial context. U is initialized with U(°) and r = 1 is set. Repeat - (a)
V (r) is computed using Equation (15). - (b)
U (r) is computed using Equation (16). - (c)
The fuzzy spatial term is computed using Equation (21). - (d)
U (r) is modified with Equation (20).
Until where is a small positive threshold.
|