Transformation Model with Constraints for High-Accuracy of 2D-3D Building Registration in Aerial Imagery

Abstract

This paper proposes a novel rigorous transformation model for 2D-3D registration to address the difficult problem of obtaining a sufficient number of well-distributed ground control points (GCPs) in urban areas with tall buildings. The proposed model applies two types of geometric constraints, co-planarity and perpendicularity, to the conventional photogrammetric collinearity model. Both types of geometric information are directly obtained from geometric building structures, with which the geometric constraints are automatically created and combined into the conventional transformation model. A test field located in downtown Denver, Colorado, is used to evaluate the accuracy and reliability of the proposed method. The comparison analysis of the accuracy achieved by the proposed method and the conventional method is conducted. Experimental results demonstrated that: (1) the theoretical accuracy of the solved registration parameters can reach 0.47 pixels, whereas the other methods reach only 1.23 and 1.09 pixels; (2) the RMS values of 2D-3D registration achieved by the proposed model are only two pixels along the x and y directions, much smaller than the RMS values of the conventional model, which are approximately 10 pixels along the x and y directions. These results demonstrate that the proposed method is able to significantly improve the accuracy of 2D-3D registration with much fewer GCPs in urban areas with tall buildings.

1. Introduction

Texturing three-dimensional (3D) buildings at a large scale for the generation of a photorealistic urban environment has been an important research topic in the computer vision [1,2,3,4], computer graphics [5] and remote sensing communities [6]. The prerequisite for texturing 3D buildings is high accuracy in the geometric alignment of 2D texture images, which are captured by different types of devices, such as airborne and spaceborne platforms, with their corresponding 3D models without textures, which are represented by various geometric data structures. This process is called 2D-3D registration. Researchers encountered various unique real-world problems and have developed a variety of approaches for 2D-3D registration.

A commonly-adopted transformation model for a given ground point G can be expressed by:

$$\left(\begin{array}{c}{X}_G\\ Y_G\\ Z_G\end{array}\right)=\left(\begin{array}{c}{X}_S\\ Y_S\\ Z_S\end{array}\right)+R(\omega ,\varphi ,\kappa )\left(\begin{array}{c}{x}_g\\ y_g\\ z_g\end{array}\right)$$

(1)

where (X_G, Y_G, Z_G)^T are the coordinates of the point G in 3D space with respect to a geographic coordinate system, (X_S, Y_S, Z_S)^T are the center of the perspective projection, which is the translation vector between the origins of the 2D image coordinate system and the geographic coordinate system, (x_g, y_g, z_g)^T are the image coordinates of the given ground point G with respect to the image coordinate system, φ, ω and k are three rotation angles and R(φ, ω, k) is a 3D orthogonal rotation matrix as follows,

$$R=\left(\begin{array}{ccc}\cos \varphi \cos k& \cos \omega \sin k+\sin \omega \sin \varphi \cos k& \sin \omega \sin k-\cos \omega \sin \varphi \cos k\\ -\cos \varphi \sin k& \cos \omega \cos k-\sin \omega \sin \varphi \sin k& \sin \omega \cos k+\cos \omega \sin \varphi \sin k\\ \sin \varphi & -\sin \omega \cos \varphi & \cos \omega \cos \varphi \end{array}\right)$$

(2)

Traditional 2D-3D registration methods solve for the camera’s position (X_S, Y_S, Z_S)^T and its orientation matrix R in Equations (1) and (2). However, none of the distortion models are perfect. Any distortion model cannot completely describe the distortion over the entire image plane, i.e., the residual errors (incomplete correction) still remain no matter what kind of distortion model is adopted. As a result, the accuracy of image coordinates in the entire image plane is asymmetric (see Figure 1). This phenomenon has been demonstrated in [7] and it becomes obvious for a big dimension of aerial images, especially in which a much higher and bigger building is imaged on a large area in the image plane [8]. Two constraint conditions are added into the traditional transformation model (Equation (1)) to increase the accuracy, reliability and robustness of the image distortion correction. For the example shown in Figure 1, the image distortion in Region 1 is different from that of Regions 2 and 3. If a conventional transformation model (e.g., photogrammetry backward intersection (PBI)) is applied to register such a 2D image that contains various and dissymmetric distortions with a 3D object represented by a rigid model, errors in the 2D-3D registration are undoubtedly unavoidable. This problem is especially profound for high-rise buildings because the bottom and top of a high-rise building are affected by different distortions in the same image. To avoid this problem, this paper presents a novel algorithm using two types of geometric constraints, i.e., co-planar and perpendicular conditions, to improve the accuracy of the 2D-3D registration. The two conditions added in the proposed transformation model, in relation to the original rigorous transformation model, can be summarized in the following.

(1)

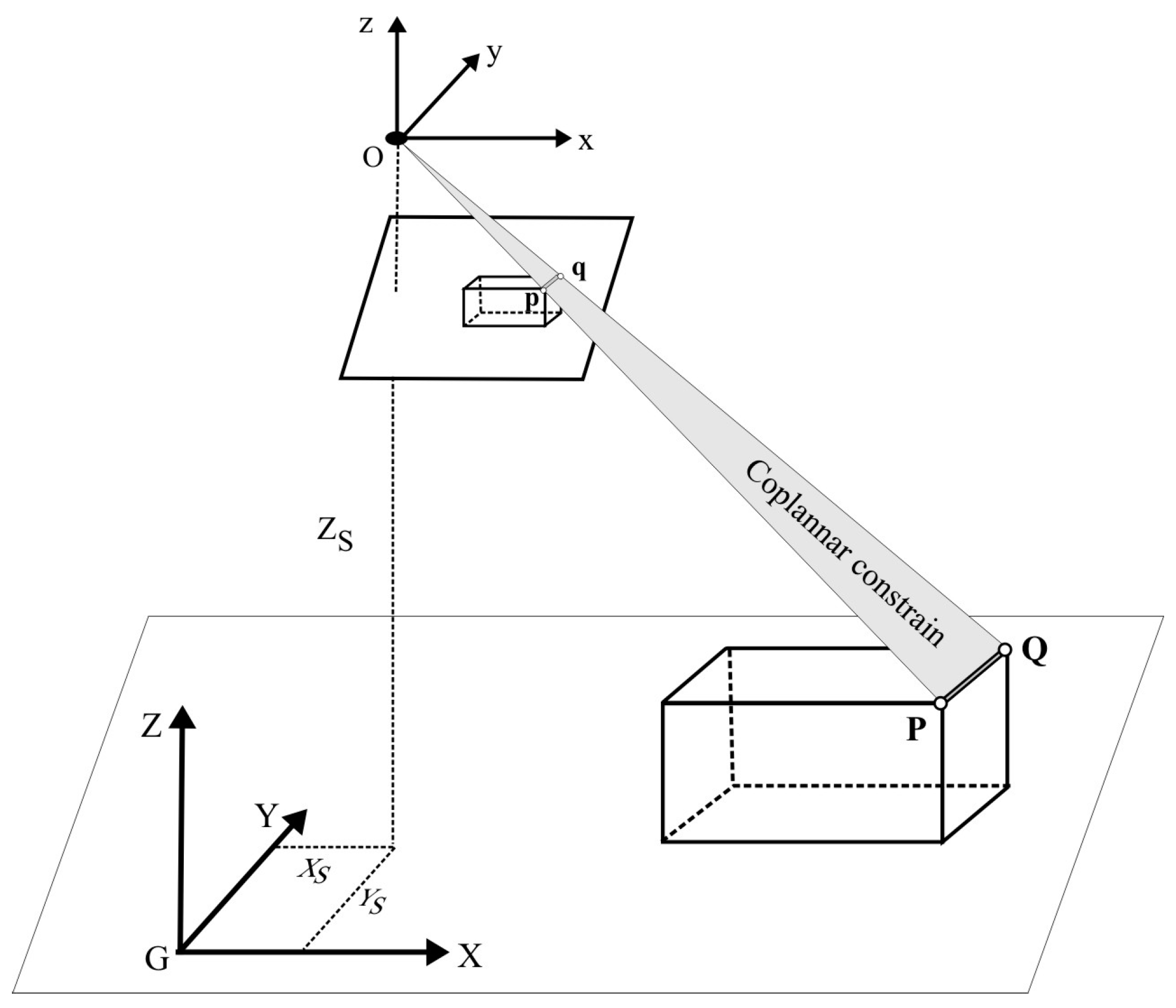
Co-planar condition: The photogrammetric center, a line in the object coordinate system and the corresponding line in the image coordinate system are in the same plane.

(2)

Perpendicular condition: The constraint requires that if two lines are perpendicular in the object coordinate system, their projections are perpendicular in the image coordinate system.

The remainder of this paper is organized as follows: Section 2 briefly overviews related work; Section 3 focuses on the development of a rigorous transformation model; Section 4 and Section 5 evaluate the correctness and accuracy of the proposed method and compare it to other existing methods; Section 6 summarizes the major contributions and advantages of the proposed method.

2. Related Work

2D-3D registration for different applications has been a very active research area in the last few decades. Researchers have developed a wide range of 2D-3D registration methods; papers in the existing literature provide an overall survey and study of various registration methods, such as [9,10,11,12,13,14,15,16,17]. Most of the registration methods consist of four steps as follows:

• Feature detection: Existing methods can be classified into feature-based or intensity-based methods. Feature-based methods use point features, linear features and areal features extracted from both the 3D urban surface/building model and 2D imagery as the common feature pairs and then align the corresponding feature pairs via a transform model. This method has been widely applied in computer vision [18,19,20,21,22,23] and medical image processing [24,25]. Intensity-based methods utilize the intensity-driven information, such as texture, reflectance, brightness, and shadow, to achieve high-accuracy in 2D-3D registration [11,13,26]. These features, which are called ground control points (GCPs) in remote sensing, can be detected manually or automatically.
• Feature matching: The relationship between the features detected from the two images is established. Different feature similarity measures are used for the estimation.
• Transform model estimation: The transform type and its parameters between two images are estimated by certain mapping functions based on the previously-established feature correspondence.
• Image resampling and transformation: The slave image is resampled and transformed into the frame of the reference image, according to the transformation model and interpolation technique.

Among the previous efforts, imaging geometry has been utilized as a rigorous transformation model by some researchers, such as [26,27,28,29,30,31,32] suggested integrating single straight lines into the orientation of images for building reconstruction and/or building recognition. Habib et al. [33] proposed that straight lines be utilized as constraints in photogrammetric bundle adjustment to solve the interior orientation parameters (IOPs) of the camera and the exterior orientation parameters (EOPs) of aerial images. Two major advantages lie in that: (1) straight lines are employed to enhance the reliability of bundle adjustment; and (2) the IOPs are considered as unknown parameters to be solved in the model. The disadvantages of this method lie in that: (1) the straight line constraint is not as strong as that of co-planarity, because this type of constraint does not combine the image space, object space and perspective center; (2) the straight line constraint enhances only the accuracy along a straight line in theory, whereas the accuracy along other directions, such as that perpendicular to the straight line, becomes relatively weak. Zhang et al. [34] developed a methodology to co-register the laser scanning data and aerial images over urban areas. The method considers a linear feature as observed primitives and uses coplanar condition as error equations to solve for the EOP of the digital image. One advantage of this method is that it extends the straight line constraint into the coplanar constraint, which in fact combines features in object space, image space and the perspective center. One disadvantage is that it considers digital cameras as a rigid body for which the IOPs are known and are computed independently.

Considering the advantages and disadvantages of the two foregoing methods (i.e., [33,34]), this paper presents two types of constraint conditions, i.e., coplanar and perpendicular conditions. This idea comes from the fact that Zhou et al. [8] demonstrated that two aerial images over an urban area will have different accuracy of registration even with the same digital building model (DBM) and the same algorithm. This implies that highly accurate 2D-3D registration will not be achievable if constraint conditions are not applied.

3. Rigorous Transformation Model

We first briefly describe the fundamental concepts of the conventional rigorous transformation model, which is based on imaging geometry. For more detailed information, please refer to existing literature [27,28,29]. This paper only considers aerial photography. The conventional rigorous transformation model is represented by:

$$\begin{array}{l}{x}_g-x_0=-f\frac{r_{11}(X_G-Xs)+r_{12}(Y_G-Ys)+r_{13}(Z_G-Zs)}{r_{31}(X_G-Xs)+r_{32}(Y_G-Ys)+r_{33}(Z_G-Zs)}=-f_x\\ y_g-y_0=-f\frac{r_{21}(X_G-Xs)+r_{22}(Y_G-Ys)+r_{23}(Z_G-Zs)}{r_{31}(X_G-Xs)+r_{32}(Y_G-Ys)+r_{33}(Z_G-Zs)}=-f_y\end{array}$$

(3)

where f, x₀, y₀ are the camera’s IOP and r_i,j (i = 1, 2, 3; j = 1, 2, 3) are components of the rotation matrix R(ω, ϕ, k), which was described in Equation (2). Considering two types of imagery distortions, radial and decentering, the image coordinates in Equation (3) can be modified by:

$$\begin{array}{l}{x}_g^{\prime }=x_g+\delta x-x_0\\ y_g^{\prime }=y_g+\delta y-y_0\end{array}$$

(4)

where (x′ g, y′ g) are the distortion-free image coordinates after correction and δx, δy are corrections through the imagery distortion models below:

$$\begin{array}{l}{\delta }_x=\stackrel{radial}{\overbrace{{\kappa }_1{x}_g(x_g^2+y_g^2)}}+\stackrel{decentering}{\overbrace{{\rho }_1(3x_g^2+y_g^2)+2{\rho }_2{x}_g{y}_g}}\\ {\delta }_y=\stackrel{radial}{\overbrace{{\kappa }_1{y}_g(x_g^2+y_g^2)}}+\stackrel{decentering}{\overbrace{{\rho }_2(3x_g^2+y_g^2)+2{\rho }_1{x}_g{y}_g}}\end{array}$$

(5)

where k₁, ρ₁ and ρ₂ are the coefficients of radial distortion and decentering, respectively, and x_g, y_g are the coordinates of a target point in a defined image coordinate system.

Because Equation (3) is not linear, it must be linearized with respect to both IOPs and EOPs. The vector form of the registration model can be expressed by:

$$V=A_1{X}_1+A_2{X}_2-L$$

(6)

where X₁ represents EOPs; X₂ denotes IOPs; V is the residual error matrix; and A₁ and A₂ are their coefficients, whose partial derivatives with respect to the registration parameters can be found in [35]. The vectors in Equation (6) are X₁ = (ϕ, ω, k, X_S, Y_S, Z_S)^T, X₁ = [k₁, ρ₁, ρ₂], $V=(V_{x_g},V_{y_g})$,

$$A_1=\left[\begin{array}{cccccc}\frac{\partial f_x}{\partial X_s}& \frac{\partial f_x}{\partial Y_s}& \frac{\partial f_x}{\partial Z_s}& \frac{\partial f_x}{\partial \varphi }& \frac{\partial f_x}{\partial \omega }& \frac{\partial f_x}{\partial \kappa }\\ \frac{\partial f_y}{\partial X_s}& \frac{\partial f_y}{\partial Y_s}& \frac{\partial f_y}{\partial Z_s}& \frac{\partial f_y}{\partial \varphi }& \frac{\partial f_y}{\partial \omega }& \frac{\partial f_y}{\partial \kappa }\end{array}\right], A_2=\left[\begin{array}{ccc}\frac{\partial f_x}{\partial {\kappa }_1}& \frac{\partial f_x}{\partial {\rho }_1}& \frac{\partial f_x}{\partial {\rho }_2}\\ \frac{\partial f_y}{\partial {\kappa }_1}& \frac{\partial f_y}{\partial {\rho }_1}& \frac{\partial f_y}{\partial {\rho }_2}\end{array}\right]$$

$$L=\left(\begin{array}{c}{L}_{x_g}\\ L_{y_g}\end{array}\right)=\left[\begin{array}{c}{x}_g^{\prime }-f\frac{r_{11}(X_G-Xs)+r_{12}(Y_G-Ys)+r_{13}(Z_G-Zs)}{r_{31}(X_G-Xs)+r_{32}(Y_G-Ys)+r_{33}(Z_G-Zs)}\\ y_g^{\prime }-f\frac{r_{21}(X_G-Xs)+r_{22}(Y_G-Ys)+r_{23}(Z_G-Zs)}{r_{31}(X_G-Xs)+r_{32}(Y_G-Ys)+r_{33}(Z_G-Zs)}\end{array}\right]$$

The registration parameters in Equation (6) are conventionally solved by least adjustment estimation using a number of well-distributed GCPs.

As mentioned previously, the conventional registration model is not robust for high-rise buildings in urban areas. Therefore, this paper proposes two types of conditions, co-planarity and perpendicularity, as constraints to the conventional model Equation (6). Mathematically, the two types of conditions are described as follows.

3.1. Coplanar Condition

The straight line condition does not combine the features in image space, object space and perspective center; thus, this paper proposes a coplanar constraint condition, which is similar to (Zhang et al., 2005). As shown in Figure 2, given two points P and Q on the object surface, their corresponding image points are p and q. Five points, O (camera exposure center), P, Q, p and q, should theoretically be coplanar. The mathematical model that describes the coplanar condition using three vectors $\overrightarrow{OP}$, $\overrightarrow{OQ}$ and $\overrightarrow{Op}$ is:

$$\left|\begin{array}{ccc}{u}_p& v_p& w_p\\ X_P-X_S& Y_P-Y_S& Z_P-Z_S\\ X_Q-X_S& Y_Q-Y_S& Z_Q-Z_S\end{array}\right|=F_p=0$$

(7)

where F_P is the residual error matrix; (X_P, Y_P, Z_P) and (X_Q, Y_Q, Z_Q) are coordinates of the ground points P, Q with respect to the ground coordinate system, respectively; (u_P, v_P, w_P) are coordinates of the image point p with respect to the camera coordinate system.

Combining Equations (1) and (3), Equation (7) yields

$$\left|\begin{array}{ccc}{u}_p& v_p& w_p\\ X_P-X_S& Y_P-Y_S& Z_P-Z_S\\ X_Q-X_S& Y_Q-Y_S& Z_Q-Z_S\end{array}\right|=\left|\begin{array}{ccc}{u}_p& v_p& w_p\\ X_P^{\prime }& Y_P^{\prime }& Z_P^{\prime }\\ X_Q^{\prime }& Y_Q^{\prime }& Z_Q^{\prime }\end{array}\right|=F_p=0$$

(8)

where:

• $(X_P^{\prime },Y_P^{\prime },Z_P^{\prime })=(X_P-X_S,Y_P-Y_S,Z_P-Z_S), (X_Q^{\prime },Y_Q^{\prime },Z_Q^{\prime })=(X_Q-X_S,Y_Q-Y_S,Z_Q-Z_S).$

Let:

• $A=Y_P^{\prime }\cdot Z_Q^{\prime }-Y_Q^{\prime }\cdot Z_P^{\prime }, B=Z_P^{\prime }\cdot X_Q^{\prime }-Z_Q^{\prime }\cdot X_P^{\prime }, C=X_P^{\prime }\cdot Y_Q^{\prime }-X_Q^{\prime }\cdot Y_P^{\prime };$

Equation (7) can be rewritten as:

$$F_P=A\cdot u_p+B\cdot v_p+C\cdot w_p$$

(9)

With the established coplanar constraint Equation (9), considering differential terms with respect to the unknown parameters when linearizing using Taylor’s series, Equation (9) can also be rewritten using a differential form as,

$$\left|\begin{array}{ccc}{u}_p+d{u}_P& v_p+d{v}_P& w_p+d{w}_P\\ X_P^{\prime }+d{X}_P-d{X}_S& Y_P^{\prime }+d{Y}_P-d{Y}_S& Z_P^{\prime }+d{Z}_P-d{Z}_S\\ X_Q^{\prime }+d{X}_Q-d{X}_S& Y_Q^{\prime }+d{Y}_Q-d{Y}_S& Z_Q^{\prime }+d{Z}_Q-d{Z}_S\end{array}\right|=F_p=0$$

(10)

where $d(.)=\frac{\partial F_p}{\partial (.)}$, and Equation (10) is rewritten as:

$$A_1^P\cdot d\varphi +A_2^P\cdot d\omega +A_3^P\cdot d\kappa +A_4^P\cdot d{X}_S+A_5^P\cdot d{Y}_S+A_6^P\cdot d{Z}_S+F_P=0$$

(11)

where:

• $A_1^p=A\cdot [-r_{31}{x}_P^{\prime }-r_{32}{y}_P^{\prime }+r_{33}f]+C\cdot [r_{11}{x}_p^{\prime }+r_{12}{y}_p^{\prime }-r_{13}f]$
• $\begin{array}{cc}{A}_2^p=\hfill & A\cdot [(-\sin \mathsf{\varphi }\cos \mathsf{\omega }\sin \mathsf{\kappa })x_p^{\prime }+(-\sin \mathsf{\varphi }\cos \mathsf{\omega }\cos \mathsf{\kappa })y_p^{\prime }-f\sin \mathsf{\varphi }\sin \mathsf{\omega }]+\hfill \\ & B\cdot [(-\sin \mathsf{\varphi }\sin \mathsf{\kappa })x_p^{\prime }+(-\sin \mathsf{\omega }\cos \mathsf{\kappa })y_p^{\prime }+f\cos \mathsf{\omega }]+\hfill \\ & C\cdot [(\cos \mathsf{\varphi }\cos \mathsf{\omega }\sin \mathsf{\kappa })x_p^{\prime }+(\cos \mathsf{\varphi }\cos \mathsf{\omega }\cos \mathsf{\kappa })y_p^{\prime }+f\cos \mathsf{\varphi }\sin \mathsf{\omega }]\hfill \end{array}$
• $A_3^p=A\cdot [r_{12}{x}_p^{\prime }-r_{11}{y}_p^{\prime }]+B\cdot [(\cos \mathsf{\omega }\cos \mathsf{\kappa })x_p^{\prime }+(-\cos \mathsf{\omega }\sin \mathsf{\kappa })y_p^{\prime }]+C\cdot [r_{32}{x}_p^{\prime }-r_{31}{y}_p^{\prime }]$
• $A_4^p=-[(Y_Q^{\prime }-Y_P^{\prime })w_p+(Z_Q^{\prime }-Z_P^{\prime })v_p], A_5^p=-[(X_Q^{\prime }-X_P^{\prime })w_p+(Z_Q^{\prime }-Z_P^{\prime })u_p]$
• $A_6^p=-[(X_Q^{\prime }-X_P^{\prime })v_p+(Y_Q^{\prime }-Y_P^{\prime })u_p], (x_p^{\prime },y_p^{\prime })$

are image coordinates of point p on the image plane after all corrections in Section 3.1; other symbols are the same as above.

Equation (11) is rewritten in vector form as below:

$$C_1{X}_1+W_1=0$$

(12)

where:

• $\begin{array}{c}{C}_1=[\begin{array}{cccccc}{A}_1^P& A_2^P& A_3^P& A_4^P& A_5^P& A_6^P\end{array}], \\ X_1=[\begin{array}{cccccc}d\omega & d\phi & dk& d{X}_S& d{Y}_S& d{Z}_s\end{array}],\end{array}$
• $W_1=F_P.$

3.2. Perpendicular Condition

The perpendicularity constraint in 3D space is added to ensure preservation of the registered 2D and 3D pairs after applying registration transformation. As shown in Figure 3, suppose that AB and BC are two edges of a flat house roof, and their corresponding edges in the 2D image plane are ab and bc. Suppose that the coordinates of A, B and C are (X_A, Y_A, Z_A), (X_B, Y_B, Z_B) and (X_C, Y_C, Z_C), respectively, in the object coordinate system. For a flat-roof, cube house, the heights (i.e., Z coordinates) of A, B and C are the same, and the line segments AB and BC are perpendicular to each other. If AB is not perpendicular to BC and the angle between them is θ, i.e., B deviates from its correct position at B′, a line from C to O is drawn, and CO is perpendicular to AB′. l is the distance between B and O and can be expressed by [8]:

$$l=(X_C-X_B)\cos \theta +(Y_C-Y_B)\sin \theta =(Y_C-Y_B)(Y_B-Y_A)/S_{AB}+(X_C-X_B)(X_B-X_A)/S_{AB}$$

(13)

where S_AB is the length of the segment AB. Theoretically, the distance l should be zero. Thus, the differential form of Equation (13) is:

$$\begin{array}{cc}\hfill l_0+\Delta l=& [(Y_C-Y_B)(Y_B-Y_A)/S_{AB}+(X_C-X_B)(X_B-X_A)/S_{AB}]+\hfill \\ & [(X_B-X_A)\Delta X_C+(Y_B-Y_A)\Delta Y_C+(X_B-X_C)\Delta X_A+(Y_B-Y_C)\Delta Y_A+\hfill \\ & (X_C-2X_B+X_A)\Delta X_B+(Y_C-2Y_B+Y_A)\Delta Y_B]/S_{AB}=0.\hfill \end{array}$$

(14)

Equation (14) can be rewritten in matrix form as below:

$${\left[\begin{array}{c}{X}_B-X_C\\ Y_B-Y_C\\ X_C-2X_B+X_A\\ Y_C-2Y_B+Y_A\\ X_B-X_A\\ Y_B-Y_A\end{array}\right]}^T\left[\begin{array}{c}\Delta X_A\\ \Delta Y_A\\ \Delta X_B\\ \Delta Y_B\\ \Delta X_C\\ \Delta Y_C\end{array}\right]+[(X_C-X_B)(X_B-X_A)+(Y_C-Y_B)(Y_B-Y_A)]=0$$

(15)

Equation (15) can be then rewritten in vector form as:

$$C_2{\widehat{X}}_2+W_2=0$$

(16)

where:

• $C_2=\left[\begin{array}{cccccc}(X_B-X_C)& (Y_B-Y_C)& (X_C-2X_B+X_A)& (Y_C-2Y_B+Y_A)& (X_B-X_A)& (Y_B-Y_A)\end{array}\right],$
• ${\widehat{X}}_2={\left[\begin{array}{cccccc}\Delta X_A& \Delta Y_A& \Delta X_B& \Delta Y_B& \Delta X_C& \Delta Y_C\end{array}\right]}^T,$
• $W_2=(X_C-X_B)(X_B-X_A)+(Y_C-Y_B)(Y_B-Y_A).$

3.3. Solution of Registration Parameters

By combining Equations (6), (12) and (16), we have:

$$\{\begin{array}{c}V=A_1{X}_1+A_2{X}_2-L\\ C_1{\widehat{X}}_1+W_1=0\\ C_2{\widehat{X}}_2+W_2=0\end{array}$$

(17)

Furthermore, Equation (17) can be rewritten as:

$$\{\begin{array}{c}V=D\delta X-L\\ C_x\delta X+W_x=0\end{array}$$

(18)

where:

• $C_x={\left(\begin{array}{cc}{C}_1& C_2\end{array}\right)}^T, W_x={\left(\begin{array}{cc}{W}_1& W_2\end{array}\right)}^T, D=\left(\begin{array}{cc}{A}_1& A_2\end{array}\right),$
• $\mathsf{\delta }X={\left(\Delta \mathsf{\varphi }\Delta \mathsf{\omega }\Delta \mathsf{\kappa }\Delta X_S\Delta Y_S\Delta Z_S\Delta X_A\Delta Y_A\Delta Z_A\cdots \Delta X_N\Delta Y_N\Delta Z_N\right)}^T$

Equation (18) is the model derived in this paper for 2D-3D registration. Distinct from the existent conventional model used for 2D-3D registration in Equation (7), this model is called the rigorous model in this paper. As can be seen in Equation (18), this registration model combines the linear edges and conventional point features of a building. This model should therefore achieve higher accuracy and reliability than the conventional model. Equation (18) is usually solved using least-squares estimation, which is expressed as [36]:

$$\Phi =V^{T}V+2K_S^T(C_X\delta X+W_X)=\min$$

(19)

With least-squares estimation, the solution normal equation matrix can be written as:

$$\{\begin{array}{c}{D}_X^T{D}_X\delta X+C_X^T{K}_S+D_{X}L=0\\ C_X\delta X+0K_S+W_X=0\end{array}$$

(20)

where K_s is an introduced unknown matrix (for its details, please refer to [37]). If the number of total observation equations is M, the dimension of K_s is M × 1, i.e., $K_S={\left(K_{S_1},K_{S_2},\cdots ,K_{S_M}\right)}^T$.

Let $N_{XX}=D_x^T{D}_x^{}$; Equation (20) can be rewritten as:

$$\left(\begin{array}{cc}{N}_{XX}& C_X^T\\ C_X& 0\end{array}\right)\left(\begin{array}{c}\delta X\\ K_S\end{array}\right)+\left(\begin{array}{c}{D}_X^{T}L\\ W_X\end{array}\right)=0$$

(21)

The solution of unknown parameters would be:

$$\{\begin{array}{c}\delta X=-(Q_{12}{D}^{T}L+Q_{12}{W}_X)\\ K_S=-(Q_{21}{D}^{T}L+Q_{22}{W}_X)\end{array}$$

(22)

where Q_ij (i, j = 1, 2) is the components of the covariance matrix, which is an inverse of the normal matrix, i.e.,

$${\left(\begin{array}{cc}{N}_{XX}& C_X^T\\ C_X^T& 0\end{array}\right)}^{-1}=\left(\begin{array}{cc}{Q}_{11}& Q_{12}\\ Q_{21}& Q_{22}\end{array}\right)$$

(23)

3.4. Accuracy Evaluation

The standard deviations of the unit weight and unknown parameters are typically used to evaluate the quality of adjustment and the accuracy of adjusted unknown parameters. The standard deviation of the unit weight δ₀ is computed by:

$${\delta }_0=\sqrt{\frac{V^{T}V}{r}}$$

(24)

where V is the residual vector and r is the redundancy of the observation equation.

3.5. Discussion

3.5.1. Coplanar and Collinear Constraint

Lines have been used as registration primitives in previous work. As shown in Figure 4, if any three points B′, E′, C′ in object space are collinear, the collinear constraint condition can be established according to the method proposed by [8,33]. We can analyze the constraint condition of lines.

• Under the collinear constraint, three points B′, E′, C′ are considered to lie on a line in object space. However, due to the incomplete camera calibration in practice, their projections b′, e′, c′ cannot be guaranteed to lie on a line in image space. This implies that the collinear constraint condition ensures their collinearity only in object space, but it does not ensure their collinearity in image space.
• If the image is completely free of distortion after processing (this is definitely impossible.), their projections b′, e′, c′ in image space should lie on a line; i.e., their projections also meet the collinear constraint condition in image space. Under this ideal condition, the collinear constraint is consistent with the coplanar constraint. In other words, the collinearity and coplanar constraint condition is highly correlated if they are simultaneously considered in a formula.
• Because the camera lens cannot be completely calibrated, the residue of image distortion still remains even though a very high accuracy of camera calibration is achieved. This fact results in a line in object space being distortion free, but its corresponding image still contains distortion in image space. That is, the coplanar constraint combines a line in object space with its corresponding one in image space, whereas the collinear constraint considers only a line in object space. Thus, the coplanar constraint condition is much stricter than the collinear constraint condition.

Given the foregoing analysis, this paper uses the coplanar condition instead of the collinear condition.

3.5.2. Perpendicular Constraint

Perspective projections do not preserve angles. For example, as shown in Figure 4, if θ = 90° in object space, β is not 90° after perspective projection. Furthermore, when θ = θ′ = 90°, the two angles’ projections are both equal to β. This means that: (1) the perpendicular constraint is capable of enhancing the registration accuracy; (2) it may result in multiple solutions of IOPs and EOPs if we consider only the perpendicular constraint condition without adding the coplanar constraint and/or GCPs. For this reason, this paper simultaneously considers the perpendicular constraint, coplanar constraint and a few GCPs. Therefore, the perpendicular constraint proposed in this paper not only enhances the registration accuracy, but will also not reduce the risk of multiple solutions of IOPs and EOPs.

In a word, the coplanarity constraint condition in Figure 2 improves the accuracy of co-registration along a line (i.e., building edge), and the perpendicular constraint condition in Figure 3 improves the accuracy of co-registration along perpendicular lines (i.e., two perpendicular building edge). The two types of constraint conditions can maximize the accuracy symmetry without the need of adding additional GCPs.

4. Experiments and Analysis

4.1. Experimental Data

The experimental field is located in downtown Denver, Colorado, where the highest buildings reach 125 m, and many buildings are approximately 100 m. The City and County of Denver, Colorado, provided us with the aerial images and digital surface model (DSM).

• Aerial images: The six aerial images, with two flight strips, at the end lap of approximately 65% and the side lap of 30%, were acquired using a Leica RC30 aerial camera at a nominal focal length of 153.022 mm on 17 April 2000 (see Figure 5). The flying height was 1650 m above the mean ground elevation of the imaged area. The aerial photos were originally recorded on film and later scanned into digital format at a pixel resolution of 25 μm.
• DSM dataset: The DSM in the central part of downtown Denver was originally acquired by LiDAR and then edited into grid format at a spacing of 0.6 m (Figure 6a). The DSM accuracy in planimetry and height was approximately 0.1 m and 0.2 m, respectively. The horizontal datum is Geodetic Reference System (GRS) 1980, and the vertical datum is North American Datum of 1983 (NAD83).

With the datasets provided, we conducted data pre-processing and 3D coordinate measurement.

• CSG representation: With the given DSM (see Figure 6a), a 3D CSG (constructive solid geometry) model was utilized to represent the building individually. The CSG is a very mature method that uses a few basic primitives to create a complex surface or object by Boolean operators [38]. The details of the CSG method can be found in [6,38]. This paper proposes a three-level data structure to represent a building based on the given DSM data. The first level is 2D primitive representation, such as rectangle, circle, triangle or polygon, accompanied with their own parameters, including length, width, radius and the position of the point. The second level is 3D primitive representation, which is created by adding height information onto the 2D primitives. For example, by adding height information onto a rectangle (2D primitive), it becomes a cube (3D primitive); by adding height information onto a circle (2D primitive), it becomes a cylinder (3D primitive). In other words, cubes, cylinders, cones, pyramids, etc., are single 3D primitives. The third level is to create a 3D CSG representation of a building by combining multiple 3D primitives. During this process, a topological relationship is created, as well, so that building data can be easily retrieved and the geometric constraints proposed in this paper can be easily constructed. Meanwhile, the attributes (e.g., length, position, direction, grey) are assigned to each building (see Figure 6b).
• Coordinate measurement of “GCPs” and checkpoints: In areas with numerous high buildings, it is impossible to find conventional photogrammetric targeted points as ground control points (GCPs). In this paper, the corner points of building roofs or bottoms are taken as “GCPs”. The 3D (XYZ) coordinates of “GCPs” are acquired from the DBM. The corresponding 2D image coordinates are automatically measured with Erdas/Imagine software. The first three “GCPs” are selected manually. First, we select their locations in DBM, and their 3D coordinates can be read directly. We then find the corresponding locations in the 2D images manually with Erdas/Imagine software. After that, all other “GCPs” can be automatically measured with Erdas/Imagine software. The 2D image coordinates of “GCP” selection and measurements are based on back-projection. The EOPs of each image are solved by the first three measured “GCPs”, and the 3D coordinates of the other corners of buildings are then back-projected onto the image plane, with which the 2D image coordinates are automatically measured (Figure 7a). The measurement accuracy of the 2D image coordinates is at the sub-pixel level. With the operation above, 321 points are measured, of which 232 points are taken as “GCPs” and 89 are used as checkpoints, which will be used to evaluate the final accuracy of 2D-3D registration (Figure 6a and Figure 7b).

4.2. Establishment of the Registration Model

With the measured “GCPs” in Section 4.1, the 2D-3D registration model in Equation (18) can be established. Meanwhile, the two types of geometric constraint conditions, co-planarity (Equation (12)) and perpendicularity (Equation (16)), can simultaneously be established using the measured “GCPs”. For example, the faces, F_a, F_b and F_c, the edges, L₁, L₂ and L₃, and their attributes are described in the CSG model (see Figure 8a,b). From the attributes of the face data structure, L₁ and L₃ are automatically recognized as the edges of roofs, and L₂ is seen as the edge of a wall. However, the control points P₁, P₃ and P₅ are extracted, and they can be automatically constructed lines, l₁, l₂ and l₃. When L₁, L₂ and L₃ are back-projected onto the original aerial image, L₁, L₂ and L₃ will be matched with lines l₁, l₂ and l₃, respectively (Figure 8b). Thus, the attributes (e.g., edges of roofs and edges of walls) and topographic relationships (i.e., perpendicularity) of l₁, l₂ and l₃ can be inherited from L₁, L₂ and L₃. Thus, l₁ and l₃ are edges in the roof, and l₂ is a vertical line in the wall. Additionally, l₂ is perpendicular to l₁ and l₃; l₁ is also perpendicular to l₃. Therefore, when l₁ ⊥ l₃, Equation (16) is applied to construct a perpendicular constraint condition by replacing A, B and C by P₅, P₃ and P₁ (see Figure 2). Similarly, the coplanar constraint condition (Equation (12)) can be established, as well. By combining all established equations above, the registration equations for Equation (18) are established.

With the registration model established above, the solution can be found using the least-squares estimation. Owing to the non-linearization of the registration model (Equation (18)), the iterative solution is needed until the convergence of the solved registration parameters is met under a given threshold. The solved results are listed in Section 5.

4.3. Experimental Results

With the solved registration parameters, we project the 3D urban model back onto the aerial image. The 106 3D CSG building models are registered onto the original 2D aerial image, as shown in Figure 9. It is noted that the 3D CSG model is in the form of transparent wireframes to avoid the impact of the occluded wireframes of buildings when verifying the accuracy of 2D-3D registration.

5. Accuracy Comparison and Analysis

The accuracy comparison analysis of the 2D-3D registration is designed through conventional registration models (i.e., Equation (1)) and three types of ground control primitives. The evaluation indices include: (1) theoretical accuracy of the solved registration parameters; (2) relative accuracy in 2D space and 3D space; and (3) visual check.

5.1. Comparison of Theoretical Accuracy

The IOPs, including focal length and principal point coordinates, were precisely calibrated and provided by the data vendor. The registration parameters (also EOPs, X_S, Y_S, Z_S, ϕ, ω and k) and image distortion parameters (k₁, ρ₁ and ρ₂) are solved using Equation (22). The results and standard deviation are listed in

Table 1. Accuracy evaluation of the 2D-3D registration parameter: image distortion parameters (focal length = 153.022 mm; x₀ = 0.002 mm; y₀ = −0.004 mm).

Methods		Lens Distortion Parameter			${\mathsf{\delta }}_0^{IOP}$ (pixel)
Registration Model	Control Primitives	k1 (×10−4)	ρ1 (×10−6)	ρ1 (×10−6)
Traditional model	12 points	0.208	−0.114	0.198	1.23
Traditional model	211 points	0.301	−0.174	0.222	1.09
Our model	32 points + constraints	0.707	−0.201	0.038	0.47

and

Table 2. Accuracy evaluation of the 2D-3D registration parameter: exterior orientation parameters (EOPs).

Methods		Exterior Orientation Parameter
Registration Model	Registration Primitives	ϕ (arc)	ω (arc)	k (arc)	XS (ft)	YS (ft)	ZS (ft)	${\mathsf{\delta }}_0^{IOP}$ (pixel)
Traditional model	12 points	0.0104	0.0158	−1.5503	3143007.3	1696340.4	9032.0	1.26
Traditional model	211 points	−0.0025	−0.0405	−1.5546	3143041.4	1696562.6	9070.7	1.02
Our model	32 points + constraints	−0.0017	−0.0322	−1.5544	3143041.2	1696533.4	9071.8	0.37

. As can be seen in Table 1 and Table 2, the proposed model has the highest accuracy at a standard deviation of 0.47 pixels for solving IOPs and 0.37 pixels for solving EOPs.

5.2. Accuracy Comparison in 2D Space

The accuracy comparison in the 2D image plane is conducted to evaluate the correctness and robustness of the proposed method. The steps of the comparison analysis in 2D space are as follows: (1) With the registration parameters solved above, 3D buildings are back-projected onto the aerial image plane; (2) XY image coordinates of the back-projected and original 59 checkpoints are measured; (3) the root mean square ($RMS$) error of 59 checkpoints is computed by $RM{S}_X=\sqrt{({\Delta }^T\Delta )/N}$, where Δ is the difference in the x coordinates between the back-projected and the original 59 checkpoints and N is the number of checkpoints used; the operation for the y coordinates is similar.

As illustrated in Table 1, the accuracy estimation for the lens distortion parameters (${\mathsf{\delta }}_0^{IOP}$) is 1.23 pixels and 1.09 pixels when using 12 GCPs and 211 GCPs with conventional model. Compared with those results, ${\mathsf{\delta }}_0^{IOP}$ is 0.47 pixel when using 32 points with the proposed model, which is an improvement of 61.8% over the conventional model when using 12 GCPs and 56.9% when using 211 GCPs.

On the similarity, from Table 2, the accuracy estimation for the exterior orientation parameters (${\mathsf{\delta }}_0^{IOP}$) is 1.26 and 1.02 when using 12 “GCPs” and 211 “GCPs” with the conventional model. Compared to those results, ${\mathsf{\delta }}_0^{IOP}$ is 0.37 pixels when using 32 points with the proposed model, an improvement of 70.6% over the conventional model when using 12 GCPs and 63.7% when using 211 GCPs.

From

Table 3. Accuracy comparison of 2D-3D registration in 2D space.

Registration Models	Control Primitives	$RM{S}_X$ (pixel)	$RM{S}_y$ (pixel)
Conventional model	12 points	9.4	10.1
Conventional model	211 points	5.2	6.7
Proposed model	32 points + constraints	1.8	2.2

, there are significant offsets between the building wireframes and the building edges for the conventional model, whose RMS values are approximately 10 pixels along the x and y directions; whereas the RMS of the proposed method is only about two pixels in both the x and y directions, an improvement of 78.0% over the conventional model when using 12 GCPs and 67.2% when using 211 GCPs. The results demonstrate that the accuracy of 2D-3D registration achieved by the proposed method has been greatly increased.

Figure 10 depicts the 2D-3D registration results for the visual check using the proposed and conventional model. Five typical buildings with different heights are represented, and they are located at different locations of the image plane. a₁ through e₁ are the 2D-3D registration results created by the proposed model, in which 32 points plus the two types of constraints are employed; a₂ through e₂ and a₃ through e₃ are the 2D-3D registration results created by conventional models, in which 211 “GCPs” and 12 “GCPs” are employed, respectively.

6. Conclusions

The major contribution of this paper is the development of a rigorous transformation model for 2D-3D registration to increase its accuracy and reliability. This model simultaneously considers two types of geometric constraints (perpendicularity and co-planarity) and utilizes both point features and linear features as registration primitives. The details of the proposed 2D-3D registration model were presented.

A test field located in downtown Denver, Colorado, has been used to evaluate the proposed methods. The comparison analysis of the accuracy achieved by the proposed method and the conventional method are conducted. The experimental results demonstrated that: (1) the theoretical accuracy of the solved registration parameters can reach 0.47 pixels, whereas other methods reach only 1.23 and 1.09 pixels; (2) the RMS of 2D-3D registration created by the conventional model is approximately 10 pixels along both x and y directions, whereas the RMS from the proposed method is only two pixels in both the x and y directions. In addition, five buildings with different heights located at different locations of the aerial image plane are visually evaluated. It is demonstrated that the method proposed in this paper achieved higher accuracy than conventional methods, and 3D buildings presented by wireframes can be exactly registered in 2D aerial imagery.