Land Surface Temperature and Emissivity Retrieval from Field-Measured Hyperspectral Thermal Infrared Data Using Wavelet Transform
Abstract
:1. Introduction
2. Methodology and Data
2.1. Radiative Transfer Theory
2.2. Wavelet Transform Method for Temperature and Emissivity Separation (WTTES)
2.3. Simulated Data
2.4. Field-Measured Data
2.5. Algorithms for Evaluation
3. Results and Discussion
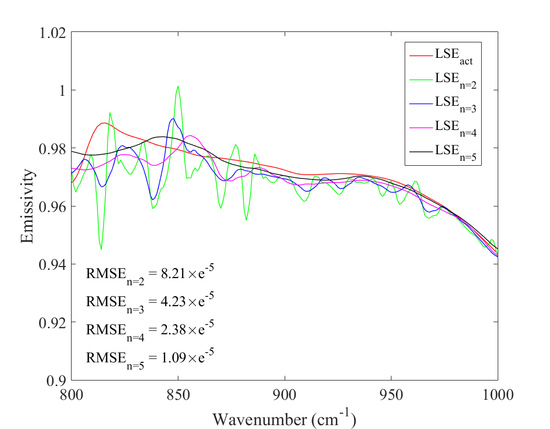
3.1. Errors introduced by the Wavelet Transform (WT)
3.2. Sensitivity to Instrument Noise
3.3. Sensitivity to the Atmospheric Downwelling Radiance
3.4. Comparison of the WTTES Algorithm with the ISSTES Algorithm
3.5. Evaluation with Field-Measured Data
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dash, P.; Olesen, F.S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Li, Z.L.; Wu, H.; Wang, N.; Shi, Q.; Sobrino, J.A.; Wan, Z.; Tang, B.H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.Z.; Yan, G.J.; Wan, Z.M.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Quattrochi, D.A.; Goel, N.S. Spatial and temporal scaling of thermal infrared remote sensing data. Remote Sens. Rev. 1995, 12, 255–286. [Google Scholar] [CrossRef]
- Hook, S.J.; Gabell, A.R.; Green, A.A.; Kealy, P.S. A comparison of techniques for extracting emissivity information from thermal infrared data for geologic studies. Remote Sens. Environ. 1992, 42, 123–135. [Google Scholar] [CrossRef]
- Hook, S.J.; Karlstrom, K.E.; Miller, C.F.; McCaffrey, K.J.W. Mapping the Piute Mountains, California, with thermal infrared multi- spectral scanner (TIMS) images. J. Geophys. Res. 1994, 99, 15605–15622. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Realmuto, V.J. Separating the effects of temperature and emissivity: Emissivity spectrum normalization. In Proceedings of the 2nd TIMS Workshop, Pasadena, CA, USA, 6 June 1990. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Wan, Z.; Li, Z.L. A physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 980–996. [Google Scholar]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Kahle, A.B.; Madura, D.P.; Soha, J.M. Middle infrared multispectral aircraft scanner data: analysis for geological applications. Appl. Opt. 1980, 19, 2279–2290. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Pippi, I. Temperature and emissivity retrieval from remotely sensed images using the “Grey body emissivity” method. IEEE Trans. Geosci. Remote Sens. 1996, 34, 681–695. [Google Scholar] [CrossRef]
- Gillespie, A.R. Lithologic mapping of silicate rocks using TIMS (Thermal Infrared Multispectral Scanner). In Proceedings of the Thermal Infrared Multispectral Scanner Data User’s Workshop, Pasadena, CA, USA, 18–19 June 1985. [Google Scholar]
- Mao, K.; Shi, J.; Tang, H.; Li, Z.L.; Wang, X.; Chen, K.S. A neural network technique for separating land surface emissivity and temperature from ASTER imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 200–208. [Google Scholar] [CrossRef]
- Li, Z.L.; Becker, F.; Stoll, M.P.; Wan, Z. Evaluation of Six Methods for Extracting Relative Emissivity Spectra from Thermal Infrared Images. Remote Sens. Environ. 1999, 69, 197–214. [Google Scholar] [CrossRef]
- Aumann, H.H.; Chahine, M.T.; Gautier, C.; Goldberg, M.D.; Kalnay, E.; McMillin, L.M.; Revercomb, H.; Rosenkranz, P.W.; Smith, W.L.; Staelin, D.H.; et al. AIRS/AMSU/HSB on the Aqua mission: Design, science objectives, data products, and processing systems. IEEE Trans. Geosci. Remote Sens. 2003, 41, 253–264. [Google Scholar] [CrossRef]
- Chalon, G.; Cayla, F.; Diebel, D. IASI-An advanced sounder for operational meteorology. In Proceedings of the 52nd IAF, International Astronautical Congress, Toulouse, France, 1–5 October 2001. [Google Scholar]
- Siméoni, D.; Singer, C.; Chalon, G. Infrared atmospheric sounding interferometer. Acta Astronaut. 1997, 40, 113–118. [Google Scholar] [CrossRef]
- Glumb, R.J.; Mantica, P. Development of the Crosstrack Infrared Sounder (CrIS) sensor design. Proc. SPIE Int. Soci. Opt. Eng. 2002, 4486, 411–424. [Google Scholar]
- Borel, C.C. Surface emissivity and temperature retrieval for a hyperspectral sensor. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seattle, WA, USA, 6–10 July 1998; pp. 546–549. [Google Scholar]
- Wang, N.; Wu, H.; Nerry, F.; Li, C.; Li, Z.L. Temperature and emissivity retrievals from hyperspectral thermal infrared data using linear spectral emissivity constraint. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1291–1303. [Google Scholar] [CrossRef]
- Wang, X.; Ouyang, X.; Tang, B.; Li, Z.L.; Zhang, R. A New Method for Temperature/Emissivity Separation from Hyperspectral Thermal Infrared Data. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 8–11 July 2008. [Google Scholar]
- Cheng, J.; Liang, S.; Wang, J.; Li, X. A Stepwise Refining Algorithm of Temperature and Emissivity Separation for Hyperspectral Thermal Infrared Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1588–1597. [Google Scholar] [CrossRef]
- Adler-golden, S.; Conforti, P.; Gagnon, M.; Tremblay, P.; Chamberland, M. Long-wave infrared surface reflectance spectra retrieved from Telops Hyper-Cam imagery. In Proceedings of the SPIE-The International Society for Optical Engineering, Baltimore, MD, USA, 5 May 2014; pp. 90880U:1–90880U:8. [Google Scholar]
- Wu, H.; Li, Z.L.; Tang, B.H.; Tang, B.L. Evaluation of the improved linear emissivity constraint temperature and emissivity separation method by using the simulated hyperspectral thermal infrared data. In Proceedings of the 2015 SPIE 9808, International Conference on Intelligent Earth Observing and Applications, Guilin, China, 23 October 2015. 98082L. [Google Scholar]
- Wu, H.; Wang, N.; Ni, L.; Tang, B.H.; Li, Z.L. Practical retrieval of land surface emissivity spectra in 8–14 μm from hyperspectral thermal infrared data. Opt. Express 2012, 20, 24761–24768. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Goldberg, M.; Barnet, C.; Cheng, Z.; Sun, F.; Wolf, W.; Divakarla, M. Regression of Surface Spectral Emissivity from Hyperspectral Instruments. IEEE Trans. Geosci. Remote Sens. 2008, 46, 328–333. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Bernstein, L.S.; Acharya, P.K.; Dothe, H.; Matthew, M.W.; Adler-Golden, S.M.; Chetwynd, J.H.; Richtsmeier, S.C.; Pukall, B.; et al. MODTRAN4 radiative transfer modeling for atmospheric correction. Proc. SPIE Int. Soc. Opt. Eng. 1999, 3756, 348–353. [Google Scholar]
- Gu, D.; Gillespie, A.R.; Kahle, A.B.; Palluconi, F.D. Autonomous Atmospheric Compensation (AAC) of high-resolution hyperspectral thermal infrared remote-sensing imagery. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2557–2570. [Google Scholar]
- Young, S.J.; Johnson, B.R.; Hackwell, J.A. An in-scene method for atmospheric compensation of thermal hyperspectral data. J. Geophys. Res. Atmos. 2002, 107, ACH 14-1–ACH 14-20. [Google Scholar] [CrossRef]
- Tonooka, H. An atmospheric correction algorithm for thermal infrared multispectral data over land-a water-vapor scaling method. IEEE Trans. Geosci. Remote Sens. 2001, 39, 682–692. [Google Scholar] [CrossRef]
- Tonooka, H.; Palluconi, F.D. Validation of ASTER/TIR Standard Atmospheric Correction Using Water Surfaces. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2769–2777. [Google Scholar] [CrossRef]
- Tonooka, H. Accurate atmospheric correction of ASTER thermal infrared imagery using the WVS method. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2778–2792. [Google Scholar] [CrossRef]
- Farge, M. Wavelet Transforms and their Applications to Turbulence. Annu. Rev. Fluid. Mech. 1992, 24, 395–457. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Borel, C. Error analysis for a temperature and emissivity retrieval algorithm for hyperspectral imaging data. Int. J. Remote Sens. 2008, 29, 5029–5045. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Matthew, M.W.; Golden, S.M. MODTRAN4 User’s Manual; Air Force Research Laboratory, Space Vehicles Directorate: HANSCOM AFB, MA, USA, 1999. [Google Scholar]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Tang, B.H.; Bi, Y.Y.; Li, Z.L.; Xia, J. Generalized Split-Window Algorithm for Estimate of Land Surface Temperature from Chinese Geostationary FengYun Meteorological Satellite (FY-2C) Data. Sensors 2008, 8, 933–951. [Google Scholar] [CrossRef] [PubMed]
- Kanani, K.; Poutier, L.; Nerry, F.; Stoll, M.P. Directional effects consideration to improve out-doors emissivity retrieval in the 3–13 µm domain. Opt. Express 2007, 15, 12464–12482. [Google Scholar] [CrossRef] [PubMed]









| Profiles | Total Water Vapor (g/cm2) | Bottom Atmospheric Temperature (K) | Latitude () |
|---|---|---|---|
| 1976 US Standard Atmosphere | 1.42 | 288.1 | -- |
| Tropical Atmosphere | 4.08 | 299.7 | 15 North |
| Mid-Latitude Summer | 2.91 | 294.2 | 45 North |
| Mid-Latitude Winter | 0.82 | 272.2 | 45 North |
| Sub-Arctic Summer | 2.08 | 287.2 | 60 North |
| Sub-Arctic Winter | 0.42 | 257.2 | 60 North |
| Name | Description |
|---|---|
| slate | Homogeneous and flat piece of slate. Composition: SiO2 (60%), Al2O3 (17%), Fe2O3 (7.6%), K2O (3.9%), MgO (2.5%), … |
| wood | Plywood. |
| water | Water. |
| sand#1 | Morocco sand. Red color. Various grain sizes < 750 μm. Composition: SiO2 (96.3%), Al2O3 (1%), ... |
| soil | Soil from the Negev desert. Various grain sizes < 2 mm. Composition: SiO2 (42.2%), CaO (22.8%), Al2O3 (5.5%), Fe2O3 (2.7%), ... |
| stone#2 | Flat rough and homogenous rock. Composition: SiO2 (77%), Al2O3 (12.6%), K2O (4.6%), Na2O (3.1%), Fe2O3 (1.2%), ... |
| sand#2 | Fontainebleau type sand. Various grain sizes < 750 μm. Composition: SiO2 (98.4%), Al2O3 (0.6%), ... |
| pstyr | Extruded polystyrene. |
| SiC | SiC Powder. Grain size ~ 120 μm. |
| Group | Method | NE∆T = 0.1 K | NE∆T = 0.2 K | NE∆T = 0.5 K | |
|---|---|---|---|---|---|
| G1 | ISSTES WTTES | 0.07 K 0.05 K | 0.13 K 0.10 K | 0.35 K 0.29 K | |
| RMSET | G2 | ISSTES WTTES | 0.07 K 0.06 K | 0.14 K 0.11 K | 0.41 K 0.34 K |
| G3 | ISSTES WTTES | 0.16 K 0.13 K | 0.31 K 0.26 K | 0.85 K 0.70 K | |
| G1 | ISSTES WTTES | 0.41% 0.31% | 0.79% 0.62% | 1.87% 1.48% | |
| RMSEε | G2 | ISSTES WTTES | 0.21% 0.17% | 0.40% 0.34% | 1.00% 0.84% |
| G3 | ISSTES WTTES | 0.35% 0.29% | 0.69% 0.58% | 1.79% 1.49% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.-Z.; Wu, H.; Jiang, X.-G.; Jiang, Y.-Z.; Liu, Z.-X.; Nerry, F. Land Surface Temperature and Emissivity Retrieval from Field-Measured Hyperspectral Thermal Infrared Data Using Wavelet Transform. Remote Sens. 2017, 9, 454. https://doi.org/10.3390/rs9050454
Zhang Y-Z, Wu H, Jiang X-G, Jiang Y-Z, Liu Z-X, Nerry F. Land Surface Temperature and Emissivity Retrieval from Field-Measured Hyperspectral Thermal Infrared Data Using Wavelet Transform. Remote Sensing. 2017; 9(5):454. https://doi.org/10.3390/rs9050454
Chicago/Turabian StyleZhang, Yu-Ze, Hua Wu, Xiao-Guang Jiang, Ya-Zhen Jiang, Zhao-Xia Liu, and Franҫoise Nerry. 2017. "Land Surface Temperature and Emissivity Retrieval from Field-Measured Hyperspectral Thermal Infrared Data Using Wavelet Transform" Remote Sensing 9, no. 5: 454. https://doi.org/10.3390/rs9050454
APA StyleZhang, Y.-Z., Wu, H., Jiang, X.-G., Jiang, Y.-Z., Liu, Z.-X., & Nerry, F. (2017). Land Surface Temperature and Emissivity Retrieval from Field-Measured Hyperspectral Thermal Infrared Data Using Wavelet Transform. Remote Sensing, 9(5), 454. https://doi.org/10.3390/rs9050454