1. Introduction
Remote sensing imagery is one important solution to maritime surveillance, because of its wide field of view, satisfying spatial resolution and update frequency. Remote sensing imagery includes various kinds, ranging from hyper-spectral imagery [
1], synthetic aperture radar (SAR) imagery [
2], to optical imagery. These kinds of imaging technology serve varying purposes according to their different characteristics, and optical imagery is applied widely for its rich presentation and similar reception frequency to that of human eyes.
There has been a considerate amount of research in optical imagery understanding focusing on detection of different types of objects, such as roads [
3,
4], buildings [
5,
6], oil tanks [
7,
8], vehicles [
9,
10,
11] and airplanes [
12,
13,
14]. Aside from detecting scattered objects, the classification of scenes also receives a lot of attention recently, such as in [
15,
16,
17], where the objective is to classify image patches into different classes, such as buildings, forest, harbor, etc.
Two of the most important tasks in understanding remote sensing images that is maritime-related, would be sea-land segmentation and ship detection. Research on ship detection originally focuses on off-shore ships with relatively simple background, majorly on SAR imagery [
2,
18,
19]. In recent literature, both sea-land segmentation [
20,
21] and ship detection [
22,
23,
24,
25,
26,
27] tasks are addressed with complex frameworks, which consists of cascaded procedures and have to be designed and fine-tuned with expert knowledge. That is, when the source sensor of the images is changed, the carefully designed framework always has to be re-calibrated or even re-designed by experts. The complex steps that constitute the framework also make the implementation difficult. Furthermore, ship detection, especially when including in-dock ships, are highly dependent of the performance of sea-land segmentation, making it less robust in precarious sea-land situation. Furthermore, to tackle the two problems separately, also inhibits the joint optimization of the designed algorithm.
The recent advancement in the deep learning community motivates us to address these problems with deep neural networks. Deep learning, as a subcategory of soft computing [
28,
29,
30,
31,
32,
33,
34], is seeing great attention. In our previous work, we focus on the detection of objects instance-wise, i.e., acquiring the location and bounding box of the objects in interest. In this paper, we propose to address the sea-land segmentation and ship detection at the same time, with a deep neural network, in a semantic labeling perspective. The network allows us to cope with these problems in an end-to-end fashion, without complex procedures, and without handcrafted features.
The semantic labeling of everyday images recently receives increasing attention [
35,
36,
37,
38] and is regarded as a more challenging task compared to object classification and detection of images. Semantic labeling provides a pixel-to-pixel label map corresponding to the input image, as opposed to only a single label in classification task. It also, from another point of view, provides the boundaries of the detected object, as opposed to only bounding boxes in detection task. This is similar to the saliency detection methods [
39,
40], with the difference that saliency detection is more general and pays less attention to object boundaries. One general approach of semantic labeling is to first process images into over-segmented areas and then classify each area with its extracted features [
35]. Yet with the fast-paced development of deep learning, it also proves to be able to achieve state-of-the-art semantic labeling in everyday images [
36,
37,
38]. Moreover, since recent research shows that neural networks based on everyday object knowledge can have satisfactory performance on remote sensing imagery [
41], the application of deep learning in remote sensing imagery is promising.
In both sea-land segmentation and ship detection tasks, semantic labeling using deep networks shows great potential. First, deep network is able to learn high level features, as opposed to that in other methods, features has to be handcrafted and are complex to implement. Second, semantic labeling’s pixel-labeling nature allows it to be independent of bounding boxes and are relatively indifference to objects’ size and shape. This helps because sea and land are of arbitrary sizes and shapes, and the bounding boxes of in-dock ships are hard to acquire.
However, the deep network, when used to address these remote sensing problems, is faced with one critical problem, to balance between the hardware requirement and the network’s efficacy. In remote sensing images, the area of interest can be of arbitrary size. This lead to the need for a network with extra-large receptive field (which will be extensively discussed in
Section 3.2), which requires increased amount of weights for the network layers, which then leads to excessive graphics processing unit (GPU) memory requirement from the network and increased computation in training and testing.
To ameliorate the trade-off between the network’s receptive field and the GPU memory requirement, we introduce a novel multi-scale structure for the semantic labeling network, which greatly increases the receptive field of the network, with only a small number of parameter increase.
The main idea of our multi-scale structure is different than those of the conventional ones, where shortcuts are created between convolution layers of different levels to utilize the finer feature maps in order to produce finer outputs. Our structure focuses on enlarging the receptive field of the network to incorporate information from larger scale, which is important for understanding remote sensing images.
In the network, the input data is processed in two separate layers, crop layer and resize layer, into different scales of data, fine-scale and coarse-scale, respectively. The fine-scale path with crop layer keeps the fine details in the data, but with small sized receptive field, while the coarse-scale path with resize layer down-samples the data, omitting high-resolution textures in exchange for large sized receptive field. In this paper, the coarse-scale path is more suitable for discriminating between sea and land, for their large proportion in area and usually obscure boundaries (near beaches and other natural shore-lines, for example). The fine-scale path is suitable for ship detection, for exactly the opposite reasons.
The main contribution of the paper is listed as follows,
Joint sea-land segmentation & in-dock ship detection. The information extracted by the network is used both for sea-land segmentation and ship detection. The sharing of the information can lead to better performance, especially in in-dock ship detection, since it is no longer dependent on other separated sea-land segmentation methods and can be trained jointly.
A different perspective into multi-scale structure for remote sensing images with small parameter number increase. The conventional multi-scale structures connect different feature maps from different layers that represents different level of semantics, aiming to fully utilize fine-scale features. The proposed structure aims to widen the receptive field of the network, designed specifically for remote sensing images. With the multi-scale structure, the network is able to achieve tasks that require different scales, while maintaining relatively small number of parameter and low calculation complexity. An extensive experiment is conducted to compare our proposed structure to several variants to show its superiority in learning speed and performance.
The following content is structured as follows. In
Section 2, a brief introduction to fully convolutional network is given. In
Section 3, the proposed multi-scale structure is described in detail and the receptive field of the network is analyzed. In
Section 4, the given framework and other methods are experimented on two remote sensing datasets. Finally,
Section 6 concludes this paper.
2. Fully Convolutional Network
In this section, we will provide a brief introduction to the fully convolutional network (FCN) upon which we construct our semantic labeling framework.
CNN proves to be extremely effective in image related tasks, such as object detection and classification [
42,
43]. Based on CNN, Fully Convolutional Networks (FCN) are designed to predict a label map rather than a single label for an input image, by replacing fully connected layers in CNN with small sized convolution layers [
44]. FCN’s pixel-to-pixel label map output naturally suits the need of semantic labeling.
Figure 1, modified from in [
44], shows a typical FCN structure, when used to semantic label a remote sensing image.
A typical FCN consists of convolution layers, pooling layers and activation layers [
44]. There are also softmax layers for output and loss layers for training. An input data matrix (say, an RGB image
or a grayscale image
) is processed through each layer in sequence in a neural network.
A convolution layer consists of an array of kernel matrices, with which the input data are convoluted. In a convolution layer, the data is processed with the following calculation,
where ∗ is a 3D (3 Dimensional) convolution operator,
X is the input matrix of the layer,
is the
lth kernel of the layer and
is the output matrix correspond to the
lth kernel. Here it is mandatory that
and
X are of the same size in 3rd dimension, so that the size of dimension 3 of
is necessarily 1. Finally, the
s of a layer are concatenated in 3rd dimension, resulting in
where
Y is the complete output matrix of the convolution layer.
x,
y and
l are indexes for
Y of dimension 1, 2 and 3, respectively. Convolution layers are designed to capture local features and are translation invariant, and the output matrix of a convolution layer is usually called a feature map, since the output represents the extracted features of each single pixels of the input image, with pixel-to-pixel correspondence.
Activate functions are often added after convolution layers to provide non-linear properties for a network to enhance the expressive ability of the features. In an activation function, an element-wise operation is conducted,
where
x,
y,
z are indexes of 3 dimensions of a matrix and
X,
Y are input and output matrices, respectively.
f is the function of the layer. In a simple but rather popular activation layer, Relu [
45],
A pooling layer, acting like a down-sampling filter, is often inserted among other layers. It is designed to progressively reduce the size of transferred data to reduce the amount of parameters and enhance the generalization of a network. The most common form of a pooling layer uses max operation to produce results for each local area of the input,
where
x,
y,
z,
i and
j are indexes of their according dimensions of the matrices and
X,
Y are input and output matrices, respectively. In addition,
where
and
are the two hyperparameters of the pooling layer, determining the stride of the output according to input and the size of
, respectively. For simplicity, the indexes here follow the convention in programming and start from zero.
In an FCN, there are no fully connected layers, which connect all the elements in the input matrix and output results that ignore all spatial information. Convolution layers with kernels of size
are implemented instead, producing an output matrix of corresponding spatial dimensions [
44]. Because some of the convolution layers at the top of the network still act as a role of traditional fully connected layers, in our paper we still distinguish these layers and symbolize them as “fc” layers following the notation in [
36].
A softmax layer is a layer for output, it takes in matrices of arbitrary-scaled elements and outputs a matrix of probabilities, with the formula of
where
X and
Y are input and output matrix of the softmax layer, respectively.
x,
y,
j and
k are indexes of their corresponding dimensions.
K is the size of dimension 3 of
X. In a semantic labeling network, the softmax layer outputs the probabilities of every pixel belonging to every category.
A loss layer takes in data both from outputs of previous layers and from ground truth labels. The gradients are firstly calculated from the difference of both sides, and then are back-propagated to previous layers. The kernels of each layer are then updated according to the gradients. This process is gone through iteratively and the network will be trained.
3. Multi-Scale Network for Semantic Labeling
The semantic labeling of maritime scenes calls for multi-scale features because of the tremendous size difference between the sea, land and ships. Sea-land identification demands wide spatial range of input for richer context and comprehensive understanding, whereas small targets, such as ships, demand context of smaller scale but more detailed information from local area. The feature of multi-scale has been extensively utilized in neural networks. Liang et al. connects output of the first few layers to the last layer for attention on fine-resolution layers [
36]. Paisitkriangkrai et al. trains several CNNs with different resolution of input images [
46]. Eigen et al. concatenates layers that are designed for different scales into a whole [
37]. These networks either are trained separately on every scale, resulting in far more parameters to train, or leave the layers trained without the knowledge of its corresponding scale information. Here we present a multi-scale FCN specifically designed for remote sensing imagery. This framework enlarges the receptive field of the network, while preserving the ability to take in fine details, with only a small increase in the number of parameters.
3.1. Network Structure
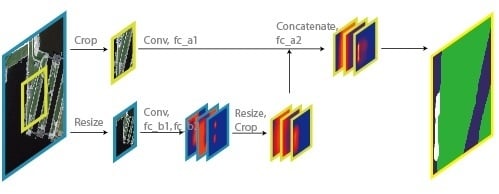
To implement the multi-scale structure in the network, we introduce two layers, crop layer and resize layer, which is illustrated in
Figure 2. In a resize layer, the input is down-sampled, and in the crop layer, the input is center-cropped. The input are separated into what we call fine and coarse scale, respectively, after these two layers.
With the two layers, we have two separate paths of images as well as ground truth labels going through the network at the same time, each representing a different scale.
In
Figure 3, the whole network is illustrated. First, an input image patch is duplicated and preprocessed in 2 separate ways, fine-scale and coarse-scale, using aforementioned crop layer and resize layer and are fed into following convolution layers. The outputs of the two preprocessing layers, although cover different areas (Area Yellow vs. Area Blue), are of the same size and thus can be fed into the same layer configuration with the same weights. The convolution layers are configured as DeepLab-LargeFOV [
36], with its first 13 convolution layers and are interlaced with Relu and pooling layers. We implement this convolution configuration because it proves to have state-of-the-art semantic labeling performance in everyday images.
In
Figure 3, some of the results of certain layers are represented as a group of 3 slices, each slice representing the probability map of a corresponding class. We name these groups as score maps for convenience. A score map, in essence, is the same as a feature map, where both maps are the output of a certain convolution layer, but the position and the configuration of the convolution layer define the semantics that the layer is to learn to output the scores of each pixel to belong to a certain category (In fact, a score map is a direct output of a softmax layer, which is placed after a convolution layer. But the function of a softmax layer is relatively trivial compared to the other layers, so the softmax layers are not mentioned either in the figure or in the text).
The network also utilizes two loss layers, each to train the layers in different scales. In
Figure 3, the score maps that are connected to a loss layers are underlined with dashed lines. As for the ground truth labels that are needed by the loss layers, they are acquired in the same way as the input patches. The original labels go through crop layer and resize layer separately, and then are fed into loss layers in fine-scale loss layer and coarse-scale loss layer, respectively. With the two loss layers, the convolution layers and fc_** layers learn to produce score maps in accordance. To be specific, the coarse-scale score map is predicted purely from coarse-scale data and then are modified with resize and crop layers, and finally are fed into fine-scale path (Layer fc_a2) to produce fine-scale score map jointly.
Although in
Figure 3 the convolution layers are divided into fine-scale and coarse-scale, it is only for clarity. In the practical implementation the fine-scale and coarse-scale data are concatenated first and fed into the same convolution layers, and then separated back to each scale before producing score maps. The weights are shared for convolution layers on the same level and also between fc_*1 layers to minimize the number of parameters. Here the feature extraction mechanism of the convolution layers are not scale specific. The feature maps extracted from different scales may share different semantics, but they are equally effective. We presume that just as deep features can generalize from everyday objects to remote sensing domains [
41], deep features can also generalize between different scales of scenes, hence the sharing weights between scales.
The crop layer we design has a simple forward function, which center crops the input with a single parameter, . The crop function only work on spatial dimensions, which means only the sizes of the first 2 dimension will change. It also has no backward function, meaning no gradient is transferred back through this layer, for simplicity. The simplification is plausible because (a) it is located in special positions in the network, twice after data layers and once after convolution layers and (b) the convolution layers before it have shared weights and can already learn from both scales and (c) coarse-scale layers should focus on sea-land classification and need to take little knowledge from fine-scale losses.
It is also worth mentioning that in [
36,
47], a ’hole algorithm’ is introduced into the deep network for convolution layers, to increase the receptive field of the layers while keeping the number of weights unchanged. A simple explanation would be to put ’holes’ in the layer kernels to enlarge the kernels spatially, while maintaining the number of parameters in a kernel,
where
x,
y,
z are indexes of their according dimensions of the matrices,
means to calculate the remainder of division and
K,
are original and modified kernel of the convolution layer with ’hole algorithm’, respectively.
is a hyperparameter of the layer, specifying how large the ’hole’ you want to insert into the kernels. In this paper, we keep the ’hole algorithm’ as is implemented in [
36], but with tuned-down size of the hole, in order to acquire more subtle details for the label result.
Table 1 lists the structure setup of the network. The layer names are either self-explanatory or mentioned in the text, so the layer types are omitted. Apart from the Relu layers after each convolution layer, the layers from conv1_1 to pool5b are listed as the exact setup order.
3.2. Receptive Field Analysis
The receptive field is a vital concept that can affect a network’s performance. It is a biologically-inspired term from animals’ visual cortex. In a network, it describes the spatial range of input pixels that can contribute to the calculation of a single element in the output. With larger receptive field, each layer can take in more context and represent more abstract meanings. For a network to determine if a pixel belongs to a ship, it is important that the network can determine if the pixel belongs to the forecastle deck or the side of a ship. For ship detection, the receptive field is best to be large enough to cover the space of ship and its context, and for sea-land segmentation, extensively larger receptive field is needed.
The crop layer and the resize layer introduced in the former section is introduced into the network to specifically enlarge the receptive field of one path, while also maintaining the detail feature in another path. The resize layer acts as a downsampling filter, which shrinks the spatial size of the input at the cost of losing detail information, while allowing enlarging the receptive field of the following network path (coarse-scale) without any modification to the existing convolutional layers. The crop layer ensures the input image is cropped to the same spatial area as the desired and maintains the detail information (for the fine-scale). In the training procedure, the parameters of the network is jointly optimized to decrease the loss to the ground truth label. With the different scale of the input data that is given to each path, the network can automatically learn the optimized task for each path, as shown in
Section 4.4.
Figure 4 also illustrates the relation between the kernel size and the receptive field of each convolution layer. The kernel size determine the area of the input data to calculate one single element in the output. We can see that with the layers going deeper, or with larger kernel size, the receptive field of the the output layer will increase. Apart from that, the pooling layer also can increase the receptive field, with the possible draw-back of lowering the layer resolution.
The whole network’s receptive field can calculated by stacking up each layer’s receptive radius,
where
R is the radius of the network receptive field (
),
l is the index of the layers and affects receptive field, including pooling layers and convolution layers.
L is the total number of the above layers, and
r is the radius of the layer’s receptive field when considering the subsampling effect of its previous pooling layers.
r is defined by
where
is the radius of the kernel of the current layer (
),
N is the number of pooling layers between the input layer and the current layer, and
is the step size of the pooling layer
n.
Apart from the crop layers and resize layers, all the layers that affect receptive field are listed in
Table 1. All the layers without
hyperparameter have an
of 1, and those with
have an
of 2. With 13 convolution layers, 5 pooling layers and 2 fc_** layers, our non-multi-scale network has a receptive field of
pixels. While the ships in our datasets average about
in size, the receptive field is suitable only for ship detection tasks. To enlarge a network’s receptive field for sea-land segmentation, traditional methods such as increasing kernel size or increasing the depth of the network all lead to huge amount of increase in weight number, which in turn leads to harder network training, higher hardware requirement and more computation complexity. The resize layer in the multi-scale structure has a similar effect on receptive fields as the pooling layer, therefore the receptive field of network is enlarged as if a pooling layer is put at the very beginning of the network. With
of both resize layer and crop layer set to 3, the receptive field is roughly scaled up by 9 times in area, into
, with only two additional layers (fc_b1 and fc_b2) with weights. The convolution layers which hold large proportion of the weights stay unchanged, and the network is still able to be fine-tuned from the pre-trained original one.
3.3. Data Preprocessing
Different from most of the previous works that focus on open datasets only containing extracted small image patches, we focus our framework on large, relatively complete images that general remote sensing images are distributed as. The network training and testing on large images brings in new problems, such as how to effectively extract samples or image patches for the network.
Because of the limitation of GPU memory, both training and testing images have to be cut into relatively small patches before being fed into the neural network. For training, we select samples from training images randomly. To be specific, for each original image in the training set, we randomly generate N triplets , with each symbol indicating pixel coordinate x, coordinate y, and the rotating angle. For each triplet one training sample is selected according to , with being the coordinate of the selected patch in the original image. Finally each sample is rotated by angle . For testing samples, the patches are extracted in a sliding-window manner, with a stride the same as the size of the fine-scale input patch, so that the fine-scale inputs has no overlaying on each other. The experiment shows that the network we train performs well on patch borders, especially with the help of the multi-scale scheme. When put back together, the label maps connects to each other well, with no obvious artifacts.
In the literature of semantic labeling, the balancing of samples is barely mentioned, because its application background is mainly on daily images in well-prepared dataset and the problem of unbalanced samples does not exist. In the remote sensing dataset, it is crucial to balance the samples (in this context, to balance the number of pixels of different categories) first for the network to learn equally from different classes. Without the balanced samples, the network will lean towards better performance on sea-land classification, neglecting the accuracy of ship category. In this experiment, firstly, we limit the number of samples that do not contain ships, secondly, we utilize one of the functions of loss layer in DeepLab’s Caffe implementation [
36], the ability to ignore the loss on the pixels that are labeled to a special class,
ignore. We randomly set the ground truth label of sea and land pixels to
ignore, so that when calculating the loss value of the network, the actual functioning ground truth pixels are category-balanced. In our experiment, without balancing the sample, the accuracy of ship detection would decrease dramatically (by 10%).
The samples that contain ships are rotated several times because a ship presented on an remote sensing image can be of arbitrary possible orientation. We also control the number of samples extracted from an image, so that the image is covered roughly twice by the training samples. Although convolution layers have the property of translation invariance, we sample the images more times to counter-act the border effect of the convolution (the borders of a input matrix has to be padded by zero before convolution to maintain output matrix size, thus compromising the effectiveness of features close to the borders).
4. Experiments
This network is implemented with Caffe [
48], on Ubuntu 14.04, with one Titan X. The network is trained with mini-batched Stochastic Gradient Descent (SGD) with momentum and step learning rate. The batch size is set to 14, base learning rate 0.001, which drops by a factor of 10 every 2000 iterations. We use momentum 0.9, weight decay 5 and doubled learning rate for biases following the implementation in [
36,
44]. The network is first initialized with pre-trained weights from ImageNet dataset and then fine-tuned with remote sensing data, to compensate the limited amount of training images. With the pre-trained weights, the network converges to a satisfactory extent at only 4000 iterations.
The selection of the Caffe framework and the training scheme follows the common acknowledgment in the deep learning community [
36,
49]. Although there are plenty of selection of deep learning framework to use (such as TensorFlow, Torch), the accuracy-wise performance has only a very limited variation [
49]. The choice of training scheme has also undergone extensive investigation [
50] and we follow [
36] because of the similar network architecture. We also experiment other modified version of SGD [
50] but yield inferior results.
We experiment our proposed method on two different datasets. The first dataset we use consists of 6 panchromatic (grayscale) images from GaoFen-1 satellite each with above
pixels and a resolution of 2.5 m/pixel. The second dataset has 21 images (RGB) from Google Map, each with above
pixels and a resolution of 1 m/pixel. Both datasets focuses on areas with harbors, where both ships and various types of terrain exist. Although datasets (such as SPOT-4) that has lower resolution can provide competitive results for sea/land segmentation [
51], we select the high resolution imagery to meet the requirement for in-shore ship detection, as proposed in [
23,
25].
Remote sensing datasets from Google Map has received extensive research in the recent days and are recognized as a valid source for remote sensing research [
52]. Although imagery from Google Map may be enhanced to different extents, we qualitatively find that the imagery are not too varied to the degree that human cannot distinguish the objects in the imagery in the way on daily life objects, i.e., objects in Google Earth still are faithful to real colors and textures. Nevertheless, we here provide the coordinates and the sensor of the images we use for the experiment. All of the images from Google Map are produced by Digital Mapping Camera (DMC) collected from United States Geological Survey (USGS) High Resolution Orthoimagery and the coordinates of the most north-west pixel of the images are listed in
Table 2.
For the Google dataset, we select 7 images as test data and the other 14 as training data. For GaoFen-1 dataset, we find that to augment the training data by including Google images can improve the performance, so we convert the 14 RGB training images to grayscale images and join them to 2 of the GaoFen-1 images as training data, and choose the remaining 4 as test data. Note that the distribution of the ships also varies across the dataset, where the dataset from Google Map has far more in-dock ships. In the test data, Google Map dataset has 55 ships in total, including 50 in-dock ships, while GaoFen-1 dataset has 160 ships in total, including only 20 in-dock ships.
As a novel effort to implement deep learning semantic labeling into the maritime area, we focus our detection target on large navy ships/oil tankers to limit the scale of the target. The length of the target ships vary from 80 m to under 200 m in Google Map dataset and around 300 m in GaoFen-1 dataset. This lead to a similar scale for ships on both datasets because of the different resolution. The ships vary from 80 to 200 pixels in length.
For performance evaluation, we follow the method that is widely used in segmentation/semantic labeling tasks [
36,
46] . We count the number of pixels that are correctly labeled and those that are not, and compute the confusion matrix and Intersection-Over-Unions (IOU) for each task. Values in a confusion matrix indicate the percentage of the pixels labeled to the column class in the pixels belonging to the row class, meaning a row of a confusion matrix sums to one. Whereas IOU is calculated as
4.1. Benefit of Multi-Class Classification
Previous in-shore ship detection methods rely heavily on the acquirement of shore-line as a 1st step. This step contributes to locating possible areas with in-shore ships and eliminating complex inland areas that could produce huge number of false alarms. Traditionally there are two options to acquire shore-line information, (a) manually labeled shore-line database, which has two problems, the need for constant update and the need for accurate registration between database and image; And (b) a separate algorithm for the detection of shore-line, which is time consuming and requires tedious optimization (possibly hand-tuned) iterated between shore-line and ship detection algorithm.
In our framework the two problems are tackled at the same time and are jointly optimized to achieve better performance. We experiment our network on GaoFen-1 dataset on two different scenarios to show the benefit of multi-class classification of our framework, (1) the network is tasked to classify only 2 classes, Non-ship and Ship and (2) the network is tasked to classify 3 classes, Sea, Land and Ship.
Table 3 shows with 3-class task, the network’s accuracy on Ship is greatly improved, the network’s learning time is also decreased. This is because with the 3-class task, the network in training is given extra information to comprehend the context of the task and by jointly classify multiple classes, the network learns the spatial relationship between the different classes (the Ship have minimal probability to appear in the middle of Land but maximal probability at the brink between Land and Sea). The 3-class problem also provides a more balanced sample pool so the network is easier to train with larger learning rate and faster converging speed.
Although in the remote sensing imagery the land area features most complex objects, we find the classification of these objects will not contribute to the performance of the task. This is because ship detection is majorly focused at the brink between land and sea. The classification of objects enclosed by land will not provide any additional information for ship-detection, while also unnecessarily taking up the capacity of the network.
4.2. Comparison between Different Realization of Multi-Scale Structure
The multi-scale structure which ensembles paths of different receptive fields has various ways of implementation. In this section we list a few different multi-scale structures and compare the convergent speeds and parameter numbers of the various structures to show the superiority of our choice. Note that although there are already many multi-scale structures proposed in literature, by creating shortcuts between layers to ensemble feature maps of different level of semantics, we here focus on multi-scale structures that use input of different scales.
Figure 5 depicts the some of the common structures feasible for multi-scale implementation that we experiment in the comparison. Network A (
Figure 5a) is the most basic multi-scale structure which simply averages the results of different scales. This network is similar to basic scale augmentation of training samples. The network does not learn the relationship between different scales. Network B (
Figure 5b) concatenate the results after the convolution layers. Here the fc_** layers start to learn the weights of different paths to classify different objects. In Network C (
Figure 5c), the concatenation takes place after the first fc_** layers. The proposed network is similar to Network C except the the network has two loss layers, each on the top of either path. In contrast, Network A, B, C only have one loss layer at the very top of the network.
We experiment the different networks on Google Map images.
Figure 6 shows the training average Accuracy/epoch, Recall/epoch and IOU/epoch curve of these networks. It shows that the proposed method, with 2 loss layers at different path, has overall faster learning speed and higher performance.
In
Table 4 we show the the numbers of parameters and the computation time of a single forward/backward routine on a
training patch of these networks. Since Network C differs from the proposed one only in that it has one fewer loss layer, its data is omitted. The table shows that our proposed multi-scale structure has relatively small number of parameters and considerate fewer computation time compared to Network B.
We also include an experiment to show the performance comparison between the usage of hole algorithm and different convolution architecture. In one of the experiment we cancel the hole implementation and in the other experiment we use Resnet [
53] as the convolution structure. The IOU is shown in
Table 5. As shown in the table, the hole implementation and the convolution structure both slightly increase the performance compared to the counterpart. The implementation with Resnet has the worst performance despite it is the more recent architecture. This is because Resnet introduce heavy pooling and the small details are further neglected. This can be seen in the 4% drop IOU in Ship performance.
4.3. Comparison with Other Methods
For a performance baseline, we also experiment the SLIC (Simple Linear Iterative Clustering) method [
35] and DenseCRF (Dense Conditional Random Field) [
54] two of the most widely used semantic labeling methods other than deep learning networks, to approach the same problem. SLIC is a widely approved way of producing superpixels as a preprocessing step for other process such as object localization and semantic labeling. We first break the large images into small, irregular segments called superpixels and then learn to classify each superpixel into different categories as described in [
35], i.e., to extract color, shape and texture info of each superpixel as features and train an adaboost classifier [
55] for classification. DenseCRF is a widely used multi-class image segmentation method based on fully connected random field. This model accounts for unary and pairwise potentials among pixels at the same time. The pairwise potential can address the difference between pixels in arbitrary feature spaces and the unary potentials are computed independently on each pixel. The unary potentials are treated as the initial guess of each pixel’s category, and the pairwise potentials are to rectify the results. The solution to this model is yielded in an iterative fashion and leads to a refined classification results of each pixel. In this experiment, we follow the implementation in [
54], in which the unary potentials are acquired using TextonBoost [
56]. Although for the unary potentials there are multiple selection such as convolutional network, we use TextonBoost for the consistency to the original paper.
Table 6 shows the comparison results. We notice that because of the nature of the categories in this problem, pixels that belongs to sea or land takes an extremely great proportion (over 99%), affecting the statistics in the evaluation. So we randomly ignore pixels belonging to sea or land in the evaluation, to ensure the numbers of pixels in different categories are of similar order of magnitude (the ratio between the areas of land, sea and ships is balanced roughly to 4:4:1). We also list the IOUs without the balanced evaluation in
Table 7 for completeness, but for future results, we will only show the ones with balanced evaluation.
We notice that the SLIC method performs poorly in this problem because a) the superpixels produced are of bad accuracy even with carefully tuned parameters (initial region size and spatial regularizer) and b) at the classification stage, the features extracted are not rich enough to distinguish each category. The DenseCRF’s iteration method relies greatly on its initial result, the unary potentials from TextonBoost, which is initially designed for everyday image circumstances. The experiment shows that TextonBoost is, however, not suitable for remote sensing images. We presume the failure of DenseCRF and SLIC is generally due to the fact that remote sensing images have scarce (if any) color information and objects are of much smaller size compared to those in everyday images.
4.4. Experiments on Multi-Scale Structure
Table 8 shows the performance comparison between the network with and without multi-scale structure. The multi-scale structure enhances the network’s ability to discriminate categories in different scales, with accuracy on sea and land greatly improved.
As is shown in
Figure 7, after the training of the network, we extracted the weights of Layer fc_a2, which is used to combine the information from fine-scale feature maps and coarse-scale score maps. Only 20 weights of each kernel are shown for clarity. The layer learns that sea and land score maps from coarse-scale have greater weights and ship score map have relatively lesser weight (as it should, intuitively, since coarse-scale network are more reliable for sea-land segmentation).
4.5. Qualitative Experiments
The qualitative performance is shown in
Figure 8 and
Figure 9.
Figure 8 features the comparison between our proposed method with and without multi-scale structure. The result with multi-scale structure tends to be more accurate and continuous, especially on GaoFen-1 dataset. Also note that images from GaoFen-1 dataset have more ships off-shore, which can be relatively easy for the network and add to better quantitative performance on GaoFen-1 dataset in
Table 6. It is also noticed that the segmentation boundaries are not quite accurate with respect to the original images. This is in accordance with the initial results of DeepLab network [
36], which, later implements DenseCRF as a post-process to acquire better segmentation boundaries. However, DenseCRF does not yield satisfactory results in our experiments, due to the fact that the objects in our dataset lack color differentiation and clear boundaries, especially in GaoFen-1 images.
Qualitative comparisons between our proposed method and DenseCRF, SLIC are shown in
Figure 10. The compared methods presents inferior results because of two aspects, the classification and the segmentation. DenseCRF and SLIC both have worse performance when compared to our deep network and can not fully identify the ship body. In addition, when the shadows on the ship is evident, these two methods often classify these shadows into sea category.
5. Feasibility of Ship Detection via Coastline Detection
Coastline detection has undergone extensive research over the last decades [
51,
57,
58] and it is possible to consider it as an approach towards ship detection to regard dynamic ships as a temporal change in multi-temporal images. The automatic coastline detection can facilitate autonomous navigation, coastal resource management and coastal environmental protection.
Although the accuracy of coastline detection is constantly increasing, it is still not enough for direct implementation for ship detection [
59]. Coastline detection methods commonly utilize image segmentation tools such as watershed transformation [
59] or graph-based discrimination [
60], which are based on the features of textures and intensities and have no knowledge to holistic objects such as ships. As a result, for instance, at the fine scale segmentation stage, shadows on the decks that are cast by ships themselves are often segmented into seas [
23]. Besides, a post-validation algorithm is still needed since not all detected changes are ships.
Moreover, single image ship detection, in contrast to multi-image ship detection, has the advantage that it does not need the multiple image registration and the storing of template images. Besides, change detection methods has the disadvantage that it is not accurate when image contrast has severe variation and that it needs constant manual power to update latest coast line.