Discriminative Feature Metric Learning in the Affinity Propagation Model for Band Selection in Hyperspectral Images

Abstract

Traditional supervised band selection (BS) methods mainly consider reducing the spectral redundancy to improve hyperspectral imagery (HSI) classification with class labels and pairwise constraints. A key observation is that pixels spatially close to each other in HSI have probably the same signature, while pixels further away from each other in the space have a high probability of belonging to different classes. In this paper, we propose a novel discriminative feature metric-based affinity propagation (DFM-AP) technique where the spectral and the spatial relationships among pixels are constructed by a new type of discriminative constraint. This discriminative constraint involves chunklet and discriminative information, which are introduced into the BS process. The chunklet information allows for grouping of spectrally-close and spatially-close pixels together without requiring explicit knowledge of their class labels, while discriminative information provides important separability information. A discriminative feature metric (DFM) is proposed with the discriminative constraints modeled in terms of an optimal criterion for identifying an efficient distance metric learning method, which involves discriminative component analysis (DCA). Following this, the representative subset of bands can be identified by means of an exemplar-based clustering algorithm, which is also known as the process of affinity propagation. Experimental results show that the proposed approach yields a better performance in comparison with several representative class label and pairwise constraint-based BS algorithms. The proposed DFM-AP improves the classification performance with discriminative constraints by selecting highly discriminative bands with low redundancy.

1. Introduction

Hyperspectral imagery (HSI) can acquire images in hundreds of narrow and adjacent spectral channels [1], which provide rich information to distinguish different ground objects and have a high potential for detailed land cover classification. However, this also involves several significant challenges for HSI classification due to the following critical factors: (1) the Hughes phenomenon [2,3] (also known as the curse of dimensionality), involving the classification accuracy possibly decreasing with an increase in the number of spectral bands when a limited number of labeled samples is available; (2) high correlation between spectral bands bringing a large amount of redundant information, which has a negative effect on classification performance; and (3) high spatial resolution increasing the intraclass variability and decreasing the interclass variability, which thus reduces the statistical separation between different land cover classes in the spectral domain [4]. Therefore, it is necessary to reduce the dimensionality and remove redundant information contained in HSI, while improving the discriminability of pixels belonging to different classes.

Dimensionality reduction (DR) is a necessary preprocessing step that decreases the number of hyperspectral channels for improving the classification performance of HSI. Generally, DR techniques can be classified into two major types: band (feature) selection (BS) or feature extraction (FE) [5,6]. The FE [7] methods use all of the features to find a transformation that maps the original data into a low-dimensional subspace. The BS [8] aims to identify a suitable subset of the original feature set, which allows optimization of the classification results. Compared to FE, the BS techniques can inherit the original spectral meanings of HSI data [9]. In this paper, we focus on BS techniques.

According to the selection strategy used, the BS techniques can be divided into ranking-based and clustering-based methods. In ranking-based BS, each band is sorted by a band prioritization criterion (e.g., the maximum variance-based criterion [10] and the non-Gaussianity (NG) [6] criterion used in information divergence (ID) [11]), before top-ranked bands are selected. However, this type of BS method does not consider spectral correlation and cannot remove the redundant bands. The clustering-based methods perform clustering on each band to group them into different clusters according to their similarity (or correlation). Accordingly, redundancy reduction can be obtained by selecting the representative bands. However, the fact that the classical clustering-based methods are sensitive to initialization implies that the selected subset of bands may be unstable and may change depending on the particular initialization. Recently, an exemplar-based clustering algorithm, namely affinity propagation (AP) [12], was applied to BS in HSI [13,14]. AP identifies clusters based on similarity measures, which is characterized by a relatively small error rate and a fast execution speed (especially for large datasets). The above AP-based methods can ensure that the selected bands have a relatively low redundancy and are stable. However, they do not consider the discriminative capability of single bands as they give the bands the same prior suitability (preference). This can significantly affect the final selection results of bands. A desirable BS process in HSI for classification tasks is to select highly discriminant bands and reduce redundant information. For achieving this goal, it is necessary to define a feature metric (or similarity measure of bands) in the AP so that both can assess the class separability of each band and the spectral correlation between two bands.

Based on the availability of prior information, BS algorithms can be further classified into supervised and unsupervised. Supervised methods [15,16] select a discriminative band subset by measuring the separation among classes with prior knowledge. In unsupervised methods [17,18], the informative bands can be evaluated by statistical measures and are selected by feature clustering. Recently, semi-supervised methods that exploit a small amount of prior information have been applied to reduce the HSI dimensions. Two main types of prior information can be used in HSI analysis: land cover class labels and pairwise constraints (i.e., positive constraints and negative constraints on pairs of pixels, which indicate only if a pair of samples belongs to the same class or not without knowing the class label). Earlier studies proposed that the metric (or similarity) should be learned in a supervised way through class labels. However, often, land cover class labels are difficult to obtain, and thus, it is difficult to define a reliable and complete training set for exploiting supervised methods. In contrast, pairwise constraints are relatively easy to achieve. Class labels and pairwise constraints are generally defined at the pixel level, with each single pixel considered as an independent information entity.

HSI represents the real land surfaces that typically extend for a few pixels in the image. Thus, nearby pixels in HSI have a high probability of belonging to the same class, indicating the existence of high spatial correlation [19,20]. Recently, a new learning paradigm, namely adjustment learning (AL), has been studied for image retrieval [21]. In the AL scheme, data points can be identified as small group sets, which are known to originate from the same class (but the label is unknown). These small group sets are termed as “chunklets”, which can be constructed by positive constraints. Following this, a simple and efficient metric learning method called relevant component analysis (RCA) was developed, which was based on the AL [22,23]. The RCA uses chunklets to find a transformation matrix, which can improve data representation. In previous work, we integrated the RCA and the AP into a joint framework for HSI band selection [24,25]. However, only considering chunklet information or positive constraints is not enough. Negative constraints play a fundamental role in defining discriminant criteria. Two extensions of the RCA have been developed, which are the discriminative component analysis (DCA) [26] and the extended relevant component analysis (ERCA) [27]. Compared with the RCA, a discriminative set can be formed in the DCA by negative constraints for describing the relationship of chunklets, which delivers a type of discriminative information. In comparison, the ERCA simply focuses on positive and negative constraints.

A desirable BS process in HSI for classification tasks is to select a subset of bands with low redundancy and a strong capability to distinguish different classes by using easily-acquired prior information. For achieving this goal, we introduce a new type of discriminative constraint, namely chunklet and discriminative information, into the BS process by modeling the spectral and spatial relationship between pixels in this paper. The chunklet method groups spectrally-close and spatially-close pixels together without requiring explicit knowledge of their class labels, while discriminative information describes the relationship between any two chunklets providing valuable information for distinguishing classes. In greater detail, a discriminative feature metric (DFM) is modeled with the discriminative constraints in terms of an optimal criterion based on the DCA. The learned DFM can effectively assess both class separability and spectral correlation associated with HSI channels. Following this, the AP is used to search the subset of high-discriminative and low-redundancy bands. The proposed BS technique is referred to as discriminative feature metric-based affinity propagation (DFM-AP). The effectiveness of the proposed BS method is analyzed on two different hyperspectral datasets in terms of accuracy and robustness with the constructed discriminative constraints.

2. Methods

In this section, the discriminative feature metric-based affinity propagation (DFM-AP) is proposed. The full implementation process of the DFM-AP consists of the following three parts: (1) construction of discriminative constraints; (2) discriminative feature metric (DFM) learning; and (3) selection of representative band subsets based on AP clustering with the DFM. A detailed description of these three parts is given in the following subsections.

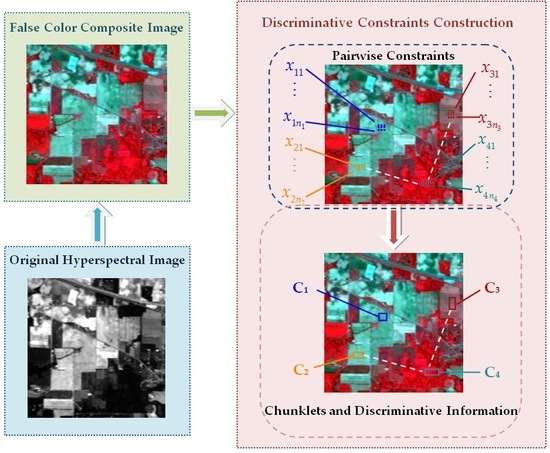
2.1. Construction of Discriminative Constraints

Let X = {x₁, x₂, …, x_N} $\subset$ R^B×N be an HSI dataset, where x_i represents a vector of spectral responses, B is the number of bands and each band contains N pixels. Two key observations on the spectral and spatial relationship information are as follows:

• Spectral similarity: HSI pixels that are similar in the feature space have a high probability of belonging to the same class (and vice versa).
• Spatial correlation: HSI pixels that are spatially near each other have a high probability of belonging to the same class, while pixels that are far away from each other in the spatial domain may belong to different classes.

Following the observations described above, two types of prior information can be derived, which naturally integrates the spectral similarity and spatial correlation information. One is expressed in terms of pairwise constraints, while the other is expressed in terms of discriminative constraints. The pairwise constraints can always be used to construct discriminative constraints without any explicit knowledge of the pixel labels. We introduce the construction process of discriminative constraints, as shown in Figure 1. In this figure, blue, orange, red and green points denote four sets of positive constraints, while orange and green, as well as red and green points are examples of negative constraints. Assuming that K chunklets are generated according to the given positive constraints, the k-th chunklet is termed as C_k = {x_k1, x_k2, …, x_knk} (k = 1, 2, …, K), where n_k is the number of pixels in the k-th chunklet. For each chunklet, a discriminative set D is formed by the negative constraints in order to represent discriminative information between any two sets of chunklets. For the k-th chunklet, each element in the discriminative set D_k indicates one of the K chunklets that can be discriminated from the k-th chunklet, which is also known as the discriminative chunklet. Two chunklets can be discriminated from each other if there is at least one negative constraint between them. As shown in Figure 1, the positive constraints can be grouped into four chunklets (i.e., C₁, C₂, C₃ and C₄), and any two chunklets with one negative constraint are discriminative chunklets (i.e., C₂ and C₄, as well as C₃ and C₄). The chunklets and the discriminative information are grouped together and termed as discriminative constraints.

Indeed, the two types of information are not equivalent since discriminative constraints should be constructed with spatially-near pairwise constraints, while pairwise constraints do not need to hold both spectral and spatial relationships. It is important to note that the discriminative constraints can reflect the spectral and spatial relationship information between pixels. However, these are not limited to a pair of pixels and can sometimes be obtained directly by photo-interpretation or by automatic image analysis techniques without knowing the specific pairwise constraints.

2.2. Learning Discriminative Feature Metric

The aim of BS is to find a subset of representative bands Y = {y₁, y₂, …, y_b} (b ≪ B), which can better reflect discriminative chunklets, where y₁, y₂, …, y_b are the selected representative bands from X.

The DFM learned here is based on the optimal criteria of the DCA and learns a distance metric by a data transformation for both minimizing the total variance of data points within the same chunklets and maximizing the total variance between the chunklets with discriminative information. To achieve this goal, two covariance matrices are introduced, which are the between-chunklets covariance matrix ${\widehat{C}}_b$ and within-chunklets covariance matrix ${\widehat{C}}_w$. They can be written as follows:

$${\widehat{C}}_b=\frac{1}{K_d}{{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{t\in D_k}\left(m_k-m_t\right)\left(m_k-m_t\right)}}}^T$$

(1)

$${\widehat{C}}_w=\frac{1}{K}{{\displaystyle \sum _{k=1}^K\frac{1}{n_k}{\displaystyle \sum _{l=1}^{n_k}\left(x_{kl}-m_k\right)\left(x_{kl}-m_k\right)}}}^T$$

(2)

where $m_k=\frac{1}{n_k}{\displaystyle \sum _{l=1}^{n_k}{x}_{kl}}$ is the mean of the k-th chunklet; m_t is the mean of the t-th chunklet; x_kl is the l-th pixel of the k-th chunklet; n_k is the total number of pixels in the k-th chunklet; $K_d={\displaystyle \sum _{k=1}^K\left|D_k\right|}$ denotes the cardinality of a set; and D_k indicates one of the K chunklets, which can be discriminated from the k-th chunklet.

The Fisher theory or criterion [28,29] and its derived algorithms such as Fisher’s linear discriminant analysis (FLDA) and some modified methods [30,31,32], have been widely accepted as effective techniques for HSI classification and analysis. According to the Fisher theory, the solution of DCA corresponds to a learned transformation matrix, which maximizes the ratio of between-chunklets and within-chunklets covariance in a matrix. Accordingly, the transformation matrix W can be defined as:

$$W={\widehat{C}}_b\cdot {\widehat{C}}_w^{-1}$$

(3)

The DFM between different bands x_i and x_j can be computed as follows:

$$\begin{gathered} \mathrm{DFM}(x_i,x_j)=W(x_i,x_j) \\ i=1,2,\cdots ,B;j=1,2,\cdots ,B;i\ne j \end{gathered}$$

(4)

The DFM of a single band x_i can be expressed as:

$$\begin{gathered} \mathrm{DFM}(x_i,x_i)=-DFTS\cdot \left|\frac{1}{W(x_i,x_i)}\cdot \frac{Max}{Min}\right| \\ i=1,2,\cdots ,B \end{gathered}$$

(5)

where Max and Min are the maximum and minimum values of 1/W(x_i,x_i). By setting an appropriate threshold, which is also known as the discriminative feature threshold scalar (DFTS), one can select the spectral band subset Y in which the classes can be well separated with discriminative constraints.

2.3. Discriminative Feature Metric-Based Affinity Propagation

AP [12] takes the similarity values between pairs of data points as input measures and aims to find exemplars to maximize the sum of similarities between data points and corresponding exemplars. A common choice for similarity is the negative Euclidean distance. It does not require that the number of clusters is prespecified, as it is controlled by setting the parameter “preference”, namely the self-similarity. The “preference” represents the prior suitability of a data point to be the exemplar, which can be set to a global (shared) value or customized for specific data points. In this present study, the learned DFM is adopted to measure the similarity of bands and is used in the AP algorithm as an input measure. The DFM between different bands denotes the band correlation, while the DFM of a single band denotes its preference (band priority), which is its prior suitability to serve as a representative band. The proposed approach is referred to as the discriminative feature metric-based affinity propagation (DFM-AP). The details and procedure associated with DFM-AP are as follows.

Proposed Discriminative Feature Metric-Based Affinity Propagation

Input:   Hyperspectral dataset X, Discriminative Constraints C and D. Output:   Representative bands set Y Procedure: Initialize values of exemplars and parameters. Let Y = X: consider all bands to be initial clustering exemplars, which are namely the representative bands; Compute the between-discriminative chunklets matrix ${\widehat{C}}_b$ and within-chunklets scatter matrix ${\widehat{C}}_w$ using Equations (1) and (2). Calculate the DFM for all spectral bands; Set DFTS to get the expected number of bands; Calculate the DFM between different bands using Equation (4); Compute the DFM of single band according to Equation (5). Update availability and responsibility.   Two types of messages, responsibility r and availability a, communicate between bands, with each taking a different kind of competition into account. Let a(xi, xj) (availability) denote the degree of band xi as the cluster center for band xj. To begin with, let a(xi, xj) = 0; r(xi, xj) (responsibility) is the degree of the band xj, which is suitable for being the cluster center for band xi. The cluster centers of all of the bands, a(xi, xj) and r(xi, xj), are computed as follows: $$a\left(x_i,x_j\right)=\{\begin{array}{cc}{\displaystyle \sum _{p\ne j}\max \left\{0,r\left(x_p,x_j\right)\right\}}& i=j\\ \min \left\{0,r\left(x_j,x_j\right)+{\displaystyle \sum _{p\ne j,i}\max \left\{0,r\left(x_p,x_j\right)\right\}}\right\}& i\ne j\end{array}$$ (6) $$r\left(x_i,x_j\right)=DFM\left(x_i,x_j\right)-\underset{p\ne j}{\max }\left\{DFM\left(x_i,x_p\right)+a\left(x_i,x_p\right)\right\}$$ (7)   The damping factor is used in over-relaxation methods to avoid numerical oscillations when computing responsibilities and availabilities with simple updating rules. The two types of messages could be damped according to the following equations: $$\begin{array}{c}{R}^{t+1}=\alpha R^{t-1}+(1-\alpha )R^t\\ A^{t+1}=\alpha A^{t-1}+(1-\alpha )A^t\end{array}$$ (8) where R and A represent responsibility and availability vectors, respectively; $\alpha$ is the factor of damping; and t is the number of iterations. 5. Obtain the cluster centers set C of all of the spectral bands.   For any band xi, a larger sum of a(xi, xj) and r(xi, xj) means a greater possibility of band xj to be the final cluster center of band xi. The band xi determines its cluster center according to the following equation: $$\underset{x_j\in C}{\max }\{a(x_i,x_j)+r(x_i,x_j)\}$$ (9) 6. Identify the representative bands Y and their number b.   Repeat Steps 4 and 5, until cluster boundaries are unchanged for a given number of iterations. At convergence, we obtain the final subset of representative bands and the number of bands to be used for HSI classification.

3. Experimental Results

3.1. Dataset Description

Two different types of hyperspectral datasets are used in the experiments.

The first dataset Indian Pines, Indian Pines 92AV3C [33], was gathered by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor over northwest Indiana on 12 June 1992. It has 145 × 145 pixels and 220 spectral bands ranging from 400–2500 nm with a spatial resolution of 20 m. After discarding the lower signal-to-noise (SNR) bands (104–108, 150–163 and 220), 200 bands were considered. The dataset includes 16 land cover classes, which represent different crop types, vegetation and man-made structures with 10,366 true ground labeled pixels. Figure 2 shows the false color composite image of Bands 57, 27 and 17 and the available true map of the Indian Pines dataset.

The second dataset, Xuzhou, was acquired by Hyperion over the city of Xuzhou, Jiangsu Province, China on 7 February 2004 (Entity ID: EO1H1210362004038110PZ_AGS_01). It has 250 × 566 pixels and shows an urban area. The original image contains 242 spectral channels with a wavelength range from 356–2577 nm with only 198 bands being calibrated. After removing uncalibrated and noisy bands (1–10, 58–81, 120–130, 165–182, 185–187, 200, 201 and 221–242), 152 channels were selected to use as input parameters in the process of band selection. The image contains 6233 ground truth pixels classified into five land cover classes, which are water, vegetation, woodland, built-up and bare land. Figure 3 shows a false color composition and the available true ground map of the Xuzhou dataset.

3.2. Experimental Design

For evaluating the performance of the proposed DFM-AP, we compared it with the seven unsupervised, semi-supervised and supervised BS methods in our experiments as described below.

Table 1. Description of the acronyms of compared methods and evaluation criteria used in experiments.

Acronyms	Description	Acronyms	Description
ID	Information divergence	LFM-AP	Label feature metric-based affinity propagation
NG	Non-Gaussianity	PFM-AP	Pairwise feature metric-based affinity propagation
MVPCA	Maximum variance-based principal component analysis	DFM-AP	Discriminative feature metric-based affinity propagation
AP	Affinity propagation	SVM	Support vector machine
AAP	Adaptive affinity propagation	AOA	Average overall accuracy
FM-AP	Feature metric-based affinity propagation	SD	Standard deviation

describes the acronyms of compared methods and evaluation criteria used in experiments.

Unsupervised BS:

• ID [6,11]: all bands are analyzed by a band prioritization criterion, known as the NG;
• Maximum variance-based principal component analysis (MVPCA) [10]: MV criteria used to prioritize bands;
• AP [12]: standard AP with the negative Euclidean distance;
• Adaptive AP (AAP) [14]: AP with the negative spectral angle mapper (SAM) and an exemplar number determination procedure for getting fixed selected band numbers;

Semi-supervised BS:

• RCA-based AP (FM-AP) [24,25]: AP using a feature metric (FM) based on the criterion of the RCA with chunklets;
• ERCA-based AP (pairwise feature metric (PFM)-AP): the similarity of bands used in AP is based on the optimization criterion of ERCA with pairwise constraints.

Supervised BS:

• FLDA-based AP (LFM-AP): the similarity in AP is based on FLDA with class labels.

We also compared the results obtained with those achieved by using all of the original bands (baseline).

For Indian Pines and Xuzhou datasets, we randomly selected 630/90 and 1980/13 pixels as positive/negative constraints from the available true ground pixels. A total of 63 and 11 chunklets (each chunklet contains 10 and 180 pixels for different land cover classes, which are unknown in advance) are formed by the given positive constraints. For each dataset, a discriminative set is formed by negative constraints, in which a chunklet is discriminated from another if there is at least one negative constraint between them. In practice, we just need to consider certain pixels in any two chunklets that have a negative relationship. The randomly-selected pairwise constraints in the experiments are used for the PFM-AP learning, while the transformed chunklets and discriminative constraints are used for the FM-AP and DFM-AP learning. In order to obtain statistically-significant results, a widely-used supervised classifier, namely the support vector machine (SVM), is employed to evaluate the performance of BS methods. The randomly-selected constraints are transformed into class labels with available ground-truth data for FLDA learning and SVM training, while the remaining pixels are used for estimating the performance of BS methods. To assess whether results were statistically significant, we repeated this process for five trials/times and used the average overall accuracy (AOA) and the related standard deviation (SD) as evaluation criteria. It is important to note that no labeled samples were used in our BS process.

3.3. Results

In the experimental analysis, we first quantified the performance of the proposed DFM-AP with respect to the other seven reference BS methods and to the baseline. Secondly, we analyzed the behavior of the AOA provided by the DFM-AP compared to the number of chunklets. Thirdly, we assessed the classification accuracy of the DFM-AP with different percentages of discriminative information. Finally, a parameter sensitivity analysis of DFM-AP is given.

3.3.1. Accuracy Compared to the Number of Selected Bands

The AOA and SD obtained by using all of the spectral channels and the selected bands subsets were compared (see Figure 4 and

Table 2. SD of the seven compared methods and proposed DFM-AP compared to the number of selected bands (NB) in the range of 10–60 for the Indian Pines and Xuzhou datasets.

Datasets		SD	MVPCA	ID	AP	AAP	LFM-AP	FM-AP	PAM-AP	DFM-AP
	NB
Indian Pines	10		1.642	1.426	1.382	2.368	2.667	2.005	1.061	1.045
	20		1.746	1.526	1.458	0.767	2.985	1.106	1.304	2.006
	40		1.996	1.129	2.126	1.831	2.480	0.910	1.398	2.205
	60		1.582	1.468	2.308	2.116	1.427	0.689	1.399	1.878
Xuzhou	10		1.860	1.757	2.363	2.972	2.437	1.661	6.476	1.812
	20		1.969	1.812	2.007	2.045	2.954	1.874	3.624	1.972
	40		1.783	1.826	1.964	2.510	2.972	1.985	3.085	1.596
	60		1.813	1.719	2.174	2.747	2.700	1.956	3.135	1.989

).

For the Indian Pines and Xuzhou datasets, we can observe that the AP-based methods yielded a higher AOA than the other two BS methods (i.e., the MVPCA and ID). In greater detail, compared with the AP, AAP and PFM-AP, the proposed DFM-AP, LFM-AP and FM-AP exhibited more stable performances with a lower SD. It is important to note that there were a few times when the PFM-AP and AAP achieved a higher AOA (when 5–8 bands were selected for the Indian Pines dataset). This is probably due to the fact that spectral values of different land cover classes (e.g., corn and soybean-types) are very close in this dataset, which thus requires more bands to discriminate them. Nevertheless, the AOA obtained by AAP shows a sharp decline and is lower than the baseline when the number of selected bands increases. Furthermore, the proposed DFM-AP approach always provides the best AOA and a lower SD compared to the FM-AP and LFM-AP with an increase in the number of selected bands. For Indian Pines and Xuzhou datasets, the DFM-AP obtained only 14 and 10 bands with AOA values (60.80% and 89.87%, respectively) that were higher than those yielded when using all 200 and 152 bands (60.55% and 89.76%, respectively). In comparison, more bands (30 and 13) have to be selected to achieve a higher accuracy for FM-AP than the baseline in the two datasets.

Figure 5 shows the wavelength of 14 selected bands compared to the radiance value of land cover classes at the sensor for the proposed DFM-AP and FM-AP in the Indian Pines dataset. It was seen the FM-AP selected many adjacent bands in each trial as it uses only chunklets, which are affected by the imbalance and small sample size of the dataset. On the contrary, the bands selected by the proposed DFM-AP have a more dispersed distribution in the five trials. Moreover, they cover regions of the spectrum with large intervals, which indicates their highly discriminative capabilities for different categories.

3.3.2. Comparison of Accuracy Compared to the Number of Chunklets

This experiment explores the effect of the number of chunklets on the AOA of DFM-AP in the two considered datasets (see Figure 6). For the Indian Pines and Xuzhou datasets, the originally generated pairwise constraints were divided into 126/189 and 55/110 chunklets (each contains 5/3 and 36/18 pixels), respectively.

3.3.3. Comparison of Accuracy with Discriminative Information

This experiment assesses the performance of the proposed DFM-AP when considering a different amount of discriminative information. We randomly generated 0.5-, 1-, 2-, 3- and 4-times the number of the original negative constraints as a discriminative set, while maintaining the number of positive constraints/chunklets attached to the Indian Pines and Xuzhou datasets (see

Table 3. AOA of the proposed DFM-AP compared to the number of negative constraints with different numbers of selected bands (NB) for the Indian Pines and Xuzhou datasets.

Dataset		AOA	Discriminative Information (# Times the Number of Original Negative Constraints)
	NB		0.5	1	2	3	4
Indian Pines	12		57.39	60.18	59.70	60.69	57.87
	20		59.60	60.11	60.21	62.23	60.90
	30		60.09	60.12	62.27	61.97	60.46
	40		61.06	61.39	62.04	62.13	60.47
	50		61.52	60.63	62.23	63.04	60.98
	60		62.18	61.06	62.11	63.45	60.14
Xuzhou	8		58.46	89.08	89.27	89.58	90.15
	20		88.02	89.79	90.41	90.93	91.07
	30		90.18	91.82	92.67	91.02	91.93
	40		91.60	93.65	93.52	93.95	93.82
	50		90.15	90.72	92.59	92.23	92.73
	60		92.07	92.43	91.86	92.52	93.37

).

3.3.4. Sensitivity Analysis

There are two user-defined parameters in the proposed DFM-AP:

• $\alpha$, which affects the convergence speed; and
• DFTS, which determines the number of selected bands (i.e., representative bands).

The parameter $\alpha$ should be at least 0.5 and less than one. In general, it can be set between 0.8 and 0.9. If the algorithm does not converge, the value can be increased, but the execution time increases as well. In the experiments, the $\alpha$ values of AP, FM-AP and DFM-AP were set to 0.85 and 0.9, while the average execution times were 6.8, 5.2 and 5.9 seconds with 14 selected bands in the Indian Pines dataset (PC workstation (Intel(R) Core(TM) i7-3720QM CPU @ 2.60 GHz, 2.60 GHz with 16.0 GB of RAM)), respectively. All software is implemented in Microsoft visual C++.Net. Generally, the α can be set to 0.9. A larger α means a better convergence of AP. If the algorithm does not converge, the value α can be increased, but numerical precision issues can arise if it goes beyond 0.99 [34]. Readers can refer to a previous study [25] for more details on the selection of the parameter $\alpha$ value. For the second parameter, the number of representative bands is close to being monotonically related to the DFTS. Lower values of DFTS resulted in the selection of many bands, while high values led to a small number of bands in all sampling conditions of the two datasets, although these had a different range of values (see Figure 7). As done in other BS techniques, one can run DFM-AP several times with different DFTS values searching for the desired number of bands. The DFTS ranges and values can also be obtained automatically [35].

4. Discussion

Based on the experimental results presented in the previous section, we can observe that the proposed DFM-AP is almost always superior to the other BS methods in terms of AOA and SD in the considered datasets. In this section, we focus our attention on a discussion of the effectiveness of BS algorithms with respect to the selection strategy and the prior information.

4.1. Clustering-Based Methods versus Ranking-Based Methods

According to the experimental results presented in the previous section, we can conclude that the clustering-based BS methods (i.e., the proposed DFM-AP, FM-AP, PFM-AP, LFM-AP, AAP and AP) produced higher classification accuracies than the ranking-based methods (i.e., ID and MVPCA). Among these BS algorithms, ranking-based methods (i.e., ID and MVPCA) obtained the lowest AOA because they neglect the redundancy of selected bands. On the contrary, redundant bands can be removed by selecting the representative bands in the clustering process. At the same time, the AP-based methods consider all data points to be equally suitable as exemplars or can use constraints to guide the clustering process for finding effective representative bands.

4.2. BS Performance Compared to Different Prior Information

From the experimental results, several conclusions can be drawn. First, we can observe from Figure 4 that, as expected, the prior information used in similarity metrics can generally improve the accuracy. The AOA of the proposed DFM-AP, FM-AP, PFM-AP and LFM-AP are higher than those of the unsupervised methods (i.e., the AAP, AP and the ID, MVPCA) with an increase in the number of selected bands.

With regards to the proposed DFM-AP, FM-AP, PFM-AP and LFM-AP methods, four different types of prior information, namely the discriminative constraints (chunklets and discriminative information), chunklets, pairwise constraints and class labels, have been used for finding subsets of bands with a relatively high capability for class discrimination. In the proposed DFM-AP, as well as LFM-AP and PFM-AP, this is done by learning the optimal data transformation matrices via both maximizing the total variance between discriminative chunklets, different classes and negative pixels in addition to minimizing the total variance of pixels in the same chunklets, the same classes and positive pixels. This leads to a final feature metric. The FM-AP only focuses on minimizing the total variance of pixels in the same chunklet. From this point of view, the organization of the modeling of the prior information in pixels plays an important role in the BS process. Discriminative constraints combine pixels into small group sets with the spectral and spatial characteristics of HSI and build the connections between pixel groups. Therefore, a higher intraclass variability and lower interclass variability between two land cover classes can be more suitable to a certain degree. However, the pairwise constraints and class labels are based on pairwise pixel connections, which cannot guarantee the spatial correction among pixels, especially when the prior information is dispersed. By analyzing Table 2 in greater detail, it was seen that the proposed DFM-AP approach always provided a higher AOA and lower SD than the PFM-AP and LFM-AP with an increase in the number of selected bands in the Xuzhou dataset. Thus, the proposed DFM-AP achieves a relatively higher stability than the other three clustering-based methods. At the same time, it improves the classification performance by selecting highly discriminative and low redundancy bands (see Figure 5).

4.3. BS Performance Compared to the Amount of Prior Information

This sub-section discusses the performances of the proposed DFM-AP with different numbers of chunklets and different discriminative information (see Figure 6 and Table 3).

From Figure 6, it was observed that the AOA of the Indian Pines dataset increases with an increase in the number of chunklets. This is due to the fact that the Indian Pines dataset shows high intraclass variability, and the diversification of chunklets models this variability. In comparison, the DFM-AP is not very sensitive to the number of chunklets for the Xuzhou dataset. This may be due to the fact that spectral values of the same land cover classes in the Xuzhou dataset are very close, as they show low intraclass variability. It is important to note that the accuracy decreases in both datasets with an increase in the number of chunklets over a given value. This is due to the fact that each chunklet contains only two pixels at this value, as seen in the case of PFM-AP.

By analyzing Table 3, it was seen that the AOA values obtained by the proposed DFM-AP on the Indian Pines and Xuzhou datasets were higher than the baseline and had a fewer number of bands (12 and eight bands, respectively). These values were also higher than those obtained with the FM-AP (+3.24% and +3.67%) when three- or four-times the number of original discriminative bands were considered on the two datasets. This proves that the performances of the proposed DFM-AP in identifying highly discriminative subsets of bands are significantly better than those obtained by the previous FM-AP when introducing a given amount of discriminative information. When using a limited (0.5-times) amount of discriminative information, more bands (about 30 bands) should be selected to obtain a higher accuracy than the baseline. Nevertheless, the proposed DFM-AP exhibited a more stable behavior with respect to the FM-AP when the number of selected bands was further increased.

According to the above-mentioned discussion, the performance of the DFM-AP technique depends on the adopted DFM and on the number of discriminative constraints. However, the desired number of discriminative constraints to be selected is not known a priori, as it varies with the HSI data considered. Determination of an optimal number of discriminative constraints will be investigated in the future. On the other hand, the proposed DFM-AP based on the solution of DCA corresponds to a learned transformation matrix needed for learning the DFM. The eigenanalysis has been used in the learning process, but the relationship between eigenvalues and eigenvectors was not fully exploited. Therefore, we will explore other FM criteria via eigen (spectral) decomposition to further improve the classification performance in future studies.

5. Conclusions

In this study, we have presented a novel DFM-AP approach to identify a high-discriminative and low-correlated subset of bands for HSI classification. Considering the difficulty in the collection of labeled pixels, new types of discriminative constraints (i.e., chunklets and discriminative information) are constructed with spectral and spatial relationship information without requiring any land cover class label. The DFM-AP learns a DFM as a similarity metric, which is based on the optimal criterion of the DCA with constructed chunklets and discriminative information that aims to measure both the correlations and the discriminative capability of bands. Following this, the subset of bands is selected by using the AP clustering. The performances of the proposed DFM-AP have been compared against seven BS methods with different types of prior information. The results show that the proposed DFM-AP achieves the highest AOA with a low SD. Furthermore, the experiments on the influence of both the number of chunklets and the discriminative information on the AOA show that the chunklet groups can improve BS performance effectively with the introduction of a small amount of discriminative information, because of the joint exploitation of pixel aggregation and separability.