Quantum Enhancement of a S/D Tunneling Model in a 2D MS-EMC Nanodevice Simulator: NEGF Comparison and Impact of Effective Mass Variation
Abstract
1. Introduction
2. Simulation Framework and Device Structures
2.1. Description of the Simulated Devices
2.2. Description of the 2D NEGF Module Inside NESS
2.3. General Overview of the 2D MS-EMC Tool
2.4. Description of the S/D Tunneling Model Inside the 2D MC-EMC Tool
2.5. Description of the Effective Mass Calculation
3. Simulation Results and Discussions
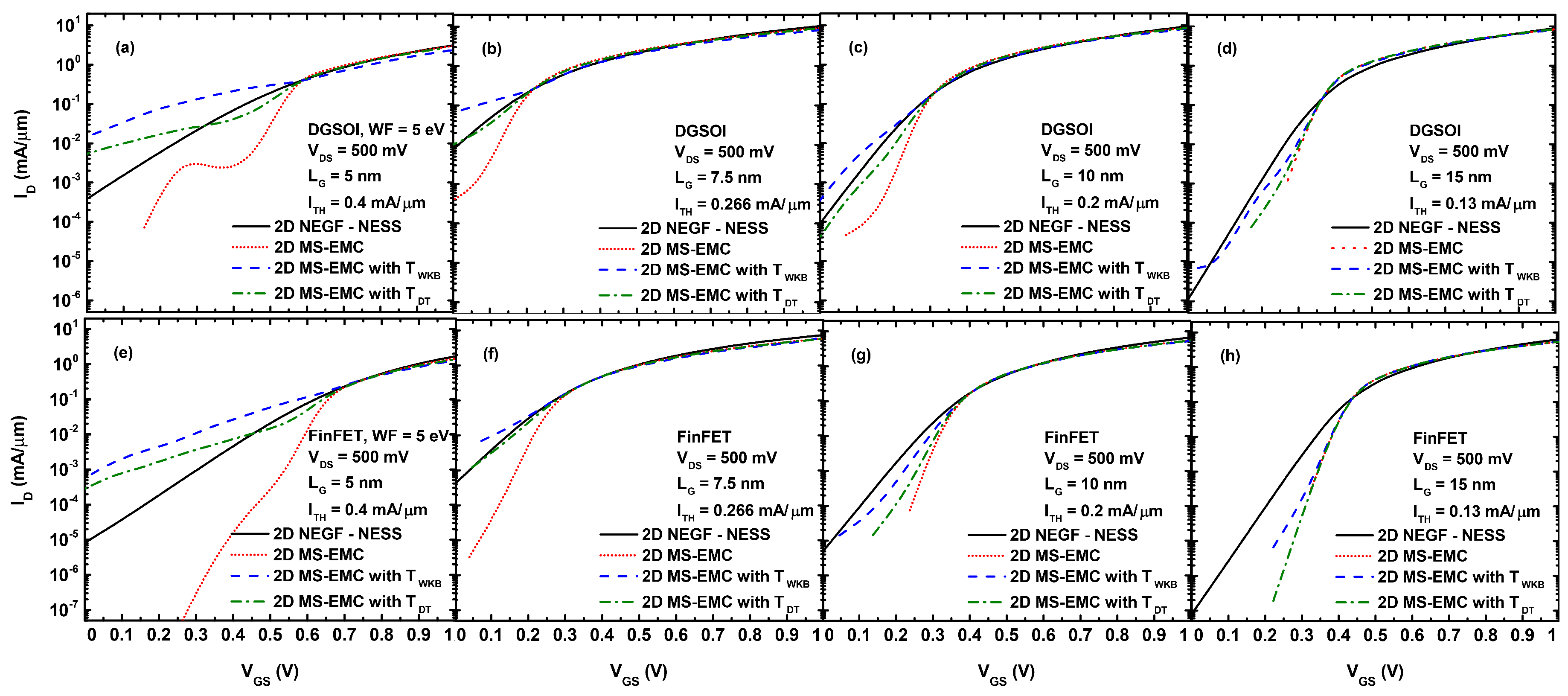
3.1. Comparison of MS-EMC with S/D Tunneling Models vs. NEGF
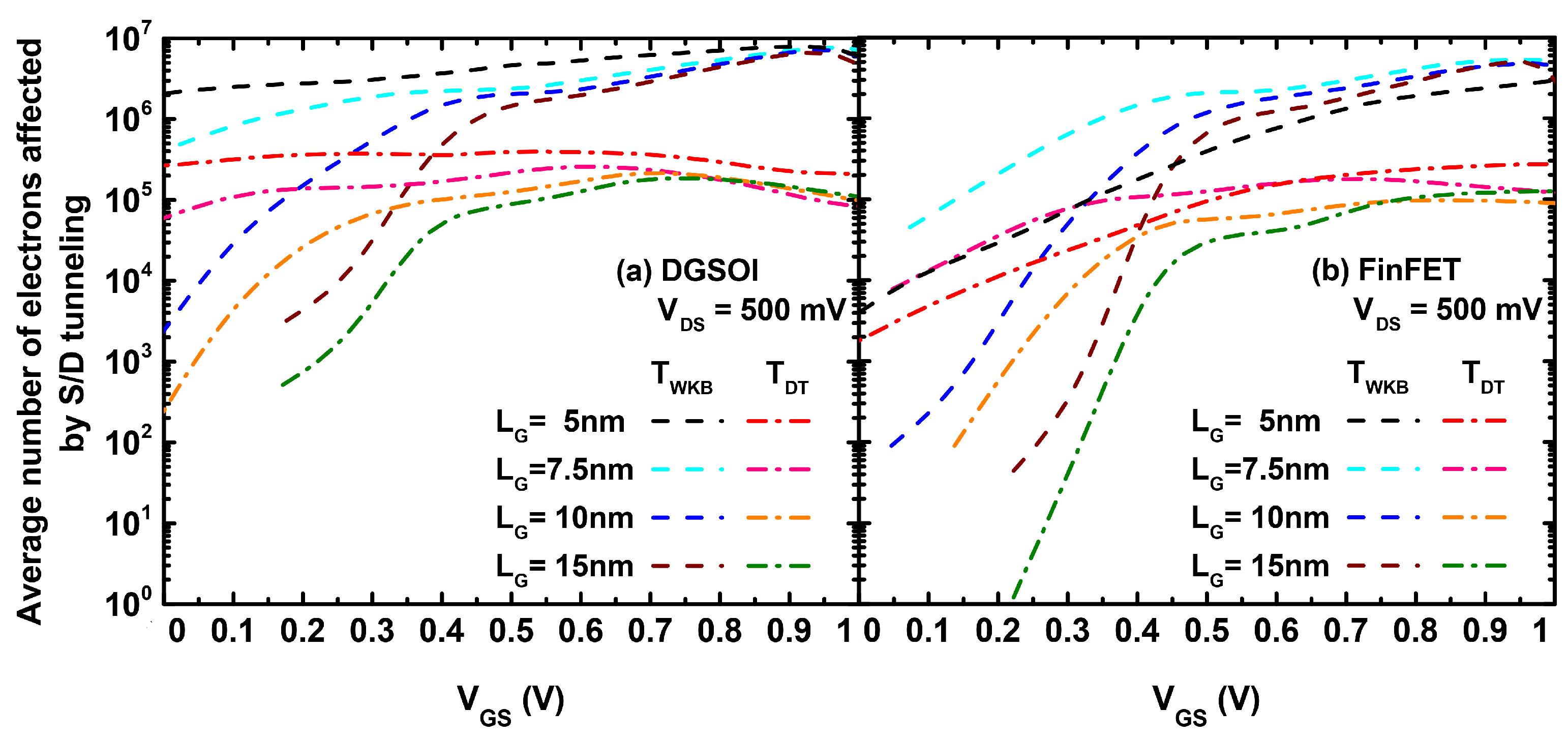
3.2. Impact of the Effective Mass Choice
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wong, H.S. Beyond the conventional transistor. IBM J. Res. Dev. 2002, 46, 133–168. [Google Scholar] [CrossRef]
- Iwai, H. Future of nano CMOS technology. Solid-State Electron. 2015, 112, 56–67. [Google Scholar] [CrossRef]
- Grillet, C.; Logoteta, D.; Cresti, A.; Pala, M.G. Assessment of the Electrical Performance of Short Channel InAs and Strained Si Nanowire FETs. IEEE Trans. Electron Devices 2017, 64, 2425–2431. [Google Scholar] [CrossRef]
- Wang, J.W.J.; Lundstrom, M. Does source-to-drain tunneling limit the ultimate scaling of MOSFETs? In Proceedings of the Technical digest–IEDM, International Electron Devices Meeting 2002, San Francisco, CA, USA, 8–11 December 2002; pp. 707–710. [Google Scholar] [CrossRef]
- Sampedro, C.; Medina-Bailon, C.; Donetti, L.; Padilla, J.; Navarro, C.; Marquez, C.; Gámiz, F. Multi-Subband Ensemble Monte Carlo Simulator for Nanodevices in the End of the Roadmap. In Proceedings of the International Conference on Large-Scale Scientific Computations, Sozopol, Bulgaria, 10–14 June 2019. Lecture Notes in Computer Science (LNCS) post-proceedings. [Google Scholar] [CrossRef]
- Berrada, S.; Dutta, T.; Carrillo-Nunez, H.; Duan, M.; Adamu-Lema, F.; Lee, J.; Georgiev, V.; Medina-Bailon, C.; Asenov, A. NESS: new flexible Nano-Electronic Simulation Software. In Proceedings of the 2018 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Austin, TX, USA, 24–26 September 2019; pp. 22–25. [Google Scholar] [CrossRef]
- Rahman, A.; Lundstrom, M.S.; Ghosh, A.W.; Rahman, A.; Lundstrom, M.S.; Ghosh, A.W. Generalized effective-mass approach for n-type metal-oxide-semiconductor field-effect transistors on arbitrarily oriented wafers. J. Appl. Phys. 2005, 97. [Google Scholar] [CrossRef]
- Sampedro, C.; Donetti, L.; Gámiz, F.; Godoy, A. 3D Multi-Subband Ensemble Monte Carlo Simulator of FinFETs and Nanowire Transistors. In Proceedings of the 2014 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), Yokohama, Japan, 9–11 September 2014; pp. 21–24. [Google Scholar] [CrossRef]
- Luisier, M.; Schenk, A.; Fichtner, W. Quantum transport in two- and three-dimensional nanoscale transistors: Coupled mode effects in the nonequilibrium Greens function formalism. J. Appl. Phys. 2006, 100, 043713. [Google Scholar] [CrossRef]
- Svizhenko, A.; Anantram, M.P. Role of scattering in nanotransistors. IEEE Trans. Electron Devices 2003, 50, 1459–1466. [Google Scholar] [CrossRef]
- Sancho, M.P.L.; Sancho, J.M.L.; Sancho, J.M.L.; Rubio, J. Highly convergent schemes for the calculation of bulk and surface Green functions. J. Phys. F Met. Phys. 1985, 15, 851–858. [Google Scholar] [CrossRef]
- Venugopal, R.; Ren, Z.; Datta, S.; Lundstrom, M.S.; Jovanovic, D. Simulating quantum transport in nanoscale transistors: Real versus mode-space approaches. J. Appl. Phys. 2002, 92, 3730–3739. [Google Scholar] [CrossRef]
- Medina-Bailon, C.; Padilla, J.; Sadi, T.; Sampedro, C.; Godoy, A.; Donetti, L.; Georgiev, V.; Gámiz, F.; Asenov, A. Multisubband Ensemble Monte Carlo Analysis of Tunneling Leakage Mechanisms in Ultrascaled FDSOI, DGSOI, and FinFET Devices. IEEE Trans. Electron Devices 2019, 66, 1145–1152. [Google Scholar] [CrossRef]
- Medina-Bailon, C.; Padilla, J.; Sampedro, C.; Godoy, A.; Donetti, L.; Gámiz, F. Source–to–Drain Tunneling Analysis in FDSOI, DGSOI and FinFET Devices by Means of Multi-Subband Ensemble Monte Carlo. IEEE Trans. Electron Devices 2018, 65, 4740–4746. [Google Scholar] [CrossRef]
- Griffiths, D.J. The WKB approximation. In Introduction to Quantum Mechanics; Prentice Hall: Bergen, NJ, USA, 1995; pp. 274–297. [Google Scholar]
- Medina-Bailon, C.; Sampedro, C.; Padilla, J.L.; Godoy, A.; Donetti, L.; Gamiz, F.; Asenov, A. MS-EMC vs. NEGF: A comparative study accounting for transport quantum corrections. In Proceedings of the EUROSOI-ULIS 2018 Joint International EUROSOI Workshop and International Conference on Ultimate Integration on Silicon (EUROSOI-ULIS 2018), Granada, Spain, 19–21 March 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Carrillo-Nunez, H.; Ziegler, A.; Luisier, M.; Schenk, A. Modeling direct band-to-band tunneling: From bulk to quantum-confined semiconductor devices. J. Appl. Phys. 2015, 117, 1234501. [Google Scholar] [CrossRef]
- Shen, C.; Yang, L.T.; Samudra, G.; Yeo, Y.C. A new robust non-local algorithm for band-to-band tunneling simulation and its application to Tunnel-FET. Solid-State Electron. 2011, 57, 23–30. [Google Scholar] [CrossRef]
- QuantumATK version O-2018.06. Available online: https://www.synopsys.com/silicon/quantumatk.html (accessed on 1 June 2019).
- Medina-Bailon, C.; Lee, J.; Sampedro, C.; Padilla, J.; Donetti, L.; Georgiev, V.; Gámiz, F.; Asenov, A. Impact of Effective Mass on Transport Properties and Direct Source-to-Drain Tunneling in Ultrascaled Double Gate Devices: a 2D Multi-Subband Ensemble Monte Carlo study. In Proceedings of the Nanotechnology Materials and Devices Conference (NMDC), Stockholm, Sweden, 27–30 October 2019; pp. 1–4. [Google Scholar]
- Schroder, D.K. Semiconductor Material and Device Characterization; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]





| Device | Valley | m | ||
|---|---|---|---|---|
| DGSOI | = 0.193 m | = 0.193 m | = 0.912 m | |
| (100)<011> | = 0.319 m | = 0.553 m | = 0.193 m | |
| FinFET | = 0.193 m | = 0.912 m | = 0.193 m | |
| (01)<011> | = 0.553 m | = 0.193 m | = 0.319 m | |
| Device | Valley | T = 3 nm | T = 5 nm | ||||
|---|---|---|---|---|---|---|---|
| DGSOI | 0.144 m | 0.144 m | 1.002 m | 0.166 m | 0.166 m | 0.93 m | |
| (100)<011> | 0.252 m | 0.573 m | 0.144 m | 0.282 m | 0.548 m | 0.166 m | |
| FinFET | 0.15 m | 1.134 m | 0.15 m | 0.171 m | 0.956 m | 0.171 m | |
| (01)<011> | 0.642 m | 0.15 m | 0.265 m | 0.563 m | 0.171 m | 0.29 m | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medina-Bailon, C.; Carrillo-Nunez, H.; Lee, J.; Sampedro, C.; Padilla, J.L.; Donetti, L.; Georgiev, V.; Gamiz, F.; Asenov, A. Quantum Enhancement of a S/D Tunneling Model in a 2D MS-EMC Nanodevice Simulator: NEGF Comparison and Impact of Effective Mass Variation. Micromachines 2020, 11, 204. https://doi.org/10.3390/mi11020204
Medina-Bailon C, Carrillo-Nunez H, Lee J, Sampedro C, Padilla JL, Donetti L, Georgiev V, Gamiz F, Asenov A. Quantum Enhancement of a S/D Tunneling Model in a 2D MS-EMC Nanodevice Simulator: NEGF Comparison and Impact of Effective Mass Variation. Micromachines. 2020; 11(2):204. https://doi.org/10.3390/mi11020204
Chicago/Turabian StyleMedina-Bailon, Cristina, Hamilton Carrillo-Nunez, Jaehyun Lee, Carlos Sampedro, Jose Luis Padilla, Luca Donetti, Vihar Georgiev, Francisco Gamiz, and Asen Asenov. 2020. "Quantum Enhancement of a S/D Tunneling Model in a 2D MS-EMC Nanodevice Simulator: NEGF Comparison and Impact of Effective Mass Variation" Micromachines 11, no. 2: 204. https://doi.org/10.3390/mi11020204
APA StyleMedina-Bailon, C., Carrillo-Nunez, H., Lee, J., Sampedro, C., Padilla, J. L., Donetti, L., Georgiev, V., Gamiz, F., & Asenov, A. (2020). Quantum Enhancement of a S/D Tunneling Model in a 2D MS-EMC Nanodevice Simulator: NEGF Comparison and Impact of Effective Mass Variation. Micromachines, 11(2), 204. https://doi.org/10.3390/mi11020204







