Experimental Characterization and Simulation of Thermoplastic Polymer Flow Hesitation in Thin-Wall Injection Molding Using Direct In-Mold Visualization Technique
Abstract
:1. Introduction
2. Materials and Methods
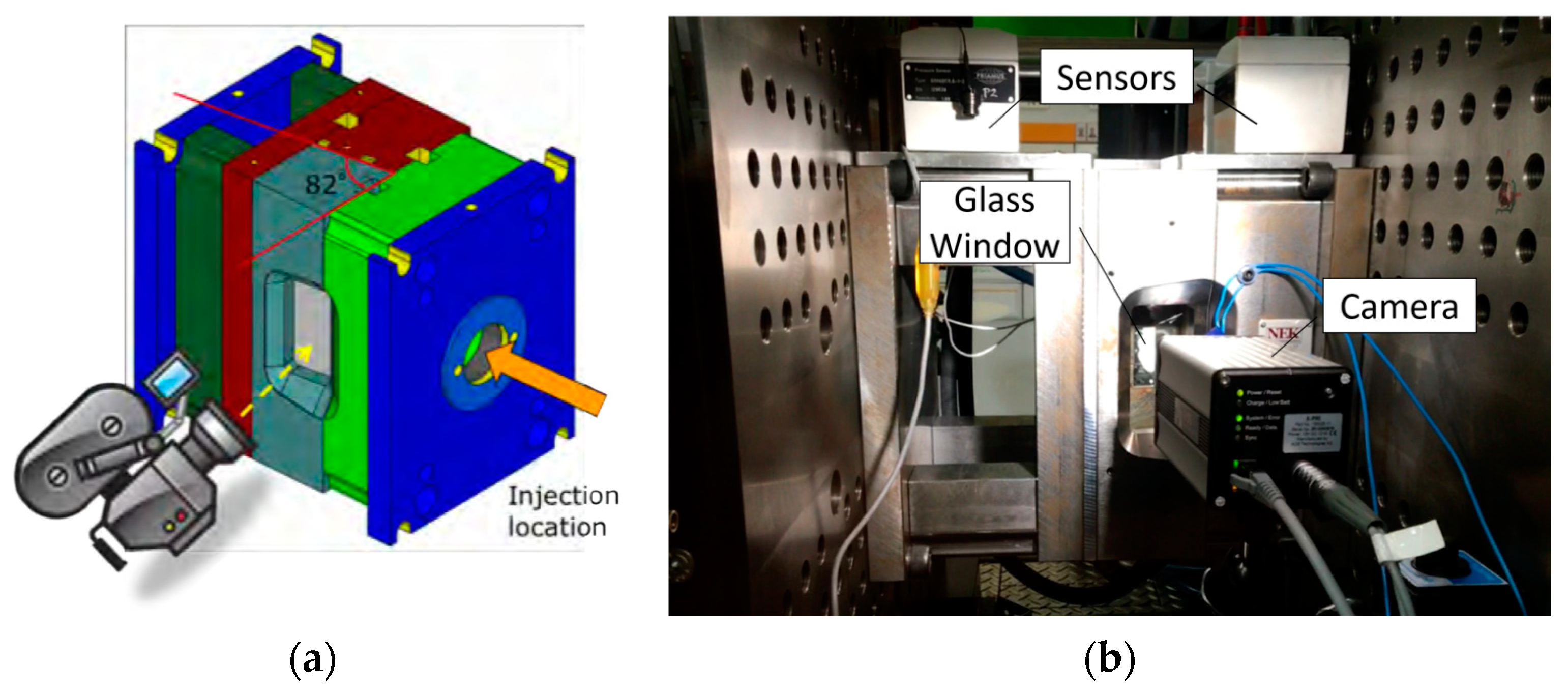
2.1. Glass Mold and Injection Molding Machine
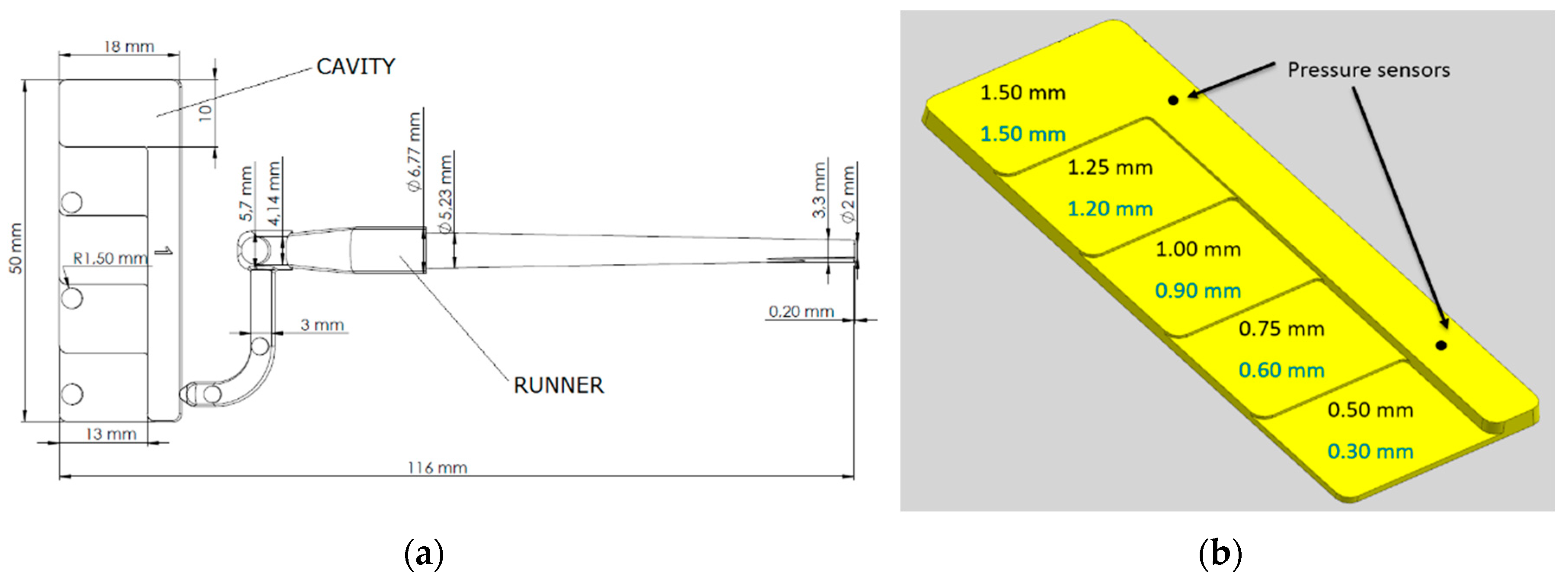
2.2. Test Parts and Materials
2.3. Experiments
- (1)
- In the maximum pressure (MP) method, the different filling percentages of the cavity were obtained limiting the maximum applied pressure and progressively raising its limit value. MP short shots were therefore produced with variable injection speeds (varying from 4 to 9 mm/s).
- (2)
- In the second method, the desired positions were obtained with consecutive increments of the stroke length at a certain injection velocity. They were addressed as Short Shots (SS). Similar to the complete experiments, SSF runs were with an injection velocity of 40 mm/s, while SSM with 10 mm/s. The velocities were chosen to allow a direct comparison between the complete and the short shot experiments.
- ComF refers to the complete filling experiments with an injection velocity of 40 mm/s;
- ComM refers to the complete filling experiments with an injection velocity of 10 mm/s;
- ComS refers to the complete filling experiments with an injection velocity of 6 mm/s;
- SSF refers to the short shots obtained varying the stroke length with injection velocity of 40 mm/s;
- SSM refers to the short shots obtained varying the stroke length with injection velocity of 10 mm/s;
- MP refers to the short shots achieved limiting the maximum applied pressure.
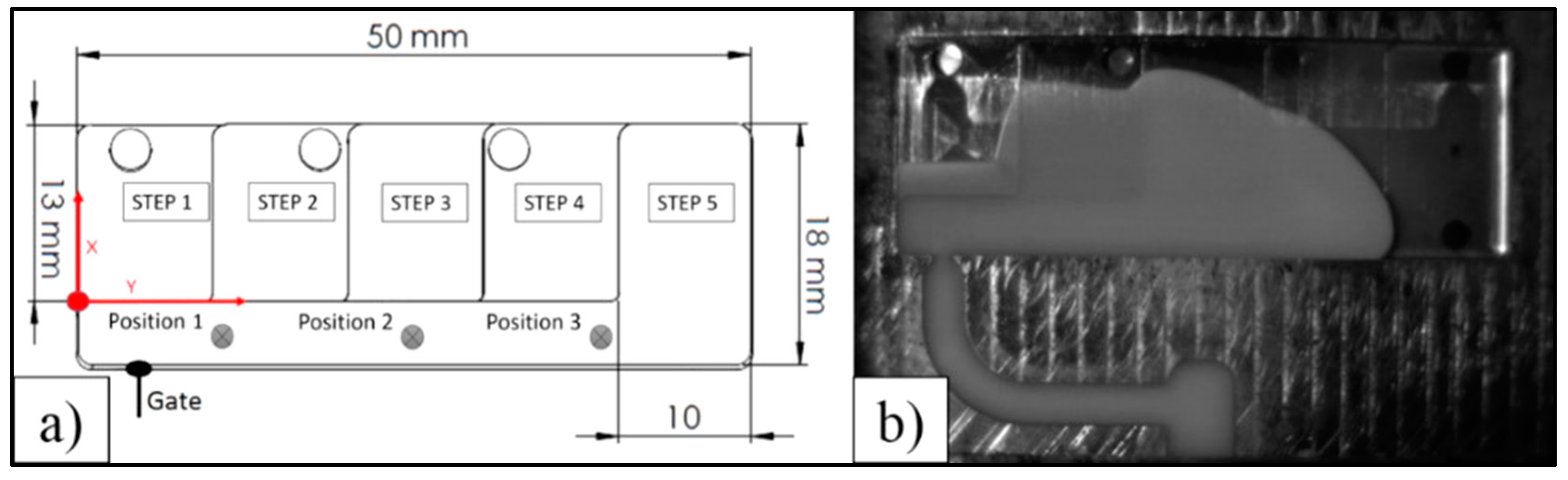
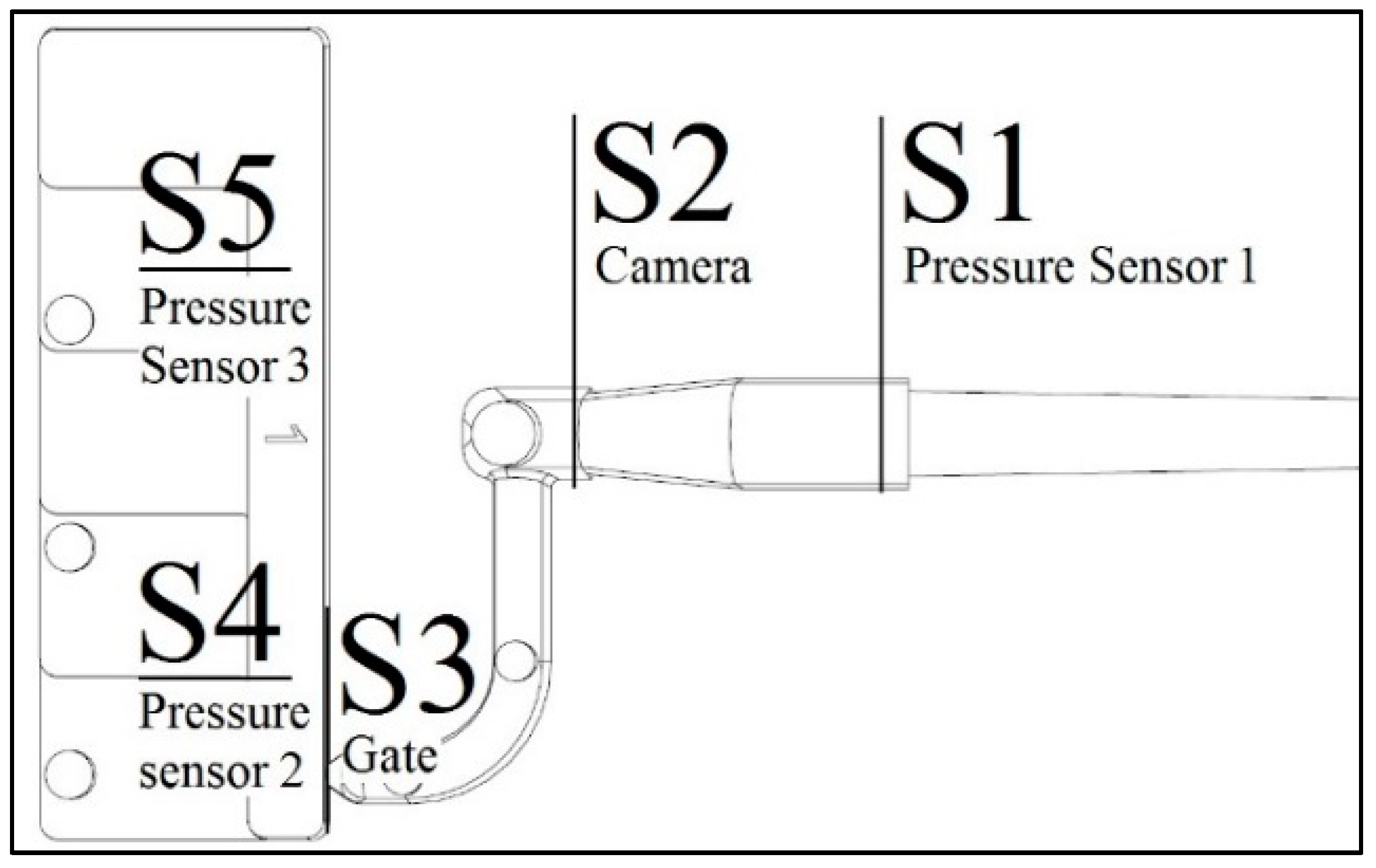
2.4. High Speed Video Analysis
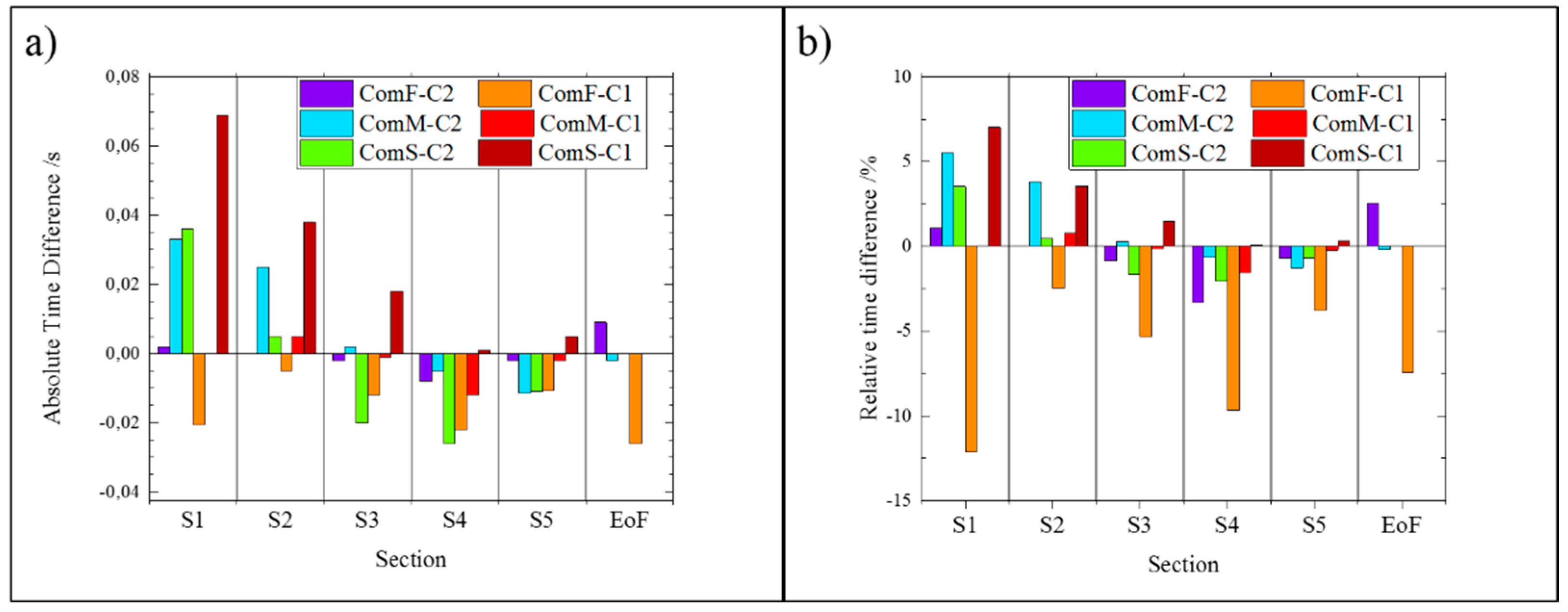
3. Results of Experiments
- Thickness variation is the most important factor affecting the hesitation effect;
- The injection velocity and the thickness are not linearly related;
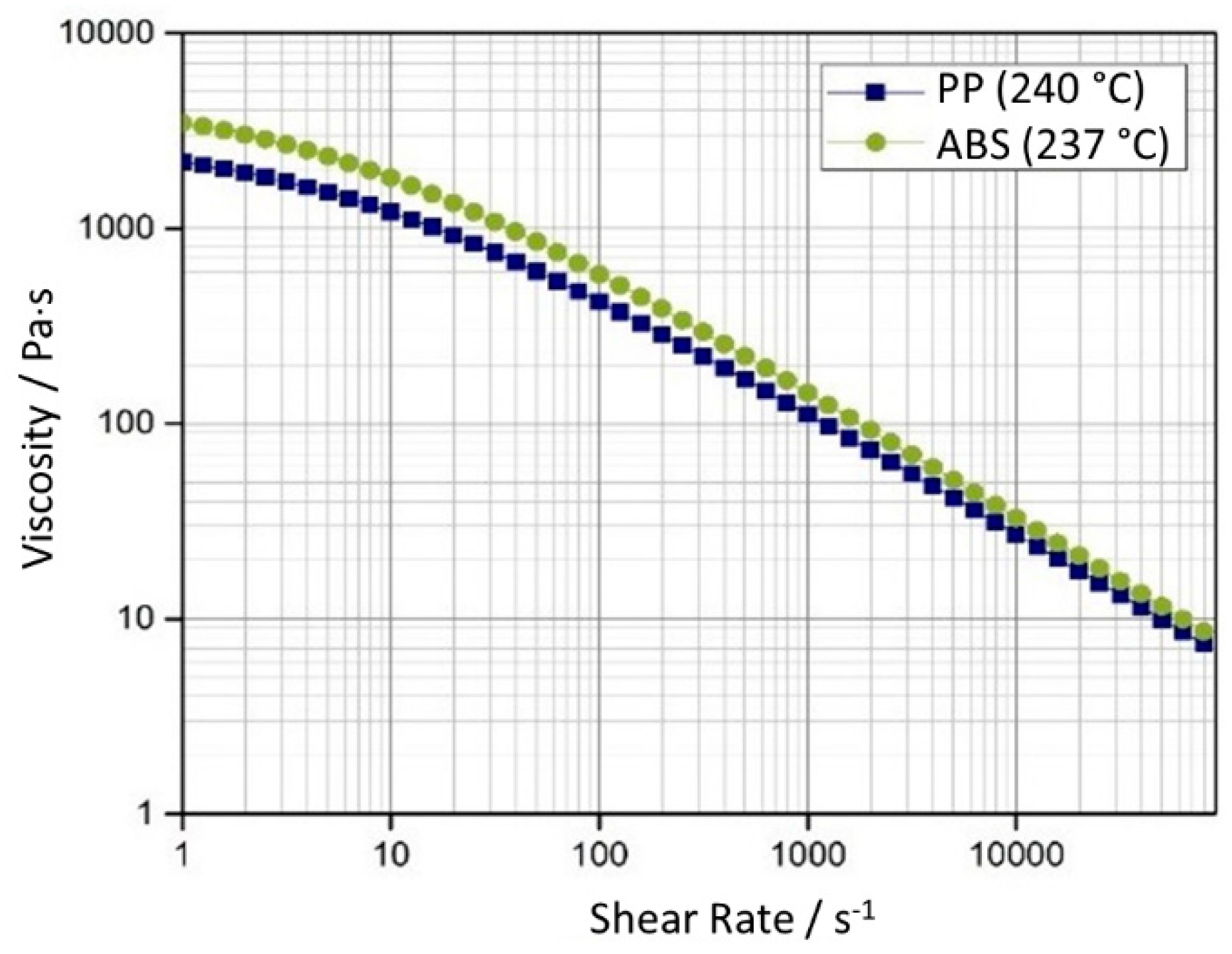
- PP showed less hesitation effect than ABS, as expected from its lower viscosity at the selected melt temperature;
- MP short shot method is not suitable for the characterization of the flow in the cavity;
- Short shots increase the hesitation effect occurring during the filling phase.
4. Simulations
4.1. Theoretical Background
4.2. Simulation Setup
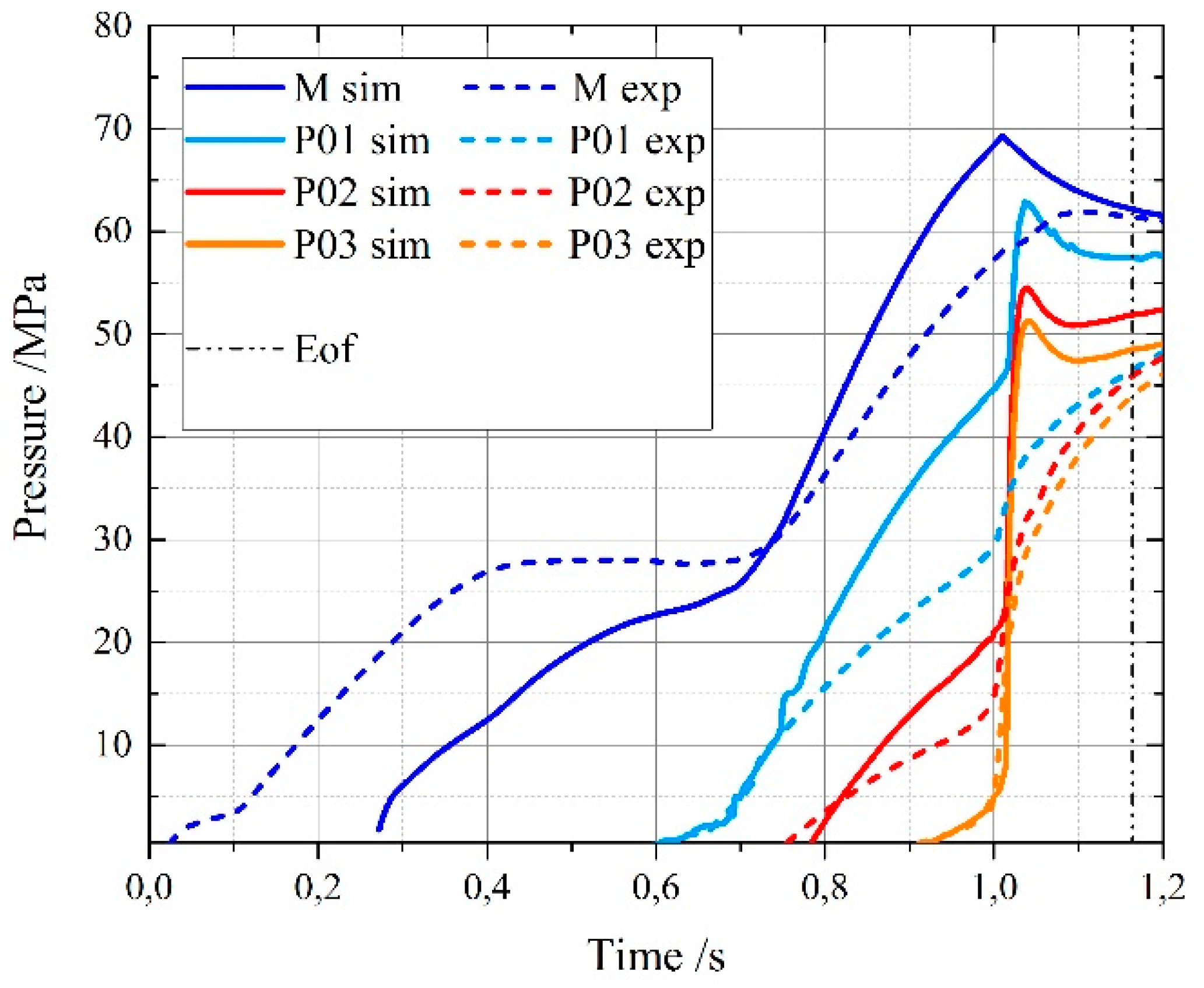
4.3. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gramann, P.J.; Osswald, T.; Turng, L.S. Injection Molding Handbook; Carl Hanser Verlag: Munich, Germany, 2008. [Google Scholar]
- Kim, H.S.; Son, J.S.; Im, Y.T. Gate Location Design in Injection Molding of an Automobile Junction Box with Integral Hinges. J. Mater. Process. Technol. 2003, 140, 110–115. [Google Scholar] [CrossRef]
- Yang, Y.J.; Huang, C.C.; Tao, J. Application of ultrasonic-assisted injection molding for improving melt flowing and floating fibers. J. Polym. Eng. 2016, 36, 119–128. [Google Scholar] [CrossRef]
- Murata, Y.; Yokoi, H.; Utaka, Y. Visual Analysis of Short-shot Front Behaviors by Glass-Inserted Mold. Seikei-kakou 1994, 6, 703–711. [Google Scholar] [CrossRef] [Green Version]
- Yokoi, H. Visualization Analysis of Undesired Phenomena on Molded Surface in Injection Molding Process. J. Surf. Finish. Soc. Jpn. 2000, 51, 1182–1186. [Google Scholar] [CrossRef]
- Yang, S.Y.; Nian, S.C.; Sun, I.C. Flow visualization of filling process during micro-injection molding. Int. Polym. Process. 2002, 4, 354–360. [Google Scholar] [CrossRef]
- Nian, S.; Yang, S.Y. Flow visualization of filling with aid of colored billets during impact micro-injection molding. Int. Polym. Process. 2004, 4, 402–407. [Google Scholar] [CrossRef]
- Han, X.; Yokoi, H. Visualization analysis of the filling behavior of melt into microscale v-grooves during the filling stage of injection molding. Polym. Eng. Sci. 2006, 46, 1590–1597. [Google Scholar] [CrossRef]
- Layser, G.S.; Coulter, J.P. Effect of processing parameters on flow hesitation with glass-filled reinforced thermoplastics: Experimental investigation with direct visualization. In Proceedings of the 67th Annual Technical Conference (ANTEC) of the Society of Plastics Engineers (SPE), Chicago, IL, USA, 22–24 June 2009; Society of Plastics Engineers (SPE) Publisher: Brookfield, CT, USA, 2009; pp. 342–348. [Google Scholar] [CrossRef]
- Spares, R.; Whiteside, B.R.; Coates, P. High speed thermal imaging of micromoulding. In Proceedings of the 67th Annual Technical Conference (ANTEC) of the Society of Plastics Engineers (SPE), Chicago, IL, USA, 22–24 June 2009; Society of Plastics Engineers (SPE) Publisher: Brookfield, CT, USA, 2009; pp. 2570–2573. [Google Scholar]
- Whiteside, B.R.; Spares, R.; Coates, P. Rheo-optical measurements in micromoulding. In Proceedings of the 67th Annual Technical Conference (ANTEC) of the Society of Plastics Engineers (SPE), Chicago, IL, USA, 22–24 June 2009; Society of Plastics Engineers (SPE) Publisher: Brookfield, CT, USA, 2009; pp. 2803–2810. [Google Scholar]
- Sorgato, M.; Babenko, M.; Lucchetta, G. Investigation of the influence of Vacuum Venting on Mould Surface Temperature. Int. J. Adv. Manuf. Technol. 2017, 88, 547–555. [Google Scholar] [CrossRef] [Green Version]
- Baruffi, F.; Gülçür, M.; Calaon, M.; Romano, J.-M.; Penchev, P.; Dimov, S.; Whiteside, B.; Tosello, G. Correlating nano-scale surface replication accuracy and cavity temperature in micro-injection moulding using in-line process control and high-speed thermal imaging. J. Manuf. Process. 2019, 47, 367–381. [Google Scholar] [CrossRef]
- Yanev, A.S.; Dias, G.R.; Cunha, A.M. Direct visualization of conventional injection molding. In Proceedings of the 65th Annual Technical Conference (ANTEC) of the Society of Plastics Engineers (SPE), Cincinnati, OH, USA, 6–10 May 2007; Society of Plastics Engineers (SPE) Publisher: Brookfield, CT, USA, 2007; pp. 1097–1101. [Google Scholar]
- Yanev, A.S.; Dias, G.R.; Cunha, A.M. Visualization of injection molding process. Mater. Sci. Forum 2008, 587–588, 716–720. [Google Scholar] [CrossRef]
- Guerrier, P.; Tosello, G.; Nielsen, K.K.; Hattel, J.H. Three-Dimensional Numerical Modeling of an Induction Heated Injection Molding Tool with Flow Visualization. Int. J. Adv. Manuf. Technol. 2016, 85, 643–660. [Google Scholar] [CrossRef] [Green Version]
- Guerrier, P.; Tosello, G.; Hattel, J.H. Flow Visualization and Simulation of the Filling Process during Injection Molding. CIRP J. Manuf. Sci. Technol. 2017, 16, 220–222. [Google Scholar] [CrossRef] [Green Version]
- Regi, F.; Tosello, G. Direct flow visualization of hesitation during injection molding of thermoplastic polymers. In AIP Conference Proceedings, Proceedings of the the 33rd International Conference of the Polymer Processing Society, Cancun, Mexico, 10–14 December 2017; Manero, O., Calderas, F., Eds.; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2139, p. 030001. [Google Scholar] [CrossRef] [Green Version]
- Schneider, A.C.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- JCGM 100:2008 Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement Joint Committee for Guides in Metrology; Bureau International des Poids et Mesures, BIPM: Sèvres, France, 2008.
- Eladl, A.; Mostafa, R.; Islam, A.; Loaldi, D.; Soltan, H.; Hansen, H.N.; Tosello, G. Effect of Process Parameters on Flow Length and Flash Formation in Injection Moulding of High Aspect Ratio Polymeric Micro Features. Micromachines 2018, 9, 58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vietri, U.; Sorrentino, A.; Speranza, V.; Pantani, R. Improving the prediction of injection molding simulation software. Polym. Eng. Sci. 2011, 51, 2542–2551. [Google Scholar] [CrossRef]
- Tosello, G.; Costa, F. High precision validation of micro injection molding process simulations. J. Manuf. Process. 2019, 48, 236–248. [Google Scholar] [CrossRef]
- Raha, S.; Sharma, H.; Senthilmurugan, M.; Bandyopadhyay, S.; Mukhopadhyay, P. Determination of the Pressure Dependence of Polymer Melt Viscosity Using a Combination of Oscillatory and Capillary Rheometer. Polym. Eng. Sci. 2019, 60, 517–523. [Google Scholar] [CrossRef]
- Gava, A.; Tosello, G.; Lucchetta, G.; Reinecke, H.; Hansen, H.N.; Schoth, A. Experimental validation of viscous and viscoelastic simulations of micro injection molding process. In Proceedings of the 67th Annual Technical Conference (ANTEC) of the Society of Plastics Engineers (SPE), Chicago, IL, USA, 22–26 June 2009; Society of Plastics Engineers (SPE) Publisher: Brookfield, CT, USA, 2009; pp. 1781–1786. [Google Scholar]
- Cao, W.; Shen, Y.; Wang, P.; Yang, H.; Zhao, S.; Shen, C. Viscoelastic modeling and simulation for polymer melt flow in injection/compression molding. J. Non-Newton. Fluid Mech. 2019, 274, 104186. [Google Scholar] [CrossRef]


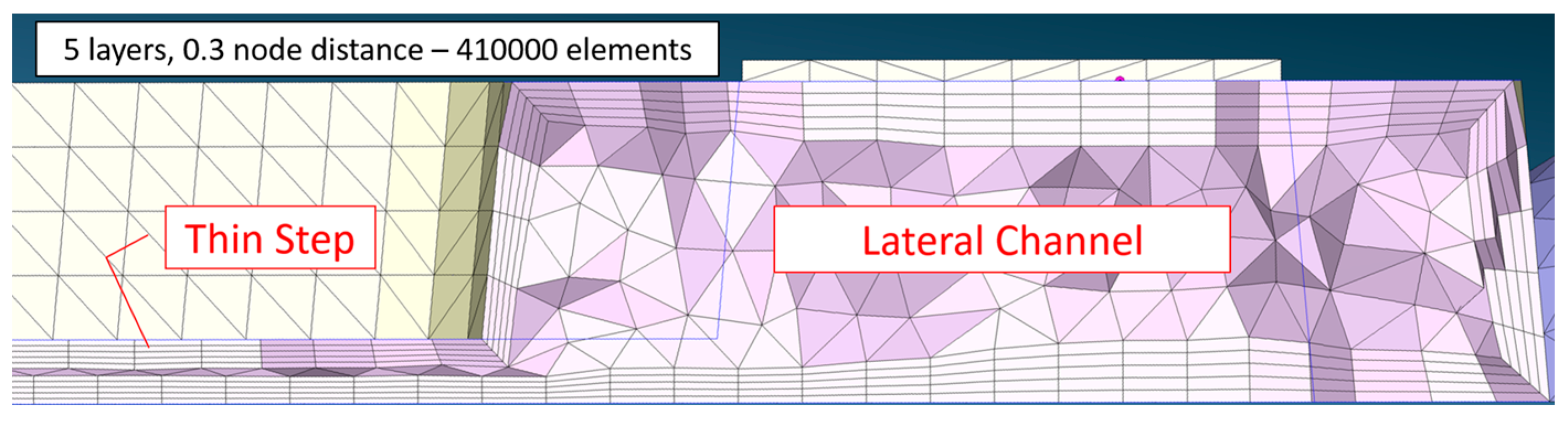


| Position | Cavity | Gate | Runner |
|---|---|---|---|
| Layers | 5 | 5 | 5 |
| Mesh size/mm | 0.3 | 0.3 | 0.5 |
| Elements/total no. | 410,000 | 255,000 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Regi, F.; Guerrier, P.; Zhang, Y.; Tosello, G. Experimental Characterization and Simulation of Thermoplastic Polymer Flow Hesitation in Thin-Wall Injection Molding Using Direct In-Mold Visualization Technique. Micromachines 2020, 11, 428. https://doi.org/10.3390/mi11040428
Regi F, Guerrier P, Zhang Y, Tosello G. Experimental Characterization and Simulation of Thermoplastic Polymer Flow Hesitation in Thin-Wall Injection Molding Using Direct In-Mold Visualization Technique. Micromachines. 2020; 11(4):428. https://doi.org/10.3390/mi11040428
Chicago/Turabian StyleRegi, Francesco, Patrick Guerrier, Yang Zhang, and Guido Tosello. 2020. "Experimental Characterization and Simulation of Thermoplastic Polymer Flow Hesitation in Thin-Wall Injection Molding Using Direct In-Mold Visualization Technique" Micromachines 11, no. 4: 428. https://doi.org/10.3390/mi11040428
APA StyleRegi, F., Guerrier, P., Zhang, Y., & Tosello, G. (2020). Experimental Characterization and Simulation of Thermoplastic Polymer Flow Hesitation in Thin-Wall Injection Molding Using Direct In-Mold Visualization Technique. Micromachines, 11(4), 428. https://doi.org/10.3390/mi11040428






