Laser Ablation of Aluminum Near the Critical Regime: A Computational Gas-Dynamical Model with Temperature-Dependent Physical Parameters
Abstract
:1. Introduction
2. Modeling Laser Ablation
2.1. Thermal Processes
2.2. Vaporization
- the necessary temperatures to attain efficient LA of metals (our situation) are very high due to their high . This implies that the interatomic potential becomes certainly negligible with respect to the atomic kinetic energy, and precisely this contributes to justify the assumption of randomly moving particle via perfectly elastic collision which the ideal gas is based on;
- modeling the vapor expansion in vacuum, using the Euler Equations (15), requires the Knudsen layer to be taken into account. Now all the quantitative relations connected to it and available in the literature, see for example [21], have been calculated under the ideal gas approximation, which is therefore normally used in the literature (see also [31]). This is the reason we have consistently used the ideal gas approximation throughout the text.
2.3. Knudsen Layer and Vapor Expansion
3. Aluminum Properties
3.1. Critical Temperature
3.2. Density
3.3. Specific Heat at Constant Pressure
3.4. Enthalpy of Vaporization
3.5. Transport Properties
3.6. Optical Properties
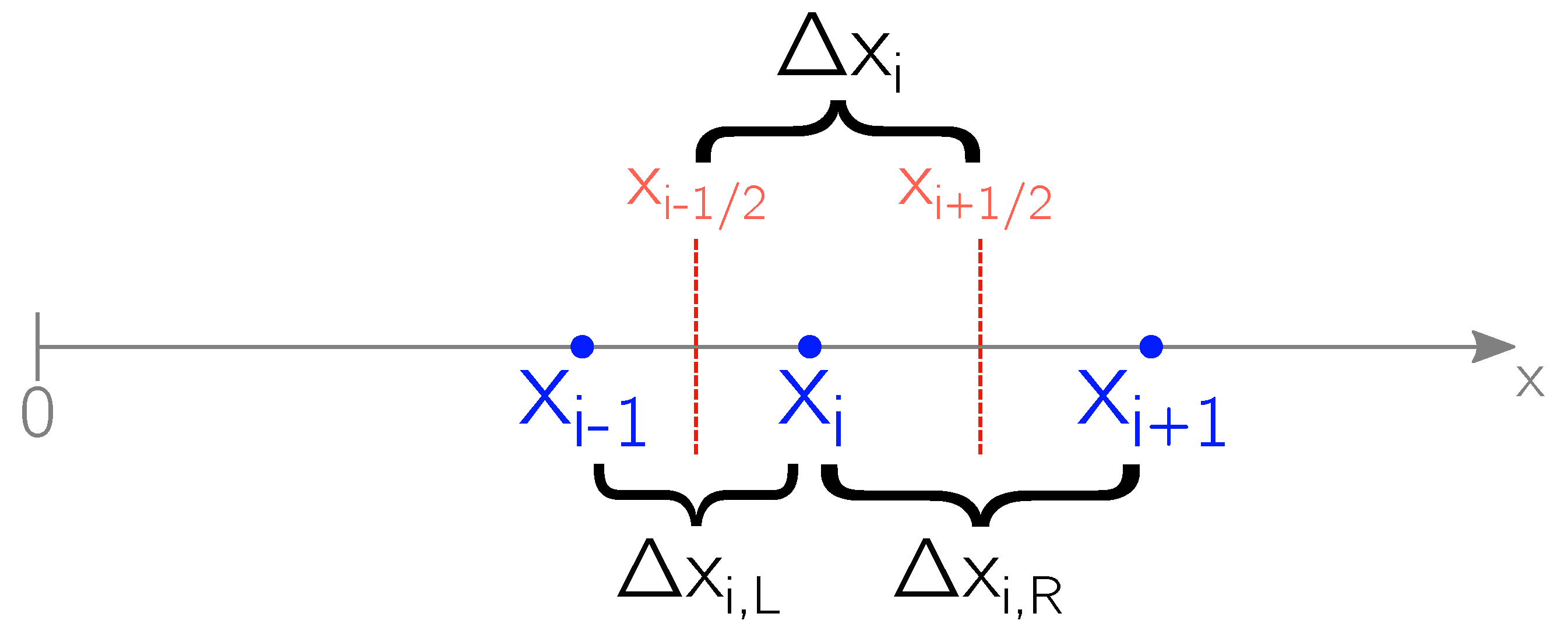
4. Numerical Methods
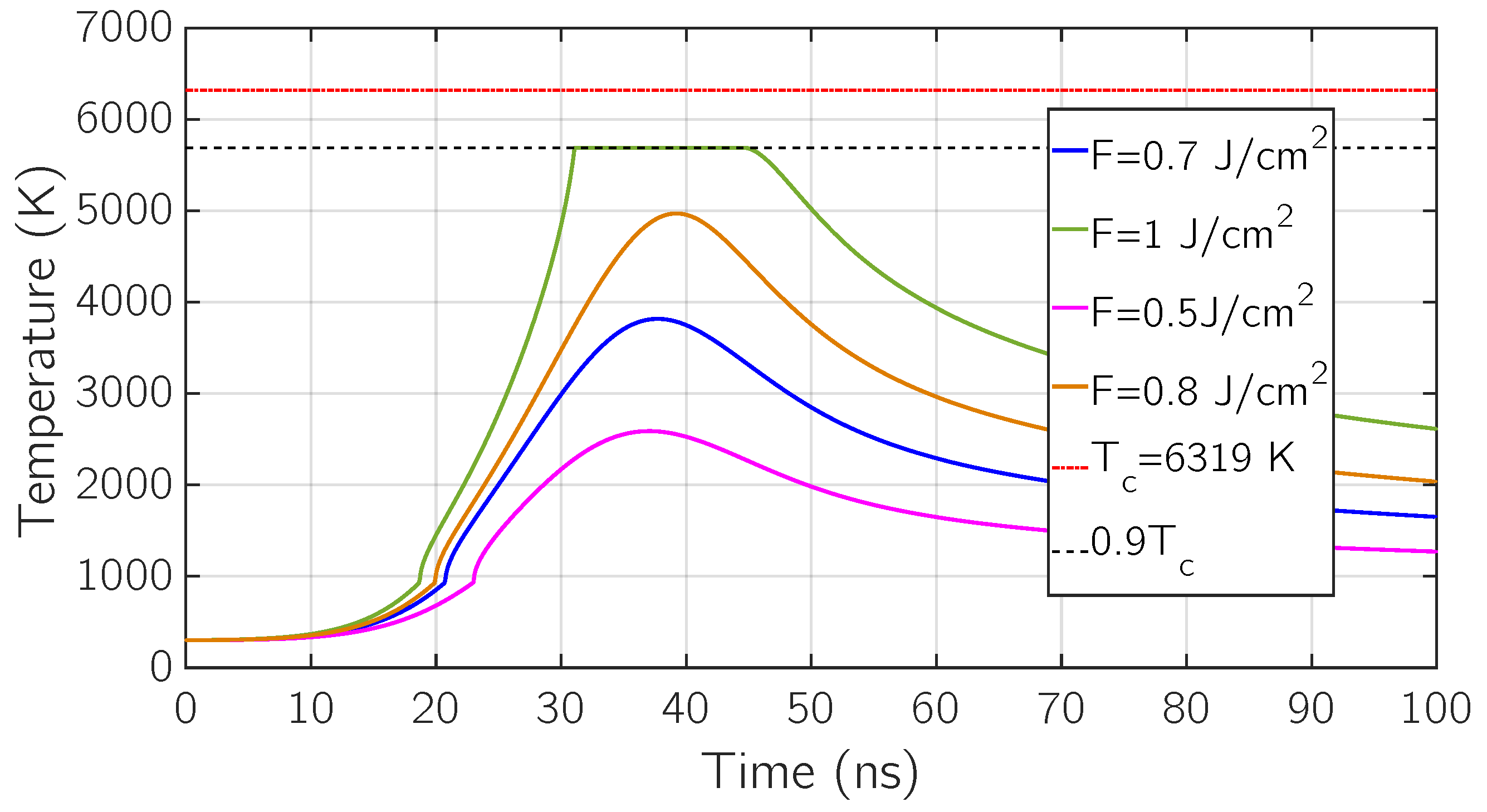
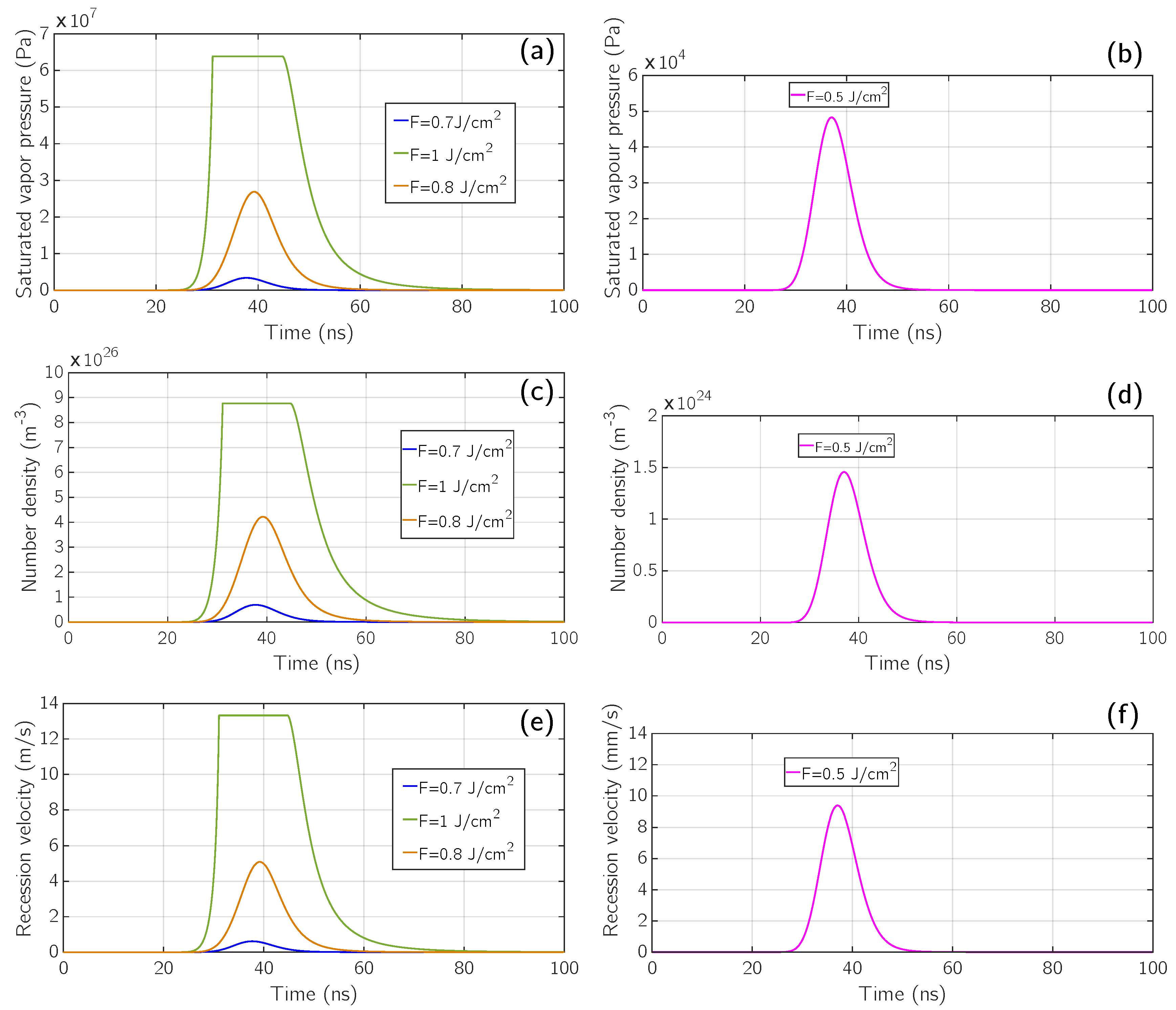
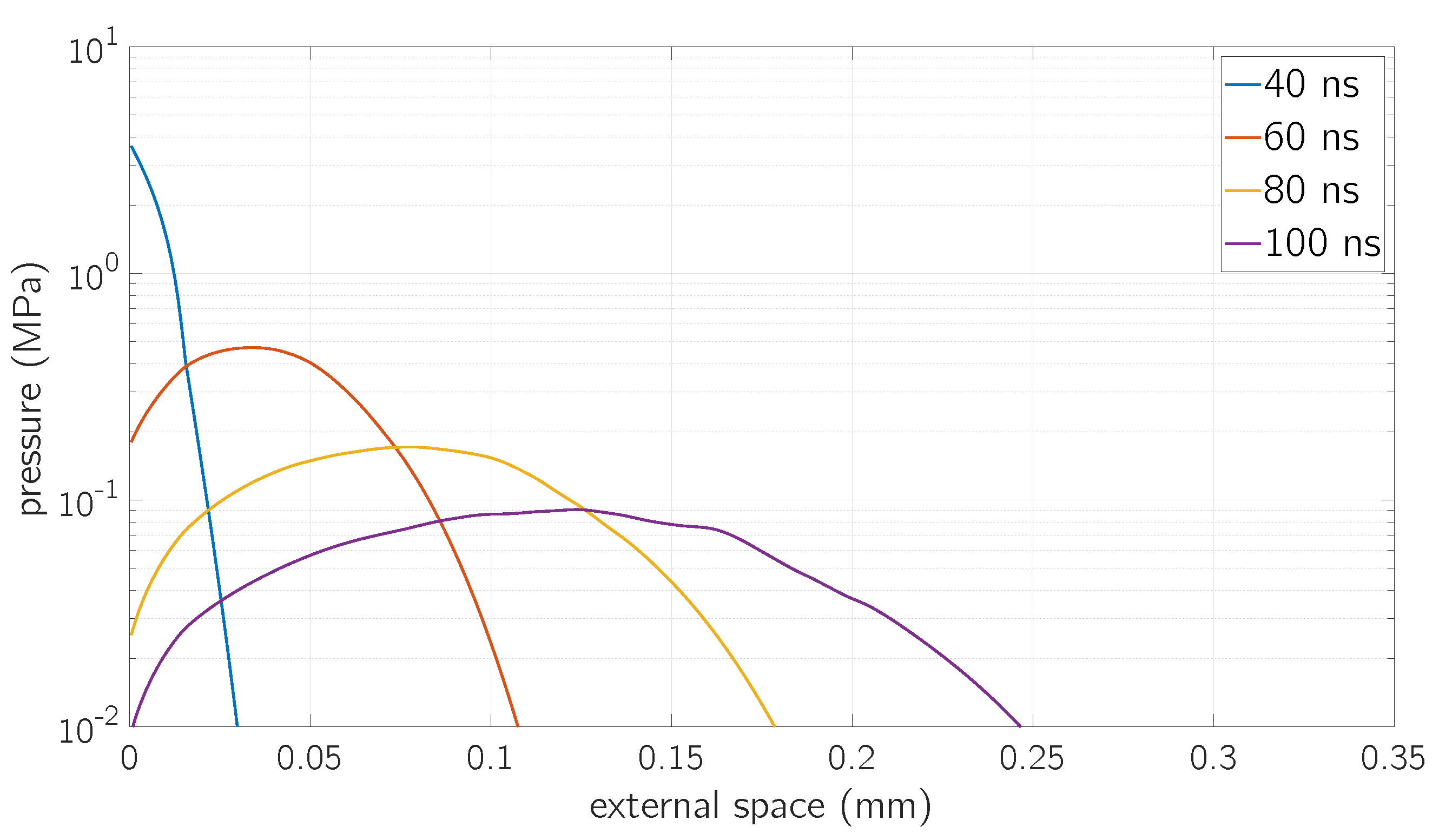
5. Results and Discussion
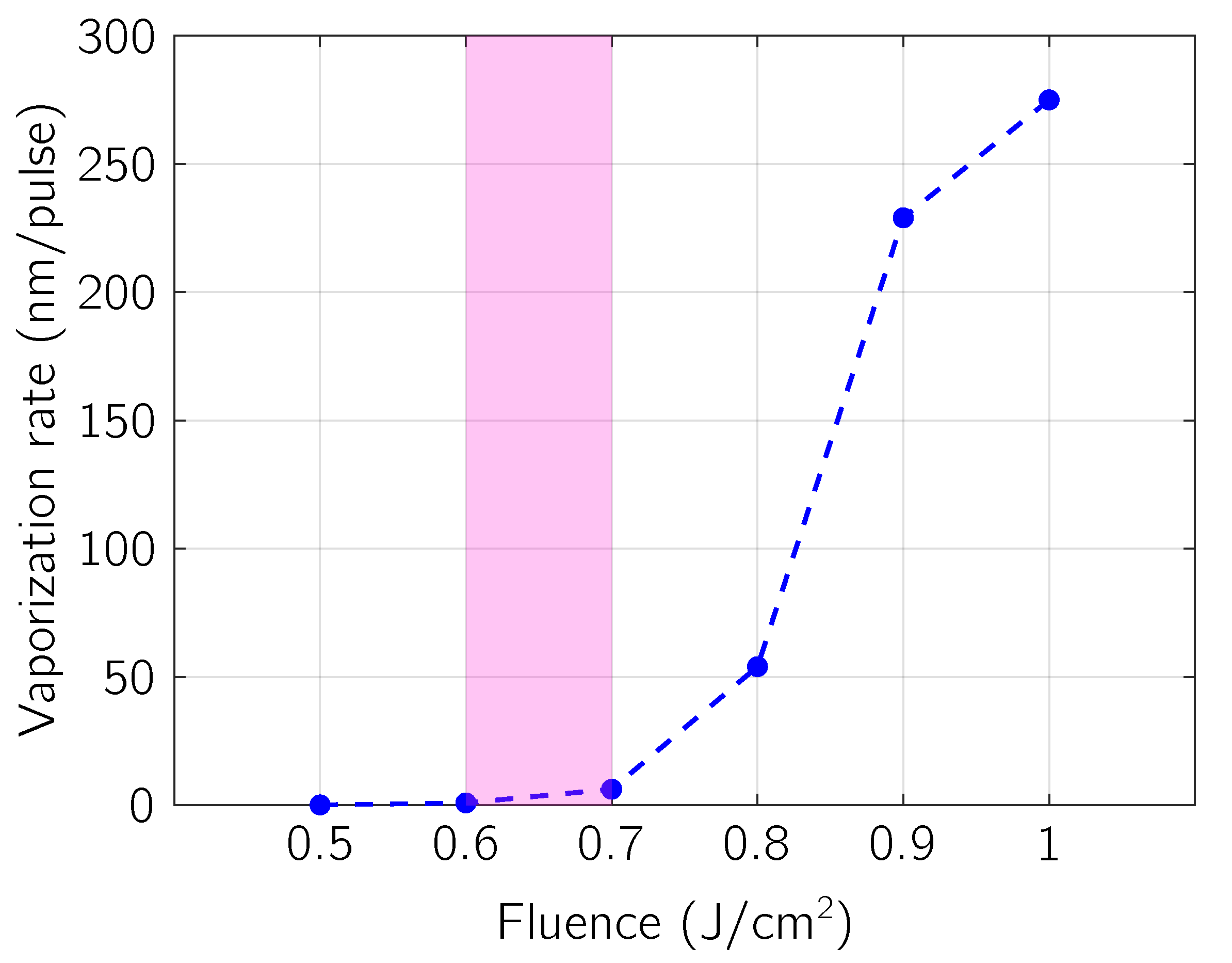
5.1. Comparison with Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| CFL | Courant-Friedrich-Levy |
| FTCS | Forward Time Centered Space |
| FV | Finite Volumes |
| FWHM | Full Width Half Maximum |
| KL | Knudsen Layer |
| LA | Laser Ablation |
| LAP | Laser Ablation Propulsion |
| LIBS | Laser Induced Breakdown Spectroscopy |
| LTP | Low Temperature Plasma |
| PLD | Pulsed Laser Deposition |
| UAE | Unsteady Adiabatic Expansion |
References
- Fazio, E.; Neri, F.; Ponterio, R.C.; Trusso, S.; Tommasini, M.; Ossi, P.M. Laser controlled synthesis of noble metal nanoparticle arrays for low concentration molecule recognition. Micromachines 2014, 5, 1296–1309. [Google Scholar] [CrossRef] [Green Version]
- Basso, L.; Sacco, M.; Bazzanella, N.; Cazzanelli, M.; Barge, A.; Orlandi, M.; Bifone, A.; Miotello, A. Laser-Synthesis of NV-Centers-Enriched Nanodiamonds: Effect of Different Nitrogen Sources. Micromachines 2020, 11, 579. [Google Scholar] [CrossRef] [PubMed]
- Bleiner, D.; Chen, Z.; Autrique, D.; Bogaerts, A. Role of laser-induced melting and vaporization of metals during ICP-MS and LIBS analysis, investigated with computer simulations and experiments. J. Anal. At. Spectrom. 2006, 21, 910–921. [Google Scholar] [CrossRef]
- Lukyanchuk, B. Laser Cleaning: Optical Physics, Applied Physics and Materials Science; World Scientific: Singapore, 2002. [Google Scholar]
- Moses, E.; Bonanno, R.; Haynam, C.; Kauffman, R.; MacGowan, B.; Patterson, R.; Sawicki, R.; Van Wonterghem, B. The national ignition facility: Path to ignition in the laboratory. Eur. Phys. J. D 2007, 44, 215–218. [Google Scholar] [CrossRef]
- Phipps, C.R.; Baker, K.L.; Libby, S.B.; Liedahl, D.A.; Olivier, S.S.; Pleasance, L.D.; Rubenchik, A.; Trebes, J.E.; George, E.V.; Marcovici, B.; et al. Removing orbital debris with lasers. Adv. Space Res. 2012, 49, 1283–1300. [Google Scholar] [CrossRef] [Green Version]
- Phipps, C.; Birkan, M.; Bohn, W.; Eckel, H.A.; Horisawa, H.; Lippert, T.; Michaelis, M.; Rezunkov, Y.; Sasoh, A.; Schall, W.; et al. Laser-ablation propulsion. J. Propuls. Power 2010, 26, 609–637. [Google Scholar] [CrossRef]
- Opiela, J.N. A study of the material density distribution of space debris. Adv. Space Res. 2009, 43, 1058–1064. [Google Scholar] [CrossRef]
- Tsuruta, H.; Wang, B.; Wang, Z.; Yokota, S.; Sasoh, A. Repetitive Pulse Performance of One-Micrometer Laser-Ablation Propulsion onto Aluminum. J. Propuls. Power 2014, 30, 1485–1489. [Google Scholar] [CrossRef]
- Yuan, H.; Tong, H.; Li, M.; Sun, C. Computational study of nanosecond pulsed laser ablation and the application to momentum coupling. J. Appl. Phys. 2012, 112, 023105. [Google Scholar] [CrossRef]
- Miotello, A.; Kelly, R. Laser-induced phase explosion: New physical problems when a condensed phase approaches the thermodynamic critical temperature. Appl. Phys. A 1999, 69, S67–S73. [Google Scholar] [CrossRef]
- Porneala, C.; Willis, D.A. Observation of nanosecond laser-induced phase explosion in aluminum. Appl. Phys. Lett. 2006, 89, 211121. [Google Scholar] [CrossRef]
- Zhigilei, L.V.; Lin, Z.; Ivanov, D.S. Atomistic modeling of short pulse laser ablation of metals: Connections between melting, spallation, and phase explosion. J. Phys. Chem. C 2009, 113, 11892–11906. [Google Scholar] [CrossRef] [Green Version]
- Anisimov, S. Evaporation of metal on absorbing laser radiation. J. Exp. Theor. Phys. 1968, 54, 339–342. [Google Scholar]
- Martynyuk, M. Mechanism for metal damage by intense electromagnetic radiation. Sov. Phys.-Tech. Phys. 1976, 21, 430–433. [Google Scholar]
- Bogaerts, A.; Chen, Z.; Gijbels, R.; Vertes, A. Laser ablation for analytical sampling: What can we learn from modeling? Spectrochim. Acta Part B At. Spectrosc. 2003, 58, 1867–1893. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, D.; Wu, J.; He, Z.; Deng, X. A thermal model for nanosecond pulsed laser ablation of aluminum. AIP Adv. 2017, 7, 075010. [Google Scholar] [CrossRef]
- Autrique, D.; Clair, G.; l’Hermite, D.; Alexiades, V.; Bogaerts, A.; Rethfeld, B. The role of mass removal mechanisms in the onset of ns-laser induced plasma formation. J. Appl. Phys. 2013, 114, 023301. [Google Scholar] [CrossRef] [Green Version]
- Gusarov, A.V.; Smurov, I. Gas-dynamic boundary conditions of evaporation and condensation: Numerical analysis of the Knudsen layer. Phys. Fluids 2002, 14, 4242–4255. [Google Scholar] [CrossRef]
- Knight, C.J. Theoretical modeling of rapid surface vaporization with back pressure. AIAA J. 1979, 17, 519–523. [Google Scholar] [CrossRef]
- Kelly, R. On the dual role of the Knudsen layer and unsteady, adiabatic expansion in pulse sputtering phenomena. J. Chem. Phys. 1990, 92, 5047–5056. [Google Scholar] [CrossRef]
- Marla, D.; Bhandarkar, U.V.; Joshi, S.S. A model of laser ablation with temperature-dependent material properties, vaporization, phase explosion and plasma shielding. Appl. Phys. A 2014, 116, 273–285. [Google Scholar] [CrossRef]
- Alves, L.; Bogaerts, A.; Guerra, V.; Turner, M. Foundations of modelling of nonequilibrium low-temperature plasmas. Plasma Sources Sci. Technol. 2018, 27, 023002. [Google Scholar] [CrossRef]
- Miotello, A.; Kelly, R. Critical assessment of thermal models for laser sputtering at high fluences. Appl. Phys. Lett. 1995, 67, 3535–3537. [Google Scholar] [CrossRef]
- Mazzi, A.; Gorrini, F.; Miotello, A. Dynamics of liquid nanodroplet formation in nanosecond laser ablation of metals. Appl. Surf. Sci. 2017, 418, 601–606. [Google Scholar] [CrossRef]
- Autrique, D.; Alexiades, V.; Khanal, H. Hydrodynamic modeling of ns-laser ablation. Electron. J. Differ. Equ. 2013, 20, 1–14. [Google Scholar]
- Marla, D.; Bhandarkar, U.V.; Joshi, S.S. Models for predicting temperature dependence of material properties of aluminum. J. Phys. D Appl. Phys. 2014, 47, 105306. [Google Scholar] [CrossRef]
- Miotello, A.; Ossi, P.M. Laser-Surface Interactions for New Materials Production; Springer: Berlin/Heidelberg, Germany, 2010; Volume 130. [Google Scholar]
- Gilgenbach, R.M.; Ventzek, P.L. Dynamics of excimer laser-ablated aluminum neutral atom plume measured by dye laser resonance absorption photography. Appl. Phys. Lett. 1991, 58, 1597–1599. [Google Scholar] [CrossRef] [Green Version]
- Peterlongo, A.; Miotello, A.; Kelly, R. Laser-pulse sputtering of aluminum: Vaporization, boiling, superheating, and gas-dynamic effects. Phys. Rev. E 1994, 50, 4716. [Google Scholar] [CrossRef] [PubMed]
- Mazzi, A.; Gorrini, F.; Miotello, A. Liquid nanodroplet formation through phase explosion mechanism in laser-irradiated metal targets. Phys. Rev. E 2015, 92, 031301. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Leitner, M.; Leitner, T.; Schmon, A.; Aziz, K.; Pottlacher, G. Thermophysical properties of liquid aluminum. Metall. Mater. Trans. A 2017, 48, 3036–3045. [Google Scholar] [CrossRef] [Green Version]
- Blairs, S.; Abbasi, M.H. Correlation between surface tension and critical temperatures of liquid metals. J. Colloid Interface Sci. 2006, 304, 549–553. [Google Scholar] [CrossRef]
- Keene, B. Review of data for the surface tension of pure metals. Int. Mater. Rev. 1993, 38, 157–192. [Google Scholar] [CrossRef]
- Haynes, W.; Lide, D.; Bruno, T. CRC Handbook of chemistry and Physics, 2009–2010. J. Am. Chem. Soc. 2009, 131, 12862. [Google Scholar]
- Pinhasi, G.; Ullmann, A.; Dayan, A. 1D plane numerical model for boiling liquid expanding vapor explosion (BLEVE). Int. J. Heat Mass Transf. 2007, 50, 4780–4795. [Google Scholar] [CrossRef]
- Gathers, G. Thermophysical properties of liquid copper and aluminum. Int. J. Thermophys. 1983, 4, 209–226. [Google Scholar] [CrossRef]
- Watson, K. Thermodynamics of the liquid state. Ind. Eng. Chem. 1943, 35, 398–406. [Google Scholar] [CrossRef]
- Velasco, S.; Román, F.; White, J.; Mulero, A. Prediction of the enthalpy of vaporization of metals and metalloids. Fluid Phase Equilib. 2006, 244, 11–15. [Google Scholar] [CrossRef]
- March, N.H. Liquid Metals: Concepts and Theory; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Vial, A.; Laroche, T. Comparison of gold and silver dispersion laws suitable for FDTD simulations. Appl. Phys. B 2008, 93, 139–143. [Google Scholar] [CrossRef]
- Quarteroni, A.; Valli, A. Numerical Approximation of Partial Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 23. [Google Scholar]
- Darwis, M.; Abdullah, K.; Mohammed, A.N. Comparative study of Roe, RHLL and Rusanov fluxes for shock-capturing schemes. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 243, p. 012007. [Google Scholar]
- Žemaitis, A.; Gaidys, M.; Brikas, M.; Gečys, P.; Račiukaitis, G.; Gedvilas, M. Advanced laser scanning for highly-efficient ablation and ultrafast surface structuring: Experiment and model. Sci. Rep. 2018, 8, 17376. [Google Scholar] [CrossRef]
- Starikov, S.V.; Pisarev, V.V. Atomistic simulation of laser-pulse surface modification: Predictions of models with various length and time scales. J. Appl. Phys. 2015, 117, 135901. [Google Scholar] [CrossRef] [Green Version]
- Ahmmed, K.T.; Ling, E.J.Y.; Servio, P.; Kietzig, A.M. Introducing a new optimization tool for femtosecond laser-induced surface texturing on titanium, stainless steel, aluminum and copper. Opt. Lasers Eng. 2015, 66, 258–268. [Google Scholar] [CrossRef]
- Sibold, D.; Urbassek, H. Kinetic study of pulsed desorption flows into vacuum. Phys. Rev. A 1991, 43, 6722. [Google Scholar] [CrossRef] [PubMed]
- Ranjbar, O.A.; Lin, Z.; Volkov, A.N. One-dimensional kinetic simulations of plume expansion induced by multi-pulse laser irradiation in the burst mode at 266 nm wavelength. Vacuum 2018, 157, 361–375. [Google Scholar] [CrossRef]
- Marine, W.; d’Aniello, J.S.; Gerri, M. Velocity measurement of the ablated particles during picosecond laser ablation. Mater. Sci. Eng. B 1992, 13, 57–62. [Google Scholar] [CrossRef]
- Wood, R.; Chen, K.R.; Leboeuf, J.; Puretzky, A.; Geohegan, D. Dynamics of plume propagation and splitting during pulsed-laser ablation. Phys. Rev. Lett. 1997, 79, 1571. [Google Scholar] [CrossRef] [Green Version]
- Fishburn, J.; Withford, M.; Coutts, D.; Piper, J. Study of the fluence dependent interplay between laser induced material removal mechanisms in metals: Vaporization, melt displacement and melt ejection. Appl. Surf. Sci. 2006, 252, 5182–5188. [Google Scholar] [CrossRef]
- Zemaitis, A.; Gaidys, M.; Gecys, P.; Gedvilas, M. Influence of nonlinear and saturable absorption on laser lift-off threshold of an oxide/metal structure. Opt. Lett. 2020, 45, 6166–6169. [Google Scholar] [CrossRef] [PubMed]




| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Melting point | 933 | ||
| Boiling Point (at ) | 2743 | ||
| Critical temperature | 6319 | ||
| Critical density | 634 | ||
| Latent heat of melting | |||
| Latent heat of vaporization |
| Parameter | Value |
|---|---|
| 0.109 | |
| 0.325 | |
| 0.51 | |
| 1.1 | |
| −0.17 | |
| 1.75 | |
| 0.08 |
| 1.0 | |||
|---|---|---|---|
| 5.2306 | 5.2704 | ||
| −0.51202 | 0.42503 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terragni, J.; Miotello, A. Laser Ablation of Aluminum Near the Critical Regime: A Computational Gas-Dynamical Model with Temperature-Dependent Physical Parameters. Micromachines 2021, 12, 300. https://doi.org/10.3390/mi12030300
Terragni J, Miotello A. Laser Ablation of Aluminum Near the Critical Regime: A Computational Gas-Dynamical Model with Temperature-Dependent Physical Parameters. Micromachines. 2021; 12(3):300. https://doi.org/10.3390/mi12030300
Chicago/Turabian StyleTerragni, Jacopo, and Antonio Miotello. 2021. "Laser Ablation of Aluminum Near the Critical Regime: A Computational Gas-Dynamical Model with Temperature-Dependent Physical Parameters" Micromachines 12, no. 3: 300. https://doi.org/10.3390/mi12030300
APA StyleTerragni, J., & Miotello, A. (2021). Laser Ablation of Aluminum Near the Critical Regime: A Computational Gas-Dynamical Model with Temperature-Dependent Physical Parameters. Micromachines, 12(3), 300. https://doi.org/10.3390/mi12030300







