Hydraulic Integrated Interconnected Regenerative Suspension: Modeling and Characteristics Analysis
Abstract
:1. Introduction
1.1. Interconnected Suspensions
1.2. Energy Harvesting Shock Absorbers
1.3. Energy Harvesting Hydraulic Interconnected Suspension
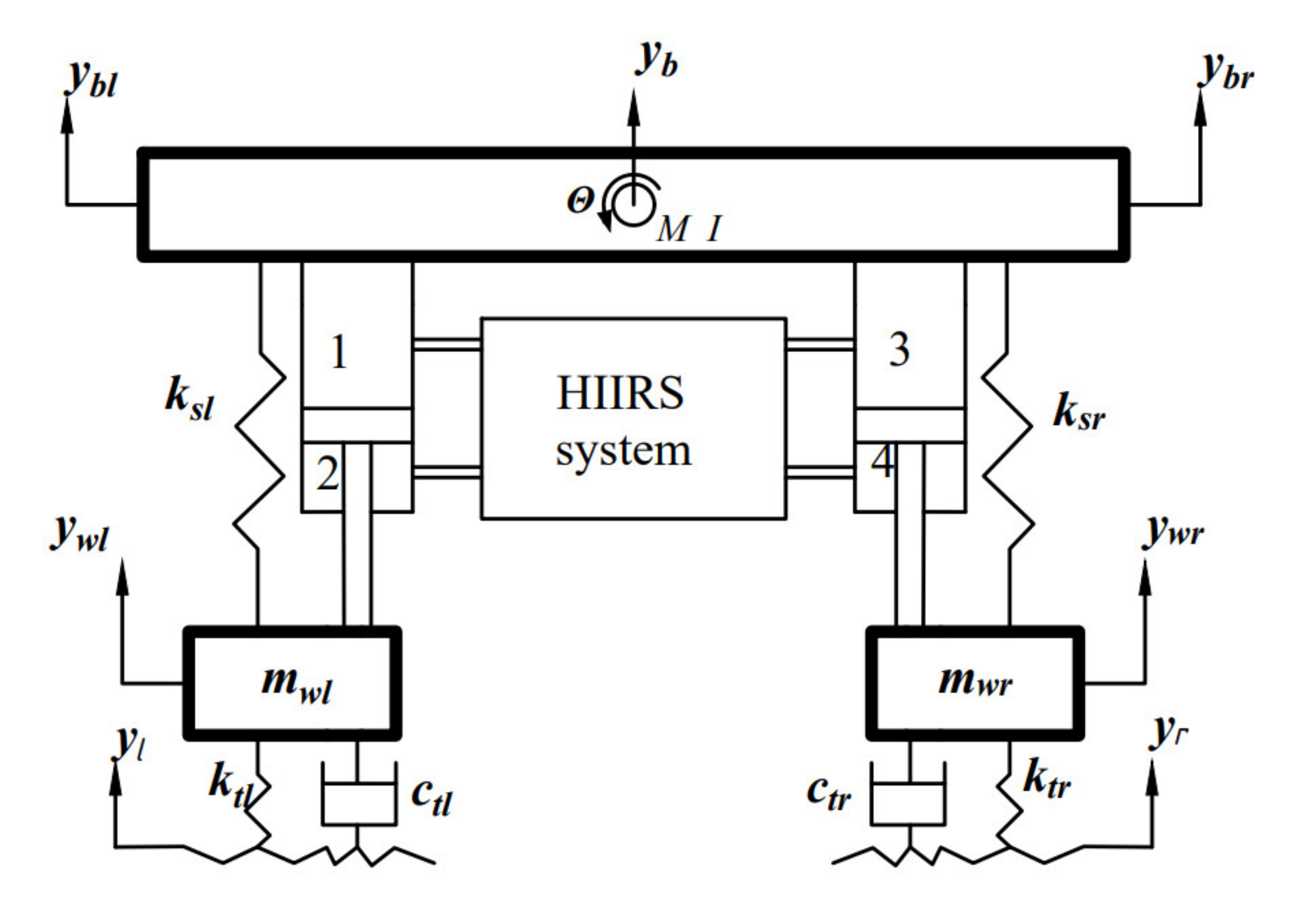
2. Modeling
2.1. Mechanical System
2.2. Mechanical–Fluid System Boundary Conditions
2.3. Fluid System
3. Vibration Analysis
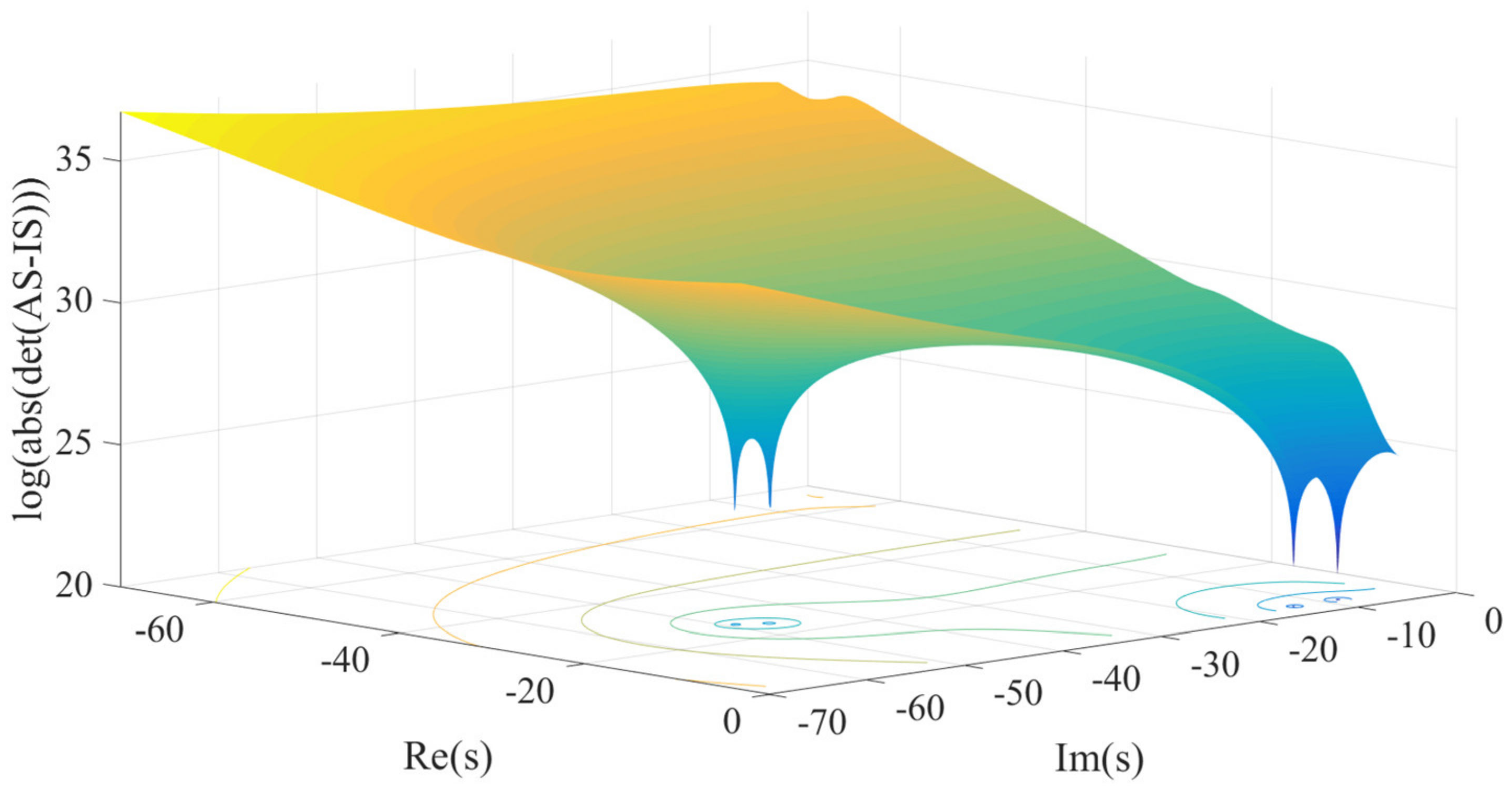
3.1. Free Vibration Analysis
3.2. Forced Vibration Analysis
3.2.1. Frequency Response Matrix
3.2.2. The Response to Random Road Excitation
4. Energy Harvesting Power of the HIIRS
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Yang, Z. Resonance Mechanism of Nonlinear Vibrational Multistable Energy Harvesters under Narrow-Band Stochastic Parametric Excitations. Complexity 2019, 2019, 1050143. [Google Scholar] [CrossRef]
- Tao, K.; Chen, Z.; Yi, H.; Zhang, R.; Shen, Q.; Wu, J.; Tang, L.; Fan, K.; Fu, Y.; Miao, J.; et al. Hierarchical Honeycomb-Structured Electret/Triboelectric Nanogenerator for Biomechanical and Morphing Wing Energy Harvesting. Nano Micro Lett. 2021, 13, 123. [Google Scholar] [CrossRef]
- Mikołaj, B.; Marcin, P. Multiaspect measurement analysis of breaking energy recovery. Energy Convers. Manag. 2016, 127, 35–42. [Google Scholar]
- Liu, X.; Deng, Y.; Li, Z.; Su, C. Performance analysis of a waste heat recovery thermoelectric generation system for automotive application. Energy Convers. Manag. 2016, 90, 121–127. [Google Scholar] [CrossRef]
- Jia, Y.; Li, S.; Shi, Y. An Analytical and Numerical Study of Magnetic Spring Suspension with Energy Recovery Capabilities. Energies 2018, 11, 3126. [Google Scholar] [CrossRef] [Green Version]
- Jolly, M.R.; Margolis, D.L. Regenerative Systems for Vibration Control. J. Vib. Acoust. 1997, 119, 208–215. [Google Scholar] [CrossRef]
- Makihara, K.; Onoda, J.; Tsuchihashi, M. Investigation of Performance in Suppressing Various Vibrations with Energy-Recycling Semi-Active Method. Acta Astronaut. 2006, 58, 506–514. [Google Scholar] [CrossRef]
- Zuo, L.; Zhang, P. Energy Harvesting, Ride Comfort, and Road Handling of Regenerative Vehicle Suspensions. J. Vib. Acoust. 2013, 135, 1060–1068. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, K.; Yu, F.; Gu, Y.; Li, D. Experimental verification of energy-regenerative feasibility for an automotive electrical suspension system. In Proceedings of the 2007 IEEE International Conference on Vehicular Electronics and Safety, Beijing, China, 13–15 December 2007; pp. 13–15. [Google Scholar]
- NHTS Administration. Traffic Safety Facts; National Highway Traffic Safety Administration: Washington, DC, USA, 2004. Available online: https://crashstats.nhtsa.dot.gov/Api/Public/ViewPublication/809919 (accessed on 10 May 2021).
- NHTSA Administration. Traffic Safety Facts 2014: A Compilation of Motor Vehicle Crash Data from the Fatality Analysis Reporting System and the General Estimates System; National Highway Traffic Safety Administration: Washington, DC, USA, 2014.
- Smith, W.A.; Zhang, N.; Hu, W. Hydraulically interconnected vehicle suspension: Handling performance. Veh. Syst. Dyn. 2011, 49, 87–106. [Google Scholar] [CrossRef]
- Moulton, A.; Best, A. Hydragas® Suspension. In 1979 Automotive Engineering Congress and Exposition; Paper Series 1979-01-790374; SAE: Detroit, MI, USA, 1979. [Google Scholar]
- Wang, L.; Zhang, N.; Du, H. Experimental Investigation of a Hydraulically Interconnected Suspension in Vehicle Dynamics and Stability Control. SAE Int. J. Passeng. Cars Mech. Syst. 2012, 5, 759–768. [Google Scholar] [CrossRef]
- Ding, F.; Han, X.; Luo, Z.; Zhang, N. Modelling and characteristic analysis of triaxle trucks with hydraulically interconnected suspensions. Veh. Syst. Dyn. 2012, 50, 1877–1904. [Google Scholar] [CrossRef]
- Cao, D.; Rakheja, S.; Su, C. Property Analysis of an X-Coupled Suspension for Sport Utility Vehicles. SAE Int. J. Passeng. Cars Mech. Syst. 2008, 1, 853–862. [Google Scholar] [CrossRef]
- Zhang, N.; Smith, W.A.; Jeyakumaran, J. Hydraulically interconnected vehicle suspension: Background and modelling. Veh. Syst. Dyn. 2010, 48, 17–40. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, B.; Chen, Y.; Zhang, N.; Zhang, J. Frequency-Based Modeling of a Vehicle Fitted with Roll-Plane Hydraulically Interconnected Suspension for Ride Comfort and Experimental Validation. IEEE Access 2020, 8, 1091–1104. [Google Scholar] [CrossRef]
- Wang, L.; Jian, S.; Qi, H.; Zhang, N. Lateral stability study of a vehicle fitted with hydraulically interconnected suspension in slalom maneuver. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 1702–1707. [Google Scholar]
- Zhang, D.; Li, H.; Dong, P.; Li, J.; Zhao, S. Study on a new damper for hydraulically interconnected suspension and its response characterization. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems, Guiyang, China, 19–22 June 2018; pp. 394–398. [Google Scholar]
- Wang, R.; Ye, Q.; Sun, Z.; Zhou, W.; Cao, Y.; Chen, L. A study of the hydraulically interconnected inerter-spring-damper suspension system. Mech. Based Des. Struct. Mach. 2017, 45, 415–429. [Google Scholar] [CrossRef]
- Cao, D.; Subhash, R.; Su, Y. Roll- and pitch-plane-coupled hydro-pneumatic suspension. Part 2: Dynamic response analyses. Veh. Syst. Dyn. 2010, 48, 507–528. [Google Scholar] [CrossRef] [Green Version]
- Wendel, G.R.; Stecklein, G.L. A regenerative active suspension system. In International Congress & Exposition; Paper Series 1991-01-910659; SAE: Detroit, MI, USA, 1991. [Google Scholar]
- Liang, X.C.; Zhao, J.S. Research on Recycling Vibration Energy of Shock Absorber. Int. J. Veh. Des. 2015, 68, 201–220. [Google Scholar] [CrossRef]
- Abdelkareem, M.; Xu, L.; Mohamed, K.A.A.; Elagouz, A.; Mi, J.; Guo, S.; Liu, Y.; Zuo, L. Vibration Energy Harvesting in Automotive Suspension System: A Detailed Review. Appl. Energy 2018, 229, 672–699. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, T.; Zhang, B.; Shi, J. Energy Harvesting from Vehicle Suspension System by Piezoelectric Harvester. Math. Probl. Eng. 2019, 2019, 1086983. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhang, T.; Zhang, Z.; Yuan, Y.; Liu, Y. A High-Efficiency Regenerative Shock Absorber Considering Twin Ball Screws Transmissions for Application in Range-Extended Electric Vehicles. Energy Built Environ. 2020, 1, 36–49. [Google Scholar] [CrossRef]
- Li, Z.; Zuo, L.; Luhrs, G.; Lin, L.; Qin, Y. Electromagnetic Energy-Harvesting Shock Absorbers: Design, Modeling, and Road Tests. IEEE Trans. Veh. Technol. 2013, 62, 1065–1074. [Google Scholar] [CrossRef]
- Lv, X.; Ji, Y.; Zhao, H.; Zhang, J.; Zhang, G.; Zhang, L. Research Review of a Vehicle Energy-Regenerative Suspension System. Energies 2020, 13, 441. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Xu, G. Modeling and Analysis of a Hydraulic Energy Regeneration Shock Absorber. Math. Probl. Eng. 2020, 2020, 1580297. [Google Scholar]
- Samn, A.; Abdelhaleem, A.; Kabeel, A.; Gad, E. Ride Comfort, Road Holding, and Energy Harvesting of a Hydraulic Regenerative Vehicle Suspension. SAE Int. J. Passeng. Cars Mech. Syst. 2020, 13, 159–171. [Google Scholar] [CrossRef]
- Fang, Z.; Guo, X.; Xu, L. An optimal algorithm for energy recovery of hydraulic electromagnetic energy-regenerative shock absorber. Appl. Math. Inf. Sci. 2013, 7, 2207–2214. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Xu, L.; Liu, Y.; Guo, X.; Zuo, L. Modeling and Experiments of a Hydraulic Electromagnetic Energy Harvesting Shock Absorber. IEEE Trans. Mechatron. 2017, 22, 2684–2694. [Google Scholar] [CrossRef]
- Zhou, Q.; Guo, S.; Xu, L.; Guo, X.; Yan, F.; Williams, H.; Xu, H. Global Optimization of the Hydraulic-electromagnetic Energy-harvesting Shock Absorber for Road Vehicles with Human-knowledge-integrated Particle Swarm Optimization Scheme. IEEE Trans. Mechatron. 2021, 2, 1580297. [Google Scholar]
- Peng, M.; Guo, X.; Zou, J.; Zhang, C. Simulation Study on Vehicle Road Performance with Hydraulic Electromagnetic Energy-Regenerative Shock Absorber. In International Congress & Exposition; Paper Series 2016-01-1550; SAE: Detroit, MI, USA, 2016. [Google Scholar]
- Chen, Y.; Qin, B.; Guo, S.; Yu, L.; Zuo, L. Asymmetric Energy Harvesting and Hydraulically Interconnected Suspension: Modeling and Validations. In Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019; Volume 3, p. V003T01A009. [Google Scholar]
- Guo, S.; Chen, Z.; Guo, X.; Zhou, Q. Vehicle Interconnected Suspension System based on Hydraulic Electromagnetic Energy Harvest: Design, Modeling and Simulation Tests. In SAE 2014 Commercial Vehicle Engineering Congress; Paper Series 2014-01-2299; SAE: Rosemont, IL, USA, 2014. [Google Scholar]
- Zou, J.; Guo, X.; Abdelkareem, M.A.A.; Xu, L.; Zhang, J. Modelling and ride analysis of a hydraulic interconnected suspension based on the hydraulic energy regenerative shock absorbers. Mech. Syst. Signal Process. 2019, 127, 345–369. [Google Scholar] [CrossRef]
- Watton, J.; Holford, K.M.; Surawattanawan, P. Electrohydraulic effects on the modelling of a vehicle active suspension. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2001, 215, 1077–1092. [Google Scholar] [CrossRef] [Green Version]
- Goodson, R.; Leonard, R. A survey of modelling techniques for fluid line transients. ASME J. Basic Eng. 1972, 94, 474–482. [Google Scholar] [CrossRef]
- Stecki, J.; Davis, D. Fluid transmission lines—Distributed parameter models part 2: Comparison of models. Proc. Inst. Mech. Eng. Part A Power Process Eng. 1986, 200, 229–236. [Google Scholar] [CrossRef]
- Stecki, J.; Davis, D. Fluid transmission lines—Distributed parameter models part 1: A review of the state of the art. Proc. Inst. Mech. Eng. Part A Power Process Eng. 1986, 200, 215–228. [Google Scholar] [CrossRef]
- Yu, B.; Wang, Z.; Wang, G.; Zhao, J.; Zhou, L.; Zhao, J. Investigation of the suspension design and ride comfort of an electric mini off-road vehicle. Adv. Mech. Eng. 2019, 11, 1–10. [Google Scholar] [CrossRef] [Green Version]






| Symbol | Values | Units | Description |
|---|---|---|---|
| M | 1400 | kg | Sprung mass |
| I | 625 | Sprung mass moment of inertia about roll axis | |
| 60 | kg | Unsprung mass | |
| 0.9 | m | Distance from gravity center to suspension strut | |
| 30 | Mechanical suspension spring stiffness | ||
| 300 | Tire spring stiffness | ||
| 870 | Density | ||
| 0.05 | Viscosity | ||
| 1400 | MPa | Bulk modulus | |
| l | 1 | m | Length of pipe |
| m | Pipeline diameter | ||
| Pre-charge gas volume of ha | |||
| 0.8 | MPa | Pre-charge pressure of ha | |
| Pre-charge gas volume of la | |||
| 0.1 | MPa | Pre-charge pressure of la | |
| ) | Upper and lower piston areas (i = 1, 3; j = 2, 4) | ||
| 0.15 | m | Stroke length | |
| Linear loss coefficient for check valve | |||
| Linear loss coefficient for accumulator valves | |||
| 10 | cc/rev | Hydraulic motor displacement | |
| 0.0005 | Motor-generator rotational inertia | ||
| 0.25 | Torque constant | ||
| 0.25 | Speed constant | ||
| 10 | Load Resistance | ||
| 0.6 | Motor internal resistance |
| Eigenvalues | First | Second | Third | Fourth |
|---|---|---|---|---|
| Real part | −3.7850 | −3.6440 | −24.4428 | −25.7550 |
| Imaginary part | −8.5587 | −13.1938 | −46.8497 | −49.1905 |
| Mode | Bounce | Roll | Wheel Hop 1 (Synchronous) | Wheel Hop 2 (Oppositional) |
|---|---|---|---|---|
| Frequency (Hz) and damping ratio | 0.40 | 0.27 | 0.46 | 0.46 |
| State variable (s) | ||||
| ) | 0.23i | 0.29 + 0.18i | 1 | 1 |
| ) | 0.23i | 0.18i | 1 | −1 |
| ) | 1 | 0 | −0.02 + 0.08i | 0 |
| Roll angle (θ) | 0 | 1 | 0 | 0.14i |
| Type of Pavement | The Value Range of c |
|---|---|
| Class A | |
| Class B | |
| Class C |
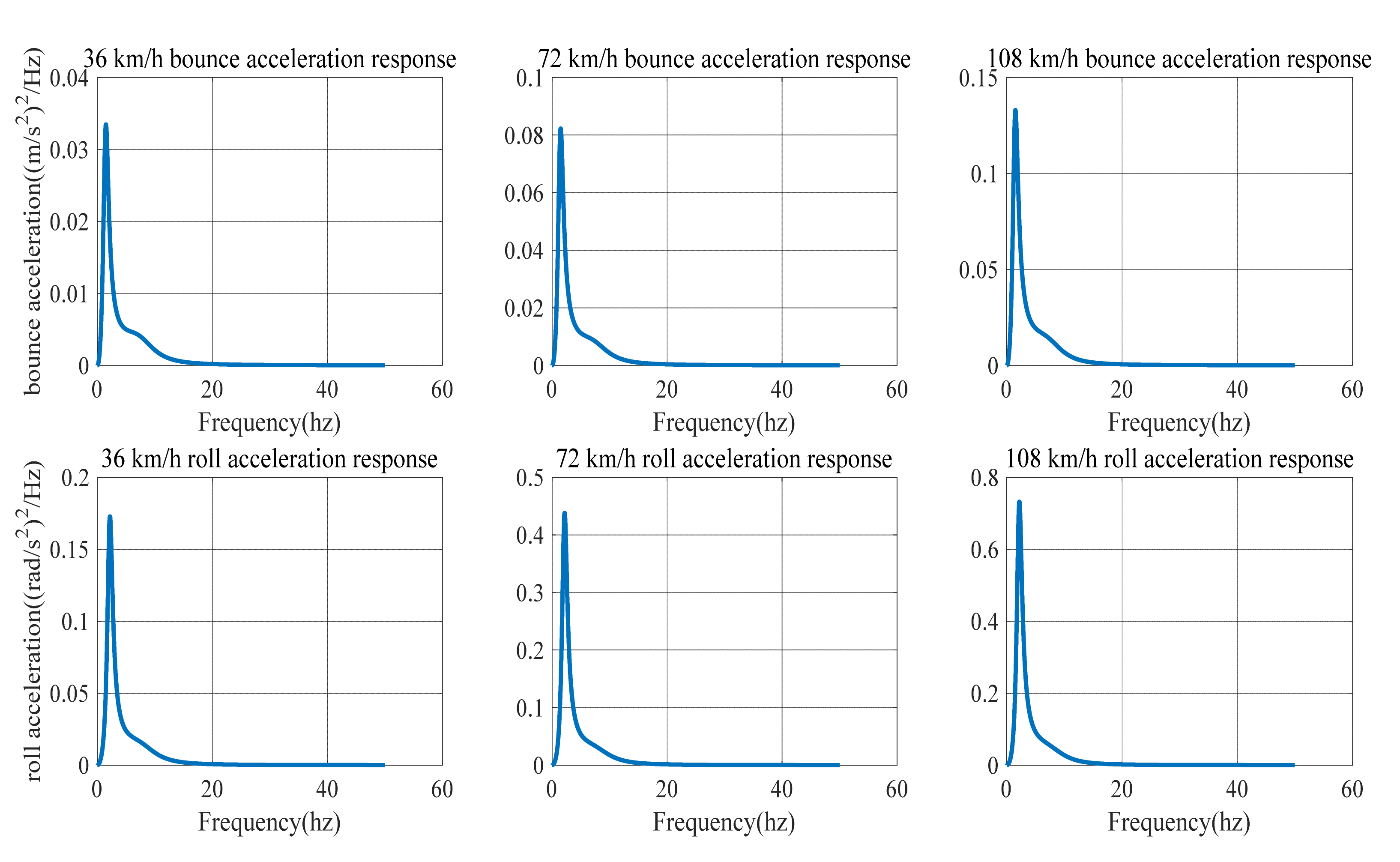
| Working Conditions | Class-B Road | Class-C Road | |||||
|---|---|---|---|---|---|---|---|
| 36 km/h | 72 km/h | 108 km/h | 36 km/h | 72 km/h | 108 km/h | ||
| Natural frequency | Bounce (Hz) | 1.48 | 1.50 | 1.51 | 1.48 | 1.50 | 1.51 |
| Roll (Hz) | 2.19 | 2.19 | 2.19 | 2.19 | 2.19 | 2.19 | |
| RMS of acceleration | 0.0049 | 0.0120 | 0.0196 | 0.0109 | 0.0480 | 0.0393 | |
| Roll () | 0.0246 | 0.0614 | 0.1029 | 0.0985 | 0.2457 | 0.2059 | |
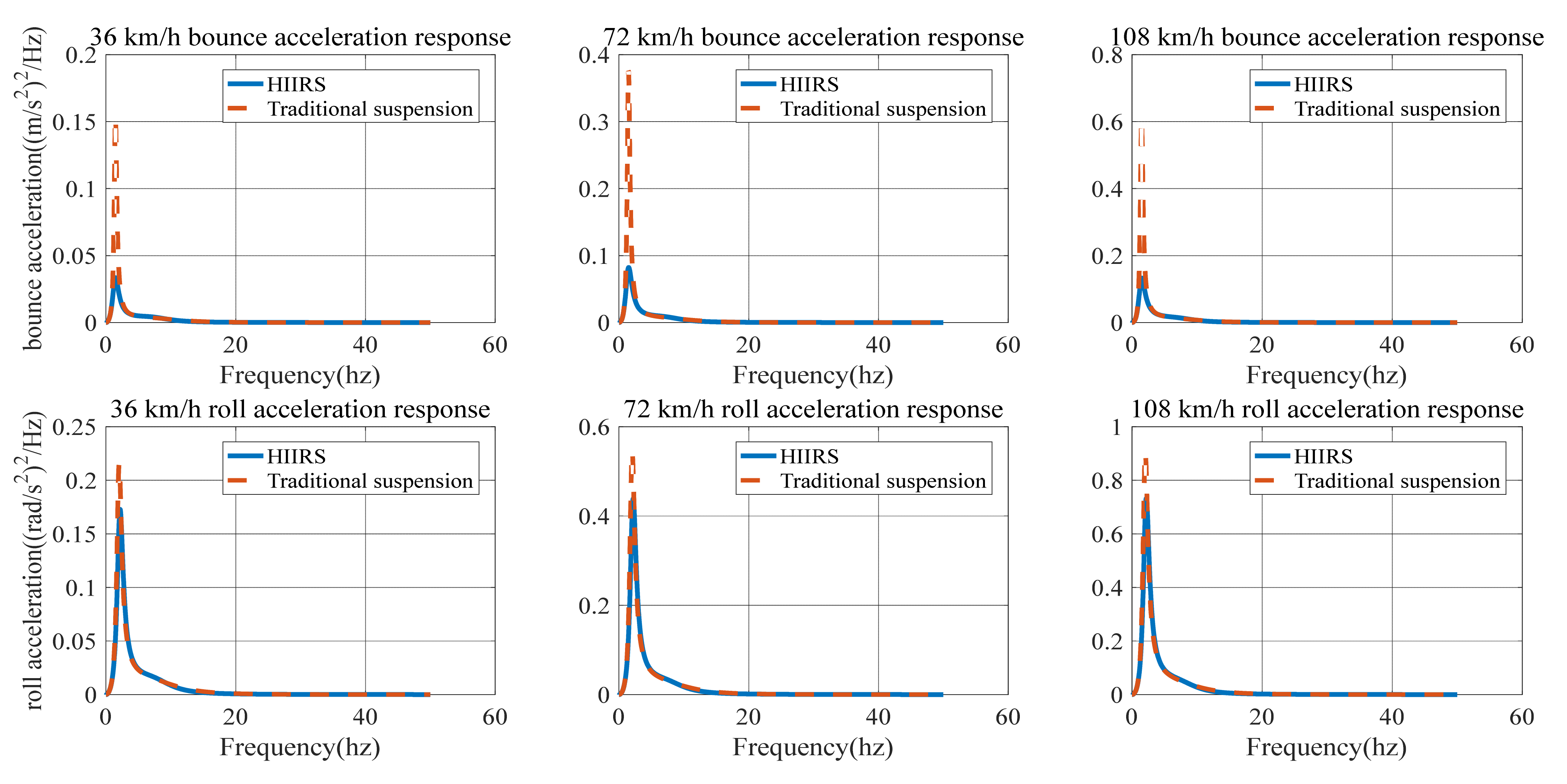
| Suspension and Speed | Natural Frequency of Bounce (Hz) | Natural Frequency of Roll (Hz) | |||
|---|---|---|---|---|---|
| HIIRS | 36 km/h | 1.48 | 2.19 | 0.0049 | 0.0246 |
| 72 km/h | 1.50 | 2.19 | 0.0120 | 0.0614 | |
| 108 km/h | 1.51 | 2.19 | 0.0196 | 0.1029 | |
| Traditional suspension | 36 km/h | 1.48 | 2.04 | 0.0139 | 0.0276 |
| 72 km/h | 1.48 | 2.04 | 0.0342 | 0.0690 | |
| 108 km/h | 1.48 | 2.04 | 0.0554 | 0.1150 | |
| Vehicle Speed | 36 km/h | 72 km/h | 108 km/h |
|---|---|---|---|
| Energy harvesting power (W) | 186.93 | 417.39 | 655.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Chen, L.; Wang, X.; Zou, J.; Hu, S. Hydraulic Integrated Interconnected Regenerative Suspension: Modeling and Characteristics Analysis. Micromachines 2021, 12, 733. https://doi.org/10.3390/mi12070733
Guo S, Chen L, Wang X, Zou J, Hu S. Hydraulic Integrated Interconnected Regenerative Suspension: Modeling and Characteristics Analysis. Micromachines. 2021; 12(7):733. https://doi.org/10.3390/mi12070733
Chicago/Turabian StyleGuo, Sijing, Liang Chen, Xikai Wang, Junyi Zou, and Sanbao Hu. 2021. "Hydraulic Integrated Interconnected Regenerative Suspension: Modeling and Characteristics Analysis" Micromachines 12, no. 7: 733. https://doi.org/10.3390/mi12070733
APA StyleGuo, S., Chen, L., Wang, X., Zou, J., & Hu, S. (2021). Hydraulic Integrated Interconnected Regenerative Suspension: Modeling and Characteristics Analysis. Micromachines, 12(7), 733. https://doi.org/10.3390/mi12070733







