Driving a Microswimmer with Wall-Induced Flow
Abstract
:1. Introduction
2. Model
3. Results
3.1. Controllability Analysis
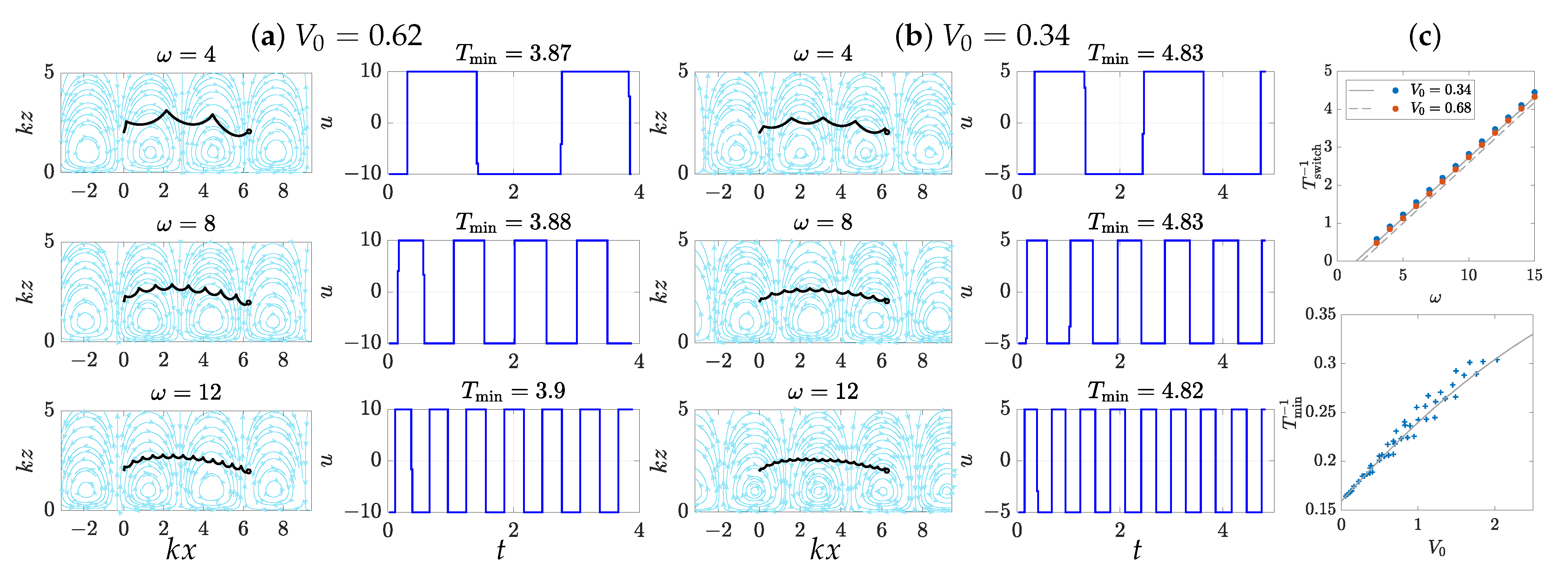
3.2. Optimal Control
- 1.
- A displacement parallel to the wall, from to at fixed distance : ;
- 2.
- A change of orientation, from to at fixed distance : ;
- 3.
- A change of distance to the wall, from to : .
3.3. Robust Driving Strategies
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Denissenko, P.; Kantsler, V.; Smith, D.J.; Kirkman-Brown, J. Human spermatozoa migration in microchannels reveals boundary-following navigation. Proc. Natl. Acad. Sci. USA 2012, 109, 8007–8010. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, H.C.; Powers, T.R.; Stocker, R. Bacterial rheotaxis. Proc. Natl. Acad. Sci. USA 2012, 109, 4780–4785. [Google Scholar] [CrossRef] [Green Version]
- Kantsler, V.; Dunkel, J.; Polin, M.; Goldstein, R.E. Ciliary contact interactions dominate surface scattering of swimming eukaryotes. Proc. Natl. Acad. Sci. USA 2013, 110, 1187–1192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Man, Y.; Ling, F.; Kanso, E. Cilia oscillations. Philos. Trans. R. Soc. B 2020, 375, 20190157. [Google Scholar] [CrossRef]
- Gilpin, W.; Prakash, V.N.; Prakash, M. Vortex arrays and ciliary tangles underlie the feeding–swimming trade-off in starfish larvae. Nat. Phys. 2017, 13, 380–386. [Google Scholar] [CrossRef]
- Darnton, N.; Turner, L.; Breuer, K.; Berg, H.C. Moving fluid with bacterial carpets. Biophys. J. 2004, 86, 1863–1870. [Google Scholar] [CrossRef] [Green Version]
- Winet, H.; Bernstein, G.S.; Head, J. Observations on the response of human spermatozoa to gravity, boundaries and fluid shear. Reproduction 1984, 70, 511–523. [Google Scholar] [CrossRef]
- Smith, D.; Gaffney, E.; Blake, J.; Kirkman-Brown, J. Human sperm accumulation near surfaces: A simulation study. J. Fluid Mech. 2009, 621, 289–320. [Google Scholar] [CrossRef] [Green Version]
- Berke, A.P.; Turner, L.; Berg, H.C.; Lauga, E. Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 2008, 101, 038102. [Google Scholar] [CrossRef] [Green Version]
- Aranda, V.; Cortez, R.; Fauci, L. A model of Stokesian peristalsis and vesicle transport in a three-dimensional closed cavity. J. Biomech. 2015, 48, 1631–1638. [Google Scholar] [CrossRef] [Green Version]
- Ishimoto, K.; Gaffney, E.A. Mechanical tuning of mammalian sperm behaviour by hyperactivation, rheology and substrate adhesion: A numerical exploration. J. R. Soc. Interface 2016, 13, 20160633. [Google Scholar] [CrossRef] [PubMed]
- Nosrati, R.; Driouchi, A.; Yip, C.M.; Sinton, D. Two-dimensional slither swimming of sperm within a micrometre of a surface. Nat. Commun. 2015, 6, 8703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miki, K.; Clapham, D.E. Rheotaxis Guides Mammalian Sperm. Curr. Biol. 2013, 23, 443–452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ishimoto, K.; Gaffney, E.A. Fluid flow and sperm guidance: A simulation study of hydrodynamic sperm rheotaxis. J. R. Soc. Interface 2015, 12, 20150172. [Google Scholar] [CrossRef] [Green Version]
- Ishimoto, K. Guidance of microswimmers by wall and flow: Thigmotaxis and rheotaxis of unsteady squirmers in two and three dimensions. Phys. Rev. E 2017, 96, 043103. [Google Scholar] [CrossRef]
- Meng, F.; Matsunaga, D.; Yeomans, J.M.; Golestanian, R. Magnetically-actuated artificial cilium: A simple theoretical model. Soft Matter 2019, 15, 3864–3871. [Google Scholar] [CrossRef] [Green Version]
- Massana-Cid, H.; Meng, F.; Matsunaga, D.; Golestanian, R.; Tierno, P. Tunable self-healing of magnetically propelling colloidal carpets. Nat. Commun. 2019, 10, 2444. [Google Scholar] [CrossRef]
- Matsunaga, D.; Hamilton, J.K.; Meng, F.; Bukin, N.; Martin, E.L.; Ogrin, F.Y.; Yeomans, J.M.; Golestanian, R. Controlling collective rotational patterns of magnetic rotors. Nat. Commun. 2019, 10, 4696. [Google Scholar] [CrossRef]
- Gu, H.; Boehler, Q.; Cui, H.; Secchi, E.; Savorana, G.; De Marco, C.; Gervasoni, S.; Peyron, Q.; Huang, T.Y.; Pane, S.; et al. Magnetic cilia carpets with programmable metachronal waves. Nat. Commun. 2020, 11, 2637. [Google Scholar] [CrossRef]
- Walker, B.J.; Ishimoto, K.; Wheeler, R.J.; Gaffney, E.A. Response of monoflagellate pullers to a shearing flow: A simulation study of microswimmer guidance. Phys. Rev. E 2018, 98, 063111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khalil, I.S.M.; Klingner, A.; Hamed, Y.; Hassan, Y.S.; Misra, S. Controlled Noncontact Manipulation of Nonmagnetic Untethered Microbeads Orbiting Two-Tailed Soft Microrobot. IEEE Trans. Robot. 2020, 6, 1–13. [Google Scholar] [CrossRef]
- Moreau, C.; Ishimoto, K.; Gaffney, E.A.; Walker, B.J. Control and controllability of microswimmers by a shearing flow. R. Soc. Open Sci. 2021, 8, 211141. [Google Scholar] [CrossRef] [PubMed]
- Shapere, A.; Wilczek, F. Efficiencies of self-propulsion at low Reynolds number. J. Fluid Mech. 1989, 198, 587–599. [Google Scholar] [CrossRef] [Green Version]
- Martín, J.; Takahashi, T.; Tucsnak, M. A control theoretic approach to the swimming of microscopic organisms. Q. Appl. Math. 2007, 65, 405–424. [Google Scholar] [CrossRef] [Green Version]
- Lohéac, J.; Scheid, J.F.; Tucsnak, M. Controllability and time optimal control for low Reynolds numbers swimmers. Acta Appl. Math. 2013, 123, 175–200. [Google Scholar] [CrossRef]
- Lohéac, J.; Munnier, A. Controllability of 3D low Reynolds number swimmers. ESAIM Control Optim. Calc. Var. 2014, 20, 236–268. [Google Scholar] [CrossRef]
- Chambrion, T.; Giraldi, L.; Munnier, A. Optimal strokes for driftless swimmers: A general geometric approach. ESAIM Control Optim. Calc. Var. 2019, 25, 6. [Google Scholar] [CrossRef] [Green Version]
- Alouges, F.; DeSimone, A.; Heltai, L.; Lefebvre-Lepot, A.; Merlet, B. Optimally swimming stokesian robots. Discret. Contin. Dyn. Syst. Ser. B 2013, 18, 1189–1215. [Google Scholar] [CrossRef] [Green Version]
- Tam, D.; Hosoi, A.E. Optimal stroke patterns for Purcell’s three-link swimmer. Phys. Rev. Lett. 2007, 98, 068105. [Google Scholar] [CrossRef] [Green Version]
- Alouges, F.; DeSimone, A.; Giraldi, L.; Zoppello, M. Self-propulsion of slender micro-swimmers by curvature control: N-link swimmers. Int. J. Non-Linear Mech. 2013, 56, 132–141. [Google Scholar] [CrossRef]
- Giraldi, L.; Martinon, P.; Zoppello, M. Controllability and optimal strokes for N-link microswimmer. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 3870–3875. [Google Scholar]
- Giraldi, L.; Pomet, J.B. Local controllability of the two-link magneto-elastic micro-swimmer. IEEE Trans. Autom. Control 2017, 62, 2512–2518. [Google Scholar] [CrossRef] [Green Version]
- Giraldi, L.; Lissy, P.; Moreau, C.; Pomet, J.B. Addendum to “Local Controllability of the Two-Link Magneto-Elastic Microswimmer”. IEEE Trans. Autom. Control 2018, 63, 2303–2305. [Google Scholar] [CrossRef] [Green Version]
- Moreau, C. Local controllability of a magnetized Purcell’s swimmer. IEEE Control Syst. Lett. 2019, 3, 637–642. [Google Scholar] [CrossRef]
- El Alaoui-Faris, Y.; Pomet, J.B.; Régnier, S.; Giraldi, L. Optimal actuation of flagellar magnetic microswimmers. Phys. Rev. E 2020, 101, 042604. [Google Scholar] [CrossRef] [Green Version]
- Papavassiliou, D.; Alexander, G.P. The many-body reciprocal theorem and swimmer hydrodynamics. EPL Europhys. Lett. 2015, 110, 44001. [Google Scholar] [CrossRef]
- Stone, H.A.; Samuel, A.D. Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 1996, 77, 4102. [Google Scholar] [CrossRef] [Green Version]
- Coron, J.M. Control and Nonlinearity; American Mathematical Society: Providence, RI, USA, 2007; Volume 136. [Google Scholar]
- Silverman, L.; Meadows, H. Controllability and time-variable unilateral networks. IEEE Trans. Circuit Theory 1965, 12, 308–314. [Google Scholar] [CrossRef]
- Chang, A. An algebraic characterization of controllability. IEEE Trans. Autom. Control 1965, 10, 112–113. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Lighthill, M. On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Math. 1952, 5, 109–118. [Google Scholar] [CrossRef]
- Blake, J.R. A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 1971, 46, 199–208. [Google Scholar] [CrossRef]
- Lauga, E. The Fluid Dynamics of Cell Motility; Cambridge University Press: Cambridge, UK, 2020; Volume 62. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreau, C.; Ishimoto, K. Driving a Microswimmer with Wall-Induced Flow. Micromachines 2021, 12, 1025. https://doi.org/10.3390/mi12091025
Moreau C, Ishimoto K. Driving a Microswimmer with Wall-Induced Flow. Micromachines. 2021; 12(9):1025. https://doi.org/10.3390/mi12091025
Chicago/Turabian StyleMoreau, Clément, and Kenta Ishimoto. 2021. "Driving a Microswimmer with Wall-Induced Flow" Micromachines 12, no. 9: 1025. https://doi.org/10.3390/mi12091025
APA StyleMoreau, C., & Ishimoto, K. (2021). Driving a Microswimmer with Wall-Induced Flow. Micromachines, 12(9), 1025. https://doi.org/10.3390/mi12091025





