A Miniaturized Quad-Stopband Frequency Selective Surface with Convoluted and Interdigitated Stripe Based on Equivalent Circuit Model Analysis
Abstract
:1. Introduction
2. Design of the FSS
2.1. Design Concept
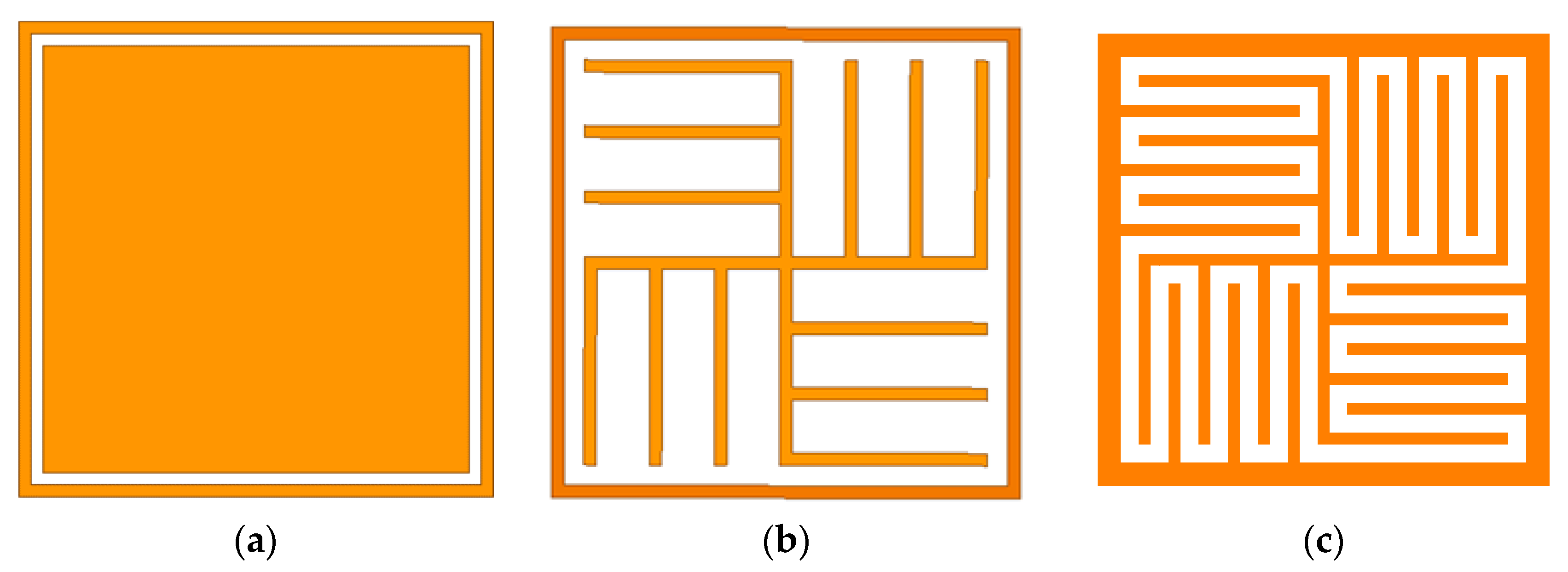
2.2. Design Evolution and Configuration
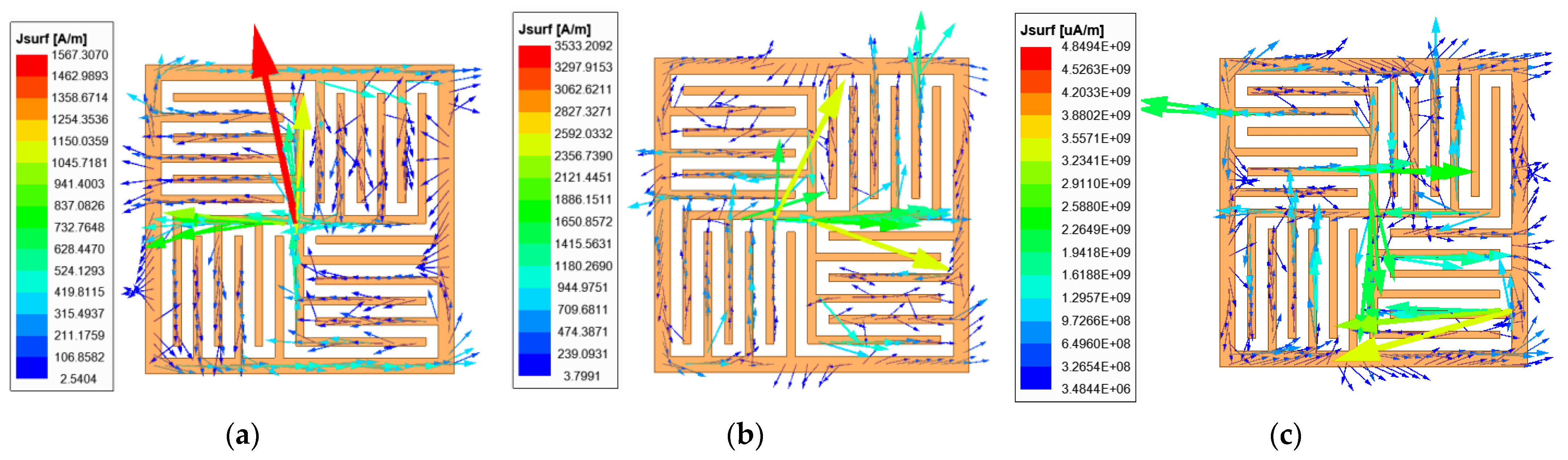
3. FSS Analysis
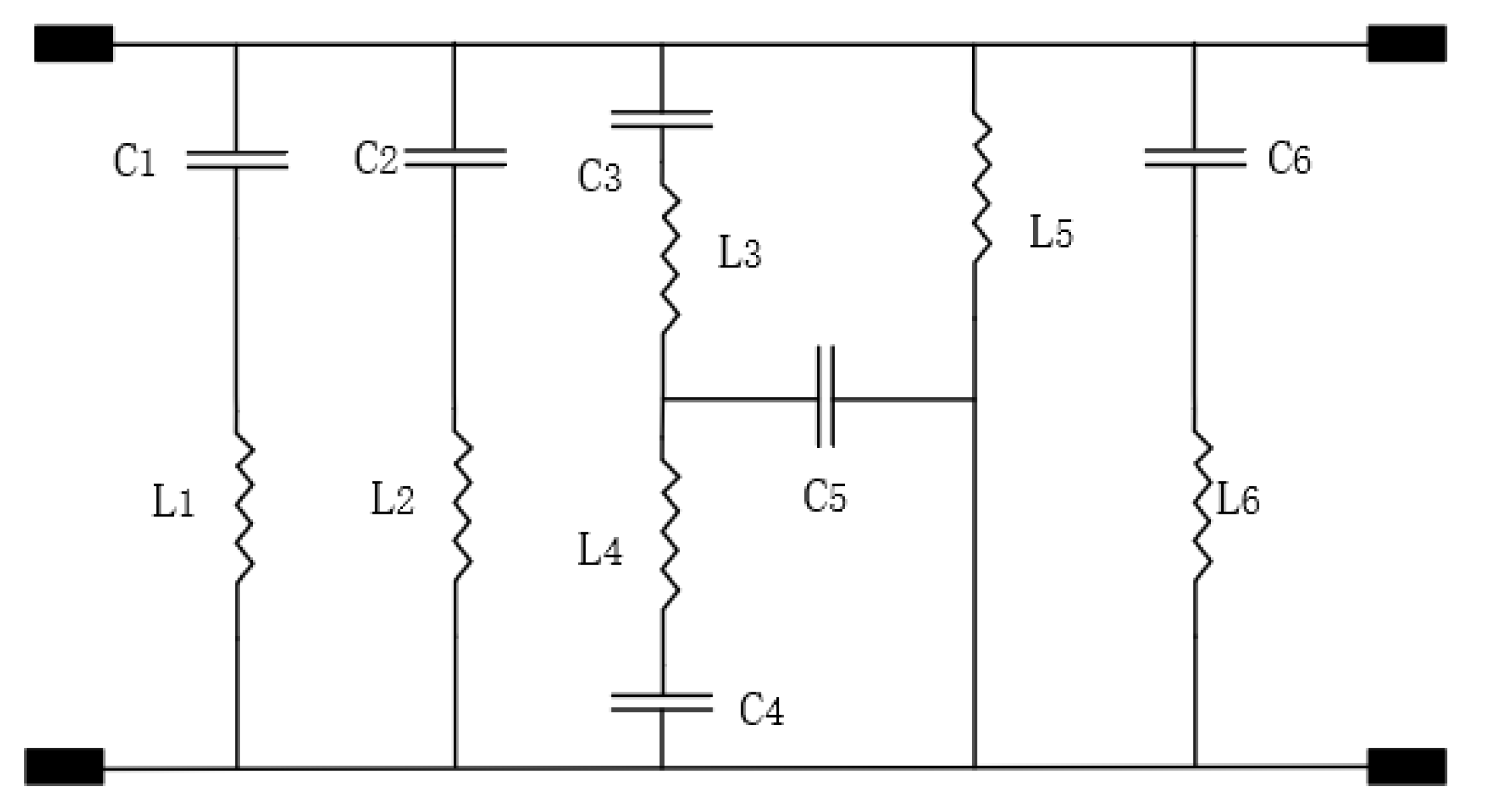
3.1. Equivalent Circuit Model Analysis
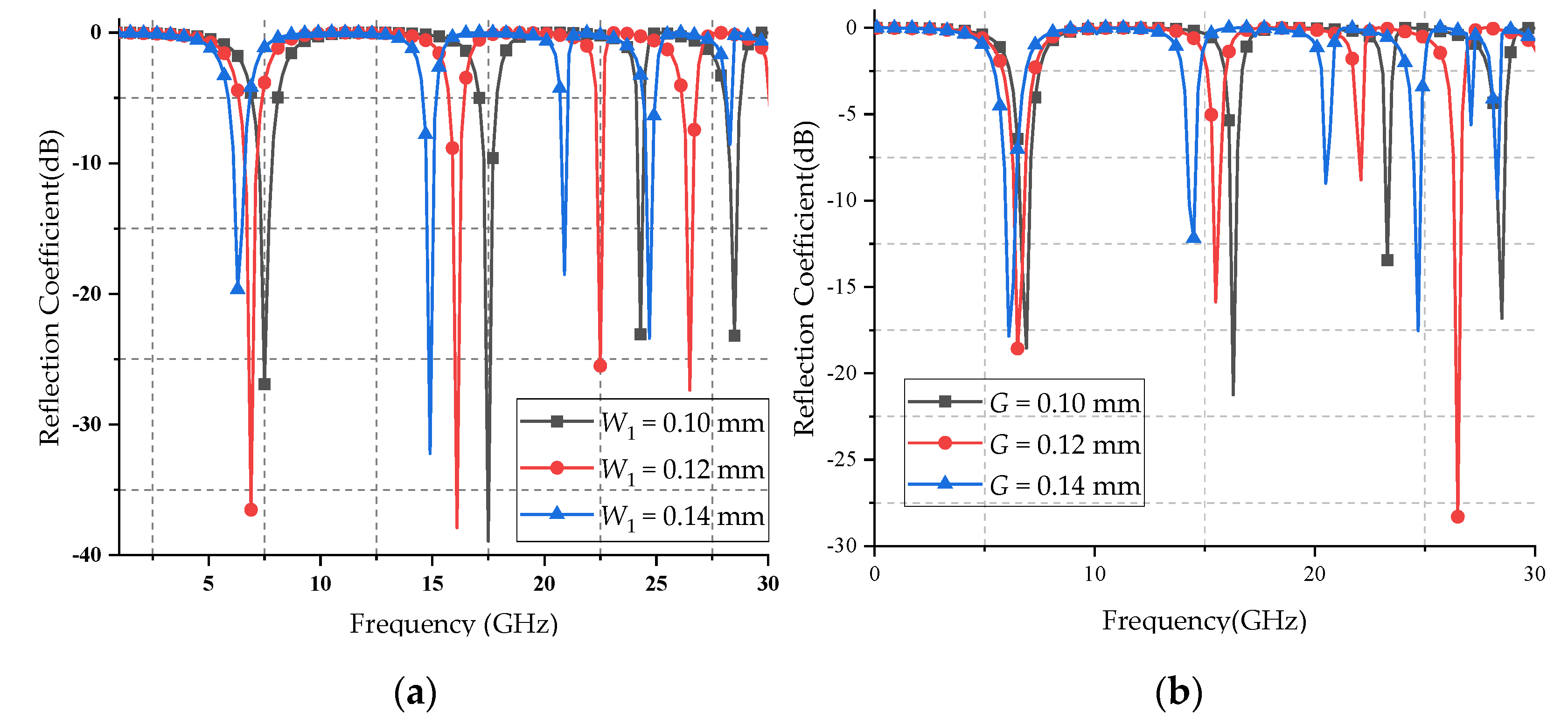
3.2. Parametric Variation
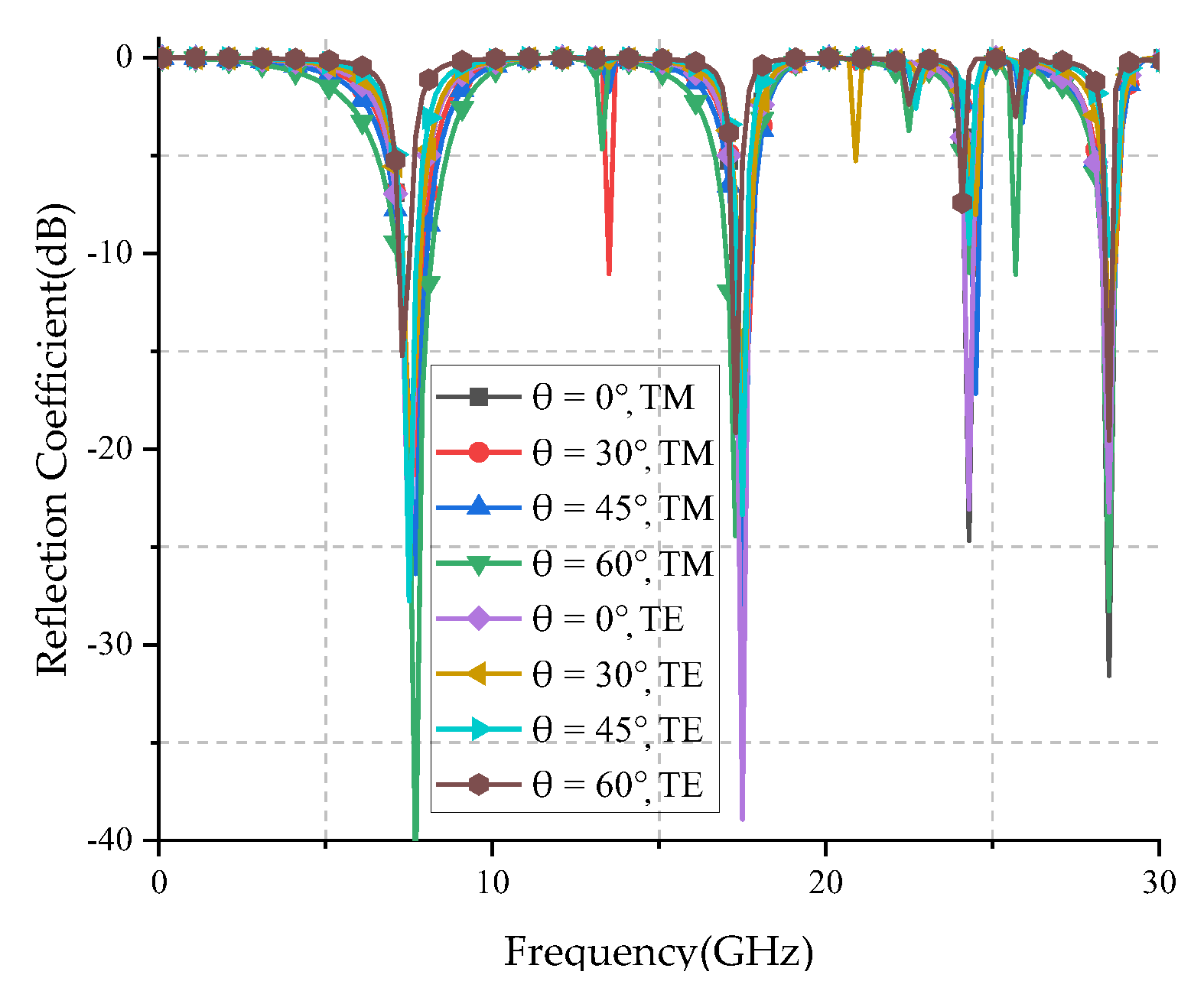
3.3. Polarization Stability
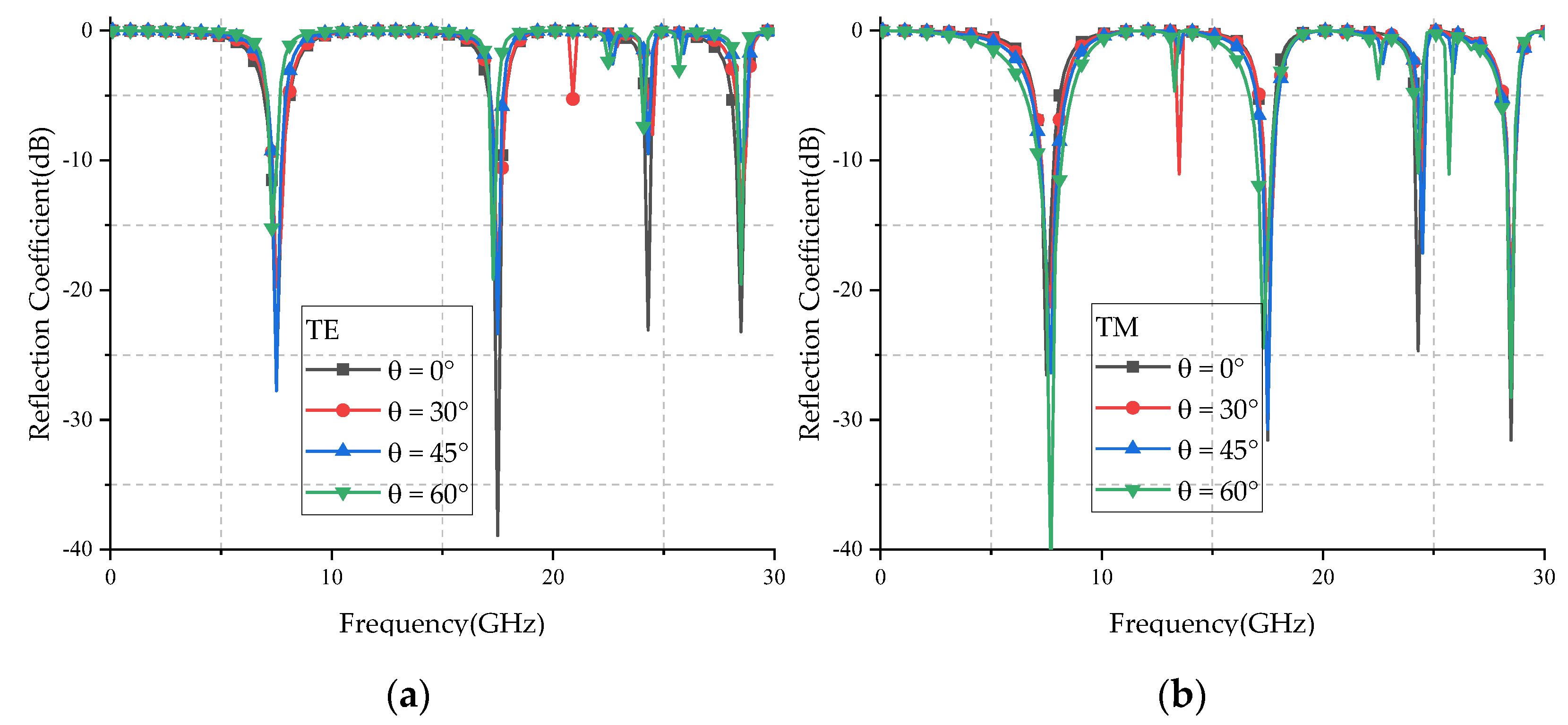
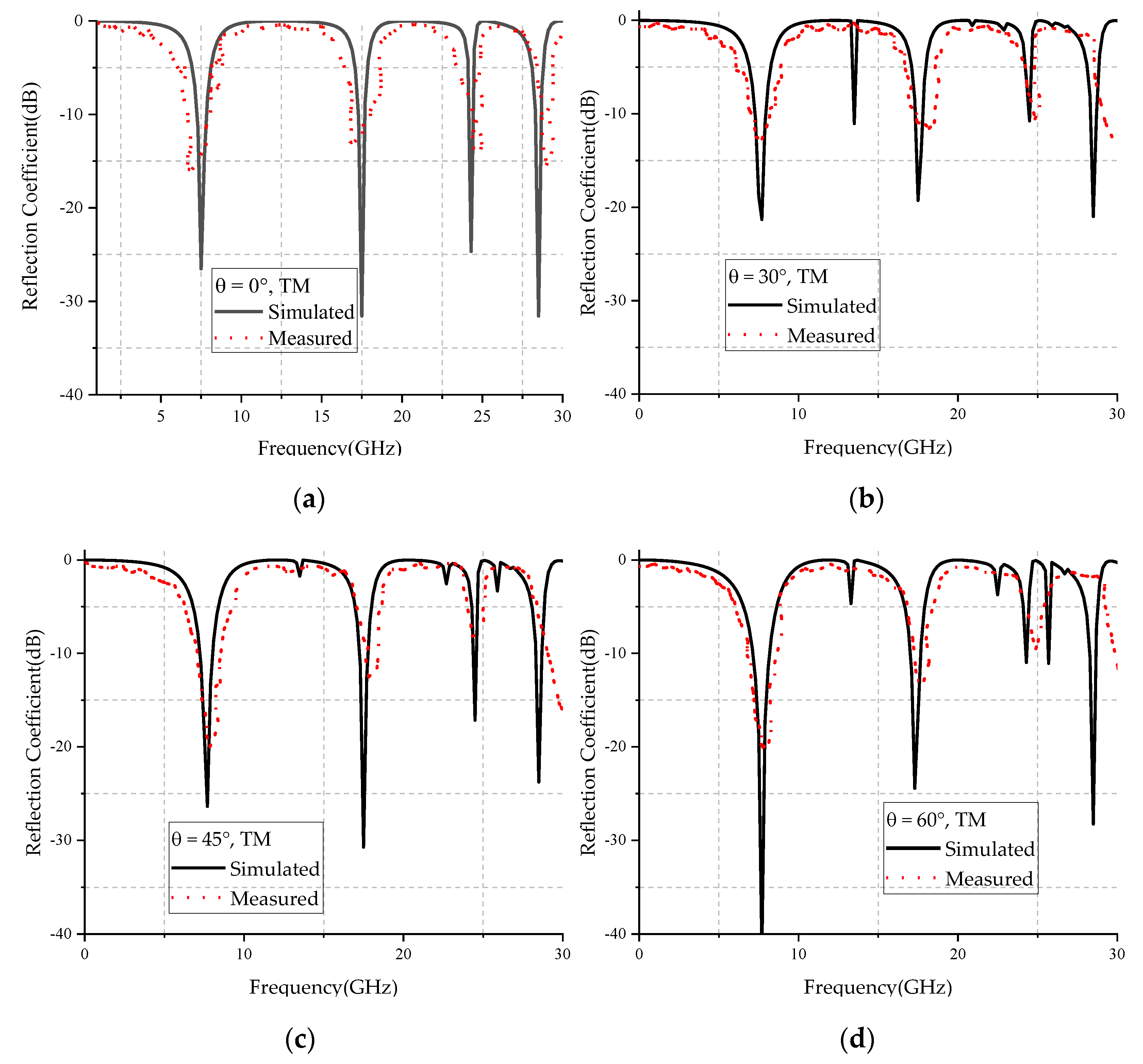
3.4. Angle Stability
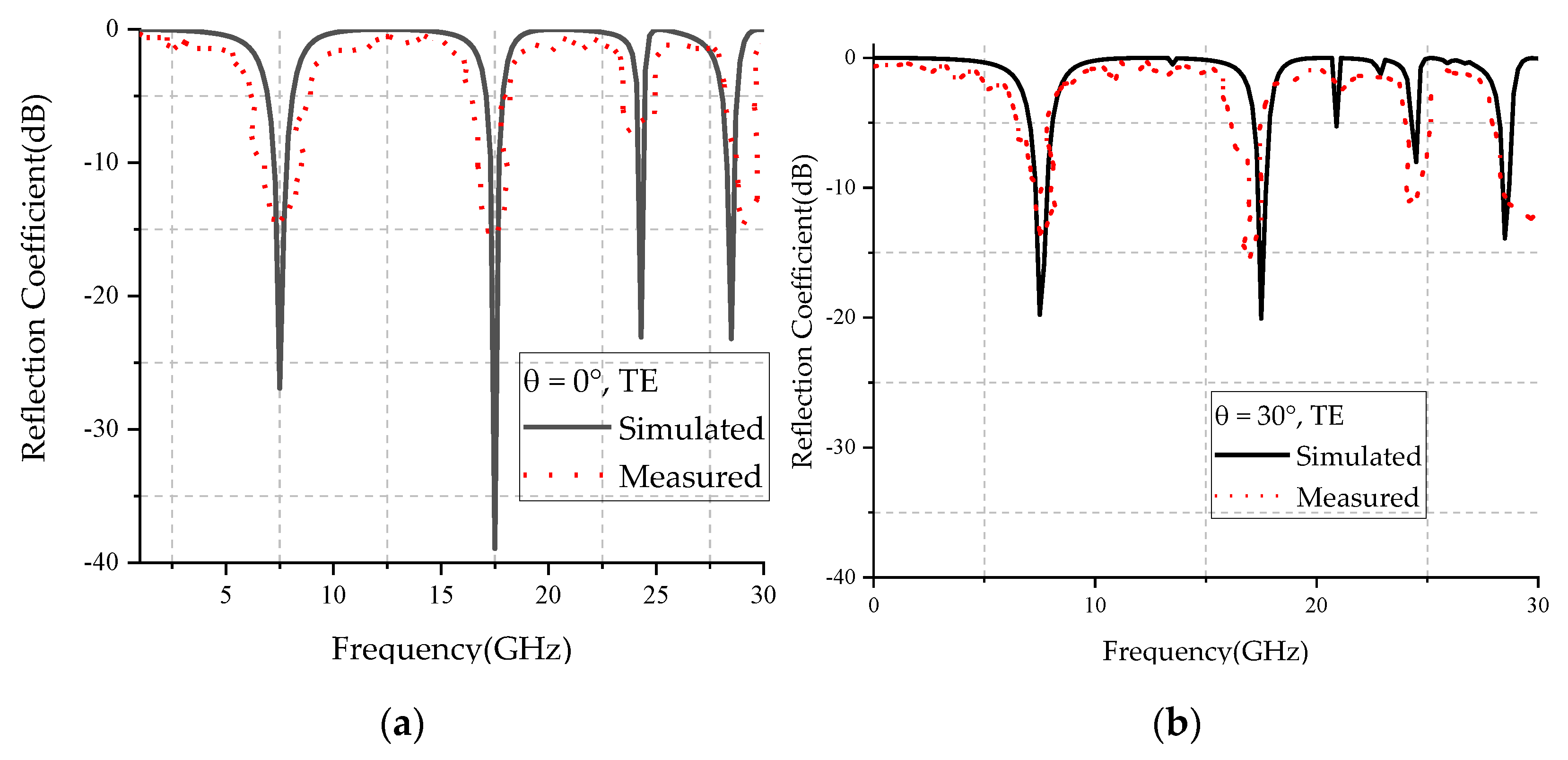
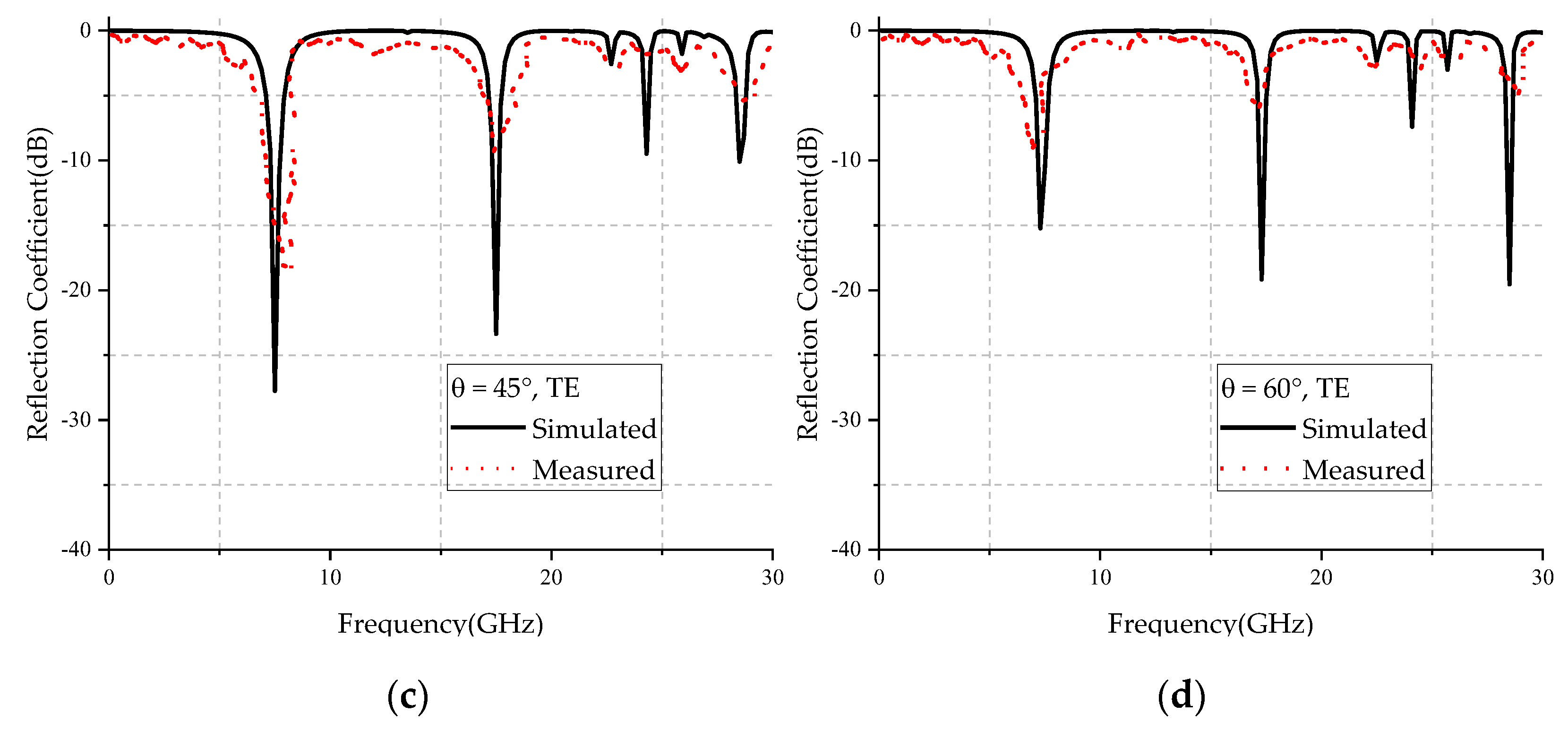
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Munk, B.A. Frequency Selective Surface: Theory and Design; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Farooq, U.; Shafique, M.F.; Mughal, M.J. Polarization insensitive dual band frequency selective surface for RF shielding through glass windows. IEEE Trans. Electromagn. Compat. 2020, 62, 93–100. [Google Scholar] [CrossRef]
- Yin, W.; Zhang, H.; Zhong, T.; Min, X. Ultra-miniaturized low-profile angularly-stable frequency selective surface design. IEEE Trans. Electromagn. Compat. 2019, 61, 1234–1238. [Google Scholar] [CrossRef]
- Li, D.; Li, T.; Li, E.; Zhang, Y. A 2.5-D angularly stable frequency selective surface using via-based structure for 5G EMI shielding. IEEE Trans. Electromagn. Compat. 2018, 60, 768–775. [Google Scholar] [CrossRef]
- Khan, J.; Nayan, N.; Kiani, G.I.; Hussaini, M.A. FSS Design for Improving Transmission of Microwave Signals and Wireless Security in Modern Buildings. J. Electron. Mater. 2021, 50, 1–9. [Google Scholar] [CrossRef]
- An, K.; Liang, T.; Zheng, G.; Yan, X.; Li, Y.; Chatzinotas, S. Performance Limits of Cognitive-Uplink FSS and Terrestrial FS for Ka-Band. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 2604–2611. [Google Scholar] [CrossRef]
- Sivasamy, R.; Moorthy, B.; Kanagasabai, M.; Samsingh, V.R.; Alsath, M.G.N. A Wideband Frequency Tunable FSS for Electromagnetic Shielding Applications. IEEE Trans. Electromagn. Compat. 2018, 60, 280–283. [Google Scholar] [CrossRef]
- Madhav, B.T.P.; Anilkumar, T. Design and study of multiband planar wheel-like fractal antenna for vehicular communication applications. Microw. Opt. Technol. Lett. 2018, 60, 1985–1993. [Google Scholar] [CrossRef]
- Aqlan, B.; Vettikalladi, H.; Alkanhal, M.A.S. Millimeter wave antenna with frequency selective surface (FSS) for 79 GHz automotive radar applications. Int. J. Microw. Wirel. Technol. 2017, 9, 281–290. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Pang, Y.; Feng, M.; Qu, S. Water-based metamaterial absorber for broadband electromagnetic wave absorption. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium (ACES), Firenze, Italy, 26–30 March 2017; pp. 1–2. [Google Scholar]
- Sheng, X.; Fan, J.; Liu, N.; Zhang, C.B. A Miniaturized Dual-Band FSS With Controllable Frequency Resonances. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 915–917. [Google Scholar] [CrossRef]
- Sampath, S.; Sivasamy, R. Design and fabrication of miniaturized tri-band frequency selective surface with polarization-independent and angularly stable response. Frequenz 2021. [Google Scholar] [CrossRef]
- Katoch, K.; Jaglan, N.; Gupta, S.D.; Sharawi, M.S. Design of a triple band notched polarization independent compact FSS at UWB frequency range. Int. J. RF Microw. Comput.-Aided Eng. 2021, 31, 22631. [Google Scholar] [CrossRef]
- Mantash, M.; Kesavan, A.; Denidni, T.A. Beam-Tilting Endfire Antenna Using a Single-Layer FSS for 5G Communication Networks. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 29–33. [Google Scholar] [CrossRef]
- Chaharmir, M.R.; Shaker, J. Design of a Multilayer X-/Ka-Band Frequency-Selective Surface-Backed Reflectarray for Satellite Applications. IEEE Trans. Antennas Propag. 2015, 63, 1255–1262. [Google Scholar] [CrossRef]
- Luo, K.; Duan, Y.T.; Xu, B.A.; Zhu, D.W.; Gao, X. Dual band single layered frequency selective surfaces. In Proceedings of the 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 3–5 October 2016; pp. 1192–1195. [Google Scholar]
- Gao, M.; Momeni Hasan Abadi, S.M.A.; Behdad, N. A Dual-Band, Inductively Coupled Miniaturized-Element Frequency Selective Surface with Higher Order Bandpass Response. IEEE Trans. Antennas Propag. 2016, 64, 3729–3734. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, L.; OuYang, J. Frequency selective surface with wide passband and stopband performance operating in L/S band. In Proceedings of the 2016 IEEE International Symposium on Antennas and Propagation (APSURSI), Fajardo, PR, USA, 26 June–1 July 2016; pp. 969–970. [Google Scholar]
- Biswas, A.N.; Ballav, S.; Parui, S.K.; Chatterjee, A. A Polarization Insensitive Frequency Selective Surface with Bandpass and Bandstop Response. In Proceedings of the 2018 IEEE Indian Conference on Antennas and Propogation (InCAP), Hyderabad, India, 16–19 December 2018; pp. 1–4. [Google Scholar]
- Suresh Kumar, T.R.; Vinoy, K.J. Tri-Band Band-Stop Frequency Selective Surface using Tortuous Jerusalem Cross with Angularly Stable Response. In Proceedings of the 2018 IEEE Indian Conference on Antennas and Propogation (InCAP), Hyderabad, India, 16–19 December 2018; pp. 1–4. [Google Scholar]
- Kartal, M.; Golezani, J.J.; Doken, B. A Triple Band Frequency Selective Surface Design for GSM Systems by Utilizing a Novel Synthetic Resonator. IEEE Trans. Antennas Propag. 2017, 65, 2724–2727. [Google Scholar] [CrossRef]
- Yan, M.; Wang, J.F.; Ma, H.; Feng, M.D.; Pang, Y.Q.; Qu, S.B.; Zhang, J.Q.; Zheng, L. A Tri-Band, Highly Selective, Bandpass FSS Using Cascaded Multilayer Loop Arrays. IEEE Trans. Antennas Propag. 2016, 64, 2046–2049. [Google Scholar] [CrossRef]
- Liu, N.; Sheng, X.; Zhang, C.; Fan, J.; Guo, D. A Miniaturized Triband Frequency Selective Surface Based on Convoluted Design. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2384–2387. [Google Scholar] [CrossRef]
- Xu, G.; Hum, S.V.; Eleftheriades, G.V. A Technique for Designing Multilayer Multistopband Frequency Selective Surfaces. IEEE Trans. Antennas Propag. 2018, 66, 780–789. [Google Scholar] [CrossRef]
- Garg, M.; Chahar, R.; Yadav, S.; Garg, S.; Noor, D. A novel polarization independent triple bandstop frequency selective surface for the mobile and wireless communication. In Proceedings of the 2017 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 5–6 May 2017; pp. 1518–1521. [Google Scholar]
- Li, Z.; Dong, J.; Mo, J. A Miniaturized Quad-Band Frequency Selective Surface. In Proceedings of the 2020 Cross Strait Radio Science & Wireless Technology Conference (CSRSWTC), Fuzhou, China, 13–16 December 2020; pp. 1–3. [Google Scholar]
- Garg, N.; Jain, S.; Yadav, A.; Sharma, M.D. Dual Band Frequency Selective Surface for WiMAX/WLAN Band Application. In Proceedings of the 2020 International Conference on Wireless Communications Signal Processing and Networking (WiSPNET), Chennai, India, 4–6 August 2020; pp. 173–176. [Google Scholar]
- Jangi Golezani, J.; Kartal, M.; Döken, B.; Paker, S. Triple-Band Frequency Selective Surface Design Effective Over Oblique Incidence Angles for GSM System. IETE J. Res. 2019, 1–5. [Google Scholar] [CrossRef]
- Liu, N.; Sheng, X.; Zhang, C.; Guo, D. Design of Frequency Selective Surface Structure with High Angular Stability for Radome Application. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 138–141. [Google Scholar] [CrossRef]
- Sheng, X.; Ge, J.; Han, K.; Zhu, X. Transmissive/Reflective Frequency Selective Surface for Satellite Applications. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1136–1140. [Google Scholar] [CrossRef]
- Mutluer, E.; Döken, B.; Kartal, M. A Dual-Band Frequency Selective Surface Design for Satellite Applications. In Proceedings of the 2018 18th Mediterranean Microwave Symposium (MMS), Istanbul, Turkey, 31 October–2 November 2018; pp. 43–46. [Google Scholar]
- Bashiri, M.; Ghobadi, C.; Nourinia, J.; Majidzadeh, M. WiMAX, WLAN, and X-Band Filtering Mechanism: Simple-Structured Triple-Band Frequency Selective Surface. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3245–3248. [Google Scholar] [CrossRef]
- Ghosh, S.; Srivastava, K.V. An angularly stable dual-band FSS with closely spaced resonances using miniaturized unit cell. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 218–220. [Google Scholar] [CrossRef]
- Ünaldı, S.; Cimen, S.; Çakır, G.; Ayten, U.E. A novel dual-band ultrathin FSS with closely settled frequency response. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1381–1384. [Google Scholar] [CrossRef]
- Xu, B.Z.; Jia, S.L.; Zheng, T. A Low Pass and Wide Angle Frequency Selective Surface with Miniaturized Elements. In Proceedings of the 2020 IEEE 3rd International Conference on Electronics Technology (ICET), Chengdu, China, 8–12 May 2020; pp. 720–723. [Google Scholar]






| Parameter | H | G | W1 | W2 | Dx | Dy |
|---|---|---|---|---|---|---|
| Value (mm) | 0.80 | 0.16 | 0.10 | 0.10 | 3.94 | 3.94 |
| Parameters (mm) | 3dB Bandwidth (GHz) | |||
|---|---|---|---|---|
| 1st Band | 2nd Band | 3rd Band | 4th Band | |
| W1 = 0.10 | 1.00–6.65 | 8.35–16.90 | 18.04–24.00 | 24.50–27.84 |
| W1 = 0.12 | 1.00–6.10 | 7.62–15.56 | 16.55–22.21 | 22.69–25.96 |
| W1 = 0.14 | 1.00–5.65 | 7.05–14.43 | 15.28–20.60 | 21.08–24.26 |
| G = 0.10 | 1.00–6.19 | 7.42–15.93 | 16.67–23.10 | 23.51–27.94 |
| G = 0.12 | 1.00–5.94 | 7.20–15.14 | 15.91–21.76 | 22.25–26.01 |
| G = 0.14 | 1.00–5.52 | 6.81–14.02 | 14.75–20.31 | 20.82–24.23 |
| Modes | TE (GHz) | TM (GHz) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Angle (deg.) | 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 | |||
| f1 | 7.5 | 7.5 | 7.5 | 7.3 | 7.5 | 7.7 | 7.7 | 7.7 | 2.60 | 0.89 | 2.67 |
| f2 | 17.5 | 17.5 | 17.5 | 17.3 | 17.5 | 17.5 | 17.5 | 17.3 | 0 | 0.38 | 0.38 |
| f3 | 24.3 | 24.5 | 24.3 | 24.1 | 24.3 | 24.5 | 24.3 | 24.3 | 0.21 | 0.55 | 0.27 |
| Ref. | Unit Cell Size (mm) | No. of Stopbands | No. of Metal Layers | No. of Substrate Layers | Operating Frequency Band | Angle Stability (deg.) |
|---|---|---|---|---|---|---|
| [11] | 6.6 × 6.6 × 1 | 2 | 1 | 1 | L, S, C, X | 60 |
| [17] | 1.9 × 1.9 × 4 | 2 | 5 | 4 | Ku, Ka | 45 |
| [21] | 50 × 50× 1 | 3 | 1 | 1 | GSM | 45 |
| [27] | 16 × 16 × 1.6 | 2 | 1 | 1 | WiMAX, WLAN | 60 |
| [28] | 46 × 46 × 1 | 3 | 1 | 1 | GSM | 45 |
| [29] | 6 × 6× 11.5 | 1 | 2 | 5 | Ku | 60 |
| [30] | 5 × 5× 0.508 | 3 | 1 | 1 | X, Ku, Ka | 80/80/60 |
| [31] | 4 × 4× 1 | 2 | 1 | 1 | Ku, Ka | 60 |
| [32] | 10 × 10 × 1.6 | 3 | 2 | 2 | WiMAX, WLAN, X | 50 |
| [33] | 8.4 × 8.4 × 0.8 | 2 | 1 | 1 | L, S | 60 |
| [34] | 8.8 × 8.8 × 0.762 | 2 | 1 | 1 | X | 60 |
| [35] | 4.0 × 4.0 × 8.78 | 1 | 4 | 9 | L, S, C, X, Ku | 30 |
| Proposed | 3.94 × 3.94 × 1.6 | 4 | 1 | 2 | L, S, C, X, Ku, K, Ka | 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Ma, Y.; Li, Z.; Mo, J. A Miniaturized Quad-Stopband Frequency Selective Surface with Convoluted and Interdigitated Stripe Based on Equivalent Circuit Model Analysis. Micromachines 2021, 12, 1027. https://doi.org/10.3390/mi12091027
Dong J, Ma Y, Li Z, Mo J. A Miniaturized Quad-Stopband Frequency Selective Surface with Convoluted and Interdigitated Stripe Based on Equivalent Circuit Model Analysis. Micromachines. 2021; 12(9):1027. https://doi.org/10.3390/mi12091027
Chicago/Turabian StyleDong, Jian, Yan Ma, Zhuangzhuang Li, and Jinjun Mo. 2021. "A Miniaturized Quad-Stopband Frequency Selective Surface with Convoluted and Interdigitated Stripe Based on Equivalent Circuit Model Analysis" Micromachines 12, no. 9: 1027. https://doi.org/10.3390/mi12091027
APA StyleDong, J., Ma, Y., Li, Z., & Mo, J. (2021). A Miniaturized Quad-Stopband Frequency Selective Surface with Convoluted and Interdigitated Stripe Based on Equivalent Circuit Model Analysis. Micromachines, 12(9), 1027. https://doi.org/10.3390/mi12091027







