Time-Domain Dynamic Characteristics Analysis and Experimental Research of Tri-Stable Piezoelectric Energy Harvester
Abstract
:1. Introduction
2. Structure and Theoretical Model of a TPEH
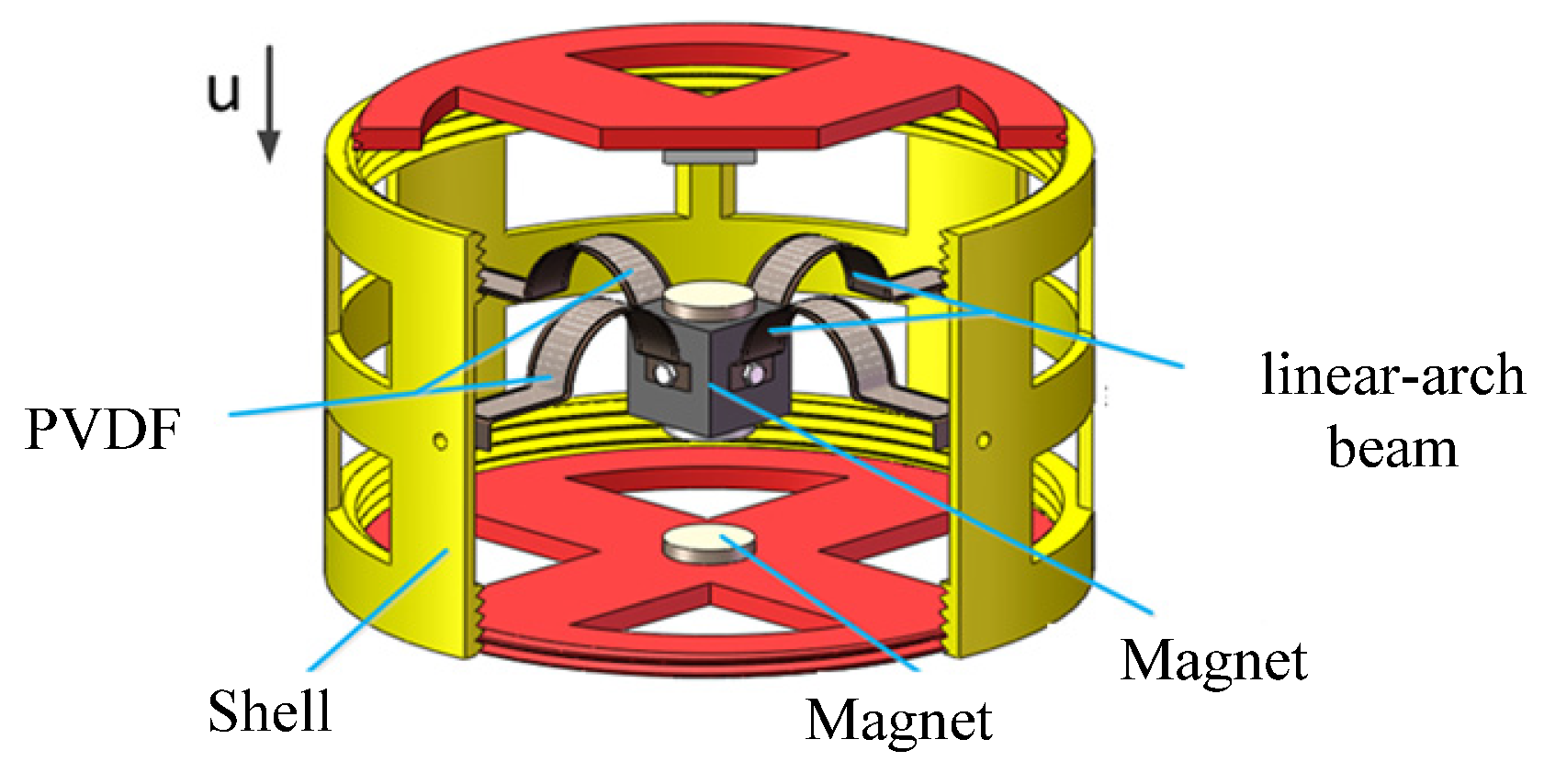
2.1. Structure of the TPEH
2.2. Theoretical Modeling
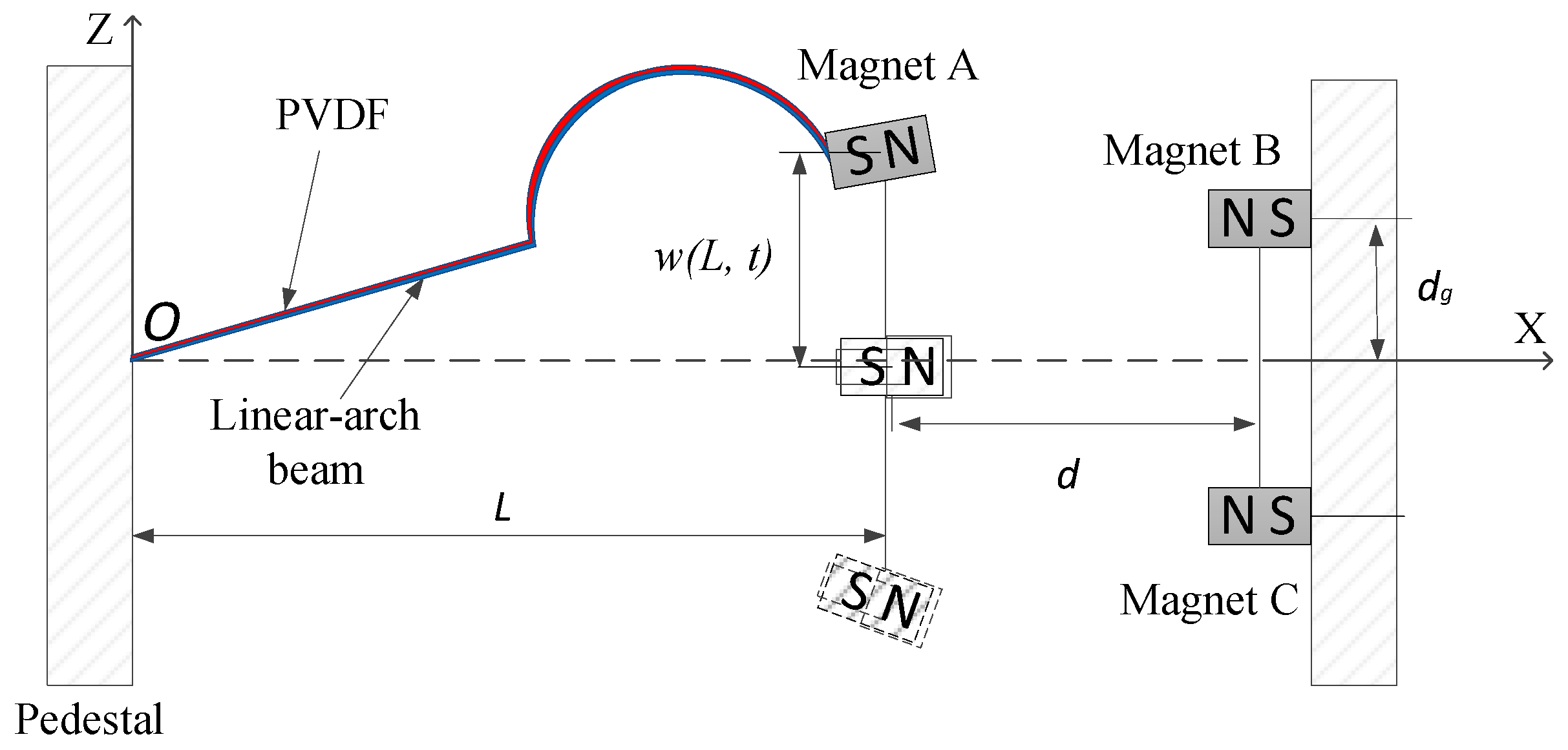
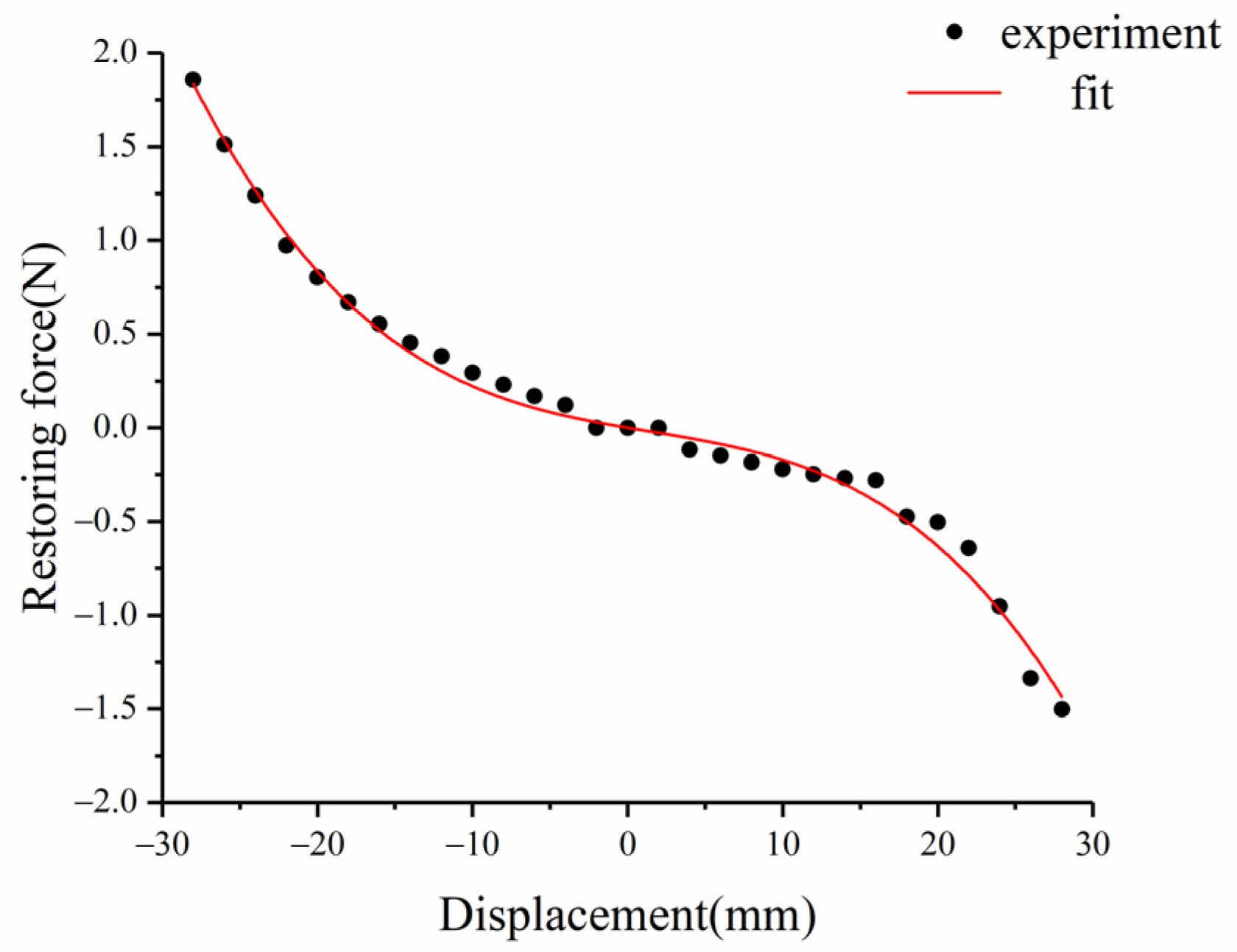
2.2.1. Nonlinear Restoring Force of Linear-Arch Beam
2.2.2. Nonlinear Magnetic Force Modeling
2.2.3. Dynamic Modeling
3. Dynamic Analysis of TPEH
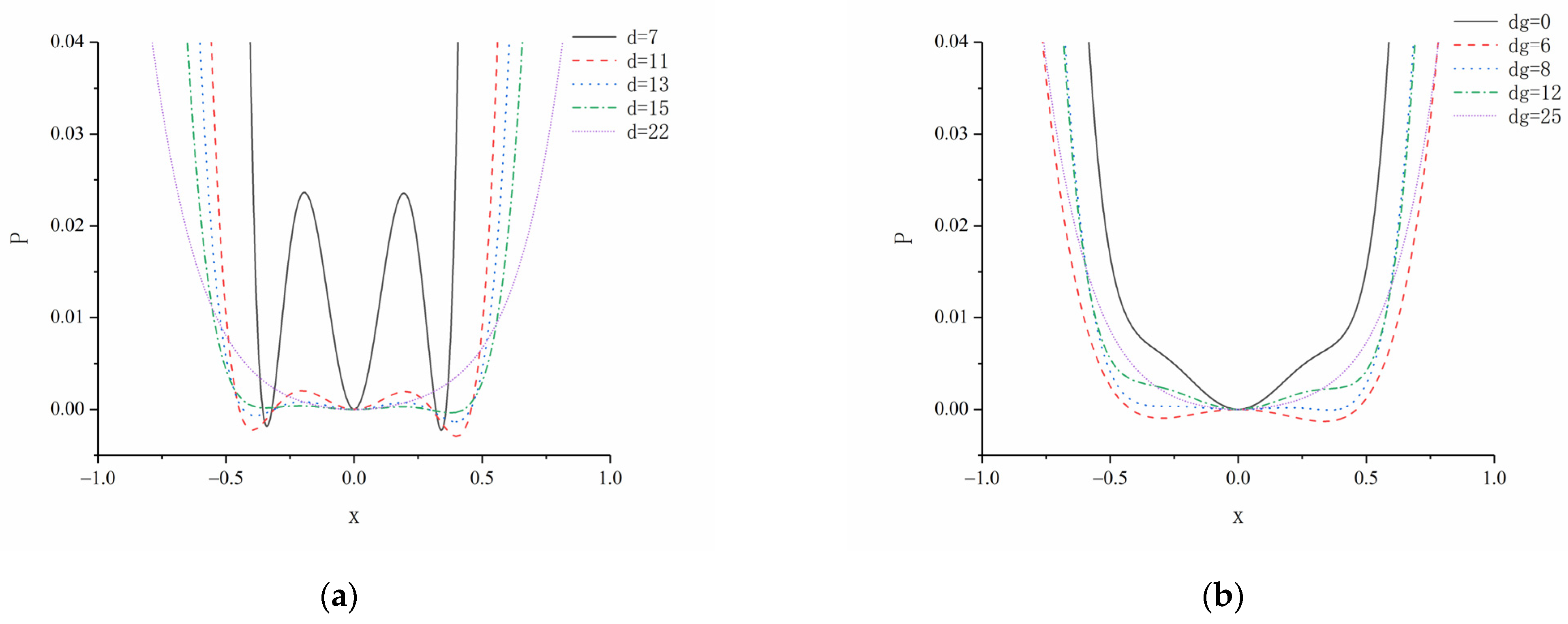
3.1. Analysis of System Potential Energy
3.2. Dynamic Analysis
3.2.1. The Influence of Horizontal Magnetic Distance
3.2.2. The Influence of Vertical Magnetic Distance
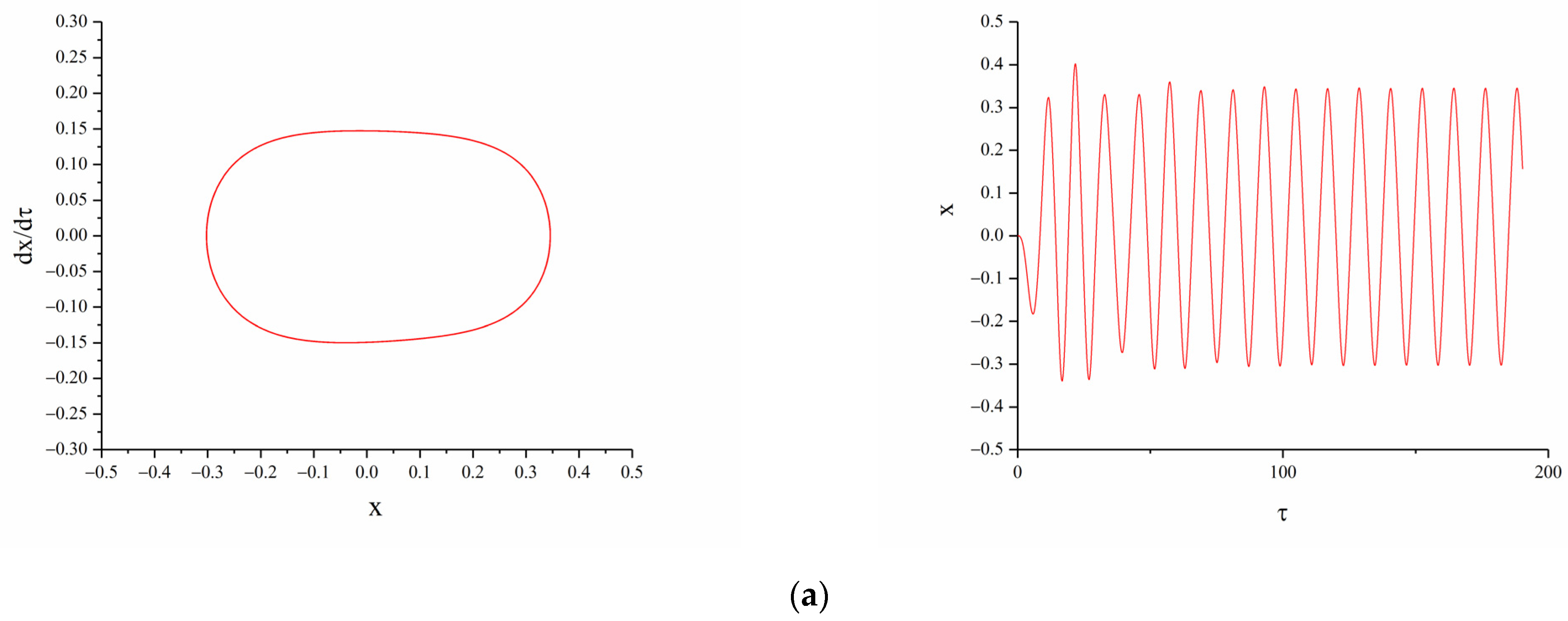
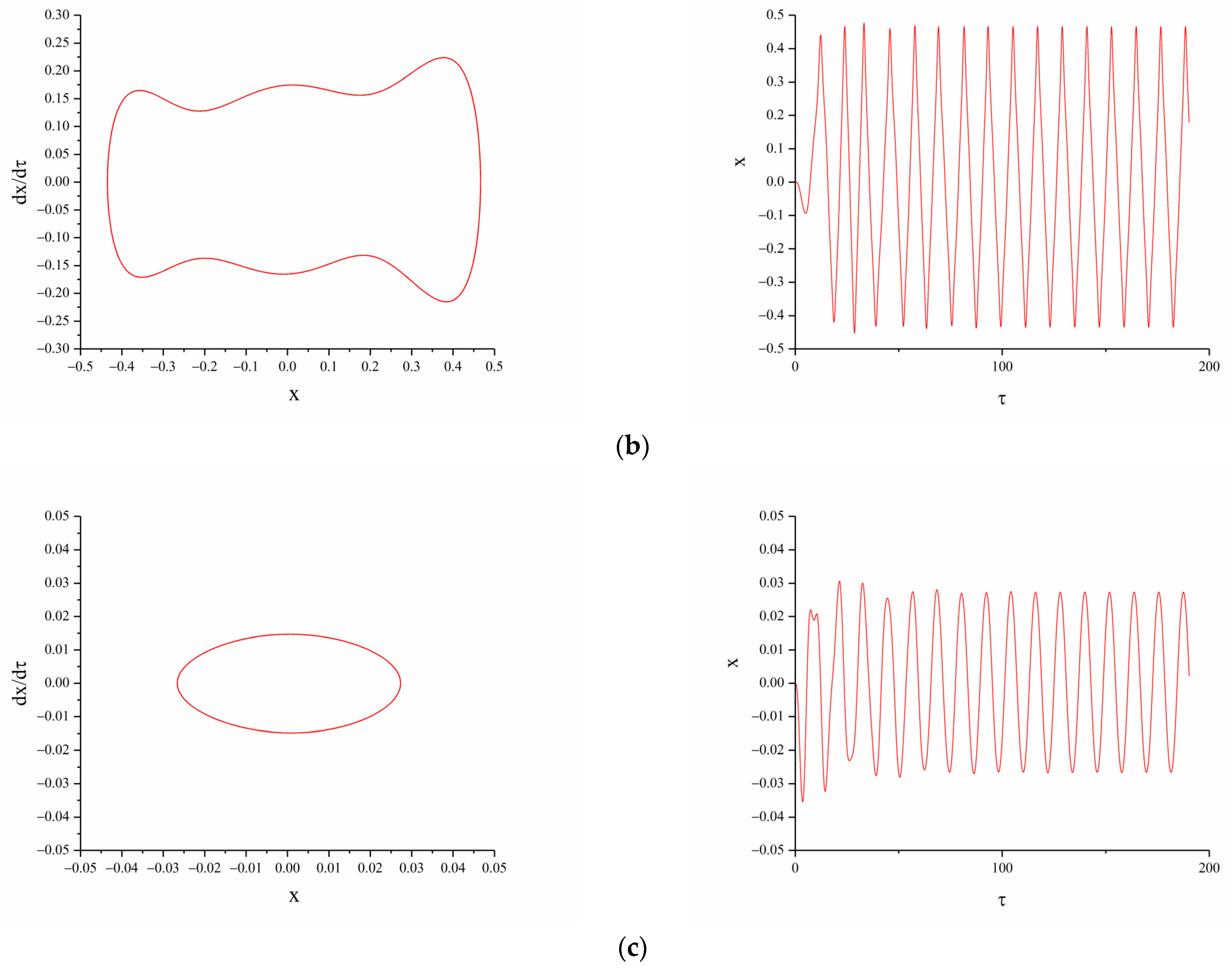
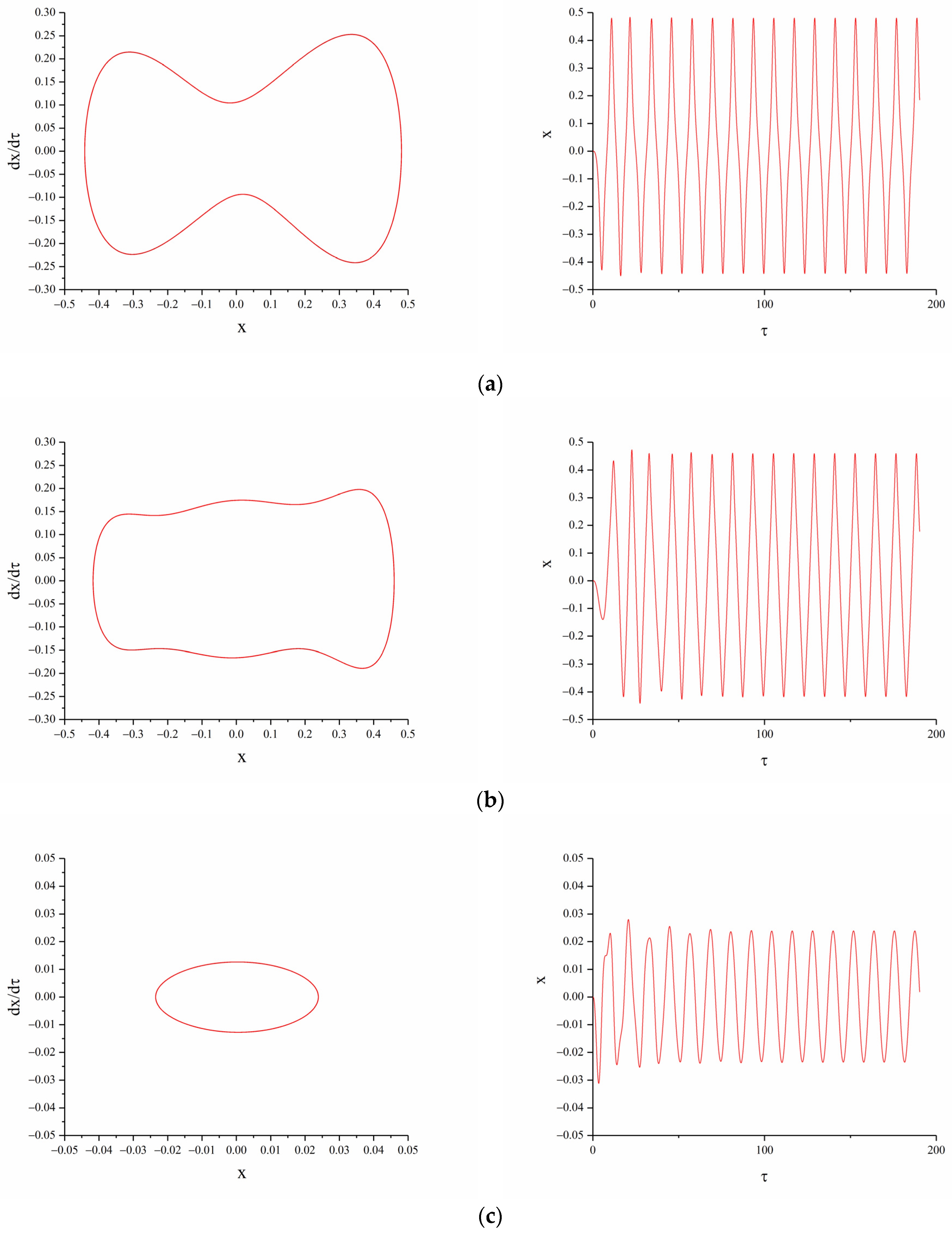
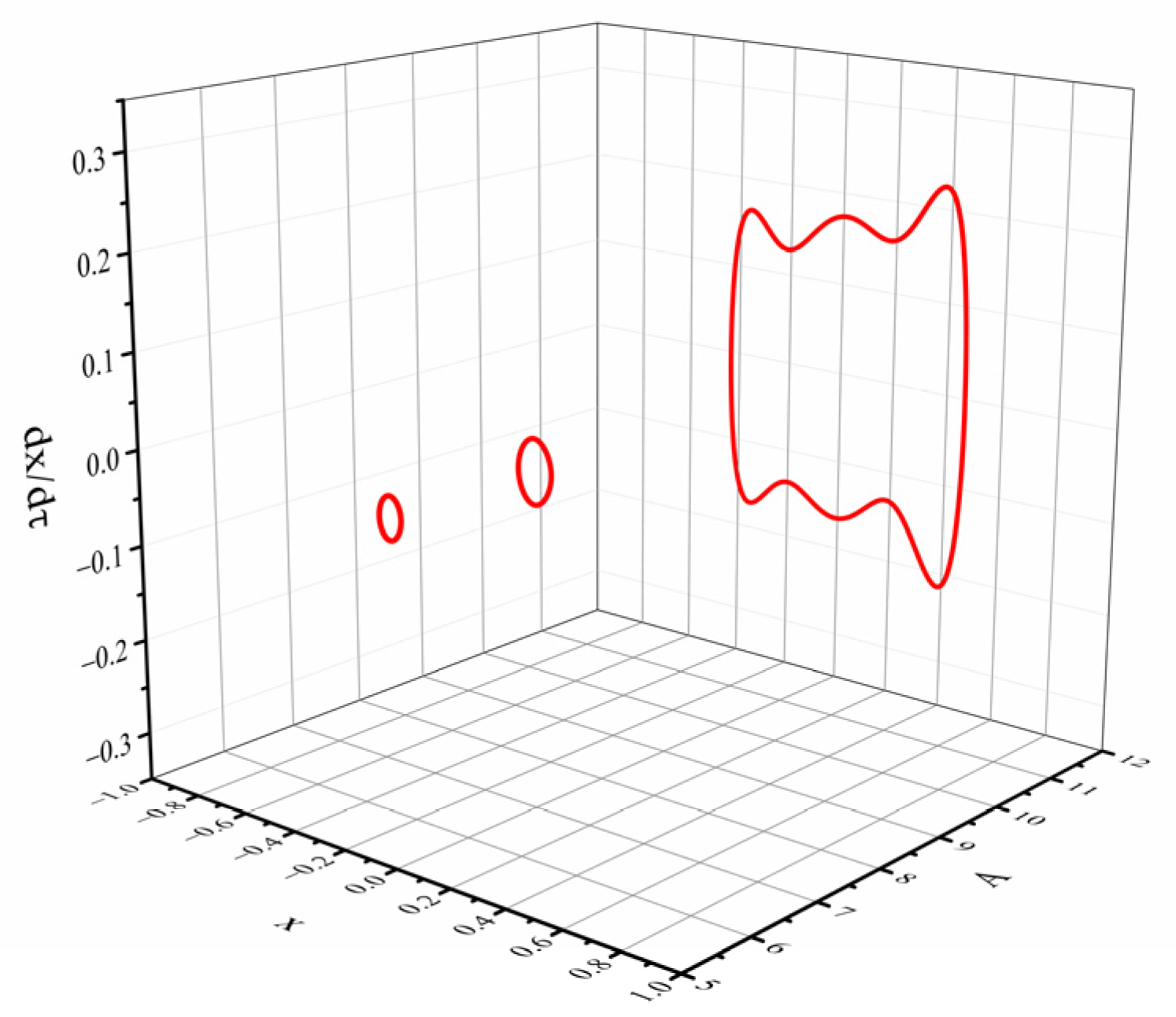
3.2.3. The Influence of Excitation Intensity
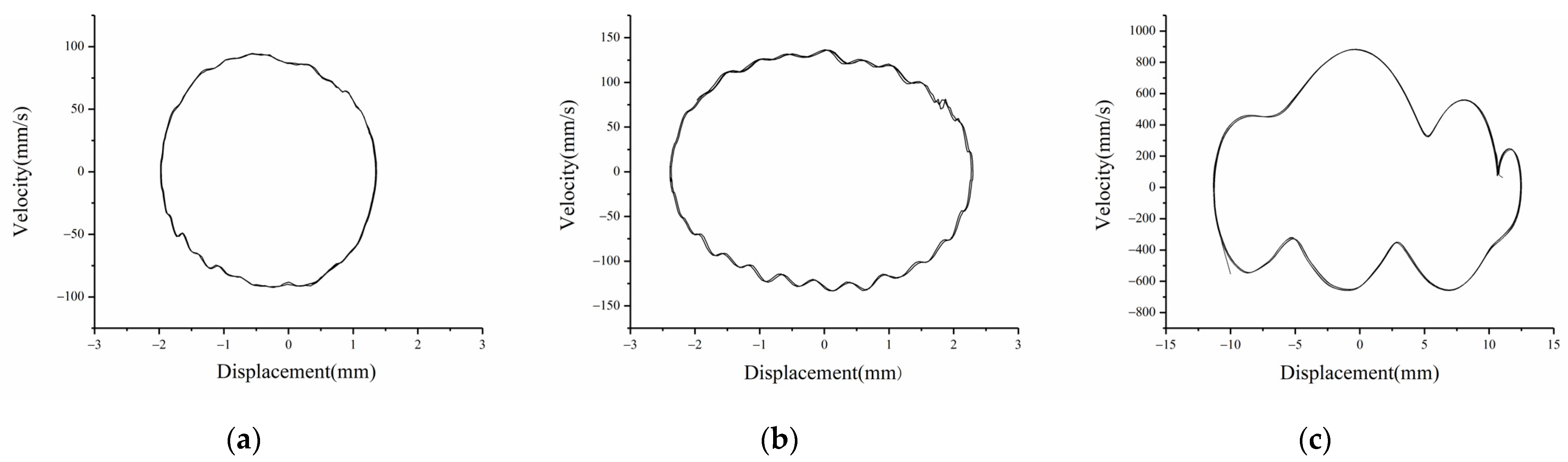
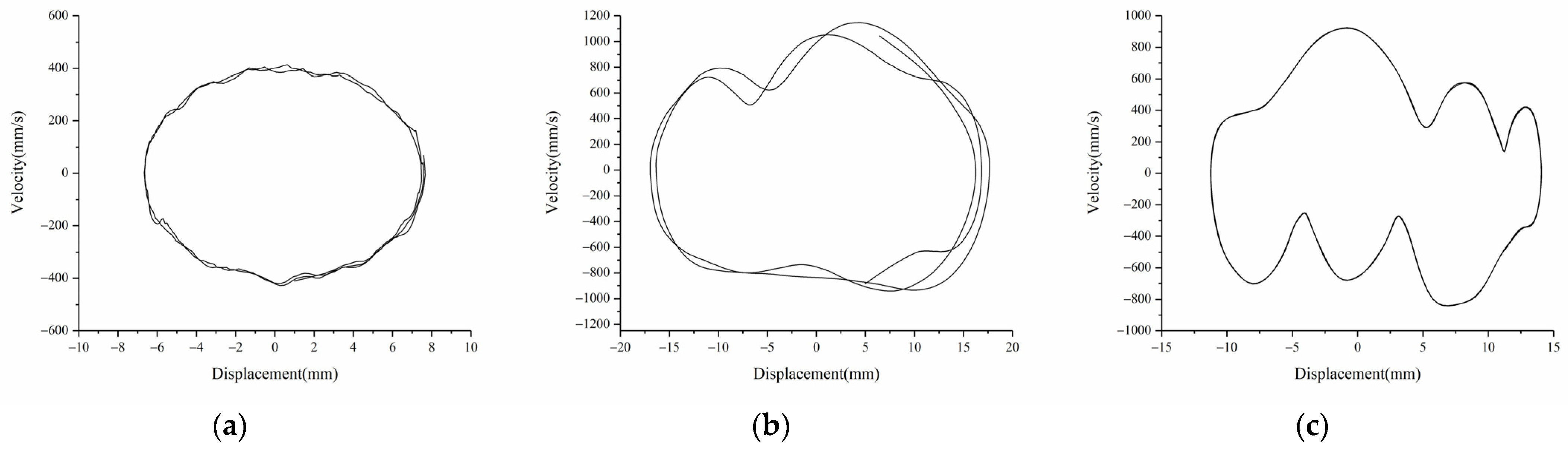
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, K.; Xie, Z.; Zeng, D.; Li, W.; Luo, J.; Wang, M.; Ren, M.; Xia, C. Power cable vibration monitoring based on wireless distributed sensor network. Procedia Comput. Sci. 2021, 183, 401–411. [Google Scholar] [CrossRef]
- Joris, L.; Dupont, F.; Laurent, P.; Bellier, P.; Stoukatch, S.; Redoute, J.-M. An Autonomous Sigfox Wireless Sensor Node for Environmental Monitoring. IEEE Sensors Lett. 2019, 3, 01–04. [Google Scholar] [CrossRef]
- Tao, K.; Chen, Z.; Yi, H.; Zhang, R.; Shen, Q.; Wu, J.; Tang, L.; Fan, K.; Fu, Y.; Miao, J.; et al. Hierarchical Honeycomb-Structured Electret/Triboelectric Nanogenerator for Biomechanical and Morphing Wing Energy Harvesting. Nano-Micro Lett. 2021, 13, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-Performance Piezoelectric Energy Harvesters and Their Applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef] [Green Version]
- Sezer, N.; Ko, M. A Comprehensive Review on the State-of-the-Art of Piezoelectric Energy Harvesting. Nano Energy 2020, 80, 1–25. [Google Scholar]
- Yu, L.; Tang, L.; Yang, T. Piezoelectric passive self-tuning energy harvester based on a beam-slider structure. J. Sound Vib. 2020, 489, 115689. [Google Scholar] [CrossRef]
- Wang, B.; Li, Z.; Yang, Z. A distributed-parameter electromechanical coupling model for a piezoelectric energy harvester with variable curvature. Smart Mater. Struct. 2020, 29, 115015. [Google Scholar] [CrossRef]
- Paknejad, A.; Rahimi, G.; Farrokhabadi, A.; Khatibi, M.M. Analytical solution of piezoelectric energy harvester patch for various thin multilayer composite beams. Compos. Struct. 2016, 154, 694–706. [Google Scholar] [CrossRef]
- Wang, G.; Liao, W.-H.; Yang, B.; Wang, X.; Xu, W.; Li, X. Dynamic and energetic characteristics of a bistable piezoelectric vibration energy harvester with an elastic magnifier. Mech. Syst. Signal Process. 2018, 105, 427–446. [Google Scholar] [CrossRef]
- Yildirim, T.; Ghayesh, M.H.; Li, W.; Alici, G. A review on performance enhancement techniques for ambient vibration energy harvesters. Renew. Sustain. Energy Rev. 2017, 71, 435–449. [Google Scholar] [CrossRef] [Green Version]
- Tran, N.; Ghayesh, M.H.; Arjomandi, M. Ambient vibration energy harvesters: A review on nonlinear techniques for performance enhancement. Int. J. Eng. Sci. 2018, 127, 162–185. [Google Scholar] [CrossRef]
- Li, P.; Liu, Y.; Wang, Y.; Luo, C.; Li, G.; Hu, J.; Liu, W.; Zhang, W. Low-frequency and wideband vibration energy harvester with flexible frame and interdigital structure. AIP Adv. 2015, 5, 047151. [Google Scholar] [CrossRef]
- Liu, D.; Al-Haik, M.; Zakaria, M.; Hajj, M.R. Piezoelectric energy harvesting using L-shaped structures. J. Intell. Mater. Syst. Struct. 2018, 29, 1206–1215. [Google Scholar] [CrossRef]
- Zhou, S.; Hobeck, J.D.; Cao, J.; Inman, D.J. Analytical and experimental investigation of flexible longitudinal zigzag structures for enhanced multi-directional energy harvesting. Smart Mater. Struct. 2017, 26, 35008. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. A novel two-degrees-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2012, 24, 357–368. [Google Scholar] [CrossRef]
- Rezaei, M.; Khadem, S.E.; Firoozy, P. Broadband and tunable PZT energy harvesting utilizing local nonlinearity and tip mass effects. Int. J. Eng. Sci. 2017, 118, 1–15. [Google Scholar] [CrossRef]
- Liu, H.; Lee, C.; Kobayashi, T.; Tay, C.J.; Quan, C. Investigation of a MEMS piezoelectric energy harvester system with a frequency-widened-bandwidth mechanism introduced by mechanical stoppers. Smart Mater. Struct. 2012, 21, 035005. [Google Scholar] [CrossRef]
- Kumar, T.; Kumar, R.; Chauhan, V.S.; Twiefel, J. Finite-Element Analysis of a Varying-Width Bistable Piezoelectric Energy Harvester. Energy Technol. 2015, 3, 1243–1249. [Google Scholar] [CrossRef]
- Singh, K.A.; Kumar, R.; Weber, R.J. A broadband bistable piezoelectric energy harvester with nonlinear high-power extraction. IEEET Power Electr. 2015, 30, 6763–6774. [Google Scholar] [CrossRef]
- Wang, G.; Ju, Y.; Liao, W.-H.; Zhao, Z.; Tan, J. A hybrid piezoelectric device combining a tri-stable energy harvester with an elastic base for low-orbit vibration energy harvesting enhancement. Smart Mater. Struct. 2021, 30, 075028. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Qin, W.Y.; Zhu, P. Energy harvesting in a quad-stable harvester subjected to random excitation. AIP Adv. 2016, 6, 025022. [Google Scholar] [CrossRef] [Green Version]
- Yao, M.; Liu, P.; Ma, L.; Wang, H.; Zhang, W. Experimental study on broadband bistable energy harvester with L-shaped piezoelectric cantilever beam. Acta Mech. Sin. 2020, 36, 557–577. [Google Scholar] [CrossRef]
- Wang, G.; Wu, H.; Liao, W.-H.; Cui, S.; Zhao, Z.; Tan, J. A modified magnetic force model and experimental validation of a tri-stable piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2020, 31, 967–979. [Google Scholar] [CrossRef]
- Zhu, P.; Ren, X.; Qin, W.; Yang, Y.; Zhou, Z. Theoretical and experimental studies on the characteristics of a tri-stable piezoelectric harvester. Arch. Appl. Mech. 2017, 87, 1541–1554. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tri-stable energy harvester: Modeling and experiment verification. Appl. Energ. 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Zhang, X.; Zuo, M.; Yang, W.; Wan, X. A Tri-Stable Piezoelectric Vibration Energy Harvester for Composite Shape Beam: Nonlinear Modeling and Analysis. Sensors 2020, 20, 1370. [Google Scholar] [CrossRef] [Green Version]
- Hai-Tao, L.; Hu, D.; Xing-Jian, J.; Wei-Yang, Q.; Li-Qun, C. Improving the performance of a tri-stable energy harvester with a staircase-shaped potential well. Mech. Syst. Signal Process. 2021, 159, 107805. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, Z.; Liao, W.-H.; Tan, J.; Ju, Y.; Li, Y. Characteristics of a tri-stable piezoelectric vibration energy harvester by considering geometric nonlinearity and gravitation effects. Mech. Syst. Signal Process. 2020, 138, 106571. [Google Scholar] [CrossRef]
- Sun, S.; Leng, Y.; Su, X.; Zhang, Y.; Chen, X.; Xu, J. Performance of a novel dual-magnet tri-stable piezoelectric energy harvester subjected to random excitation. Energy Convers. Manag. 2021, 239, 114246. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, W.; Zuo, M.; Tan, H.; Fan, H.; Mao, Q.; Wan, X. An Arc-shaped Piezoelectric Bistable Vibration Energy Harvester: Modeling and Experiments. Sensors 2018, 18, 4472. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zhu, P.; Ren, X.; Qin, W.; Zhou, Z. Improving energy harvesting in a tri-stable piezomagnetoelastic beam with two attractive external magnets subjected to random excitation. Arch. Appl. Mech. 2017, 87, 45–57. [Google Scholar] [CrossRef]
- Wang, W.; Cao, J.; Bowen, C.R.; Litak, G. Multiple solutions of asymmetric potential bistable energy harvesters: Numerical simulation and experimental validation. Eur. Phys. J. B 2018, 91, 254. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| linear-arch beam | Piezoelectric layer | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, L.; Chen, X.; Zhu, F.; Guo, Y. Time-Domain Dynamic Characteristics Analysis and Experimental Research of Tri-Stable Piezoelectric Energy Harvester. Micromachines 2021, 12, 1045. https://doi.org/10.3390/mi12091045
Zhang X, Chen L, Chen X, Zhu F, Guo Y. Time-Domain Dynamic Characteristics Analysis and Experimental Research of Tri-Stable Piezoelectric Energy Harvester. Micromachines. 2021; 12(9):1045. https://doi.org/10.3390/mi12091045
Chicago/Turabian StyleZhang, Xuhui, Luyang Chen, Xiaoyu Chen, Fulin Zhu, and Yan Guo. 2021. "Time-Domain Dynamic Characteristics Analysis and Experimental Research of Tri-Stable Piezoelectric Energy Harvester" Micromachines 12, no. 9: 1045. https://doi.org/10.3390/mi12091045
APA StyleZhang, X., Chen, L., Chen, X., Zhu, F., & Guo, Y. (2021). Time-Domain Dynamic Characteristics Analysis and Experimental Research of Tri-Stable Piezoelectric Energy Harvester. Micromachines, 12(9), 1045. https://doi.org/10.3390/mi12091045







