Predicting Cutting Force and Primary Shear Behavior in Micro-Textured Tools Assisted Machining of AISI 630: Numerical Modeling and Taguchi Analysis
Abstract
:1. Introduction
2. Numerical Design
2.1. Simulation Setup and Taguchi Design of Experiment (DoE)
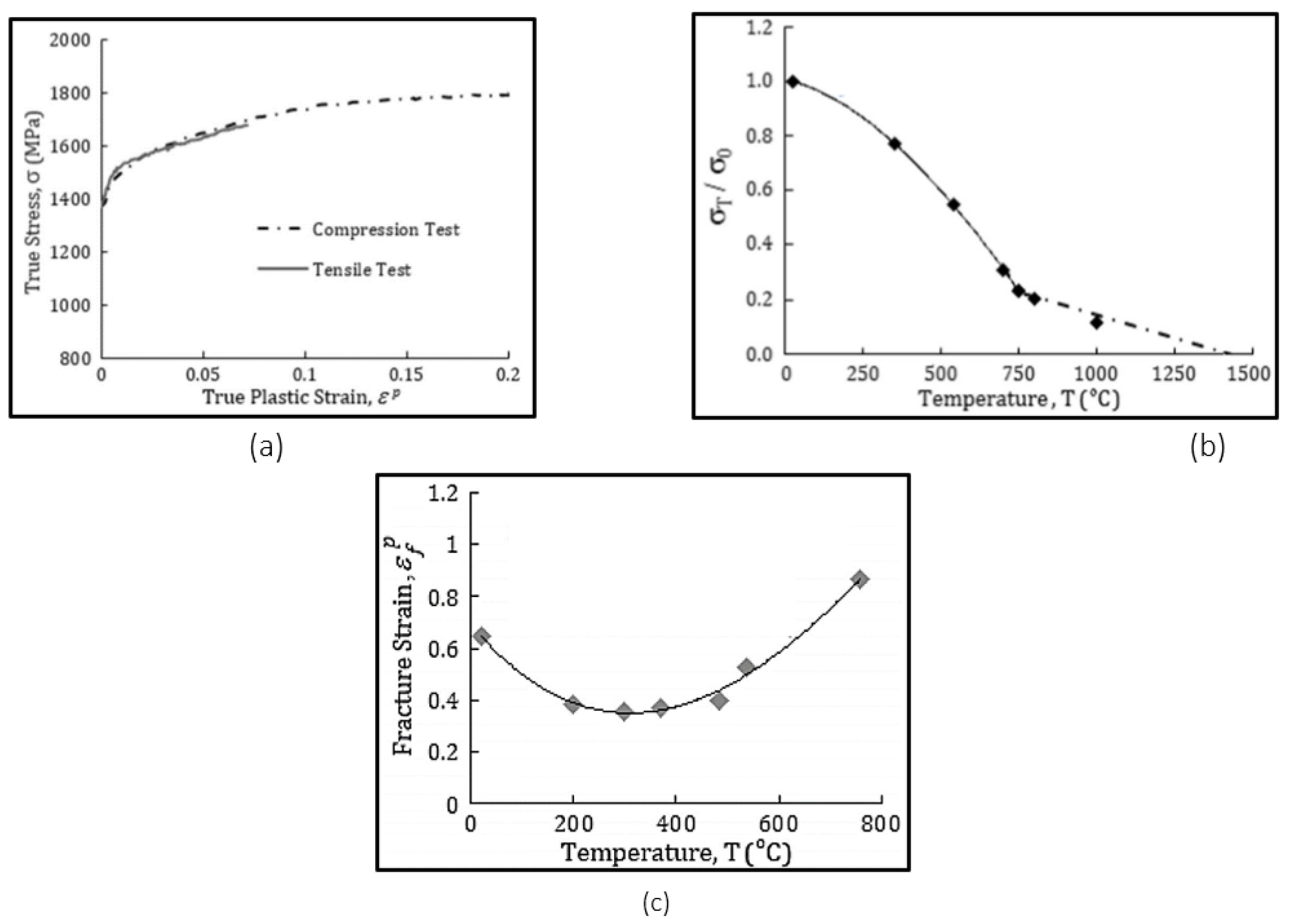
2.2. Material Model
3. Results and Discussion
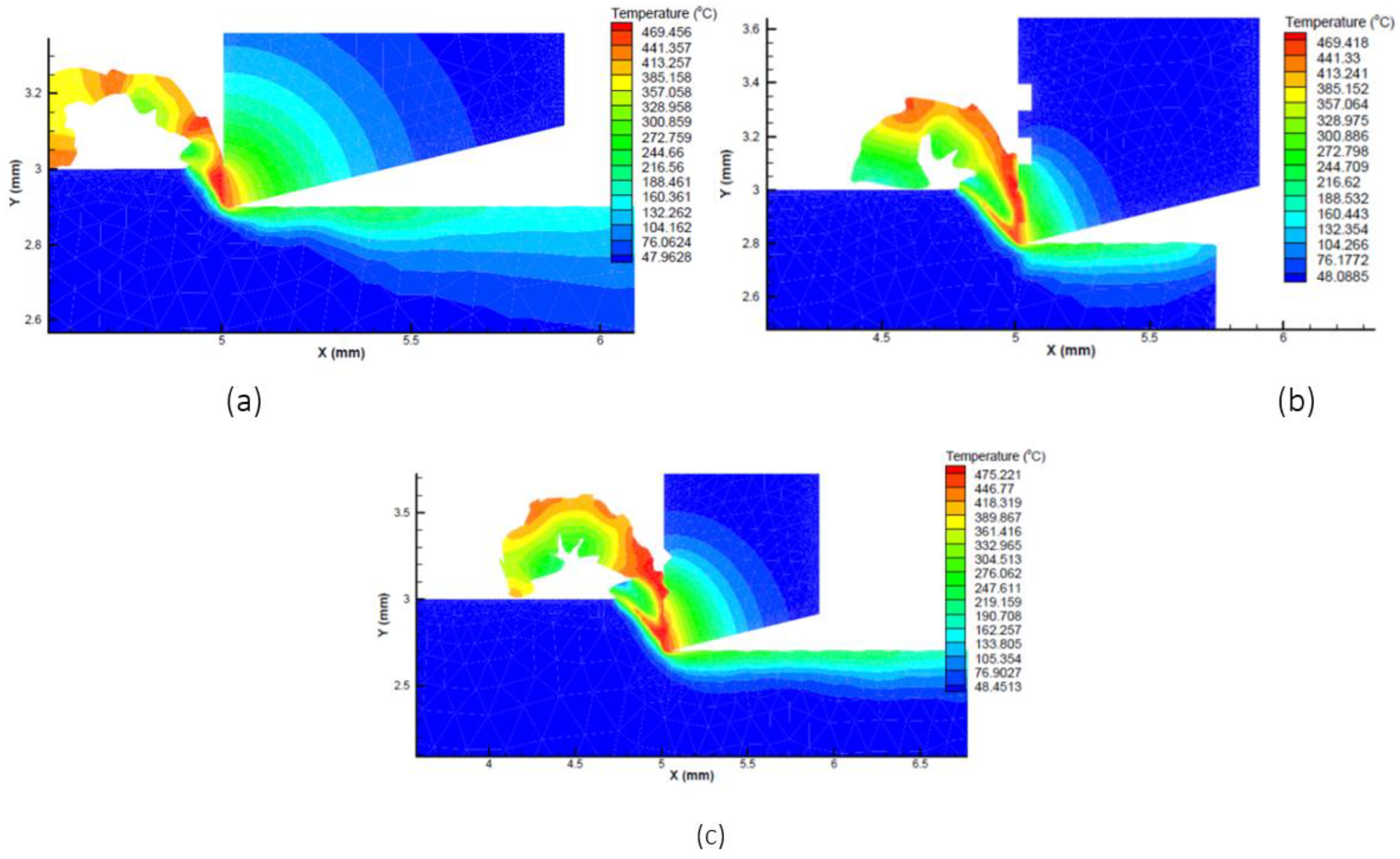
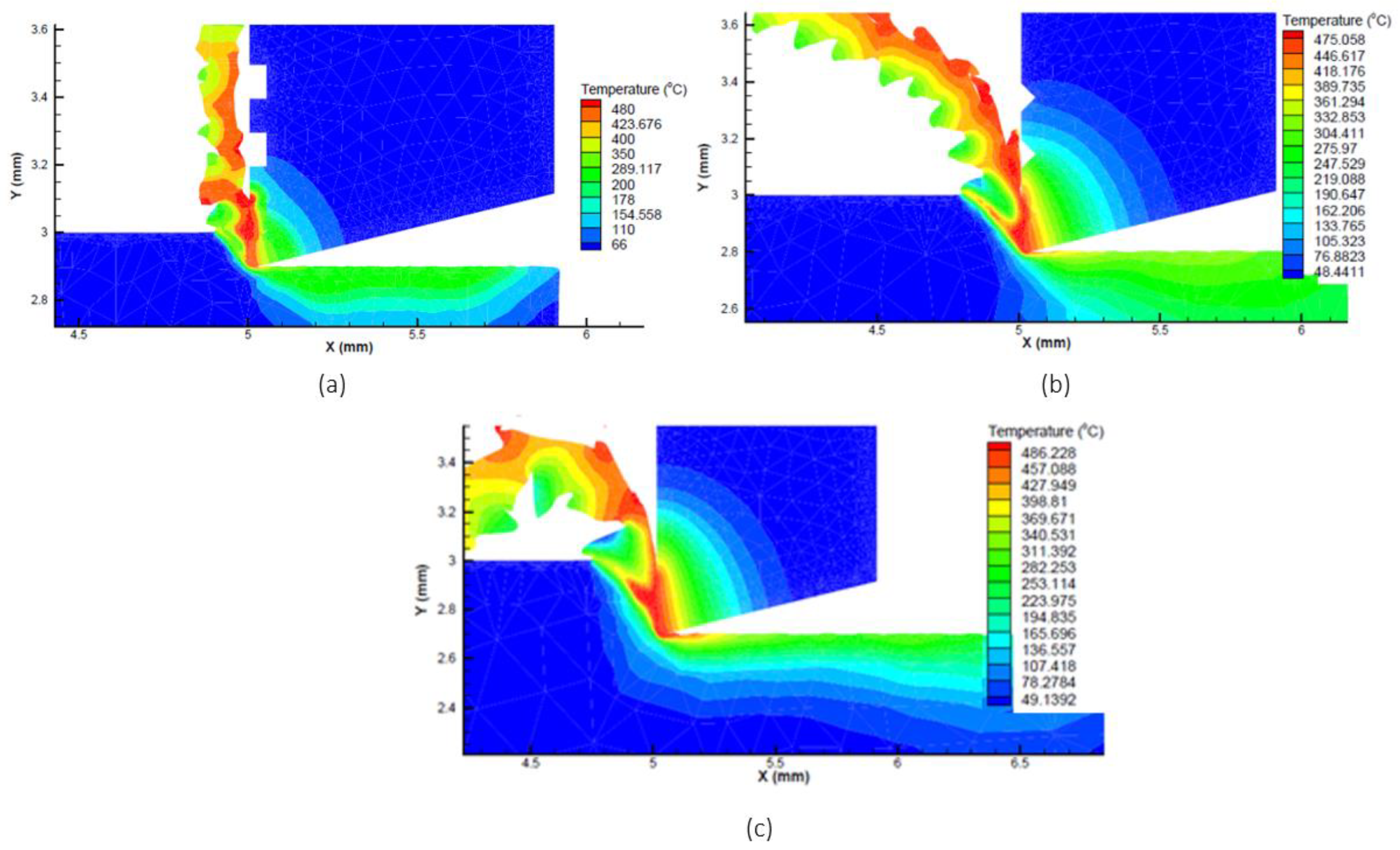
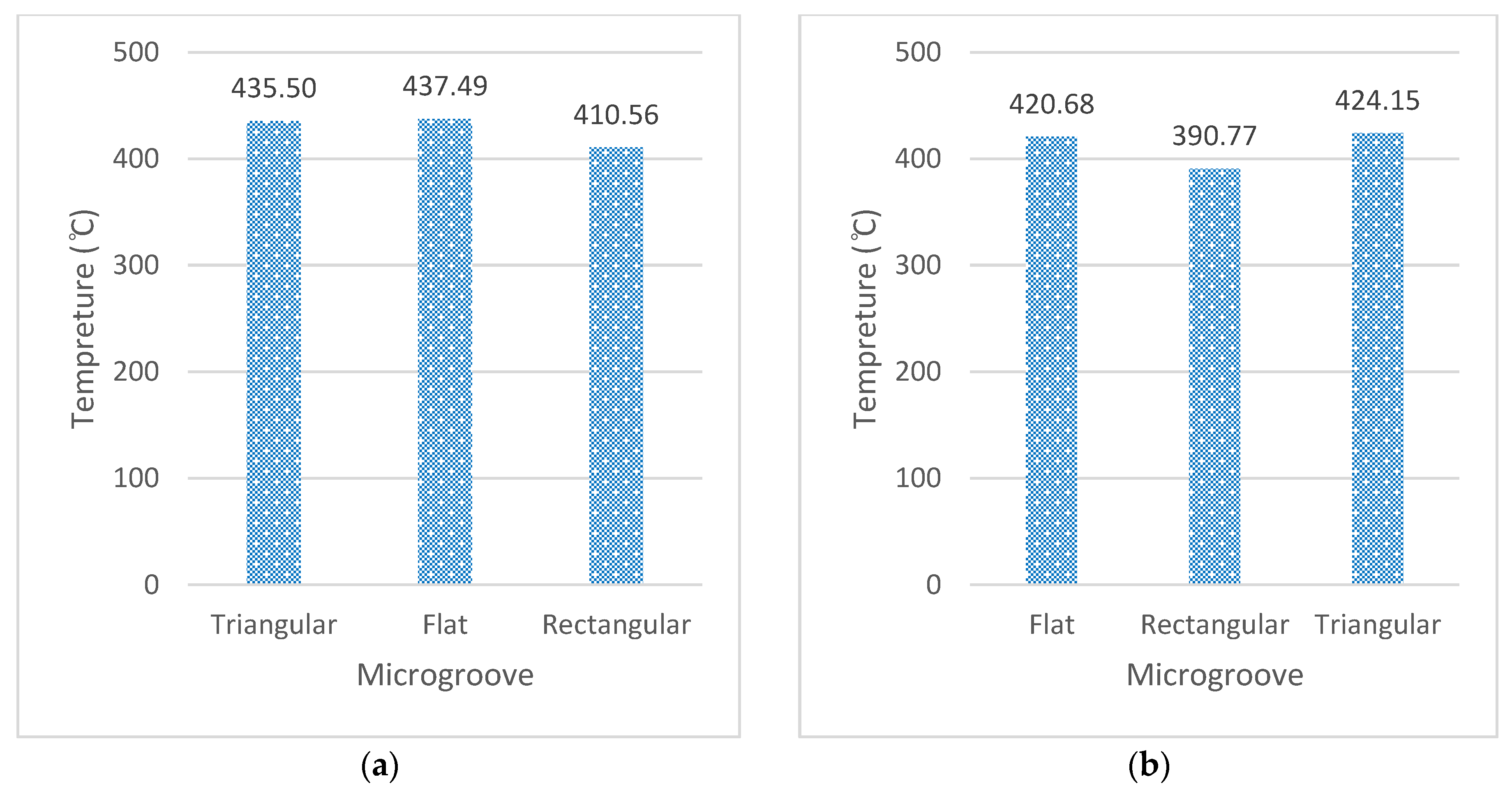
3.1. Cutting Temperature
3.2. Chip Ratio and Shear Angle
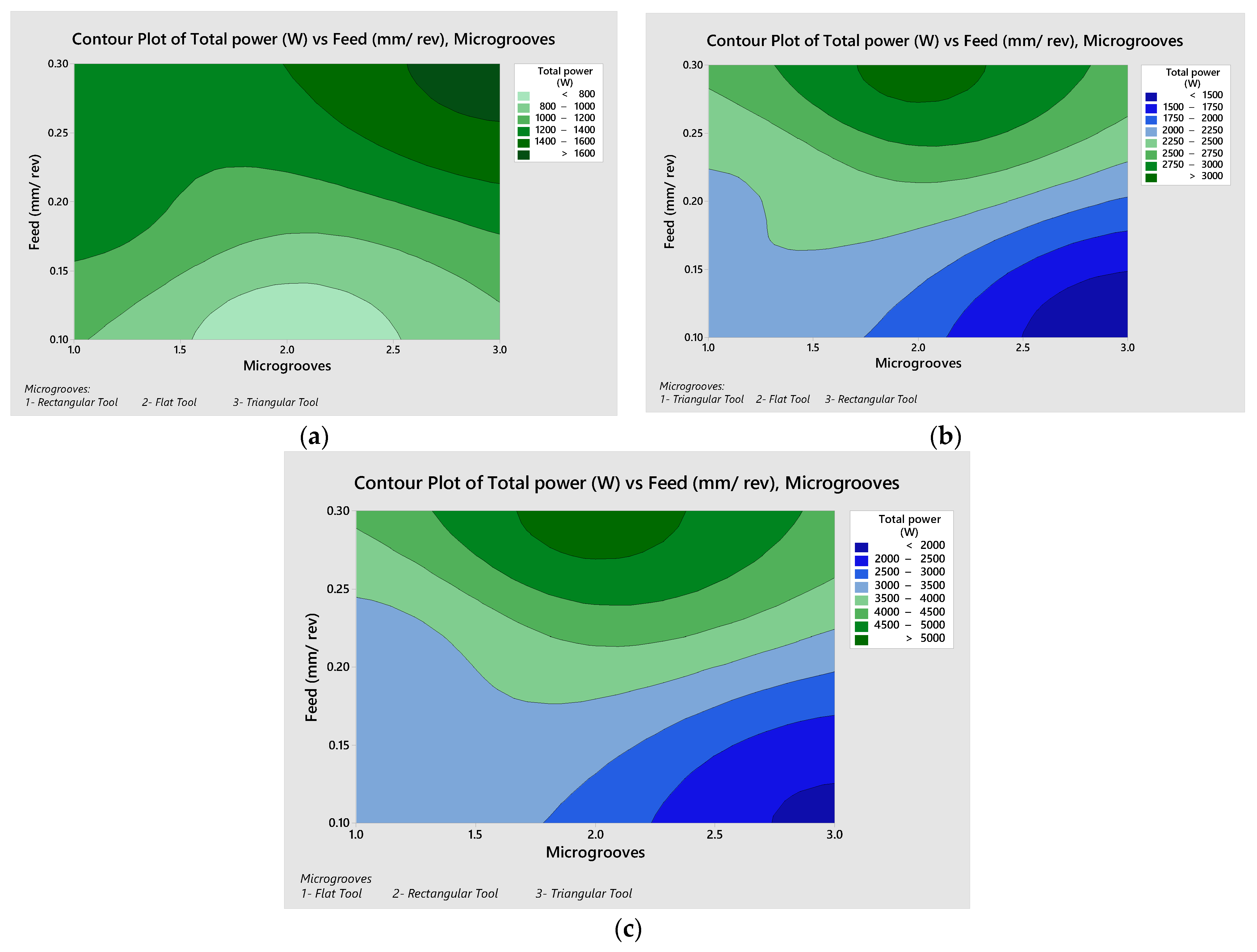
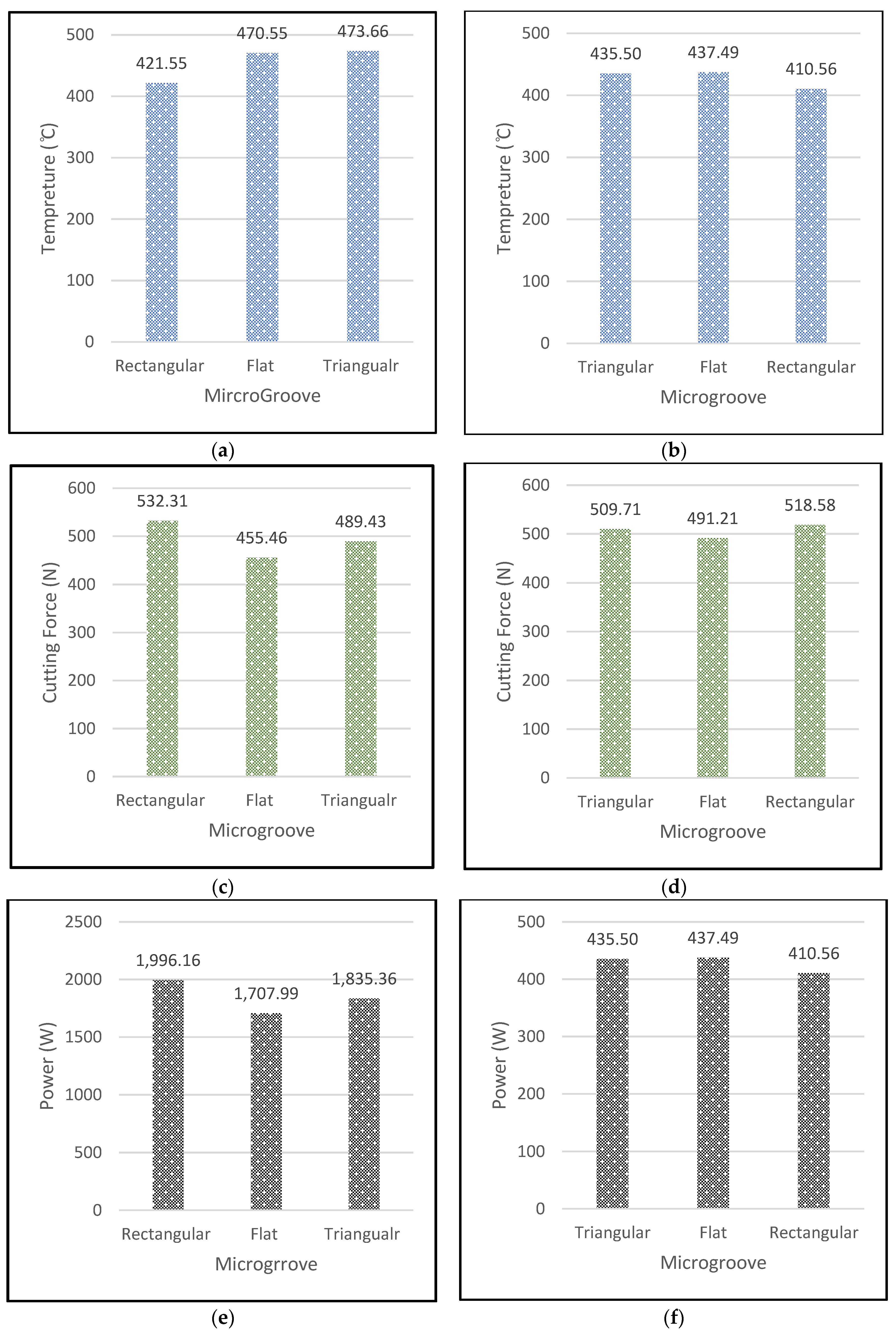
3.3. Cutting Force and Power Consumption
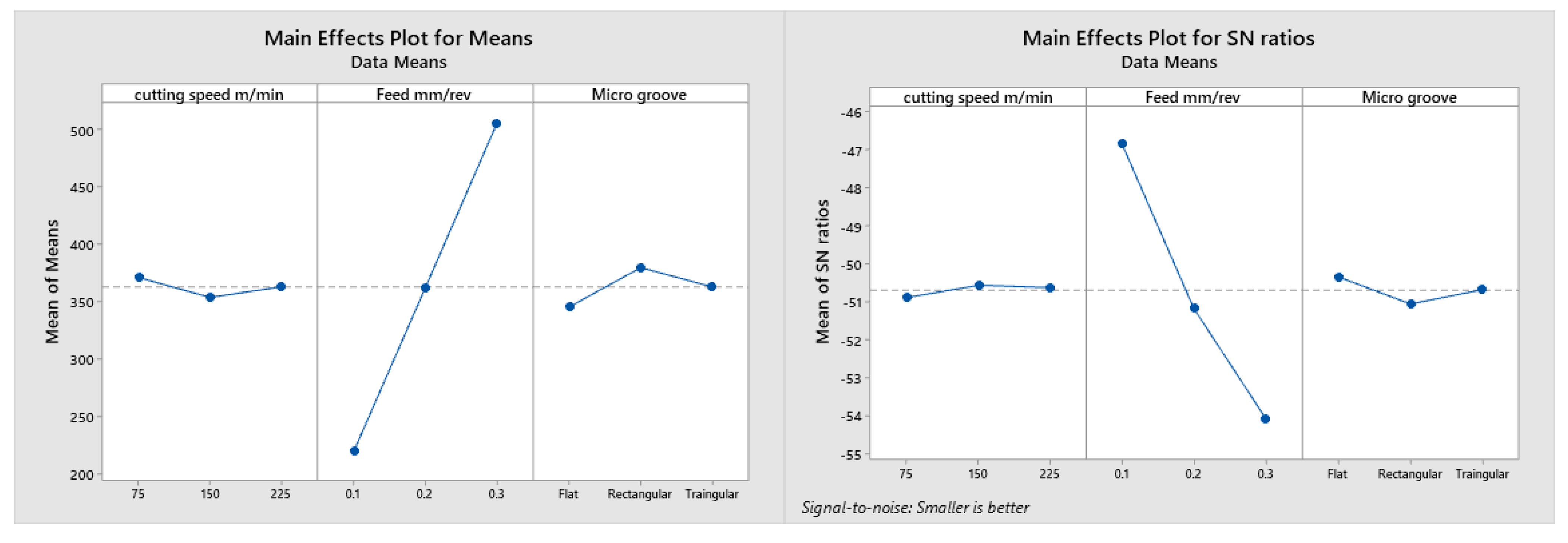
3.4. Effect of Cutting Speed vs. Microgroove on Different Parameters
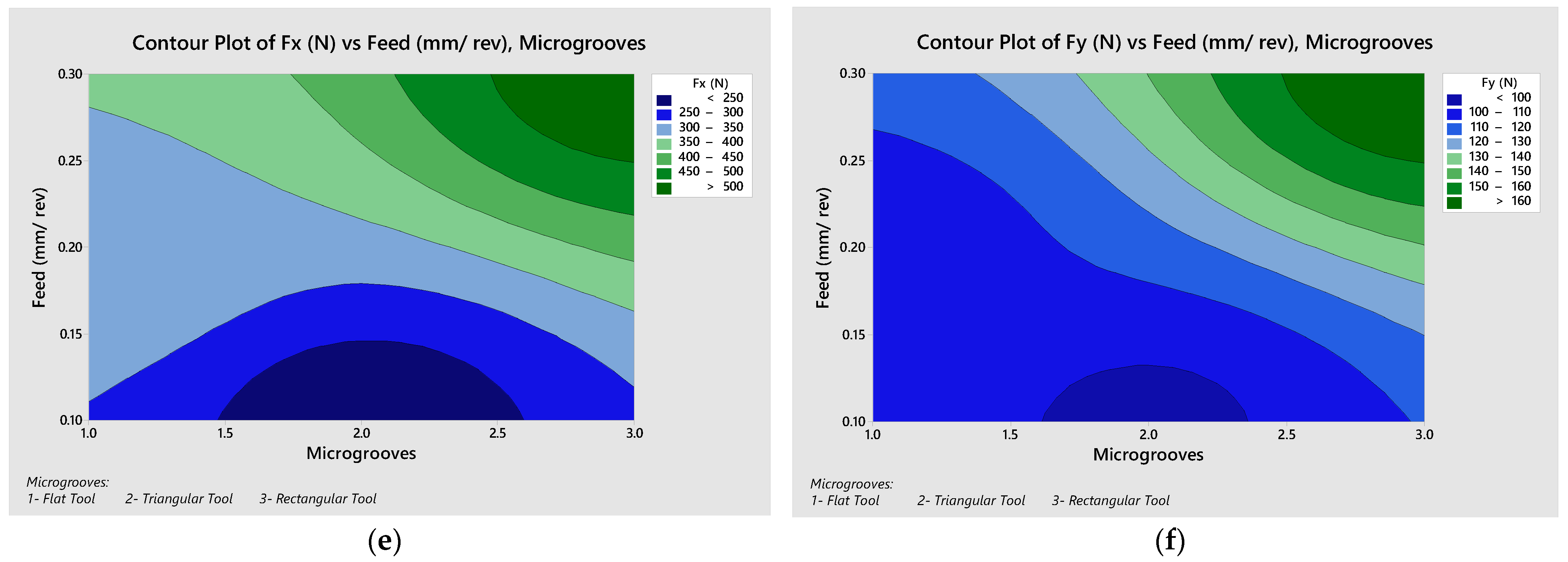
3.5. Effect of Feed Rate vs. Microgrooves on Different Cutting Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, K.; Yang, F.; Zhang, N.; Liu, Q.; Jiang, F. Study on the cutting performance of micro textured tools on cutting Ti-6Al-4V titanium alloy. Micromachines 2020, 11, 137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mishra, S.K.; Ghosh, S.; Aravindan, S. Performance of laser processed carbide tools for machining of Ti6Al4V alloys: A combined study on experimental and finite element analysis. Precis. Eng. 2019, 56, 370–385. [Google Scholar] [CrossRef]
- Krolczyk, G.M.; Maruda, R.W.; Krolczyk, J.B.; Wojciechowski, S.; Mia, M.; Nieslony, P.; Budzik, G. Ecological trends in machining as a key factor in sustainable production—A review. J. Clean. Prod. 2019, 218, 601–615. [Google Scholar] [CrossRef]
- Chen, G.; Lu, L.; Ke, Z.; Qin, X.; Ren, C. Influence of constitutive models on finite element simulation of chip formation in orthogonal cutting of Ti-6Al-4V alloy. Procedia Manuf. 2019, 33, 530–537. [Google Scholar] [CrossRef]
- Lu, J.; Chen, J.; Fang, Q.; Liu, B.; Liu, Y.; Jin, T. Finite element simulation for Ti-6Al-4V alloy deformation near the exit of orthogonal cutting. Int. J. Adv. Manuf. Technol. 2016, 85, 2377–2388. [Google Scholar] [CrossRef]
- Mishra, S.K.; Ghosh, S.; Aravindan, S. 3D finite element investigations on textured tools with different geometrical shapes for dry machining of titanium alloys. Int. J. Mech. Sci. 2018, 141, 424–449. [Google Scholar] [CrossRef]
- Tamil Alagan, N.; Zeman, P.; Hoier, P.; Beno, T.; Klement, U. Investigation of micro-textured cutting tools used for face turning of alloy 718 with high-pressure cooling. J. Manuf. Process. 2019, 37, 606–616. [Google Scholar] [CrossRef]
- Machai, C.; Iqbal, A.; Biermann, D.; Upmeier, T.; Schumann, S. On the effects of cutting speed and cooling methodologies in grooving operation of various tempers of β-titanium alloy. J. Mater. Process. Technol. 2013, 213, 1027–1037. [Google Scholar] [CrossRef]
- Rathod, P.; Aravindan, S.; Paruchuri, V.R. Multi-objective optimization for creating a low-carbon logistics system through community-based action. J. Adv. Mech. Des. Syst. Manuf. 2015, 9, 1–12. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, X.; Zhang, K.; Wu, Y.; Huang, Q. Enhancing cutting performance of uncoated cemented carbide tools by joint-use of magnetic nanofluids and micro-texture under magnetic field. J. Mater. Process. Technol. 2020, 284, 116764. [Google Scholar] [CrossRef]
- Hao, X.; Chen, X.; Xiao, S.; Li, L.; He, N. Cutting performance of carbide tools with hybrid texture. Int. J. Adv. Manuf. Technol. 2018, 97, 3547–3556. [Google Scholar] [CrossRef]
- Lian, Y.; Mu, C.; Wang, L.; Yao, B.; Deng, J.; Lei, S. Numerical simulation and experimental investigation on friction and wear behaviour of micro-textured cemented carbide in dry sliding against TC4 titanium alloy balls. Int. J. Refract. Met. Hard Mater. 2018, 73, 121–131. [Google Scholar] [CrossRef]
- Duan, R.; Deng, J.; Lei, S.; Ge, D.; Liu, Y.; Li, X. Effect of derivative cutting on machining performance of micro textured tools. J. Manuf. Process. 2019, 45, 544–556. [Google Scholar] [CrossRef]
- Ranjan, P.; Hiremath, S.S. Role of textured tool in improving machining performance: A review. J. Manuf. Process. 2019, 43, 47–73. [Google Scholar] [CrossRef]
- Kawasegi, N.; Kawashima, T.; Morita, N.; Nishimura, K.; Yamaguchi, M.; Takano, N. Effect of texture shape on machining performance of textured diamond cutting tool. Precis. Eng. 2019, 60, 21–27. [Google Scholar] [CrossRef]
- Xing, Y.; Deng, J.; Wang, X.; Ehmann, K.; Cao, J. Experimental assessment of laser textured cutting tools in dry cutting of aluminum alloys. J. Manuf. Sci. Eng. Trans. ASME 2016, 138, 071006. [Google Scholar] [CrossRef]
- Xing, Y.; Deng, J.; Zhao, J.; Zhang, G.; Zhang, K. Cutting performance and wear mechanism of nanoscale and microscale textured Al2O3/TiC ceramic tools in dry cutting of hardened steel. Int. J. Refract. Met. Hard Mater. 2014, 43, 46–58. [Google Scholar] [CrossRef]
- Sugihara, T.; Kobayashi, R.; Enomoto, T. Direct observations of tribological behavior in cutting with textured cutting tools. Int. J. Mach. Tools Manuf. 2021, 168, 103726. [Google Scholar] [CrossRef]
- ThirdWaveSystems. Third Wave AdvantEdgeTM; User’s Manual Version 7.0; Third Wave: Palo Alto, CA, USA, 2015; 378p. [Google Scholar]
- Schmid, S.; Kalpakjian, S. Manufacturing Processes for Engineering Materials; Pearson: London, UK, 2008; ISBN 0132272717. [Google Scholar]
- Ebrahimi, S.M.; Araee, A.; Hadad, M. Investigation of the effects of constitutive law on numerical analysis of turning processes to predict the chip morphology, tool temperature, and cutting force. Int. J. Adv. Manuf. Technol. 2019, 105, 4245–4264. [Google Scholar] [CrossRef]
- Laakso, S.V.A.; Niemi, E. Modified Johnson-Cook flow stress model with thermal softening damping for finite element modeling of cutting. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 241–253. [Google Scholar] [CrossRef]
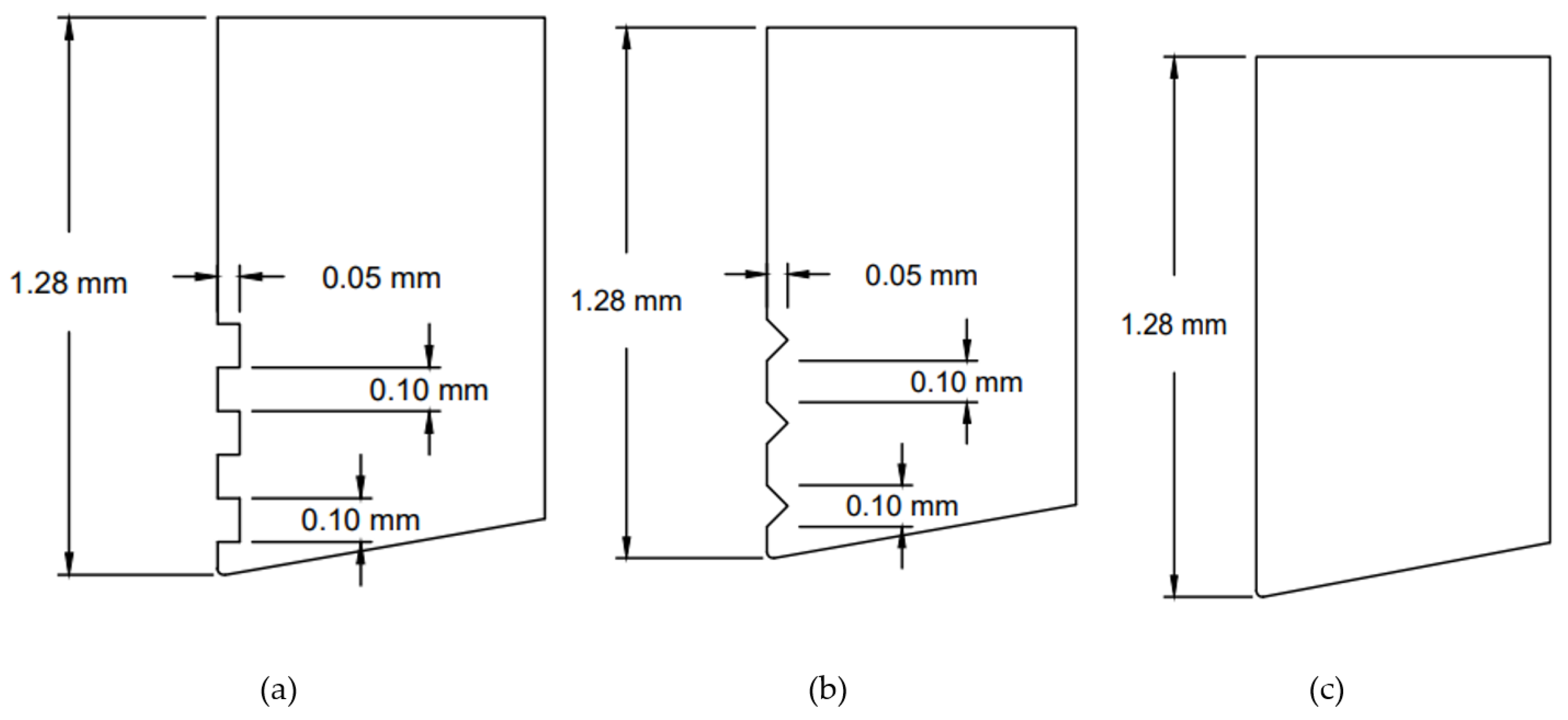






| Parameters | RT Tool | VT Tool |
|---|---|---|
| Width of groove (mm) | 0.1 | 0.2 |
| Depth of groove (mm) | 0.05 | 0.05 |
| Distance between groove (mm) | 0.2 | 0.2 |
| Radius at tip of cutting tool (mm) | 0.015 | 0.015 |
| Relief angle (degree) | 10 | 10 |
| Sr. No. | Cutting Speed (m/min) | Feed (mm/rev) | Microgroove |
|---|---|---|---|
| Vc | (to) | ||
| 1 | 75 | 0.1 | Flat |
| 2 | 75 | 0.2 | Rectangular |
| 3 | 75 | 0.3 | Triangular |
| 4 | 150 | 0.1 | Rectangular |
| 5 | 150 | 0.2 | Triangular |
| 6 | 150 | 0.3 | Flat |
| 7 | 225 | 0.1 | Triangular |
| 8 | 225 | 0.2 | Flat |
| 9 | 225 | 0.3 | Rectangular |
| Level | Cutting Speed m/min | Feed mm/rev | Micro Groove |
|---|---|---|---|
| 1 | −52.30 | −52.89 | −53.07 |
| 2 | −53.10 | −52.76 | −52.33 |
| 3 | −53.09 | −52.85 | −53.09 |
| Delta | 0.79 | 0.13 | 0.75 |
| Rank | 1 | 3 | 2 |
| Level | Cutting Speed m/min | Feed mm/rev | Micro Groove |
|---|---|---|---|
| 1 | 412.9 | 441.3 | 450.9 |
| 2 | 451.8 | 436.1 | 414.4 |
| 3 | 452.1 | 439.4 | 451.5 |
| Delta | 39.1 | 5.2 | 37.0 |
| Rank | 1 | 3 | 2 |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Cutting speed m/min | 2 | 1.25 | 48.72% | 1.25 | 0.62 | 7.03 | 0.12 |
| Feed mm/rev | 2 | 0.03 | 1.06% | 0.03 | 0.01 | 0.15 | 0.87 |
| Micro groove | 2 | 1.11 | 43.29% | 1.11 | 0.56 | 6.25 | 0.14 |
| Error | 2 | 0.18 | 6.93% | 0.18 | 0.09 | ||
| Total | 8 | 2.57 | 100.00% |
| Sr. No. | Cutting Speed (m/min) | Microgroove | Feed (mm/rev) | Undeformed Chip Thickness (mm) | Chip Ratio | Shear Angle (Degree) |
|---|---|---|---|---|---|---|
| Vc | to | tc | r | |||
| 1 | 75 | Flat | 0.1 | 0.11 | 0.901 | 42.01 |
| 2 | 75 | Rectangular | 0.2 | 0.214 | 0.934 | 43.06 |
| 3 | 75 | Triangular | 0.3 | 0.325 | 0.923 | 42.70 |
| 4 | 150 | Rectangular | 0.1 | 0.123 | 0.813 | 39.11 |
| 5 | 150 | Triangular | 0.2 | 0.244 | 0.818 | 39.28 |
| 6 | 150 | Flat | 0.3 | 0.333 | 0.901 | 42.02 |
| 7 | 225 | Triangular | 0.1 | 0.129 | 0.775 | 37.78 |
| 8 | 225 | Flat | 0.2 | 0.221 | 0.903 | 42.08 |
| 9 | 225 | Rectangular | 0.3 | 0.326 | 0.920 | 42.62 |
| Sr. No. | Cutting Power W | Shear Velocity m/min | Shear Power W | Chip Velocity m/min | Friction Power W | Total Power W |
|---|---|---|---|---|---|---|
| Pc | Vs | Ps | Vf | Pf | Pt | |
| 1 | 275.89 | 100.947 | 135.886 | 67.56 | 125.226 | 537.002 |
| 2 | 480.64 | 102.655 | 281.575 | 70.09 | 186.051 | 948.266 |
| 3 | 637.13 | 102.068 | 444.000 | 69.23 | 178.281 | 1259.411 |
| 4 | 557.2 | 193.319 | 277.950 | 121.95 | 227.032 | 1062.183 |
| 5 | 906.81 | 193.791 | 616.175 | 122.69 | 237.750 | 1760.736 |
| 6 | 1190.68 | 201.895 | 884.375 | 135.13 | 275.946 | 2351.001 |
| 7 | 813.24 | 284.687 | 446.737 | 174.42 | 284.099 | 1544.076 |
| 8 | 1277.58 | 303.149 | 884.137 | 203.16 | 355.259 | 2516.977 |
| 9 | 1996.16 | 305.773 | 1364.175 | 207.05 | 581.583 | 3941.919 |
| Level | Cutting Speed m/min | Feed mm/rev | Micro Groove |
|---|---|---|---|
| 1 | −50.90 | −46.84 | −50.35 |
| 2 | −50.57 | −51.18 | −51.06 |
| 3 | −50.63 | −54.08 | −50.69 |
| Delta | 0.33 | 7.23 | 0.71 |
| Rank | 3 | 1 | 2 |
| Level | Cutting Speed m/min | Feed mm/rev | Micro Groove |
|---|---|---|---|
| 1 | 371.4 | 219.9 | 345.6 |
| 2 | 354.0 | 362.6 | 379.9 |
| 3 | 363.3 | 506.1 | 363.1 |
| Delta | 17.4 | 286.2 | 34.3 |
| Rank | 3 | 1 | 2 |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Cutting speed m/min | 2 | 0.181 | 0.22% | 0.181 | 0.090 | 1.57 | 0.389 |
| Feed mm/rev | 2 | 79.450 | 98.69% | 79.495 | 39.747 | 691.12 | 0.001 |
| Micro groove | 2 | 0.760 | 0.94% | 0.760 | 0.378 | 6.60 | 0.132 |
| Error | 2 | 0.115 | 0.14% | 0.115 | 0.057 | ||
| Total | 8 | 80.550 | 100.00% |
| Microgroove | Cutting Speed (m/min) | Feed Rate (mm/rev) | Fx (N) | Fy (N) | Power (W) | Temperature (°C) |
|---|---|---|---|---|---|---|
| Rectangular | 225 | 0.3 | 523.31 | 168.53 | 1996.16 | 421.55 |
| Flat | 225 | 0.3 | 455.46 | 109.39 | 1707.98 | 470.55 |
| Triangle | 225 | 0.3 | 489.43 | 119.34 | 1835.36 | 470.66 |
| Triangular | 75 | 0.3 | 509.71 | 154.51 | 637.13 | 435.5 |
| Flat | 75 | 0.3 | 491.208 | 151.298 | 614.010 | 437.493 |
| Rectangular | 75 | 0.3 | 518.582 | 170.725 | 648.227 | 410.555 |
| Microgroove | Cutting Speed m/min | Feed Rate mm/rev | Fx (N) | Fy (N) | Power (W) | Temperature (°C) |
|---|---|---|---|---|---|---|
| Flat | 75 | 0.1 | 219.91 | 111.201 | 275.89 | 420.68 |
| Rectangular | 75 | 0.1 | 233.77 | 124.373 | 292.224 | 390.771 |
| Triangle | 75 | 0.1 | 231.38 | 120.37 | 289.231 | 424.148 |
| Triangular | 75 | 0.3 | 509.71 | 154.51 | 637.13 | 435.5 |
| Flat | 75 | 0.3 | 491.208 | 151.298 | 614.011 | 437.493 |
| Rectangular | 75 | 0.3 | 518.582 | 170.725 | 648.227 | 410.555 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, S.; Abdallah, S.; Pervaiz, S. Predicting Cutting Force and Primary Shear Behavior in Micro-Textured Tools Assisted Machining of AISI 630: Numerical Modeling and Taguchi Analysis. Micromachines 2022, 13, 91. https://doi.org/10.3390/mi13010091
Ali S, Abdallah S, Pervaiz S. Predicting Cutting Force and Primary Shear Behavior in Micro-Textured Tools Assisted Machining of AISI 630: Numerical Modeling and Taguchi Analysis. Micromachines. 2022; 13(1):91. https://doi.org/10.3390/mi13010091
Chicago/Turabian StyleAli, Shafahat, Said Abdallah, and Salman Pervaiz. 2022. "Predicting Cutting Force and Primary Shear Behavior in Micro-Textured Tools Assisted Machining of AISI 630: Numerical Modeling and Taguchi Analysis" Micromachines 13, no. 1: 91. https://doi.org/10.3390/mi13010091
APA StyleAli, S., Abdallah, S., & Pervaiz, S. (2022). Predicting Cutting Force and Primary Shear Behavior in Micro-Textured Tools Assisted Machining of AISI 630: Numerical Modeling and Taguchi Analysis. Micromachines, 13(1), 91. https://doi.org/10.3390/mi13010091







