MEMS-Based Tactile Sensors: Materials, Processes and Applications in Robotics
Abstract
:1. Introduction
1.1. Principles of Tactile Sensing: A Summary
1.2. Types of Tactile Sensors: A Brief Look
1.3. Analysis and Design Principles of MEMS Devices

2. MEMS-Based Barometers and Their Recent Applications in Tactile Sensing
3. Flexible MEMS-Based Tactile Sensors
3.1. A Brief Review of Principles and Applications of Flexible Capacitor, Piezoelectric, Magnetic and Conductive Pressure/Force Sensors
3.2. MEMS Tactile Sensors Utilizing Triboelectric Effect
4. Hardness/Stiffness Sensing by MEMS Devices
5. Textile Integrated MEMS Sensors
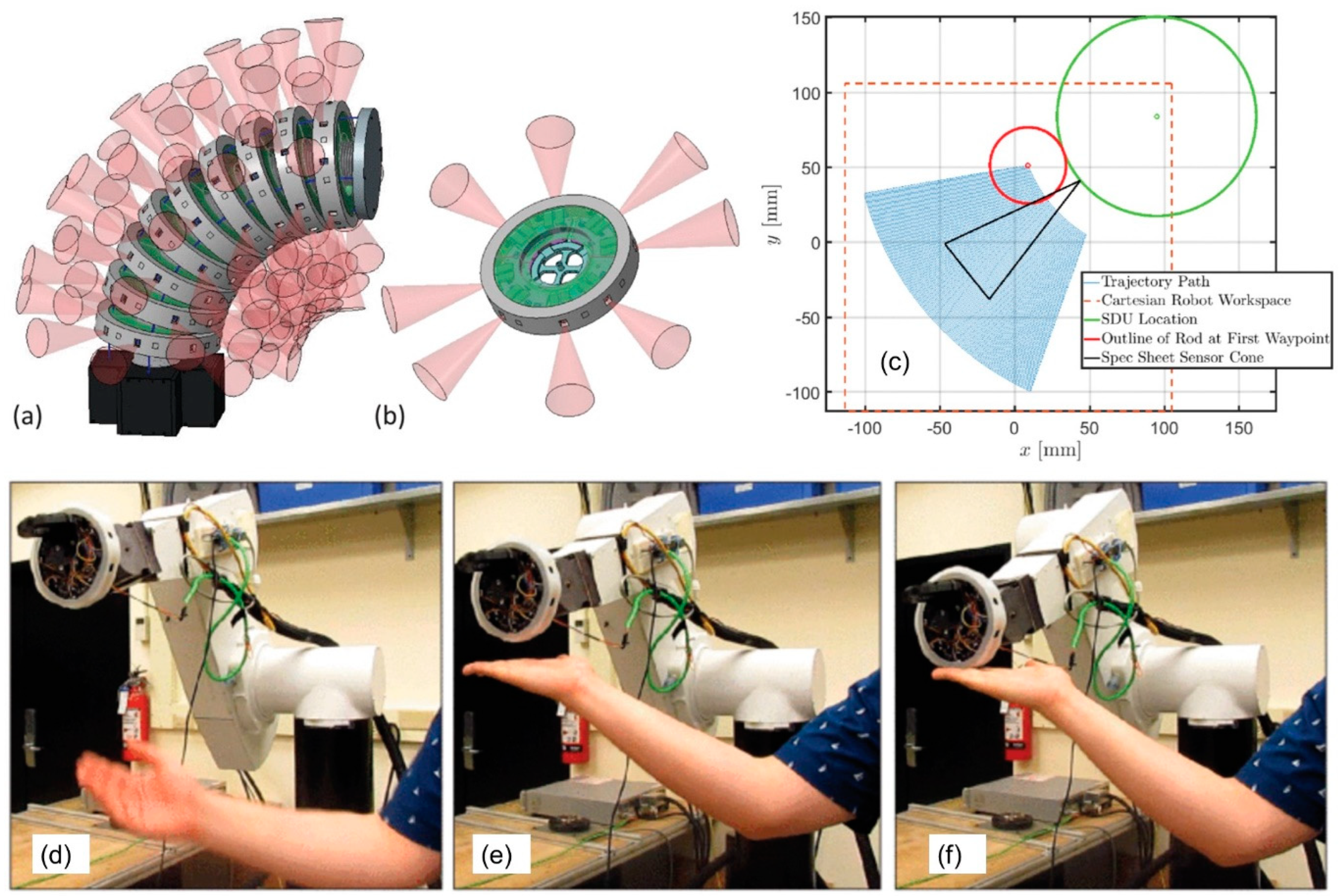
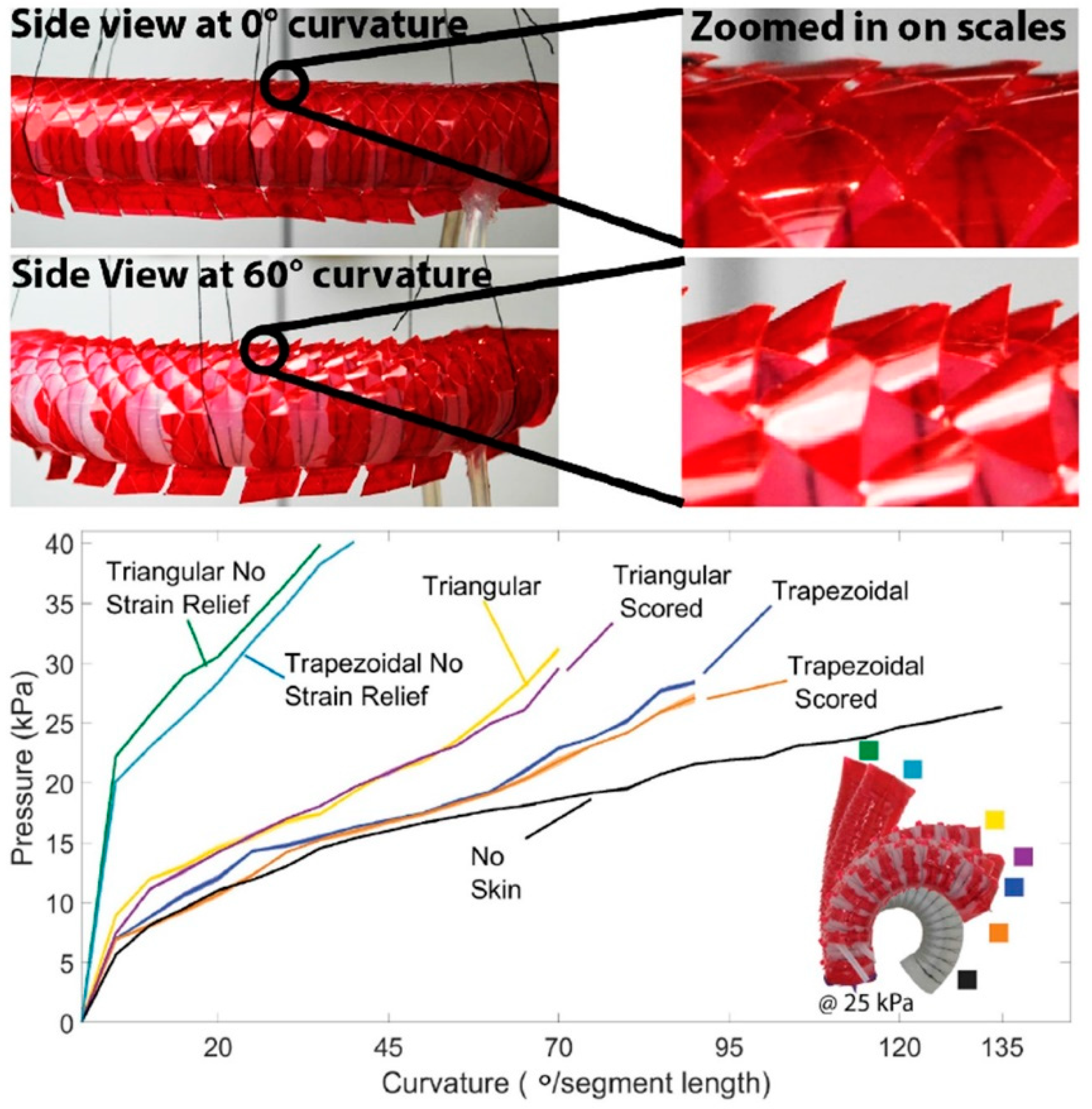
6. MEMS Tactile Sensors on Robotic Platforms: Demonstrators
7. Summary and Outlook
- Very low noise and unique relative accuracy;
- Very low power;
- Improved gyroscope temperature stability;
- Obstacle detection with advanced color and light manipulation;
- Terrain recognition with integrated ultrasonics;
- On board instant IMU data computation;
- Easier and faster robot motor control;
- Noise filter and noise cancellation;
- Robot operating system drivers for all on-board sensors.
Funding
Data Availability Statement
Conflicts of Interest
References
- Dahiya, R.S.; Metta, G.; Valle, M.; Sandini, G. Tactile sensing—From humans to humanoids. IEEE Trans. Robot. 2009, 26, 1–20. [Google Scholar] [CrossRef]
- Dargahi, J.; Najarian, S. Human tactile perception as a standard for artificial tactile sensing—A review. Int. J. Med. Robot. Comput. Assist. Surg. 2004, 1, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Westling, G.; Johansson, R.S. Factors influencing the force control during precision grip. Exp. Brain Res. 1984, 53, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Francomano, M.T.; Accoto, D.; Guglielmelli, E. Artificial sense of slip—A review. IEEE Sens. J. 2013, 13, 2489–2498. [Google Scholar] [CrossRef]
- Lederman, S.J.; Klatzky, R.L. Extracting object properties through haptic exploration. Acta Psychol. 1993, 84, 29–40. [Google Scholar] [CrossRef] [PubMed]
- Catania, K.C. Evolution of brains and behavior for optimal foraging: A tale of two predators. Proc. Natl. Acad. Sci. USA 2012, 109 (Suppl. S1), 10701–10708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maheshwari, V.; Saraf, R. Tactile Devices to Sense Touch on a Par with a Human Finger. Angew. Chem. Int. Ed. 2008, 47, 7808–7826. [Google Scholar] [CrossRef]
- Sun, J.Y.; Keplinger, C.; Whitesides, G.M.; Suo, Z. Ionic skin. Adv. Mater. 2014, 26, 7608–7614. [Google Scholar] [CrossRef]
- Carpenter, C.W.; Dhong, C.; Root, N.B.; Rodriquez, D.; Abdo, E.E.; Skelil, K.; Alkhadra, M.A.; Ramírez, J.; Ramachandran, V.S.; Lipomi, D.J. Human ability to discriminate surface chemistry by touch. Mater. Horizons 2017, 5, 70–77. [Google Scholar] [CrossRef]
- Mate, C.M.; Carpick, R.W. A sense for touch. Nature 2011, 480, 189–190. [Google Scholar] [CrossRef]
- Petersen, E.N.; Chung, H.-W.; Nayebosadri, A.; Hansen, S.B. Kinetic disruption of lipid rafts is a mechanosensor for phospholipase D. Nat. Commun. 2016, 7, 13873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Welsh, M.J.; Price, M.P.; Xie, J. Biochemical Basis of Touch Perception: Mechanosensory Function of Degenerin/Epithelial Na+ Channels. J. Biol. Chem. 2002, 277, 2369–2372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fearing, R.S.; Hollerbach, J.M. Basic solid mechanics for tactile sensing. Int. J. Robot. Res. 1985, 4, 40–54. [Google Scholar] [CrossRef]
- Cutkosky, M.R.; Howe, R.D.; Provancher, W.R. Force and Tactile Sensors. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Lee, M.H. Tactile sensing: New directions, new challenges. Int. J. Robot. Res. 2000, 19, 636–643. [Google Scholar] [CrossRef]
- Luo, S.; Bimbo, J.; Dahiya, R.; Liu, H. Robotic tactile perception of object properties: A review. Mechatronics 2017, 48, 54–67. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.H.; Nicholls, H.R. Review Article Tactile sensing for mechatronics—A state of the art survey. Mechatronics 1999, 9, 1–31. [Google Scholar] [CrossRef]
- Jara, C.A.; Pomares, J.; Candelas-Herías, F.A.; Torres, F. Control Framework for Dexterous Manipulation Using Dynamic Visual Servoing and Tactile Sensors’ Feedback. Sensors 2014, 14, 1787–1804. [Google Scholar] [CrossRef] [Green Version]
- Howe, R.D.; Cutkosky, M.R. Dynamic tactile sensing: Perception of fine surface features with stress rate sensing. IEEE Trans. Robot. Autom. 1993, 9, 140–151. [Google Scholar] [CrossRef]
- Zhang, J.; Yao, H.; Mo, J.; Chen, S.; Xie, Y.; Ma, S.; Chen, R.; Luo, T.; Ling, W.; Qin, L.; et al. Finger-inspired rigid-soft hybrid tactile sensor with superior sensitivity at high frequency. Nat. Commun. 2022, 13, 5076. [Google Scholar] [CrossRef]
- Cutkosky, M.R.; Ulmen, J. Dynamic tactile sensing. In The Human Hand as an Inspiration for Robot Hand Development; Springer: Cham, Switzerland, 2014; pp. 389–403. [Google Scholar]
- Lee, W.W.; Kukreja, S.L.; Thakor, N.V. Discrimination of Dynamic Tactile Contact by Temporally Precise Event Sensing in Spiking Neuromorphic Networks. Front. Neurosci. 2017, 11, 5. [Google Scholar] [CrossRef] [Green Version]
- Trinh, H.X.; Iwamoto, Y.; Ho, V.A.; Shibuya, K. Localization of Sliding Movements Using Soft Tactile Sensing Systems with Three-axis Accelerometers. Sensors 2019, 19, 2036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chi, C.; Sun, X.; Xue, N.; Li, T.; Liu, C. Recent Progress in Technologies for Tactile Sensors. Sensors 2018, 18, 948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Girão, P.S.; Ramos, P.M.P.; Postolache, O.; Pereira, J. Tactile sensors for robotic applications. Measurement 2013, 46, 1257–1271. [Google Scholar] [CrossRef]
- Saccomandi, P.; Schena, E.; Oddo, C.M.; Zollo, L.; Silvestri, S.; Guglielmelli, E. Microfabricated Tactile Sensors for Biomedical Applications: A Review. Biosensors 2014, 4, 422–448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krishna, G.; Rajanna, K. Tactile Sensor Based on Piezoelectric Resonance. IEEE Sensors J. 2004, 4, 691–697. [Google Scholar] [CrossRef]
- Salim, A.; Lim, S. Review of Recent Inkjet-Printed Capacitive Tactile Sensors. Sensors 2017, 17, 2593. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, H.; Recchiuto, C.; Oddo, C.; Beccai, L.; Anthony, C.; Adams, M.; Carrozza, M.; Ward, M. A capacitive tactile sensor array for surface texture discrimination. Microelectron. Eng. 2011, 88, 1811–1813. [Google Scholar] [CrossRef]
- Sferrazza, C.; D’Andrea, R. Design, Motivation and Evaluation of a Full-Resolution Optical Tactile Sensor. Sensors 2019, 19, 928. [Google Scholar] [CrossRef] [Green Version]
- Lepora, N.F. Soft Biomimetic Optical Tactile Sensing with the TacTip: A Review. IEEE Sensors J. 2021, 21, 21131–21143. [Google Scholar] [CrossRef]
- Begej, S. Planar and finger-shaped optical tactile sensors for robotic applications. IEEE J. Robot. Autom. 1988, 4, 472–484. [Google Scholar] [CrossRef]
- Wang, H.; De Boer, G.; Kow, J.; Alazmani, A.; Ghajari, M.; Hewson, R.; Culmer, P. Design Methodology for Magnetic Field-Based Soft Tri-Axis Tactile Sensors. Sensors 2016, 16, 1356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Y.; Hu, Z.; Yang, Z.; Yuan, W.; Song, C.; Pan, J.; Shen, Y. Soft magnetic skin for super-resolution tactile sensing with force self-decoupling. Sci. Robot. 2021, 6, eabc8801. [Google Scholar] [CrossRef] [PubMed]
- Maita, F.; Maiolo, L.; Minotti, A.; Pecora, A.; Ricci, D.; Metta, G.; Scandurra, G.; Giusi, G.; Ciofi, C.; Fortunato, G. Ultraflexible Tactile Piezoelectric Sensor Based on Low-Temperature Polycrystalline Silicon Thin-Film Transistor Technology. IEEE Sensors J. 2015, 15, 3819–3826. [Google Scholar] [CrossRef]
- Yu, P.; Liu, W.; Gu, C.; Cheng, X.; Fu, X. Flexible Piezoelectric Tactile Sensor Array for Dynamic Three-Axis Force Measurement. Sensors 2016, 16, 819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, N.; Dou, W.; Hao, S.; Cheng, Y.; Zhou, D.; Huang, X.; Jiang, C.; Cao, X. Tactile sensor from self-chargeable piezoelectric supercapacitor. Nano Energy 2019, 56, 868–874. [Google Scholar] [CrossRef]
- Howe, R.; Cutkosky, M. Sensing skin acceleration for slip and texture perception. In Proceedings of the 1989 International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; pp. 145–150. [Google Scholar] [CrossRef]
- Chen, W.; Khamis, H.; Birznieks, I.; Lepora, N.F.; Redmond, S.J. Tactile Sensors for Friction Estimation and Incipient Slip Detection—Toward Dexterous Robotic Manipulation: A Review. IEEE Sensors J. 2018, 18, 9049–9064. [Google Scholar] [CrossRef] [Green Version]
- Shibuya, K.; Iwamoto, Y.; Trinh, H.X. Detecting sliding movement location on morphologically changeable soft tactile sensing system with three-axis accelerometer. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Republic of Korea, 14–18 April 2019; pp. 337–342. [Google Scholar]
- Scherge, M.; Gorb, S.N. Using biological principles to design MEMS. J. Micromech. Microeng. 2000, 10, 359. [Google Scholar] [CrossRef]
- Mishra, M.K.; Dubey, V.; Mishra, P.M.; Khan, I. MEMS Technology: A Review. J. Eng. Res. Rep. 2019, 4, 1–24. [Google Scholar] [CrossRef]
- Albarbar, A.; Badri, A.; Sinha, J.K.; Starr, A. Performance evaluation of MEMS accelerometers. Measurement 2009, 42, 790–795. [Google Scholar] [CrossRef] [Green Version]
- Jachowicz, R.S.; Weremczuk, J.; Paczesny, D.; Tarapata, G. A MEMS-based super fast dew point hygrometer—Construction and medical applications. Meas. Sci. Technol. 2009, 20, 124008. [Google Scholar] [CrossRef]
- Balavalad, K.B.; Sheeparamatti, B.G. A critical review of MEMS capacitive pressure sensors. Sens. Transducers 2015, 187, 120. [Google Scholar]
- Mehmood, Z.; Haneef, I.; Udrea, F. Material selection for optimum design of MEMS pressure sensors. Microsyst. Technol. 2020, 26, 2751–2766. [Google Scholar] [CrossRef] [Green Version]
- Song, P.; Ma, Z.; Ma, J.; Yang, L.; Wei, J.; Zhao, Y.; Zhang, M.; Yang, F.; Wang, X. Recent Progress of Miniature MEMS Pressure Sensors. Micromachines 2020, 11, 56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albarbar, A.; Mekid, S.; Starr, A.; Pietruszkiewicz, R. Suitability of MEMS Accelerometers for Condition Monitoring: An experimental study. Sensors 2008, 8, 784–799. [Google Scholar] [CrossRef] [Green Version]
- Miller, K.; Erdos, D. Technology Update: The Dawn of MEMS Sensors for Directional Drilling. J. Pet. Technol. 2018, 70, 18–19. [Google Scholar] [CrossRef]
- Ciuti, G.; Ricotti, L.; Menciassi, A.; Dario, P. MEMS Sensor Technologies for Human Centred Applications in Healthcare, Physical Activities, Safety and Environmental Sensing: A Review on Research Activities in Italy. Sensors 2015, 15, 6441–6468. [Google Scholar] [CrossRef] [Green Version]
- Dheringe, N.; Rahane, S. Recent advances in mems sensor technology biomedical mechanical thermo-fluid & electromagnetic sensors. Int. J. Electron. Commun. Instrum. Eng. Res. Dev. 2013, 3, 73–90. [Google Scholar]
- Mishra, R.B.; El-Atab, N.; Hussain, A.M.; Hussain, M.M. Recent progress on flexible capacitive pressure sensors: From design and materials to applications. Adv. Mater. Technol. 2021, 6, 2001023. [Google Scholar] [CrossRef]
- Xu, F.; Li, X.; Shi, Y.; Li, L.; Wang, W.; He, L.; Liu, R. Recent Developments for Flexible Pressure Sensors: A Review. Micromachines 2018, 9, 580. [Google Scholar] [CrossRef] [Green Version]
- Jiménez, S.; Cole, M.O.; Keogh, P.S. Vibration sensing in smart machine rotors using internal MEMS accelerometers. J. Sound Vib. 2016, 377, 58–75. [Google Scholar] [CrossRef]
- Tenzer, Y.; Jentoft, L.P.; Howe, R.D. The Feel of MEMS Barometers: Inexpensive and Easily Customized Tactile Array Sensors. IEEE Robot. Autom. Mag. 2014, 21, 89–95. [Google Scholar] [CrossRef]
- Kumar, S.S.; Tanwar, A. Development of a MEMS-based barometric pressure sensor for micro air vehicle (MAV) altitude measurement. Microsyst. Technol. 2020, 26, 901–912. [Google Scholar] [CrossRef]
- Zaliva, V.; Franchetti, F. Barometric and GPS altitude sensor fusion. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 7525–7529. [Google Scholar] [CrossRef]
- Tian, X.; Chen, J.; Han, Y.; Shang, J.; Li, N. Pedestrian navigation system using MEMS sensors for heading drift and altitude error correction. Sens. Rev. 2017, 37, 270–281. [Google Scholar] [CrossRef]
- Manivannan, A.; Chin, W.C.B.; Barrat, A.; Bouffanais, R. On the Challenges and Potential of Using Barometric Sensors to Track Human Activity. Sensors 2020, 20, 6786. [Google Scholar] [CrossRef] [PubMed]
- Guggenheim, J.W.; Jentoft, L.P.; Tenzer, Y.; Howe, R.D. Robust and Inexpensive Six-Axis Force–Torque Sensors Using MEMS Barometers. IEEE/ASME Trans. Mechatronics 2017, 22, 838–844. [Google Scholar] [CrossRef]
- Grover, A.; Nadeau, P.; Grebe, C.; Kelly, J. Learning to Detect Slip with Barometric Tactile Sensors and a Temporal Convolutional Neural Network. arXiv 2022, arXiv:2202.09549. [Google Scholar] [CrossRef]
- De Oliveira, T.E.A.; Cretu, A.-M.; Petriu, E.M. Multimodal Bio-Inspired Tactile Sensing Module for Surface Characterization. Sensors 2017, 17, 1187. [Google Scholar] [CrossRef] [Green Version]
- De Clercq, T.; Sianov, A.; Crevecoeur, G. A Soft Barometric Tactile Sensor to Simultaneously Localize Contact and Estimate Normal Force with Validation to Detect Slip in a Robotic Gripper. IEEE Robot. Autom. Lett. 2022, 7, 11767–11774. [Google Scholar] [CrossRef]
- Song, A.; Fu, L. Multi-dimensional force sensor for haptic interaction: A review. Virtual Real. Intell. Hardw. 2019, 1, 121–135. [Google Scholar] [CrossRef]
- Kõiva, R.; Schwank, T.; Walck, G.; Meier, M.; Haschke, R.; Ritter, H. Barometer-based tactile skin for anthropomorphic robot hand. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2020; pp. 9821–9826. [Google Scholar]
- Nguyen, D.-S.; Pillatsch, P.; Zhu, Y.; Paprotny, I.; Wright, P.K.; White, R.D. MEMS-based capacitive pressure sensors with pre-stressed sensing diaphragms. In Proceedings of the IEEE Sensors, Busan, Republic of Korea, 1–4 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Bhandari, B.; Lee, M. Haptic identification of objects using tactile sensing and computer vision. Adv. Mech. Eng. 2019, 11, 1687814019840468. [Google Scholar] [CrossRef] [Green Version]
- Pelliccia, L.; Schumann, M.; Dudczig, M.; Lamonaca, M.; Klimant, P.; Di Gironimo, G. Implementation of tactile sensors on a 3-Fingers Robotiq® adaptive gripper and visualization in VR using Arduino controller. Procedia CIRP 2018, 67, 250–255. [Google Scholar] [CrossRef]
- Claver, U.P.; Zhao, G. Recent Progress in Flexible Pressure Sensors Based Electronic Skin. Adv. Eng. Mater. 2021, 23, 2001187. [Google Scholar] [CrossRef]
- Ashruf, C.M.A. Thin flexible pressure sensors. Sens. Rev. 2002, 22, 322–327. [Google Scholar] [CrossRef]
- Lakamraju, N.V.; Phillips, S.M.; Venugopal, S.M.; Allee, D.R. MEMS shock sensor fabricated on flexible substrate. In Proceedings of the 2009 Flexible Electronics & Displays Conference and Exhibition, Pheonix, AZ, USA, 2–5 February 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Sriphan, S.; Charoonsuk, T.; Khaisaat, S.; Sawanakarn, O.; Pharino, U.; Phunpruch, S.; Maluangnont, T.; Vittayakorn, N. Flexible capacitive sensor based on 2D-titanium dioxide nanosheets/bacterial cellulose composite film. Nanotechnology 2021, 32, 155502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Howver, R.; Gogoi, B.; Yazdi, N. A high-sensitive ultra-thin MEMS capacitive pressure sensor. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 112–115. [Google Scholar] [CrossRef]
- Lee, H.-K.; Chang, S.-I.; Yoon, E. A Flexible Polymer Tactile Sensor: Fabrication and Modular Expandability for Large Area Deployment. J. Microelectromech. Syst. 2006, 15, 1681–1686. [Google Scholar] [CrossRef]
- El-Molla, S.; Albrecht, A.; Cagatay, E.; Mittendorfer, P.; Cheng, G.; Lugli, P.; Salmerón, J.F.; Rivadeneyra, A. Integration of a thin film pdms-based capacitive sensor for tactile sensing in an electronic skin. J. Sens. 2016, 2016, 1736169. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Huang, X.H.; Ma, C.W.; Yang, Y.J. A flexible capacitive tactile sensing array with floating electrodes. J. Micromech. Microeng. 2009, 19, 115001. [Google Scholar] [CrossRef]
- Zhang, Y.; Sezen, S.; Ahmadi, M.; Cheng, X.; Rajamani, R. Paper-based supercapacitive mechanical sensors. Sci. Rep. 2018, 8, 16284. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Sun, X.; Hubbe, M.; Pal, L. Flexible and pressure-responsive sensors from cellulose fibers coated with multiwalled carbon nanotubes. ACS Appl. Electron. Mater. 2019, 1, 1179–1188. [Google Scholar] [CrossRef]
- Qin, Y.; Peng, Q.; Ding, Y.; Lin, Z.; Wang, C.; Li, Y.; Xu, F.; Li, J.; Yuan, Y.; He, X.; et al. Lightweight, superelastic, and mechanically flexible graphene/polyimide nanocomposite foam for strain sensor application. ACS Nano 2015, 9, 8933–8941. [Google Scholar] [CrossRef]
- Tian, H.; Shu, Y.; Wang, X.-F.; Mohammad, M.A.; Bie, Z.; Xie, Q.-Y.; Li, C.; Mi, W.-T.; Yang, Y.; Ren, T.-L. A graphene-based resistive pressure sensor with record-high sensitivity in a wide pressure range. Sci. Rep. 2015, 5, 8603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, H.; Xie, Y.; Zhu, E.; Liu, Y.; Shi, Z.; Xiong, C.; Yang, Q. Supertough and ultrasensitive flexible electronic skin based on nanocellulose/sulfonated carbon nanotube hydrogel films. J. Mater. Chem. A 2020, 8, 6311–6318. [Google Scholar] [CrossRef]
- Khalifa, M.; Wuzella, G.; Lammer, H.; Mahendran, A.R. Smart paper from graphene coated cellulose for high-performance humidity and piezoresistive force sensor. Synth. Met. 2020, 266, 116420. [Google Scholar] [CrossRef]
- Chitra, L.; Ramakrishnan, V. A novel design of capacitive MEMS pressure sensor for lubricating system. In Proceedings of the 2014 IEEE National Conference on Emerging Trends in New & Renewable Energy Sources and Energy Management (NCET NRES EM), Chennai, India, 16–17 December 2014; pp. 204–208. [Google Scholar] [CrossRef]
- Baek, S.; Jang, H.; Kim, S.Y.; Jeong, H.; Han, S.; Jang, Y.; Kim, D.H.; Lee, H.S. Flexible piezocapacitive sensors based on wrinkled microstructures: Toward low-cost fabrication of pressure sensors over large areas. RSC Adv. 2017, 7, 39420–39426. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Zhuo, B.; Guo, X. Large Area One-Step Facile Processing of Microstructured Elastomeric Dielectric Film for High Sensitivity and Durable Sensing over Wide Pressure Range. ACS Appl. Mater. Interfaces 2016, 8, 20364–20370. [Google Scholar] [CrossRef] [PubMed]
- Bijender; Kumar, A. One-Rupee Ultrasensitive Wearable Flexible Low-Pressure Sensor. ACS Omega 2020, 5, 16944–16950. [Google Scholar] [CrossRef] [PubMed]
- Jang, Y.; Jo, J.; Woo, K.; Lee, S.-H.; Kwon, S.; Kim, H.; Lee, H.S. Fabrication of Highly Sensitive Piezocapacitive Pressure Sensors using a Simple and Inexpensive Home Milk Frother. Phys. Rev. Appl. 2019, 11, 014037. [Google Scholar] [CrossRef]
- Kumar, A. Flexible and wearable capacitive pressure sensor for blood pressure monitoring. Sens. Bio-Sensing Res. 2021, 33, 100434. [Google Scholar] [CrossRef]
- Abels, C.; Mastronardi, V.M.; Guido, F.; Dattoma, T.; Qualtieri, A.; Megill, W.M.; De Vittorio, M.; Rizzi, F. Nitride-Based Materials for Flexible MEMS Tactile and Flow Sensors in Robotics. Sensors 2017, 17, 1080. [Google Scholar] [CrossRef] [Green Version]
- Manikandan, N.; Valleti, K.; Karupasamy, K.; Divagar, M.; Subramaniam, S. The monolithic α, β crystal structural design of piezoelectric poly (vinylidene fluoride) (PVDF) polymer/fullerene based sensor array for the measurement of lung pressure. Sens. Bio-Sensing Res. 2021, 32, 100418. [Google Scholar] [CrossRef]
- Patil, S.; Chu, V.; Conde, J. Performance of thin film silicon MEMS on flexible plastic substrates. Sens. Actuators A Phys. 2008, 144, 201–206. [Google Scholar] [CrossRef]
- Engel, J.; Chen, J.; Fan, Z.; Liu, C. Polymer micromachined multimodal tactile sensors. Sens. Actuators A Phys. 2005, 117, 50–61. [Google Scholar] [CrossRef]
- Kim, S.-H.; Engel, J.; Liu, C.; Jones, D.L. Texture classification using a polymer-based MEMS tactile sensor. J. Micromech. Microeng. 2005, 15, 912. [Google Scholar] [CrossRef] [Green Version]
- Khoshnoud, F.; de Silva, C.W. Recent advances in MEMS sensor technology-mechanical applications. IEEE Instrum. Meas. Mag. 2012, 15, 14–24. [Google Scholar] [CrossRef]
- Takao, H.; Yawata, M.; Kodama, R.; Sawada, K.; Ishida, M. Multi-functional Monolithic-MEMS Tactile Imager Using Flexible Deformation of Silicon IC. In Proceedings of the 2007 IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 16–19 September 2007; pp. 131–134. [Google Scholar] [CrossRef]
- Wang, J.; Qian, S.; Yu, J.; Zhang, Q.; Yuan, Z.; Sang, S.; Zhou, X.; Sun, L. Flexible and Wearable PDMS-Based Triboelectric Nanogenerator for Self-Powered Tactile Sensing. Nanomaterials 2019, 9, 1304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, N.; Yin, Z.; Zhang, W.; Xing, C.; Peng, T.; Meng, B.; Yang, J.; Peng, Z. A triboelectric-inductive hybrid tactile sensor for highly accurate object recognition. Nano Energy 2022, 96, 107063. [Google Scholar] [CrossRef]
- Maeda, Y.; Terao, K.; Shimokawa, F.; Takao, H. A MEMS hardness sensor with reduced contact force dependence based on the reference plane concept aimed for medical applications. Jpn. J. Appl. Phys. 2016, 55, 04EF11. [Google Scholar] [CrossRef]
- Zhao, S.; Parks, D.; Liu, C. Design and Modeling of a Wide Dynamic-Range Hardness Sensor for Biological Tissue Assessment. IEEE Sensors J. 2013, 13, 4613–4620. [Google Scholar] [CrossRef]
- Peng, P.; Sezen, A.; Rajamani, R.; Erdman, A. Novel MEMS stiffness sensor for force and elasticity measurements. Sensors Actuators A Phys. 2010, 158, 10–17. [Google Scholar] [CrossRef]
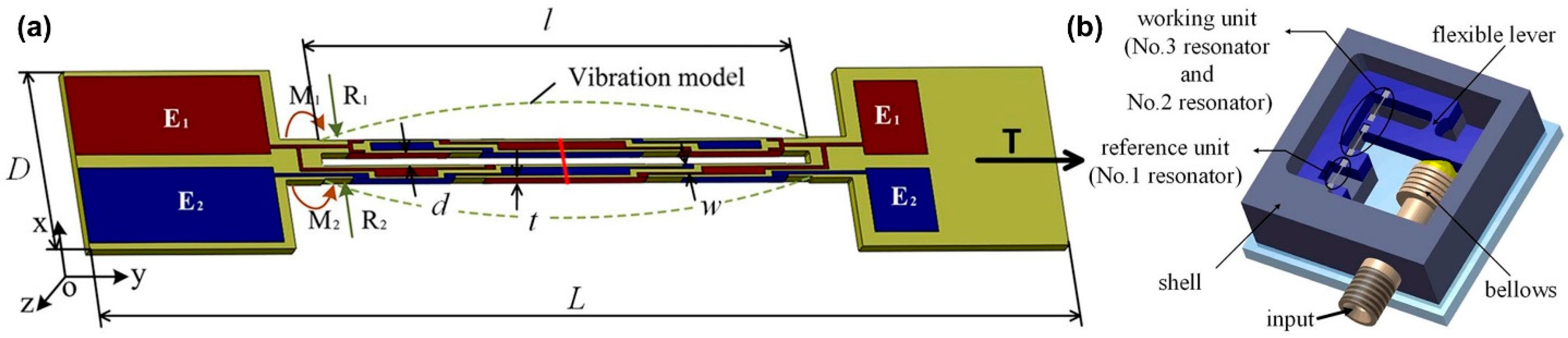
- Zhao, C.; Montaseri, M.H.; Wood, G.S.; Pu, S.H.; Seshia, A.A.; Kraft, M. A review on coupled MEMS resonators for sensing applications utilizing mode localization. Sensors Actuators A Phys. 2016, 249, 93–111. [Google Scholar] [CrossRef]
- Pattnaik, P.; Vijayaaditya, B.; Srinivas, T.; Selvarajan, A. Optical MEMS pressure sensor using ring resonator on a circular diaphragm. In Proceedings of the 2005 International Conference on MEMS, NANO and Smart Systems, Banff, AB, Canada, 24–27 July 2005; pp. 277–280. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhao, C.; Zhao, G.; Jin, X.; Zhang, S.; Zou, J. All-Quartz High Accuracy MEMS Pressure Sensor Based on Double-Ended Tuning Fork Resonator. Procedia Eng. 2015, 120, 857–860. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.H.; Alsaleem, F.M.; Ouakad, H.M. Novel threshold pressure sensors based on nonlinear dynamics of MEMS resonators. J. Micromech. Microeng. 2018, 28, 065007. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, L.; Takagi, H.; Itoh, T.; Maeda, R. Hybrid piezoelectric MEMS resonators for application in bio-chemical sensing. J. Appl. Sci. Eng. 2014, 17, 17–24. [Google Scholar] [CrossRef]
- Miller, J.M.L.; Ansari, A.; Heinz, D.B.; Chen, Y.; Flader, I.B.; Shin, D.D.; Villanueva, L.G.; Kenny, T.W. Effective quality factor tuning mechanisms in micromechanical resonators. Appl. Phys. Rev. 2018, 5, 041307. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, C.; Zhao, Y.; Li, B.; Han, C. A high sensitivity quartz resonant pressure sensor with differential output and self-correction. Rev. Sci. Instruments 2019, 90, 065003. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Wang, L.; Li, A.; Wang, L.; Sun, D. High Accuracy Resonant Pressure Sensor with Balanced-Mass DETF Resonator and Twinborn Diaphragms. J. Microelectromech. Syst. 2016, 26, 235–245. [Google Scholar] [CrossRef]
- Xing, Y.; Xie, B.; Chen, J.; Deyong, C.; Junbo, W. A differential resonant pressure micro sensor with identical sensitivity of two resonant beams, High Power Laser Part. Beams 2016, 28, 064130. [Google Scholar]
- Ellis, R.; Ganeshan, S.; Lederman, S. A tactile sensor based on thin-plate deformation. Robotica 1994, 12, 343–351. [Google Scholar] [CrossRef]
- Fouly, A.; El-Bab, A.F.; Nasr, M.N.; Abouelsoud, A. Modeling and experimental testing of three-tip configuration tactile sensor for compensating the error due to soft tissue surface irregularities during stiffness detection. Measurement 2017, 98, 112–122. [Google Scholar] [CrossRef]
- Sul, O.; Choi, E.; Lee, S.-B. A Portable Stiffness Measurement System. Sensors 2017, 17, 2686. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, M.-L.; Yeh, S.-K.; Lee, J.-H.; Cheng, M.-C.; Fang, W. CMOS-MEMS capacitive tactile sensor with vertically integrated sensing electrode array for sensitivity enhancement. Sensors Actuators A: Phys. 2021, 317, 112350. [Google Scholar] [CrossRef]
- Wang, C.; Hao, Y.; Sun, Z.; Zu, L.; Yuan, W.; Chang, H. Design of a Capacitive MEMS Accelerometer with Softened Beams. Micromachines 2022, 13, 459. [Google Scholar] [CrossRef] [PubMed]
- Maroufi, M.; Alemansour, H.; Coskun, M.B.; Moheimani, S.O.R. An adjustable-stiffness MEMS force sensor: Design, characterization, and control. Mechatronics 2018, 56, 198–210. [Google Scholar] [CrossRef]
- Watatani, K.; Terao, K.; Shimokawa, F.; Takao, H. Simultaneous Measurement of Surface Texture and Elasticity Using Tactile Sensor with Differently Protruded Contactor Array. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 454–457. [Google Scholar] [CrossRef]
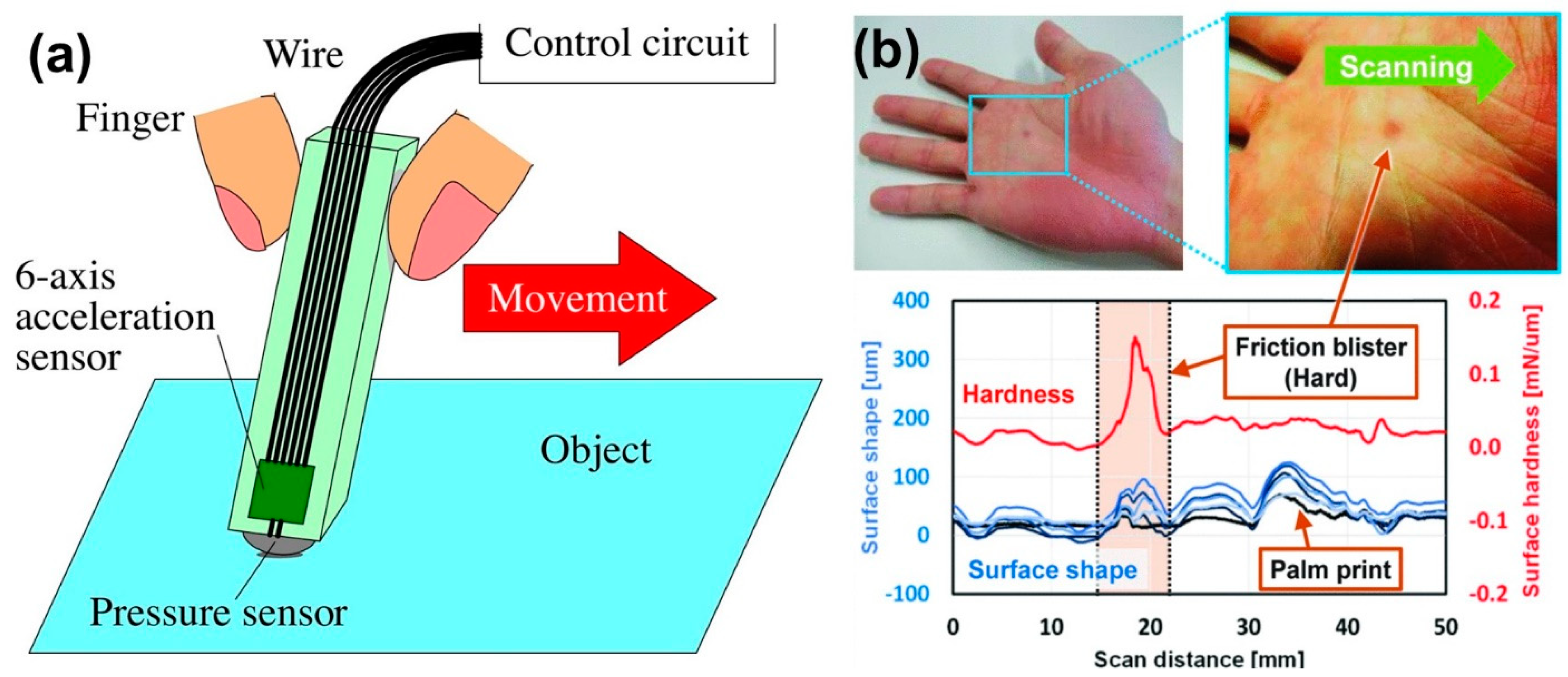
- Nishida, Y.; Watatani, K.; Terao, K.; Shimokawa, F.; Takao, H. Mems-Based “Multi-Tactile Scanner” with 100μm Spatial Resolution of Hardness. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), Gainesville, FL, USA, 25–29 January 2021; pp. 693–696. [Google Scholar] [CrossRef]
- Tsuji, S.; Kohama, T. Using a convolutional neural network to construct a pen-type tactile sensor system for roughness recognition. Sensors Actuators A: Phys. 2019, 291, 7–12. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Cattin, D.; Adami, A.; Collini, C.; Barboni, L.; Valle, M.; Lorenzelli, L.; Oboe, R.; Metta, G.; Brunetti, F. Towards tactile sensing system on chip for robotic applications. IEEE Sens. J. 2011, 11, 3216. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Shikida, M.; Sasaki, H.; Itoigawa, K.; Sato, K. An active tactile sensor for detecting mechanical characteristics of contacted objects. J. Micromech. Microeng. 2006, 16, 1625. [Google Scholar] [CrossRef]
- Bauer, F.; Fousson, E.; Zhang, Q.M. Recent advances in highly electrostrictive P(VDF-TrFE-CFE) terpolymers. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 1149–1154. [Google Scholar] [CrossRef]
- Khudiyev, T.; Clayton, J.D.; Levy, E.C.; Chocat, N.; Gumennik, A.; Stolyarov, A.M.; Joannopoulos, J.; Fink, Y. Electrostrictive microelectromechanical fibres and textiles. Nat. Commun. 2017, 8, 1435. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Wang, Y.; Mei, D.; Jiang, C. Development of Fully Flexible Tactile Pressure Sensor with Bilayer Interlaced Bumps for Robotic Grasping Applications. Micromachines 2020, 11, 770. [Google Scholar] [CrossRef]
- Najafi, M.; Zahid, M.; Ceseracciu, L.; Safarpour, M.; Athanassiou, A.; Bayer, I.S. Polylactic acid-graphene emulsion ink based conductive cotton fabrics. J. Mater. Res. Technol. 2022, 18, 5197–5211. [Google Scholar] [CrossRef]
- Yaragalla, S.; Dussoni, S.; Zahid, M.; Maggiali, M.; Metta, G.; Athanasiou, A.; Bayer, I.S. Stretchable graphene and carbon nanofiber capacitive touch sensors for robotic skin applications. J. Ind. Eng. Chem. 2021, 101, 348–358. [Google Scholar] [CrossRef]
- Shayganpour, A.; Naderizadeh, S.; Grasselli, S.; Malchiodi, A.; Bayer, I.S. Stacked-Cup Carbon Nanotube Flexible Paper Based on Soy Lecithin and Natural Rubber. Nanomaterials 2019, 9, 824. [Google Scholar] [CrossRef] [PubMed]
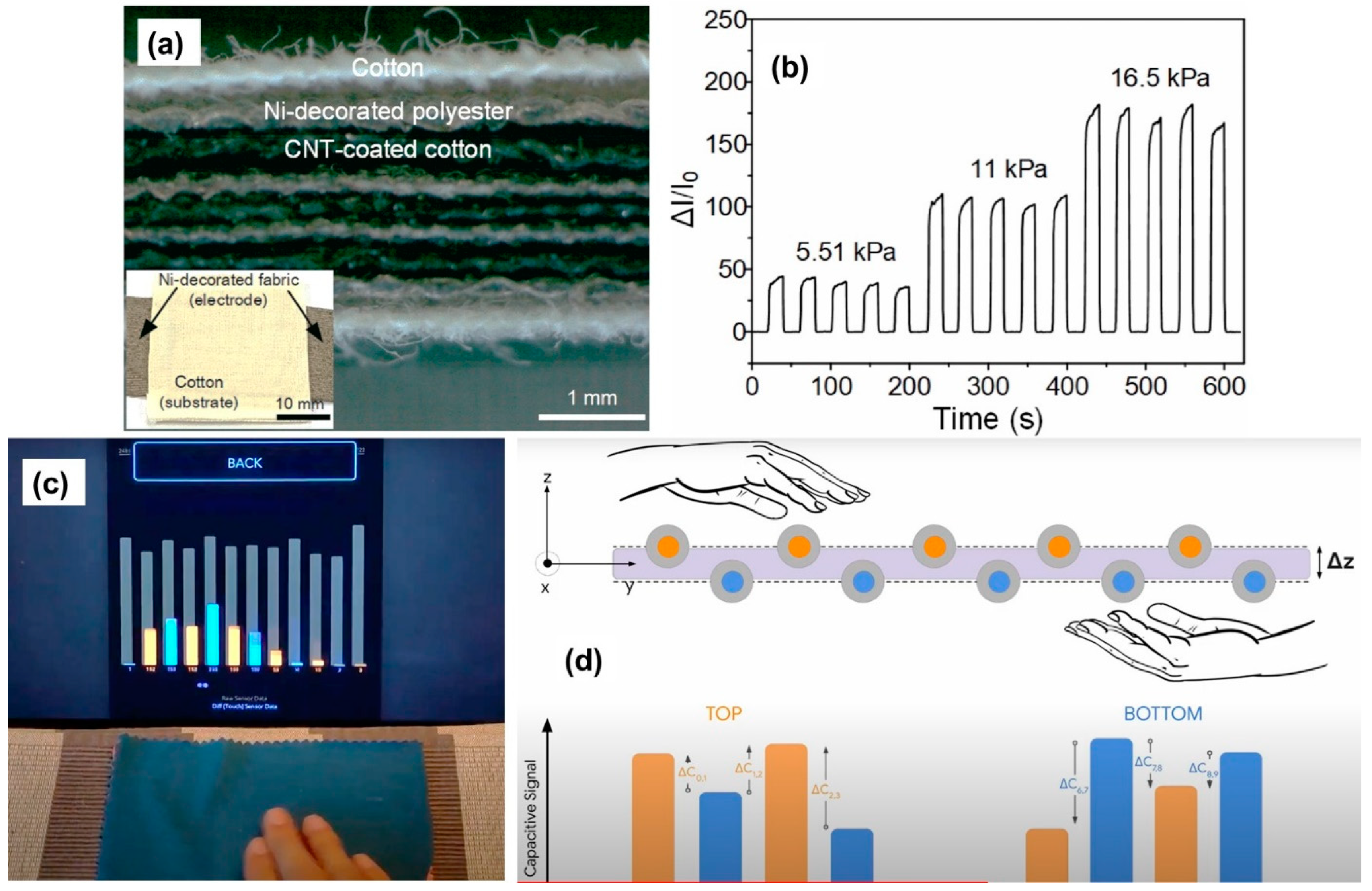
- Zahid, M.; Papadopoulou, E.L.; Athanassiou, A.; Bayer, I.S. Strain-responsive mercerized conductive cotton fabrics based on PEDOT:PSS/graphene. Mater. Des. 2017, 135, 213–222. [Google Scholar] [CrossRef]
- Cataldi, P.; Ceseracciu, L.; Marras, S.; Athanassiou, A.; Bayer, I.S. Electrical conductivity enhancement in thermoplastic polyurethane-graphene nanoplatelet composites by stretch-release cycles. Appl. Phys. Lett. 2017, 110, 121904. [Google Scholar] [CrossRef]
- Pei, Z.; Xiong, X.; He, J.; Zhang, Y. Highly Stretchable and Durable Conductive Knitted Fabrics for the Skins of Soft Robots. Soft Robot. 2019, 6, 687–700. [Google Scholar] [CrossRef] [PubMed]
- Ma, R.; Lee, J.; Choi, D.; Moon, H.; Baik, S. Knitted Fabrics Made from Highly Conductive Stretchable Fibers. Nano Lett. 2014, 14, 1944–1951. [Google Scholar] [CrossRef]
- Wang, X.; Sun, F.; Yin, G.; Wang, Y.; Liu, B.; Dong, M. Tactile-Sensing Based on Flexible PVDF Nanofibers via Electrospinning: A Review. Sensors 2018, 18, 330. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.R.; Zheng, J.M.; Ren, G.Y.; Zhang, P.H.; Xu, C. A flexible piezoelectric force sensor based on PVDF fabrics. Smart Mater. Struct. 2011, 20, 045009. [Google Scholar] [CrossRef]
- Fang, J.; Niu, H.; Wang, H.; Wang, X.; Lin, T. Enhanced mechanical energy harvesting using needleless electrospun poly(vinylidene fluoride) nanofibre webs. Energy Environ. Sci. 2013, 6, 2196–2202. [Google Scholar] [CrossRef]
- Wu, D.; Huang, S.; Xiao, Z.; Yu, L.; Wang, L.; Sun, D.; Lin, L. Poly (vinylidene fluoride) piezoelectric nanofibers fabricated by non-uniform field electrospinning. Int. J. Nanomanuf. 2015, 11, 297–310. [Google Scholar] [CrossRef]
- Edmondson, D.; Cooper, A.; Jana, S.; Wood, D.; Zhang, M. Centrifugal electrospinning of highly aligned polymer nanofibers over a large area. J. Mater. Chem. 2012, 22, 18646–18652. [Google Scholar] [CrossRef]
- Yu, H.; Huang, T.; Lu, M.; Mao, M.; Zhang, Q.; Wang, H. Enhanced power output of an electrospun PVDF/MWCNTs-based nanogenerator by tuning its conductivity. Nanotechnology 2013, 24, 405401. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.M.; Yousefi, A.A. Piezoelectric sensor based on electrospun PVDF-MWCNT-Cloisite 30B hybrid nanocomposites. Org. Electron. 2017, 50, 121–129. [Google Scholar] [CrossRef]
- Li, B.; Zheng, J.; Xu, C. Silver nanowire dopant enhancing piezoelectricity of electrospun PVDF nanofiber web. Proc. SPIE 2013, 8793, 879314. [Google Scholar] [CrossRef]
- Merlini, C.; dos Santos Almeida, R.; D’Ávila, M.A.; Schreiner, W.H.; de Oliveira Barra, G.M. Development of a novel pressure sensing material based on polypyrrole-coated electrospun poly (vinylidene fluoride) fibers. Mater. Sci. Eng. B 2014, 179, 52–59. [Google Scholar] [CrossRef]
- Merlini, C.; Barra, G.M.O.; Araujo, T.M.; Pegoretti, A. Electrically pressure sensitive poly(vinylidene fluoride)/polypyrrole electrospun mats. RSC Adv. 2014, 4, 15749–15758. [Google Scholar] [CrossRef]
- Persano, L.; Dagdeviren, C.; Su, Y.; Zhang, Y.; Girardo, S.; Pisignano, D.; Huang, Y.; Rogers, J.A. High performance piezoelectric devices based on aligned arrays of nanofibers of poly(vinylidenefluoride-co-trifluoroethylene). Nat. Commun. 2013, 4, 1633. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-H.; Lee, H.B.; Yeon, S.M.; Park, J.; Lee, N.K. Flexible and Stretchable Piezoelectric Sensor with Thickness-Tunable Configuration of Electrospun Nanofiber Mat and Elastomeric Substrates. ACS Appl. Mater. Interfaces 2016, 8, 24773–24781. [Google Scholar] [CrossRef]
- Ren, G.; Cai, F.; Li, B.; Zheng, J.; Xu, C. Flexible Pressure Sensor Based on a Poly (VDF-TrFE) Nanofiber Web. Macromol. Mater. Eng. 2013, 298, 541–546. [Google Scholar] [CrossRef]
- Mandal, D.; Yoon, S.; Kim, K.J. Origin of Piezoelectricity in an Electrospun Poly(vinylidene fluoride-trifluoroethylene) Nanofiber Web-Based Nanogenerator and Nano-Pressure Sensor. Macromol. Rapid Commun. 2011, 32, 831–837. [Google Scholar] [CrossRef]
- Lou, Z.; Chen, S.; Wang, L.; Jiang, K.; Shen, G. An ultra-sensitive and rapid response speed graphene pressure sensors for electronic skin and health monitoring. Nano Energy 2016, 23, 7–14. [Google Scholar] [CrossRef]
- Wang, X.; Yang, B.; Liu, J.; Zhu, Y.; Yang, C.; He, Q. A flexible triboelectric-piezoelectric hybrid nanogenerator based on P (VDF-TrFE) nanofibers and PDMS/MWCNT for wearable devices. Sci. Rep. 2016, 6, 36409. [Google Scholar] [CrossRef] [PubMed]
- Sharma, T.; Langevine, J.; Naik, S.; Aroom, K.; Gill, B.; Zhang, J.X.J. Aligned electrospun PVDF-TrFE nanofibers for flexible pressure sensors on catheter. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 422–425. [Google Scholar]
- Ke, J.-Y.; Chu, H.-J.; Hsu, Y.-H.; Lee, C.-K. A Highly Flexible Piezoelectret-Fiber Pressure Sensor Based on Highly Aligned P (VDF-TrFE) Electrospun Fibers; SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring; International Society for Optics and Photonics: Bellingham, WA, USA, 2017. [Google Scholar]
- Han Bit, L.; Young Won, K.; Jonghun, Y.; Nak Kyu, L.; Suk-Hee, P. 3D customized and flexible tactile sensor using a piezoelectric nanofiber mat and sandwich-molded elastomer sheets. Smart Mater. Struct. 2017, 26, 045032. [Google Scholar]
- Sharma, T.; Naik, S.; Langevine, J.; Gill, B.; Zhang, J.X. Aligned PVDF-TrFE nanofibers with high-density PVDF nanofibers and PVDF core-shell structures for endovascular pressure sensing. IEEE Trans. Biomed. Eng. 2015, 62, 188–195. [Google Scholar] [CrossRef] [PubMed]
- Chee, Y.A.; Bakir, A.A.; Wicaksono, D.H.B. Proprioceptive sensing system for therapy assessment using textile-based biomedical Micro Electro Mechanical System (MEMS). In Proceedings of the SENSORS, 2012 IEEE, Taipei, Taiwan, 28–31 October 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Pacelli, M.; Loriga, G.; Taccini, N.; Paradiso, R. Sensing fabrics for monitoring physiological and biomechanical variables: E-textile solutions. In Proceedings of the 3rd IEEE-EMBS International Summer School on Medical Devices and Biosensors, MIT, Boston, MA, USA, 4–6 September 2006; pp. 1–4. [Google Scholar]
- Zulkepli, N.; Rajdi, N.N.Z.M.; Wicaksono, D.H.B. The effect of processing parameters on the performance of cotton-fabric-based MEMS fabricated using stamped silver nanoparticles. In Proceedings of the 2014 IEEE REGION 10 SYMPOSIUM, Kuala Lumpur, Malaysia, 14–16 April 2014; pp. 29–33. [Google Scholar] [CrossRef]
- Hasegawa, Y.; Shikida, M.; Ogura, D.; Suzuki, Y.; Sato, K. Fabrication of a wearable fabric tactile sensor produced by artificial hollow fiber. J. Micromech. Microeng. 2008, 18, 085014. [Google Scholar] [CrossRef]
- Suzumori, K.; Iikura, S.; Tanaka, H. Flexible microactuator for miniature robots. In Proceedings of the 1991 Proceedings IEEE Micro Electro Mechanical Systems, Nara, Japan, 30 December 1990–2 January 1991; pp. 204–209. [Google Scholar] [CrossRef]
- Kaltsas, P.I.; Koustoumpardis, P.N.; Nikolakopoulos, P.G. A Review of Sensors Used on Fabric-Handling Robots. Machines 2022, 10, 101. [Google Scholar] [CrossRef]
- Wei, D.; Challa, S.; Islam, M.S.; Beharic, J.; Harnett, C.K.; Popa, D.O. Multi-Robot Collaboration for Electronic Textile Fabrication. In Proceedings of the 2022 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Toronto, ON, Canada, 25–29 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Katragadda, R.B.; Xu, Y. A novel intelligent textile technology based on silicon flexible skins. Sensors Actuators A: Phys. 2008, 143, 169–174. [Google Scholar] [CrossRef]
- Briand, D.; Molina-Lopez, F.; Quintero, A.V.; Ataman, C.; Courbat, J.; de Rooij, N.F. Why Going Towards Plastic and Flexible Sensors? Procedia Eng. 2011, 25, 8–15. [Google Scholar] [CrossRef]
- Khumpuang, S.; Ohtomo, A.; Miyake, K.; Itoh, T. Fabrication and evaluation of a microspring contact array using a reel-to-reel continuous fiber process. J. Micromech. Microeng. 2011, 21, 105019. [Google Scholar] [CrossRef]
- Bifulco, P.; Cesarelli, M.; Fratini, A.; Ruffo, M.; Pasquariello, G.; Gargiulo, G. A wearable device for recording of biopotentials and body movements. In Proceedings of the 2011 IEEE International Symposium on Medical Measurements and Applications, Bari, Italy, 30–31 May 2011; pp. 469–472. [Google Scholar]
- Yang, K.; Torah, R.; Wei, Y.; Beeby, S.; Tudor, J. Water Based PVA Sacrificial Material for Low Temperature MEMS Fabrication and Applications on e-textiles. Procedia Eng. 2014, 87, 1565–1568. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Sharma, V.; Young, D.J. A Paper-Based Flexible Tactile Sensor Array for Low-Cost Wearable Human Health Monitoring. J. Microelectromech. Syst. 2020, 29, 825–831. [Google Scholar] [CrossRef]
- Ojuroye, O.; Torah, R.; Beeby, S. Modified PDMS packaging of sensory e-textile circuit microsystems for improved robustness with washing. Microsyst. Technol. 2019, 28, 1467–1484. [Google Scholar] [CrossRef] [Green Version]
- Uz Zaman, S.; Tao, X.; Cochrane, C.; Koncar, V. Understanding the Washing Damage to Textile ECG Dry Skin Electrodes, Embroidered and Fabric-Based; set up of Equivalent Laboratory Tests. Sensors 2020, 20, 1272. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Gao, Z.; Yao, K.; Hou, S.; Liu, Y.; Li, D.; He, J.; Huang, X.; Song, E.; Yu, J.; et al. Thin, soft, skin-integrated foam-based triboelectric nanogenerators for tactile sensing and energy harvesting. Mater. Today Energy 2021, 20, 100657. [Google Scholar] [CrossRef]
- Kirthika, S.K.; Ponraj, G.; Ren, H. Fabrication and Comparative Study on Sensing Characteristics of Soft Textile-Layered Tactile Sensors. IEEE Sens. Lett. 2017, 1, 2500304. [Google Scholar] [CrossRef]
- Kumar, K.S.; Chen, P.-Y.; Ren, H. A Review of Printable Flexible and Stretchable Tactile Sensors. Research 2019, 2019, 3018568. [Google Scholar] [CrossRef] [Green Version]
- Castano, L.M.; Flatau, A.B. Smart fabric sensors and e-textile technologies: A review. Smart Mater. Struct. 2014, 23, 053001. [Google Scholar] [CrossRef]
- Gonçalves, C.; da Silva, A.F.; Gomes, J.; Simoes, R. Wearable E-Textile Technologies: A Review on Sensors, Actuators and Control Elements. Inventions 2018, 3, 14. [Google Scholar] [CrossRef] [Green Version]
- Possanzini, L.; Tessarolo, M.; Mazzocchetti, L.; Campari, E.G.; Fraboni, B. Impact of Fabric Properties on Textile Pressure Sensors Performance. Sensors 2019, 19, 4686. [Google Scholar] [CrossRef]
- Zhang, J.-W.; Zhang, Y.; Li, Y.-Y.; Wang, P. Textile-Based Flexible Pressure Sensors: A Review. Polym. Rev. 2022, 62, 65–94. [Google Scholar] [CrossRef]
- Parameswaran, C.; Gupta, D. Large area flexible pressure/strain sensors and arrays using nanomaterials and printing techniques. Nano Converg. 2019, 6, 28. [Google Scholar] [CrossRef] [Green Version]
- Wu, T.; Fukuhara, S.; Gillian, N.; Sundara-Rajan, K.; Poupyrev, I. ZebraSense: A double-sided textile touch sensor for smart clothing. In Proceedings of the 33rd Annual ACM Symposium on User Interface Software and Technology, Virtual, 20–23 October 2020; pp. 662–674. [Google Scholar]
- Takamatsu, S.; Kobayashi, T.; Shibayama, N.; Miyake, K.; Itoh, T. Fabric pressure sensor array fabricated with die-coating and weaving techniques. Sens. Actuators A Phys. 2012, 184, 57–63. [Google Scholar] [CrossRef]
- Ge, C.; Cretu, E. Bionic MEMS for Touching and Hearing Sensations: Recent Progress, Challenges, and Solutions. J. Bionic Eng. 2022, 19, 590–615. [Google Scholar] [CrossRef]
- Cerveri, P.; Quinzi, M.; Bovio, D.; Frigo, C.A. A Novel Wearable Apparatus to Measure Fingertip Forces in Manipulation Tasks Based on MEMS Barometric Sensors. IEEE Trans. Haptics 2016, 10, 317–324. [Google Scholar] [CrossRef]
- Walker, J.M.; Blank, A.A.; Shewokis, P.A.; O’Malley, M.K. Tactile Feedback of Object Slip Facilitates Virtual Object Manipulation. IEEE Trans. Haptics 2015, 8, 454–466. [Google Scholar] [CrossRef] [PubMed]
- Yeo, J.C.; Liu, Z.; Zhang, Z.-Q.; Zhang, P.; Wang, Z.; Lim, C.T. Wearable Mechanotransduced Tactile Sensor for Haptic Perception. Adv. Mater. Technol. 2017, 2, 1700006. [Google Scholar] [CrossRef]
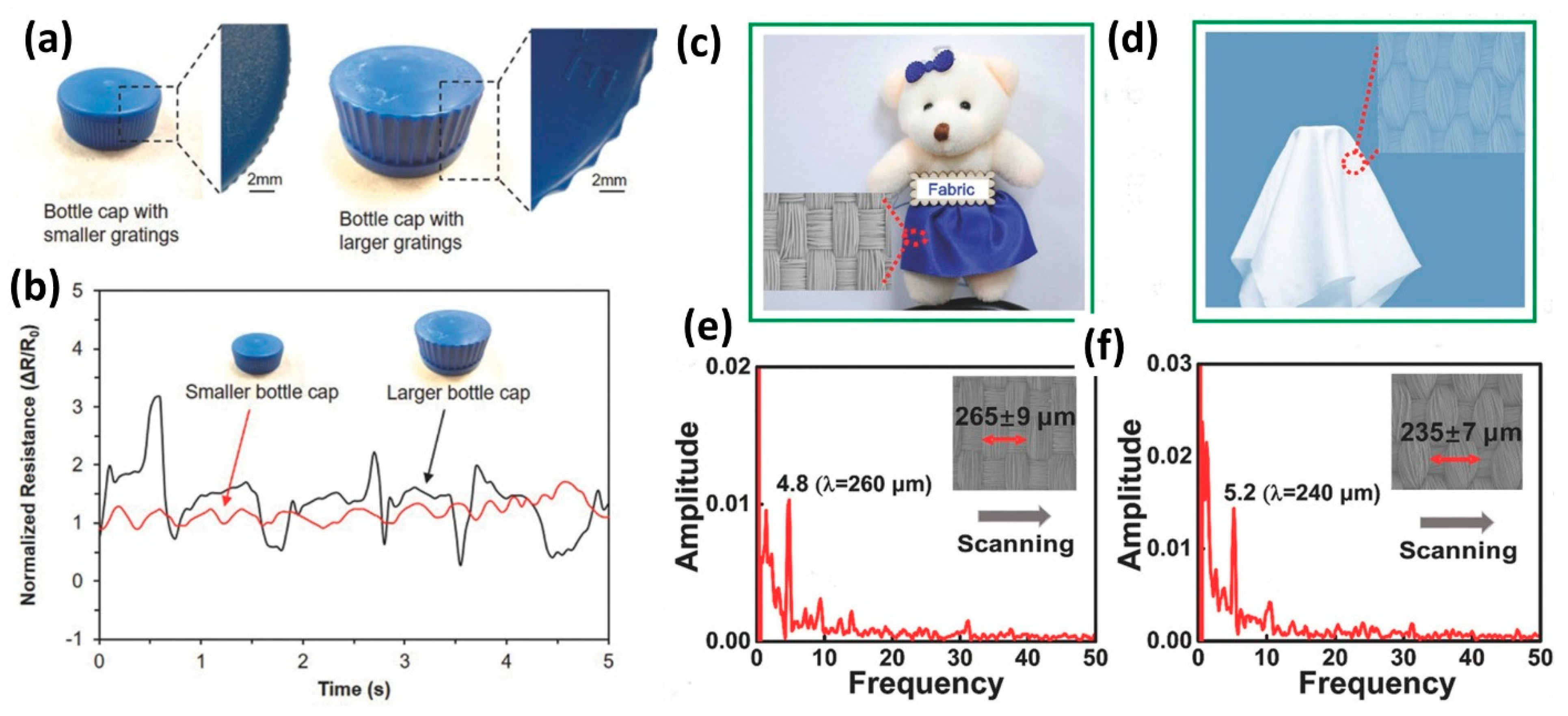
- Cao, Y.; Li, T.; Gu, Y.; Luo, H.; Wang, S.; Zhang, T. Fingerprint-Inspired Flexible Tactile Sensor for Accurately Discerning Surface Texture. Small 2018, 14, e1703902. [Google Scholar] [CrossRef] [PubMed]
- Pastor, F.; Gandarias, J.M.; García-Cerezo, A.J.; Gómez-de-Gabriel, J.M. Using 3D convolutional neural networks for tactile object recognition with robotic palpation. Sensors 2019, 19, 5356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, X.; Zhang, M. Review of flexible microelectromechanical system sensors and devices. Nanotechnol. Precis. Eng. 2021, 4, 025001. [Google Scholar] [CrossRef]
- Caeiro-Rodríguez, M.; Otero-González, I.; Mikic-Fonte, F.A.; Llamas-Nistal, M. A systematic review of commercial smart gloves: Current status and applications. Sensors 2021, 21, 2667. [Google Scholar] [CrossRef] [PubMed]
- Saudabayev, A.; Varol, H.A. Sensors for Robotic Hands: A Survey of State of the Art. IEEE Access 2015, 3, 1765–1782. [Google Scholar] [CrossRef]
- Bogue, R. Tactile sensing for surgical and collaborative robots and robotic grippers. Ind. Robot. 2019, 46, 1–6. [Google Scholar] [CrossRef]
- Massari, L.; Oddo, C.M.; Sinibaldi, E.; Detry, R.; Bowkett, J.; Carpenter, K.C. Tactile Sensing and Control of Robotic Manipulator Integrating Fiber Bragg Grating Strain-Sensor. Front. Neurorobotics 2019, 13, 8. [Google Scholar] [CrossRef] [PubMed]
- Ubeda, R.P.; Rubert, S.C.G.; Stanisic, R.Z.; Ivars, P. Design and Manufacturing of an Ultra-Low-Cost Custom Torque Sensor for Robotics. Sensors 2018, 18, 1786. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, G.; Gorjup, G.; Yu, R.; Jarvis, P.; Liarokapis, M. Modular, Accessible, Sensorized Objects for Evaluating the Grasping and Manipulation Capabilities of Grippers and Hands. IEEE Robot. Autom. Lett. 2020, 5, 6105–6112. [Google Scholar] [CrossRef]
- Belford, A.; Moshizi, S.A.; Razmjou, A.; Asadnia, M. Using Miniaturized Strain Sensors to Provide a Sense of Touch in a Humanoid Robotic Arm. Front. Mech. Eng. 2020, 6, 550328. [Google Scholar] [CrossRef]
- He, L.; Lu, Q.; Abad, S.-A.; Rojas, N.; Nanayakkara, T. Soft Fingertips with Tactile Sensing and Active Deformation for Robust Grasping of Delicate Objects. IEEE Robot. Autom. Lett. 2020, 5, 2714–2721. [Google Scholar] [CrossRef] [Green Version]
- Friedl, W.A.; Roa, M.A. Experimental Evaluation of Tactile Sensors for Compliant Robotic Hands. Front. Robot. AI 2021, 8, 704416. [Google Scholar] [CrossRef] [PubMed]
- Pang, G.; Deng, J.; Wang, F.; Zhang, J.; Pang, Z.; Yang, G. Development of Flexible Robot Skin for Safe and Natural Human–Robot Collaboration. Micromachines 2018, 9, 576. [Google Scholar] [CrossRef]
- Zimmer, J.; Hellebrekers, T.; Asfour, T.; Majidi, C.; Kroemer, O. Predicting Grasp Success with a Soft Sensing Skin and Shape-Memory Actuated Gripper. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 7120–7127. [Google Scholar] [CrossRef]
- Yang, W.; Xie, M.; Zhang, X.; Sun, X.; Zhou, C.; Chang, Y.; Zhang, H.; Duan, X. Multifunctional Soft Robotic Finger Based on a Nanoscale Flexible Temperature–Pressure Tactile Sensor for Material Recognition. ACS Appl. Mater. Interfaces 2021, 13, 55756–55765. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, H.; Jiang, L.; Fan, S.; Yang, J. Development of a Flexible 3-D Tactile Sensor System for Anthropomorphic Artificial Hand. IEEE Sens. J. 2012, 13, 510–518. [Google Scholar] [CrossRef]
- Jin, T.; Sun, Z.; Li, L.; Zhang, Q.; Zhu, M.; Zhang, Z.; Yuan, G.; Chen, T.; Tian, Y.; Hou, X.; et al. Triboelectric nanogenerator sensors for soft robotics aiming at digital twin applications. Nat. Commun. 2020, 11, 5381. [Google Scholar] [CrossRef] [PubMed]
- Homberg, B.S.; Katzschmann, R.K.; Dogar, M.R.; Rus, D. Robust proprioceptive grasping with a soft robot hand. Auton. Robot. 2019, 43, 681–696. [Google Scholar] [CrossRef] [Green Version]
- Sohgawa, M.; Nozawa, A.; Yokoyama, H.; Kanashima, T.; Okuyama, M.; Abe, T.; Noma, H.; Azuma, T. Multimodal measurement of proximity and touch force by light- and strain-sensitive multifunctional MEMS sensor. In Proceedings of the SENSORS 2014, Valencia, Spain, 2–5 November 2014; IEEE: Piscataway, NJ, USA; pp. 1749–1752. [Google Scholar] [CrossRef]
- Araki, R.; Abe, T.; Noma, H.; Sohgawa, M. Miniaturization and High-Density Arrangement of Microcantilevers in Proximity and Tactile Sensor for Dexterous Gripping Control. Micromachines 2018, 9, 301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Araki, R.; Abe, T.; Noma, H.; Sohgawa, M. Electromotive Manipulator Control by Detection of Proximity, Contact, and Slipping Using MEMS Multiaxial Tactile Sensor. Electr. Eng. Jpn. 2018, 204, 44–49. [Google Scholar] [CrossRef]
- Baldini, G.; Albini, A.; Maiolino, P.; Cannata, G. An Atlas for the Inkjet Printing of Large-Area Tactile Sensors. Sensors 2022, 22, 2332. [Google Scholar] [CrossRef]
- Roberts, P.; Zadan, M.; Majidi, C. Soft Tactile Sensing Skins for Robotics. Curr. Robot. Rep. 2021, 2, 343–354. [Google Scholar] [CrossRef]
- Park, M.; Bok, B.-G.; Ahn, J.-H.; Kim, M.-S. Recent Advances in Tactile Sensing Technology. Micromachines 2018, 9, 321. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wu, X.; Mei, D.; Zhu, L.; Chen, J. Flexible tactile sensor array for distributed tactile sensing and slip detection in robotic hand grasping. Sens. Actuators A Phys. 2019, 297, 111512. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Song, P.; Li, X.; Ru, C.; Ferrari, G.; Balasubramanian, P.; Amabili, M.; Sun, Y.; Liu, X. A Paper-Based Piezoelectric Accelerometer. Micromachines 2018, 9, 19. [Google Scholar] [CrossRef] [Green Version]
- Ren, T.-L.; Tian, H.; Xie, D.; Yang, Y. Flexible Graphite-on-Paper Piezoresistive Sensors. Sensors 2012, 12, 6685–6694. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Mwangi, M.; Li, X.; O’Brien, M.; Whitesides, G.M. Paper-based piezoresistive MEMS sensors. Lab Chip 2011, 11, 2189–2196. [Google Scholar] [CrossRef] [Green Version]
- Lessing, J.; Glavan, A.C.; Walker, S.B.; Keplinger, C.; Lewis, J.A.; Whitesides, G.M. Inkjet Printing of conductive inks with high lateral resolution on omniphobic “Rf paper” for paper-based electronics and MEMS. Adv. Mater. 2014, 26, 4677–4682. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forestier, E.M.; Najafi, S.; Dussoni, M.; Maggiali, A.; Athanassiou, I.; Bayer, S. Characterization and performance of silicone modified Polylactic acid (PLA)-graphene nanoplatelet ink coatings for flexible elastomeric substrates. Prog. Org. Coat. 2023, 174, 107251. [Google Scholar] [CrossRef]
- Meiss, T.; Wertschützky, R.; Stoeber, B. Rapid prototyping of resistive MEMS sensing devices on paper substrates. In Proceedings of the 2014 IEEE 27th international conference on micro electro mechanical systems (MEMS), San Francisco, CA, USA, 26–30 January 2014; pp. 536–539. [Google Scholar]
- Ahmed, M.; Gonenli, I.E.; Nadvi, G.S.; Kilaru, R.; Butler, D.P.; Celik-Butler, Z. MEMS sensors on flexible substrates towards a smart skin. In Proceedings of the SENSORS 2012, Taipei, Taiwan, 28–31 October 2012; IEEE: Piscataway, NJ, USA; pp. 1–4. [Google Scholar] [CrossRef]
- Fujita, H.; Triggs, B.; Laugier, C. What can MEMS do for Robotics. In Robotics Research; Springer: London, UK, 2000; pp. 428–439. [Google Scholar] [CrossRef]
- Liljebäck, P.; Pettersen, K.Y.; Stavdahl, Ø.; Gravdahl, J.T. Snake Robots: Modelling, Mechatronics, and Control; Springer: London, UK, 2013; pp. 29–37. [Google Scholar]
- Zhao, X.; Dou, L.; Su, Z.; Liu, N. Study of the Navigation Method for a Snake Robot Based on the Kinematics Model with MEMS IMU. Sensors 2018, 18, 879. [Google Scholar] [CrossRef]
- Yang, W.; Bajenov, A.; Shen, Y. Improving low-cost inertial-measurement-unit (IMU)-based motion tracking accuracy for a biomorphic hyper-redundant snake robot. Robot. Biomimetics 2017, 4, 16. [Google Scholar] [CrossRef] [Green Version]
- Liljeback, P.; Stavdahl, O.; Pettersen, K.Y.; Gravdahl, J.T. Mamba—A waterproof snake robot with tactile sensing. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 294–301. [Google Scholar] [CrossRef] [Green Version]
- Albini, A.; Grella, F.; Maiolino, P.; Cannata, G. Exploiting Distributed Tactile Sensors to Drive a Robot Arm Through Obstacles. IEEE Robot. Autom. Lett. 2021, 6, 4361–4368. [Google Scholar] [CrossRef]
- Pettersen, K.Y. Snake Robots. Annu. Rev. Control. 2017, 44, 19–44. [Google Scholar] [CrossRef]
- Branyan, C.; Hatton, R.L.; Menguc, Y. Snake-Inspired Kirigami Skin for Lateral Undulation of a Soft Snake Robot. IEEE Robot. Autom. Lett. 2020, 5, 1728–1733. [Google Scholar] [CrossRef]
- Yousef, H.; Boukallel, M.; Althoefer, K. Tactile sensing for dexterous in-hand manipulation in robotics—A review. Sens. Actuators A Phys. 2011, 167, 171–187. [Google Scholar] [CrossRef]
- Noda, K.; Hashimoto, Y.; Tanaka, Y.; Shimoyama, I. MEMS on robot applications. In Proceedings of the TRANSDUCERS 2009-2009 International Solid-State Sensors, Actuators and Microsystems Conference, Denver, CO, USA, 21–25 June 2009; pp. 2176–2181. [Google Scholar] [CrossRef]
- Mei, T.; Li, W.J.; Ge, Y.; Chen, Y.; Ni, L.; Chan, M.H. An integrated MEMS three-dimensional tactile sensor with large force range. Sensors Actuators A Phys. 2000, 80, 155–162. [Google Scholar] [CrossRef]
- Makihata, M.; Tanaka, S.; Muroyama, M.; Matsuzaki, S.; Yamada, H.; Nakayama, T.; Yamaguchi, U.; Mima, K.; Nonomura, Y.; Esashi, M.; et al. Integration and packaging technology of MEMS-on-CMOS capacitive tactile sensor for robot application using thick BCB isolation layer and backside-grooved electrical connection. Sensors Actuators A Phys. 2012, 188, 103–110. [Google Scholar] [CrossRef]
- Muhammad, H.; Oddo, C.; Beccai, L.; Recchiuto, C.; Anthony, C.; Adams, M.; Carrozza, M.; Hukins, D.; Ward, M. Development of a bioinspired MEMS based capacitive tactile sensor for a robotic finger. Sensors Actuators A Phys. 2011, 165, 221–229. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, X.; Shi, Q.; He, T.; Sun, Z.; Guo, X.; Liu, W.; Bin Sulaiman, O.; Dong, B.; Lee, C. Development Trends and Perspectives of Future Sensors and MEMS/NEMS. Micromachines 2019, 11, 7. [Google Scholar] [CrossRef] [Green Version]
- Pagliano, S.; Marschner, D.E.; Maillard, D.; Ehrmann, N.; Stemme, G.; Braun, S.; Villanueva, L.G.; Niklaus, F. Micro 3D printing of a functional MEMS accelerometer. Microsyst. Nanoeng. 2022, 8, 105. [Google Scholar] [CrossRef]
- Pulskamp, J.S.; Polcawich, R.G.; Rudy, R.Q.; Bedair, S.S.; Proie, R.M.; Ivanov, T.; Smith, G.L. Piezoelectric PZT MEMS technologies for small-scale robotics and RF applications. MRS Bull. 2012, 37, 1062–1070. [Google Scholar] [CrossRef]
- Pang, G.; Liu, H. Evaluation of a Low-cost MEMS Accelerometer for Distance Measurement. J. Intell. Robot. Syst. 2001, 30, 249–265. [Google Scholar] [CrossRef]
- Liu, C. Recent Developments in Polymer MEMS. Adv. Mater. 2007, 19, 3783–3790. [Google Scholar] [CrossRef]
- Le, X.; Shi, Q.; Sun, Z.; Xie, J.; Lee, C. Noncontact Human–Machine Interface Using Complementary Information Fusion Based on MEMS and Triboelectric Sensors. Adv. Sci. 2022, 9, 2201056. [Google Scholar] [CrossRef]
- Mousavi, M.; Alzgool, M.; Towfighian, S. Autonomous shock sensing using bi-stable triboelectric generators and MEMS electrostatic levitation actuators. Smart Mater. Struct. 2021, 30, 065019. [Google Scholar] [CrossRef]
- Tai, K.; El-Sayed, A.-R.; Shahriari, M.; Biglarbegian, M.; Mahmud, S. State of the Art Robotic Grippers and Applications. Robotics 2016, 5, 11. [Google Scholar] [CrossRef] [Green Version]
- Fujita, H. A decade of MEMS and its future. In Proceedings of the Proceedings IEEE The Tenth Annual International Workshop on Micro Electro Mechanical Systems. An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Nagoya, Japan, 26–30 January 1997; pp. 1–7. [Google Scholar] [CrossRef]
- Al-Handarish, Y.; Omisore, O.M.; Igbe, T.; Han, S.; Li, H.; Du, W.; Zhang, J.; Wang, L. A Survey of Tactile-Sensing Systems and Their Applications in Biomedical Engineering. Adv. Mater. Sci. Eng. 2020, 2020, 4047937. [Google Scholar] [CrossRef]

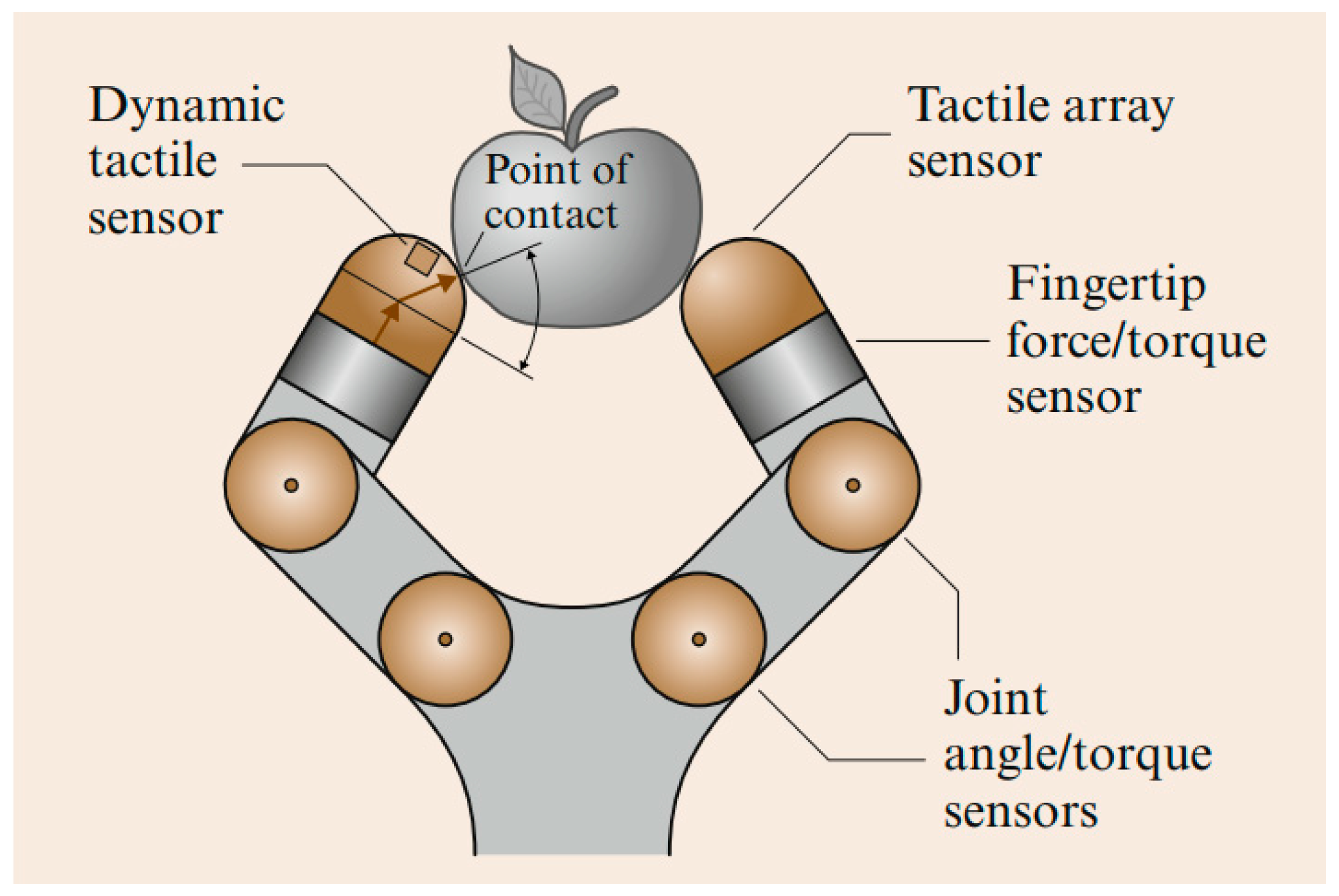
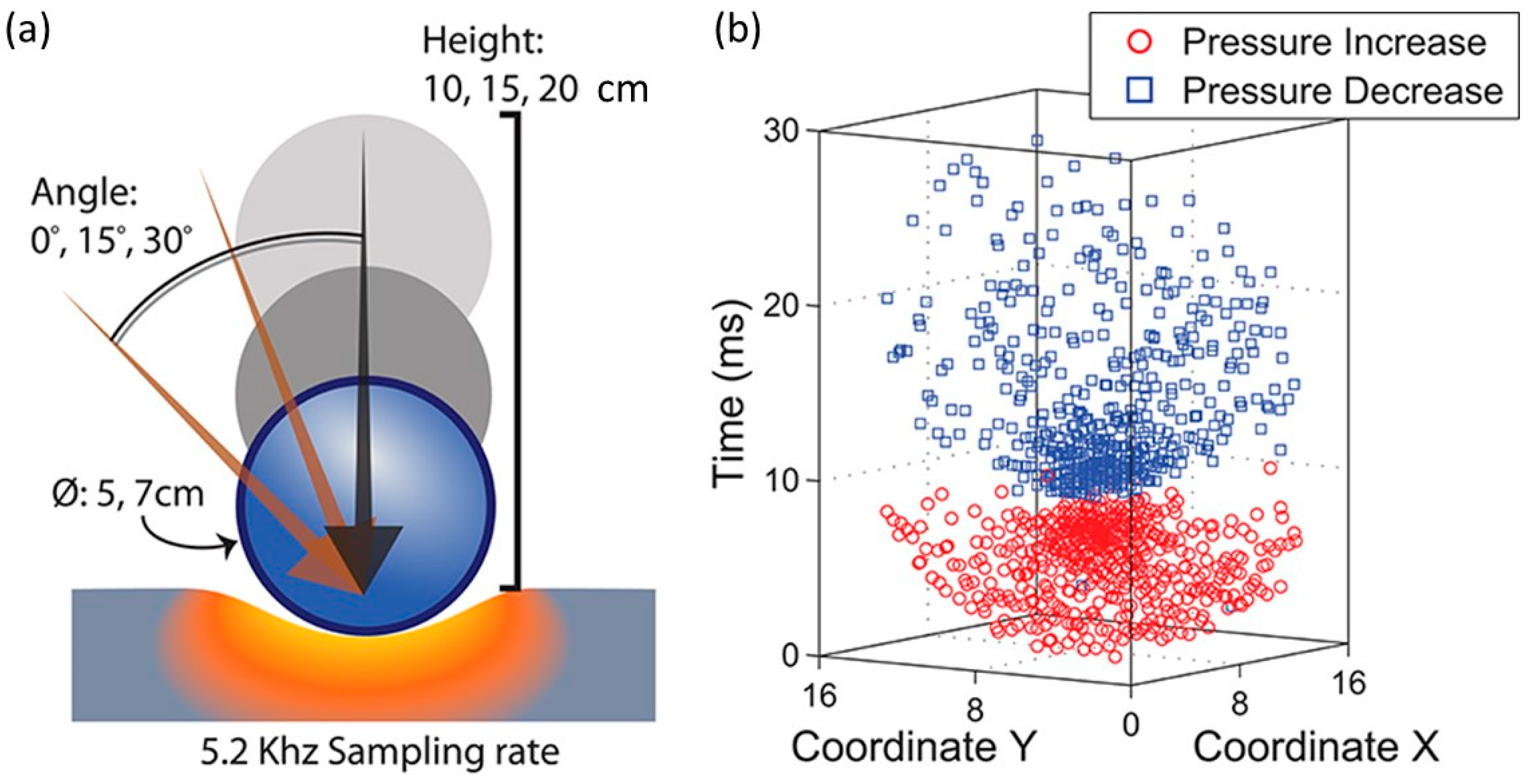

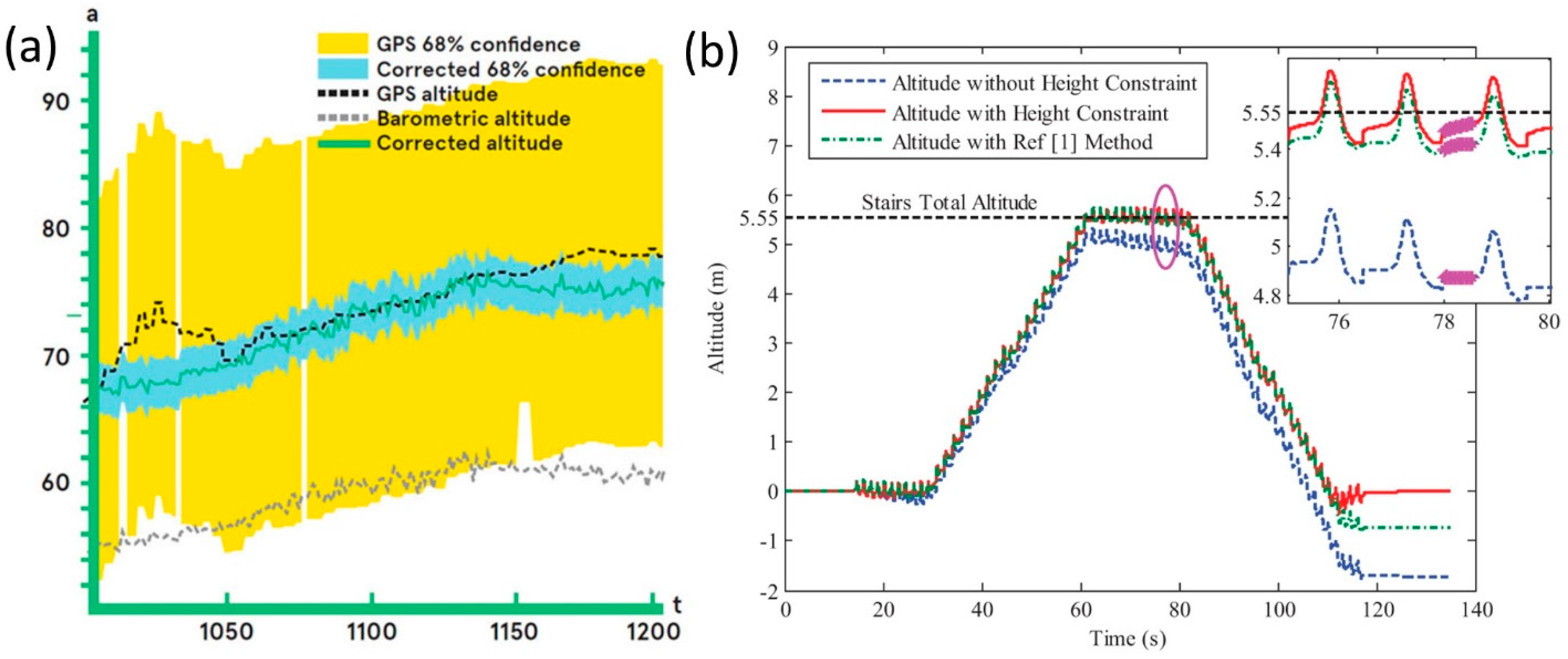
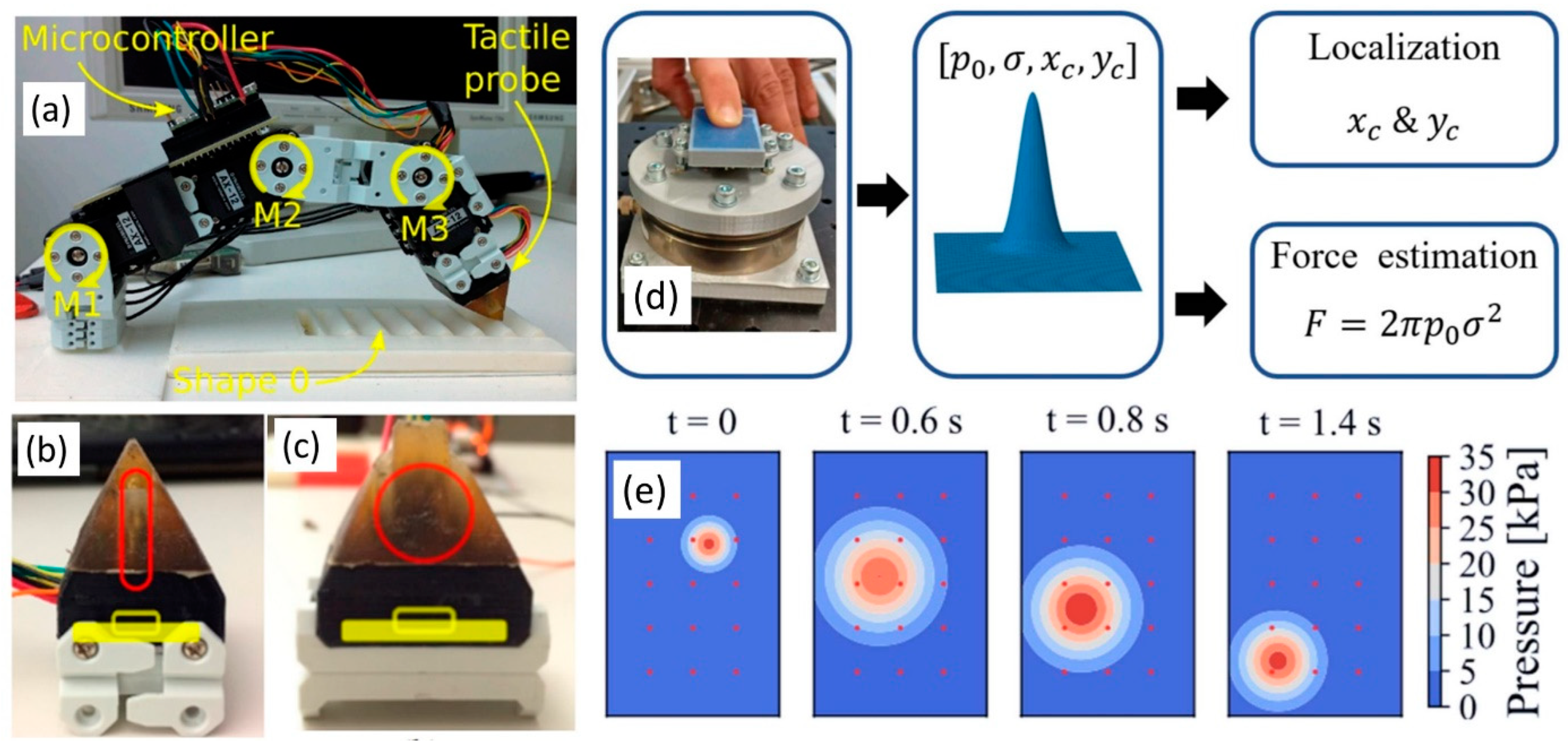

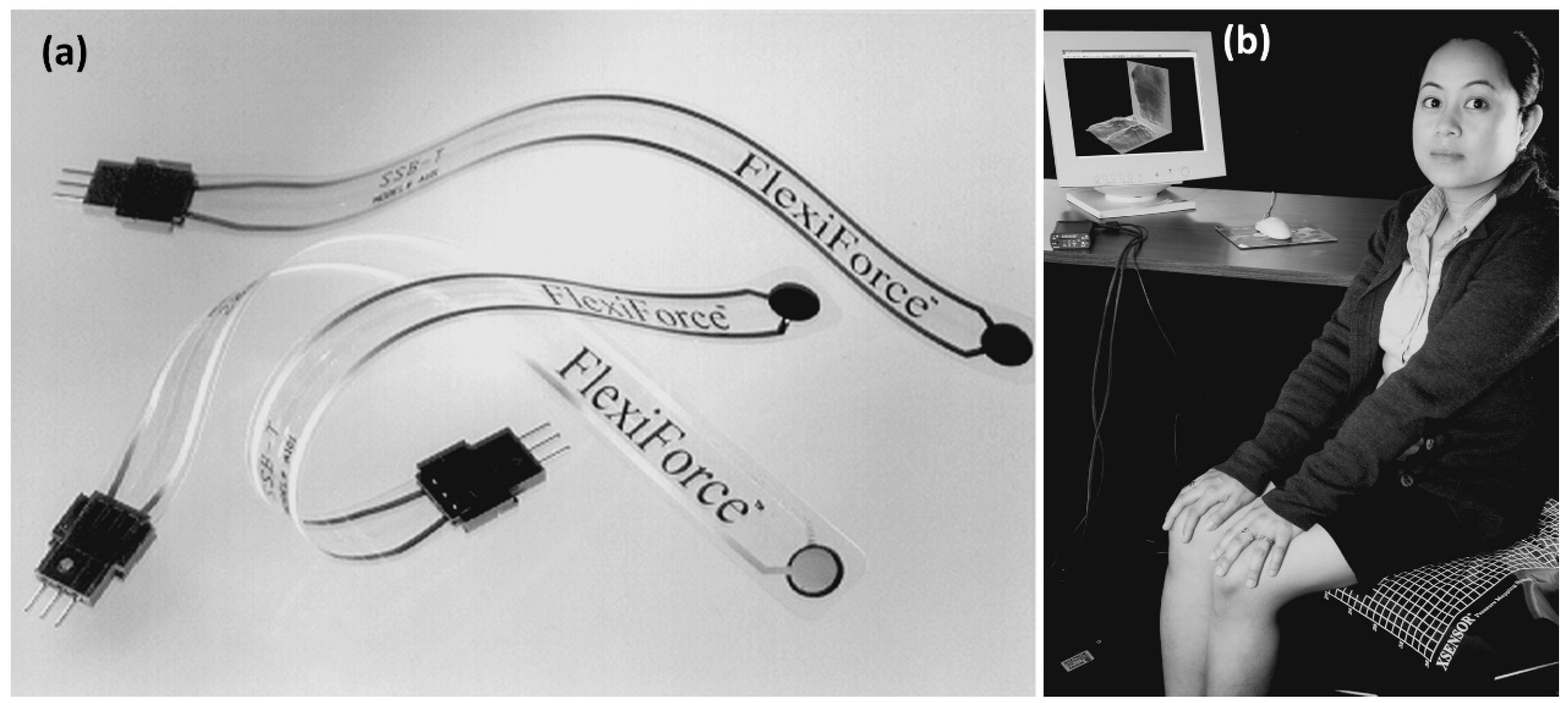
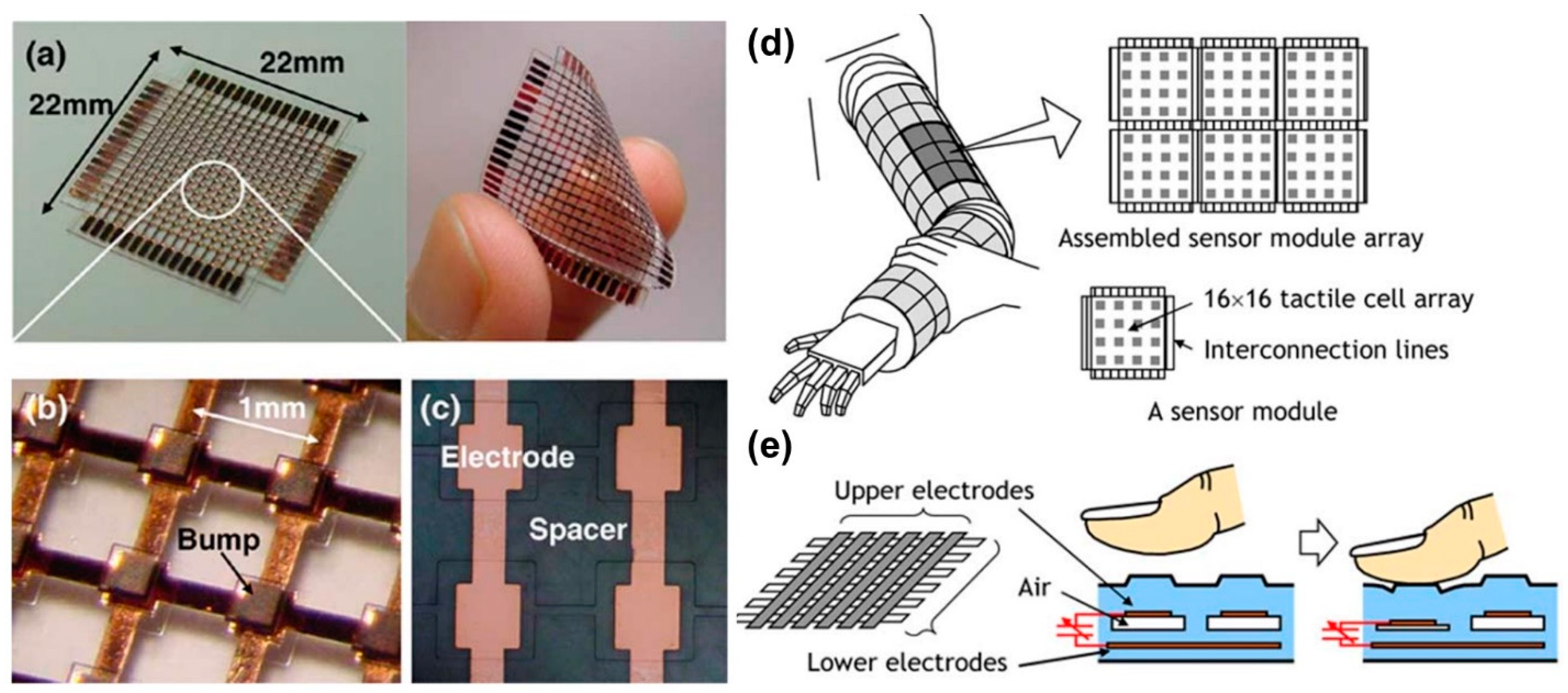
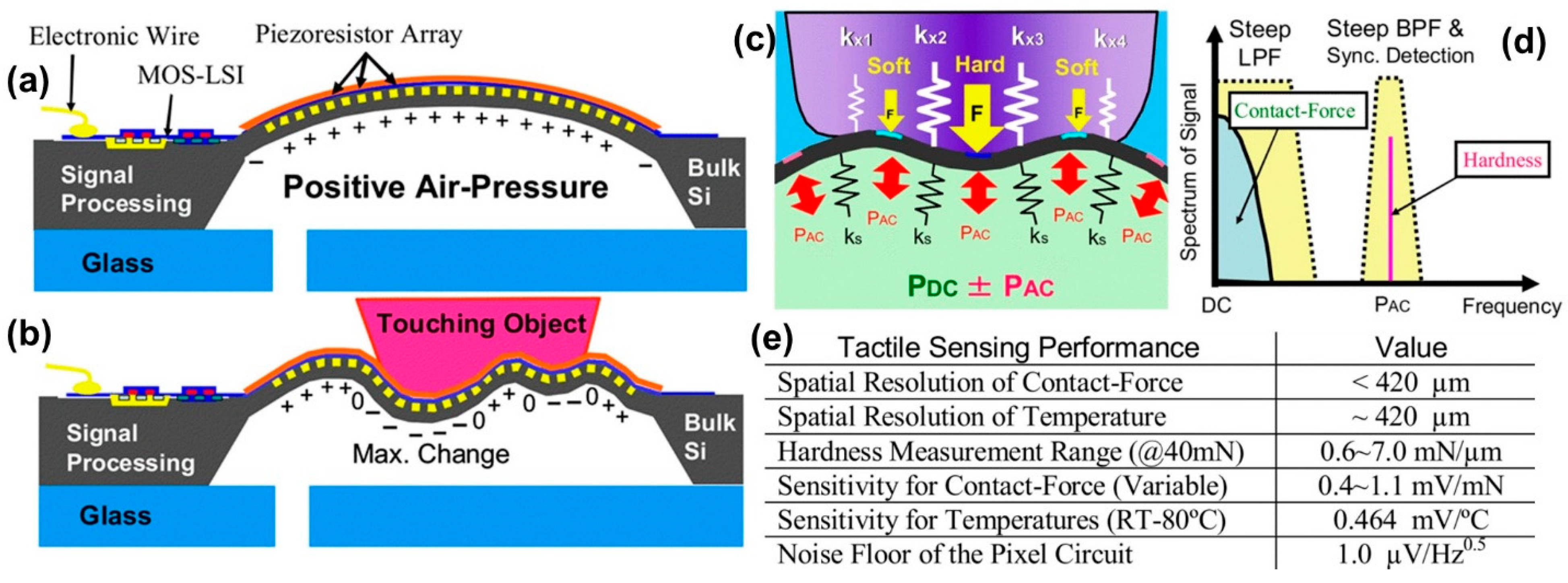
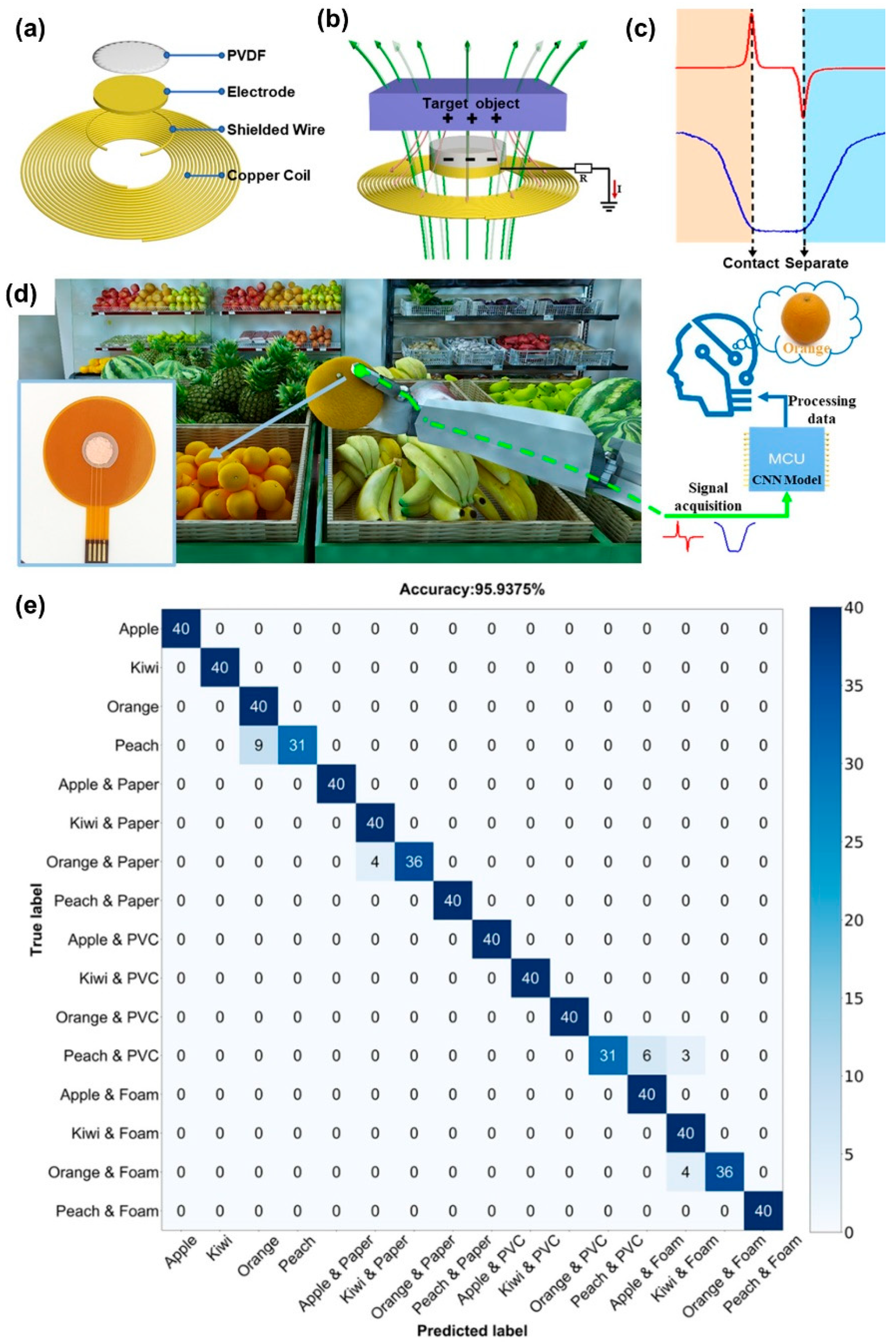


| Modality | Sensor Type | Advantages | Disadvantages |
|---|---|---|---|
| Normal pressure | Piezoresistive array | Simple signal conditioning, mass production adaptable | Temperature sensitive, reproducibility issues and signal drift |
| Capacitive array | Good sensitivity | Complex circuitry required | |
| Optical | No interconnects to break | Requires on board computation devices for applied force | |
| Skin deformation | Optical | Compliant membrane and no electrical interconnects to be damaged | Complex computations required and needs customized hand design |
| Magnetic | Array to hall-effect sensors possible | Complex computations required and needs customized hand design | |
| Resistive Tomography | Good coverage, manufacturability and robustness | Poor spatial resolution | |
| Piezoresistive (curvature) | Directly measure curvature | Frailty of electrical interconnects | |
| Dynamic tactile sensing | Piezoelectric (stress rate) | High bandwidth | Frailty of electrical junctions |
| Skin (vector) acceleration | Simple | Gets complicated for large spatial mapping |
| Year | 1st Milestone | 2nd Milestone | 3rd Milestone | 4th Milestone | 5th Milestone |
|---|---|---|---|---|---|
| 1950s | 1958 Silicon strain gauges commercialized | 1959 Richard Feynman issues a challenge to make an electrical motor smaller than 1/64th of an inch. | n/a | n/a | n/a |
| 1960s | 1961 First silicon pressure sensor fabricated | 1967 Invention of surface micromachining and Resonant Gate Field Effect Transistor, (RGT). | 1968 Development of sacrificial materials to free MEMS from the silicon substrate. | n/a | n/a |
| 1970s | 1970 First silicon accelerometer demonstrated | 1979 First micro machined inkjet nozzle | n/a | n/a | n/a |
| 1980s | 1980–1982 First experiments in surface micro machined silicon. | 1982 Disposable blood pressure transducer | 1982 Silicon etching standards established | 1982 LIGA process (fabrication of high-aspect-ratio microstructures) | 1988 First MEMS conference |
| 1990s | 1992 First micro machined hinge | 1993 First surface micro machined accelerometer sold (Analog Devices, ADXL50) | 1994 Deep Reactive Ion Etching is patented | 1995 BioMEMS emerge and grow fast | |
| 2000s | 2000 MEMS optical-networking components industrialized in large scales | 2010 MEMS adapted to handheld electronic devices | 2015 MEMS adapted to wearable and human centric technologies | 2020 MEMS as smart sensors and MEMS in robotic servants |
| Sensor Type | Active Layer | Sensitivity (kPa−1) | Detection Limit (kPa) | Reference |
|---|---|---|---|---|
| Capacitive | Ti0.91O2 NSs/BC paper | 2.44 × 10−3 | 166 | [72] |
| Capacitive | MEMs-based film | 7.10 × 10−4 | 1 | [73] |
| Capacitive | Bump PDMS film | 6 × 10−3 | 250 | [74] |
| Capacitive | Thin PDMS film | 6.13 × 10−3 | 45 | [75] |
| Capacitive | Bump PDMS film | 0.03 | 430 | [76] |
| Capacitive | Electrolyte/filter paper | 0.04 | 19 | [77] |
| Resistive | MWCNTs/cotton cellulose | 0.02 | 20 | [78] |
| Resistive | Graphene/polyimide | 0.18 | 2 | [79] |
| Resistive | LSG/GO film | 0.96 | 50 | [80] |
| Piezoresistive | SCNTs/cellulose nanofibrils | 4.40 | 0.5 | [81] |
| Piezoresistive | Graphene/cellulose paper | 9.83 | 1.7 | [82] |
| Application | Pressure |
|---|---|
| Vascular pulse (75–150 mmHg) | 10–20 kPa |
| Human fingertip texture, shape sensing | 10–40 kPa |
| Hand grip | 0–100 kPa |
| Fingerprint sensor | 1–2 kPa |
| In-shoe pressures | <1 MPa |
| Tactile robotics | 10–100 kPa |
| Material/Structure | Sensitivity (kPa−1) | Range (kPa) | Response/Recovery Time | Minimum Detection | Reference |
|---|---|---|---|---|---|
| PDMS/Wrinkled microstructure | 0.0012 4.2 × 10−6 | <1 >8 | 578/782 ms | n/a | [84] |
| Porous PDMS | 0.26 0.01 | 0–0.33 0.33–250 | 15/− ms | 1 Pa | [85] |
| Porous PDMS | 0.046 0.051 | 0.01–0.05 0.1–0.5 | NA | 5 Pa | [86] |
| Bubble trapped PDMS | 5.5 × 10−3 | 0–10.20 | ~351/386 ms | NA | [87] |
| PDMS/DIW | 0.068 0.095 | 0.01–0.05 0.1–0.5 | ~110/110 ms | 1 Pa | [88] |
| Basic Accuracy | Output Conformity Error | Hysteresis Error | Repeatability Error | Sensitivity (Hz/kPa) | Range (kPa) | Operating Temperature (°C) | Reference |
|---|---|---|---|---|---|---|---|
| n/a | 0.021 | n/a | n/a | 7.35 | <250 | −40 to +60 | [103] |
| n/a | 0.021 | n/a | n/a | 20 | <180 | −20 to +80 | [108] |
| n/a | n/a | n/a | n/a | 45 | <110 | n/a | [109] |
| 0.045 | 0.0102 | 0.0045 | 0.044 | n/a | <400 | −20 to +60 | [107] |
| 0.064 | 0.0148 | 0.0525 | 0.0315 | 36.58 | <100 | −20 to +60 | [107] |
| Nanofiber Substrate | Operation Voltage/Resistance | Applied Current | Sensitivity | Detection Limit | Cyclic Stability | Reference |
|---|---|---|---|---|---|---|
| PVDF | 140 mV | n/a | 42.00 mV/N | n/a | n/a | [132] |
| PVDF | 1–2.6 V | 1.4–4.5 μA | n/a | n/a | n/a | [133] |
| PVDF/PET and PDMS | 100 mV at 0.025 MPa | n/a | 5.812 mV kPa−1 | n/a | n/a | [134] |
| PVDF | ~3 mV | n/a | n/a | n/a | n/a | [135] |
| PVDF/MWCNT | 6 V | n/a | the volume conductivity is 5 orders higher than pure PVDF nanofibers | n/a | n/a | [136] |
| PVDF-0.05MWCNT-0.1OMMT | 58 ± 2.5 mV 48 ± 4.7 mV (pure PVDF) | n/a | 10.9 ± 1.25 mV/N 8.84 ± 1.57 mV/N (pure PVDF) | n/a | n/a | [137] |
| AgNWs doped PVDF | n/a | n/a | 29.8 pC/N (for d33) 18.1 pC/N (pure PVDF) | n/a | n/a | [138] |
| PVDF/PPy | 1.6 S·cm−1 3.2 × 10−16 S·cm−1 (pure PVDF) | n/a | 40-fold increase in the relative conductivity | n/a | n/a | [139] |
| PVDF/PPy | 107 Ω·cm 1017 Ω·cm (pure PVDF) | n/a | 200 Ω·cm/Pa 20 Ω·cm/Pa (pure PVDF) | <0.02 MPa | >25 | [140] |
| P(VDF-TrFE)/PI | 0.5–1.5 V | 6–40 nA | <0.1 Pa | 1000 | [141] | |
| P(VDF-TrFE)/PDMS | ~2000 mV | n/a | 120 mV/µm | >1000 | [142] | |
| P(VDF-TrFE) | ~5 mV | n/a | 60.5 mV/N | n/a | n/a | [143] |
| P(VDF-TrFE) | ~0.7 V | n/a | n/a | n/a | n/a | [144] |
| P(VDF-TrFE) | n/a | n/a | 15.6 kPa−1 | 1.2 Pa | 100,000 | [145] |
| P(VDF-TrFE)/PDMS-MWCNT membrane | 25 V (triboelectric voltage) 2.5 V (piezoelectric voltage) | ~6.5 μA (triboelectric current) ~2.3 μA (piezoelectric current) | n/a | n/a | [146] | |
| P(VDF-TrFE) | 300 ± 5 mV | n/a | n/a | n/a | n/a | [147] |
| P(VDF-TrFE) | n/a | n/a | 110.37 pC/Pa | n/a | n/a | [148] |
| P(VDF-TrFE) (3D sensor)/PDMS | >1200 mV (flat shape) ~1000 mV (wrist shape) ~500 mV (finger shape) | n/a | 23 VN−1 (flat shape) 20 VN−1 (wrist shape) 12 VN−1 (finger shape) | n/a | n/a | [149] |
| P(VDF-TrFE) (shell)-PVP/PEDOT: PSS (core) | >1.6 V | n/a | 4 mV/mmHg | n/a | n/a | [150] |
| Fabrication | Components | Sensitivity | Pressure Range | Size | Comments |
|---|---|---|---|---|---|
| Embroidery | Conductive thread | Switching threshold | Contact sensing | mm2–cm2 range | Electrical contact |
| Patterned electrodes | Conductive ink | 0.214 V/pF | 0–13 kPa | 32 mm2 | Thickness compression |
| Surface touch | PEDOT Nylon | 0.02 pf/mm | 0–2 Pa | Diameter = 5 cm | Capacitance fingers/surface |
| Laminated electrodes | Thin film deposited metals | 0.01 ΔC/mN | 0–50 N/cm2 | Diameter = 250 µm | Capacitance at intersecting points |
| 3D textile capacitor | Conductive fabric 3D textile | 2 pF/N/cm2 | 0–0.75 N/cm2 | 9 cm2 | Thickness compression |
| CrossliteTM capacitor | Silver-coated textile PCCR | 0.05 pF/N/cm2 | 0–30 N/cm2 | 100 mm2 | Thickness compression |
| Switch tactile sensor | Plated fabric Cu, Ni | Threshold at 500 g/mm2 | 70–500 g/mm2 | 8 mm2 | Active sensing cells |
| Tooth structured | Conductive fabric | 2.98 × 10−3 kPa−1 | –2000 kPa | 760 mm3 | Strain in under pressure fabric |
| Polyurethane foam | PPy-Polyurethane | 0:0007 mS/N | 1–7 kN/m2 | 4 cm3 | Conductance increases with compression |
| Conductive Rubber-based | Carbon polymer | 250 Ω/MPa | 0–0.2 MPa | 9 mm2 | Resistance changes with applied load |
| QTC-Ni-based | Pressure composite | ~106 Ω/1% compression | 25% compression | Diameter = 5.5 mm | Switching behavior |
| MEMS Elements | Operation Principle | Robotic Platform | Touch/Grip Object Type | Sensitivity | Reference |
|---|---|---|---|---|---|
| Optical fiber | Bragg’s grating | Four finger gripper | Metal, rubber, plastic | 139 nm/N | [186] |
| Beam deformation strain gauge | Wheatstone bridge | Manufacturing robotic arm | None/Torque sensor | 1–3 mV/Nm | [187] |
| Optical/magnetic | Retroreflective markers/Electromagnetic field | Two finger gripper | 3D printed plastics | 0.01/0.6 mm/deg. | [188] |
| Resistive sensors | Conductivity changes | Master-slave robotic hand system | Plastics and metals | 0.1 N | [189] |
| Graphene/Nanosilver electrodes | Nanoparticle/elastomer composite resistance change | Humanoid robotic hand | Ceramics, plastics | 1.32–3.40% kPa−1 | [123] |
| Capacitive/pneumatic | pneumatic deformation sensing | Two finger gripper | 3D printed soft plastics | 0.03 N | [190] |
| Resistive/magnetic | Capacitance/magnet displacement | Two finger gripper | Metal, wood plastic | n/a | [191] |
| Resistive | Nanoparticle/elastomer composite resistance change | YuMi robot | Skin-like soft rubbers | 18.83% N−1 | [192] |
| Magnetic/barometric | Liquid metal sensing/electrical resistance | Two finger gripper | Plastic objects | 85% accuracy | [193] |
| Resistive | Conductive foam compression | Two finger gripper | Metals, rubber, wood | 1.196%/°C and 13.29%/kPa | [194] |
| Resistive | Resistance change under pressure | anthropomorphic artificial hand | Rigid objects | 0.47, 0.45, 0.16 mV/mN for the x-, y- and z-directions | [195] |
| Tribolectric nanogenerator | Electrostatic induction | Three finger gripper | Plastic, fruits, aluminum, paper | 98.1% accuracy | [196] |
| Resistive | Resistance variation upon compression | Soft robotic hand | 100 objects of all sorts | 94% basic grasping, 50–80% identification-grasping | [197] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayer, I.S. MEMS-Based Tactile Sensors: Materials, Processes and Applications in Robotics. Micromachines 2022, 13, 2051. https://doi.org/10.3390/mi13122051
Bayer IS. MEMS-Based Tactile Sensors: Materials, Processes and Applications in Robotics. Micromachines. 2022; 13(12):2051. https://doi.org/10.3390/mi13122051
Chicago/Turabian StyleBayer, Ilker S. 2022. "MEMS-Based Tactile Sensors: Materials, Processes and Applications in Robotics" Micromachines 13, no. 12: 2051. https://doi.org/10.3390/mi13122051
APA StyleBayer, I. S. (2022). MEMS-Based Tactile Sensors: Materials, Processes and Applications in Robotics. Micromachines, 13(12), 2051. https://doi.org/10.3390/mi13122051






