Isolation Enhancement of a Two-Monopole MIMO Antenna Array with Various Parasitic Elements for Sub-6 GHz Applications
Abstract
1. Introduction
- (1)
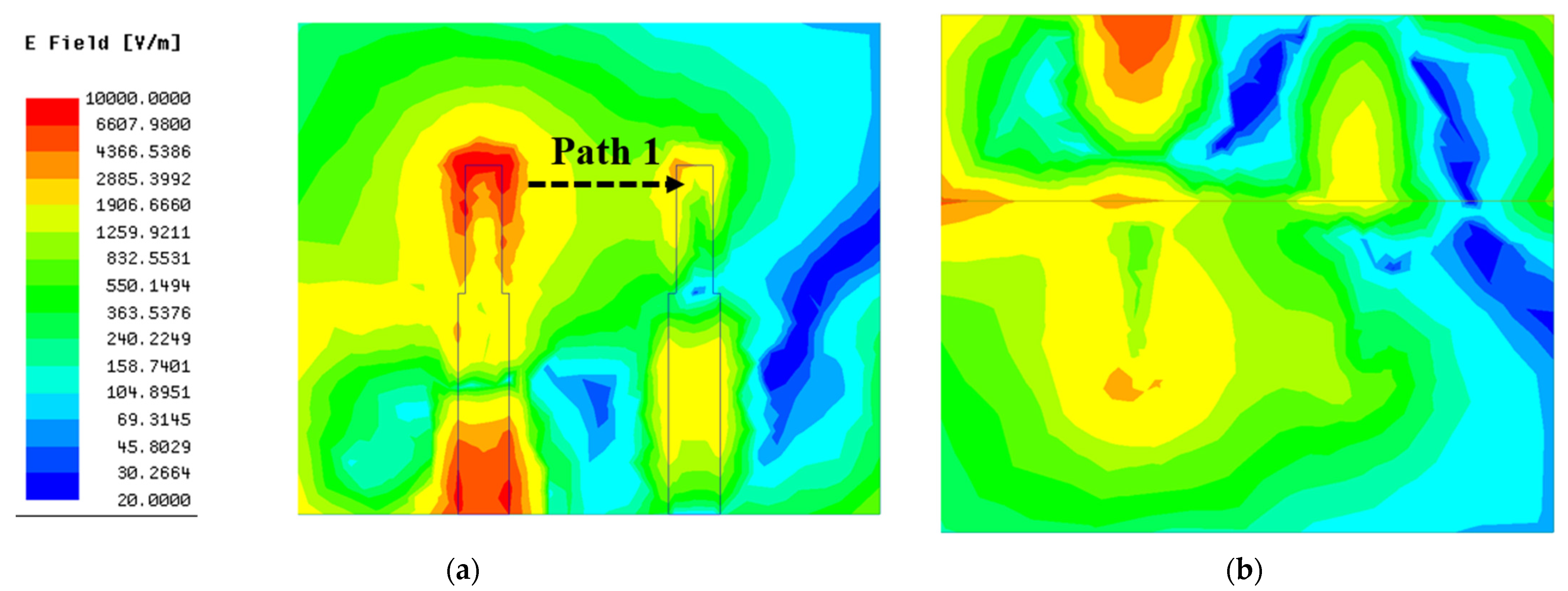
- Unlike past parasitic elements devoted to MIMO decoupling, the combination of the T-shaped ground branch and the isolated branch can be regarded as a three-dimensional composite parasitic element. The field generated by the induced current in the T-shaped ground branch can counteract the surface coupling field between antenna elements, while the isolated branch can eliminate the coupling field inside the substrate. Consequently, a unique three-dimensional weak field is created between two monopole elements, which has the distinguished ability to suppress the electromagnetic interference between antenna elements. Simulated results indicate that the highest isolation level of the final designed MIMO antenna exceeds 42.5 dB, MIMO isolation within the whole operating band is over 20 dB, and the average isolation improvement is approximately 16 dB compared to the original antenna.
- (2)
- Since the T-shaped ground branch shares a common microstrip stem with the isolated branch integrated into the substrate of antenna, the proposed antenna has a comparatively compact structure, where only a single PCB is employed in antenna design. The overall size of the proposed antenna is 0.55λ0 × 0.46λ0 × 0.018λ0 (λ0 is the free space wavelength at the center frequency).
2. MIMO Design
2.1. MIMO Antenna Configuration
2.2. MIMO Antenna Design Procedures
2.3. Simulation Results of the MIMO Antennas
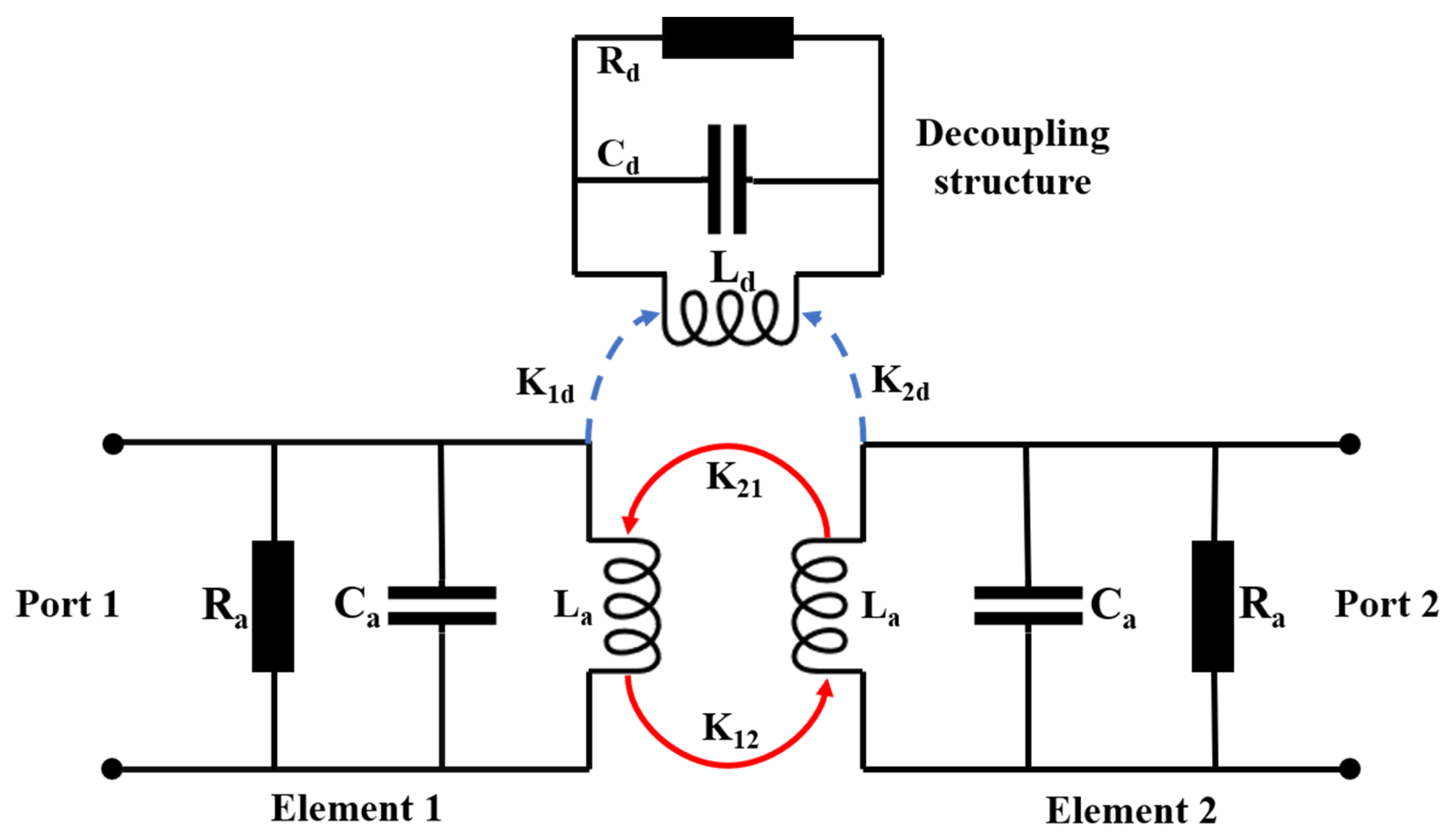
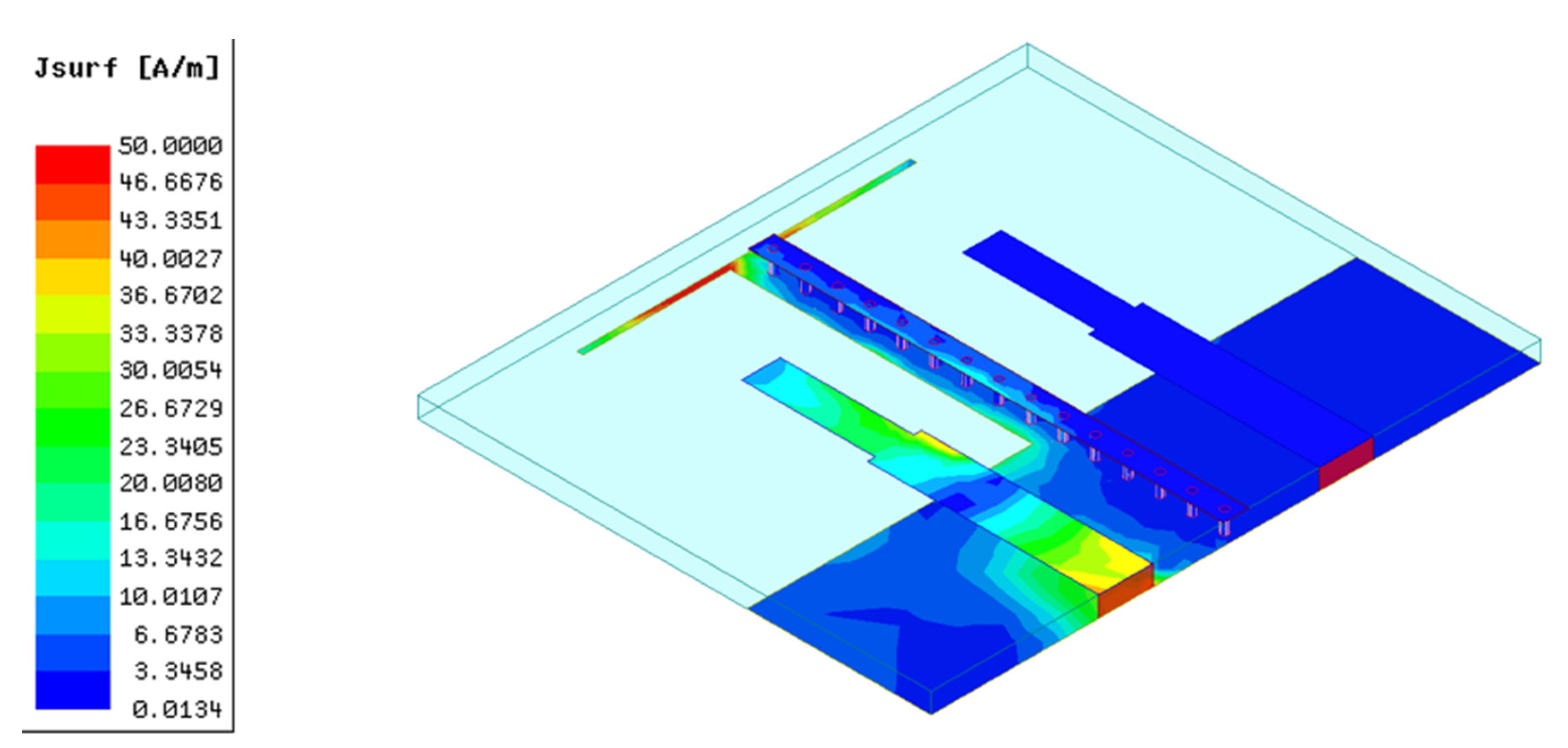
2.4. Decoupling Concept
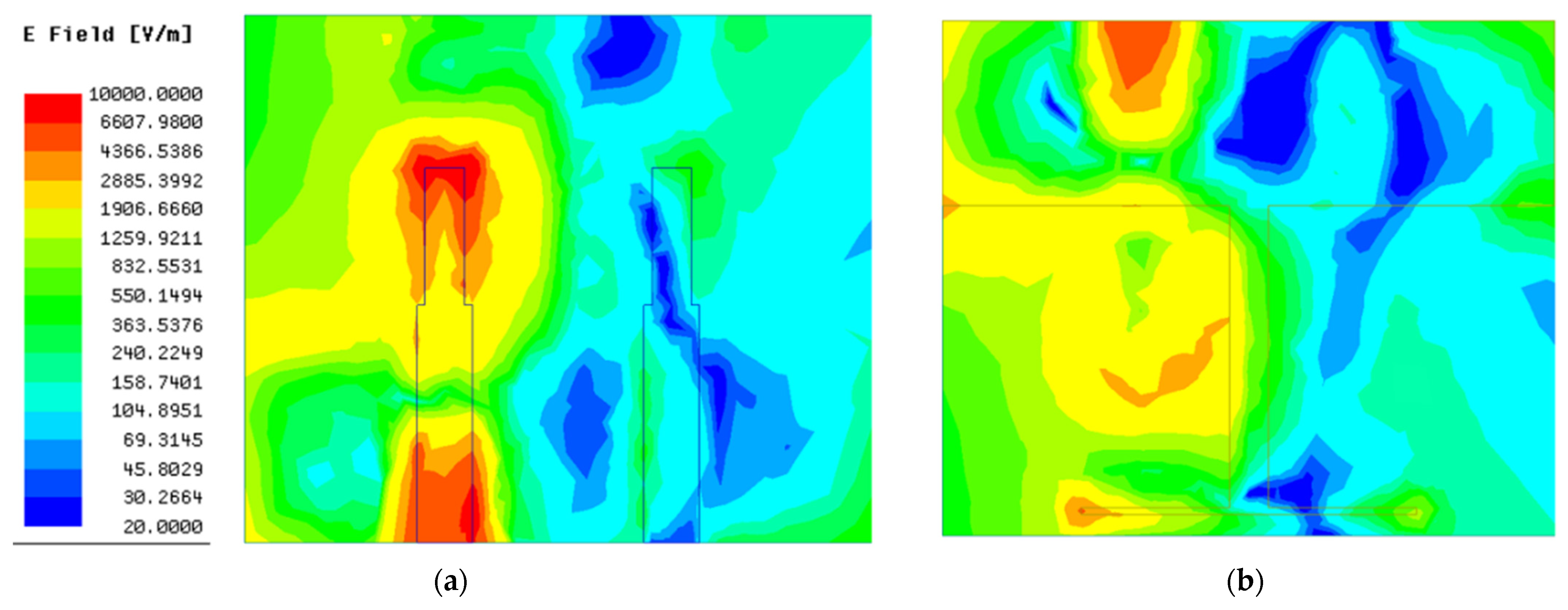
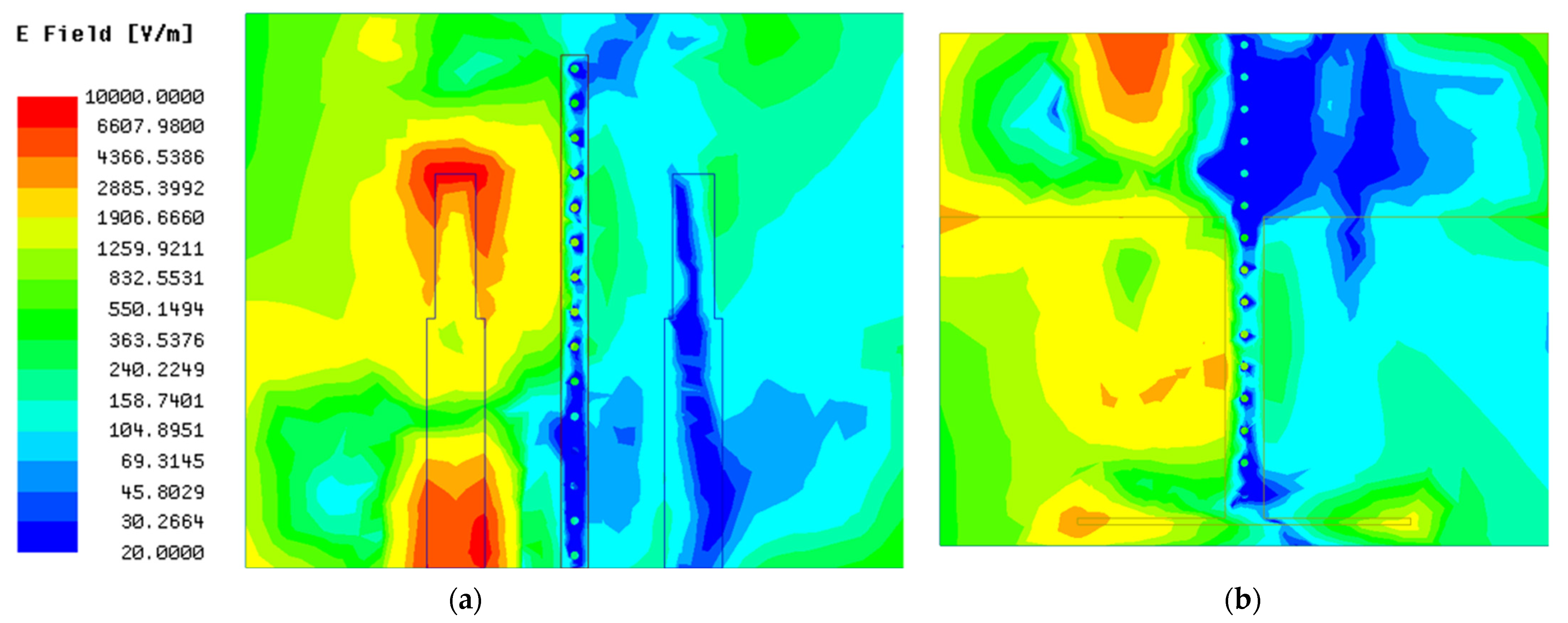
2.5. Investigation of the MIMO Antennas in Different Design Phases
2.5.1. The Antenna without Decoupling Structure
2.5.2. The Decoupling Effect of the I-Shaped Ground Branch
2.5.3. The Decoupling Effect of the T-Shaped Ground Branch
2.5.4. The Decoupling Effect of the Composite Parasitic Element
3. Parametric Analysis and Discussion
3.1. Effect of the Metallic via Diameter d2 and Periodic Distance p
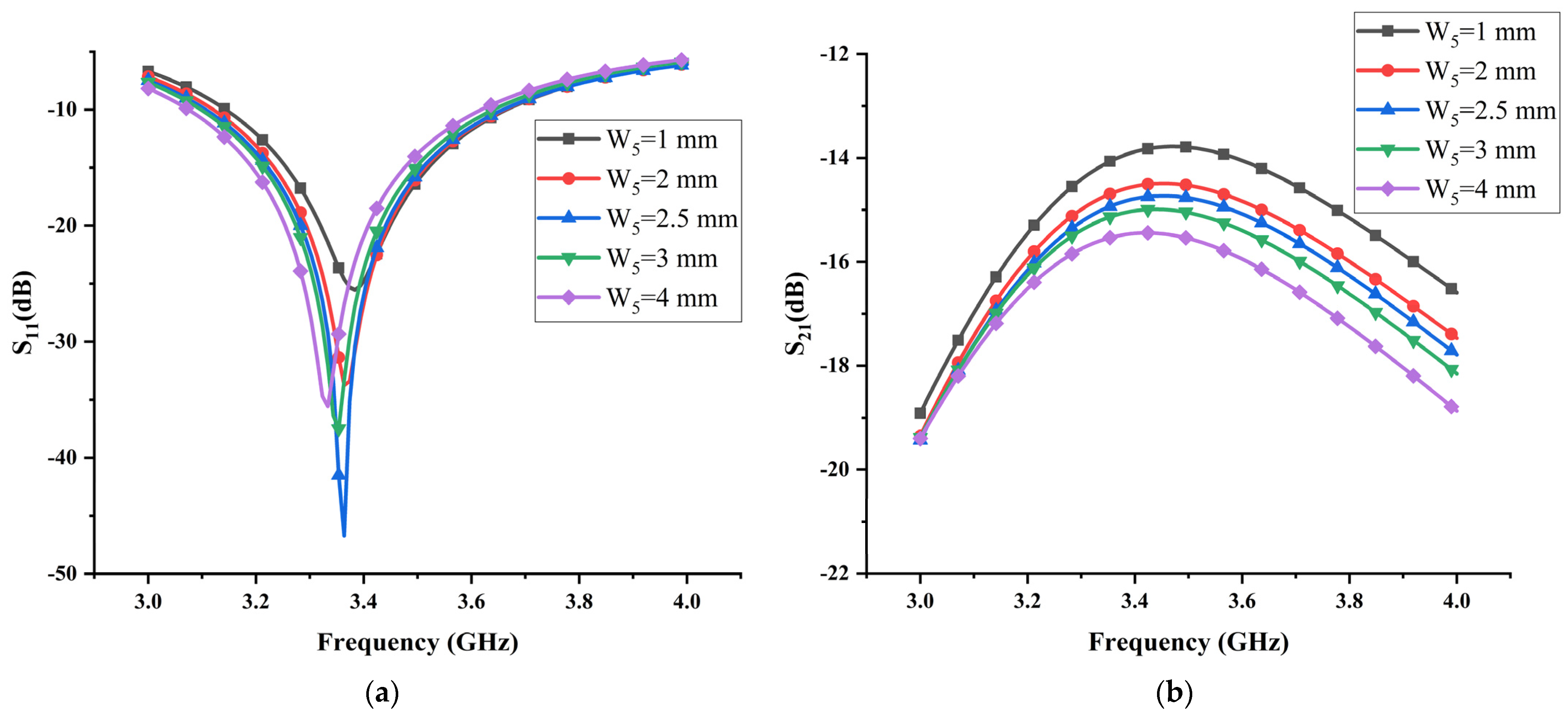
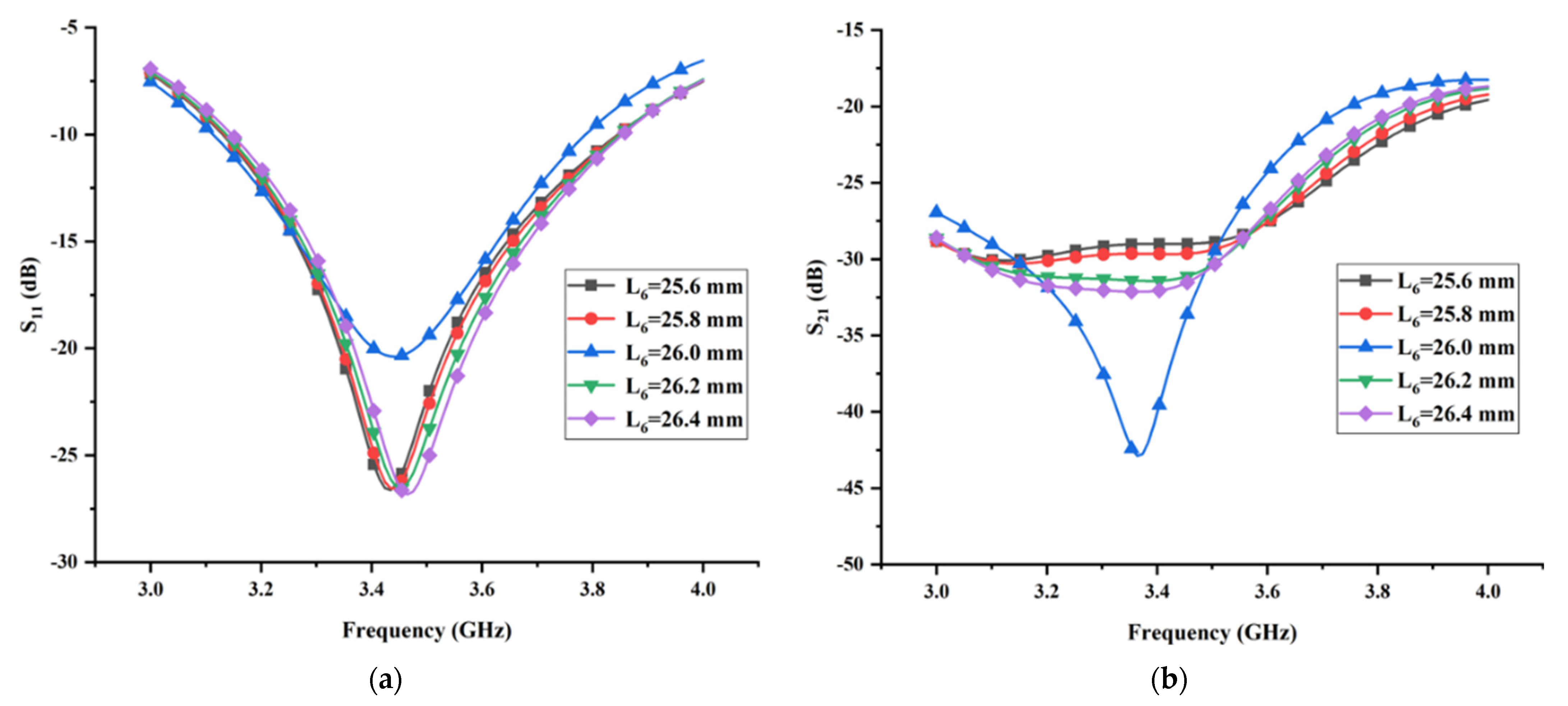
3.2. Effect of the Length L6 and Width W6 of the Thin Horizontal Stub
4. Experimental Results
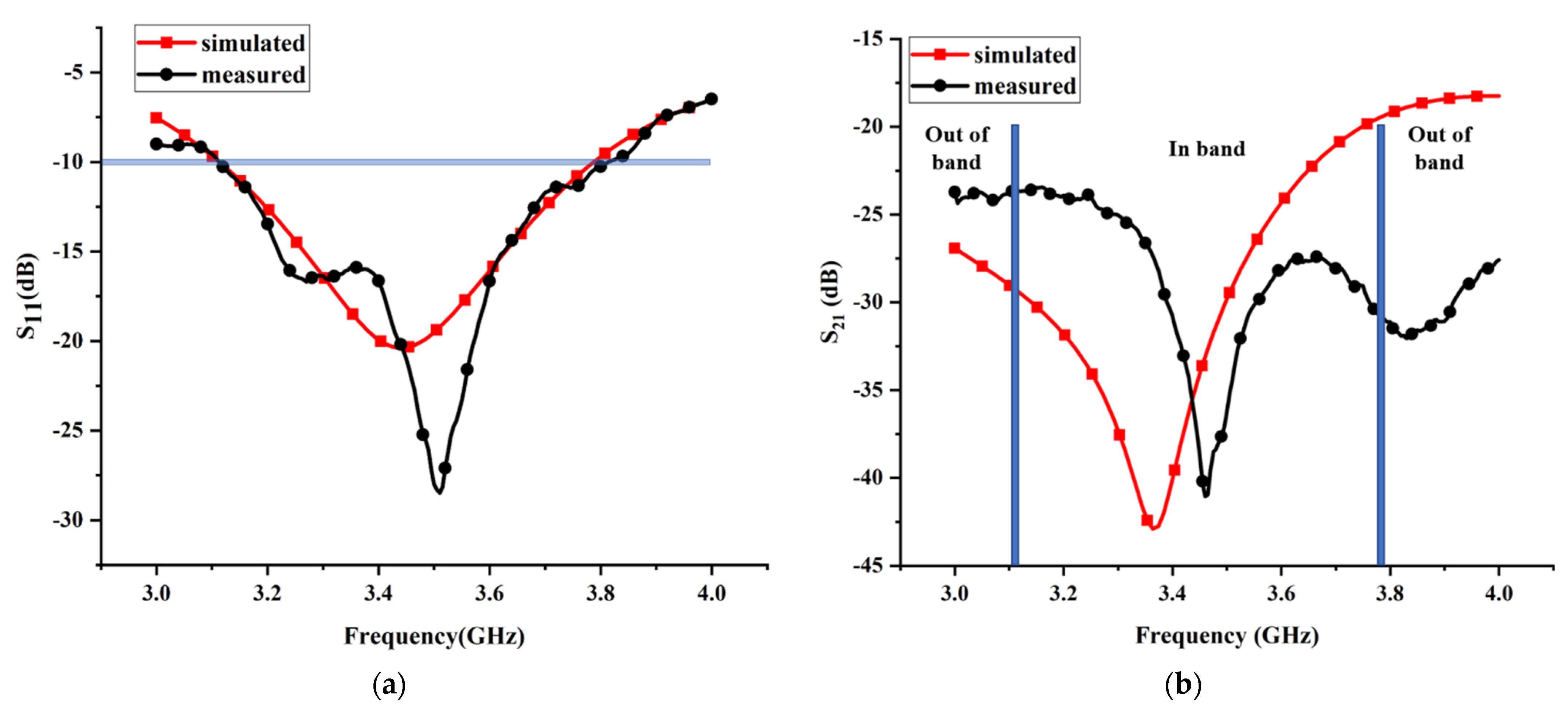
4.1. Scattering Parameters
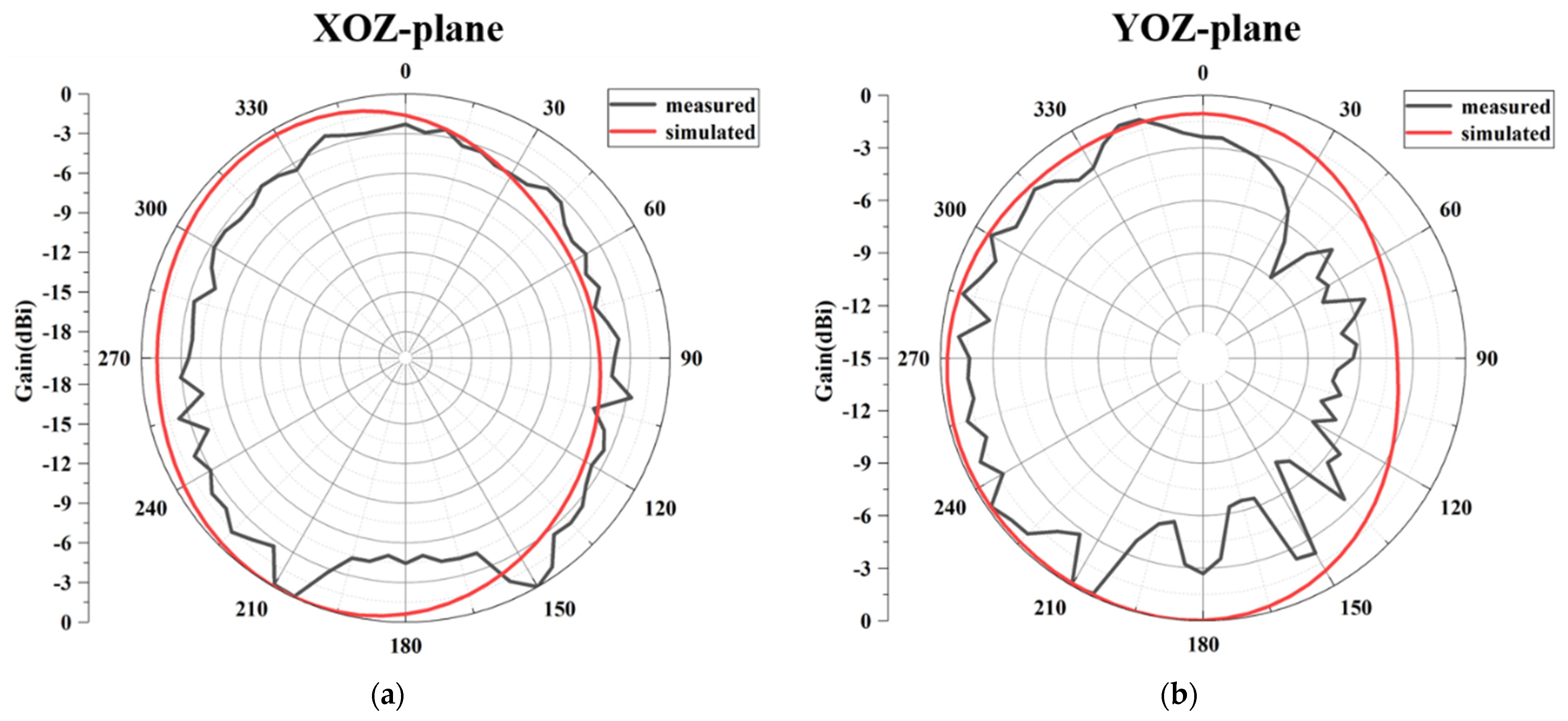
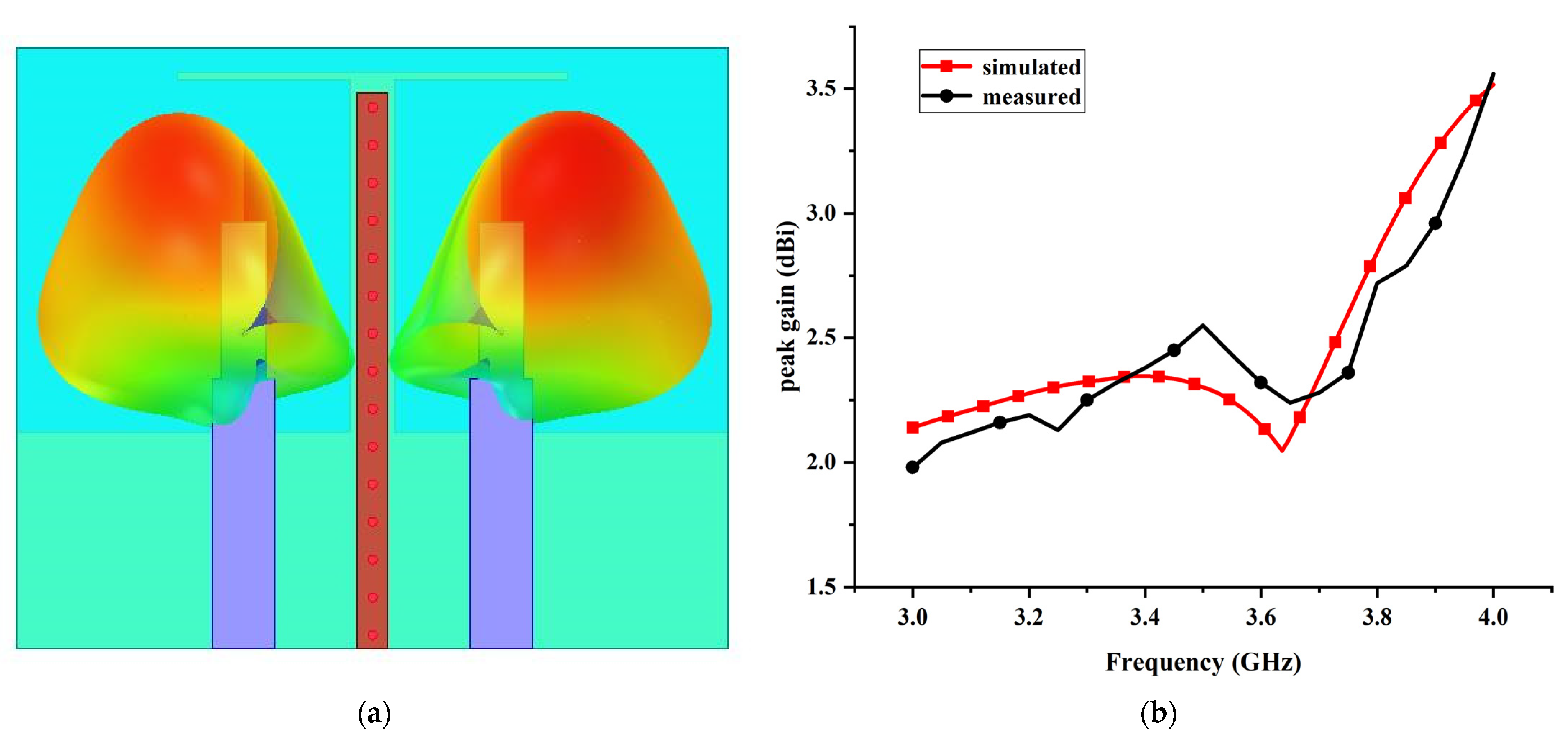
4.2. Radiation Performance
4.3. Envelope Correlation Coefficient (ECC)
4.4. Diversity Gain (DG)
4.5. Mean Effective Gain (MEG)
5. Comparison with Previous Design
- (1)
- A comparative small dimension is achieved in our design, in which the corresponding electrical size is 0.55 λ0 × 0.46 λ0.
- (2)
- A fabulous 20 dB isolation bandwidth is realized in this work, which reaches 19.4% with moderate edge separation.
- (3)
- The highest isolation level reaches 42.9 dB in this work, which is far superior to other designs accompanied by low design complexity.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahboob, S.; Vaughan, R.G. Fiber-Fed Distributed Antenna System in an FPGA Software Defined Radio for 5G Demonstration. IEEE Trans. Circuits Syst. II 2020, 67, 280–284. [Google Scholar] [CrossRef]
- Singh, H.V.; Siva Prasad, D.V.; Tripathi, S. Wideband MIMO Antenna Isolation Enhancement Using 4th-Order Cross-Coupled Decoupling Circuit. IEEE Can. J. Electr. Comput. Eng. 2022, 45, 114–123. [Google Scholar] [CrossRef]
- Lin, J.-F.; Deng, H.; Zhu, L. Design of Low-Profile Compact MIMO Antenna on a Single Radiating Patch Using Simple and Systematic Characteristic Modes Method. IEEE Trans. Antennas Propag. 2022, 70, 1612–1622. [Google Scholar] [CrossRef]
- Savy, L.; Lesturgie, M. Coupling effects in MIMO phased array. In Proceedings of the 2016 IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Chen, X.; Zhang, S.; Li, Q. A Review of Mutual Coupling in MIMO Systems. IEEE Access 2018, 6, 24706–24719. [Google Scholar] [CrossRef]
- Nadeem, I.; Choi, D. Study on Mutual Coupling Reduction Technique for MIMO Antennas. IEEE Access 2019, 7, 563–586. [Google Scholar] [CrossRef]
- Sufian, M.A.; Askari, N.H.; Park, S.G.; Shin, K.S.; Kim, N. Isolation Enhancement of a Metasurface-Based MIMO Antenna Using Slots and Shorting Pins. IEEE Access 2021, 9, 73533–73543. [Google Scholar] [CrossRef]
- Gao, D.; Cao, Z.-X.; Fu, S.-D.; Quan, X.; Chen, P. A Novel Slot-Array Defected Ground Structure for Decoupling Microstrip Antenna Array. IEEE Trans. Antennas Propag. 2020, 68, 7027–7038. [Google Scholar] [CrossRef]
- Kowalewski, J.; Atuegwu, J.; Mayer, J.; Mahler, T.; Zwick, T. A Low-Profile Pattern Reconfigurable Antenna System for Automotive MIMO Applications. Prog. Electromagn. Res. 2018, 161, 41–55. [Google Scholar] [CrossRef]
- Liu, K.; Liu, N.-W.; Fu, G. Isolation Improvement of Dual-polarized Microstrip Array Antenna by Using DGS Scheme. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 514–516. [Google Scholar]
- Bait-Suwailam, M.M.; Boybay, M.S.; Ramahi, O.M. Electromagnetic Coupling Reduction in High-Profile Monopole Antennas Using Single-Negative Magnetic Metamaterials for MIMO Applications. IEEE Trans. Antennas Propag. 2010, 58, 2894–2902. [Google Scholar] [CrossRef]
- Yang, F.; Peng, L.; Liao, X.; Mo, K.; Jiang, X.; Li, S. Coupling Reduction for a Wideband Circularly Polarized Conformal Array Antenna with a Single-Negative Structure. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 991–995. [Google Scholar] [CrossRef]
- Niu, Z.; Zhang, H.; Chen, Q.; Zhong, T. Isolation Enhancement in Closely Coupled Dual-Band MIMO Patch Antennas. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1686–1690. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, Z.; Wu, K. Phase Compensation for Decoupling of Large-Scale Staggered Dual-Polarized Dipole Array Antennas. IEEE Trans. Antennas Propag. Mag. 2020, 68, 2822–2831. [Google Scholar] [CrossRef]
- Yin, B.; Zhao, S.; Wang, P.; Feng, X. Isolation Improvement of Compact Microbase Station Antenna Based on Metasurface Spatial Filtering. IEEE Trans. Electromagn. Compat. 2021, 63, 57–65. [Google Scholar] [CrossRef]
- Huang, H. A Decoupling Method for Antennas with Different Frequencies in 5G Massive MIMO Application. IEEE Access 2020, 8, 140273–140278. [Google Scholar] [CrossRef]
- Farahani, M.; Pourahmadazar, J.; Akbari, M.; Nedil, M.; Sebak, A.R.; Denidni, T.A. Mutual Coupling Reduction in Millimeter-Wave MIMO Antenna Array Using a Metamaterial Polarization-Rotator Wall. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2324–2327. [Google Scholar] [CrossRef]
- Hasan, M.; Islam, M.T.; Samsuzzaman, M.; Baharuddin, M.H.; Soliman, M.S.; Alzamil, A.; Abu Sulayman, I.I.M.; Islam, S. Gain and isolation enhancement of a wideband MIMO antenna using metasurface for 5G sub-6 GHz communication systems. Sci. Rep. 2022, 12, 9433. [Google Scholar] [CrossRef]
- Yin, B.; Feng, X.; Gu, J. A Metasurface Wall for Isolation Enhancement: Minimizing mutual coupling between MIMO antenna elements. IEEE Antennas Propag. 2020, 62, 14–22. [Google Scholar] [CrossRef]
- Tan, X.; Wang, W.; Wu, Y.; Liu, Y.; Kishk, A.A. Enhancing Isolation in Dual-Band Meander-Line Multiple Antenna by Employing Split EBG Structure. IEEE Trans. Antennas Propag. 2019, 67, 2769–2774. [Google Scholar] [CrossRef]
- Bayarzaya, B.; Hussain, N.; Awan, W.A.; Sufian, M.A.; Abbas, A.; Choi, D.; Lee, J.; Kim, N. A Compact MIMO Antenna with Improved Isolation for ISM, Sub-6 GHz, and WLAN Application. Micromachines 2022, 13, 1355. [Google Scholar] [CrossRef]
- Wang, L.; Du, Z.; Yang, H.; Ma, R.; Zhao, Y.; Cui, X.; Xi, X. Compact UWB MIMO Antenna With High Isolation Using Fence-Type Decoupling Structure. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1641–1645. [Google Scholar] [CrossRef]
- Yang, Z.; Xiao, J.; Ye, Q. Enhancing MIMO Antenna Isolation Characteristic by Manipulating the Propagation of Surface Wave. IEEE Access 2020, 8, 115572–115581. [Google Scholar] [CrossRef]
- Sun, L.; Li, Y.; Zhang, Z. Wideband Decoupling of Integrated Slot Antenna Pairs for 5G Smartphones. IEEE Trans. Antennas Propag. 2021, 69, 2386–2391. [Google Scholar] [CrossRef]
- Li, M.; Jiang, L.; Yeung, K.L. A General and Systematic Method to Design Neutralization Lines for Isolation Enhancement in MIMO Antenna Arrays. IEEE Trans. Veh. Technol. 2020, 69, 6242–6253. [Google Scholar] [CrossRef]
- See, C.H.; Abd-Alhameed, R.A.; Abidin, Z.Z.; McEwan, N.J.; Excell, P.S. Wideband Printed MIMO/Diversity Monopole Antenna for WiFi/WiMAX Applications. IEEE Trans. Antennas Propag. 2012, 60, 2028–2035. [Google Scholar] [CrossRef]
- Wang, Y.; Du, Z. A Wideband Printed Dual-Antenna with Three Neutralization Lines for Mobile Terminals. IEEE Trans. Antennas Propag. 2014, 62, 1495–1500. [Google Scholar] [CrossRef]
- Su, S.-W.; Lee, C.-T.; Hsiao, Y.-W. Compact Two-Inverted-F-Antenna System With Highly Integrated π/pi-Shaped Decoupling Structure. IEEE Trans. Antennas Propag. 2019, 67, 6182–6186. [Google Scholar] [CrossRef]
- Khan, A.; Bashir, S.; Ghafoor, S.; Qureshi, K.K. Mutual Coupling Reduction Using Ground Stub and EBG in a Compact Wideband MIMO-Antenna. IEEE Access 2021, 9, 40972–40979. [Google Scholar] [CrossRef]
- Cheng, Y.; Cheng, K.M. Compact Wideband Decoupling and Matching Network Design for Dual-Antenna Array. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 791–795. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, K. A Decoupling Technique for Four-Element Symmetric Arrays with Reactively Loaded Dummy Elements. IEEE Trans. Antennas Propag. 2014, 62, 4416–4421. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, Q.; Guo, L. A Compact 5G Decoupling MIMO Antenna Based on Split-Ring Resonators. Int. J. Antennas Propag. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Cheng, Y.-F.; Liu, J.; Wei, C.; Wu, W.-J.; Sun, L.; Wang, G. Interplanted Patch-Monopole Array with Enhanced Isolation. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 1664–1668. [Google Scholar] [CrossRef]
- Tran, H.H.; Nguyen-Trong, N. Performance Enhancement of MIMO Patch Antenna Using Parasitic Elements. IEEE Access 2021, 9, 30011–30016. [Google Scholar] [CrossRef]
- Ding, C.F.; Zhang, X.Y.; Xue, C.; Sim, C. Novel Pattern-Diversity-Based Decoupling Method and Its Application to Multielement MIMO Antenna. IEEE Trans. Antennas Propag. 2018, 66, 4976–4985. [Google Scholar] [CrossRef]
- Zhao, X.; Yeo, S.P.; Ong, L.C. Planar UWB MIMO Antenna with Pattern Diversity and Isolation Improvement for Mobile Platform Based on the Theory of Characteristic Modes. IEEE Trans. Antennas Propag. 2018, 66, 420–425. [Google Scholar] [CrossRef]
- Hu, Y.; Pan, Y.M.; Yang, M. Circularly Polarized MIMO Dielectric Resonator Antenna With Reduced Mutual Coupling. IEEE Trans. Antennas Propag. 2021, 69, 3811–3820. [Google Scholar] [CrossRef]
- Sharma, A.; Kalaskar, K.P.; Gangane, J.R. Analysis of MIMO antennas with parasitic elements for wireless applications. In Proceedings of the 2016 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Chennai, India, 15–17 December 2016; pp. 1–4. [Google Scholar]
- Ahmad, A.; Choi, D.; Ullah, S.A. compact two elements MIMO antenna for 5G communication. Sci. Rep. 2022, 12, 3608. [Google Scholar] [CrossRef]
- Lin, H.; Chen, Q.; Ji, Y.; Yang, X.; Wang, J.; Ge, L. Weak-Field-Based Self-Decoupling Patch Antennas. IEEE Trans. Antennas Propag. 2020, 68, 4208–4217. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Y.; Yang, S. A Self-Decoupling Method for Antenna Arrays Using High-Order Characteristic Modes. IEEE Trans. Antennas Propag. 2022, 70, 2760–2769. [Google Scholar] [CrossRef]
- Yang, W.; Chen, L.; Pan, S.; Che, W.; Xue, Q. Novel Decoupling Method Based on Coupling Energy Cancellation and its Application in 5G Dual-Polarized High-Isolation Antenna Array. IEEE Trans. Antennas Propag. 2022, 70, 2686–2697. [Google Scholar] [CrossRef]
- Abbas, A.; Hussain, N.; Sufian, M.A.; Jung, J.; Park, S.M.; Kim, N. Isolation and Gain Improvement of a Rectangular Notch UWB-MIMO Antenna. Sensors 2022, 22, 1460. [Google Scholar] [CrossRef]
- Khalid, M.; Iffat Naqvi, S.; Hussain, N.; Rahman, M.; Fawad; Mirjavadi, S.S.; Khan, M.J.; Amin, Y. 4-Port MIMO Antenna with Defected Ground Structure for 5G Millimeter Wave Applications. Electronics 2020, 9, 71. [Google Scholar] [CrossRef]
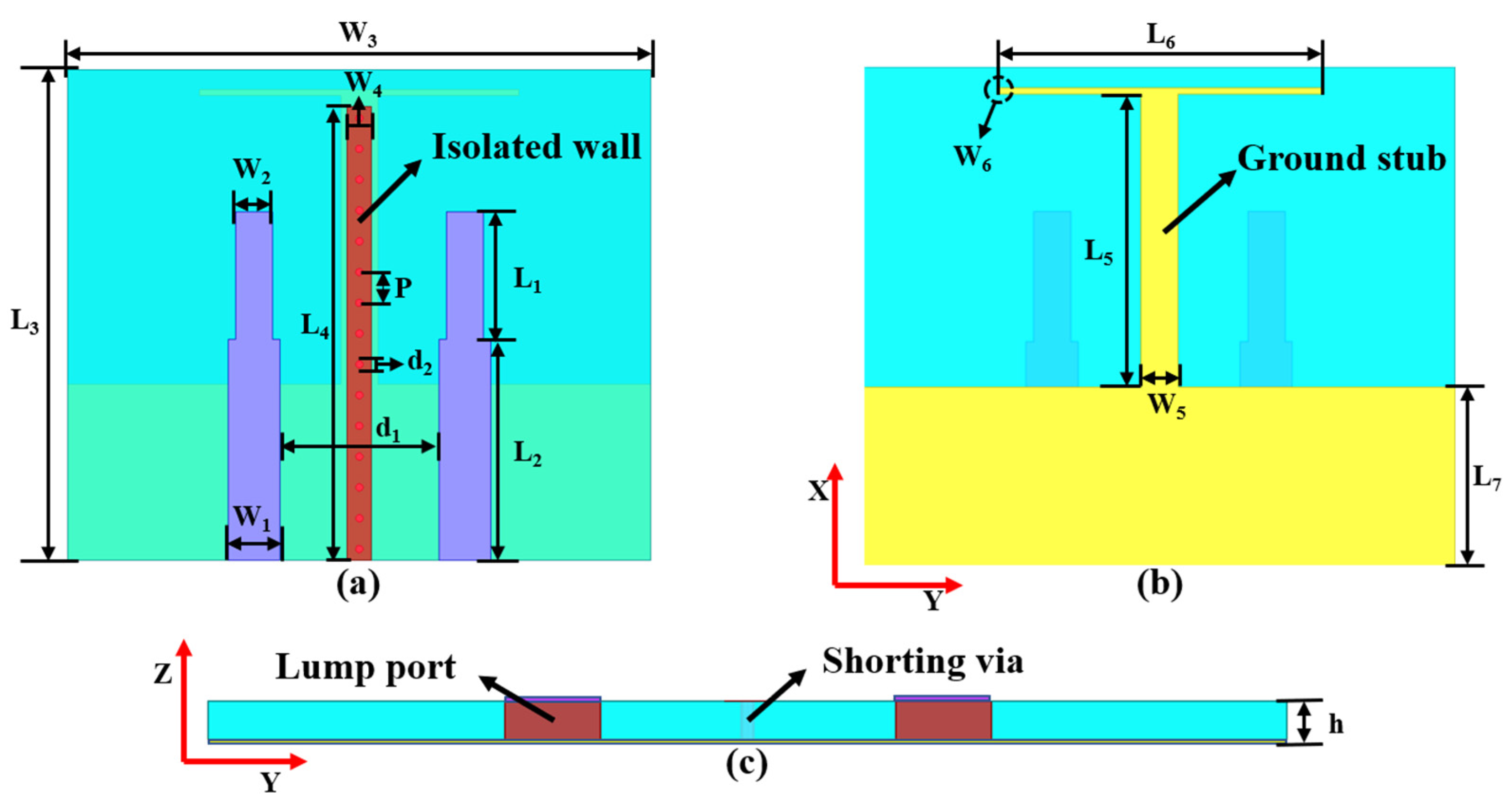










| Parameters | ||||||
|---|---|---|---|---|---|---|
| Value (mm) | 10.4 | 18 | 40 | 37 | 24 | 26 |
| Parameters | ||||||
| Value (mm) | 4.2 | 3 | 47.5 | 2 | 3 | 0.5 |
| Parameters | ||||||
| Value (mm) | 13 | 0.6 | 2.51 | 1.6 | 14.36 |
| Ref. | [26] | [27] | [28] | [29] | [31] | [32] | This Work |
|---|---|---|---|---|---|---|---|
| Antenna type | monopole | monopole | monopole | monopole | monopole | monopole | monopole |
| Method | NL | NL | DN | EBG | PE | PE | PE |
| Frequence (GHz) | 3.3 | 2.3 | 2.4 | 6.9 | 2.6 | 3.5 | 3.45 |
| Electrical dimension (λ0) | 0.99 × 0.44 | 0.88 × 0.46 | 0.3 × 0.04 | 0.6 × 0.72 | 0.76 × 0.76 | 0.99 × 0.75 | 0.55 × 0.46 |
| Profile (λ0) | 0.009 | 0.006 | 0.003 | 0.018 | 0.25 | 0.005 | 0.018 |
| Edge separation (λ0) | 0.3 | 0.04 | 0.02 | 0.19 | 0.21 | 0.06 | 0.15 |
| 20 dB isolation BW (%) | 26.7 | 11.1 | 12 | 109 | 1.5 | 5.7 | 19.4 |
| Highest isolation level (dB) | 36 | 35 | 20 | 60 | 28 | 30 | 42.9 |
| Design complexity | Moderate | High | Low | Low | Moderate | Moderate | Low |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yang, Z.; Chen, P.; Xiao, J.; Ye, Q. Isolation Enhancement of a Two-Monopole MIMO Antenna Array with Various Parasitic Elements for Sub-6 GHz Applications. Micromachines 2022, 13, 2123. https://doi.org/10.3390/mi13122123
Liu Y, Yang Z, Chen P, Xiao J, Ye Q. Isolation Enhancement of a Two-Monopole MIMO Antenna Array with Various Parasitic Elements for Sub-6 GHz Applications. Micromachines. 2022; 13(12):2123. https://doi.org/10.3390/mi13122123
Chicago/Turabian StyleLiu, Yitao, Zhuo Yang, Ping Chen, Jun Xiao, and Qiubo Ye. 2022. "Isolation Enhancement of a Two-Monopole MIMO Antenna Array with Various Parasitic Elements for Sub-6 GHz Applications" Micromachines 13, no. 12: 2123. https://doi.org/10.3390/mi13122123
APA StyleLiu, Y., Yang, Z., Chen, P., Xiao, J., & Ye, Q. (2022). Isolation Enhancement of a Two-Monopole MIMO Antenna Array with Various Parasitic Elements for Sub-6 GHz Applications. Micromachines, 13(12), 2123. https://doi.org/10.3390/mi13122123







