Time-Modulated Antenna Arrays for Ultra-Wideband 5G Applications
Abstract
1. Introduction
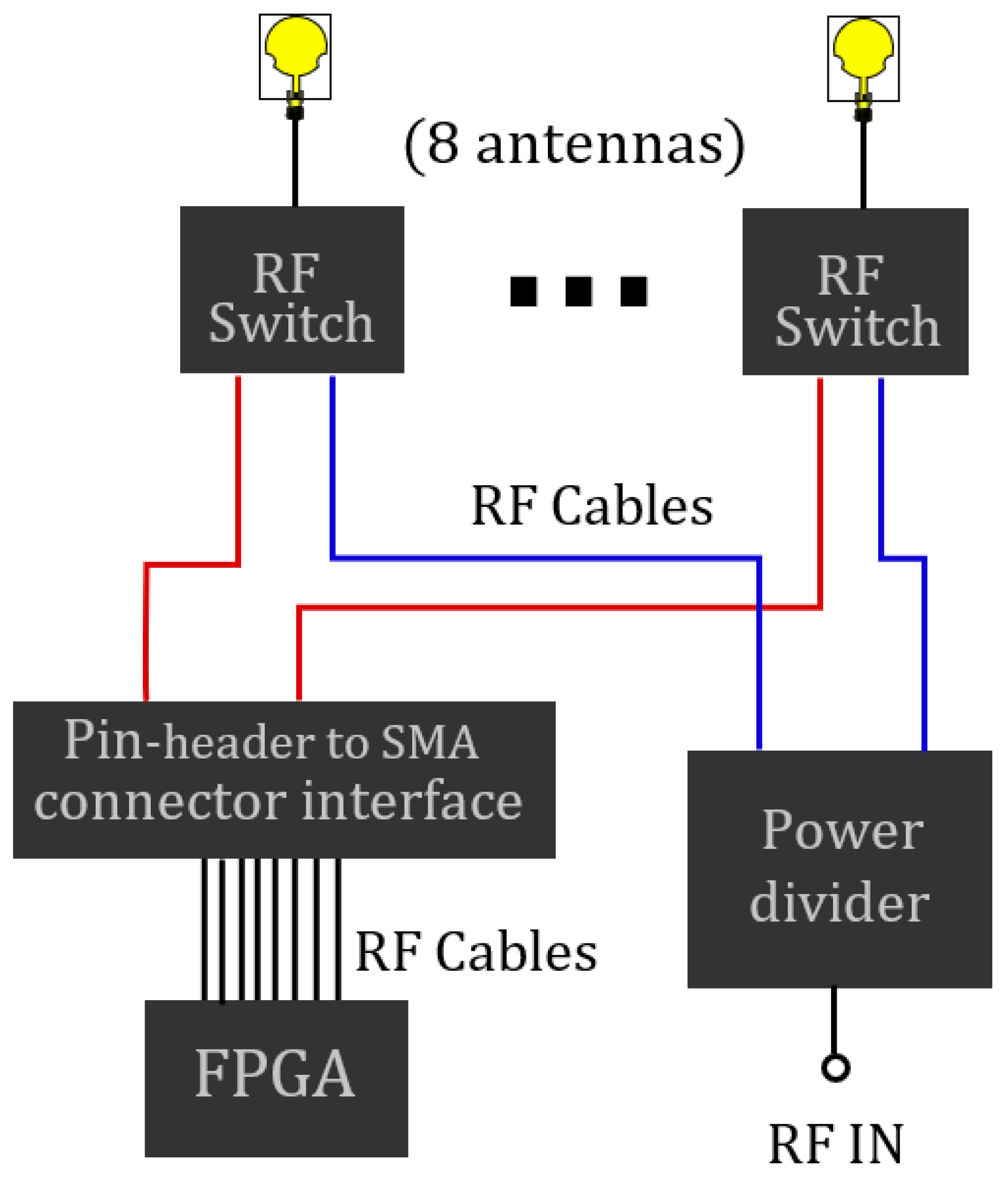
2. Time Modulated Array Model
3. Problem Statement and Optimization Algorithm
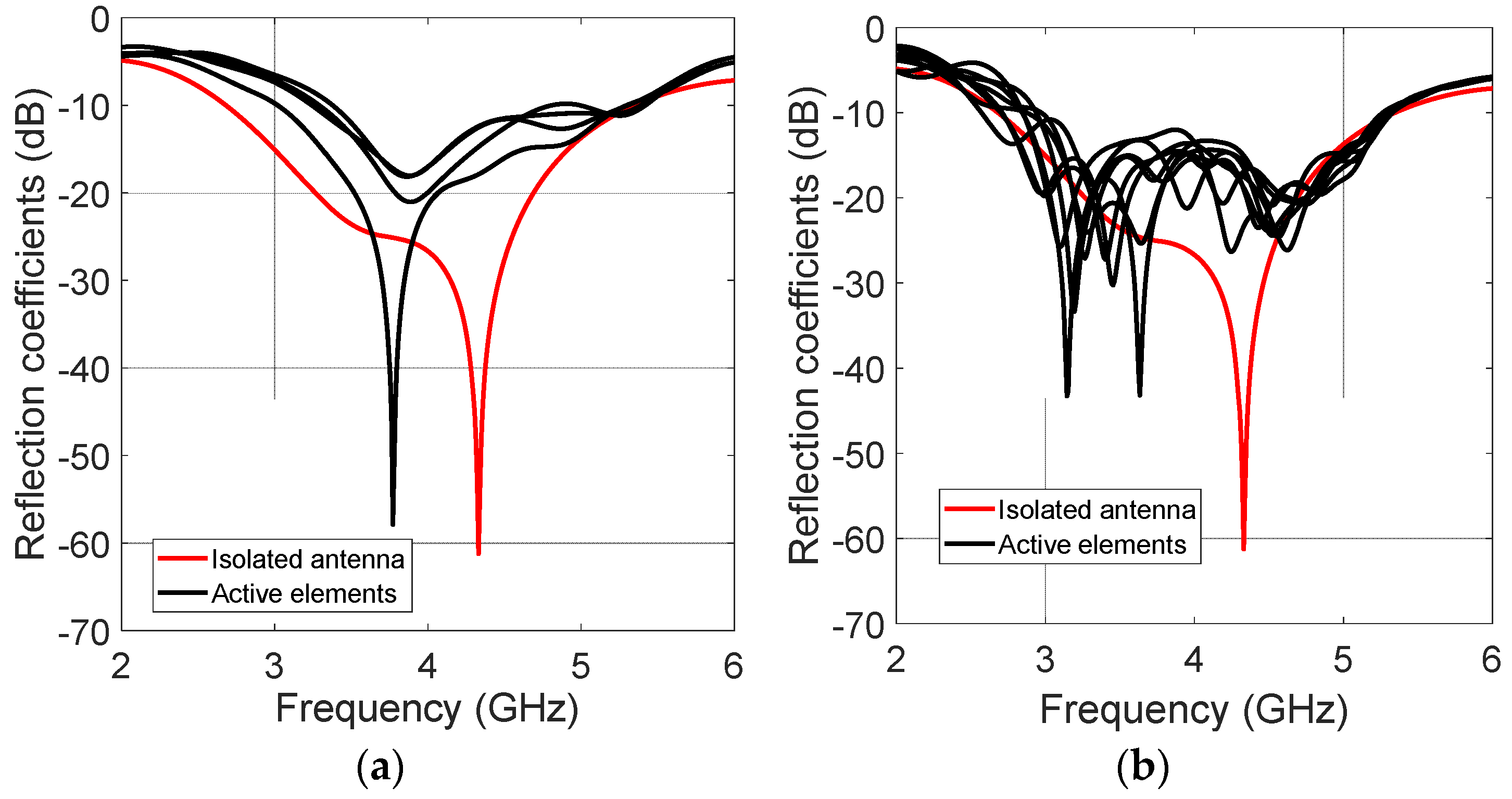
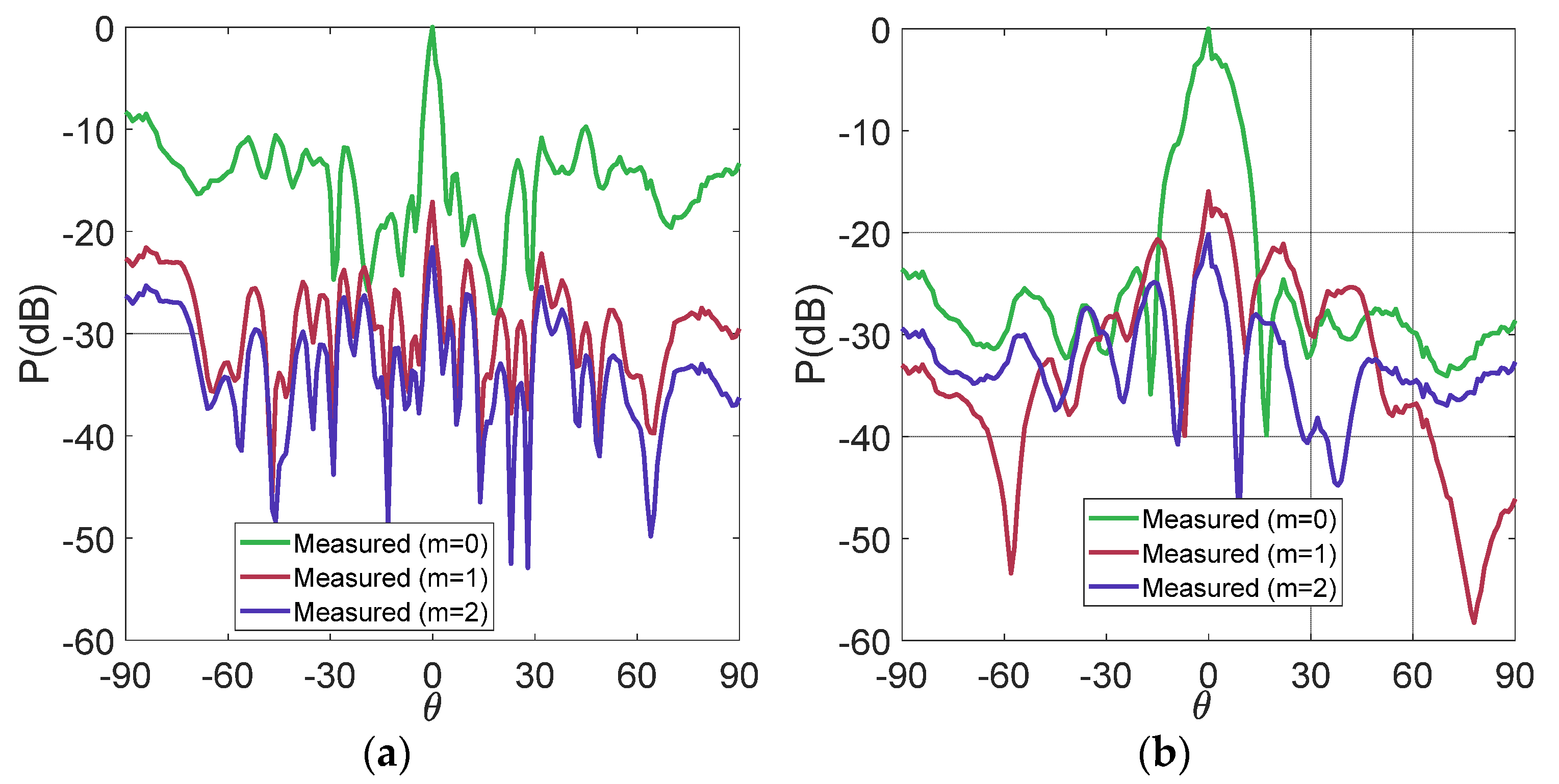
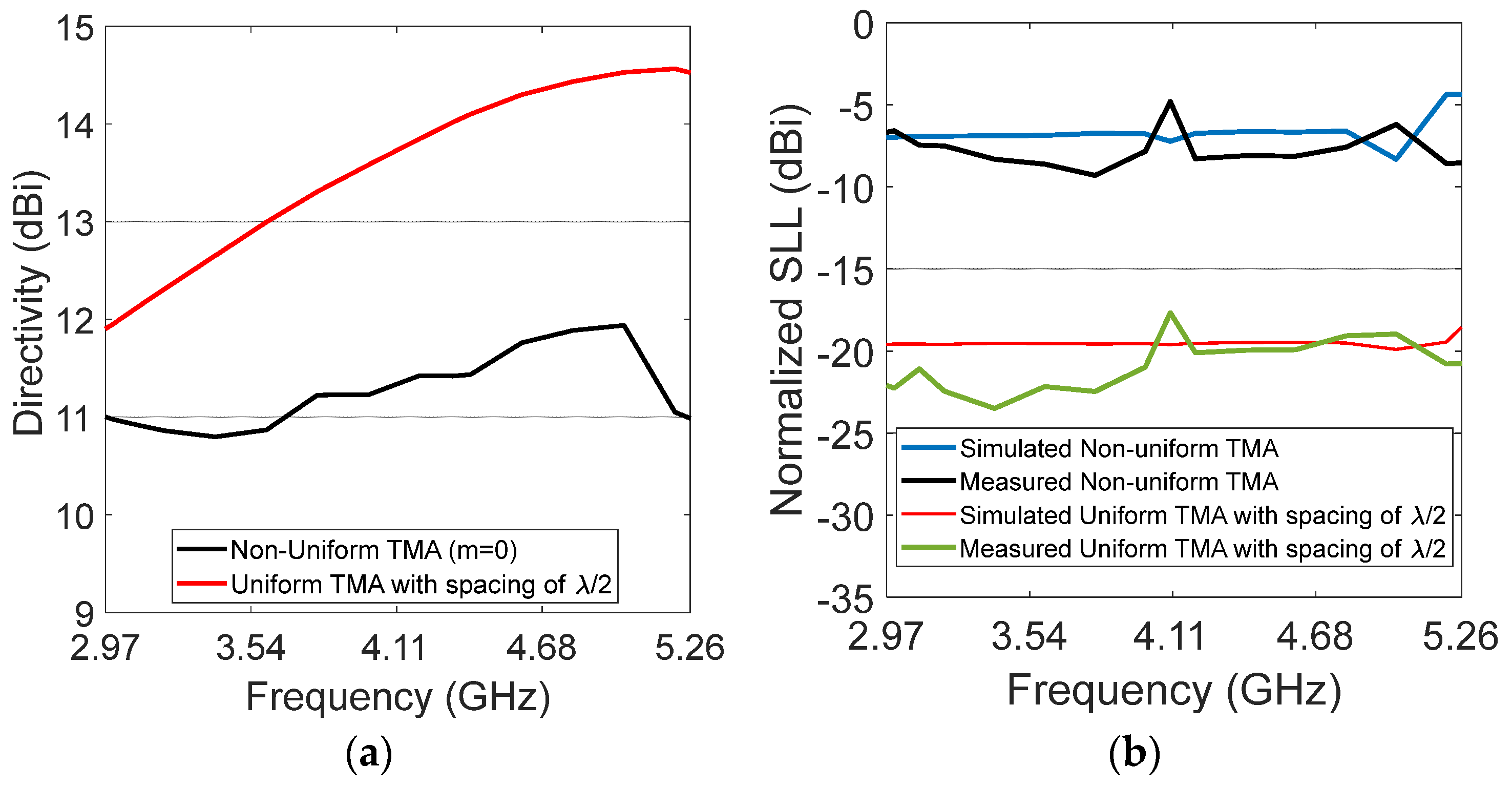
4. Design Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Johannsen, N.L.; Peitzmeier, N.; Hoeher, P.A.; Manteuffel, D. On the Feasibility of Multi-Mode Antennas in UWB and IoT Applications below 10 GHz. IEEE Commun. Mag. 2020, 58, 69–75. [Google Scholar] [CrossRef]
- Chettri, L.; Bera, R. A Comprehensive Survey on Internet of Things (IoT) Toward 5G Wireless Systems. IEEE Internet Things J. 2020, 7, 16–32. [Google Scholar] [CrossRef]
- Yang, S.; Gan, Y.B.; Qing, A. Sideband suppression in time-modulated linear arrays by the differential evolution algorithm. IEEE Antennas Wirel. Propag. Lett. 2002, 1, 173–175. [Google Scholar] [CrossRef]
- Poli, L.; Rocca, P.; Oliveri, G.; Massa, A. Harmonic Beamforming in Time-Modulated Linear Arrays. IEEE Trans. Antennas Propag. 2011, 59, 2538–2545. [Google Scholar] [CrossRef]
- Capolino, F.; Felsen, L.B. Time Domain Green’s Function for an Infinite Sequentially Excited Periodic Planar Array of Dipoles. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Transmitting Waves of Progress to the Next Millennium. 2000 Digest. Held in Conjunction with: USNC/URSI National Radio Science Meeting (Cat. No.00CH37118). Salt Lake City, UT, USA, 16–21 July 2000; pp. 2054–2057. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, S.; Huang, M.; Nie, Z. Synthesis of low sidelobe time modulated planar arrays with uniform amplitude and sub-sectional optimized time steps. In Proceedings of the 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, Harbin, China, 26–30 July 2011; pp. 498–501. [Google Scholar] [CrossRef]
- Yang, J.; Li, W.T.; Shi, X.W.; Ren, Z. Artificial bee colony algorithm for time-modulated circular antenna array synthesis. In Proceedings of the 2012 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shenzhen, China, 5–8 May 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Guney, K.; Basbug, S. Null Synthesis of Time-Modulated Circular Antenna Arrays Using an Improved Differential Evolution Algorithm. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 817–820. [Google Scholar] [CrossRef]
- Mandal, S.; Kumar Mandal, S. A Comparative Analysis of Power Losses in Time-Modulated Arrays with Uniform, Non-Uniform and Optimized Time-Modulation. In Proceedings of the 2019 International Workshop on Antenna Technology (IWAT), Miami, FL, USA, 3–6 March 2019; pp. 206–209. [Google Scholar] [CrossRef]
- Mukherjee, A.; Mandal, S.K.; Ghatak, R. Differential evolution to synthesize low sidelobe thinned isophoric time-modulated planar array with increased directivity. Int. J. RF Microw. Comput.-Aided Eng. 2019, 29, e21938. [Google Scholar] [CrossRef]
- Fondevila, J.; Bregains, J.C.; Ares, F.; Moreno, E. Optimizing uniformly excited linear arrays through time modulation. IEEE Antennas Wirel. Propag. Lett. 2004, 3, 298–301. [Google Scholar] [CrossRef]
- Aksoy, E.; Afacan, E. Thinned Nonuniform Amplitude Time-Modulated Linear Arrays. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 514–517. [Google Scholar] [CrossRef]
- Oraizi, H.; Fallahpour, M. Sum, Difference and Shaped Beam Pattern Synthesis by Non-Uniform Spacing and Phase Control. IEEE Trans. Antennas Propag. 2011, 59, 4505–4511. [Google Scholar] [CrossRef]
- Yang, Q.; Gu, P.; Li, M.; Fan, Z.; Chen, R. Synthesis of Nonuniformly Spaced Wideband Linear Arrays with MSM-FOCUSS Algorithm. In Proceedings of the 2018 IEEE International Conference on Computational Electromagnetics (ICCEM), Chengdu, China, 26–28 March 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Chen, M.Z.; Tang, W.; Dai, J.Y.; Ke, J.C.; Zhang, L.; Zhang, C.; Yang, J.; Li, L.; Cheng, Q.; Jin, S.; et al. Accurate and broadband manipulations of harmonic amplitudes and phases to reach 256 QAM millimeter-wave wireless communications by time-domain digital coding metasurface. Natl. Sci. Rev. 2022, 9, nwab134. [Google Scholar] [CrossRef]
- Ke, J.C.; Dai, J.Y.; Chen, M.Z.; Wang, L.; Zhang, C.; Tang, W.; Yang, J.; Liu, W.; Li, X.; Lu, Y.; et al. Linear and Nonlinear Polarization Syntheses and Their Programmable Controls based on Anisotropic Time-Domain Digital Coding Metasurface. Small Struct. 2021, 2, 2000060. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, J.; Yang, L.X.; Ke, J.C.; Chen, M.Z.; Cao, W.K.; Chen, M.; Wu, Z.H.; Chen, J.F.; Cheng, Q.; et al. Convolution operations on time-domain digital coding metasurface for beam manipulations of harmonics. Nanophotonics 2020, 9, 2771–2781. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, F.; Tennant, A. Increasing the energy efficiency of time-modulated reflector-arrays using double layer designs. In Proceedings of the 2016 10th European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Bogdan, G.; Yashchyshyn, Y.; Jarzynka, M. Time-Modulated Antenna Array with Lossless Switching Network. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1827–1830. [Google Scholar] [CrossRef]
- Chen, K.; Yang, S.; Chen, Y.; Qu, S.-W.; Hu, J. Hybrid Directional Modulation and Beamforming for Physical Layer Security Improvement Through 4-D Antenna Arrays. IEEE Trans. Antennas Propag. 2021, 69, 5903–5912. [Google Scholar] [CrossRef]
- Bogdan, G.; Jarzynka, M.; Yashchyshyn, Y. Experimental study of signal reception by means of time-modulated antenna array. In Proceedings of the 2016 21st International Conference on Microwave, Radar and Wireless Communications (MIKON), Krakow, Poland, 9–11 May 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Yashchyshyn, Y.; Derzakowski, K.; Bajurko, P.R.; Marczewski, J.; Kozlowski, S. Time-Modulated Reconfigurable Antenna Based on Integrated S-PIN Diodes for mm-Wave Communication Systems. IEEE Trans. Antennas Propag. 2015, 63, 4121–4131. [Google Scholar] [CrossRef]
- Zhu, Q.; Yang, S.; Zheng, L.; Nie, Z. Design of a Low Sidelobe Time Modulated Linear Array with Uniform Amplitude and Sub-Sectional Optimized Time Steps. IEEE Trans. Antennas Propag. 2012, 60, 4436–4439. [Google Scholar] [CrossRef]
- Bogdan, G.; Godziszewski, K.; Yashchyshyn, Y. Time-Modulated Antenna Array for Real-Time Adaptation in Wideband Wireless Systems—Part II: Adaptation Study. IEEE Trans. Antennas Propag. 2020, 68, 6973–6981. [Google Scholar] [CrossRef]
- Mukherjee, A.; Mandal, S.K.; Ghatak, R. A Fractal-Based Time-Modulated Multiband Linear Array for Interband Communication. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 918–922. [Google Scholar] [CrossRef]
- Revna, A.; Balderas, L.I.; Panduro, M.A. 4D Antenna Array of UWB Vivaldi Elements with Low Side Lobes and Harmonic Suppresion. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation and USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018; pp. 1505–1506. [Google Scholar] [CrossRef]
- Shiju, R.M.; Venkateswaran, N. Optimization of linear array antenna pattern synthesis using bacterial foraging algorithm. In Proceedings of the 2012 International Conference on Recent Advances in Computing and Software Systems, Chennai, India, 25–27 April 2012; pp. 130–134. [Google Scholar] [CrossRef]
- Kumar, N.A.; Gandhi, A.S. Small size planar monopole antenna for high speed UWB applications. In Proceedings of the 2016 Twenty Second National Conference on Communication (NCC), Guwahati, India, 4–6 March 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Acharya, O.P.; Patnaik, A.; Choudhury, B. Fault finding in antenna arrays using bacteria foraging optimization technique. In Proceedings of the 2011 National Conference on Communications (NCC), Bangalore, India, 28–30 January 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Farzaneh, S.; Ozturk, A.K.; Sebak, A.R.; Paknys, R. Antenna-Pattern Measurement Using Spectrum Analyzer for Systems with Frequency Translation [Measurements Corner. IEEE Antennas Propag. Mag. 2009, 51, 126–131. [Google Scholar] [CrossRef]
- Bogdan, G.; Godziszewski, K.; Yashchyshyn, Y. Feasibility of standard instrumentation for radiation pattern measurement of time modulated antenna array. In Proceedings of the 2018 22nd International Microwave and Radar Conference (MIKON), Poznan, Poland, 14–17 May 2018; pp. 420–423. [Google Scholar] [CrossRef]
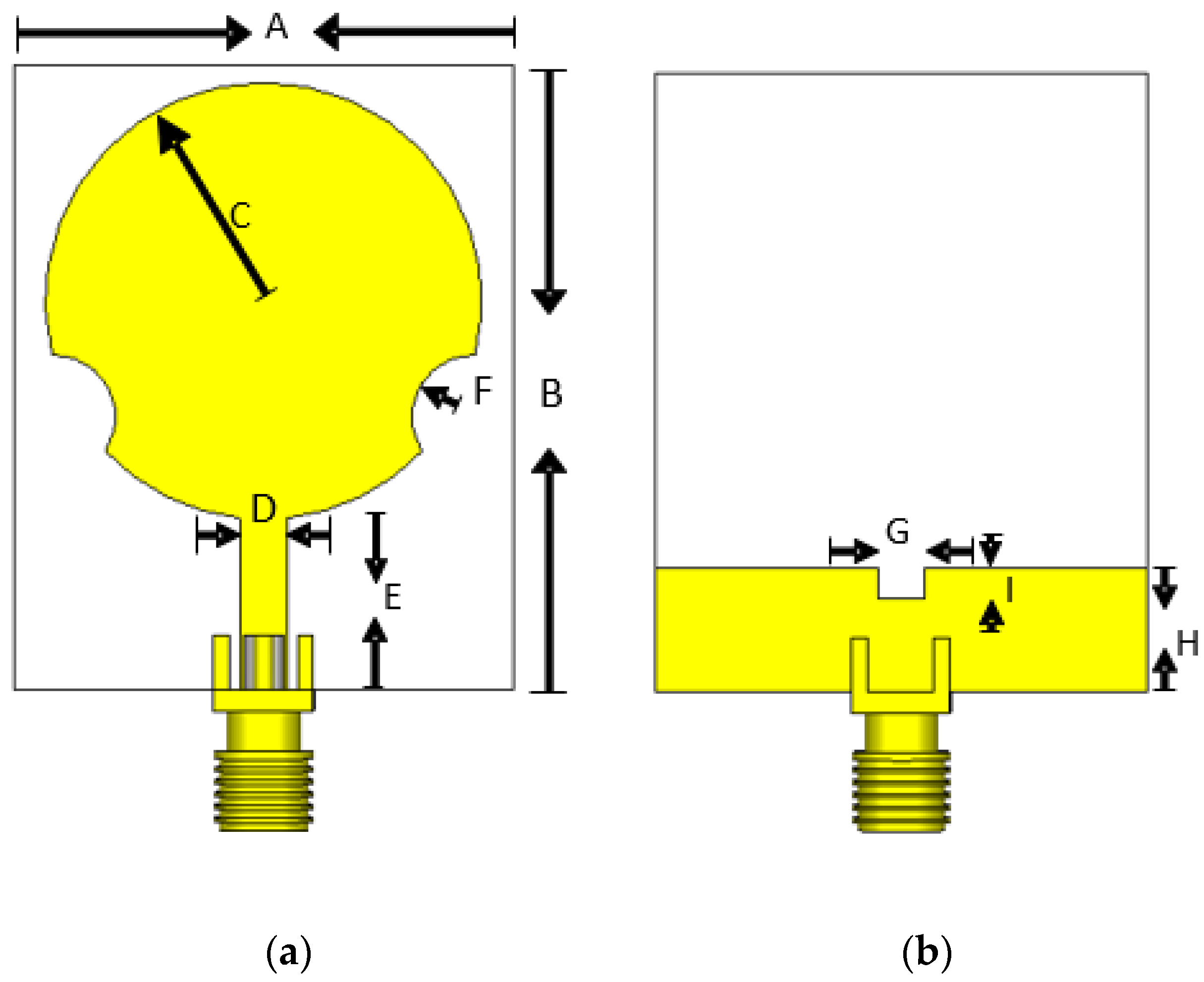
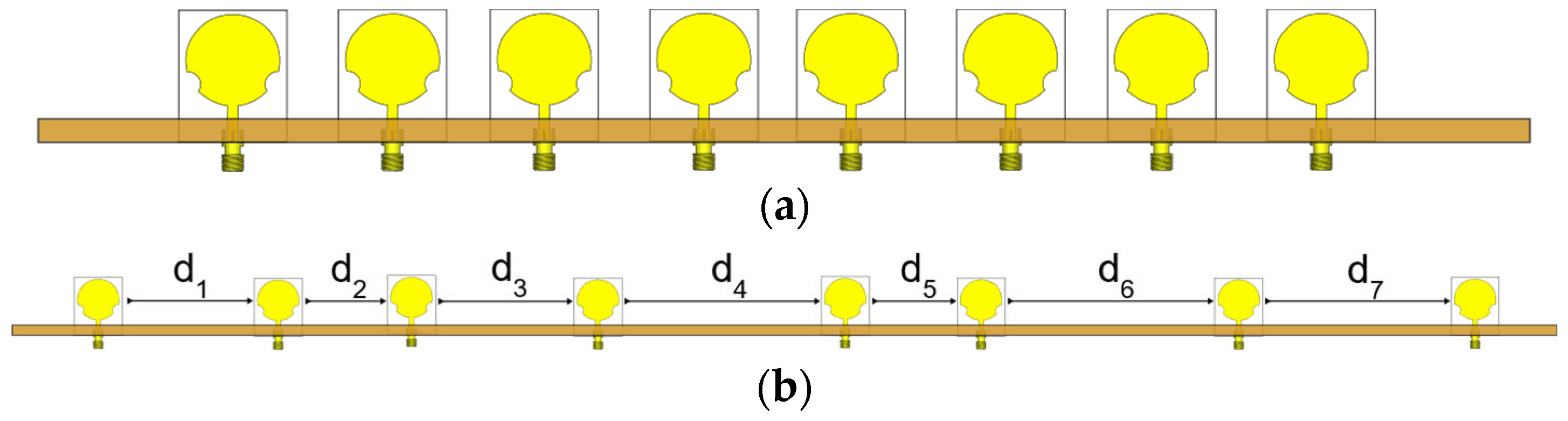



| A | B | C | D | E | F | G | H | I |
|---|---|---|---|---|---|---|---|---|
| 32 mm | 40 mm | 14 mm | 3 mm | 10.97 mm | 4 mm | 3 mm | 8 mm | 2 mm |
| Variable | Non-Uniform | Uniform Spacing of λ/2 |
|---|---|---|
| tn (us) | 0.72, 0.9998, 0.9956, 0.9711, 0.6857, 0.96, 0.8334, 0.7169 | 0.7066, 0.7399, 0.9800, 1.0000, 1.0000, 0.8611, 0.5883, 0.2692 |
| xn (λ @ 3.1 GHz) | 0, 1.3521, 2.3535, 3.76, 5.6241, 6.6395, 8.5758, 10.357 | 0, 0.5 λ, λ, 1.5 λ, 2 λ, 2.5 λ, 3 λ, 3.5 λ |
| xn (mm) | 0, 130.76, 227.60, 363.62, 543.89, 642.09, 829.34,1001.60 | 0, 48.38, 96.77, 145.15, 193.53, 241.91, 290.29, 338.67 |
| Design | N-Antenna | Freq. (GHz) | Size (mm) | Material | Switch | SLL (dB) | SBL (dB) |
|---|---|---|---|---|---|---|---|
| Uniform linear [22] | 2-Dipole | 2.45 and 5.8 | 136 × 37 | FR4 | Pin diode BAR63-02 | −7.1 and −7.68, for each frequency | −26.28 and −24.53 |
| Uniform linear [21] | 8-Dipole | 2 | 525 | R4003 | AS179-92LF | −11.25 | −16.9 |
| Uniform linear [18] | 8-Dipole | 2.6 | 403.8 | Not provided | Not provided | Not provided | Not provided |
| Uniform linear [19] | 8-Square patch | 2.6 | 403.8 | FR4 | MAPS-010144-TR0500 | Not provided | Not provided |
| Uniform linear [20] | 8-Dipole | 2.6 | 403.8 | FR4 | Not provided | −22 | −25 |
| Uniform square [24] | 16-Square patch | 5.6 | Not provided | Not provided | ADRF5020 | 14 | 14 |
| Uniform linear [25] | 9-Vivaldi | 3.3 and 9.9 | 121.2 | Not provided | Not provided | −18.8 | −16.8 |
| Uniform linear [26] | 8-Vivaldi | 2.65 to 17.26 | 205.8 | FR4 | Not provided | −44.95 and −27.88, for each frequency | −14.41 and −14.09 |
| Uniform linear [23] | 16-Dipole | 3.25 | 692.3 | Not provided | Not provided | −29.1 | −28 |
| Nonuniform linear (this work) | 8-Disk notch Patch | 2.97 to 5.26 | 1032 | FR4 | ZFSWA2R-63DR+ | −7 (average value) | −17 (average value) |
| Uniform linear (this work) | 8-Disk notch Patch | 3.37 to 4.8 | 38.5 | FR4 | ZFSWA2R-63DR+ | −21 (average value) | −17 (average value) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado, G.; Maldonado, A.R.; Balderas, L.I.; Panduro, M.A. Time-Modulated Antenna Arrays for Ultra-Wideband 5G Applications. Micromachines 2022, 13, 2233. https://doi.org/10.3390/mi13122233
Maldonado G, Maldonado AR, Balderas LI, Panduro MA. Time-Modulated Antenna Arrays for Ultra-Wideband 5G Applications. Micromachines. 2022; 13(12):2233. https://doi.org/10.3390/mi13122233
Chicago/Turabian StyleMaldonado, Gonzalo, Alberto Reyna Maldonado, Luz I. Balderas, and Marco A. Panduro. 2022. "Time-Modulated Antenna Arrays for Ultra-Wideband 5G Applications" Micromachines 13, no. 12: 2233. https://doi.org/10.3390/mi13122233
APA StyleMaldonado, G., Maldonado, A. R., Balderas, L. I., & Panduro, M. A. (2022). Time-Modulated Antenna Arrays for Ultra-Wideband 5G Applications. Micromachines, 13(12), 2233. https://doi.org/10.3390/mi13122233







