Soliton Microcomb on Chip Integrated Si3N4 Microresonators with Power Amplification in Erbium-Doped Optical Mono-Core Fiber
Abstract
:1. Introduction
2. Results
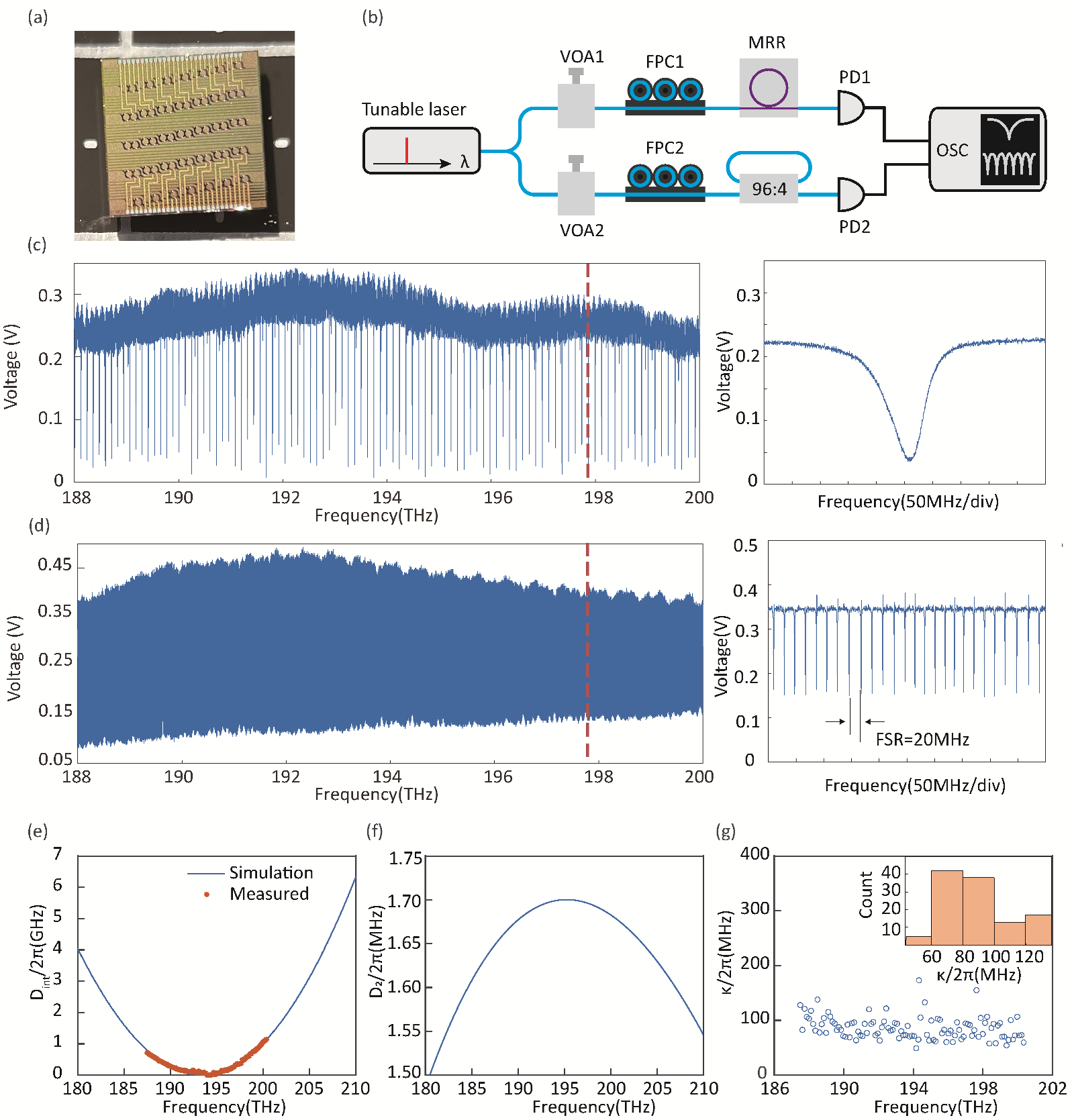
2.1. Characterization of Photonic Chip Integrated Microresonators
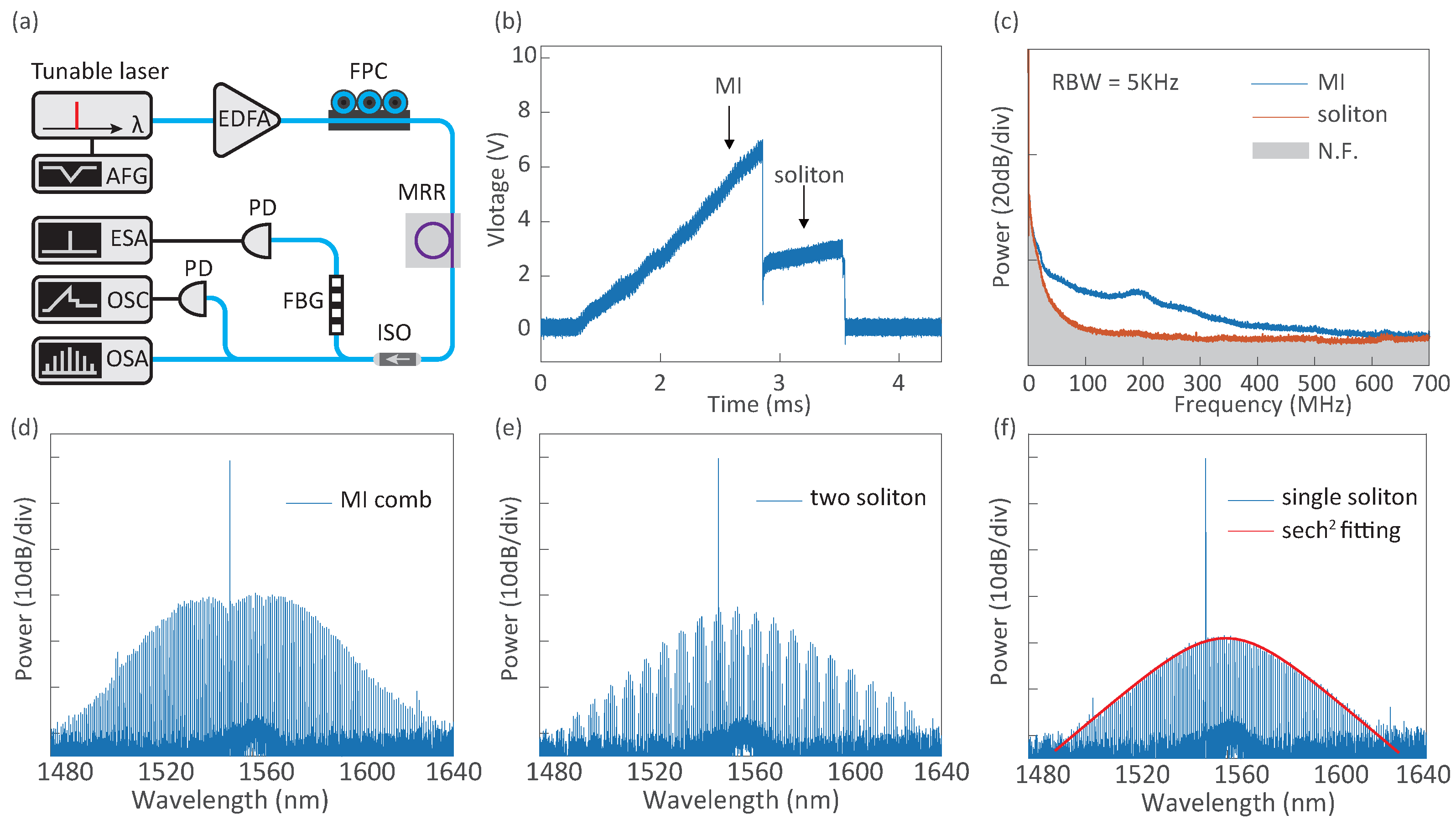
2.2. Soliton Microcomb Generation
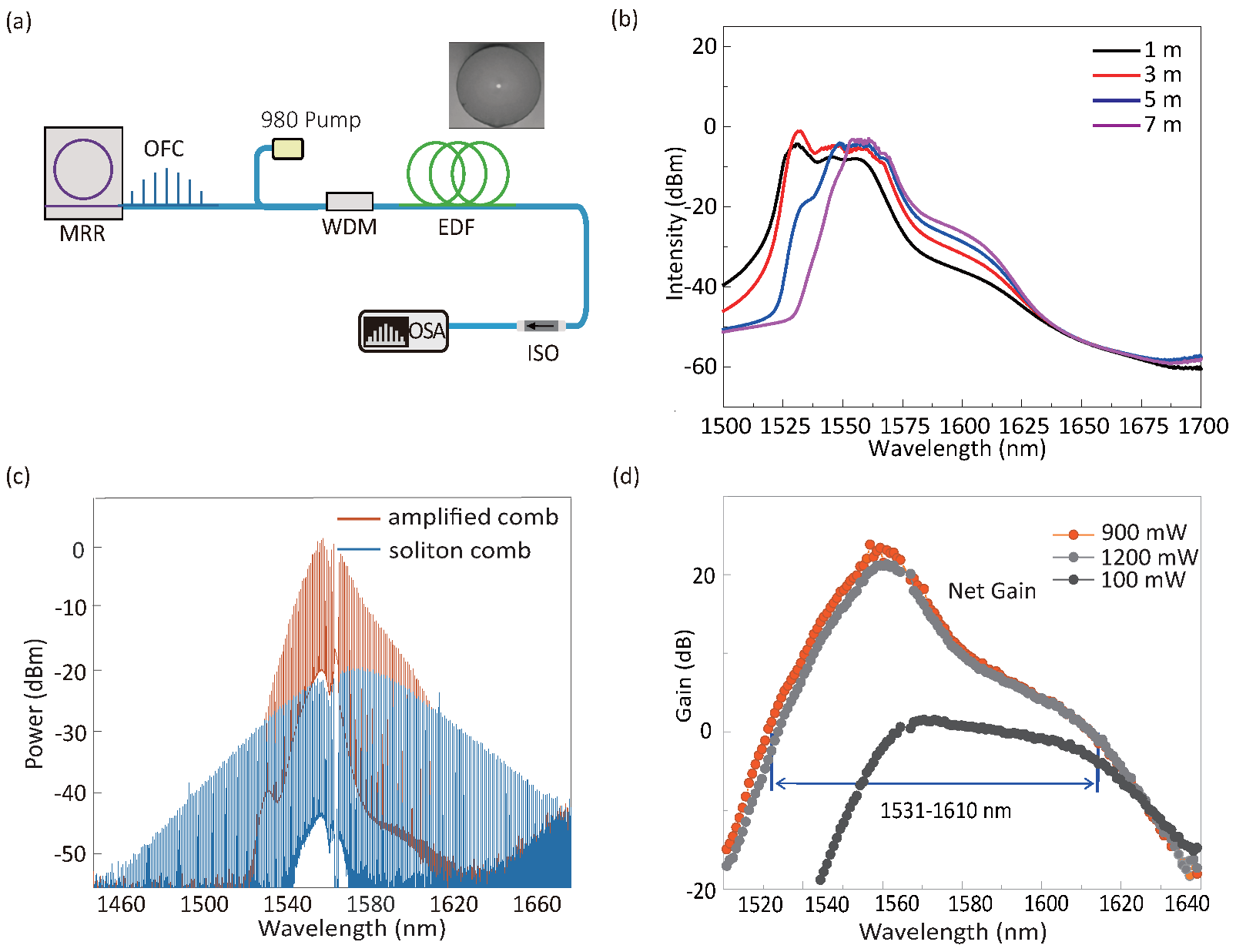
2.3. Fabrication of Home-Developed Erbium-Doped Mono-Core Fiber
2.4. Full-Wave Amplification of Soliton Comb with Home-Developed Erbium-Fiber
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marin-Palomo, P.; Kemal, J.N.; Karpov, M.; Kordts, A.; Pfeifle, J.; Pfeiffer, M.H.P.; Trocha, P.; Wolf, S.; Brasch, V.; Anderson, M.H.; et al. Microresonator-based solitons for massively parallel coherent optical communications. Nature 2017, 546, 274–279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lundberg, L.; Mazur, M.; Mirani, A.; Foo, B.; Schröder, J.; Torres-Company, V.; Karlsson, M.; Andrekson, P.A. Phase-coherent lightwave communications with frequency combs. Nat. Commun. 2020, 11, 201. [Google Scholar] [CrossRef] [Green Version]
- Mazur, M.; Suh, M.G.; Fulop, A.; Schroder, J.; Torres-Company, V.; Karlsson, M.; Vahala, K.; Andrekson, P. High Spectral Efficiency Coherent Superchannel Transmission With Soliton Microcombs. J. Light. Technol. 2021, 39, 4367–4373. [Google Scholar] [CrossRef]
- Shao, W.; Wang, Y.; Jia, S.; Xie, Z.; Gao, D.; Wang, W.; Zhang, D.; Liao, P.; Little, B.; Chu, S.T.; et al. Terabit FSO communication based on a soliton microcomb. Photonics Res. 2022, 10, 2802–2808. [Google Scholar] [CrossRef]
- Geng, Y.; Zhou, H.; Han, X.; Cui, W.; Zhang, Q.; Liu, B.; Deng, G.; Zhou, Q.; Qiu, K. Coherent optical communications using coherence-cloned Kerr soliton microcombs. Nat. Commun. 2022, 13, 1070. [Google Scholar] [CrossRef] [PubMed]
- Trocha, P.; Karpov, M.; Ganin, D.; Pfeiffer, M.H.P.; Kordts, A.; Wolf, S.; Krockenberger, J.; Marin-Palomo, P.; Weimann, C.; Randel, S.; et al. Ultrafast optical ranging using microresonator soliton frequency combs. Science 2018, 359, 887–891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Lu, Z.; Wang, W.; Zhang, F.; Chen, J.; Wang, Y.; Zheng, J.; Chu, S.T.; Zhao, W.; Little, B.E.; et al. Long-distance ranging with high precision using a soliton microcomb. Photonics Res. 2020, 8, 1964. [Google Scholar] [CrossRef]
- Riemensberger, J.; Lukashchuk, A.; Karpov, M.; Weng, W.; Lucas, E.; Liu, J.; Kippenberg, T.J. Massively parallel coherent laser ranging using a soliton microcomb. Nature 2020, 581, 164–170. [Google Scholar] [CrossRef]
- Raja, A.S.; Lange, S.; Karpov, M.; Shi, K.; Fu, X.; Behrendt, R.; Cletheroe, D.; Lukashchuk, A.; Haller, I.; Karinou, F.; et al. Ultrafast optical circuit switching for data centers using integrated soliton microcombs. Nat. Commun. 2021, 12, 5867. [Google Scholar] [CrossRef]
- JΦrgensen, A.A.; Kong, D.; Henriksen, M.R.; Klejs, F.; Ye, Z.; Helgason, O.B.; Hansen, H.E.; Hu, H.; Yankov, M.; Forchhammer, S.; et al. Petabit-per-second data transmission using a chip-scale microcomb ring resonator source. Nat. Photonics 2022, 16, 798–802. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Feldmann, J.; Youngblood, N.; Karpov, M.; Gehring, H.; Li, X.; Stappers, M.; Le Gallo, M.; Fu, X.; Lukashchuk, A.; Raja, A.S.; et al. Parallel convolutional processing using an integrated photonic tensor core. Nature 2021, 589, 52–58. [Google Scholar] [CrossRef] [PubMed]
- Dutt, A.; Joshi, C.; Ji, X.; Cardenas, J.; Okawachi, Y.; Luke, K.; Gaeta, A.L.; Lipson, M. On-chip dual-comb source for spectroscopy. Sci. Adv. 2018, 4, e1701858. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Obrzud, E.; Rainer, M.; Harutyunyan, A.; Anderson, M.H.; Liu, J.; Geiselmann, M.; Chazelas, B.; Kundermann, S.; Lecomte, S.; Cecconi, M.; et al. A microphotonic astrocomb. Nat. Photonics 2019, 13, 31–35. [Google Scholar] [CrossRef] [Green Version]
- Suh, M.G.; Yi, X.; Lai, Y.H.; Leifer, S.; Grudinin, I.S.; Vasisht, G.; Martin, E.C.; Fitzgerald, M.P.; Doppmann, G.; Wang, J.; et al. Searching for exoplanets using a microresonator astrocomb. Nat. Photonics 2019, 13, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Lucas, E.; Raja, A.S.; He, J.; Riemensberger, J.; Wang, R.N.; Karpov, M.; Guo, H.; Bouchand, R.; Kippenberg, T.J. Photonic microwave generation in the X- and K-band using integrated soliton microcombs. Nat. Photonics 2020, 14, 486–491. [Google Scholar] [CrossRef]
- Bao, C.; Yuan, Z.; Wu, L.; Suh, M.G.; Wang, H.; Lin, Q.; Vahala, K.J. Architecture for microcomb-based GHz-mid-infrared dual-comb spectroscopy. Nat. Commun. 2021, 12, 6573. [Google Scholar] [CrossRef]
- Brasch, V.; Geiselmann, M.; Herr, T.; Lihachev, G.; Pfeiffer, M.H.P.; Gorodetsky, M.L.; Kippenberg, T.J. Photonic chip–based optical frequency comb using soliton Cherenkov radiation. Science 2016, 351, 357–360. [Google Scholar] [CrossRef] [Green Version]
- Kippenberg, T.J.; Gaeta, A.L.; Lipson, M.; Gorodetsky, M.L. Dissipative Kerr solitons in optical microresonators. Science 2018, 361, eaan8083. [Google Scholar] [CrossRef] [Green Version]
- Chang, L.; Liu, S.; Bowers, J.E. Integrated optical frequency comb technologies. Nat. Photonics 2022, 16, 95–108. [Google Scholar] [CrossRef]
- Yi, X.; Yang, Q.F.; Yang, K.Y.; Suh, M.G.; Vahala, K. Soliton frequency comb at microwave rates in a high-Q silica microresonator. Optica 2015, 2, 1078. [Google Scholar] [CrossRef] [Green Version]
- Gong, Z.; Bruch, A.; Shen, M.; Guo, X.; Jung, H.; Fan, L.; Liu, X.; Zhang, L.; Wang, J.; Li, J.; et al. High-fidelity cavity soliton generation in crystalline AlN micro-ring resonators. Opt. Lett. 2018, 43, 4366. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhang, M.; Yu, M.; Zhu, R.; Hu, H.; Loncar, M. Monolithic lithium niobate photonic circuits for Kerr frequency comb generation and modulation. Nat. Commun. 2019, 10, 978. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, L.; Xie, W.; Shu, H.; Yang, Q.F.; Shen, B.; Boes, A.; Peters, J.D.; Jin, W.; Xiang, C.; Liu, S.; et al. Ultra-efficient frequency comb generation in AlGaAs-on-insulator microresonators. Nat. Commun. 2020, 11, 1331. [Google Scholar] [CrossRef] [Green Version]
- Lukin, D.M.; Dory, C.; Guidry, M.A.; Yang, K.Y.; Mishra, S.D.; Trivedi, R.; Radulaski, M.; Sun, S.; Vercruysse, D.; Ahn, G.H.; et al. 4H-silicon-carbide-on-insulator for integrated quantum and nonlinear photonics. Nat. Photonics 2020, 14, 330–334. [Google Scholar] [CrossRef]
- Zheng, Y.; Sun, C.; Xiong, B.; Wang, L.; Hao, Z.; Wang, J.; Han, Y.; Li, H.; Yu, J.; Luo, Y. Integrated Gallium Nitride Nonlinear Photonics. Laser Photonics Rev. 2022, 16, 2100071. [Google Scholar] [CrossRef]
- Xia, D.; Yang, Z.; Zeng, P.; Zhang, B.; Wu, J.; Wang, Z.; Zhao, J.; Gao, M.; Huang, Y.; Huang, J.; et al. Integrated Chalcogenide Photonics for Microresonator Soliton Combs. Laser Photonics Rev. 2022, 16, 2200219. [Google Scholar] [CrossRef]
- Levy, J.S.; Gondarenko, A.; Foster, M.A.; Turner-Foster, A.C.; Gaeta, A.L.; Lipson, M. CMOS-compatible multiple-wavelength oscillator for on-chip optical interconnects. Nat. Photonics 2010, 4, 37–40. [Google Scholar] [CrossRef]
- Liu, J.; Huang, G.; Wang, R.N.; He, J.; Raja, A.S.; Liu, T.; Engelsen, N.J.; Kippenberg, T.J. High-yield, wafer-scale fabrication of ultralow-loss, dispersion-engineered silicon nitride photonic circuits. Nat. Commun. 2021, 12, 2236. [Google Scholar] [CrossRef]
- Gondarenko, A.; Levy, J.S.; Lipson, M. High confinement micron-scale silicon nitride high Q ring resonator. Opt. Express 2009, 17, 11366. [Google Scholar] [CrossRef]
- Xuan, Y.; Liu, Y.; Varghese, L.T.; Metcalf, A.J.; Xue, X.; Wang, P.H.; Han, K.; Jaramillo-Villegas, J.A.; Al Noman, A.; Wang, C.; et al. High-Q silicon nitride microresonators exhibiting low-power frequency comb initiation. Optica 2016, 3, 1171. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Raja, A.S.; Karpov, M.; Ghadiani, B.; Pfeiffer, M.H.P.; Engelsen, N.J.; Guo, H.; Zervas, M.; Kippenberg, T.J. Ultralow-power chip-based soliton microcombs for photonic integration. Optica 2018, 5, 1347. [Google Scholar] [CrossRef] [Green Version]
- Pfeiffer, M.H.P.; Liu, J.; Raja, A.S.; Morais, T.; Ghadiani, B.; Kippenberg, T.J. Ultra-smooth silicon nitride waveguides based on the Damascene reflow process: Fabrication and loss origins. Optica 2018, 5, 884. [Google Scholar] [CrossRef]
- Pfeiffer, M.H.P.; Herkommer, C.; Liu, J.; Morais, T.; Zervas, M.; Geiselmann, M.; Kippenberg, T.J. Photonic Damascene Process for Low-Loss, High-Confinement Silicon Nitride Waveguides. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–11. [Google Scholar] [CrossRef]
- Ye, Z.; Twayana, K.; Andrekson, P.A.; Torres-Company, V. High-Q Si3N4 microresonators based on a subtractive processing for Kerr nonlinear optics. Opt. Express 2019, 27, 35719. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Barashenkov, I.V.; Smirnov, Y.S. Existence and stability chart for the ac-driven, damped nonlinear Schrödinger solitons. Phys. Rev. E 1996, 54, 5707–5725. [Google Scholar] [CrossRef]
- Wabnitz, S. Suppression of interactions in a phase-locked soliton optical memory. Opt. Lett. 1993, 18, 601. [Google Scholar] [CrossRef]
- Herr, T.; Brasch, V.; Jost, J.D.; Wang, C.Y.; Kondratiev, N.M.; Gorodetsky, M.L.; Kippenberg, T.J. Temporal solitons in optical microresonators. Nat. Photonics 2014, 8, 145–152. [Google Scholar] [CrossRef] [Green Version]
- Stone, J.R.; Briles, T.C.; Drake, T.E.; Spencer, D.T.; Carlson, D.R.; Diddams, S.A.; Papp, S.B. Thermal and Nonlinear Dissipative-Soliton Dynamics in Kerr-Microresonator Frequency Combs. Phys. Rev. Lett. 2018, 121, 063902. [Google Scholar] [CrossRef]
- Joshi, C.; Jang, J.K.; Luke, K.; Ji, X.; Miller, S.A.; Klenner, A.; Okawachi, Y.; Lipson, M.; Gaeta, A.L. Thermally controlled comb generation and soliton modelocking in microresonators. Opt. Lett. 2016, 41, 2565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Tian, H.; Lucas, E.; Raja, A.S.; Lihachev, G.; Wang, R.N.; He, J.; Liu, T.; Anderson, M.H.; Weng, W.; et al. Monolithic piezoelectric control of soliton microcombs. Nature 2020, 583, 385–390. [Google Scholar] [CrossRef] [PubMed]
- Liang, W.; Eliyahu, D.; Ilchenko, V.S.; Savchenkov, A.A.; Matsko, A.B.; Seidel, D.; Maleki, L. High spectral purity Kerr frequency comb radio frequency photonic oscillator. Nat. Commun. 2015, 6, 7957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raja, A.S.; Voloshin, A.S.; Guo, H.; Agafonova, S.E.; Liu, J.; Gorodnitskiy, A.S.; Karpov, M.; Pavlov, N.G.; Lucas, E.; Galiev, R.R.; et al. Electrically pumped photonic integrated soliton microcomb. Nat. Commun. 2019, 10, 680. [Google Scholar] [CrossRef] [Green Version]
- Shen, B.; Chang, L.; Liu, J.; Wang, H.; Yang, Q.F.; Xiang, C.; Wang, R.N.; He, J.; Liu, T.; Xie, W.; et al. Integrated turnkey soliton microcombs. Nature 2020, 582, 365–369. [Google Scholar] [CrossRef]
- Voloshin, A.S.; Kondratiev, N.M.; Lihachev, G.V.; Liu, J.; Lobanov, V.E.; Dmitriev, N.Y.; Weng, W.; Kippenberg, T.J.; Bilenko, I.A. Dynamics of soliton self-injection locking in optical microresonators. Nat. Commun. 2021, 12, 235. [Google Scholar] [CrossRef]
- Lihachev, G.; Weng, W.; Liu, J.; Chang, L.; Guo, J.; He, J.; Wang, R.N.; Anderson, M.H.; Liu, Y.; Bowers, J.E.; et al. Platicon microcomb generation using laser self-injection locking. Nat. Commun. 2022, 13, 1771. [Google Scholar] [CrossRef]
- Xiang, C.; Liu, J.; Guo, J.; Chang, L.; Wang, R.N.; Weng, W.; Peters, J.; Xie, W.; Zhang, Z.; Riemensberger, J.; et al. Laser soliton microcombs heterogeneously integrated on silicon. Science 2021, 373, 99–103. [Google Scholar] [CrossRef]
- Jin, W.; Yang, Q.F.; Chang, L.; Shen, B.; Wang, H.; Leal, M.A.; Wu, L.; Gao, M.; Feshali, A.; Paniccia, M.; et al. Hertz-linewidth semiconductor lasers using CMOS-ready ultra-high-Q microresonators. Nat. Photonics 2021, 15, 346–353. [Google Scholar] [CrossRef]
- Briles, T.C.; Yu, S.P.; Chang, L.; Xiang, C.; Guo, J.; Kinghorn, D.; Moille, G.; Srinivasan, K.; Bowers, J.E.; Papp, S.B. Hybrid InP and SiN integration of an octave-spanning frequency comb. APL Photonics 2021, 6, 026102. [Google Scholar] [CrossRef]
- Brasch, V.; Geiselmann, M.; Pfeiffer, M.H.P.; Kippenberg, T.J. Bringing short-lived dissipative Kerr soliton states in microresonators into a steady state. Opt. Express 2016, 24, 29312. [Google Scholar] [CrossRef] [PubMed]
- Wildi, T.; Brasch, V.; Liu, J.; Kippenberg, T.J.; Herr, T. Thermally stable access to microresonator solitons via slow pump modulation. Opt. Lett. 2019, 44, 4447. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Geng, Y.; Cui, W.; Huang, S.W.; Zhou, Q.; Qiu, K.; Wei Wong, C. Soliton bursts and deterministic dissipative Kerr soliton generation in auxiliary-assisted microcavities. Light. Sci. Appl. 2019, 8, 50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.; Silver, J.M.; Del Bino, L.; Copie, F.; Woodley, M.T.M.; Ghalanos, G.N.; Svela, A.P.; Moroney, N.; Del’Haye, P. Sub-milliwatt-level microresonator solitons with extended access range using an auxiliary laser. Optica 2019, 6, 206–212. [Google Scholar] [CrossRef]
- Weng, H.; Liu, J.; Afridi, A.A.; Li, J.; Dai, J.; Ma, X.; Zhang, Y.; Lu, Q.; Donegan, J.F.; Guo, W. Directly accessing octave-spanning dissipative Kerr soliton frequency combs in an AlN microresonator. Photonics Res. 2021, 9, 1351. [Google Scholar] [CrossRef]
- Lei, F.; Ye, Z.; Torres-Company, V. Thermal noise reduction in soliton microcombs via laser self-cooling. Opt. Lett. 2022, 47, 513. [Google Scholar] [CrossRef]
- Pfeiffer, M.H.P.; Herkommer, C.; Liu, J.; Guo, H.; Karpov, M.; Lucas, E.; Zervas, M.; Kippenberg, T.J. Octave-spanning dissipative Kerr soliton frequency combs in Si_3N_4 microresonators. Optica 2017, 4, 684. [Google Scholar] [CrossRef]
- Li, Q.; Briles, T.C.; Westly, D.A.; Drake, T.E.; Stone, J.R.; Ilic, B.R.; Diddams, S.A.; Papp, S.B.; Srinivasan, K. Stably accessing octave-spanning microresonator frequency combs in the soliton regime. Optica 2017, 4, 193. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Karpov, M.; Lucas, E.; Kordts, A.; Pfeiffer, M.H.P.; Brasch, V.; Lihachev, G.; Lobanov, V.E.; Gorodetsky, M.L.; Kippenberg, T.J. Universal dynamics and deterministic switching of dissipative Kerr solitons in optical microresonators. Nat. Phys. 2016, 13, 94. [Google Scholar] [CrossRef]
- Lucas, E.; Karpov, M.; Guo, H.; Gorodetsky, M.L.; Kippenberg, T.J. Breathing dissipative solitons in optical microresonators. Nat. Commun. 2017, 8, 736. [Google Scholar] [CrossRef]
- Yu, M.; Jang, J.K.; Okawachi, Y.; Griffith, A.G.; Luke, K.; Miller, S.A.; Ji, X.; Lipson, M.; Gaeta, A.L. Breather soliton dynamics in microresonators. Nat. Commun. 2017, 8, 14569. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Lucas, E.; Pfeiffer, M.H.; Karpov, M.; Anderson, M.; Liu, J.; Geiselmann, M.; Jost, J.D.; Kippenberg, T.J. Intermode Breather Solitons in Optical Microresonators. Phys. Rev. X 2017, 7, 041055. [Google Scholar] [CrossRef] [Green Version]
- Wan, S.; Niu, R.; Wang, Z.Y.; Peng, J.L.; Li, M.; Li, J.; Guo, G.C.; Zou, C.L.; Dong, C.H. Frequency stabilization and tuning of breathing solitons in Si 3 N 4 microresonators. Photonics Res. 2020, 8, 1342. [Google Scholar] [CrossRef]
- Karpov, M.; Guo, H.; Kordts, A.; Brasch, V.; Pfeiffer, M.H.; Zervas, M.; Geiselmann, M.; Kippenberg, T.J. Raman Self-Frequency Shift of Dissipative Kerr Solitons in an Optical Microresonator. Phys. Rev. Lett. 2016, 116, 103902. [Google Scholar] [CrossRef] [Green Version]
- Yi, X.; Yang, Q.F.; Yang, K.Y.; Vahala, K. Theory and measurement of the soliton self-frequency shift and efficiency in optical microcavities. Opt. Lett. 2016, 41, 3419. [Google Scholar] [CrossRef] [PubMed]
- Weng, W.; Lucas, E.; Lihachev, G.; Lobanov, V.E.; Guo, H.; Gorodetsky, M.L.; Kippenberg, T.J. Spectral Purification of Microwave Signals with Disciplined Dissipative Kerr Solitons. Phys. Rev. Lett. 2019, 122, 013902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, X.; Zheng, X.; Zhou, B. Super-efficient temporal solitons in mutually coupled optical cavities. Nat. Photonics 2019, 13, 616–622. [Google Scholar] [CrossRef] [Green Version]
- Komagata, K.; Tusnin, A.; Riemensberger, J.; Churaev, M.; Guo, H.; Tikan, A.; Kippenberg, T.J. Dissipative Kerr solitons in a photonic dimer on both sides of exceptional point. Commun. Phys. 2021, 4, 159. [Google Scholar] [CrossRef]
- Helgason, Ó.B.; Arteaga-Sierra, F.R.; Ye, Z.; Twayana, K.; Andrekson, P.A.; Karlsson, M.; Schröder, J.; Victor Torres-Company. Dissipative solitons in photonic molecules. Nat. Photonics 2021, 15, 305–310. [Google Scholar] [CrossRef]
- Mittal, S.; Moille, G.; Srinivasan, K.; Chembo, Y.K.; Hafezi, M. Topological frequency combs and nested temporal solitons. Nat. Physics 2021, 17, 1169–1176. [Google Scholar] [CrossRef]
- Tikan, A.; Tusnin, A.; Riemensberger, J.; Churaev, M.; Ji, X.; Komagata, K.N.; Wang, R.N.; Liu, J.; Kippenberg, T.J. Protected generation of dissipative Kerr solitons in supermodes of coupled optical microresonators. Sci. Adv. 2022, 8, eabm6982. [Google Scholar] [CrossRef] [PubMed]
- Helgason, Ó.B.; Girardi, M.; Ye, Z.; Lei, F.; Schröder, J.; Company, V.T. Power-efficient soliton microcombs. arXiv 2022, arXiv:2202.09410. [Google Scholar]
- Hu, Y.; Yu, M.; Buscaino, B.; Sinclair, N.; Zhu, D.; Cheng, R.; Shams-Ansari, A.; Shao, L.; Zhang, M.; Kahn, J.M.; et al. High-efficiency and broadband on-chip electro-optic frequency comb generators. Nat. Photonics 2022, 16, 679–685. [Google Scholar] [CrossRef]
- Zhao, P.; Ye, Z.; Karlsson, M.; Torres-Company, V.; Andrekson, P.A. Low-Noise Phase-sensitive Parametric Amplifiers Based on Integrated Silicon-Nitride-Waveguides for Optical Signal Processing. J. Light. Technol. 2022, 40, 1847–1854. [Google Scholar] [CrossRef]
- Liu, Y.; Qiu, Z.; Ji, X.; He, J.; Riemensberger, J.; Hafermann, M.; Wang, R.N.; Liu, J.; Ronning, C.; Kippenberg, T.J. A photonic integrated circuit based erbium-doped amplifier. Science 2022, 376, 1309–1313. [Google Scholar] [CrossRef]
- Del’Haye, P.; Arcizet, O.; Gorodetsky, M.L.; Holzwarth, R.; Kippenberg, T.J. Frequency comb assisted diode laser spectroscopy for measurement of microcavity dispersion. Nat. Photonics 2009, 3, 529–533. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Brasch, V.; Pfeiffer, M.H.P.; Kordts, A.; Kamel, A.N.; Guo, H.; Geiselmann, M.; Kippenberg, T.J. Frequency-comb-assisted broadband precision spectroscopy with cascaded diode lasers. Opt. Lett. 2016, 41, 3134. [Google Scholar] [CrossRef]
- Wen, J.; Wang, J.; Dong, Y.; Chen, N.; Luo, Y.; Peng, G.d.; Pang, F.; Chen, Z.; Wang, T. Photoluminescence properties of Bi/Al-codoped silica optical fiber based on atomic layer deposition method. Appl. Surf. Sci. 2015, 349, 287–291. [Google Scholar] [CrossRef]
- Zheng, Z.; Pan, X.; Ji, W.; Dong, Y.; Wen, J.; Chen, W.; Huang, S.; Peng, G.; Wang, T.Y. Co-Doping Effect of Bismuth Ions on the Gain Characteristics of Er-Doped Silica Optical Fiber. IEEE Photonics J. 2022, 14, 1–8. [Google Scholar] [CrossRef]
- Yan, C.; Huang, S.J.; Miao, Z.; Chang, Z.; Zeng, J.Z.; Wang, T.Y. 3D refractive index measurements of special optical fibers. Opt. Fiber Technol. 2016, 31, 65–73. [Google Scholar] [CrossRef]
- Wen, J.; Wan, Y.; Dong, Y.; Zhan, H.; Luo, Y.; Tang, F.; West, G.D.; Pang, F.; Peng, G.; Wang, T. Spectroscopy of Pb/Bi co-doped silica optical fibers fabricated via atom layer deposition with modified chemical vapour deposition. J. Lumin. 2021, 231, 117768. [Google Scholar] [CrossRef]

| Item | ER16-8/125 * | ER30-4/125 * | Our Er-Fiber |
|---|---|---|---|
| Peak core absorption (@ ) | |||
| Mode field diameter (MFD) | |||
| Numerical aperture (NA, Nominal) | 0.13 | 0.20 | 0.16 |
| Cut-off wavelength | 1100–1400 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Sun, S.; Ji, W.; Ding, X.; Gao, Y.; Liu, T.; Wen, J.; Guo, H.; Wang, T. Soliton Microcomb on Chip Integrated Si3N4 Microresonators with Power Amplification in Erbium-Doped Optical Mono-Core Fiber. Micromachines 2022, 13, 2125. https://doi.org/10.3390/mi13122125
Chen X, Sun S, Ji W, Ding X, Gao Y, Liu T, Wen J, Guo H, Wang T. Soliton Microcomb on Chip Integrated Si3N4 Microresonators with Power Amplification in Erbium-Doped Optical Mono-Core Fiber. Micromachines. 2022; 13(12):2125. https://doi.org/10.3390/mi13122125
Chicago/Turabian StyleChen, Xinpeng, Suwan Sun, Weizhu Ji, Xingxing Ding, You Gao, Tuo Liu, Jianxiang Wen, Hairun Guo, and Tingyun Wang. 2022. "Soliton Microcomb on Chip Integrated Si3N4 Microresonators with Power Amplification in Erbium-Doped Optical Mono-Core Fiber" Micromachines 13, no. 12: 2125. https://doi.org/10.3390/mi13122125
APA StyleChen, X., Sun, S., Ji, W., Ding, X., Gao, Y., Liu, T., Wen, J., Guo, H., & Wang, T. (2022). Soliton Microcomb on Chip Integrated Si3N4 Microresonators with Power Amplification in Erbium-Doped Optical Mono-Core Fiber. Micromachines, 13(12), 2125. https://doi.org/10.3390/mi13122125







