Continuous Particle Aggregation and Separation in Acoustofluidic Microchannels Driven by Standing Lamb Waves
Abstract
:1. Introduction
2. Materials and Methods
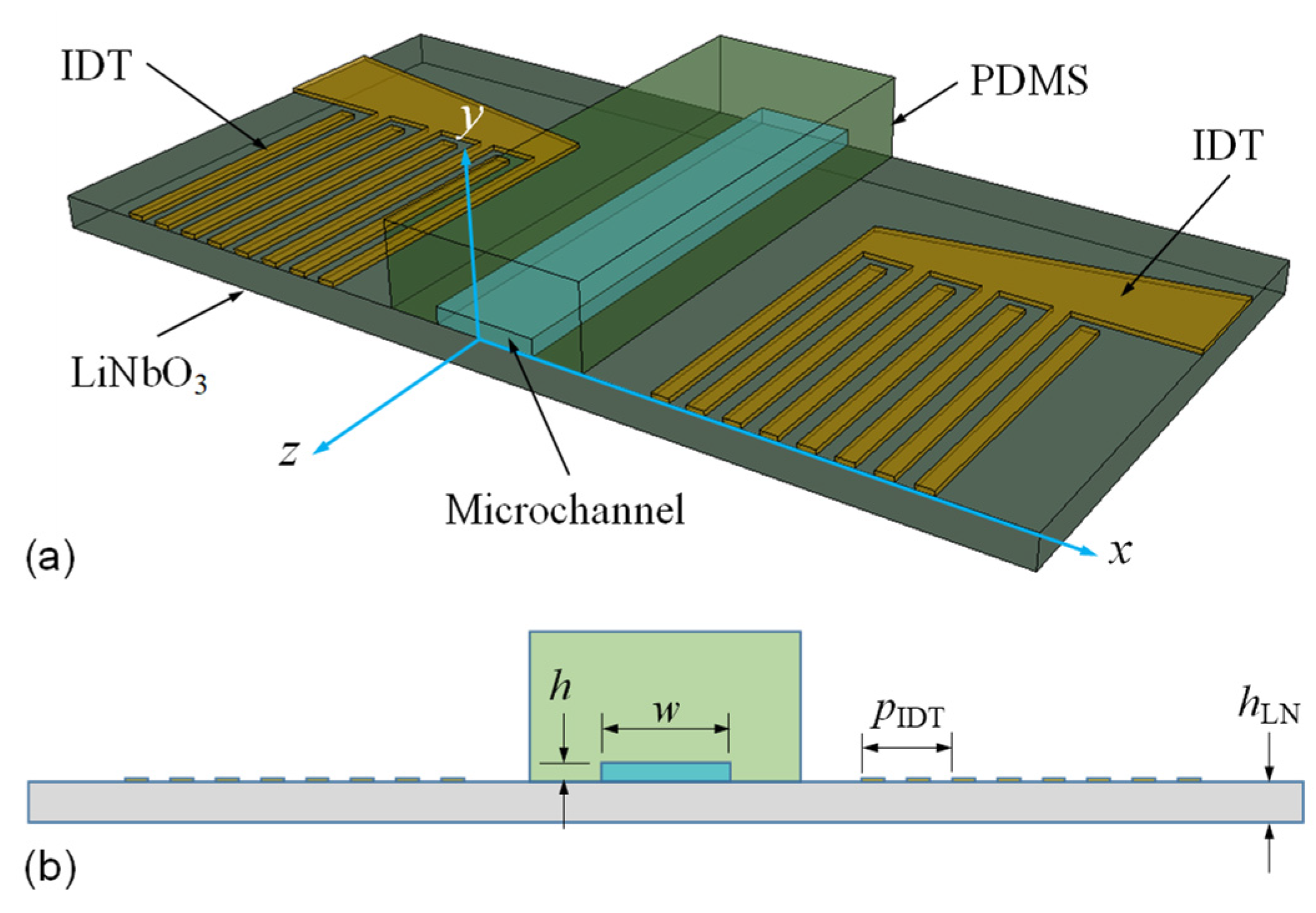
2.1. Working Principle and Numerical Approach
2.2. Device Fabrication and Experimental Procedure
3. Results and Discussions
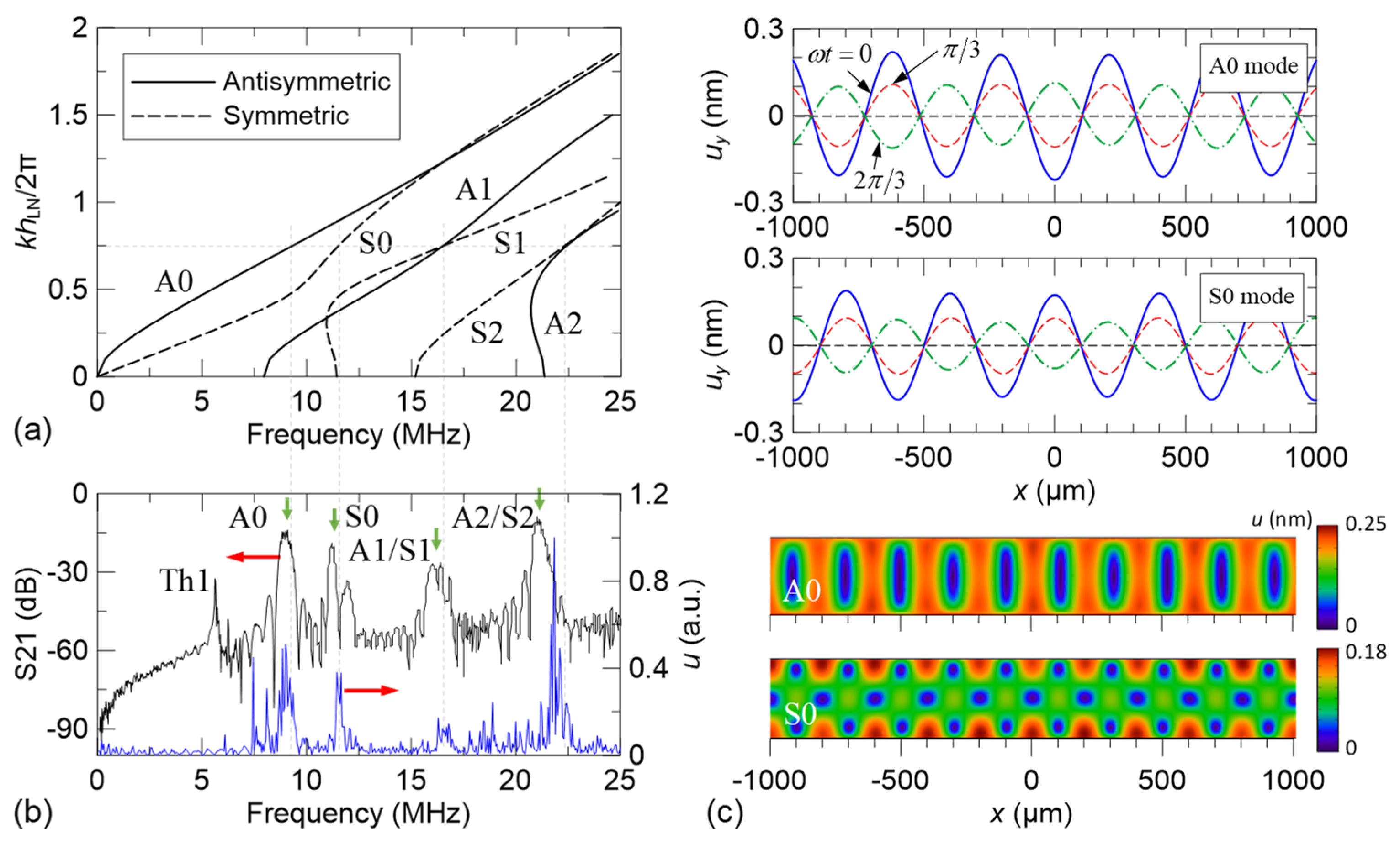
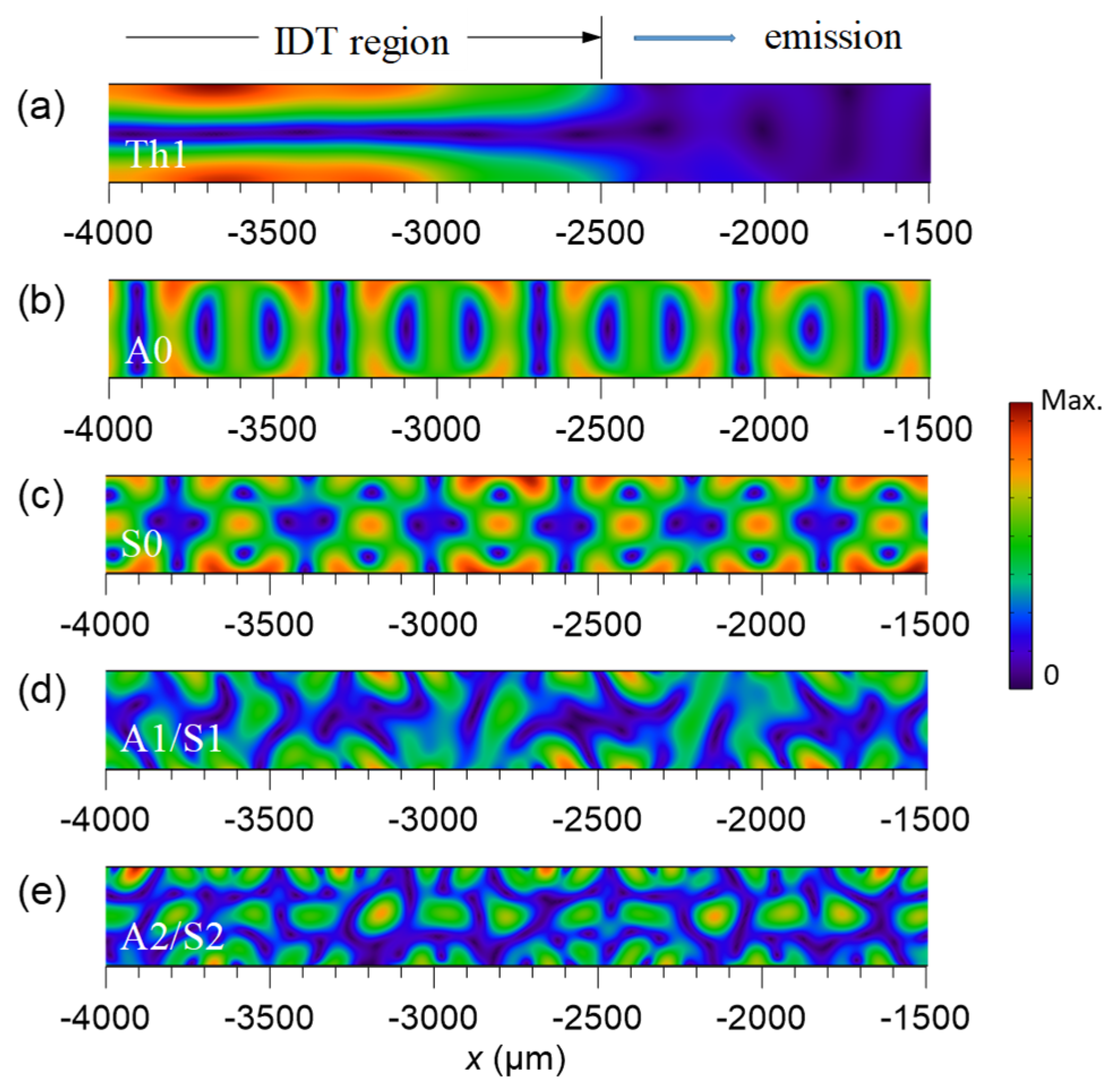
3.1. Excitation of Standing Lamb Modes in a LiNbO3 Plate
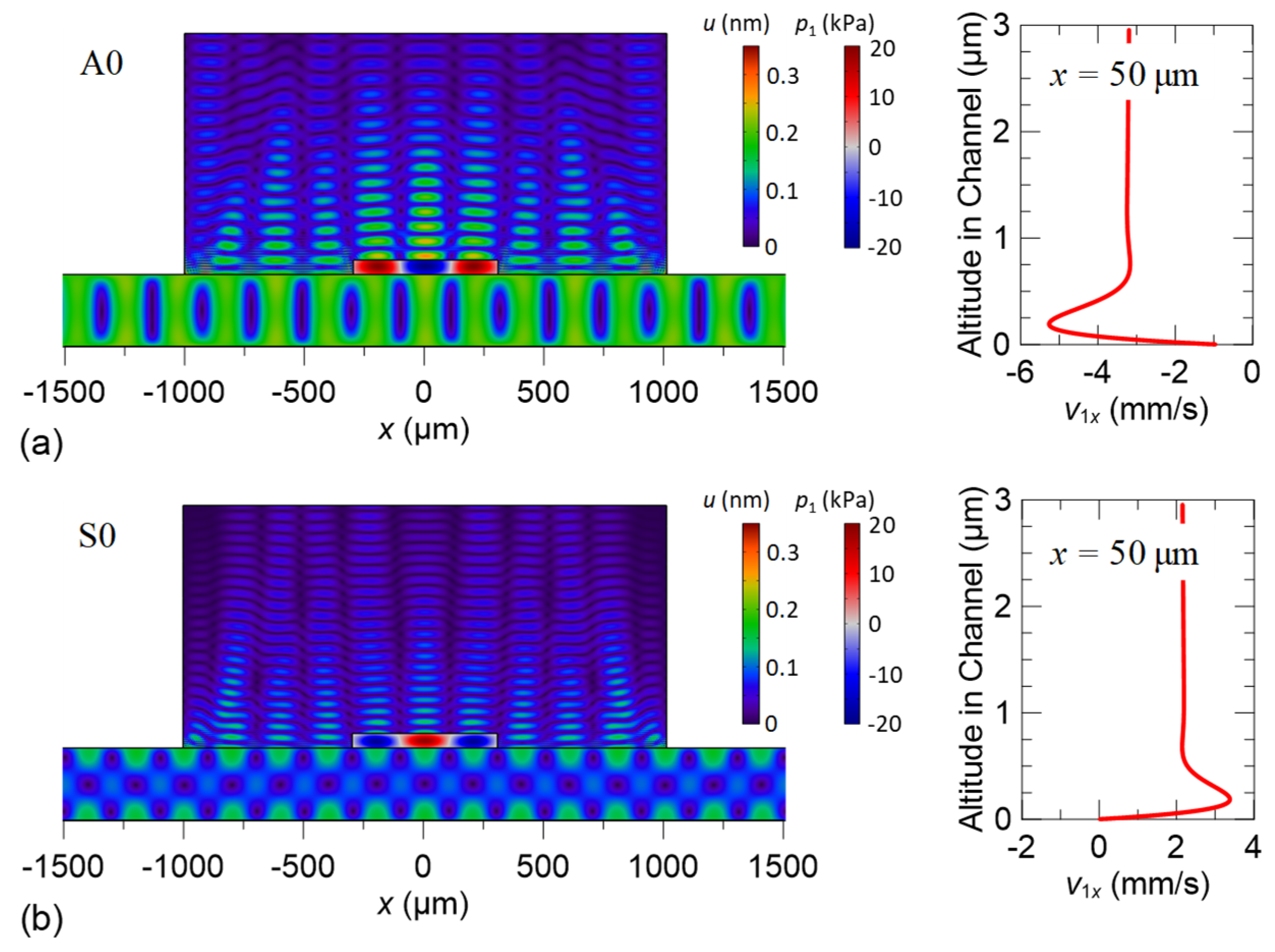
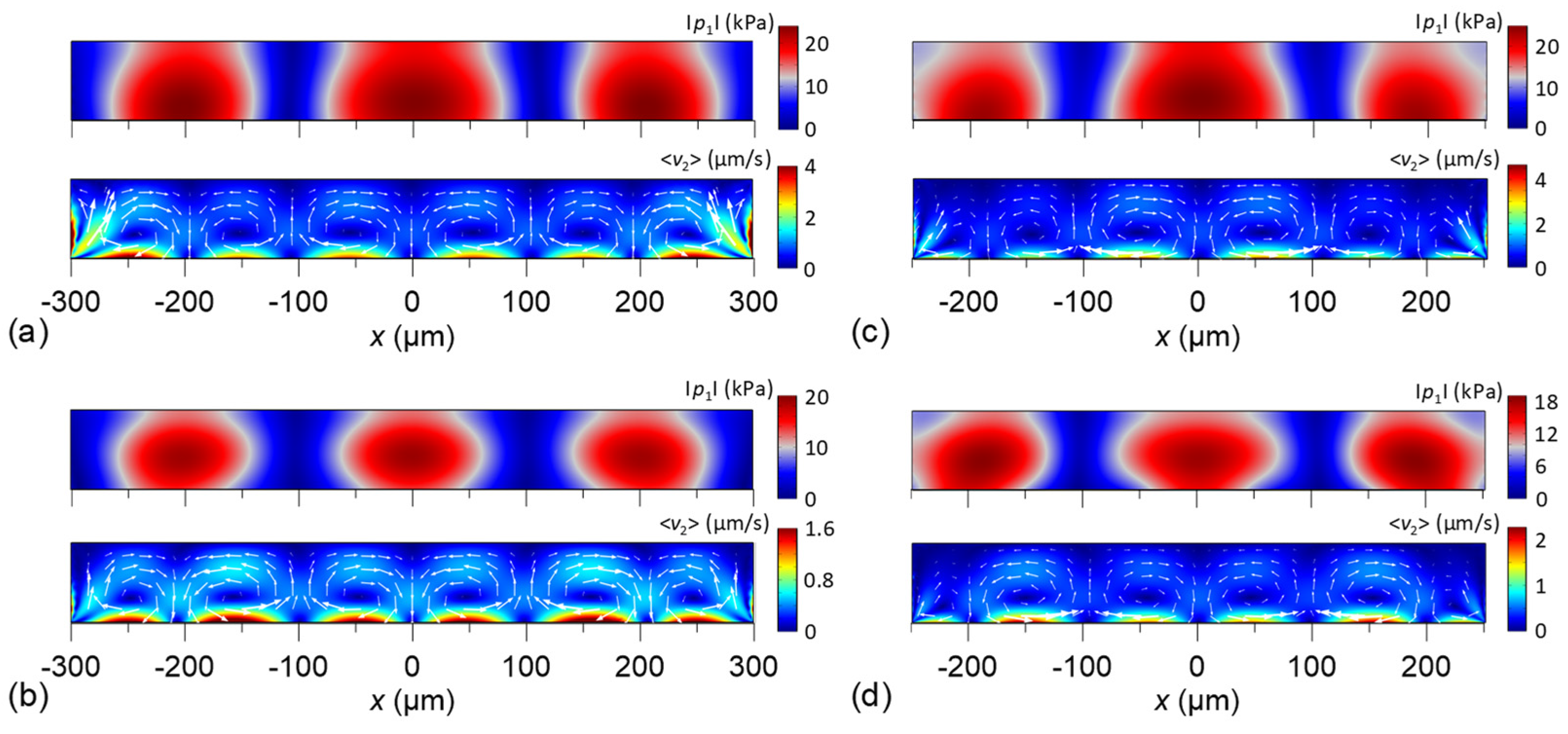
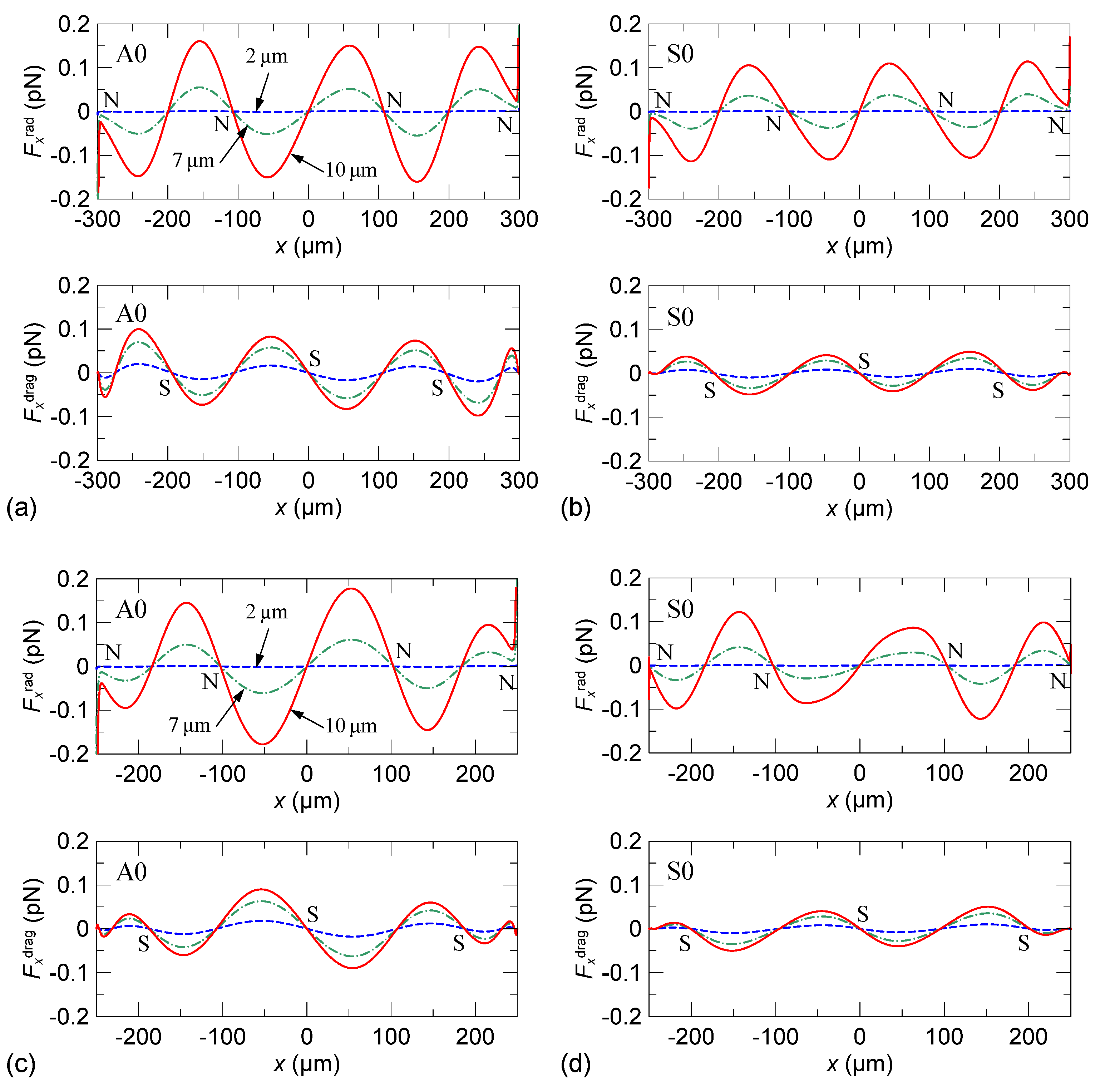
3.2. Acoustic Field, Streaming Flow, and Acoustophoretic Forces
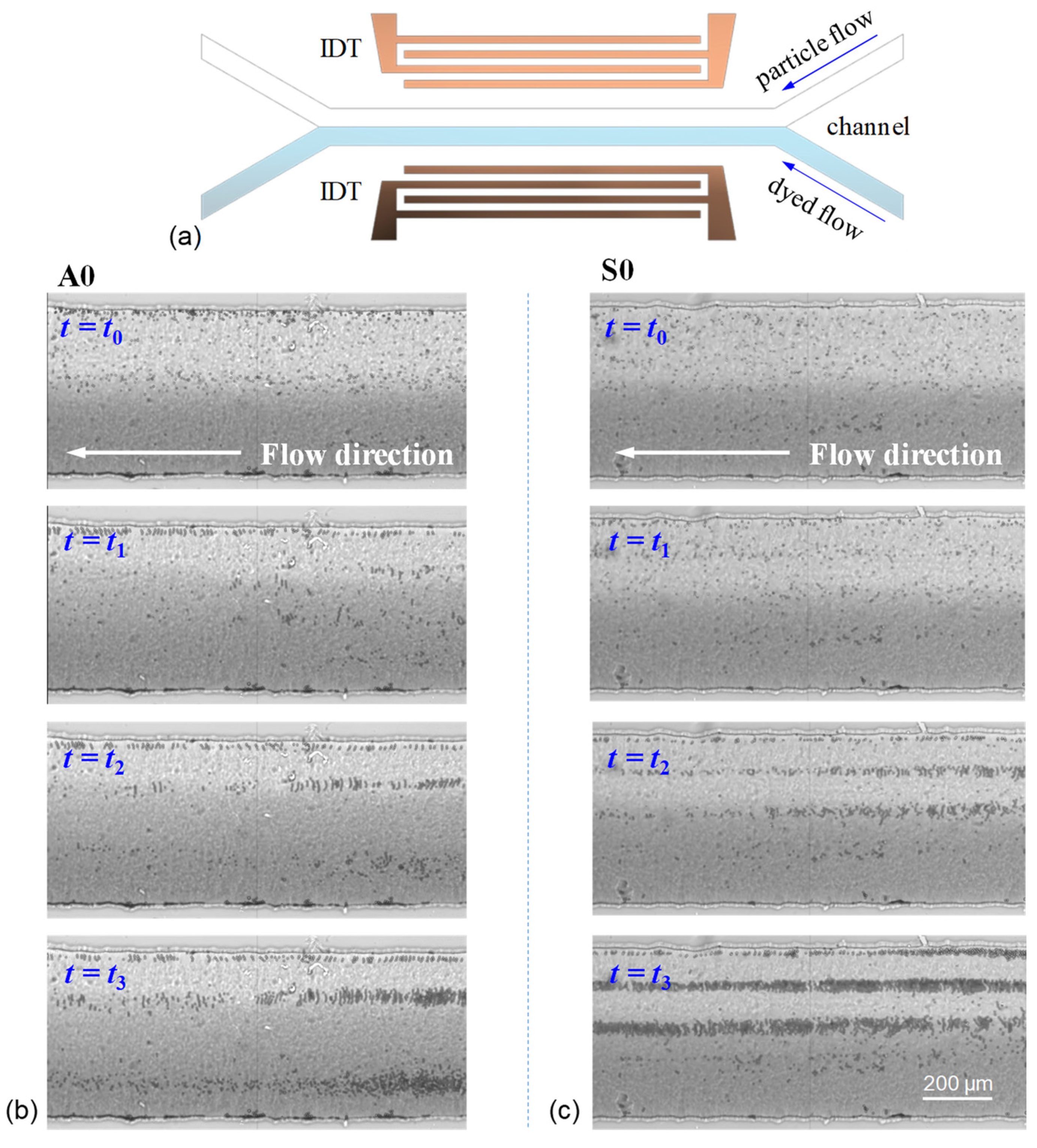
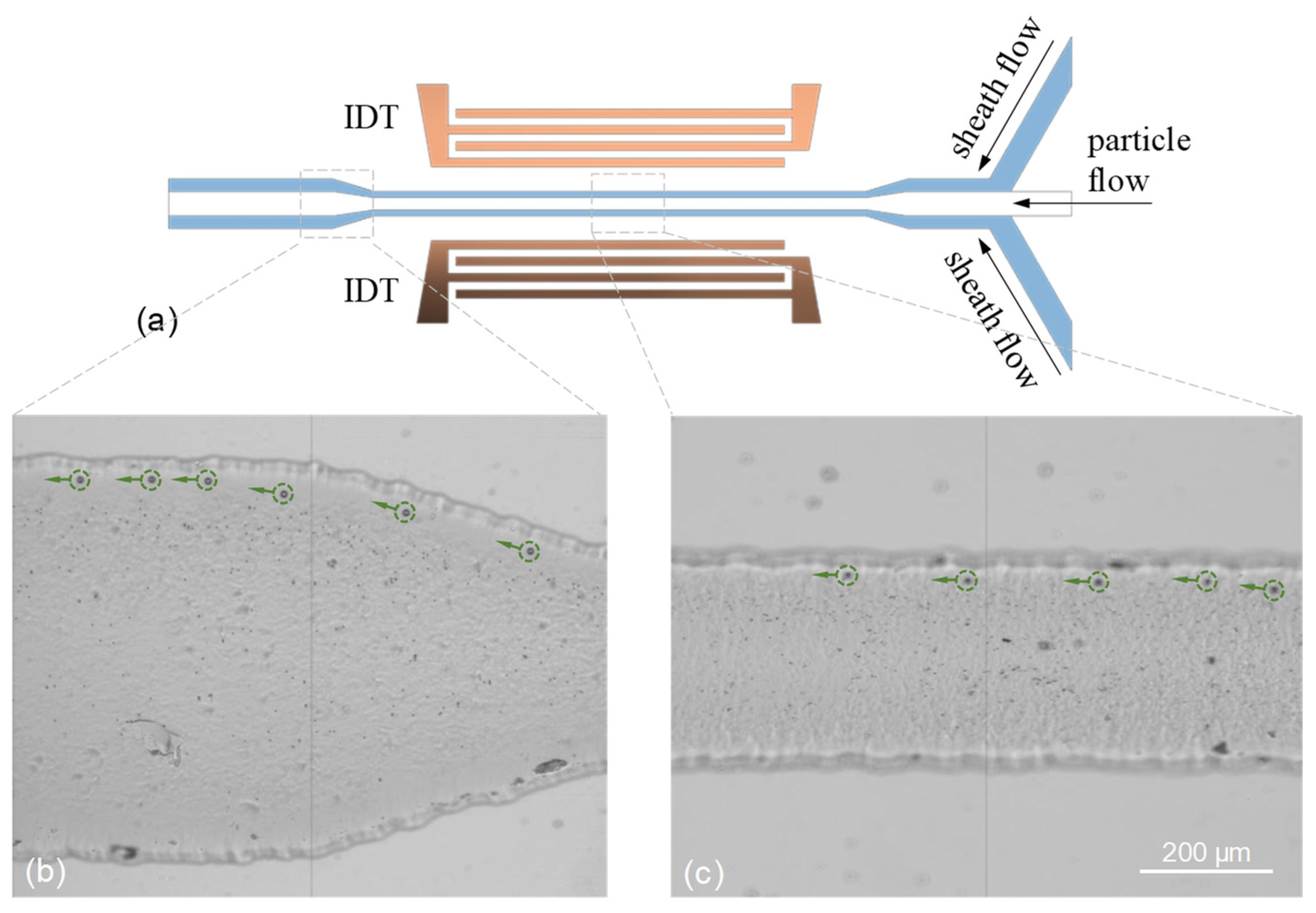
3.3. Aggregation and Separation of Microparticles
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gossett, D.R.; Weaver, W.M.; Mach, A.J.; Hur, S.C.; Tse, H.T.K.; Lee, W.; Amini, H.; Carlo, D.D. Label-free cell separation and sorting in microfluidic systems. Anal. Bioanal. Chem. 2010, 397, 3249–3267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shields, C.W., IV; Reyes, C.D.; López, G.P. Microfluidic cell sorting: A review of the advances in the separation of cells from debulking to rare cell isolation. Lab Chip 2015, 15, 1230–1249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sajeesh, P.; Sen, A.K. Particle separation and sorting in microfluidic devices: A review. Microfluid. Nanofluid. 2014, 17, 1–52. [Google Scholar] [CrossRef]
- Takagi, J.; Yamada, M.; Yasuda, M.; Seki, M. Continuous particle separation in a microchannel having asymmetrically arranged multiple branches. Lab Chip 2005, 5, 778–784. [Google Scholar] [CrossRef] [PubMed]
- Choi, S.; Park, J.K. Continuous hydrophoretic separation and sizing of microparticles using slanted obstacles in a microchannel. Lab Chip 2007, 7, 890–897. [Google Scholar] [CrossRef]
- Inglis, D.W. Efficient microfluidic particle separation arrays. Appl. Phys. Lett. 2009, 94, 013510. [Google Scholar] [CrossRef] [Green Version]
- McGrath, J.; Jimenez, M.; Bridle, H. Deterministic lateral displacement for particle separation: A review. Lab Chip 2014, 14, 4139–4158. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; Ji, X.-H.; Liu, K.; He, R.-X.; Zhao, L.-B.; Guo, Z.-X.; Liu, W.; Guo, S.-S.; Zhao, X.-Z. Droplet electric separator microfluidic device for cell sorting. Appl. Phys. Lett. 2010, 96, 193701. [Google Scholar] [CrossRef]
- Cui, H.H.; Voldman, J.; He, X.F.; Lim, K.M. Separation of particles by pulsed dielectrophoresis. Lab Chip 2009, 9, 2306–2312. [Google Scholar] [CrossRef]
- Lenshof, A.; Magnusson, C.; Laurell, T. Acoustofluidics 8: Applications of acoustophoresis in continuous flow microsystems. Lab Chip 2012, 12, 1210–1223. [Google Scholar] [CrossRef]
- Zeng, J.; Deng, Y.; Vedantam, P.; Tzeng, T.R.; Xuan, X. Magnetic separation of particles and cells in ferrofluid flow through a straight microchannel using two offset magnets. J. Magn. Magn. Mater. 2013, 346, 118–123. [Google Scholar] [CrossRef]
- Huang, K.W.; Wu, Y.C.; Lee, J.A.; Chiou, P.Y. Microfluidic integrated optoelectronic tweezers for single-cell preparation and analysis. Lab Chip 2013, 13, 3721–3727. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Ozcelik, A.; Rufo, J.; Wang, Z.; Fang, R.; Huang, T.J. Acoustofluidic separation of cells and particles. Microsyst. Nanoeng. 2019, 5, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Raeymaekers, B.; Pantea, C.; Sinha, D.N. Manipulation of diamond nanoparticles using bulk acoustic waves. J. Appl. Phys. 2011, 109, 014317. [Google Scholar] [CrossRef]
- Destgeer, G.; Alazzam, A.; Sung, H.J. High frequency travelling surface acoustic waves for microparticle separation. J. Mech. Sci. Technol. 2016, 30, 3945–3952. [Google Scholar] [CrossRef]
- Shi, J.; Huang, H.; Stratton, Z.; Huang, Y.; Huang, T.J. Continuous particle separation in a microfluidic channel via standing surface acoustic waves (SSAW). Lab Chip 2009, 9, 3354–3359. [Google Scholar] [CrossRef]
- Simon, G.; Andrade, M.A.; Reboud, J.; Marques-Hueso, J.; Desmulliez, M.P.; Cooper, J.M.; Riehle, M.O.; Bernassau, A.L. Particle separation by phase modulated surface acoustic waves. Biomicrofluidics 2017, 11, 054115. [Google Scholar] [CrossRef]
- Simon, G.; Pailhas, Y.; Andrade, M.A.; Reboud, J.; Marques-Hueso, J.; Desmulliez, M.P.; Cooper, J.M.; Riehle, M.O.; Bernassau, A.L. Particle separation in surface acoustic wave microfluidic devices using reprogrammable, pseudo-standing waves. Appl. Phys. Lett. 2018, 113, 044101. [Google Scholar] [CrossRef] [Green Version]
- Sriphutkiat, Y.; Zhou, Y. The effect of phase modulation in dual-frequency excited standing surface acoustic wave (SSAW) on microparticle manipulation. Sens. Actuator A-Phys. 2021, 332, 113072. [Google Scholar] [CrossRef]
- Lee, J.; Rhyou, C.; Kang, B.; Lee, H. Continuously phase-modulated standing surface acoustic waves for separation of particles and cells in microfluidic channels containing multiple pressure nodes. J. Phys. D-Appl. Phys. 2017, 50, 165401. [Google Scholar] [CrossRef]
- Ng, J.W.; Devendran, C.; Neild, A. Acoustic tweezing of particles using decaying opposing travelling surface acoustic waves (DOTSAW). Lab Chip 2017, 17, 3489–3497. [Google Scholar] [CrossRef] [PubMed]
- Joshi, S.G.; Jin, Y. Propagation of ultrasonic Lamb waves in piezoelectric plates. J. Appl. Phys. 1991, 70, 4113–4120. [Google Scholar] [CrossRef]
- Ni, Z.; Xu, G.; Huang, J.; Yao, G.; Tu, J.; Guo, X.; Zhang, D. Lamb wave coupled resonance for SAW acoustofluidics. Appl. Phys. Lett. 2021, 118, 051103. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Chang, C.-Y. Enhanced acoustofluidic mixing in a semicircular microchannel using plate mode coupling in a surface acoustic wave device. Sens. Actuator A-Phys. 2022, 336, 113401. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Chao, C.-L. Acoustophoretic patterning of microparticles in a microfluidic chamber driven by standing Lamb waves. Appl. Phys. Lett. 2021, 119, 103504. [Google Scholar] [CrossRef]
- Hsu, J.C.; Huang, Y.W.; Hsu, C.H. Transportation control of microfluidic particles using mode switching between surface acoustic waves and plate waves. Jpn. J. Appl. Phys. 2017, 56, 07JD05. [Google Scholar] [CrossRef]
- Moiseyenko, R.P.; Bruus, H. Whole-system ultrasound resonances as the basis for acoustophoresis in all-polymer microfluidic devices. Phys. Rev. Appl. 2019, 11, 014014. [Google Scholar] [CrossRef] [Green Version]
- Hsu, J.-C.; Chao, C.-L. Full-wave modeling of micro-acoustofluidic devices driven by standing surface acoustic waves for microparticle acoustophoresis. J. Appl. Phys. 2020, 128, 124502. [Google Scholar] [CrossRef]
- Muller, P.B.; Barnkob, R.; Jensen, M.J.H.; Bruus, H. A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab Chip 2012, 12, 4617–4627. [Google Scholar] [CrossRef] [Green Version]
- Nama, N.; Barnkob, R.; Mao, Z.; Kähler, C.J.; Costanzo, F.; Huang, T.J. Numerical study of acoustophoretic motion of particles in a PDMS microchannel driven by surface acoustic waves. Lab Chip 2015, 15, 2700–2709. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids, 2nd ed.; R. E. Krieger: Malabar, FL, USA, 1990; Volume I, pp. 101–124. [Google Scholar]
- Royer, D.; Dieulesaint, E. Elastic Waves in Solids I; Springer: Berlin/Heidelberg, Germany, 2000; pp. 133–165. [Google Scholar]
- Simulate Real-World Designs, Devices, and Processes with Multiphysics Software from COMSOL. Available online: https://www.comsol.com (accessed on 1 October 2022).
- Hsu, J.-C.; Hsu, C.-H.; Huang, Y.-W. Acoustophoretic control of microparticle transport using dual-wavelength surface acoustic wave devices. Micromachines 2019, 10, 52. [Google Scholar] [CrossRef] [PubMed]



| Wave Type | SAW | Lamb Wave |
|---|---|---|
| Characteristics | single mode (Rayleigh mode) | multimode (antisymmetric, symmetric) |
| surface localized (half-space) | plate borne (plate thickness) | |
| nondispersive (constant sound speed) | dispersive | |
| electrically excitable | electrically excitable |
| Geometry | Value | Unit |
|---|---|---|
| LN substrate thickness | 300 | μm |
| IDT pitch | 400 | μm |
| IDT electrode pairs | 20 | |
| Electrode linewidth | 100 | μm |
| IDT aperture | 4400 | μm |
| Electrode thickness (Cu/Ti) | 150/50 | nm |
| Frequency (MHz) | ||||||
|---|---|---|---|---|---|---|
| Substrate | Th1 | A0 | S0 | A1/S1 | A2/S2 | |
| 128°Y-X LiNbO3 | eigenfrequency | - | 9.3 | 11.5 | 16.6 | 22.4 |
| calculated spectrum | 6.1 † | 8.85 | 11.65 | 16.8 | 21.85 | |
| measured spectrum | 5.61 | 8.9 | 11.2 | 16.1 | 21.0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, J.-C.; Chang, C.-Y. Continuous Particle Aggregation and Separation in Acoustofluidic Microchannels Driven by Standing Lamb Waves. Micromachines 2022, 13, 2175. https://doi.org/10.3390/mi13122175
Hsu J-C, Chang C-Y. Continuous Particle Aggregation and Separation in Acoustofluidic Microchannels Driven by Standing Lamb Waves. Micromachines. 2022; 13(12):2175. https://doi.org/10.3390/mi13122175
Chicago/Turabian StyleHsu, Jin-Chen, and Chih-Yu Chang. 2022. "Continuous Particle Aggregation and Separation in Acoustofluidic Microchannels Driven by Standing Lamb Waves" Micromachines 13, no. 12: 2175. https://doi.org/10.3390/mi13122175






