Phononic-Crystal-Based Particle Sieving in Continuous Flow: Numerical Simulations
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
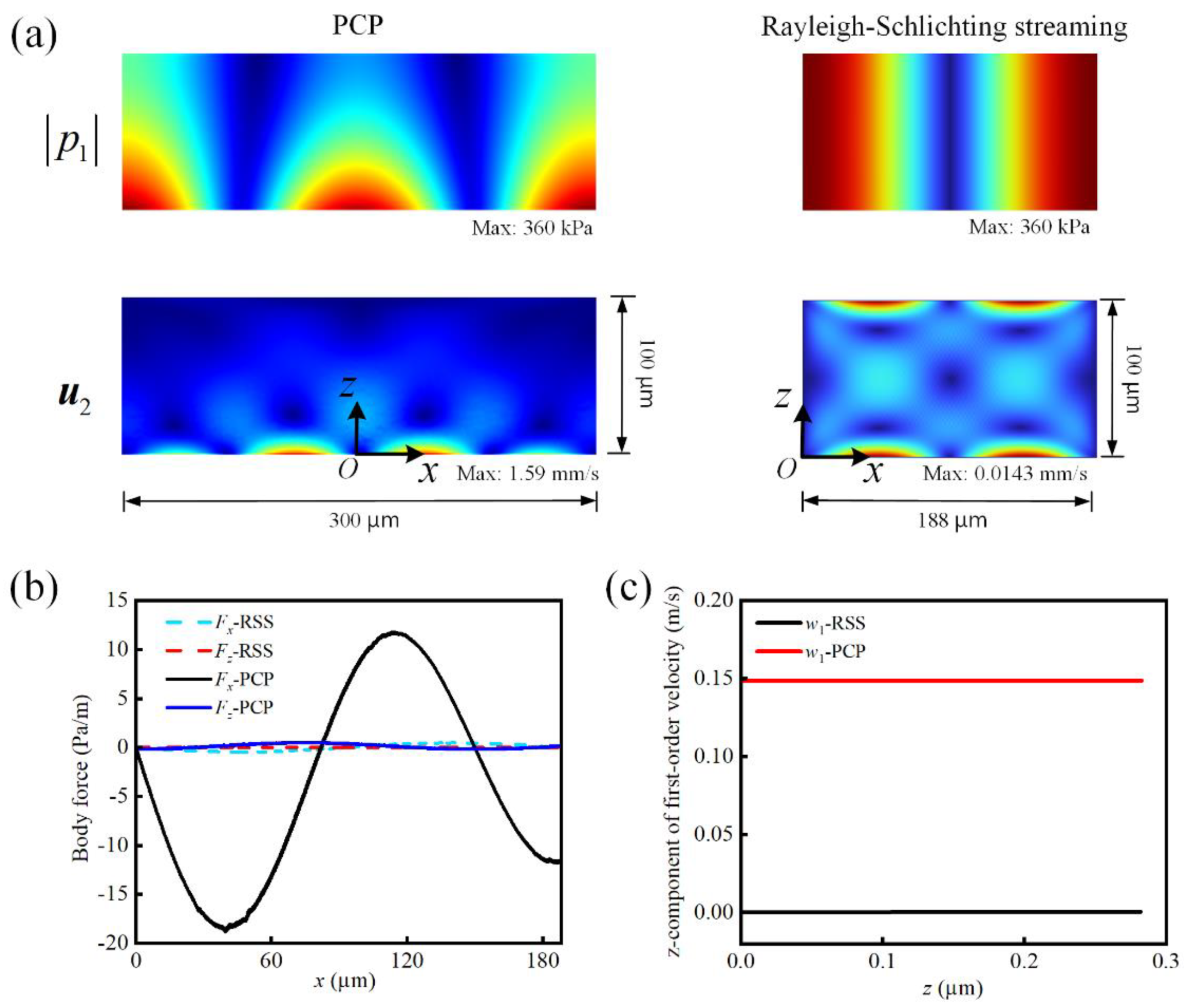
3.1. Transmission Spectrum of the PCP and Acoustic Field
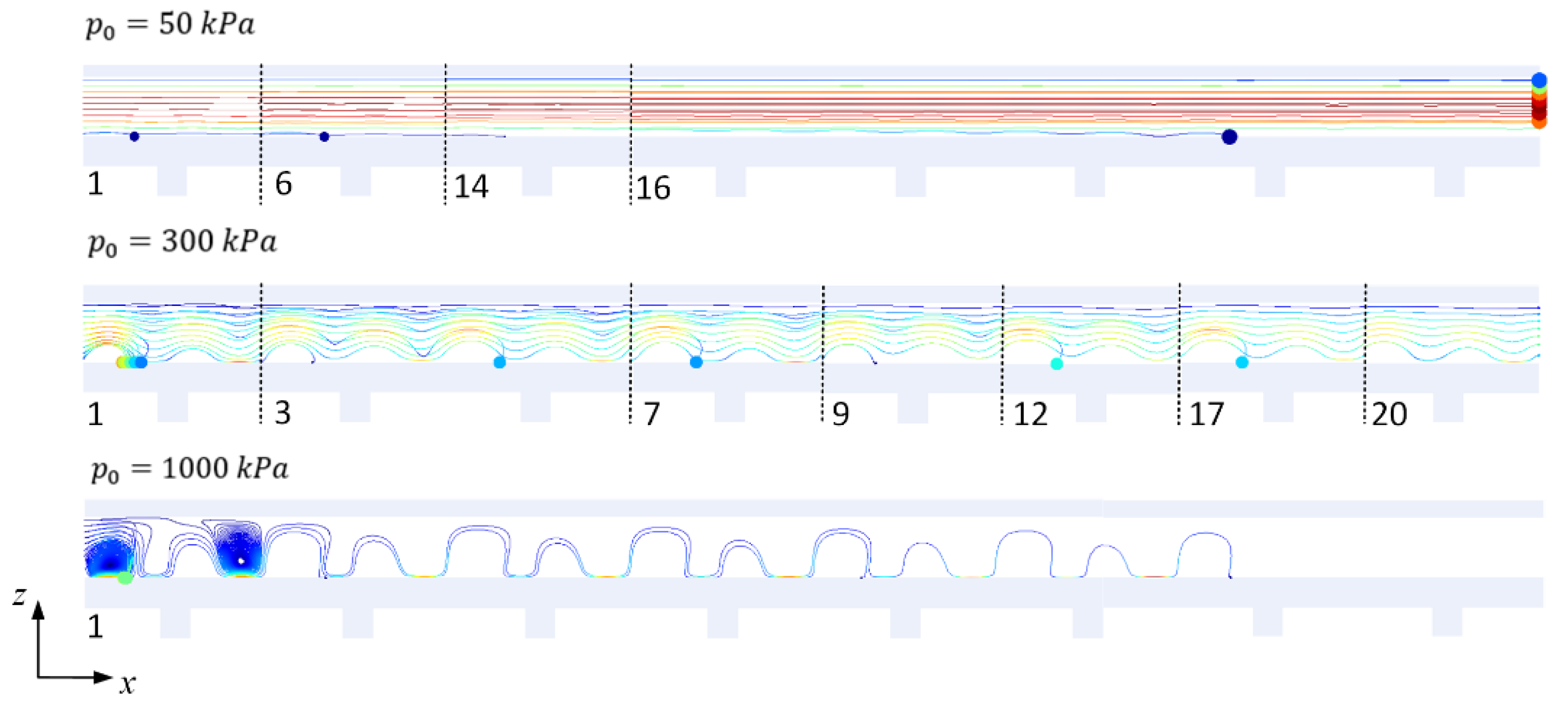
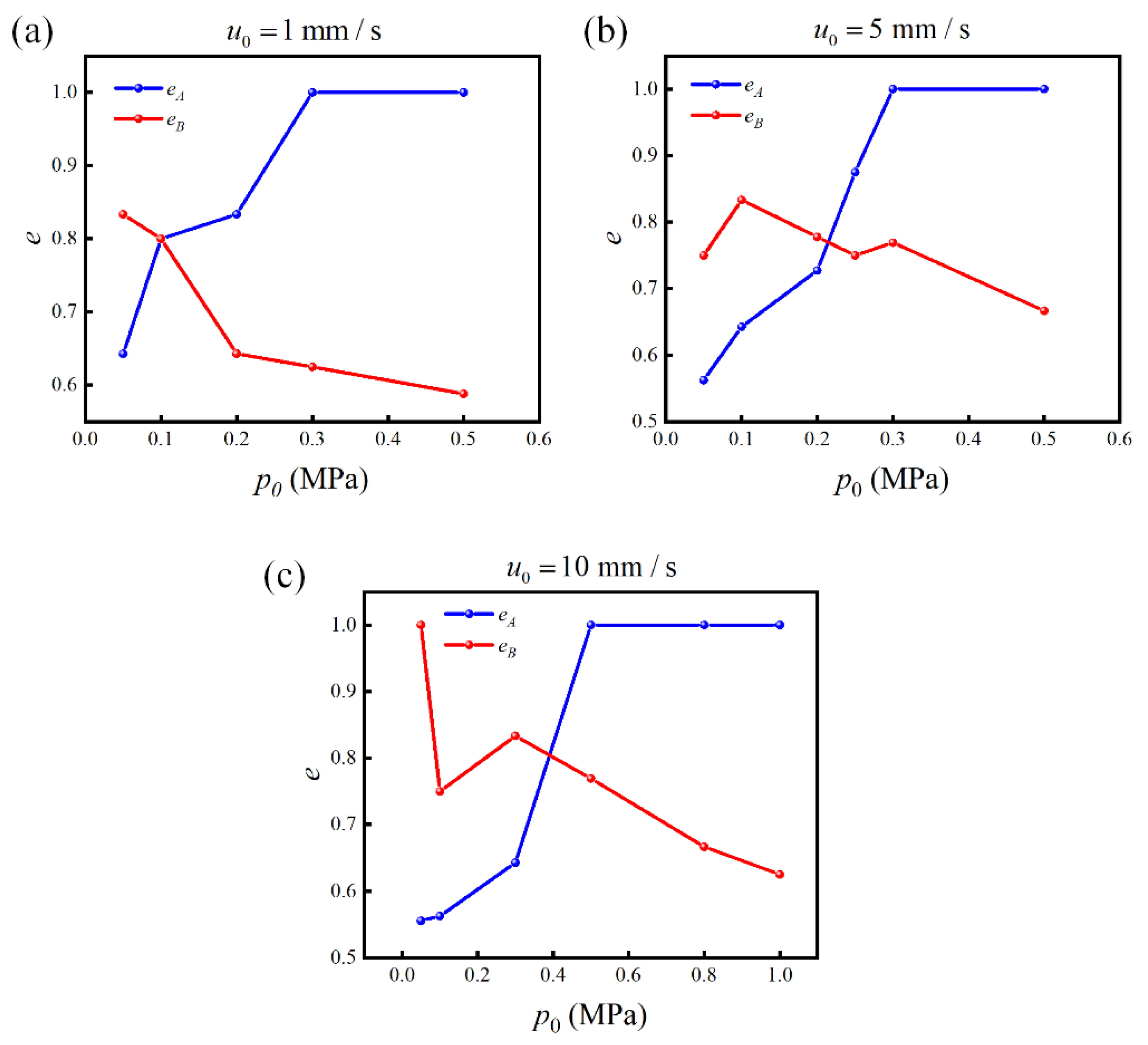
3.2. Motion of Particles and Separation Efficiency
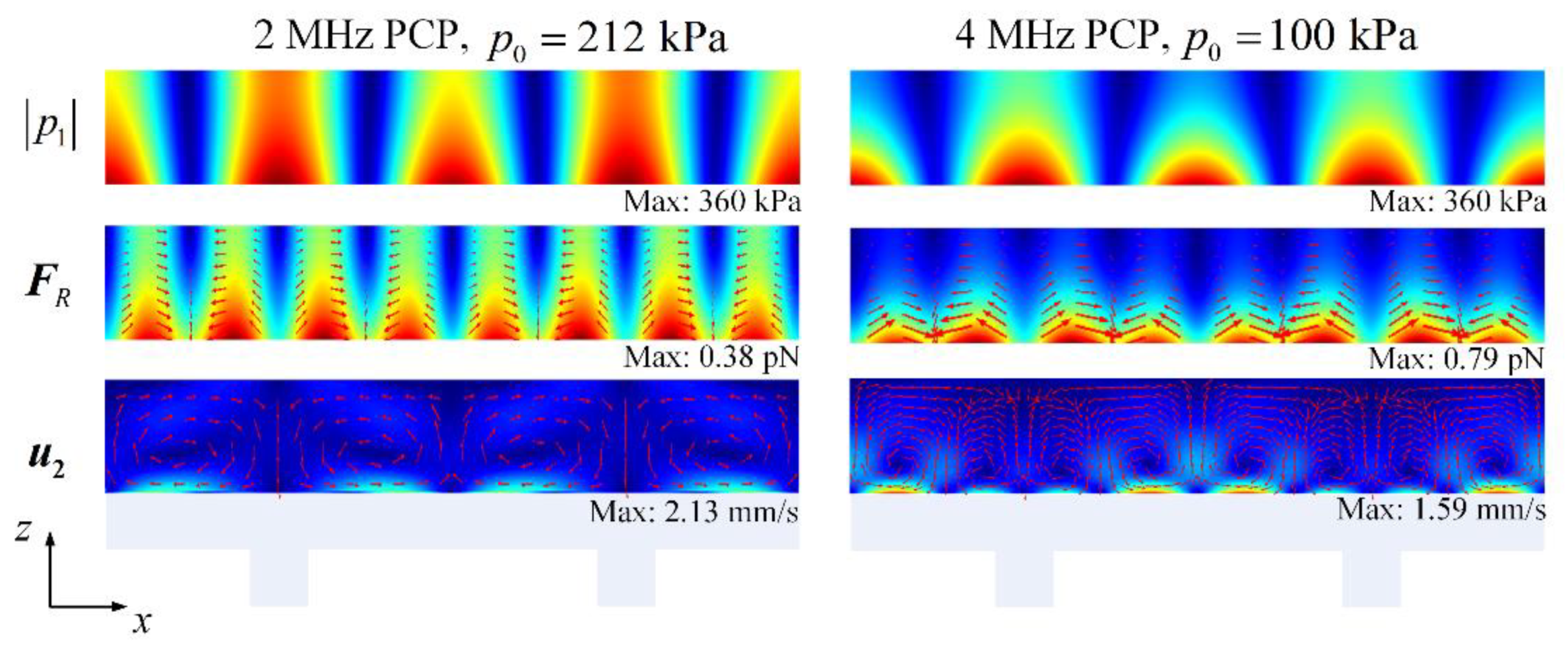
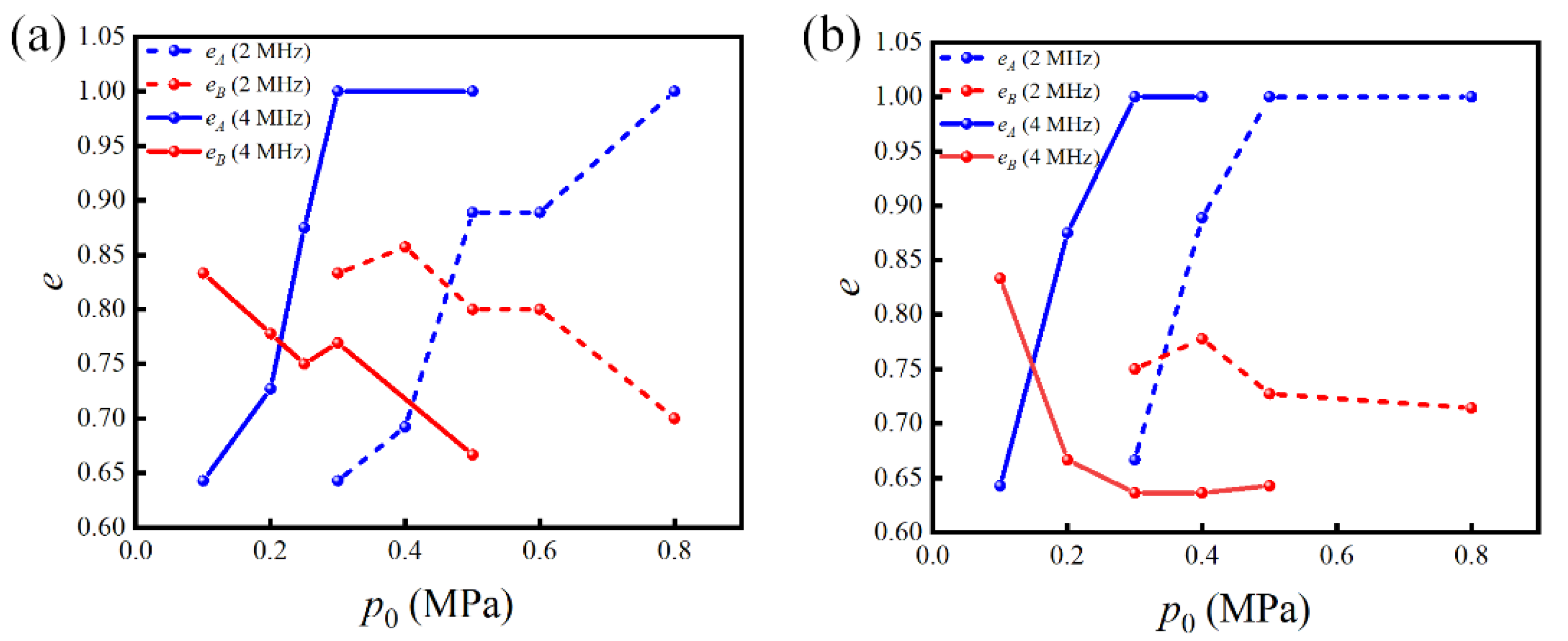
3.3. Acoustic Separation via PCPs with Different Resonant Frequencies
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harrison, D.J.; Fluri, K.; Seiler, K.; Fan, Z.; Effenhauser, C.S.; Manz, A. Micromachining a miniaturized capillary electrophoresis-based chemical analysis system on a chip. Science 1993, 261, 895–897. [Google Scholar] [CrossRef] [PubMed]
- Hafez, A.; Khedr, M.; Gadallah, H. Wastewater treatment and water reuse of food processing industries.Part II:Techno-economic study of a membrane separation technique. Desalination 2007, 214, 261–272. [Google Scholar] [CrossRef]
- Cheng, X.; Irimia, D.; Dixon, M.; Sekine, K.; Demirci, U.; Zamir, L.; Tompkins, R.G.; Rodriguez, W.; Toner, M. A microfluidic device for practical label-free CD4(+) T cell counting of HIV-infected subjects. Lab Chip 2007, 7, 170–178. [Google Scholar] [CrossRef] [PubMed]
- Gascoyne, P.; Mahidol, C.; Ruchirawat, M.; Satayavivad, J.; Watcharasit, P.; Becker, F. Microsample preparation by dielectrophoresis: Isolation of malaria. Lab Chip 2002, 2, 70–75. [Google Scholar] [CrossRef] [Green Version]
- Dassey, A.J.; Theegala, C.S. Harvesting economics and strategies using centrifugation for cost effective separation of microalgae cells for biodiesel applications. Bioresour. Technol. 2013, 128, 241–245. [Google Scholar] [CrossRef]
- Jirage, K.B.; Hulteen, J.C.; Martin, C.R. Nanotubule-Based Molecular-Filtration membranes. Science 1997, 2784, 655–658. [Google Scholar] [CrossRef]
- Yao, Y.; Hou, J.; Xu, Z.; Li, G.; Yang, Y. Effects of Solvent Mixtures on the Nanoscale Phase Separation in Polymer Solar Cells. Adv. Funct. Mater. 2008, 18, 1783–1789. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, M.; Lin, Y.; Xu, J. Acoustic Microfluidic Separation Techniques and Bioapplications: A Review. Micromachines 2020, 11, 921. [Google Scholar] [CrossRef]
- Shi, L.; Zhong, X.; Ding, H.; Yu, Z.; Jin, J.; Zhou, T.; Zhu, Y.; Liu, Z. Continuous separation of microparticles based on optically induced dielectrophoresis. Microfluid. Nanofluidics 2022, 26, 6. [Google Scholar] [CrossRef]
- Zabetian, M.; Saidi, M.S.; Shafii, M.B.; Saidi, M.H. Separation of microparticles suspended in a minichannel using laser radiation pressure. Applies Opt. 2013, 52, 4950–4958. [Google Scholar] [CrossRef]
- Khoshmanesh, K.; Zhang, C.; Tovar-Lopez, F.J.; Nahavandi, S.; Baratchi, S.; Kalantar-zadeh, K.; Mitchell, A. Dielectrophoretic manipulation and separation of microparticles using curved microelectrodes. Electrophoresis 2009, 30, 3707–3717. [Google Scholar] [CrossRef] [PubMed]
- Kang, K.H.; Kang, Y.; Xuan, X.; Li, D. Continuous separation of microparticles by size with Direct current-dielectrophoresis. Electrophoresis 2006, 27, 694–702. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Bai, F.; Wang, C. Magnetic separation of microparticles by shape. Lab Chip 2017, 17, 401–406. [Google Scholar] [CrossRef] [PubMed]
- Watarai, H.; Suwa, M.; Iiguni, Y. Magnetophoresis and electromagnetophoresis of microparticles in liquids. Anal. Bioanal. Chem. 2004, 378, 1693–1699. [Google Scholar] [CrossRef]
- Murata, M.; Okamoto, Y.; Park, Y.S.; Kaji, N.; Tokeshi, M.; Baba, Y. Cell separation by the combination of microfluidics and optical trapping force on a microchip. Anal. Bioanal. Chem. 2009, 394, 277–283. [Google Scholar] [CrossRef]
- Lewpiriyawong, N.; Yang, C.; Lam, Y.C. Continuous sorting and separation of microparticles by size using AC dielectrophoresis in a PDMS microfluidic device with 3-D conducting PDMS composite electrodes. Electrophoresis 2010, 31, 2622–2631. [Google Scholar] [CrossRef]
- Zeng, L.; Chen, X.; Du, J.; Yu, Z.; Zhang, R.; Zhang, Y.; Yang, H. Label-free separation of nanoscale particles by an ultrahigh gradient magnetic field in a microfluidic device. Nanoscale 2021, 13, 4029–4037. [Google Scholar] [CrossRef]
- Liu, J.; Qu, Y.; Wang, H. Immuno-Acoustic Sorting of Disease-Specific Extracellular Vesicles by Acoustophoretic Force. Micromachines 2021, 12, 1534. [Google Scholar] [CrossRef]
- González, I.; Earl, J.; Fernández, L.J.; Sainz, B.; Pinto, A.; Monge, R.; Alcalá, S.; Castillejo, A.; Soto, J.L.; Carrato, A. A Label Free Disposable Device for Rapid Isolation of Rare Tumor Cells from Blood by Ultrasounds. Micromachines 2018, 9, 129. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, H.; Destgeer, G.; Park, J.; Afzal, M.; Sung, H.J. Sheathless Focusing and Separation of Microparticles Using Tilted-Angle Traveling Surface Acoustic Waves. Anal. Chem. 2018, 90, 8546–8552. [Google Scholar] [CrossRef]
- Wu, M.; Ouyang, Y.; Wang, Z.; Zhang, R.; Huang, P.H.; Chen, C.; Li, H.; Li, P.; Quinn, D.; Dao, M.; et al. Isolation of exosomes from whole blood by integrating acoustics and microfluidics. Proc. Natl. Acad. Sci. USA 2017, 114, 10584–10589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, P.; Mao, Z.; Peng, Z.; Zhou, L.; Chen, Y.; Huang, P.H.; Truica, C.I.; Drabick, J.J.; El-Deiry, W.S.; Dao, M.; et al. Acoustic separation of circulating tumor cells. Proc. Natl. Acad. Sci. USA 2015, 112, 4970–4975. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fornell, A.; Cushing, K.; Nilsson, J.; Tenje, M. Binary particle separation in droplet microfluidics using acoustophoresis. Appl. Phys. Lett. 2018, 112, 063701. [Google Scholar] [CrossRef]
- Lu, X.; Martin, A.; Soto, F.; Angsantikul, P.; Li, J.; Chen, C.; Liang, Y.; Hu, J.; Zhang, L.; Wang, J. Parallel Label-Free Isolation of Cancer Cells Using Arrays of Acoustic Microstreaming Traps. Adv. Mater. Technol. 2019, 4, 1800374. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Lin, Y.-D. Microparticle concentration and separation inside a droplet using phononic-crystal scattered standing surface acoustic waves. Sens. Actuators A Phys. 2019, 300, 111651. [Google Scholar] [CrossRef]
- Korozlu, N.; Biçer, A.; Sayarcan, D.; Kaya, O.A.; Cicek, A. Acoustic sorting of airborne particles by a phononic crystal waveguide. Ultrasonics 2022, 124, 106777. [Google Scholar] [CrossRef]
- Li, F.; Cai, F.; Liu, Z.; Meng, L.; Qian, M.; Wang, C.; Cheng, Q.; Qian, M.; Liu, X.; Wu, J. Phononic-crystal-based acoustic sieve for tunable manipulations of particles by a highly localized radiation force. Phys. Rev. Appl. 2014, 1, 051001. [Google Scholar] [CrossRef]
- He, Z.; Jia, H.; Qiu, C.; Peng, S.; Mei, X.; Cai, F.; Peng, P.; Ke, M.; Liu, Z. Acoustic transmission enhancement through a periodically structured stiff plate without any opening. Phys. Rev. Lett. 2010, 105, 074301. [Google Scholar] [CrossRef]
- Li, F.; Cai, F.; Zhang, L.; Liu, Z.; Li, F.; Meng, L.; Wu, J.; Li, J.; Zhang, X.; Zheng, H. Phononic-Crystal-Enabled Dynamic Manipulation of Microparticles and Cells in an Acoustofluidic Channel. Phys. Rev. Appl. 2020, 13, 044077. [Google Scholar] [CrossRef]
- Huang, L.; Li, F.; Cai, F.; Meng, L.; Zhou, W.; Kong, D.; Zheng, H. Phononic crystal-induced standing Lamb wave for the translation of subwavelength microparticles. Appl. Phys. Lett. 2022, 121, 023505. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Cai, F.; Meng, L.; Jiang, C.; Pan, Y.; Zheng, H. Computation of the acoustic radiation force using the finite-difference time-domain method. J. Acoust. Soc. Am. 2010, 128, 1617–1622. [Google Scholar] [CrossRef] [PubMed]
- Gor’kov, L.P. On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov. Phys.-Dokl. 1962, 6, 773–775. [Google Scholar]
- Li, F.; Yan, F.; Chen, Z.; Lei, J.; Yu, J.; Chen, M.; Zhou, W.; Meng, L.; Niu, L.; Wu, J.; et al. Phononic crystal-enhanced near-boundary streaming for sonoporation. Appl. Phys. Lett. 2018, 113, 083701. [Google Scholar] [CrossRef]
- Li, F.; Xiao, Y.; Lei, J.; Xia, X.; Zhou, W.; Meng, L.; Niu, L.; Wu, J.; Li, J.; Cai, F.; et al. Rapid acoustophoretic motion of microparticles manipulated by phononic crystals. Appl. Phys. Lett. 2018, 113, 173503. [Google Scholar] [CrossRef]
- Ni, Z.; Yin, C.; Xu, G.; Xie, L.; Huang, J.; Liu, S.; Tu, J.; Guo, X.; Zhang, D. Modelling of SAW-PDMS acoustofluidics: Physical fields and particle motions influenced by different descriptions of the PDMS domain. Lab Chip 2019, 19, 2728–2740. [Google Scholar] [CrossRef]
- Lei, J.; Glynne-Jones, P.; Hill, M. Comparing methods for the modelling of boundary-driven streaming in acoustofluidic devices. Microfluid. Nanofluidics 2017, 21, 23. [Google Scholar] [CrossRef] [Green Version]
- Baasch, T.; Doinikov, A.A.; Dual, J. Acoustic streaming outside and inside a fluid particle undergoing monopole and dipole oscillations. Phys. Rev. E 2020, 101, 013108. [Google Scholar] [CrossRef]
- Lee, C.P.; Wang, T.G. Outer acoustic streaming. J. Acoust. Soc. Am. 1990, 88, 2367–2375. [Google Scholar] [CrossRef]
- Lei, J.; Glynne-Jones, P.; Hill, M. Acoustic streaming in the transducer plane in ultrasonic particle manipulation devices. Lab Chip 2013, 13, 2133–2143. [Google Scholar] [CrossRef] [Green Version]
- Devendran, C.; Choi, K.; Han, J.; Ai, Y.; Neild, A.; Collins, D.J. Diffraction-based acoustic manipulation in microchannels enables continuous particle and bacteria focusing. Lab Chip 2020, 20, 2674–2688. [Google Scholar] [CrossRef]
- Muller, P.B.; Barnkob, R.; Jensen, M.J.H.; Bruus, H. A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab Chip 2012, 12, 4617–4627. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Zhou, J.; Kong, D.; Li, F. Phononic-Crystal-Based Particle Sieving in Continuous Flow: Numerical Simulations. Micromachines 2022, 13, 2181. https://doi.org/10.3390/mi13122181
Huang L, Zhou J, Kong D, Li F. Phononic-Crystal-Based Particle Sieving in Continuous Flow: Numerical Simulations. Micromachines. 2022; 13(12):2181. https://doi.org/10.3390/mi13122181
Chicago/Turabian StyleHuang, Laixin, Juan Zhou, Deqing Kong, and Fei Li. 2022. "Phononic-Crystal-Based Particle Sieving in Continuous Flow: Numerical Simulations" Micromachines 13, no. 12: 2181. https://doi.org/10.3390/mi13122181




