Structural Optimization and Mechanical Simulation of MEMS Thin-Film Getter–Heater Unit
Abstract
:1. Introduction
2. Geometric and Physical Model Construction
2.1. Geometric Model Construction
2.2. Physical Model Construction
2.2.1. Solid Heat Conduction
2.2.2. Solid Thermodynamics
3. Model Simulation and Optimization
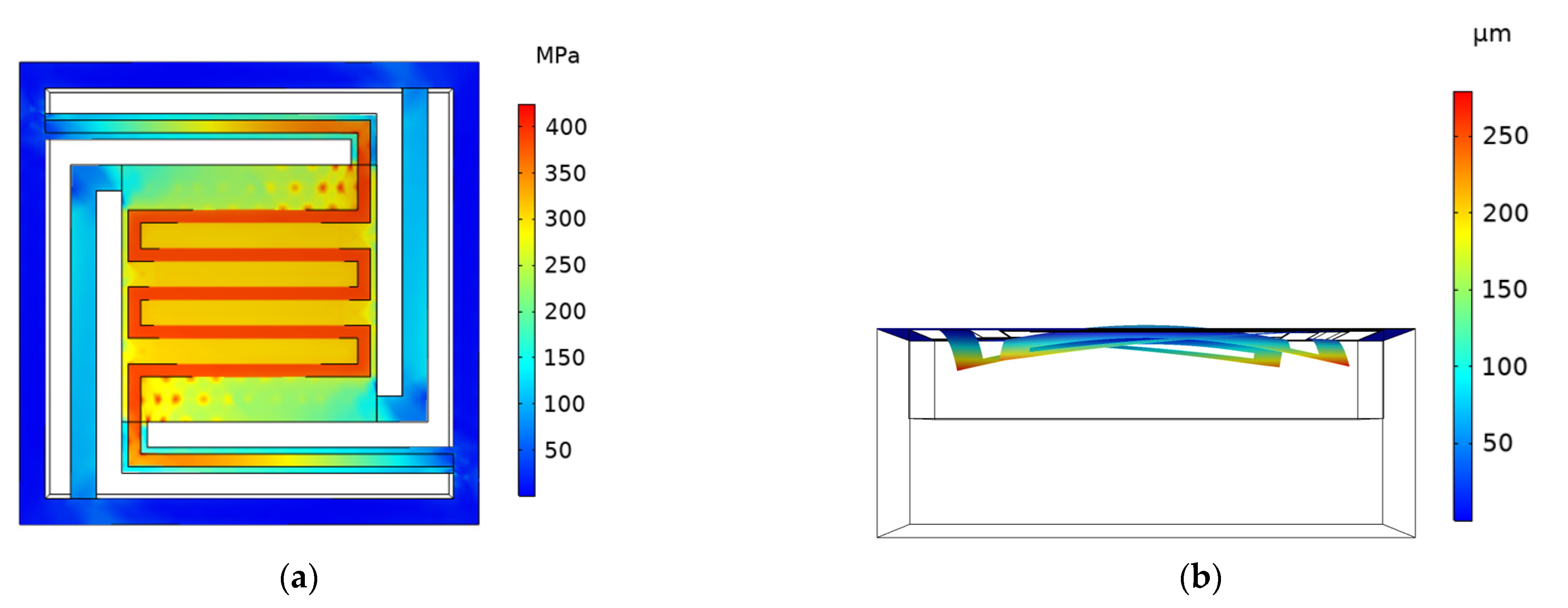
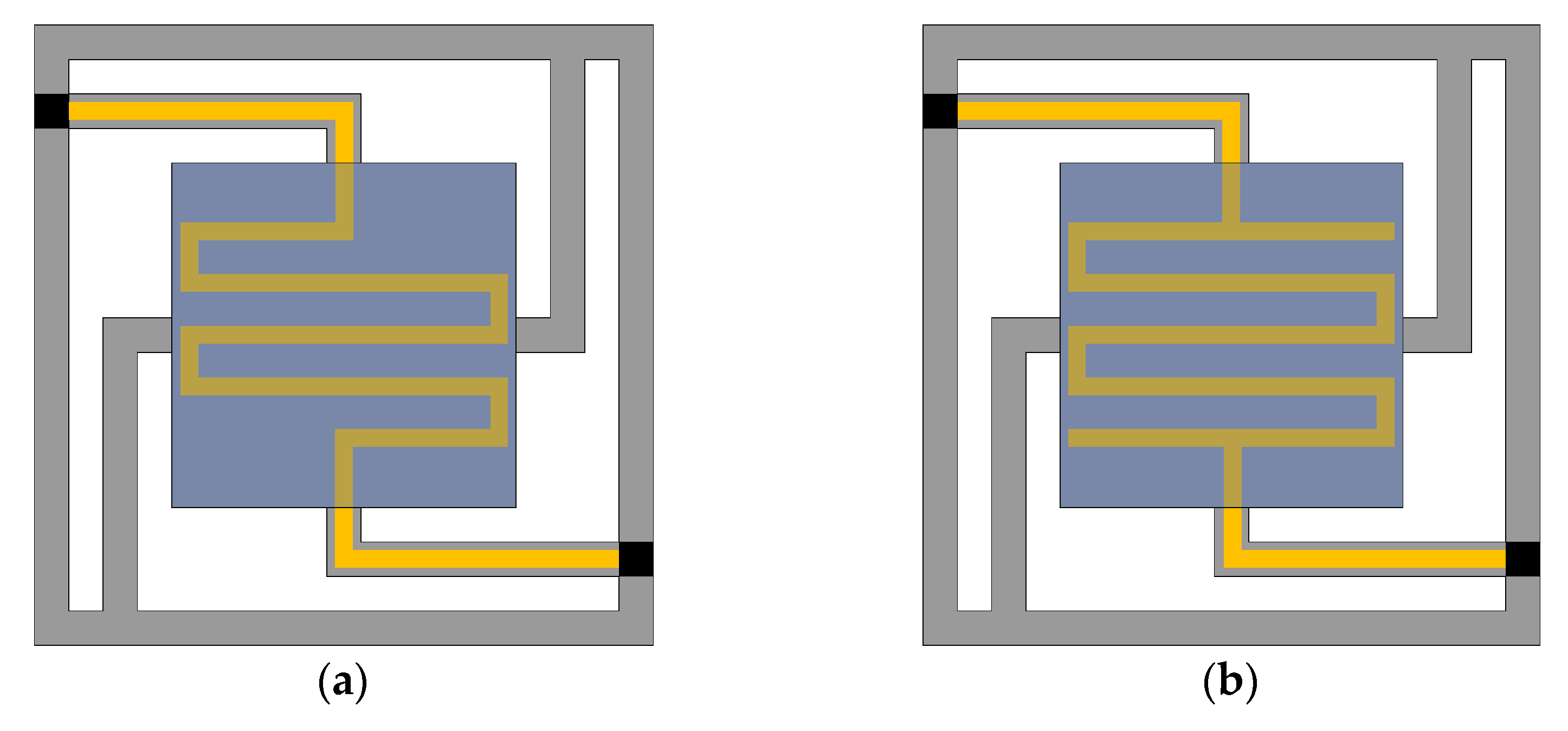
3.1. The Edge–Edge-Located Cantilever Model
3.2. The Corner–Corner-Located Cantilever Model
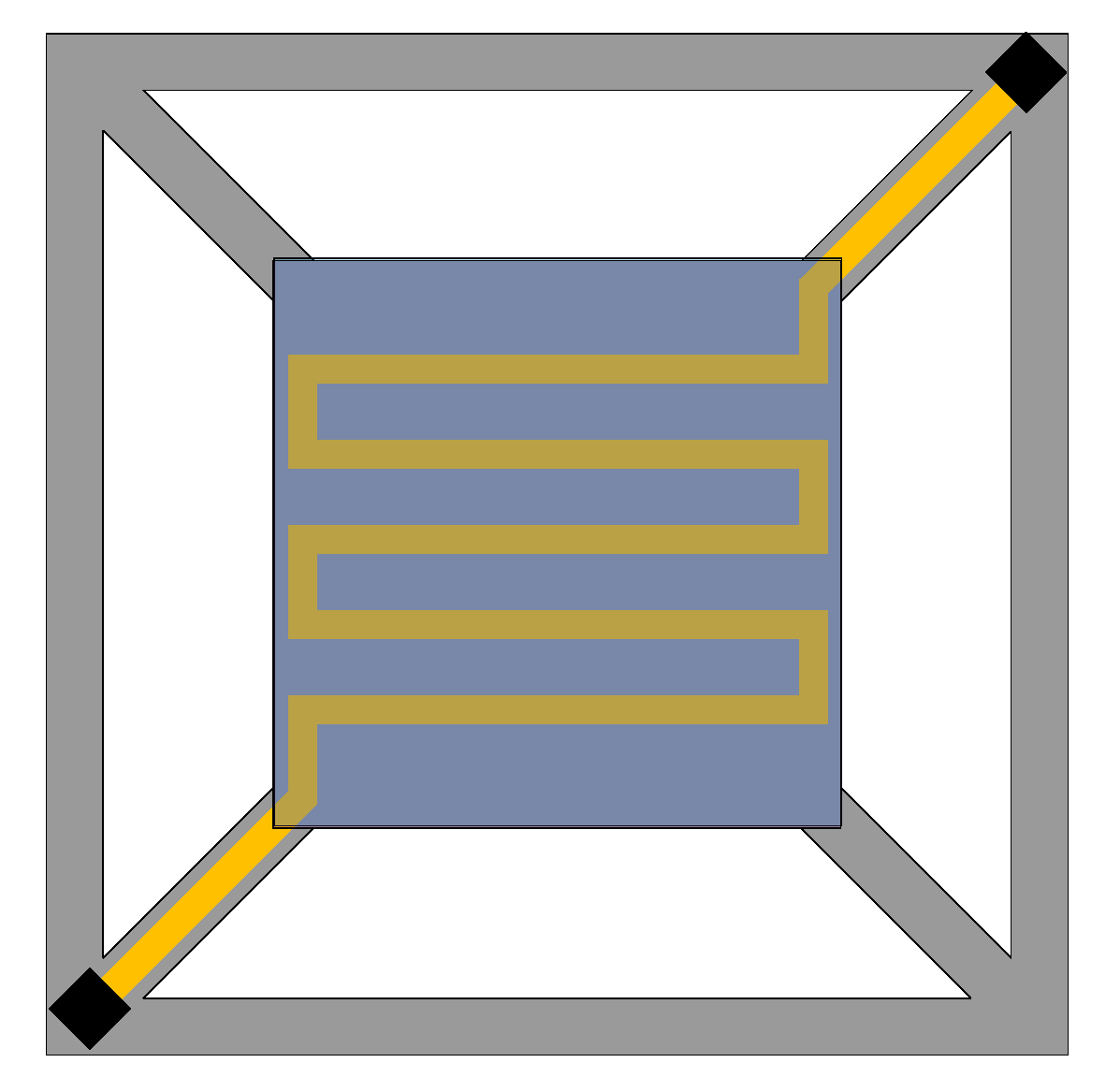
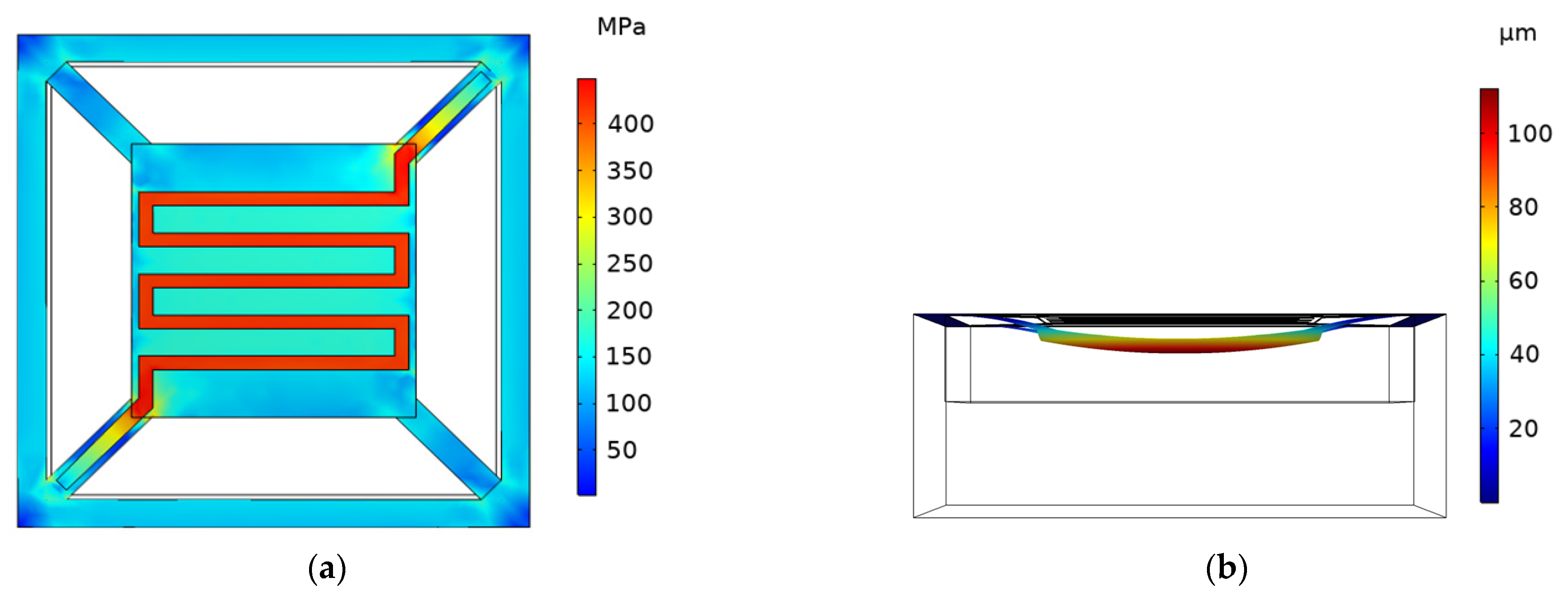
3.3. The Edge–Center-Located Cantilever Model
4. Thermodynamic Simulation and Analysis of II-ECLC Model
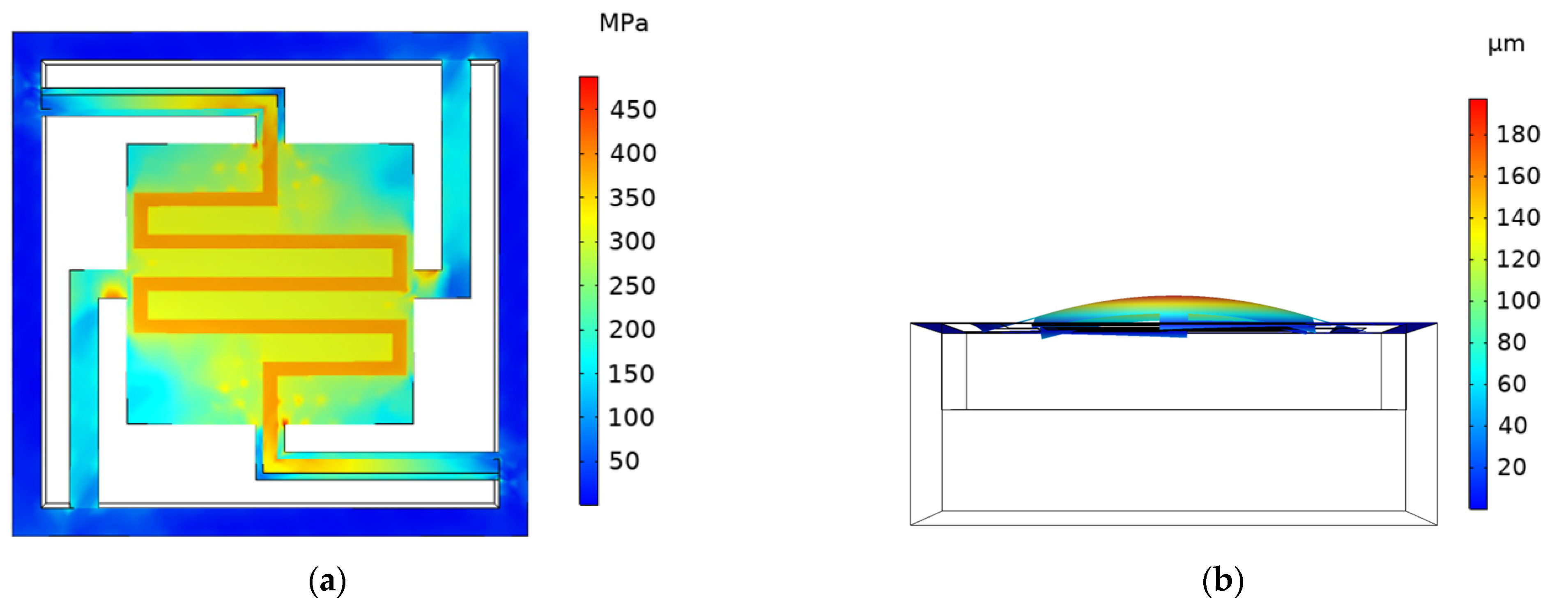
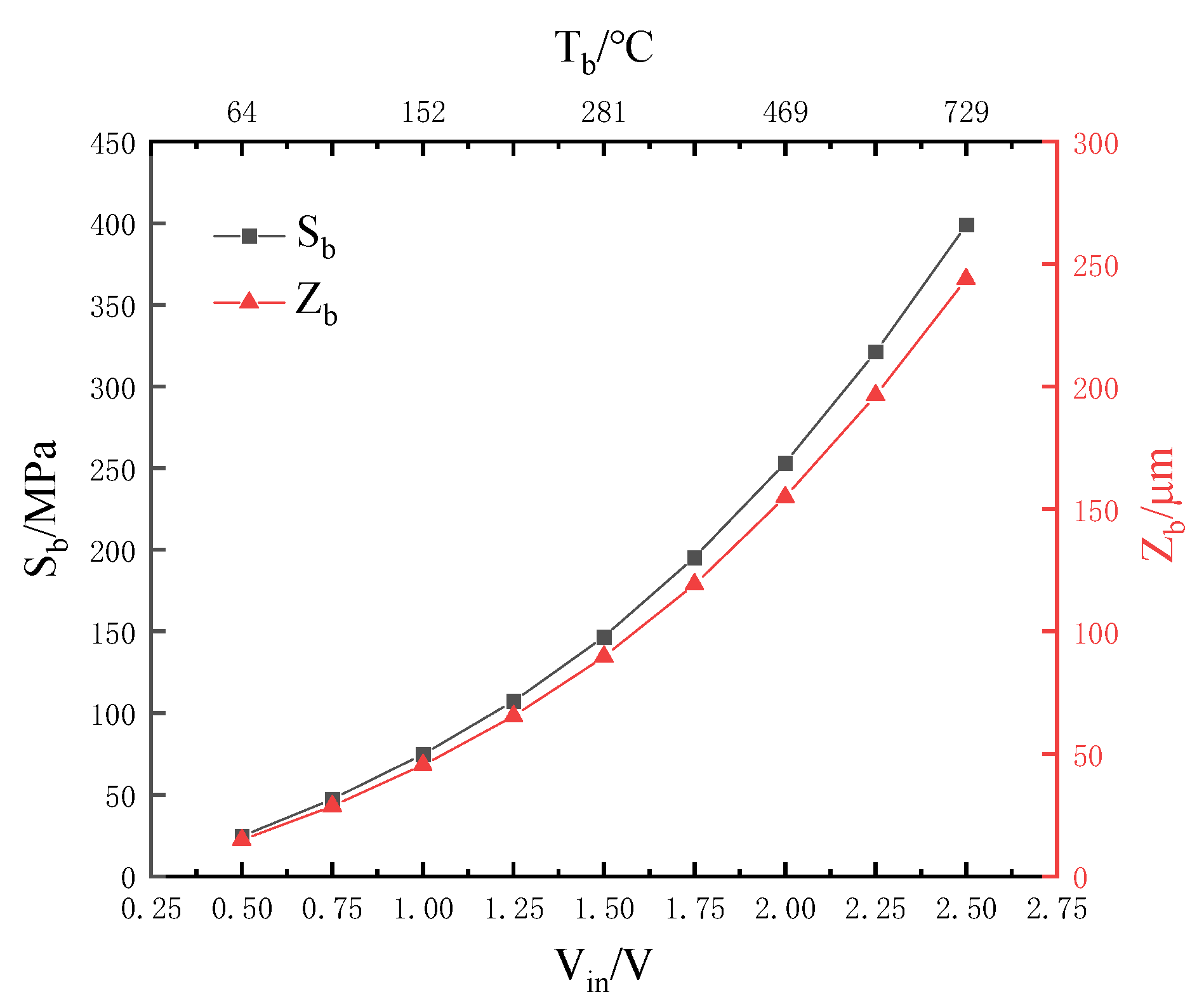
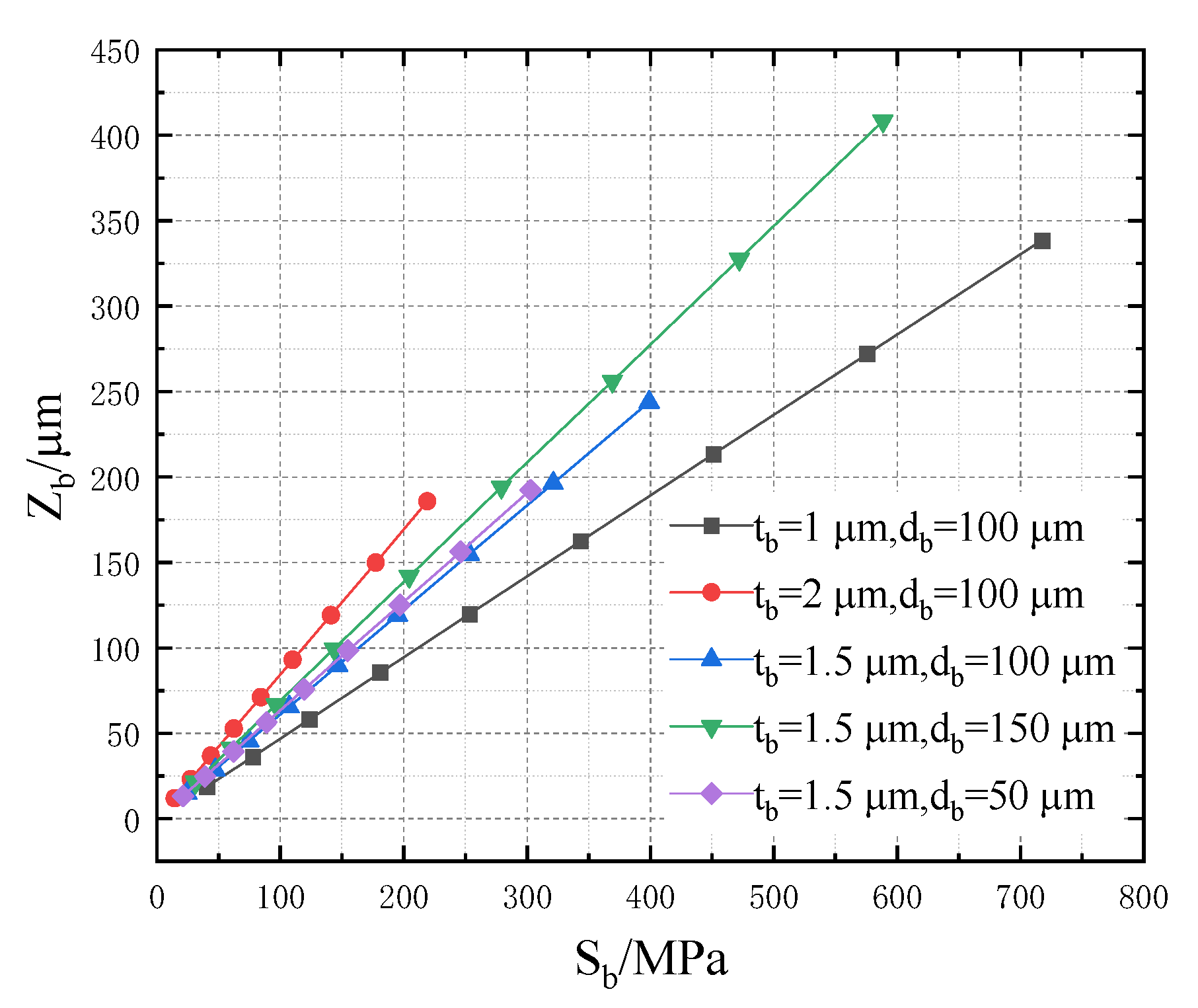
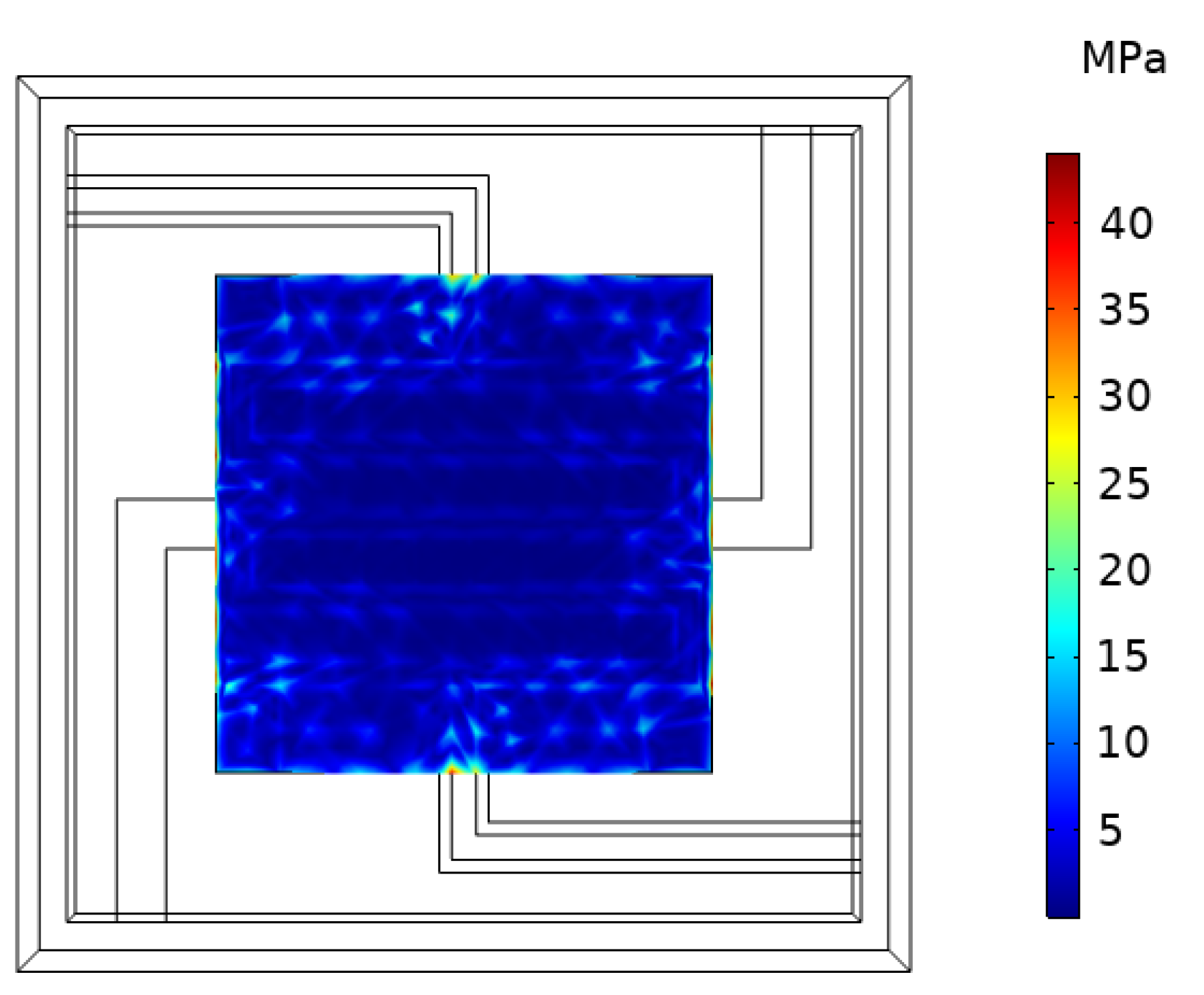
4.1. Simulation of Stress and Deformation Displacement of Cantilever Structure
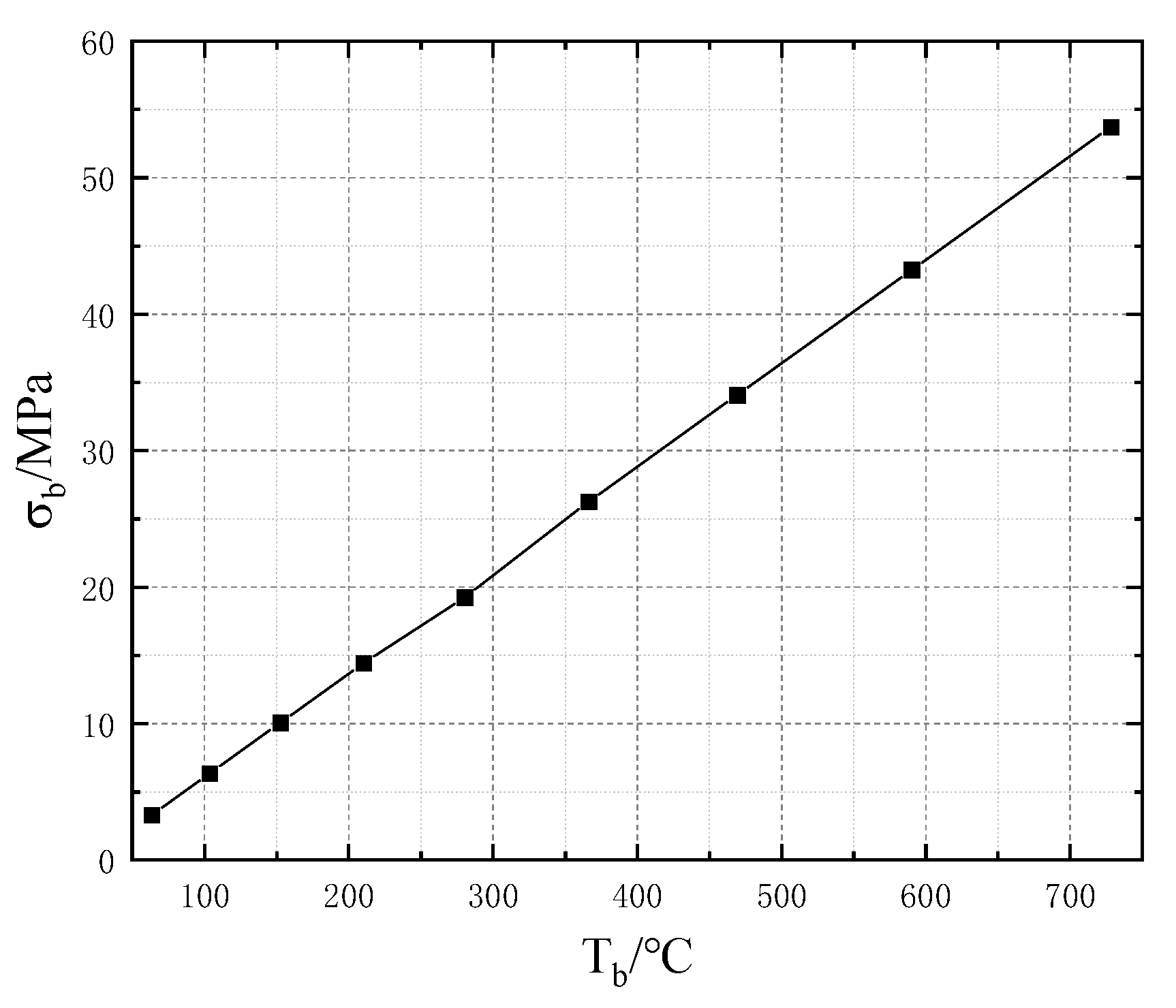
4.2. Simulation and Analysis of Interfacial Stress between Insulating Layer and Getter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shao, P. Microscale Hemispherical Shell Resonating Gyroscopes; Georgia Institute of Technology: Atlanta, GA, USA, 2014. [Google Scholar]
- Sarcan, F. ZnO nanoparticles-based vacuum pressure sensor. Nanotechnology 2020, 31, 435502. [Google Scholar] [CrossRef] [PubMed]
- Manh, C.H.; Hane, K. Vacuum operation of comb-drive micro display mirrors. J. Micromechanics Microengineering 2009, 19, 105018. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, M.; Wei, Q.; Yu, J.; Chen, J.; Chen, D.; Wang, J. Wireless Passive Intracranial Pressure Sensor Based on Vacuum Packaging. IEEE Sens. J. 2020, 20, 11247–11255. [Google Scholar] [CrossRef]
- Shan, R.; Qi, T.; Li, B.; Guo, J.; Yuan, J. Research status and application progress of non-evaporable film getter. J. Funct. Mater. 2018, 49, 05049–05055. [Google Scholar]
- Xiong, Y.; Gu, W.; Wei, X.; Yuan, P.; Qin, G. Activation process and mechanism of ZrVFe getter. Chin. J. Nonferrous Met. 2008, 18, 1358–1363. [Google Scholar]
- Ramesham, R.; Kullberg, R.M. Review of vacuum packaging and maintenance of MEMS and the use of getters therein. J. Micro/Nanolithography MEMS MOEMS 2009, 8, 031307. [Google Scholar]
- Knight, R.R.; Polcawich, R.G. A new approach to vacuum packaging of getter-less and gettered ceramic chip carriers. In Proceedings of the 2017 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27–30 March 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Knight, R.R.; DeVoe, D.D.; Polcawich, R.G.; Pulskamp, J.S.; Power, B.K. micro-Torr vacuum packaging of gettered ceramic chip carriers. In Proceedings of the 2019 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Naples, FL, USA, 1–5 April 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Ge, X.; Wang, Y.; Shao, J.; Wei, W.; Zhang, B.; Wang, S.; Zhang, Y.; Li, W.; Wang, Y. Testing the activation temperature of non-evaporable Ti-Zr-Hf-V getter films by XPS. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 967, 163864. [Google Scholar] [CrossRef]
- Ji, Y.; Feng, L.; Guo, S.; Peng, X.; Chen, S.; Li, W.; Wang, S. A micro-thin-film getter–heater unit for high vacuum capsulation of MEMS devices. AIP Adv. 2022, 12, 015105. [Google Scholar] [CrossRef]
- Elies, S. Performance analysis of commercial accelerometers: A parameter review. Sens. Transducers 2015, 193, 179. [Google Scholar]
- Völklein, F.; Grau, M.; Meier, A.; Hemer, G.; Breuer, L.; Woias, P. Optimized MEMS Pirani sensor with increased pressure measurement sensitivity in the fine and high vacuum regime. J. Vac. Sci. Technol. A 2013, 31, 061604. [Google Scholar] [CrossRef]
- Huang, K. Tensor Analysis, 3rd ed.; Tsinghua University Press: Beijing, China, 2020. [Google Scholar]
- Kshirsagar, A.; Nyaupane, P.; Bodas, D.; Duttagupta, S.; Gangal, S. Deposition and characterization of low temperature silicon nitride films deposited by inductively coupled plasma CVD. Appl. Surf. Sci. 2011, 257, 5052–5058. [Google Scholar] [CrossRef]
- Kim, Y.-H. Adhesion of titanium thin film to oxide substrates. J. Vac. Sci. Technol. A Vac. Surf. Films 1987, 5, 2890–2893. [Google Scholar] [CrossRef]
- Buchwalter, L. Chromium and tantalum adhesion to plasma-deposited silicon dioxide and silicon nitride. J. Adhes. Sci. Technol. 1995, 9, 97–116. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, P. Calculation and simulation of thermal stress of multilayer films. Chin. J. Appl. Mech. 2020, 37, 743–749. [Google Scholar]
- An, B.; Zhang, T.; Cui, K. A Study of Determination of Solid-Solid Interfacial Energies by Zero Creep Measurements. Mater. Rev. 2002, 4, 19–21. [Google Scholar]
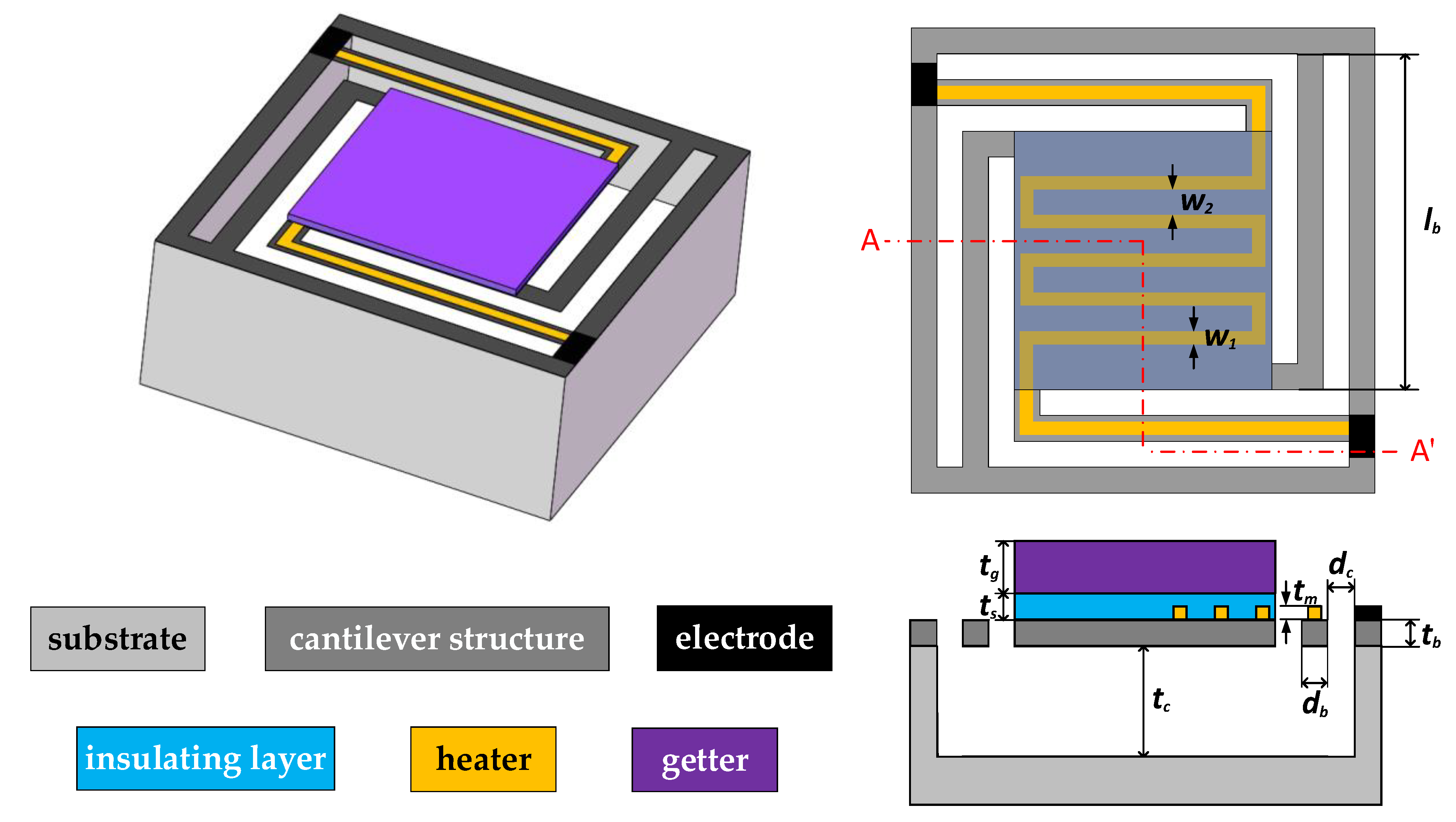


| Structure | Material | Dimensions [μm] | Thermal Conductivity [W/m·K] | Thermal Expansion Coefficient [1/K] |
|---|---|---|---|---|
| Substrate | Silicon | 1800 × 1800 × 700 | 131 | 2.33 × 10−6 |
| Cavity | … | 300 × 50 (tc × dc) | 0.01 | … |
| Cantilever structure | Silicon nitride | 1.5 × 50 × 1150 (tb × db × lb) | 20 | 2.3 × 10−6 |
| Heater | Titanium | 0.2 × 50 × 100 (tm × w1 × w2) | 21.9 | 8.6 × 10−6 |
| Insulating layer | Silicon nitride | 0.4 (ts) | 20 | 2.3 × 10−6 |
| Getter | Titanium-based alloy | 3 (tg) | 21.9 | 8.6 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Ji, Y.; Chen, S.; Guo, S.; Feng, L.; Xu, Y.; Wang, S. Structural Optimization and Mechanical Simulation of MEMS Thin-Film Getter–Heater Unit. Micromachines 2022, 13, 2252. https://doi.org/10.3390/mi13122252
Peng X, Ji Y, Chen S, Guo S, Feng L, Xu Y, Wang S. Structural Optimization and Mechanical Simulation of MEMS Thin-Film Getter–Heater Unit. Micromachines. 2022; 13(12):2252. https://doi.org/10.3390/mi13122252
Chicago/Turabian StylePeng, Xinlin, Yucheng Ji, Shuo Chen, Song Guo, Liuhaodong Feng, Yang Xu, and Shinan Wang. 2022. "Structural Optimization and Mechanical Simulation of MEMS Thin-Film Getter–Heater Unit" Micromachines 13, no. 12: 2252. https://doi.org/10.3390/mi13122252
APA StylePeng, X., Ji, Y., Chen, S., Guo, S., Feng, L., Xu, Y., & Wang, S. (2022). Structural Optimization and Mechanical Simulation of MEMS Thin-Film Getter–Heater Unit. Micromachines, 13(12), 2252. https://doi.org/10.3390/mi13122252






