Extraction of Interface-Trap Densities of the Stacked Bonding Structure in 3D Integration Using High-Frequency Capacitance-Voltage Technique
Abstract
:1. Introduction
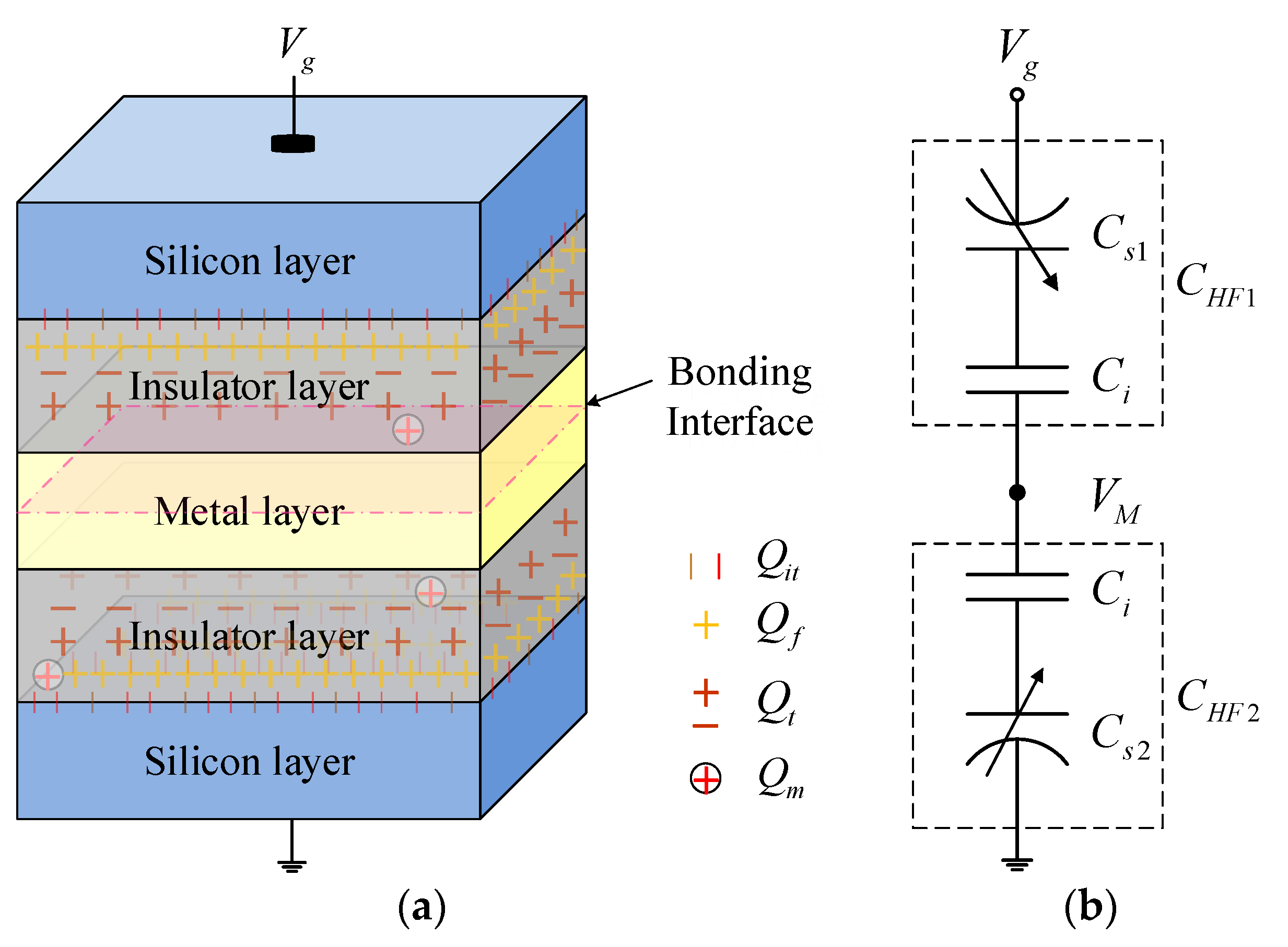
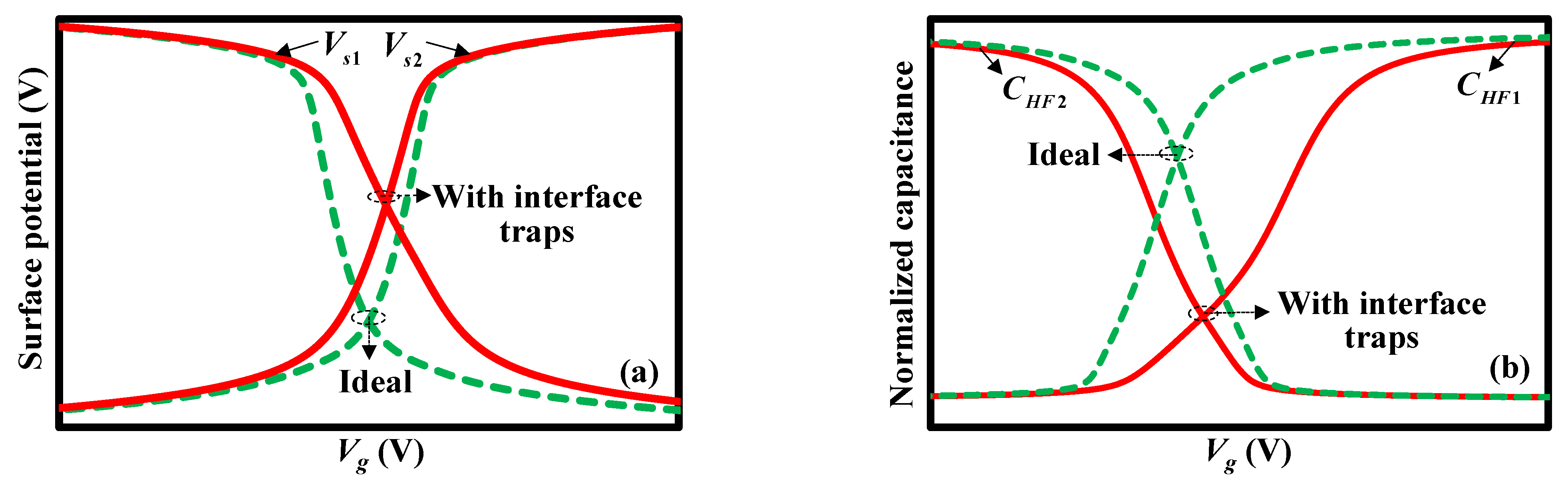
2. Theoretical Models
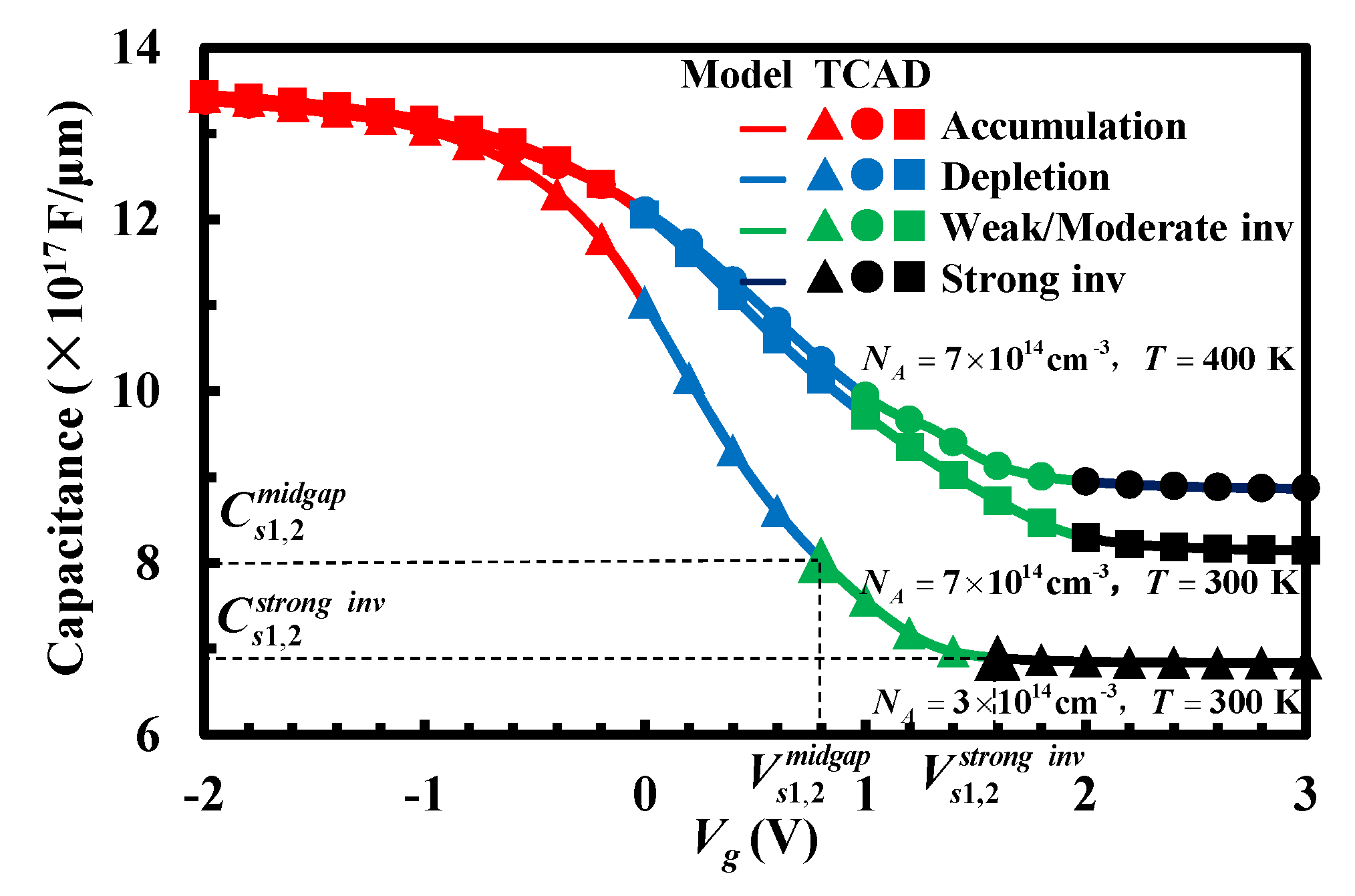
2.1. Accurate High-Frequency Capacitance–Voltage Model
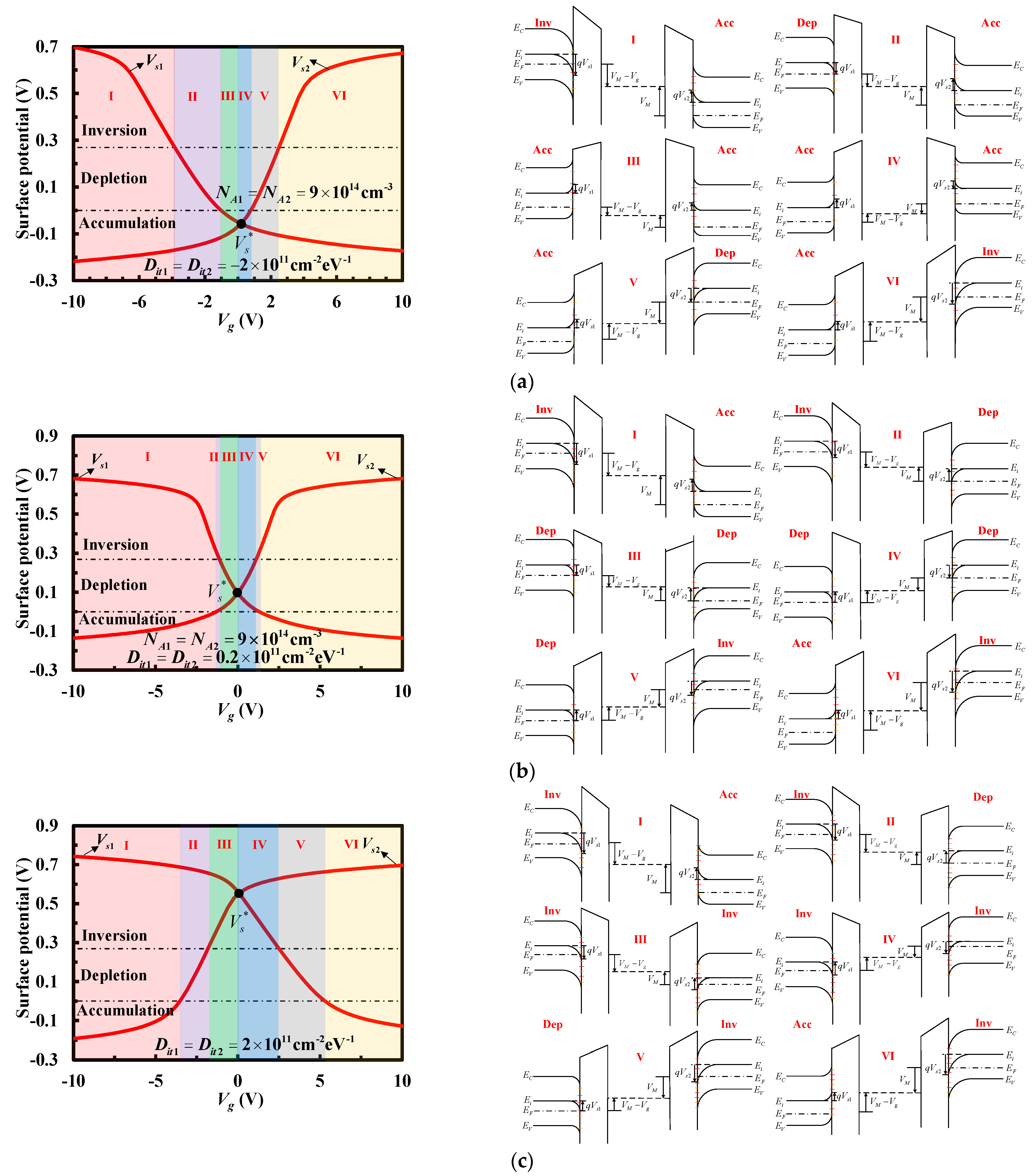
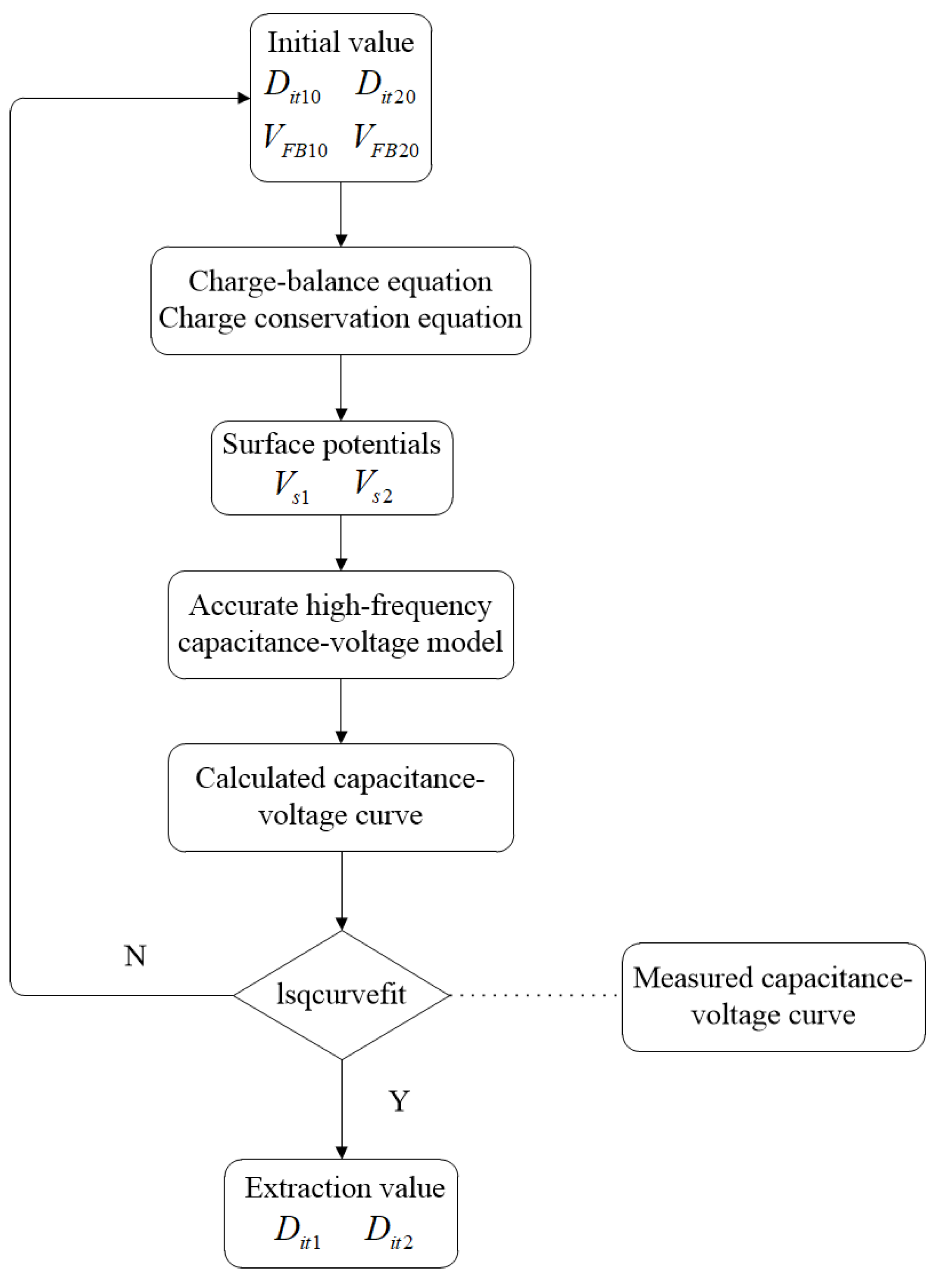
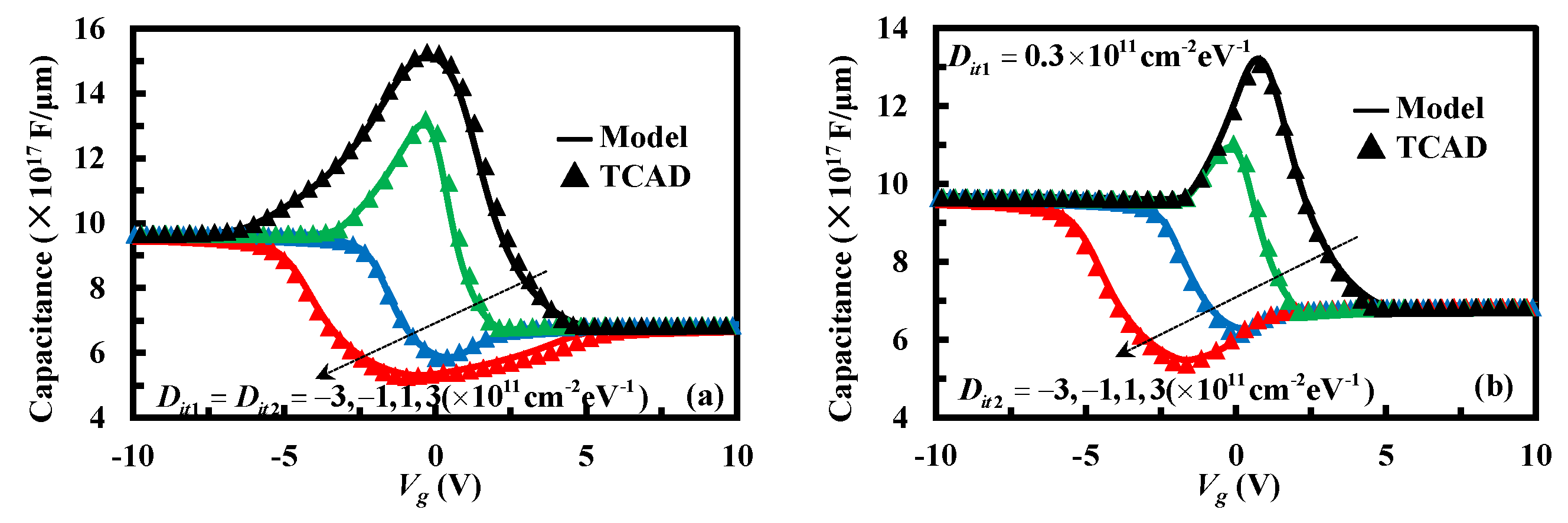
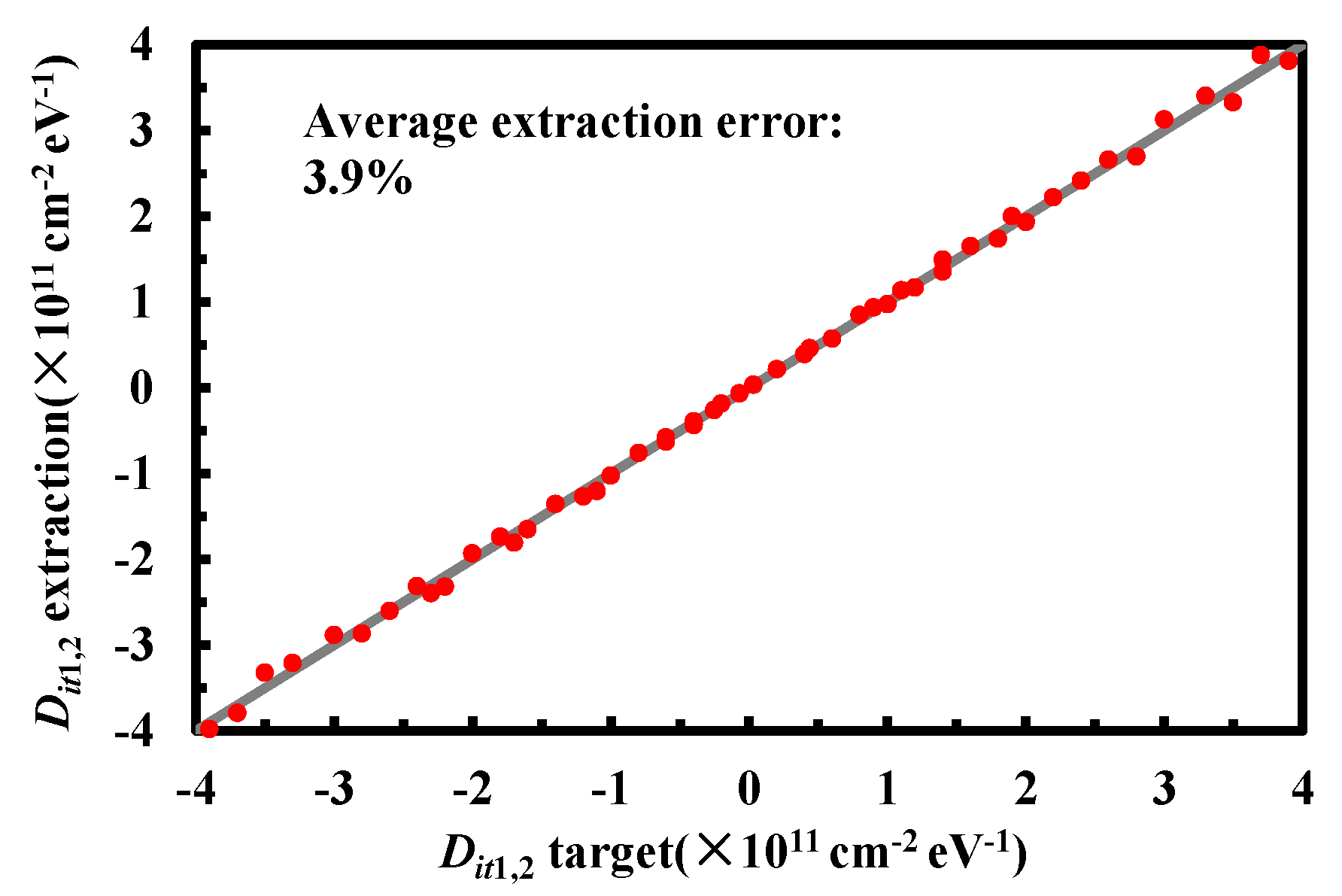
2.2. Dit Extraction
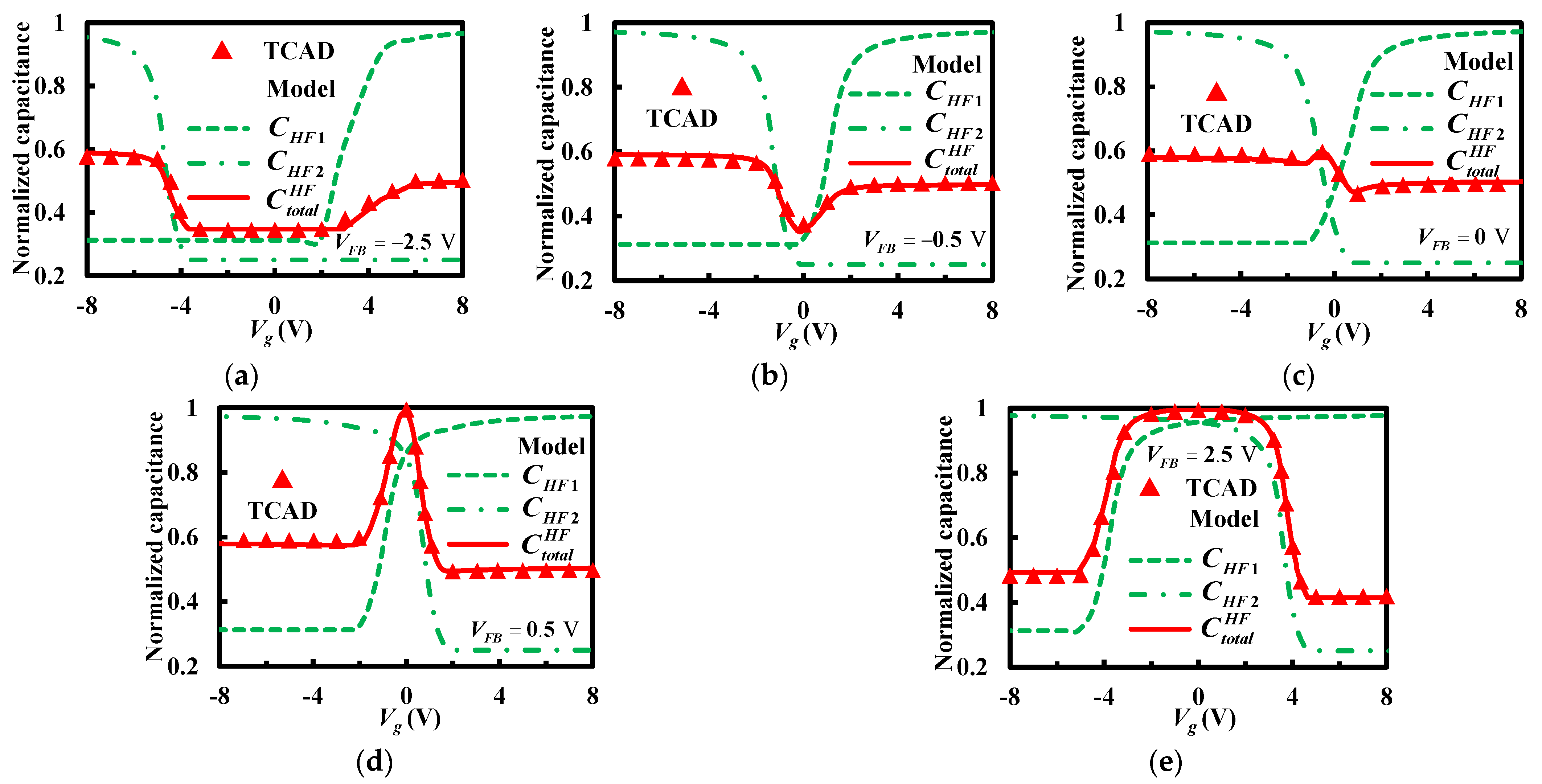
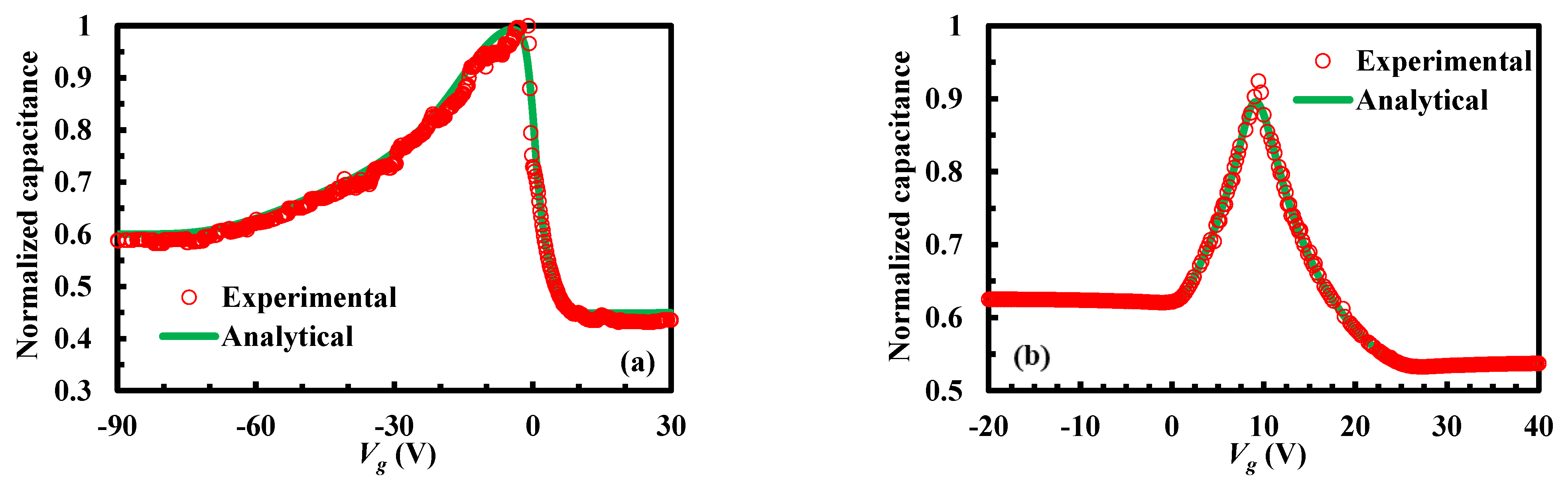
3. Results and Discussion
4. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, Z.Q.; Ding, Y.T.; Xiao, L.; Yang, B.Y.; Chen, Z.M. Study on atomic migration of copper through-silicon-vias with Bosch scallops. Microelectron. Reliab. 2021, 123, 114178. [Google Scholar] [CrossRef]
- Cai, T.; Zhang, J.Q.; Wang, Q. Experimental and computational investigation of low temperature CuSn solid-state-diffusion bonding for 3D integration. Microelectron. Eng. 2021, 236, 111479. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Z.Q.; Chen, S.W.; Wang, Y.D.; Long, W.M.; Guo, Y.H.; Wang, S.Q.; Ye, G.; Liu, W.Y. Materials, processing and reliability of low temperature bonding in 3D chip stacking. J. Alloys Compd. 2018, 750, 980–995. [Google Scholar] [CrossRef]
- Wang, C.Q.; Zhang, M.; Ming, X.F.; Ma, S.Y.; Yu, D.Q. Development of three-dimensional wafer level chip scale packaging using via last TSV and UV laser releasable temporary bonding technologies. Microsyst. Technol. 2021, 27, 4121–4125. [Google Scholar] [CrossRef]
- Jangam, S.; Iyer, S.S. Silicon-Interconnect fabric for fine-pitch (≤10 μm) heterogeneous integration. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 727–738. [Google Scholar] [CrossRef]
- Tofteberg, H.R.; Schjølberg-Henriksen, K.; Fasting, E.J.; Moen, A.S.; Taklo, M.M.V.; Poppe, E.U.; Simensen, C.J. Wafer-level Au-Au bonding in the 350–450℃ temperature range. J. Micromech. Microeng. 2014, 24, 084002. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.S.; Chang, Y.J.; Chen, K.N. Wafer-level Cu-Cu bonding technology. Microelectron. Reliab. 2012, 52, 312–320. [Google Scholar] [CrossRef]
- Liu, D.; Chen, P.C.; Liu, Y.W.; Hu, H.W.; Chen, K.N. Low-temperature (70°C) Cu-to-Cu direct bonding by capping metal layers. IEEE Electron Device Lett. 2021, 42, 1524–1527. [Google Scholar] [CrossRef]
- Malik, N.; Schjølberg-Henriksen, K.; Poppe, E.U.; Taklo, M.M.V.; Finstad, T.G. Impact of SiO2 on Al-Al thermocompression wafer bonding. J. Micromech. Microeng. 2015, 25, 035025. [Google Scholar] [CrossRef]
- Wangkheirakpam, V.D.; Bhowmick, B.; Pukhrambam, P.D. Noise behavior of vertical tunnel FETs under the influence of interface trap states. Microelectron. J. 2021, 114, 105124. [Google Scholar] [CrossRef]
- Velayudhan, V.; Gamiz, F.; Martín-Martínez, J.; Rodriguez, R.; Nafria, M.; Aymerich, X. Influence of the interface trap location on the performance and variability of ultra-scaled MOSFETs. Microelectron. Reliab. 2013, 53, 1243–1246. [Google Scholar] [CrossRef]
- Sharma, S.; Shukla, R.; Tripathy, M.R. Analog/RF performance and effect of interface trap charges in dielectric engineered gate all around junctionless MOSFET with ZrTiO4 as gate dielectric. Indian J. Pure Appl. Phys. 2018, 56, 869–874. [Google Scholar]
- Deen, D.A.; Chanplain, J.G. High frequency capacitance-voltage technique for the extraction of interface trap density of the heterojunction capacitor:Terman’s method revised. Appl. Phys. Lett. 2011, 99, 053501. [Google Scholar] [CrossRef]
- Takenaka, M.; Ozawa, Y.; Han, J.; Takagi, S. Quantitative evaluation of energy distribution of interface trap density at MoS2 MOS interfaces by the Terman method. IEEE Int. Electron Devices Meet. 2016, 053501. [Google Scholar] [CrossRef]
- Hyunsoo, K.; Seo, Y.; Shin, H. Extraction of average interface trap density using capacitance-voltage characteristic at SiGe p-FinFET and verification using Terman’s method. J. Inst. Electron. Inf. Eng. 2015, 52, 56–61. [Google Scholar]
- Engel-Herbert, R.; Hwang, Y.; Stemmer, S. Quantification of trap densities at dielectric/III–V semiconductor interfaces. Appl. Phys. Lett. 2010, 97, 062905. [Google Scholar] [CrossRef] [Green Version]
- Kuma, V.; Agawal, S.K. Physics of Semiconductor Devices, 3rd ed.; Physics Today: College Park, MD, USA, 2003. [Google Scholar]
- Wangkheirakpam, V.D.; Bhowmick, B.; Pukhrambam, P.D. Investigation of temperature variation and interface trap charges in dual MOSCAP TFET. Silicon 2020, 13, 2971–2978. [Google Scholar] [CrossRef]
- Neamen, D.A. An Introduction to Semiconductor Devices; McGraw-Hill Education: New York, USA, 2006. [Google Scholar]
- Li, M.; Guo, Y.F.; Chen, J.; Zhang, Y.F.; Gao, Z.Y.; Jiang, Y.J. A low frequency capacitance-voltage method for extracting fixed charge densities of symmetric stacked bonding structure in 3D integration. In Proceedings of the International Conference on Intelligent Materials and Mechatronics and International Conference on Solar Energy Materials and Energy Engineering, Hong Kong, China, 15–16 October 2015. [Google Scholar]
- Coleman, T.F.; Zhang, Y. Optimization Toolbox for Use With MATLAB; The MathWorks, Inc.: Natick, MA, USA, 2021. [Google Scholar]
- Sentaurus Device User Guide Version: H-2016.03; Synopsys: Mountain View, CA, USA, 2016.



| Symbols | Quantity | Value |
|---|---|---|
| ti | thickness of the insulator layer | 200 nm |
| tm | thickness of the metal layer | 80 nm |
| NA | doping concentration of the silicon layer | 1.5 × 1014–9 × 1014 cm−3 |
| T | absolute temperature | 300–400 K |
| VFB | flat-band voltage | −2.5–2.5 V |
| φm | work function of the metal | 4.65 eV |
| Qf | fixed charge density in the insulator layer | 1010 cm−2 |
| Dit | interface-trapped charge density (simulation) | −4 × 1011–4 × 1011 cm−2 eV−1 |
| εs | permittivity of silicon | 11.9 |
| εi | permittivity of insulator | 3.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Guo, Y.; Yao, J.; Zhang, J.; Liu, F.; Tang, W. Extraction of Interface-Trap Densities of the Stacked Bonding Structure in 3D Integration Using High-Frequency Capacitance-Voltage Technique. Micromachines 2022, 13, 262. https://doi.org/10.3390/mi13020262
Li M, Guo Y, Yao J, Zhang J, Liu F, Tang W. Extraction of Interface-Trap Densities of the Stacked Bonding Structure in 3D Integration Using High-Frequency Capacitance-Voltage Technique. Micromachines. 2022; 13(2):262. https://doi.org/10.3390/mi13020262
Chicago/Turabian StyleLi, Man, Yufeng Guo, Jiafei Yao, Jun Zhang, Fanyu Liu, and Weihua Tang. 2022. "Extraction of Interface-Trap Densities of the Stacked Bonding Structure in 3D Integration Using High-Frequency Capacitance-Voltage Technique" Micromachines 13, no. 2: 262. https://doi.org/10.3390/mi13020262
APA StyleLi, M., Guo, Y., Yao, J., Zhang, J., Liu, F., & Tang, W. (2022). Extraction of Interface-Trap Densities of the Stacked Bonding Structure in 3D Integration Using High-Frequency Capacitance-Voltage Technique. Micromachines, 13(2), 262. https://doi.org/10.3390/mi13020262








