Investigation of the Contact Characteristics of Silicon–Gold in an Anodic Bonding Structure
Abstract
:1. Introduction
2. Contact Characteristics Analysis
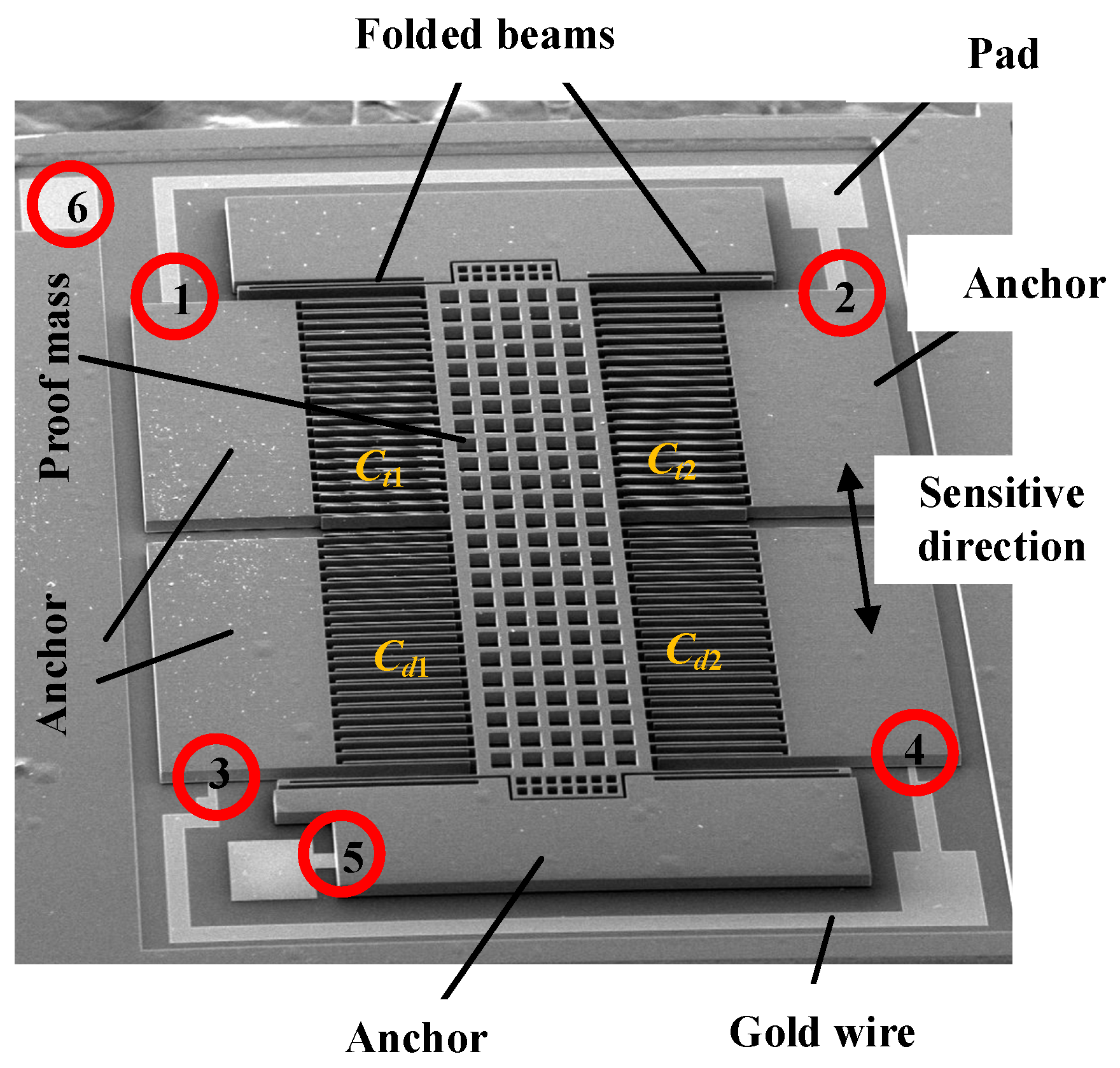
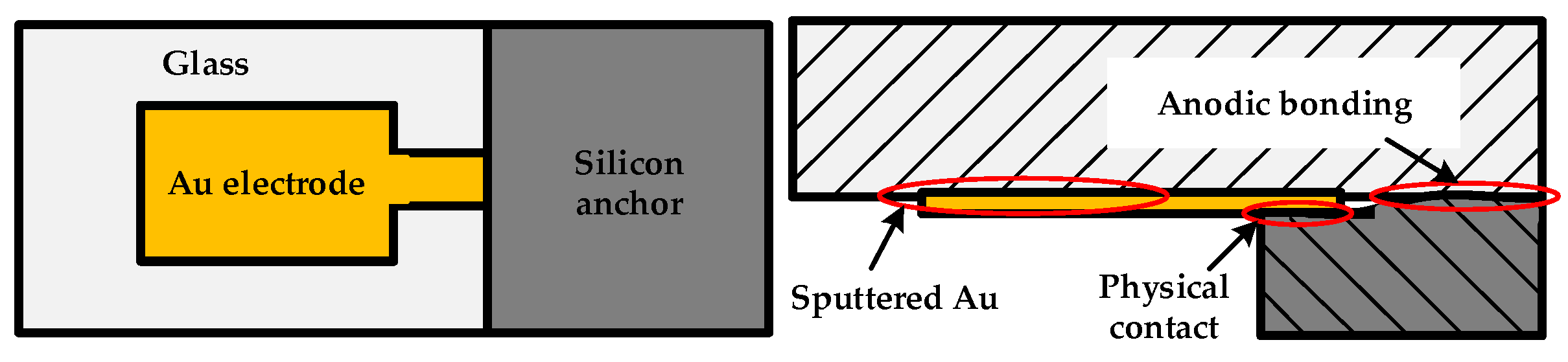
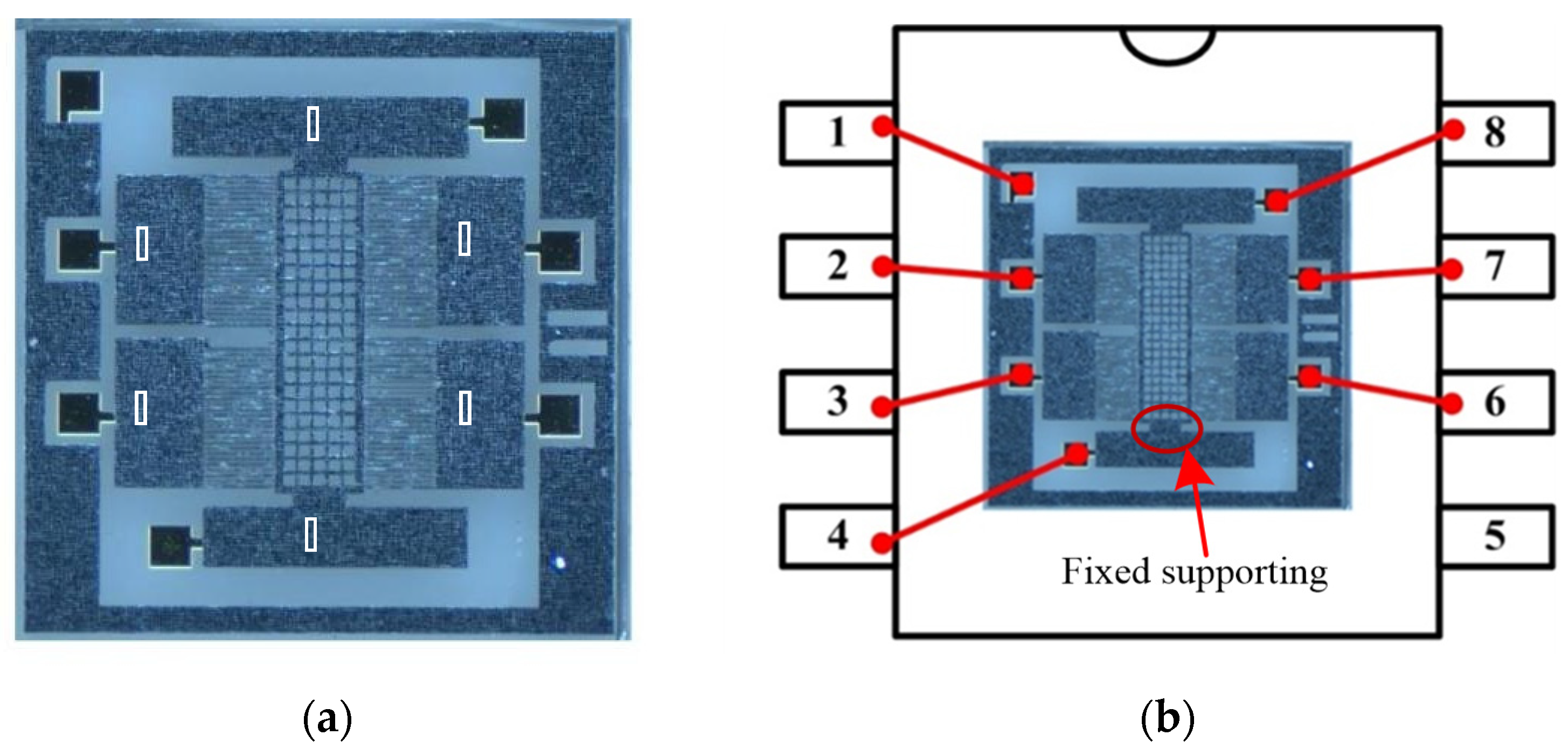
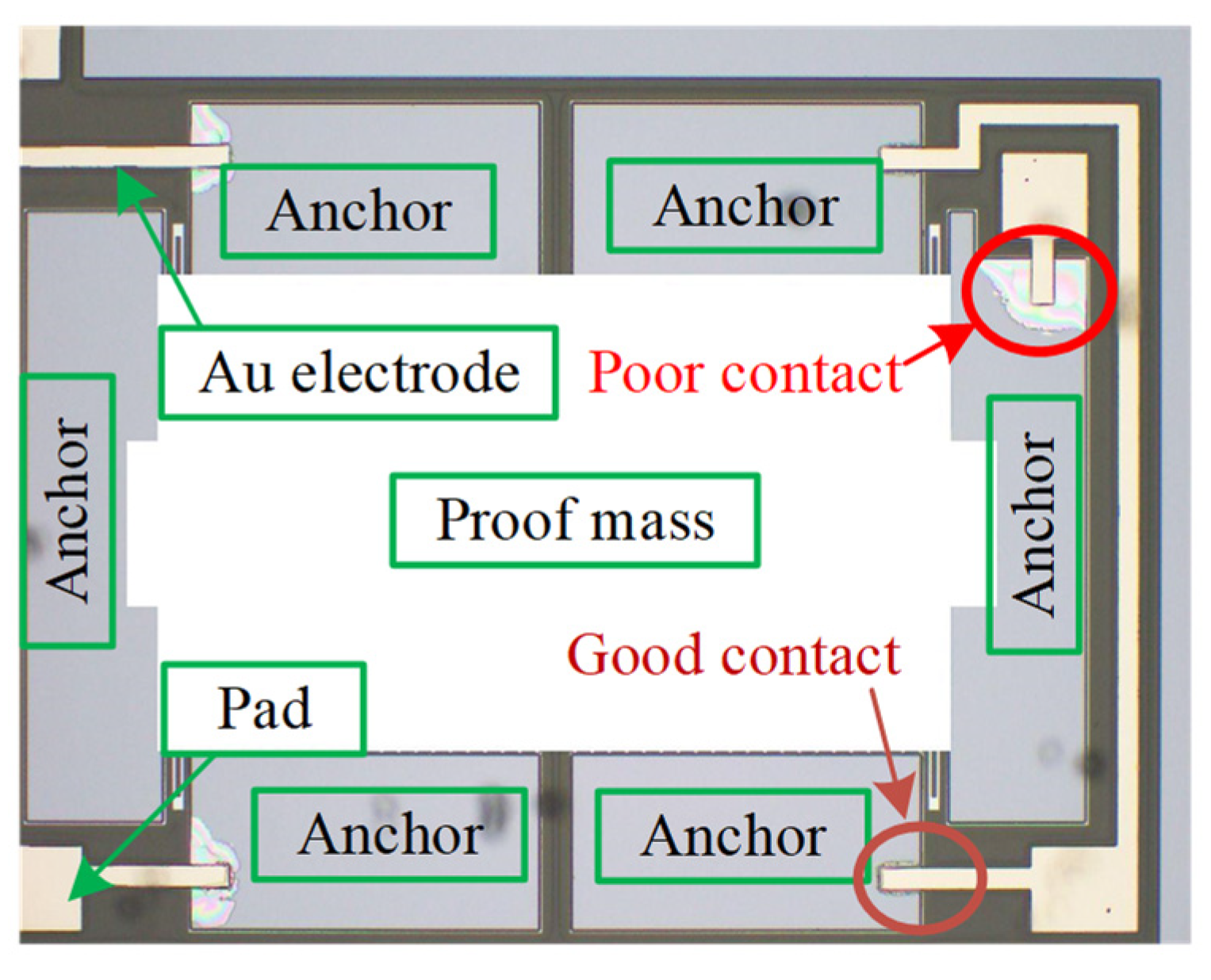
2.1. Bonding Structure
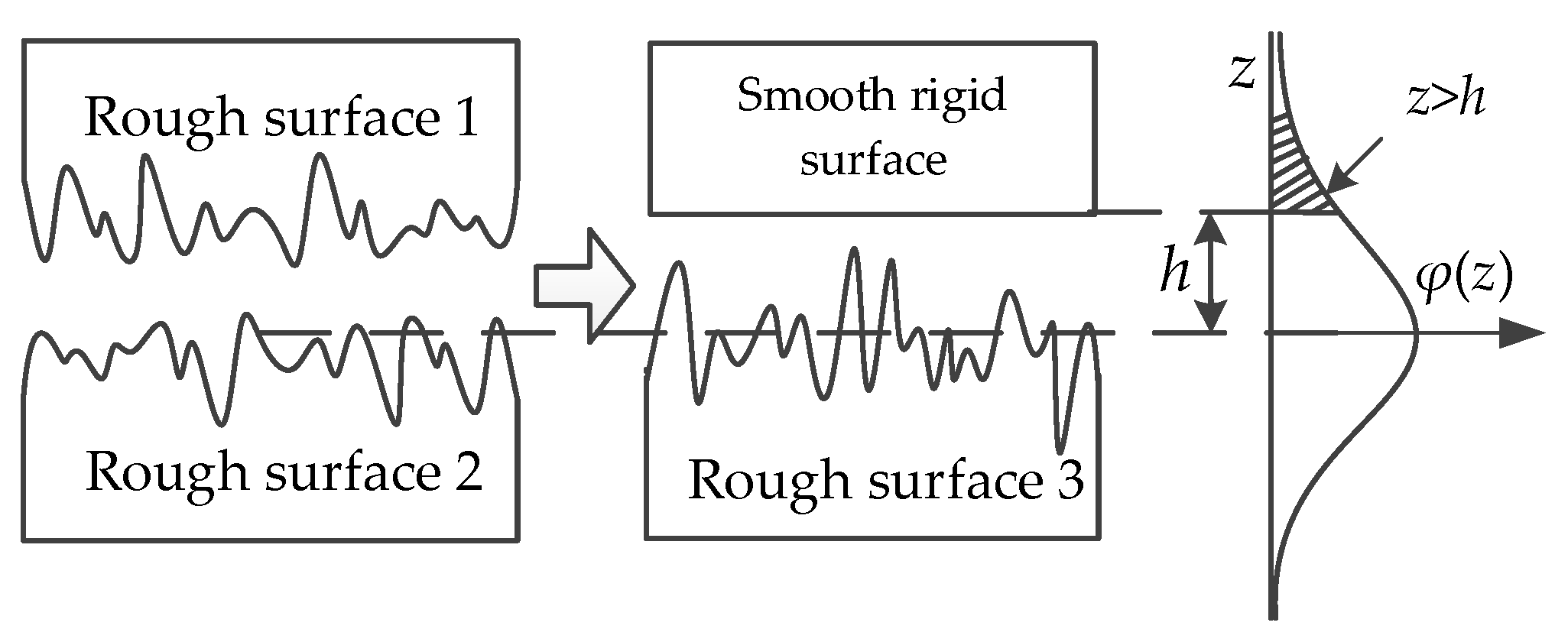
2.2. Model of Contacting Area
2.3. Model of Contacting Resistance
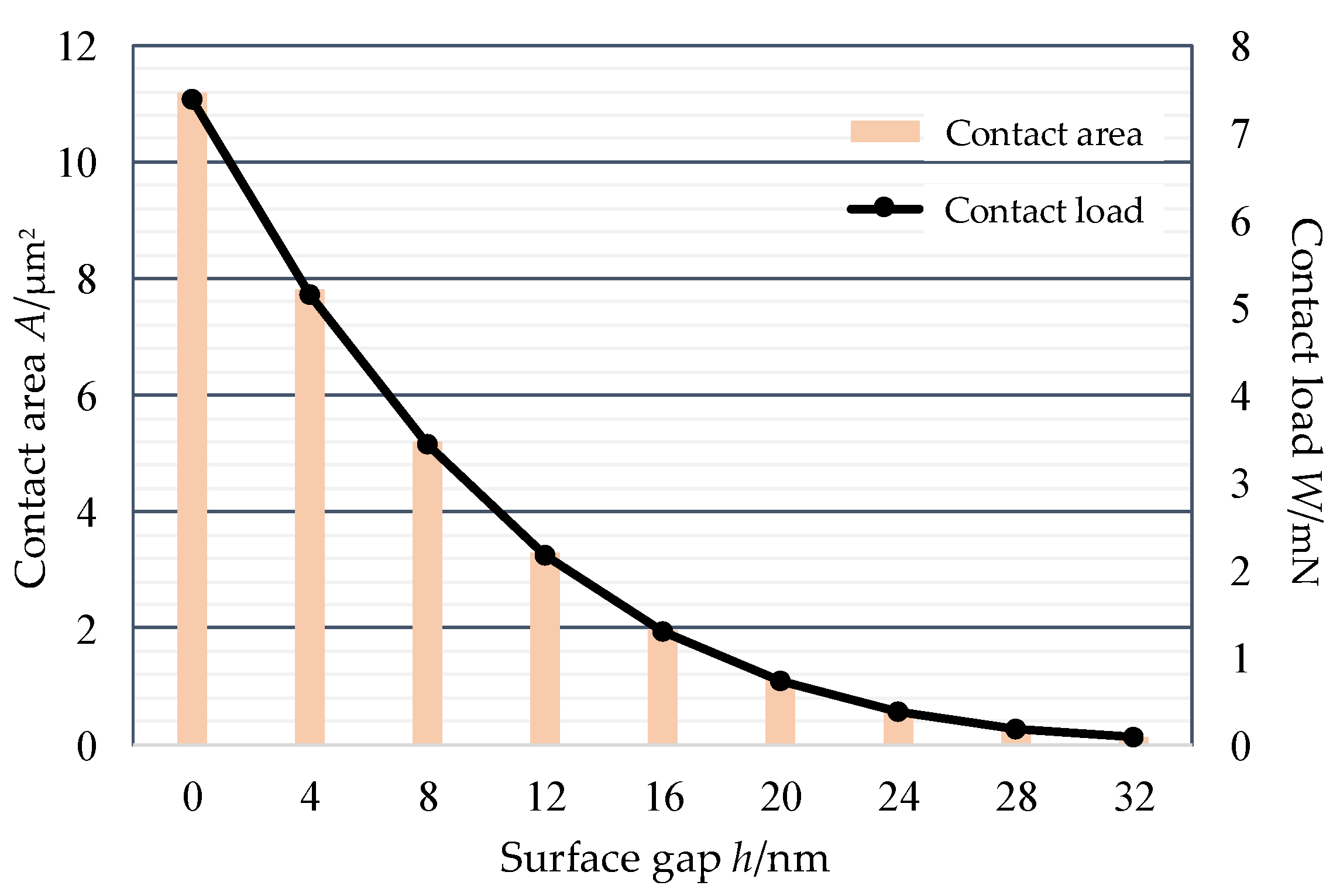
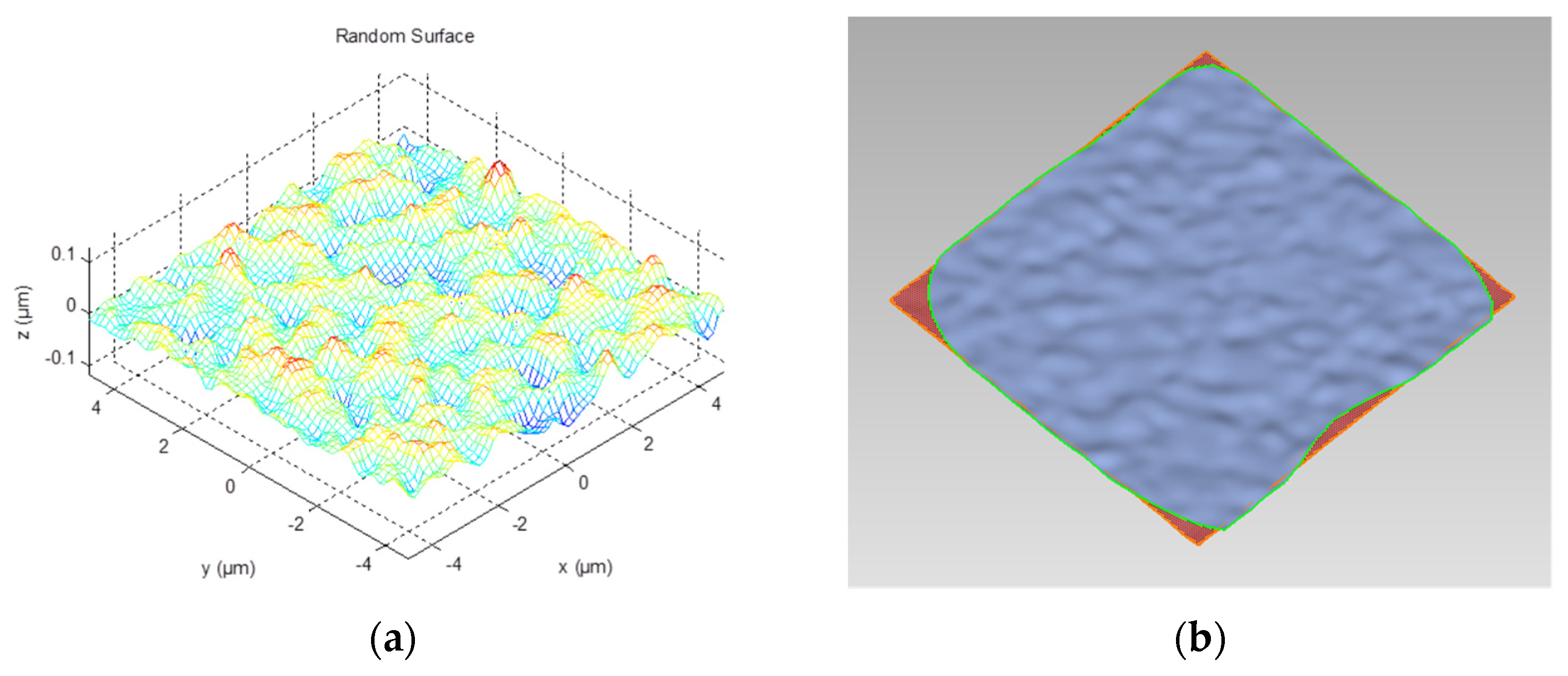
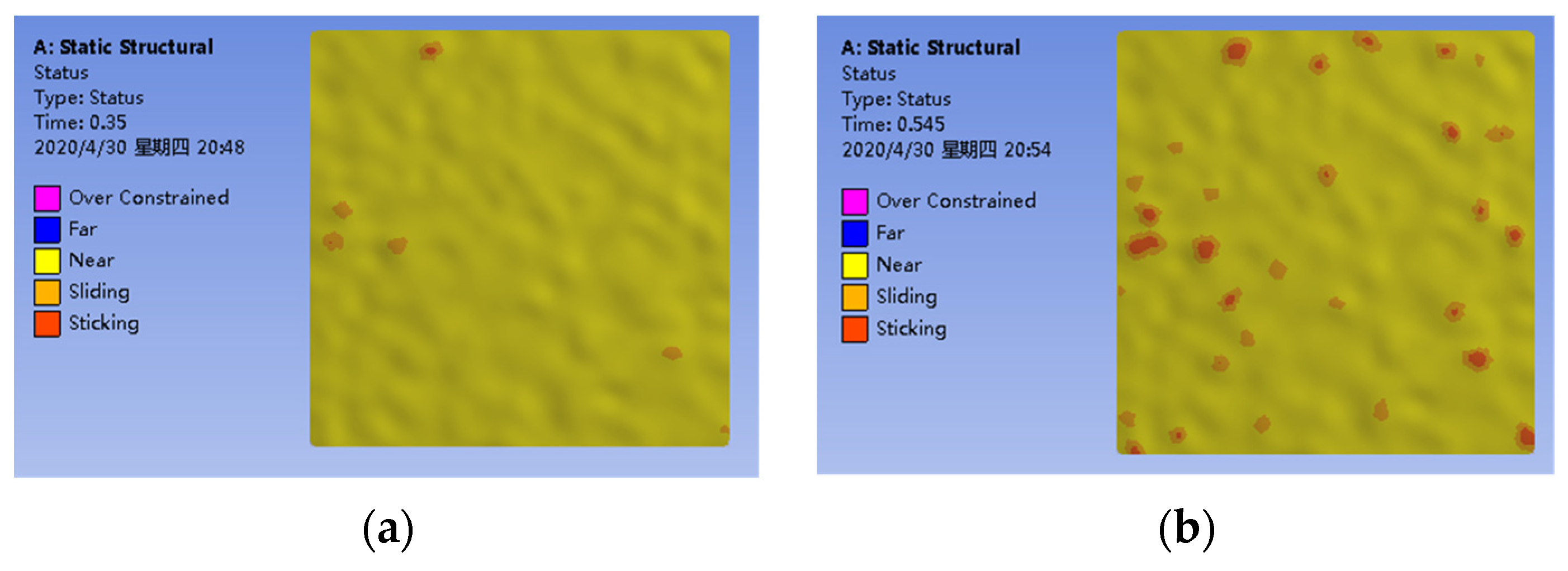
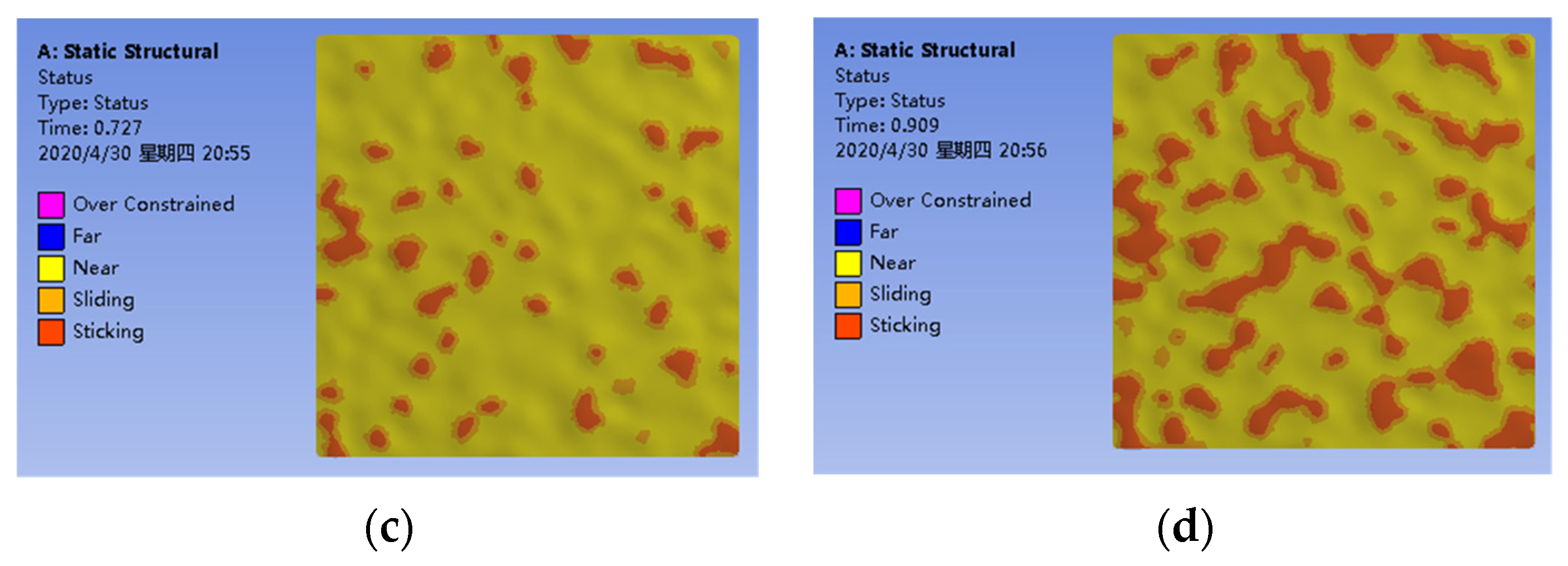
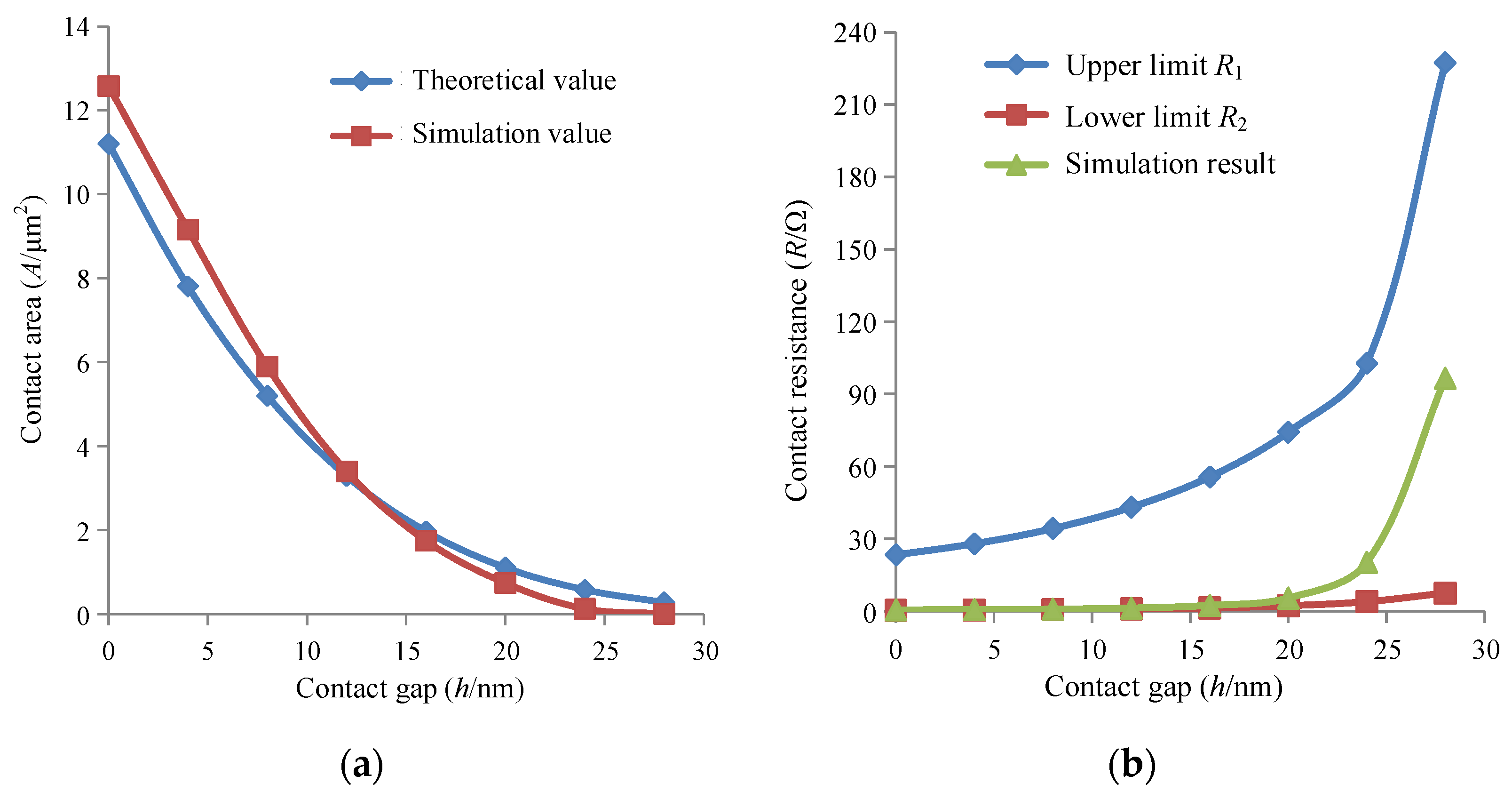
3. Contact Modelling and Simulation
4. Experiments and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aljancic, U.; Resnik, D.; Vrtacnik, D.; Mozek, M.; Amon, S. Silicon-glass anodic bonding. Inform. Midem. 2004, 34, 168–173. [Google Scholar]
- Mouskeftaras, A.; Beurthey, S.; Cogan, J.; Hallewell, G.; Leroy, O.; Grojo, D.; Perrin-Terrin, M. Short-Pulse Laser-Assisted Fabrication of a Si-SiO2 Microcooling Device. Micromachines 2021, 12, 1054. [Google Scholar] [CrossRef]
- Prasad, M.; Khanna, V.K. Development of MEMS Acoustic Sensor with Microtunnel for High SPL Measurement. IEEE Trans. Ind. Electron. 2022, 69, 3142–3150. [Google Scholar] [CrossRef]
- Almeida, L.; Ramadoss, R.; Jackson, R.; Ishikawa, K.; Yu, Q. Study of the electrical contact resistance of multi-contact MEMS relays fabricated using the MetalMUMPs process. J. Micromechanics Microengineering 2006, 16, 1189–1194. [Google Scholar] [CrossRef]
- Li, H.; Ruan, Y.; You, Z.; Song, Z. Design and Fabrication of a Novel MEMS Relay with Low Actuation Voltage. Micromachines 2020, 11, 171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, L.F.; Wang, H.; Xue, Y.Z.; Shi, F.R.; Chen, S.P. Study on the mechanism of Si-glass-Si two step anodic bonding process. J. Micromechanics Microengineering 2018, 28, 045003. [Google Scholar] [CrossRef]
- Sundaresh, S.; Deshpande, M.G.; Sundaram, K.B. New Inexpensive Simple Experimental Setup for Anodic Bonding of Silicon-Glass. ECS J. Solid State Sci. 2021, 10, 054002. [Google Scholar] [CrossRef]
- Gao, C.W.; Yang, F.; Zhang, D.C. Modeling of anodic bonding with SiO2 dielectric as interlayer. J. Micromechanics Microengineering 2020, 30, 105003. [Google Scholar] [CrossRef]
- Tang, J.L.; Cai, C.; Ming, X.X.; Yu, X.H.; Zhao, S.L.; Tu, S.T.; Liu, H.L. Morphology and stress at silicon-glass interface in anodic bonding. Appl. Surf. Sci. 2016, 387, 139–148. [Google Scholar] [CrossRef]
- Wang, C. Fabrication and Tests of Ohmic Contacts for MEMS Accelerometers. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2015. [Google Scholar]
- Li, H.; Shi, Y. Measurement and Calculation of Specific Contact Resistance in Metal-Semiconductor Contacts. Semicond. Technol. 2008, 33, 155–159. [Google Scholar]
- Jia, D. Electrothermomechanical Research of Metal Microcontacts in MEMS Switch. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2011. [Google Scholar]
- Zhu, Y. On Key Technology of MEMS Switches. Ph.D. Thesis, Xidan University, Xi’an, China, 2013. [Google Scholar]
- Pennec, F.; Peyrou, D.; Broue, A.; Dhennin, J.; Pons, P.; Plana, R.; Courtade, F. RF MEMS electrical contact resistance calculation using mechanical contact simulations and analytical models. In Proceedings of the International Collaborative Aerospace Development Micro Nanotechnologies: From Concepts to Systems (CANEUS 2009), Moffett Field, CA, USA, 1–6 March 2009. ffhal-00431027f. [Google Scholar]
- Ardito, R.; Corigliano, A.; Frangi, A. Finite Element modelling of adhesion phenomena in MEMS. In Proceedings of the 11th International Thermal, Mechanical & Multi-Physics Simulation, and Experiments in Microelectronics and Microsystems, Bordeaux, France, 26–28 April 2010; pp. 1–6. [Google Scholar]
- Cui, T.; Li, Q.; Xuan, Y.; Zhang, P. Multiscale simulation of thermal contact resistance in electronic packaging. Int. J. Therm. Sci. 2014, 83, 16–24. [Google Scholar] [CrossRef]
- Zhang, P.; Lau, Y.Y. Scaling laws for electrical contact resistance with dissimilar materials. J. Appl. Phys. 2010, 108, 85. [Google Scholar] [CrossRef]
- Lumbantobing, A.; Kogut, L.; Komvopoulos, K. Electrical contact resistance as a diagnostic tool for MEMS contact interfaces. J. Microelectromechanical Syst. 2004, 13, 77–987. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. A statistical model of elasto-plastic asperity contact between rough surfaces. Tribol. Int. 2006, 39, 906–914. [Google Scholar] [CrossRef]
- Kogut, L.; Komvopoulos, K. Electrical contact resistance theory for conductive rough surfaces. J. Appl. Phys. 2004, 95, 576–585. [Google Scholar] [CrossRef]
- Rezvanian, O.; Zikry, M.A.; Brown, C.; Krim, J. Surface roughness, asperity contact and gold RF MEMS switch behavior. J. Micromechanics Microengineering 2007, 17, 2006–2015. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.W.; Bhushan, B.; Cho, Y.J. The contact behavior of elastic/plastic non-Gaussian rough surfaces. Tribol. Lett. 2006, 22, 1–13. [Google Scholar] [CrossRef]
- Zhou, W.; He, J.; Yu, H.; He, X.; Peng, P. Analytical study of temperature coefficients of bulk MEMS capacitive accelerometers operating in closed-loop mode. Sensor Actuat. A-Phys. 2019, 290, 239–247. [Google Scholar] [CrossRef]
- Liu, H.; Liang, X.; Liu, G.; Chai, G.; Huang, M. Development of Anodic Bonding in MEMS Packaging. Meas. Control Technol. 2020, 39, 69–74. [Google Scholar]
- Greewood, J.A.; Williamson, J.B.P. Contact of nominally flat surface. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 30–319. [Google Scholar]
- Yan, J. The Mechanics of Interface; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Yi, T.; Xing, P.; Zheng, F.; Xie, J.; Li, C.; Yang, M. Preparation of Continuous Gold Nano-films by Magnetron Sputtering. At. Energy Sci. Technol. 2010, 44, 479–483. [Google Scholar]
- Nikolic, B.; Allen, P.B. Electron transport through a circular constriction. Phys. Rev. B 1999, 60, 3963–3969. [Google Scholar] [CrossRef] [Green Version]
- Książkiewicz, A. Change of electric contact resistance of an electromagnetic relay during switching operations without electric load. In Proceedings of the 5th International Interdisciplinary Technical Conference of Young Scientists, Poznan, Poland, 16–18 May 2012. [Google Scholar]
- He, J.; Xie, J.; He, X.; Du, L.; Zhou, W. Analytical study and compensation for temperature drifts of a bulk silicon MEMS capacitive accelerometer. Sensor Actuat. A-Phys. 2016, 239, 174–184. [Google Scholar] [CrossRef]


| Quantity | n | Σ (nm) | E (GPa) | R (nm) | v | σs (MPa) |
|---|---|---|---|---|---|---|
| Silicon | 200 | 15 | 169 | 1515 | 0.22 | / |
| Gold (Au) | / | 0.7 | 74.46 | / | 0.3 | 660 |
| No. # | Leg Resistance (Ω) | Mass Resistance (Ω) | Contact Resistance (Ω) |
|---|---|---|---|
| 1 | 4.68 | 3.26 | 0.71 |
| 2 | 5.14 | 3.12 | 0.99 |
| 3 | 243 | 2.98 | 120.01 |
| 4 | 4.52 | 3.11 | 0.71 |
| 5 | 4.66 | 3.05 | 0.81 |
| 6 | 4.63 | 3.38 | 0.63 |
| 7 | 5.10 | 3.71 | 0.70 |
| 8 | 4.89 | 3.00 | 0.95 |
| 9 | 4.82 | 3.63 | 0.60 |
| 10 | 5.03 | 3.51 | 0.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Cao, K.; Ran, L.; Yu, H.; Zhou, W. Investigation of the Contact Characteristics of Silicon–Gold in an Anodic Bonding Structure. Micromachines 2022, 13, 264. https://doi.org/10.3390/mi13020264
Zhang L, Cao K, Ran L, Yu H, Zhou W. Investigation of the Contact Characteristics of Silicon–Gold in an Anodic Bonding Structure. Micromachines. 2022; 13(2):264. https://doi.org/10.3390/mi13020264
Chicago/Turabian StyleZhang, Lin, Kaicong Cao, Longqi Ran, Huijun Yu, and Wu Zhou. 2022. "Investigation of the Contact Characteristics of Silicon–Gold in an Anodic Bonding Structure" Micromachines 13, no. 2: 264. https://doi.org/10.3390/mi13020264
APA StyleZhang, L., Cao, K., Ran, L., Yu, H., & Zhou, W. (2022). Investigation of the Contact Characteristics of Silicon–Gold in an Anodic Bonding Structure. Micromachines, 13(2), 264. https://doi.org/10.3390/mi13020264






