High-Performance Piezoelectric-Type MEMS Vibration Sensor Based on LiNbO3 Single-Crystal Cantilever Beams
Abstract
:1. Introduction
2. Methods
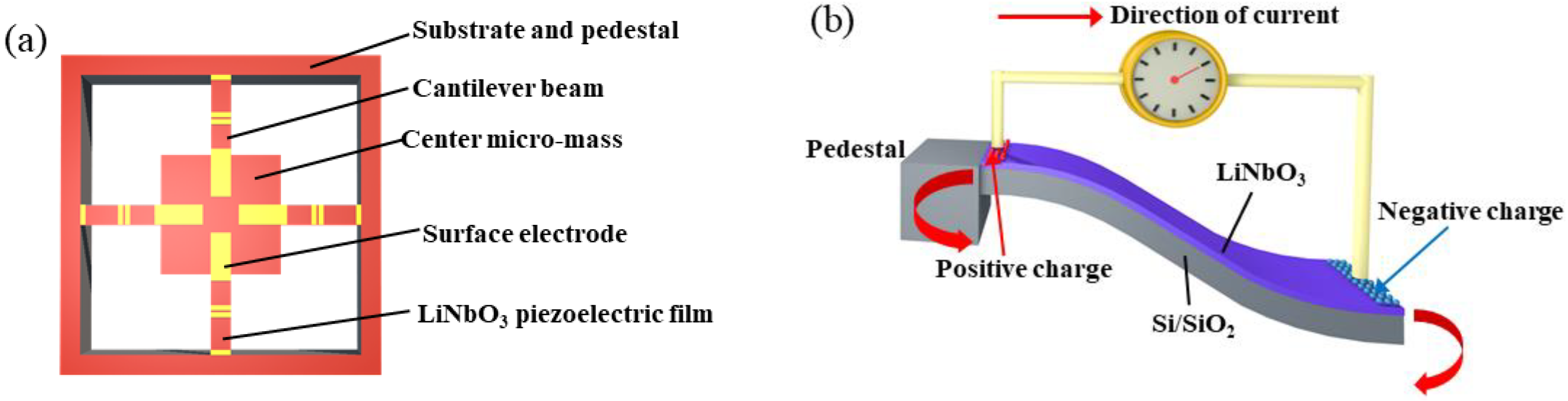
2.1. Working Principle
2.2. Design of the Vibration Sensor
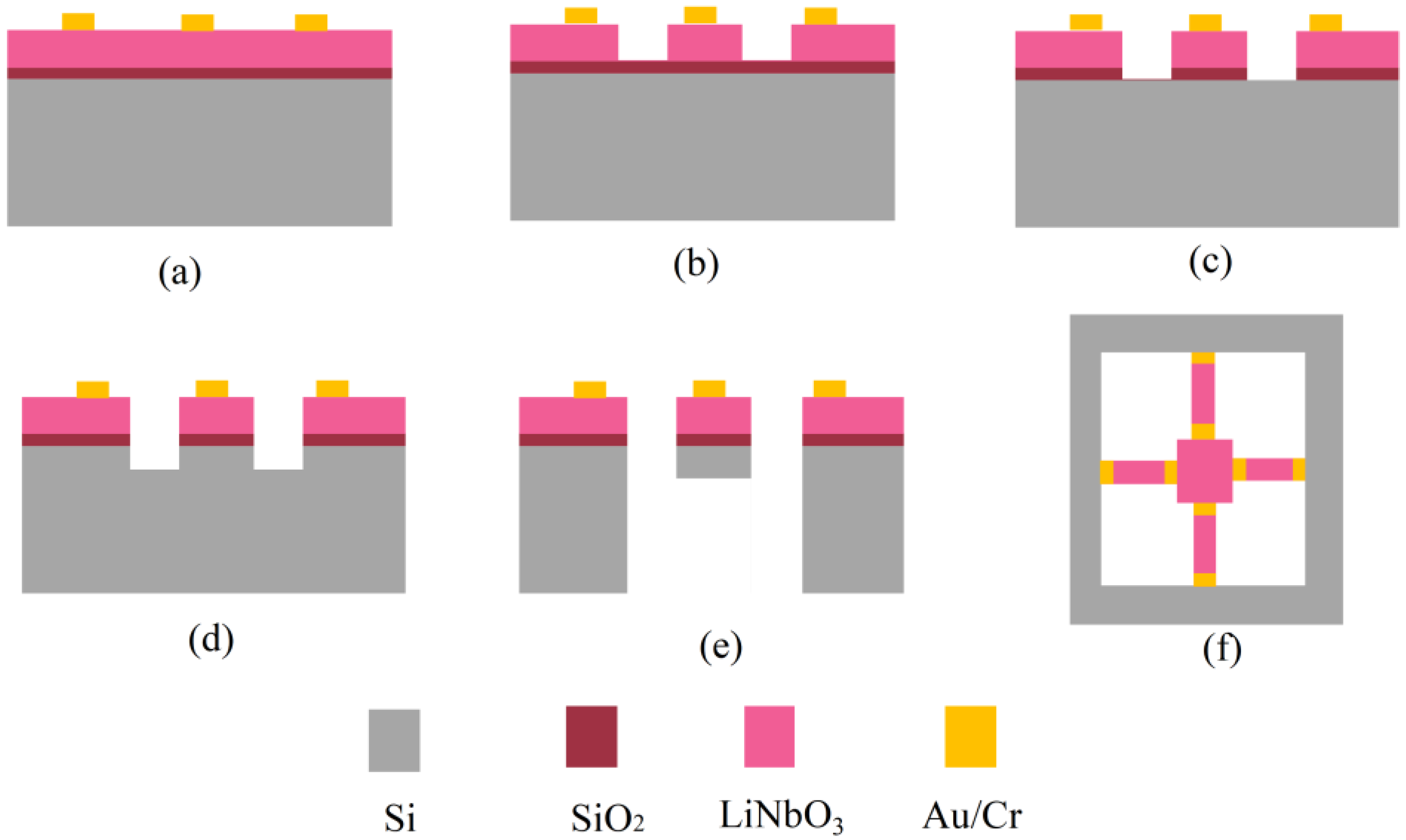
2.3. Fabrication of the Vibration Sensor
2.4. Morphology Characterization of the Vibration Sensor
2.5. Testing of the Performance of the Vibration Sensor
3. Results and Discussion
3.1. Morphology of the Vibration Sensor
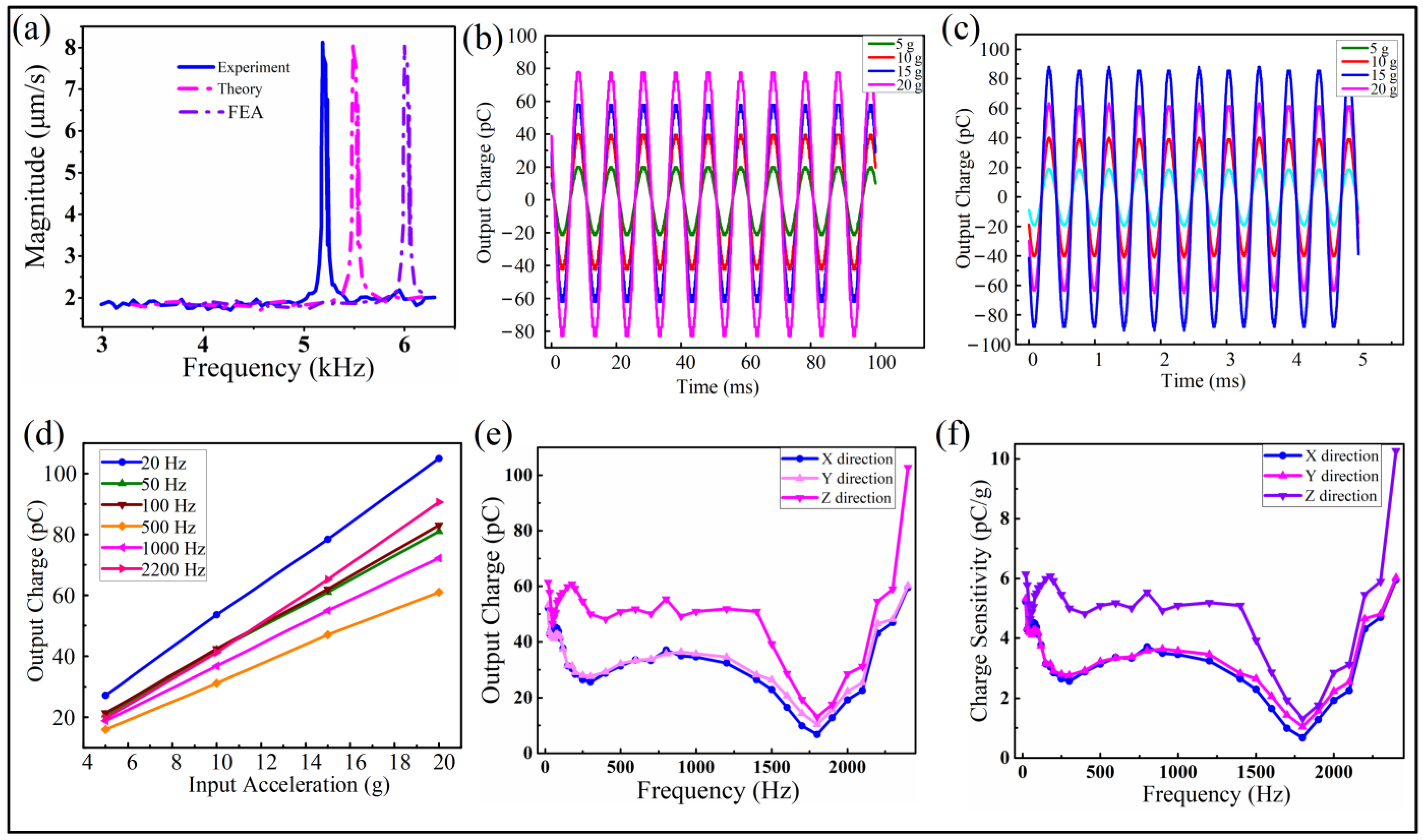
3.2. Performance of the Vibration Sensor
3.3. Effect of the Temperature on the Performance the Vibration Sensor
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Campeiro, L.; Silveira, R.; Baptista, F.G. Impedance-based damage detection under noise and vibration effects. Struct. Health Monit. 2017, 17, 654–667. [Google Scholar] [CrossRef]
- Fatima, S.; Guduri, B.; Mohanty, A.; Naikan, V. Transducer invariant multi-class fault classification in a rotor-bearing system using support vector machines. Measurement 2014, 58, 363–374. [Google Scholar] [CrossRef]
- Wang, F.; Song, G. Bolt early looseness monitoring using modified vibro-acoustic modulation by time-reversal. Mech. Syst. Signal Process. 2019, 130, 349–360. [Google Scholar] [CrossRef]
- Zarnik, M.S.; Novak, F. Effect of condensing environments on characteristics of piezoresistive ceramic pressure sensors. Sens. Actuators A Phys. 2017, 267, 385–392. [Google Scholar] [CrossRef]
- Lian, Y.-S.; Sun, J.-Y.; Ge, X.-M.; Yang, Z.-X.; He, X.-T.; Zheng, Z.-L. A theoretical study of an improved capacitive pressure sensor: Closed-form solution of uniformly loaded annular membranes. Measurement 2017, 111, 84–92. [Google Scholar] [CrossRef]
- Kuo, C.-L.; Lin, S.-C.; Wu, W.-J. Fabrication and performance evaluation of a metal-based bimorph piezoelectric MEMS generator for vibration energy harvesting. Smart Mater. Struct. 2016, 25, 105016. [Google Scholar] [CrossRef]
- Grall, S.; Dufour, I.; Aubry, V.; Debéda, H. Fabrication and characterisation of piezoelectric screen-printed in plane resonant microcantilevers used as gravimetric sensors. Smart Mater. Struct. 2019, 28, 105055. [Google Scholar] [CrossRef]
- Li, M.; Gao, R.; Liu, S.; Tong, L. Modeling, analysis and validation of a novel asymmetric cruciform harvester with d 15 mode. Smart Mater. Struct. 2019, 29, 025014. [Google Scholar] [CrossRef]
- Derakhshani, M.; Momenzadeh, N.; Berfield, T.A. Analytical and experimental study of a clamped-clamped, bistable buckled beam low-frequency PVDF vibration energy harvester. J. Sound Vib. 2021, 497, 115937. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, W.; Ghosh, A.; Wang, G.; Wu, F.; Zhang, H. Miniaturized langasite MEMS micro-cantilever beam structured resonator for high temperature gas sensing. Smart Mater. Struct. 2020, 29, 055002. [Google Scholar] [CrossRef]
- Shen, D.; Park, J.-H.; Ajitsaria, J.; Choe, S.-Y.; Wikle, H.; Kim, D.-J. The design, fabrication and evaluation of a MEMS PZT cantilever with an integrated Si proof mass for vibration energy harvesting. J. Micromechan. Microeng. 2008, 18, 055017. [Google Scholar] [CrossRef]
- Shen, D.; Park, J.-H.; Noh, J.H.; Choe, S.-Y.; Kim, S.-H.; Wikle, H.; Kim, D.-J. Micromachined PZT cantilever based on SOI structure for low frequency vibration energy harvesting. Sens. Actuators A Phys. 2009, 154, 103–108. [Google Scholar] [CrossRef]
- Jeon, Y.; Sood, R.; Jeong, J.-H.; Kim, S.-G. MEMS power generator with transverse mode thin film PZT. Sens. Actuators A Phys. 2005, 122, 16–22. [Google Scholar] [CrossRef]
- Ren, B.; Or, S.W.; Zhang, Y.; Zhang, Q.; Li, X.; Jiao, J.; Wang, W.; Liu, D.; Zhao, X.; Luo, H. Piezoelectric energy harvesting using shear mode 0.71Pb(Mg1/3Nb2/3)O3∓0.29PbTiO3 single crystal cantilever. Appl. Phys. Lett. 2010, 96, 083502. [Google Scholar] [CrossRef]
- Zhou, L.; Sun, J.; Zheng, X.; Deng, S.; Zhao, J.; Peng, S.; Zhang, Y.; Wang, X.; Cheng, H. A model for the energy harvesting performance of shear mode piezoelectric cantilever. Sens. Actuators A Phys. 2012, 179, 185–192. [Google Scholar] [CrossRef]
- Islam, M.S.; Beamish, J. Shear Piezoelectric and Dielectric Properties of LN, PMN-PT and PZT-5A at Low Temperatures. J. Low Temp. Phys. 2018, 194, 285–301. [Google Scholar] [CrossRef]
- Qu, M.; Shen, Y.; Wu, L.; Fu, X.; Cheng, X.; Wang, Y. Homogenous and ultra-shallow lithium niobate etching by focused ion beam. Precis. Eng. 2020, 62, 10–15. [Google Scholar] [CrossRef]
- Li, Y.; Lan, T.; Yang, D.; Xiang, M.; Dai, J.; Li, C.; Wang, Z. Research of selective etching in LiNbO3 using proton-exchanged wet etching technique. Mater. Res. Express 2020, 7, 056202. [Google Scholar] [CrossRef]
- Xiang, B.-X.; Wang, L.; Ma, Y.-J.; Yu, L.; Han, H.-P.; Ruan, S.-C. Supercontinuum Generation in Lithium Niobate Ridge Waveguides Fabricated by Proton Exchange and Ion Beam Enhanced Etching. Chin. Phys. Lett. 2017, 34, 24203. [Google Scholar] [CrossRef]
- Kim, S.-B.; Park, H.; Kim, S.-H.; Wikle, H.; Park, J.-H.; Kim, D.-J. Comparison of MEMS PZT Cantilevers Based on d31 and d33 Modes for Vibration Energy Harvesting. J. Microelectromechan. Syst. 2012, 22, 26–33. [Google Scholar] [CrossRef]
- Shivashankar, P.; Gopalakrishnan, S. Design, modeling and testing of d33-mode surface-bondable multilayer piezoelectric actuator. Smart Mater. Struct. 2019, 29, 045016. [Google Scholar] [CrossRef]
- Payam, A.F.; Trewby, W.; Voïtchovsky, K. Simultaneous viscosity and density measurement of small volumes of liquids using a vibrating microcantilever. Analyst 2017, 142, 1492–1498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Z.; Liu, J.; Yu, C.; Zheng, Y. A Small Range Six-Axis Accelerometer Designed with High Sensitivity DCB Elastic Element. Sensors 2016, 16, 1552. [Google Scholar] [CrossRef] [PubMed]
- Altieri, L.; Tonoli, A. Piezoelectric Injectors for Automotive Applications: Modeling and Experimental Validation of Hysteretic Behavior and Temperature Effects. J. Dyn. Syst. Meas. Control 2012, 135, 011005. [Google Scholar] [CrossRef]



| Materials | Parameters | Values |
|---|---|---|
| Silicon layer | Density (kg/m3) | |
| Young’s modulus (GPa) | ||
| LiNbO3 layer | Piezoelectric coefficients (×pC/N) | |
| Density (kg/m3) | ||
| Young’s modulus (GPa) |
| Parameters for Scanning | Range of Parameter | Steps |
|---|---|---|
| Length of cantilever beams | 1860 to 2260 μm | 50 μm |
| Length of proof mass | 3000 to 4000 μm | 50 μm |
| Widths of cantilever beam | 300 to 600 μm | 20 μm |
| Thicknesses of cantilever beam | 30 to 60 μm | 5 μm |
| Thicknesses of proof mass | 30 to 60 μm | 5 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Geng, W.; Bi, K.; Li, T.; Li, X.; Qiao, X.; Shi, Y.; Zhang, H.; Zhao, C.; Xue, G.; et al. High-Performance Piezoelectric-Type MEMS Vibration Sensor Based on LiNbO3 Single-Crystal Cantilever Beams. Micromachines 2022, 13, 329. https://doi.org/10.3390/mi13020329
Wei H, Geng W, Bi K, Li T, Li X, Qiao X, Shi Y, Zhang H, Zhao C, Xue G, et al. High-Performance Piezoelectric-Type MEMS Vibration Sensor Based on LiNbO3 Single-Crystal Cantilever Beams. Micromachines. 2022; 13(2):329. https://doi.org/10.3390/mi13020329
Chicago/Turabian StyleWei, Huifen, Wenping Geng, Kaixi Bi, Tao Li, Xiangmeng Li, Xiaojun Qiao, Yikun Shi, Huiyi Zhang, Caiqin Zhao, Gang Xue, and et al. 2022. "High-Performance Piezoelectric-Type MEMS Vibration Sensor Based on LiNbO3 Single-Crystal Cantilever Beams" Micromachines 13, no. 2: 329. https://doi.org/10.3390/mi13020329
APA StyleWei, H., Geng, W., Bi, K., Li, T., Li, X., Qiao, X., Shi, Y., Zhang, H., Zhao, C., Xue, G., & Chou, X. (2022). High-Performance Piezoelectric-Type MEMS Vibration Sensor Based on LiNbO3 Single-Crystal Cantilever Beams. Micromachines, 13(2), 329. https://doi.org/10.3390/mi13020329







