Recent Progress in Silicon-Based Slow-Light Electro-Optic Modulators
Abstract
:1. Introduction
2. Principle of Slow-Light Effect
2.1. Basic Theory of Slow-Light Effect
2.2. Basic Structure of Slow-Light Modulators
3. Silicon Photonic Crystal Modulators
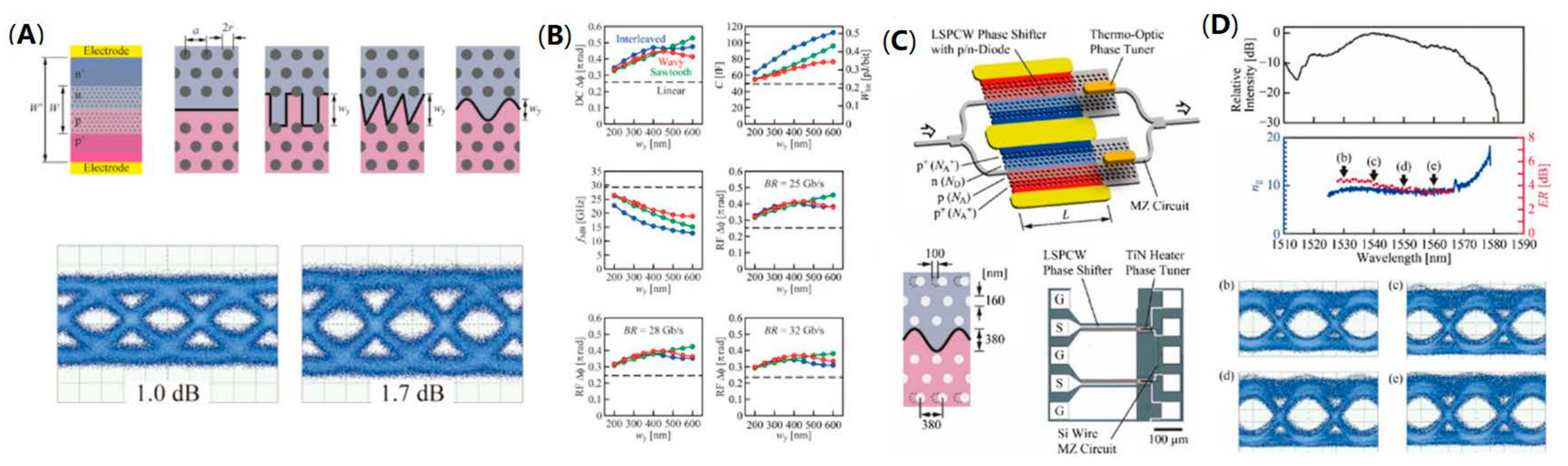
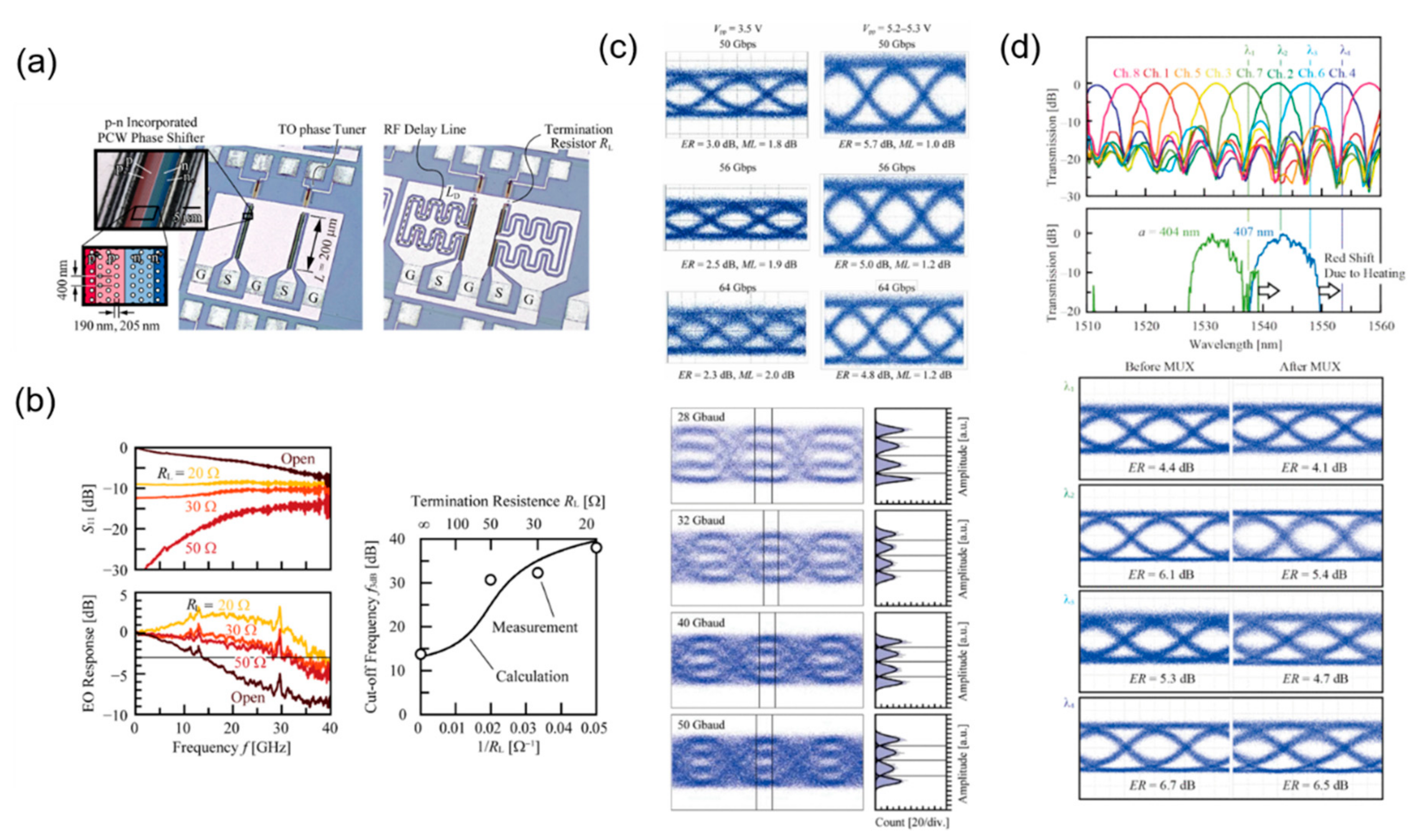
3.1. All-Silicon Photonic Crystal Modulators
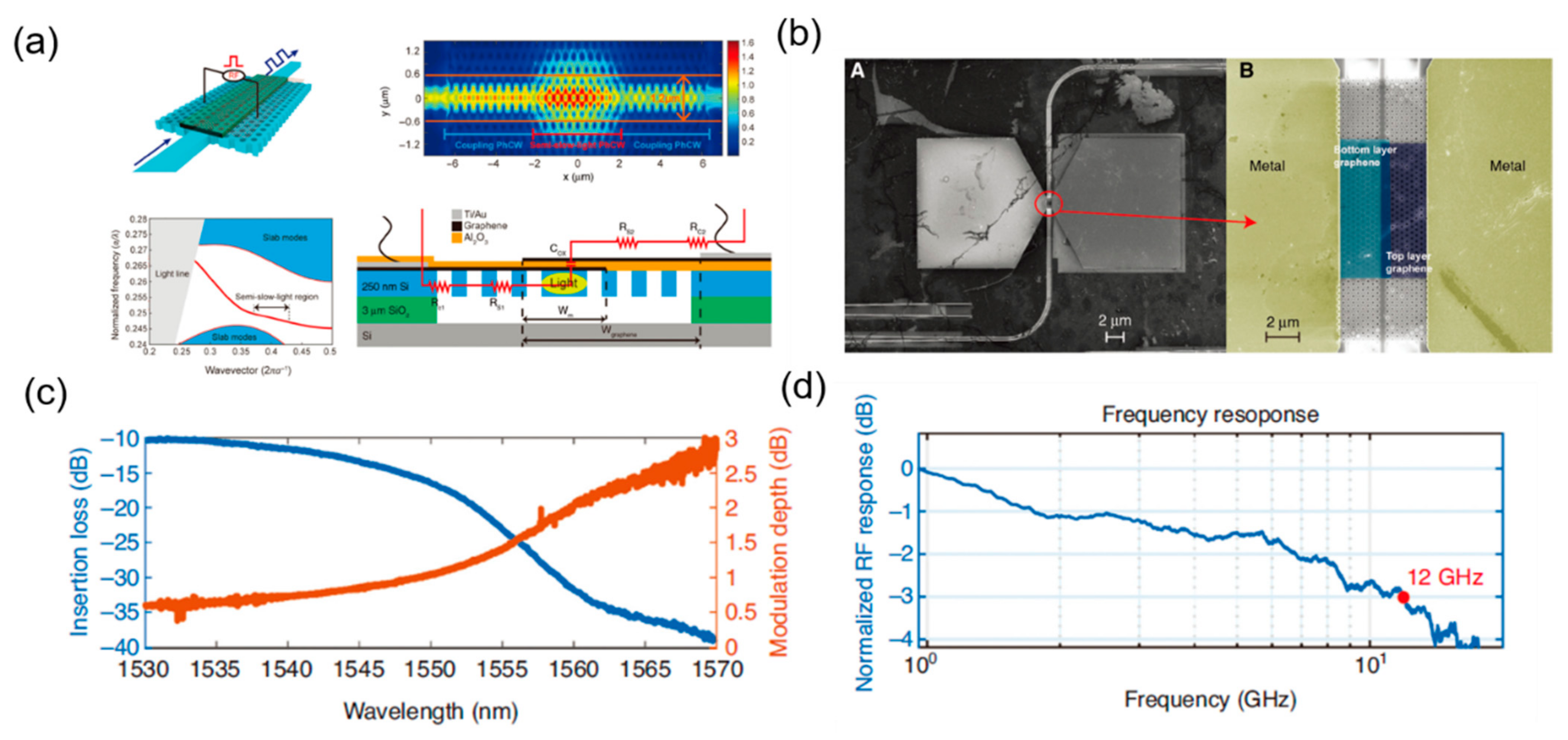
3.2. Silicon-Based Hybrid Photonic Crystal Modulators
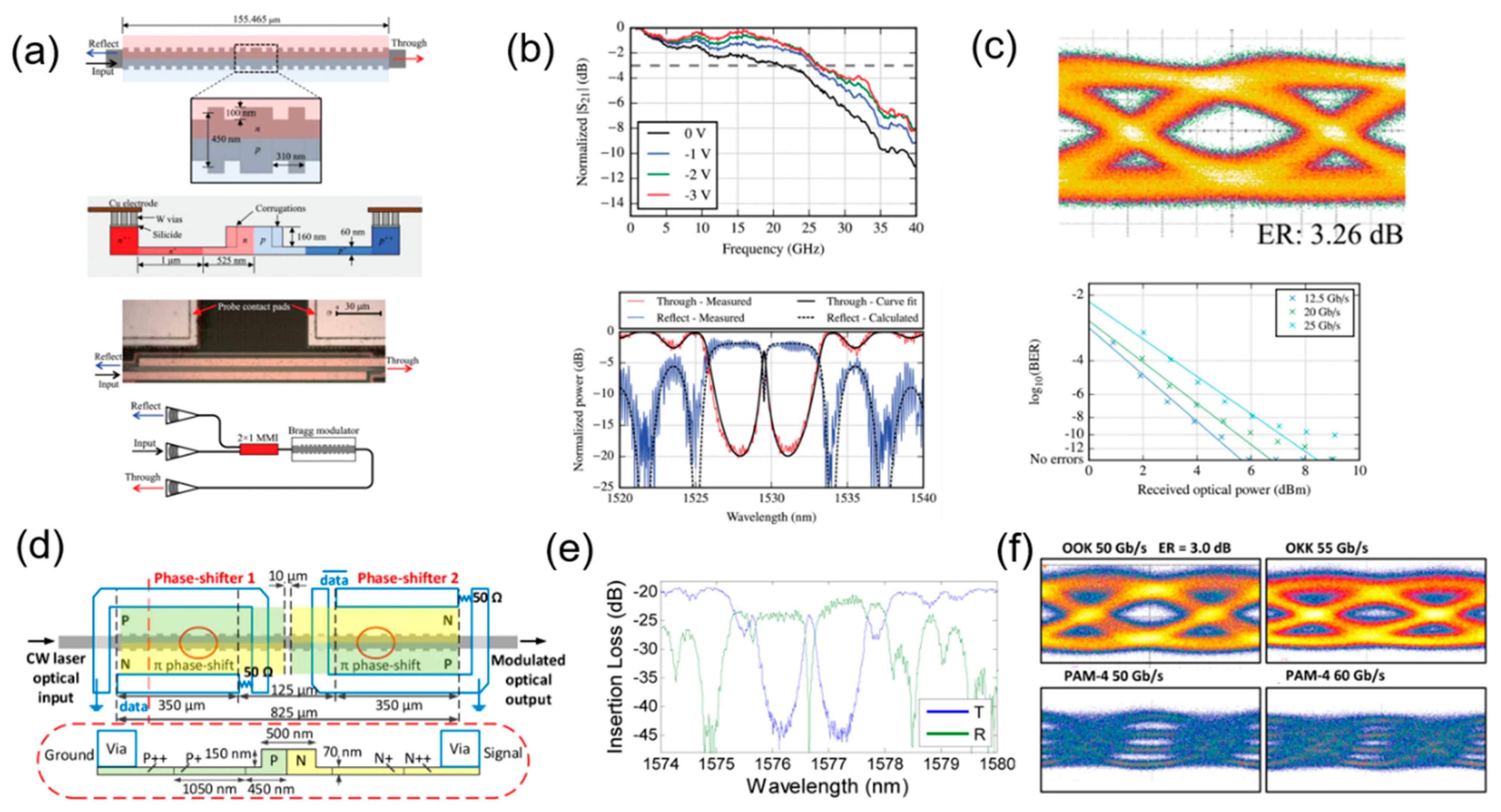
4. Silicon Waveguide Grating Modulators
4.1. All-Silicon Waveguide Grating Modulators
4.2. Silicon-Based Hybrid Waveguide Grating Modulators
5. Discussion
- Complex format transmission: The primary advantage of silicon slow-light modulators is their ultra-compact footprint, while silicon MRMs are also with an advantage in size, so compared with the silicon MRMs, the advantages of function for the slow-light modulator need to be demonstrated clearly. The silicon slow-light modulator is conducive to realizing phase modulation, thereby transmitting signals such as BPSK and QPSK, and realizing the fabrication of coherent transmitters. Although there exists research on silicon photonic crystal modulators to obtain QPSK constellation pattern, the research on high-order data transmission is relatively limited, and there is still no phase modulation experiment for silicon waveguide grating modulators. Therefore, developing the complex signal transmission function of silicon slow-light modulators to realize silicon coherent transmitters of slow light is an important research direction.
- System integration: The ultra-compact footprint of silicon slow-light modulators has intrinsic advantages in further optoelectronic integration, but currently there are few silicon system integrations based on slow-light modulators. Large-scale system integration is an important direction for the further development of phonics chip and optical communication systems. Practically, in the current silicon optoelectronics integrated systems, conventional silicon MZMs are always the main limiting factor. If the silicon slow-light modulator an order of magnitude smaller than the conventional silicon MZMs can be used as a unit device, the area of the system integration chip will be reduced significantly and the advantages of slow-light modulators will be maximized.
- Reduce loss: Although the loss of the silicon slow-light modulators is not particularly high compared to that of the conventional silicon modulators, it is based on an extremely short length. Indeed, the silicon slow-light modulator is sensitive to the length of slow-light waveguide. If the waveguide length increases, the loss will increase accordingly. This condition limits the length of the silicon slow-light modulators. However, if the length of the silicon slow-light modulators can be increased enough on the premise of controlling the loss, according to the extremely high modulation efficiency brought by slow-light effect, a very low half-wave voltage will be obtained, which is very suitable for optoelectronic integration.
Autor Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Cheng, Q.X.; Bahadori, M.; Glick, M.; Rumley, S.; Bergman, K. Recent advances in optical technologies for data centers: A review. Optica 2018, 5, 1354–1370. [Google Scholar] [CrossRef]
- Tkach, R.W. Scaling optical communications for the next decade and beyond. Bell Labs Tech. J. 2010, 14, 3–9. [Google Scholar] [CrossRef]
- Reed, G.T.; Mashanovich, G.; Gardes, F.Y.; Thomson, D.J. Silicon optical Modulators. Nat. Photonics 2010, 4, 518–526. [Google Scholar] [CrossRef] [Green Version]
- Reed, G.T.; Mashanovich, G.Z.; Gardes, F.Y.; Nedeljkovic, M.; Hu, Y.F.; Thomson, D.J.; Li, K.; Wilson, P.R.; Chen, S.W.; Hsu, S.S. Recent breakthroughs in carrier depletion based silicon optical modulators. Nanophotonics 2014, 3, 229–245. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.C.; Harris, N.C.; Skirlo, S.; Prabhu, M.; Baehr-Jones, T.; Hochberg, M.; Sun, X.; Zhao, S.J.; Larochelle, H.; Englund, D.; et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 2017, 11, 441–446. [Google Scholar] [CrossRef]
- Marpaung, D.; Yao, J.P.; Capmany, J. Integrated microwave photonics. Nat. Photonics 2019, 12, 80–90. [Google Scholar] [CrossRef]
- Tao, Y.S.; Shu, H.W.; Wang, X.J.; Jin, M.; Tao, Z.H.; Yang, F.H.; Shi, J.B.; Qin, J. Hybrid-integrated high-performance microwave photonic filter with switchable response. Photonics Res. 2021, 9, 1569–1580. [Google Scholar] [CrossRef]
- Jin, M.; Tang, S.J.; Chen, J.H.; Yu, X.C.; Shu, H.W.; Tao, Y.S.; Chen, A.K.; Gong, Q.H.; Wang, X.J.; Xiao, Y.F. 1/f-noise-free optical sensing with an integrated heterodyne interferometer. Nat. Commun. 2021, 12, 1973. [Google Scholar] [CrossRef]
- Soref, R.A.; Bennett, B.R. Electrooptical effects in silicon. IEEE J. Quantum Electron. 1987, 23, 123–129. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.F.; Ji, R.Q.; Zhang, L.; Yang, L. Electro-optical response analysis of a 40 Gb∕s silicon Mach-Zehnder optical modulator. J. Lightwave Technol. 2013, 31, 2434–2440. [Google Scholar] [CrossRef]
- Patel, D.; Ghosh, S.; Chagnon, M.; Samani, A.; Veerasubramanian, V.; Osman, M.; Plant, D.V. Design, analysis, and transmission system performance of a 41 GHz silicon photonic modulator. Opt. Express 2015, 23, 14263–14287. [Google Scholar] [CrossRef] [Green Version]
- Deniel, L.; Gay, M.; Galacho, D.P.; Baudot, C.; Bramerie, L.; Ozolins, O.; Boeuf, F.; Vivien, L.; Peucheret, C.; Marris-Morini, D. DAC-less PAM-4 generation in the O-band using a silicon Mach-Zehnder modulator. Opt. Express 2019, 27, 9740–9748. [Google Scholar] [CrossRef]
- Rosenberg, J.C.; Green, W.M.J.; Assefa, S.; Gill, D.M.; Barwicz, T.; Yang, M.; Shank, S.M.; Vlasov, Y.A. A 25 Gbps silicon microring modulator based on an interleaved junction. Opt. Express 2012, 20, 26411–26423. [Google Scholar] [CrossRef]
- Li, R.; Patel, D.; El-Fiky, E.; Samani, A.; Xing, Z.P.; Morsy-Osman, M.; Plant, D.V. High-speed low-chirp PAM-4 transmission based on push-pull silicon photonic microring modulators. Opt. Express 2017, 25, 13222–13229. [Google Scholar] [CrossRef]
- Sun, J.; Kumar, R.; Sakib, M.; Driscoll, J.B.; Jayatilleka, H.; Rong, H.S. A 128 Gb∕s PAM4 silicon microring modulator with integrated thermo-optic resonance tuning. J. Lightwave Technol. 2019, 37, 110–115. [Google Scholar] [CrossRef]
- He, M.B.; Xu, M.Y.; Ren, Y.X.; Jian, J.; Ruan, Z.L.; Xu, Y.S.; Gao, S.Q.; Sun, S.H.; Wen, X.Q.; Zhou, L.D.; et al. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photonics 2019, 13, 359–364. [Google Scholar] [CrossRef]
- Lu, G.W.; Hong, J.X.; Qiu, F.; Spring, A.M.; Kashino, T.; Oshima, J.; Ozawa, M.; Nawata, H.; Yokoyama, S. High-temperature-resistant silicon-polymer hybrid modulator operating at up to 200 Gbit s−1 for energy-efficient datacentres and harsh-environment applications. Nat. Commun. 2020, 11, 4224. [Google Scholar]
- Liu, M.; Yin, X.B.; Ulin-Avila, E.; Geng, B.S.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef]
- Krauss, T.F. Why do we need slow light. Nat. Photonics 2008, 2, 448–450. [Google Scholar] [CrossRef]
- Baba, T. Slow light in photonic crystals. Nat. Photonics 2008, 2, 465–473. [Google Scholar] [CrossRef]
- Thevenaz, L. Slow and fast light in optical fibres. Nat. Photonics 2008, 2, 474–481. [Google Scholar] [CrossRef] [Green Version]
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Zhu, Z.M.; Gauthier, D.J.; Boyd, R.W. Stored Light in an Optical Fiber via Stimulated Brillouin Scattering. Science 2007, 318, 1748–1750. [Google Scholar] [CrossRef]
- Kowsari, A.; Ahmadi, V.; Darvish, G.; Moravvej-Farshi, M.K. All-optical tunable delay line based on nonlinearities in a chalcogenide microfiber coil resonator. J. Opt. Soc. Am. B 2017, 34, 1199–1205. [Google Scholar] [CrossRef]
- Sharping, J.E.; Okawachi, Y.; Gaeta, A.L. Wide bandwidth slow light using a Raman fiber amplifier. Opt. Express 2005, 13, 6092–6098. [Google Scholar] [CrossRef]
- Yanik, M.F.; Suh, W.; Wang, Z.; Fan, S.H. Stopping Light in a Waveguide with an All-Optical Analog of Electromagnetically Induced Transparency. Phys. Rev. Lett. 2004, 93, 233903. [Google Scholar] [CrossRef]
- Xu, Q.F.; Sandhu, S.; Povinelli, M.L.; Shakya, J.; Fan, S.H.; Lipson, M. Experimental Realization of an On-Chip All-Optical Analogue to Electromagnetically Induced Transparency. Phys. Rev. Lett. 2006, 96, 123901. [Google Scholar] [CrossRef]
- Xiang, C.; Davenport, M.L.; Khurgin, J.B.; Morton, P.A.; Bowers, J.E. Low-Loss Continuously Tunable Optical True Time Delay Based on Si3N4 Ring Resonators. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 5900109. [Google Scholar] [CrossRef]
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Selvaraja, S.K.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Ohtaka, K. Energy band of photons and low-energy photon diffraction. Phys. Rev. B 1979, 19, 5057–5067. [Google Scholar] [CrossRef]
- Gerace, D.; Andreani, L.C. Gap maps and intrinsic diffraction losses in one-dimensional photonic crystal slabs. Phys. Rev. E 2004, 69, 56603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Notomi, M.; Yamada, K.; Shinya, A.; Takahashi, J.; Takahashi, C.; Yokohama, I. Extremely Large Group-Velocity Dispersion of Line-Defect Waveguides in Photonic Crystal Slabs. Phys. Rev. Lett. 2001, 87, 253902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Colman, P.; Combrie, S.; Lehoucq, G.; De Rossi, A. Control of dispersion in photonic crystal waveguides using group symmetry theory. Opt. Express 2012, 20, 13108–13114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsakmakidis, K.L.; Hess, O.; Boyd, R.W.; Zhang, X. Ultraslow waves on the nanoscale. Science 2017, 358, eaan5196. [Google Scholar] [CrossRef] [Green Version]
- O’Faolain, L.; Schulz, S.A.; Beggs, D.M.; White, T.P.; Spasenovic, M.; Kuipers, L.; Morichetti, F.; Melloni, A.; Mazoyer, S.; Hugonin, J.P.; et al. Loss engineered slow light waveguides. Opt. Express 2010, 18, 27627–27638. [Google Scholar] [CrossRef] [Green Version]
- Li, J.T.; O’Faolain, L.; Schulz, S.A.; Krauss, T.F. Low loss propagation in slow light photonic crystal waveguides at group indices up to 60. Photonics Nanostruct.-Fundam. Appl. 2012, 10, 589–593. [Google Scholar] [CrossRef]
- Tamura, T.; Kondo, K.; Terada, Y.; Hinakura, Y.; Ishikura, N.; Baba, T. Silica-Clad Silicon Photonic Crystal Waveguides for Wideband Dispersion-Free Slow Light. J. Lightwave Technol. 2015, 33, 3034–3040. [Google Scholar] [CrossRef]
- Passoni, M.; Gerace, D.; O’Faolain, L.; Andreani, L.C. Optimizing band-edge slow light in silicon-on-insulator waveguide gratings. Opt. Express 2018, 26, 8470–8478. [Google Scholar] [CrossRef]
- Jean, P.; Gervais, A.; LaRochelle, S.; Shi, W. Slow Light in Subwavelength Grating Waveguides. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 8200108. [Google Scholar] [CrossRef] [Green Version]
- Yablonovitch, E. Photonic band-gap structures. J. Opt. Soc. Am. B 1993, 10, 283–295. [Google Scholar] [CrossRef]
- Baba, T.; Motegi, A.; Iwai, T.; Fukaya, N.; Watanabe, Y.; Sakai, A. Light propagation characteristics of straight single line defect optical waveguides in a photonic crystal slab fabricated into a silicon-on-insulator substrate. IEEE J. Quantum Electron. 2002, 38, 743–752. [Google Scholar] [CrossRef]
- Jiang, Y.Q.; Jiang, W.; Gu, L.L.; Chen, X.N.; Chen, R.T. 80-micron interaction length silicon photonic crystal waveguide modulator. Appl. Phys. Lett. 2005, 87, 221105. [Google Scholar] [CrossRef] [Green Version]
- Opheij, A.; Rotenberg, N.; Beggs, D.M.; Rey, I.H.; Krauss, T.F.; Kuipers, L. Ultracompact (3 μm) silicon slow-light optical modulator. Sci. Rep. 2013, 3, 3546. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.C.; Hashimoto, S.; Shinkawa, M.; Baba, T. Compact and fast photonic crystal silicon optical modulators. Opt. Express 2012, 20, 22465–22474. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.C.; Yazawa, N.; Hashimoto, S.; Otsuka, S.; Baba, T. Sub-100 μm Photonic Crystal Si Optical Modulators: Spectral, Athermal, and High-Speed Performance. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 3400811. [Google Scholar] [CrossRef]
- Hojo, K.; Terada, Y.; Yazawa, N.; Watanabe, T.; Baba, T. Compact QPSK and PAM Modulators with Si Photonic Crystal Slow-Light Phase Shifters. IEEE Photonics Technol. Lett. 2016, 28, 1438–1441. [Google Scholar] [CrossRef]
- Terada, Y.; Tatebe, T.; Hinakura, Y.; Baba, T. Si Photonic Crystal Slow-Light Modulators with Periodic p–n Junctions. J. Lightwave Technol. 2017, 35, 1684–1692. [Google Scholar] [CrossRef]
- Terada, Y.; Kondo, K.; Abe, R.; Baba, T. Full C-band Si photonic crystal waveguide modulator. Opt. Lett. 2017, 42, 5110–5112. [Google Scholar] [CrossRef]
- Hinakura, Y.; Arai, H.; Baba, T. 64 Gbps Si photonic crystal slow light modulator by electro-optic phase matching. Opt. Express 2019, 27, 14321–14327. [Google Scholar] [CrossRef]
- Hinakura, Y.; Akiyama, D.; Ito, H.; Baba, T. Silicon Photonic Crystal Modulators for High-Speed Transmission and Wavelength Division Multiplexing. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 4900108. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Shams-Ansari, A.; Chandrasekhar, S.; Winzer, P.; Loncar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104. [Google Scholar] [CrossRef]
- Li, M.X.; Ling, J.W.; He, Y.; Javid, U.A.; Xue, S.X.; Lin, Q. Lithium niobate photonic-crystal electro-optic modulator. Nat. Commun. 2020, 11, 4123. [Google Scholar] [CrossRef]
- Lee, M.; Katz, H.E.; Erben, C.; Gill, D.M.; Gopalan, P.; Heber, J.D.; McGee, D.J. Broadband modulation of light by using an electro-optic polymer. Science 2002, 298, 1401–1403. [Google Scholar] [CrossRef]
- Brosi, J.M.; Koos, C.; Andreani, L.C.; Waldow, M.; Leuthold, J.; Freude, W. High-speed low-voltage electro-optic modulator with a polymer-infiltrated silicon photonic crystal waveguide. Opt. Express 2008, 16, 4177–4191. [Google Scholar] [CrossRef]
- Lin, C.Y.; Wang, X.L.; Chakravarty, S.; Lee, B.S.; Lai, W.C.; Luo, J.D.; Jen, A.K.Y.; Chen, R.T. Electro-optic polymer infiltrated silicon photonic crystal slot waveguide modulator with 23 dB slow light enhancement. Appl. Phys. Lett. 2010, 97, 93304. [Google Scholar] [CrossRef]
- Wang, X.L.; Lin, C.Y.; Chakravarty, S.; Luo, J.D.; Jen, A.K.Y.; Chen, R.T. Effective in-device r(33) of 735 pm/V on electro-optic polymer infiltrated silicon photonic crystal slot waveguides. Opt. Lett. 2011, 36, 882–884. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Hosseini, A.; Chakravarty, S.; Luo, J.D.; Jen, A.K.Y.; Chen, R.T. Wide optical spectrum range, subvolt, compact modulator based on an electro-optic polymer refilled silicon slot photonic crystal waveguide. Opt. Lett. 2013, 38, 4931–4934. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.Y.; Chung, C.J.; Hosseini, A.; Subbaraman, H.; Luo, J.D.; Jen, A.K.Y.; Nelson, R.L.; Lee, C.Y.C.; Chen, R.T. High performance optical modulator based on electro-optic polymer filled silicon slot photonic crystal waveguide. J. Lightwave Technol. 2016, 34, 2941–2951. [Google Scholar] [CrossRef]
- Phare, C.T.; Lee, Y.H.D.; Cardenas, J.; Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photonics 2015, 9, 511–514. [Google Scholar] [CrossRef]
- Lee, B.S.; Kim, B.; Freitas, A.P.; Mohanty, A.; Zhu, Y.B.; Bhatt, G.R.; Hone, J.; Lipson, M. High-performance integrated graphene electro-optic modulator at cryogenic temperature. Nanophotonics 2021, 10, 99–104. [Google Scholar] [CrossRef]
- Sorianello, V.; Contestabile, G.; Midrio, M.; Pantouvaki, M.; Asselbergs, I.; Van Campenhout, J.; Huyghebaerts, C.; D’Errico, A.; Galli, P.; Romagnoli, M. Chirp management in silicon-graphene electro absorption modulators. Opt. Express 2017, 25, 19371–19381. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Zhu, X.L.; Galili, M.; Frandsen, L.H.; Hu, H.; Xiao, S.S.; Dong, J.J.; Ding, Y.H.; Oxenlowe, L.K.; Zhang, X.L. Double-layer graphene on photonic crystal waveguide electro-absorption modulator with 12 GHz bandwidth. Nanophotonics 2020, 9, 2377–2385. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Recent advances and progress in photonic crystalbased gas sensors. J. Phys. D 2017, 50, 203001. [Google Scholar] [CrossRef]
- Brimont, A.; Thomson, D.J.; Sanchis, P.; Herrera, J.; Gardes, F.Y.; Fedeli, J.M.; Reed, G.T.; Marti, J. High speed silicon electro-optical modulators enhanced via slow light propagation. Opt. Express 2011, 19, 20876–20885. [Google Scholar] [CrossRef] [Green Version]
- Brimont, A.; Thomson, D.J.; Gardes, F.Y.; Fedeli, J.M.; Reed, G.T.; Marti, J.; Sanchis, P. High-contrast 40 Gb ∕ s operation of a 500 μm long silicon carrier-depletion slow wave modulator. Opt. Lett. 2012, 37, 3504–3506. [Google Scholar] [CrossRef] [Green Version]
- Brimont, A.; Gutierrez, A.M.; Aamer, M.; Thomson, D.J.; Gardes, F.Y.; Fedeli, J.M.; Reed, G.T.; Marti, J.; Sanchis, P. Slow-Light-Enhanced Silicon Optical Modulators Under Low-Drive-Voltage Operation. IEEE Photonics J. 2012, 4, 1306–1315. [Google Scholar] [CrossRef]
- Caverley, M.; Wang, X.; Murray, K.; Jaeger, N.A.F.; Chrostowski, L. Silicon-on-Insulator Modulators Using a Quarter-Wave Phase-Shifted Bragg Grating. IEEE Photonics Technol. Lett. 2015, 27, 2331–2334. [Google Scholar] [CrossRef]
- Bedard, K.; Simard, A.D.; Filion, B.; Painchaud, Y.; Rusch, L.A.; LaRochelle, S. Dual phase-shift Bragg grating silicon photonic modulator operating up to 60 Gb/s. Opt. Express 2016, 24, 2413–2419. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, R.; Mirzoyan, L.; Jamshidi, K. Energy Consumption Enhancement of Reverse-Biased Silicon-Based Mach–Zehnder Modulators Using Corrugated Slow Light Waveguides. IEEE Photonics J. 2018, 10, 8200207. [Google Scholar] [CrossRef]
- Jafari, O.; Sepehrian, H.; Shi, W.; LaRochelle, S. High-Efficiency Silicon Photonic Modulator Using Coupled Bragg Grating Resonators. J. Lightwave Technol. 2019, 37, 2065–2075. [Google Scholar] [CrossRef]
- Jafari, O.; Shi, W.; LaRochelle, S. Efficiency-Speed Tradeoff in Slow-Light Silicon Photonic Modulators. IEEE J. Sel. Top. Quantum Electron. 2020, 27, 3400611. [Google Scholar] [CrossRef]
- Passoni, M.; Gerace, D.; O’Faolain, L.; Andreani, L.C. Slow light with interleaved p-n junction to enhance performance of integrated Mach-Zehnder silicon modulators. Nanophotonics 2019, 8, 1485–1494. [Google Scholar] [CrossRef] [Green Version]
- Passoni, M.; Gerace, D.; O’Faolain, L.; Andreani, L.C. Optimizing an interleaved p-n junction to reduce energy dissipation in silicon slow-light modulators. Photonics Res. 2020, 8, 457–467. [Google Scholar] [CrossRef]
- Jafari, O.; Shi, W.; LaRochelle, S. Mach-Zehnder Silicon Photonic Modulator Assisted by Phase-Shifted Bragg Gratings. IEEE Photonics Technol. Lett. 2020, 32, 445–448. [Google Scholar] [CrossRef]
- Jafari, O.; Zhalehpour, S.; Shi, W.; LaRochelle, S. DAC-Less PAM-4 Slow-Light Silicon Photonic Modulator Providing High Efficiency and Stability. J. Lightwave Technol. 2021, 39, 5074–5082. [Google Scholar] [CrossRef]
- Jafari, O.; Zhalehpour, S.; Shi, W.; LaRochelle, S. Mode-conversion-based silicon photonic modulator loaded by a combination of lateral and interleaved p-n junctions. Photonics Res. 2021, 9, 471–476. [Google Scholar] [CrossRef]
- Huang, X.R.; Liu, Y.; Guan, H.; Yu, Z.G.; Tan, M.Q.; Li, Z.Y. High-Efficiency, Slow-Light Modulator on Hybrid Thin-Film Lithium Niobate Platform. IEEE Photonics Technol. Lett. 2021, 33, 1093–1096. [Google Scholar] [CrossRef]


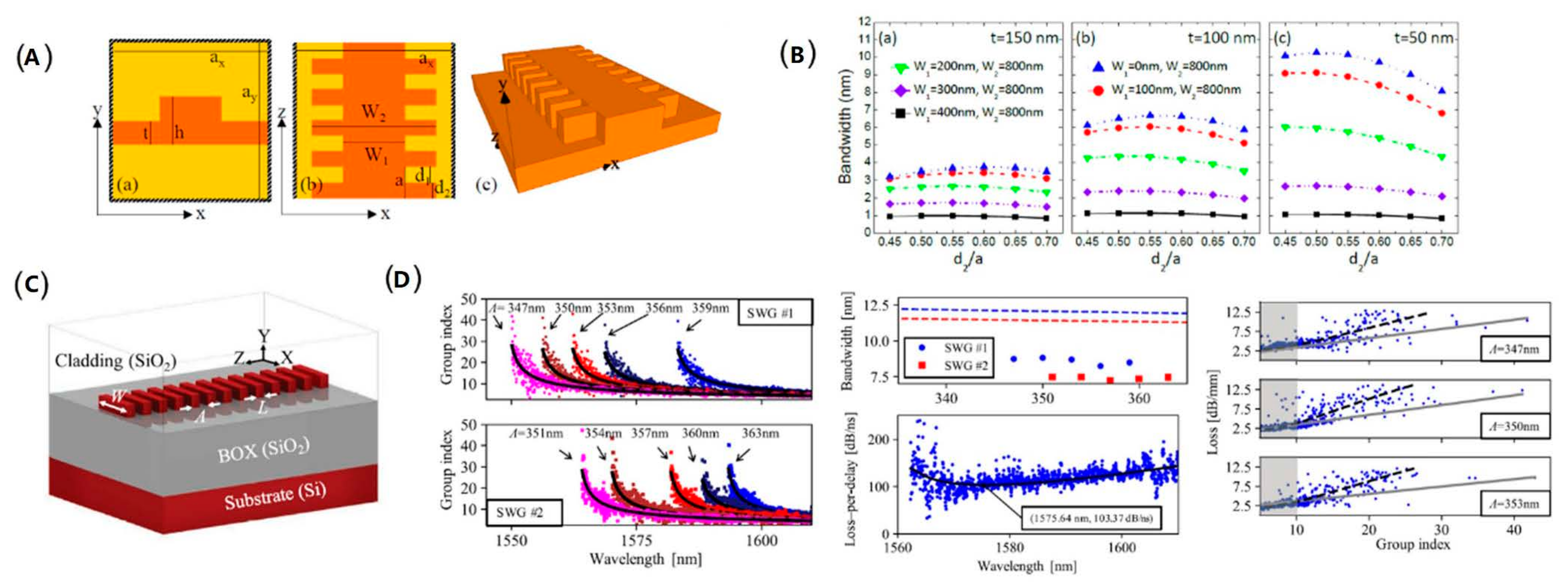
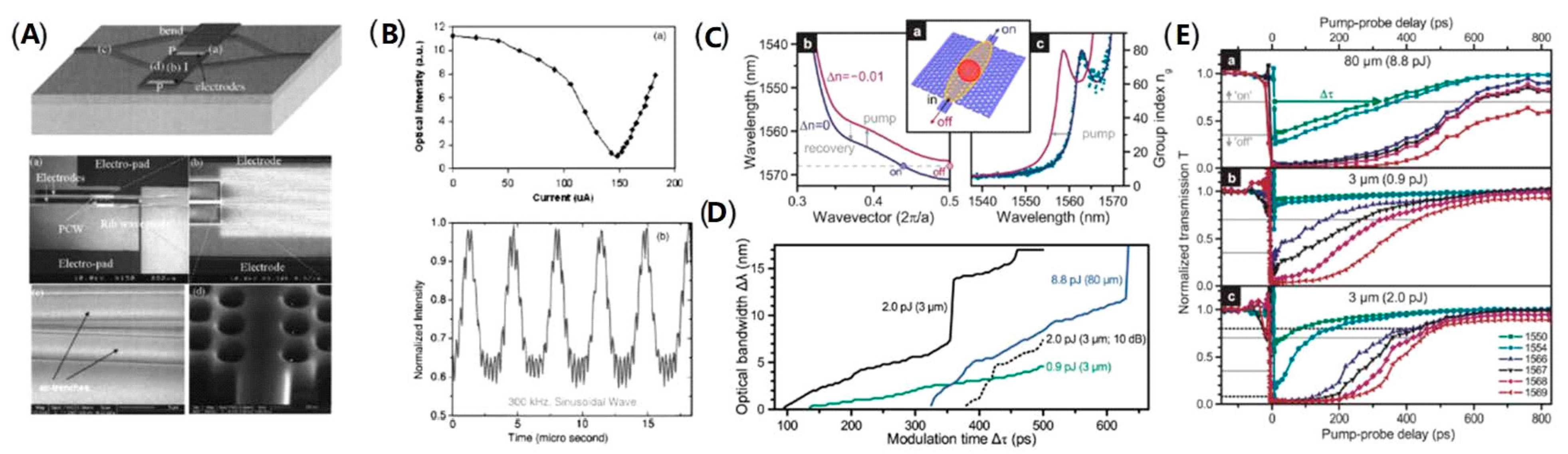
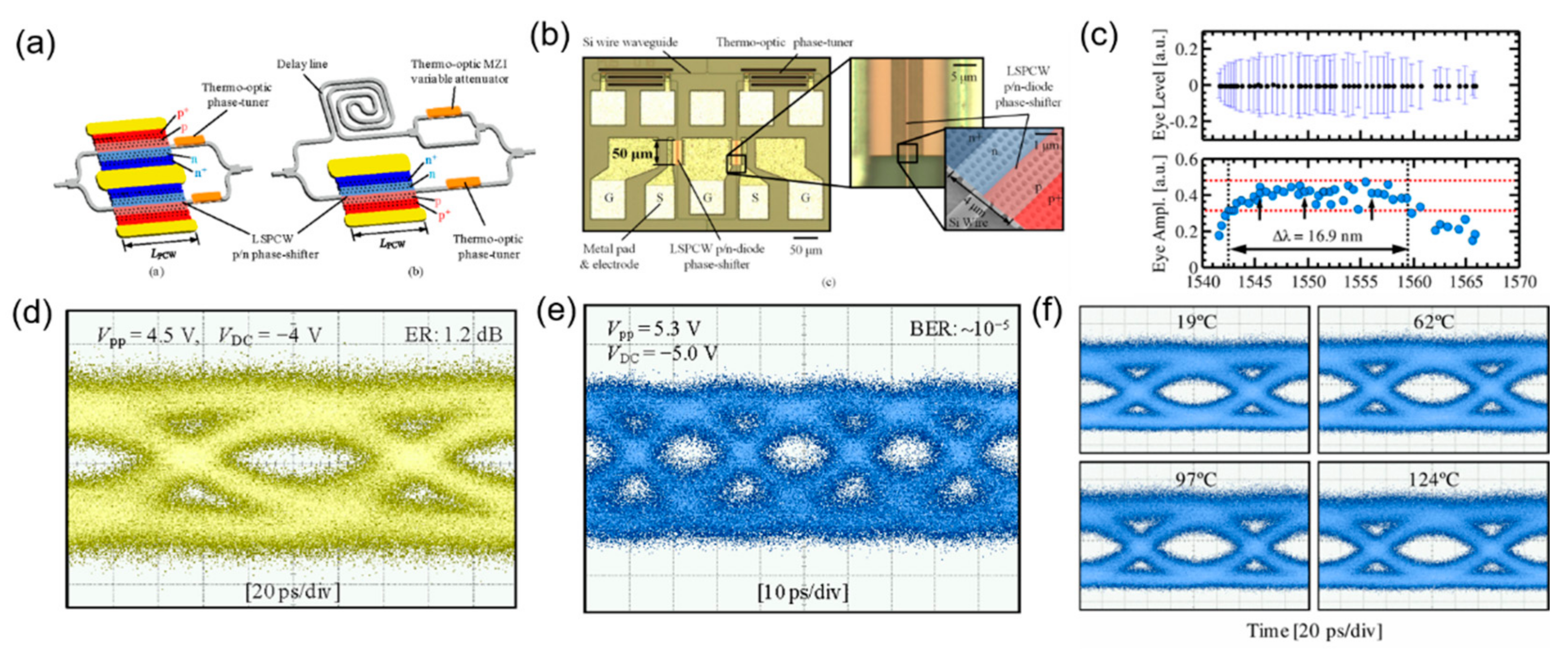
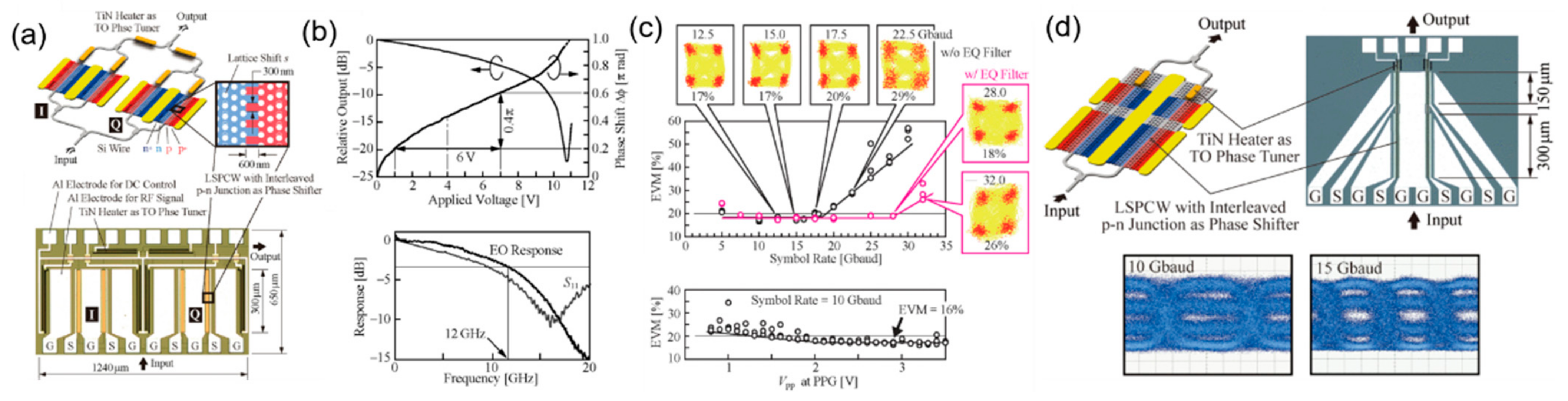



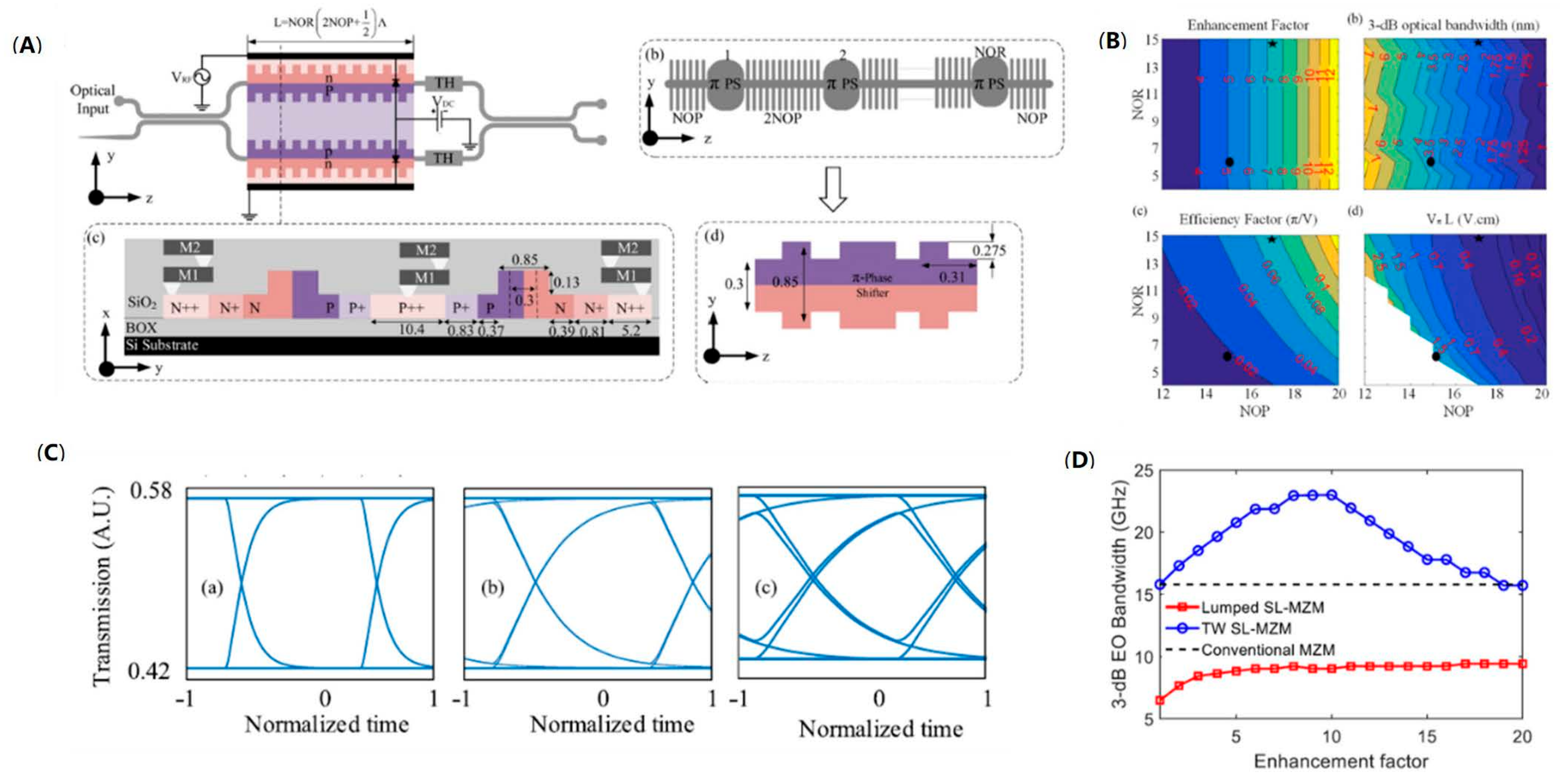
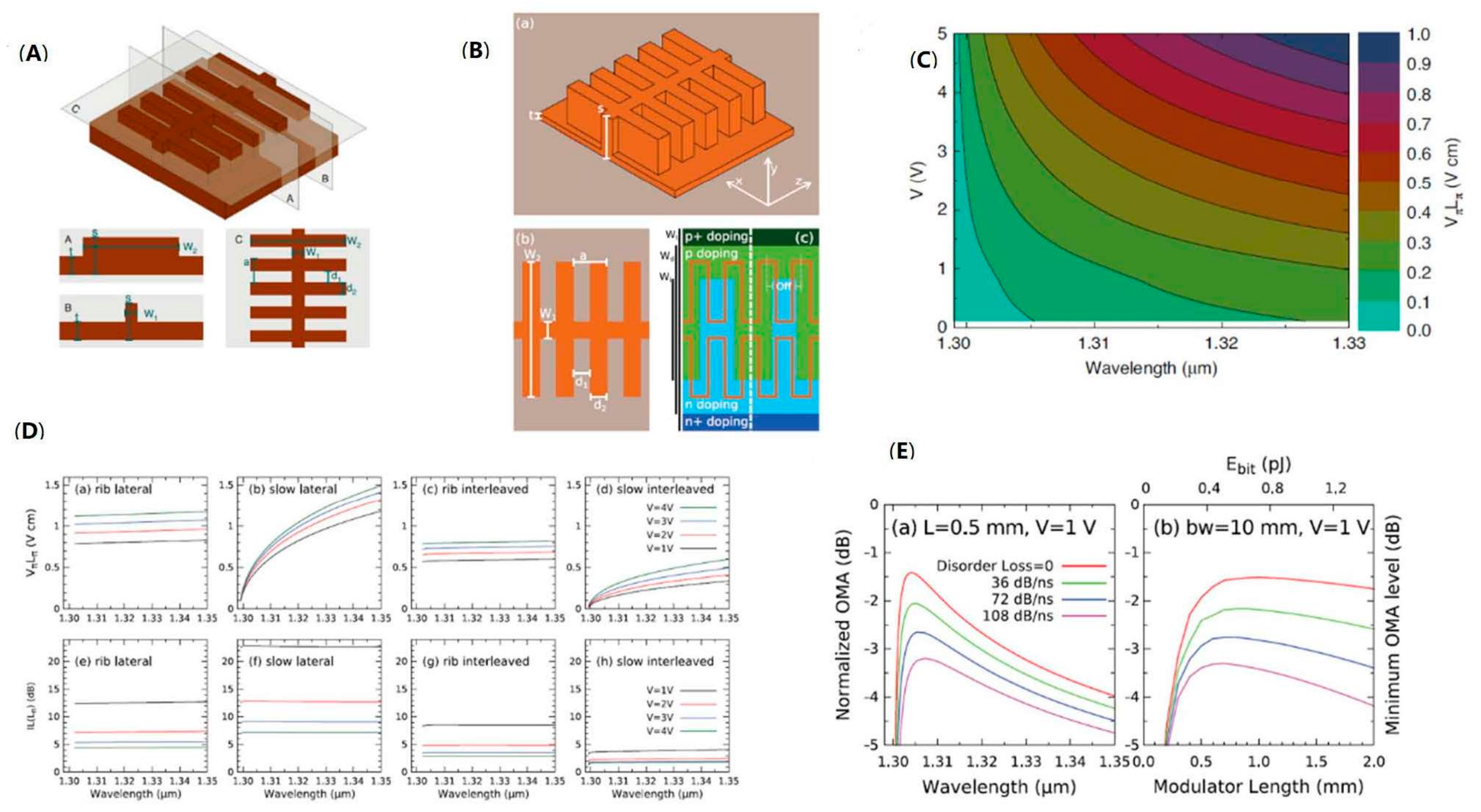
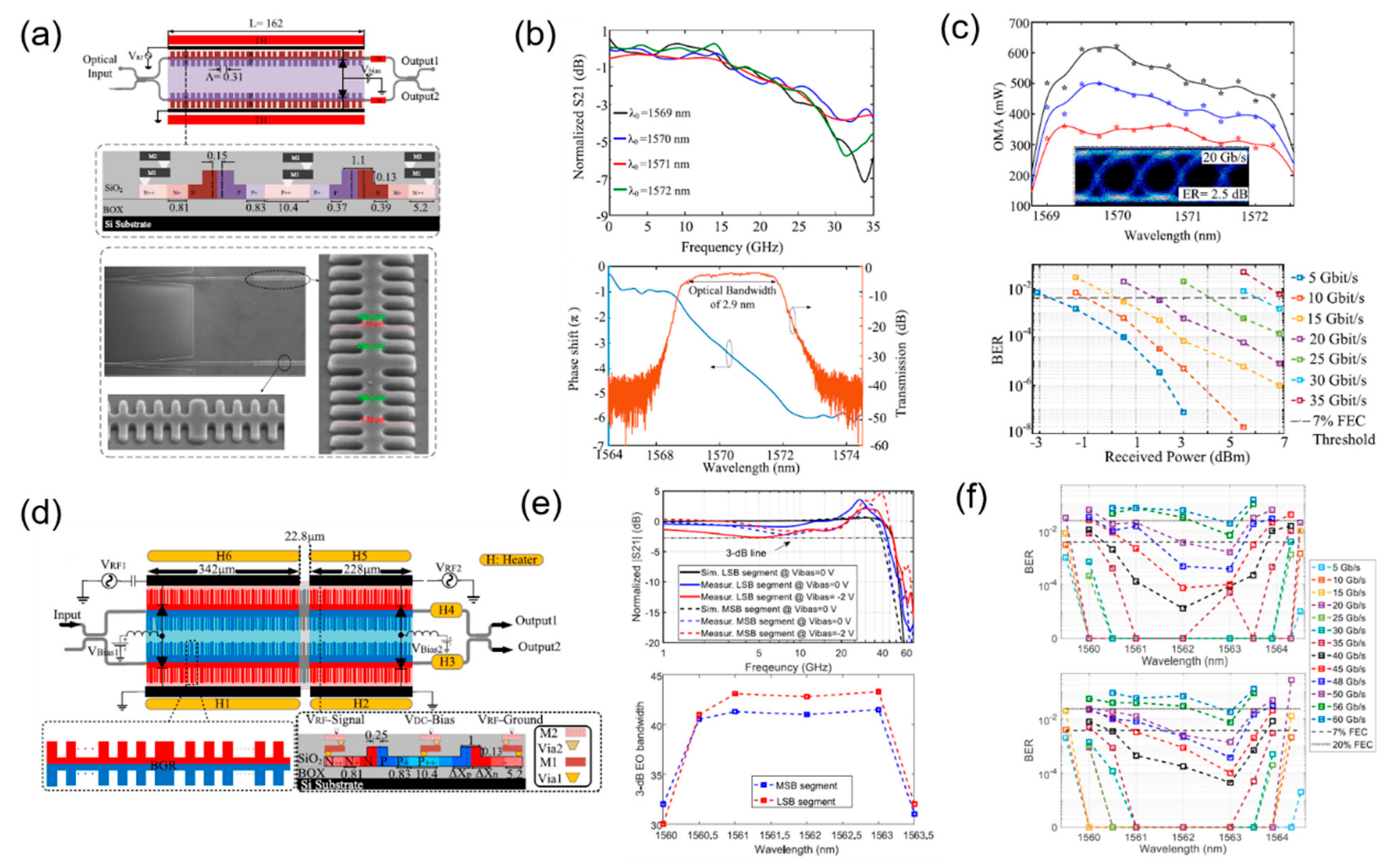
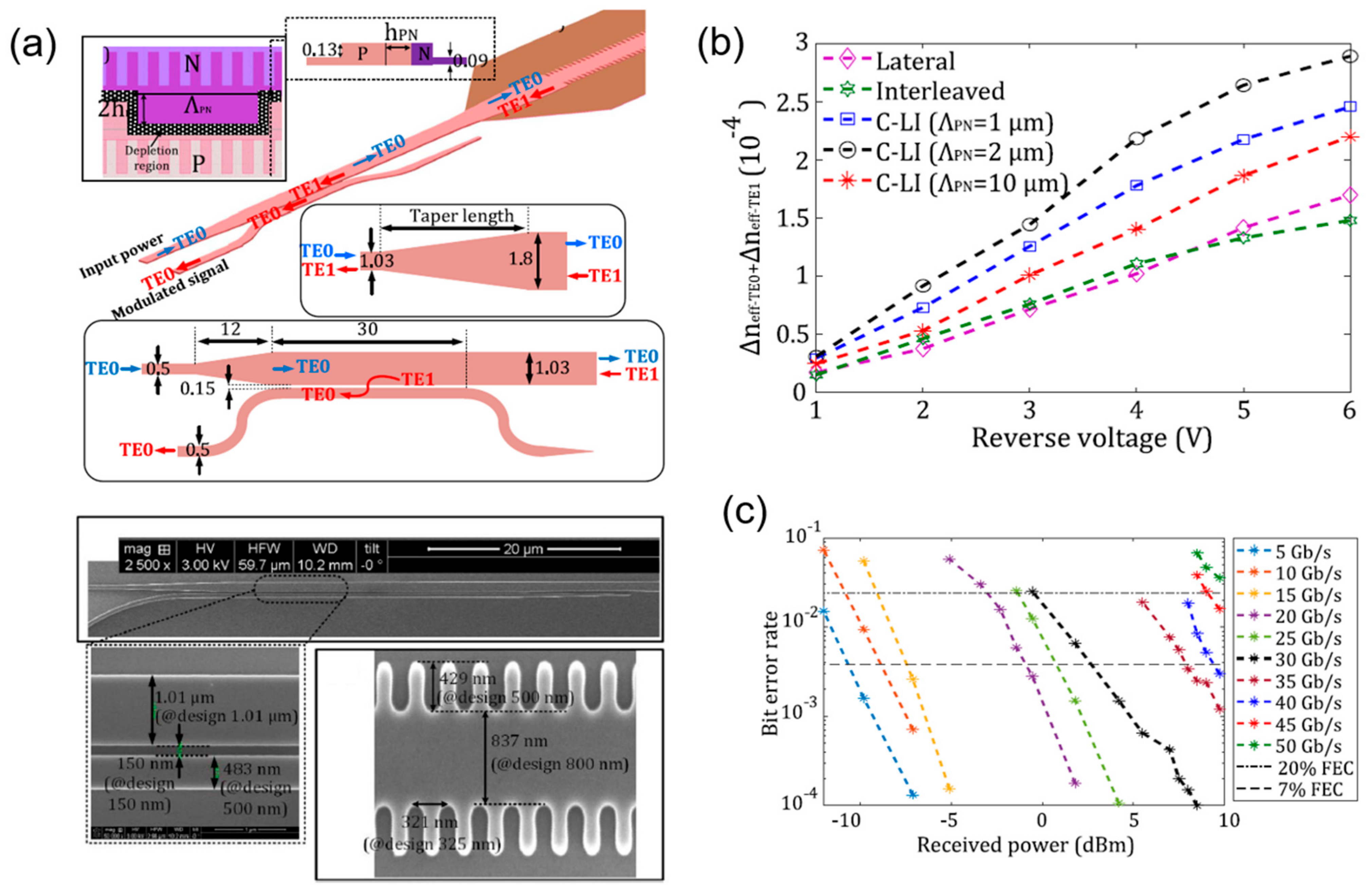

| Ref. | Structure | Footprint | EO Bandwidth | Optical Bandwidth | Modulation Efficiency | Loss | Speed |
|---|---|---|---|---|---|---|---|
| [44] | Photonic crystal | 50 μm/ 90 μm | NA | 12.5 nm/2 nm | NA | 9.1 dB/6.2 dB | 10 Gb/s OOK 40 Gb/s OOK |
| [45] | Photonic crystal | 90 μm | NA | 16.9 nm | NA | 8 dB | 40 Gb/s OOK |
| [46] | Photonic crystal | 300 μm/ 450 μm | 12 GHz | NA | 0.32 V·cm | 14 dB | 56 Gb/s QPSK 30 Gb/s PAM-4 |
| [48] | Photonic crystal | 200 μm | NA | 42 nm | NA | 4–5 dB | 25 Gb/s OOK |
| [49] | Photonic crystal | 200 μm | 31 GHz/ 38 GHz | 15 nm | 0.6 V·cm | 6–8 dB | 64 Gb/s OOK |
| [50] | Photonic crystal | 200 μm | 32–38 GHz | 15 nm | 0.44 V·cm | 6 dB | 64 Gb/s OOK 100 Gb/s PAM-4 4 × 50 Gb/s WDM |
| [64] | Waveguide grating | 500 μm/ 1000 μm | 16 GHz/ 11 GHz | NA | 0.45 V·cm | 13 dB (1000 μm) | 40 Gb/s OOK 30 Gb/s OOK |
| [65] | Waveguide grating | 500 μm | NA | 1.3 nm | 0.85 V·cm | 6 dB | 40 Gb/s OOK |
| [66] | Waveguide grating | 1000 μm | NA | NA | 0.6 V·cm | 12 dB | 25 Gb/s OOK |
| [67] | Waveguide grating | 155 μm | 26.5 GHz | NA | NA | 45.3 dB/cm | 32 Gb/s OOK |
| [68] | Waveguide grating | 825 μm | NA | NA | NA | 2.8 dB | 55 Gb/s OOK 60 Gb/s PAM-4 |
| [74] | Waveguide grating | 162 μm | 28 GHz | 2.9 nm | 0.18 V·cm | 2 dB | 30 Gb/s OOK |
| [75] | Waveguide grating | 570 μm | >40 GHz | 2 nm | 0.51 V·cm | 5.5 dB | 90 Gb/s PAM-4 |
| [76] | Waveguide grating | 290 μm | 11.2 GHz | NA | NA | 2 dB | 55 Gb/s OOK |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.; Jin, M.; Tao, Y.; Shen, B.; Wang, X. Recent Progress in Silicon-Based Slow-Light Electro-Optic Modulators. Micromachines 2022, 13, 400. https://doi.org/10.3390/mi13030400
Han C, Jin M, Tao Y, Shen B, Wang X. Recent Progress in Silicon-Based Slow-Light Electro-Optic Modulators. Micromachines. 2022; 13(3):400. https://doi.org/10.3390/mi13030400
Chicago/Turabian StyleHan, Changhao, Ming Jin, Yuansheng Tao, Bitao Shen, and Xingjun Wang. 2022. "Recent Progress in Silicon-Based Slow-Light Electro-Optic Modulators" Micromachines 13, no. 3: 400. https://doi.org/10.3390/mi13030400
APA StyleHan, C., Jin, M., Tao, Y., Shen, B., & Wang, X. (2022). Recent Progress in Silicon-Based Slow-Light Electro-Optic Modulators. Micromachines, 13(3), 400. https://doi.org/10.3390/mi13030400







