Hardware Demonstration of SRDP Neuromorphic Computing with Online Unsupervised Learning Based on Memristor Synapses
Abstract
:1. Introduction
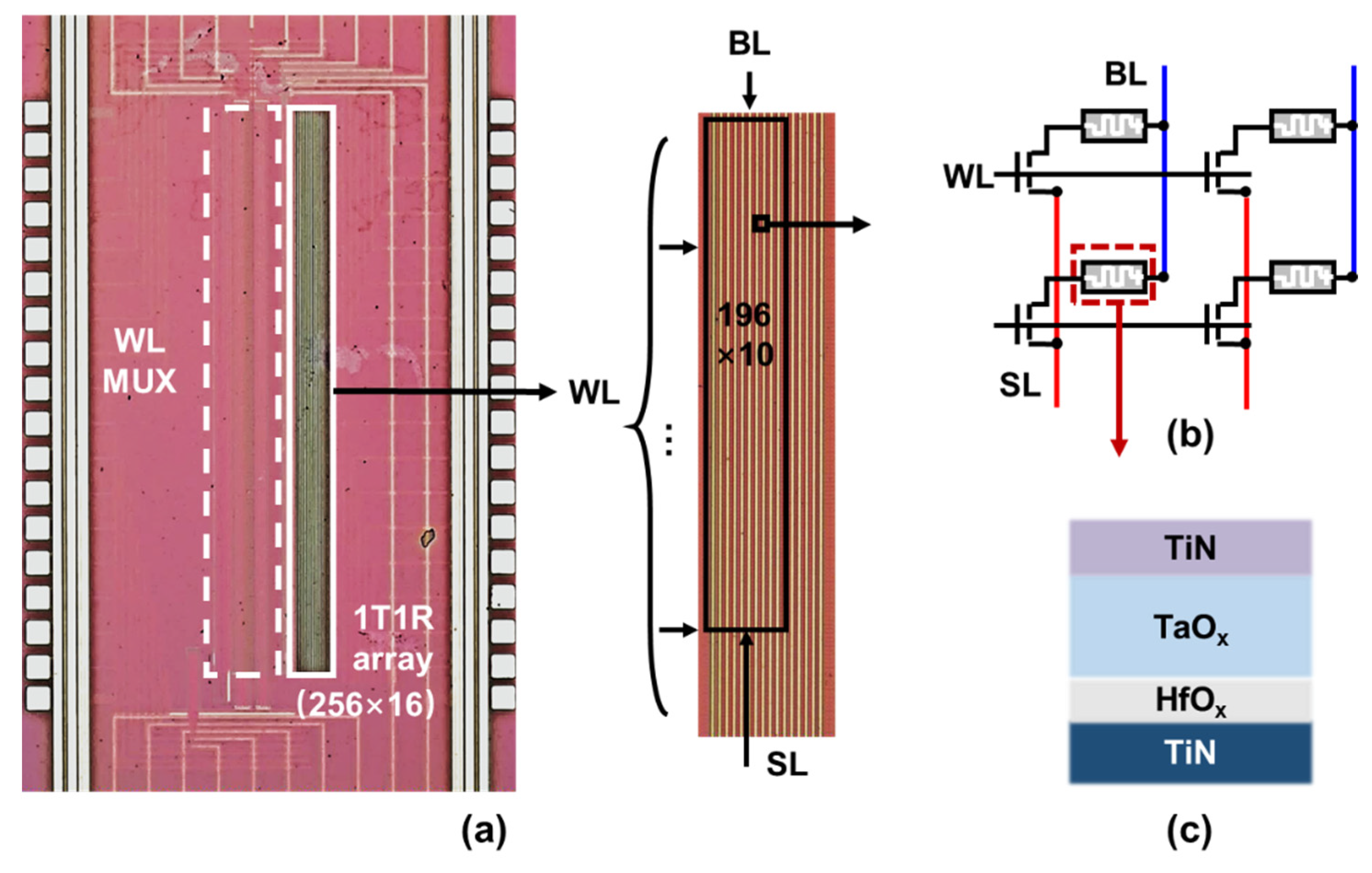
2. Memristor-Based Neuromorphic Hardware System
3. Memristor Synapse with SRDP Characteristic
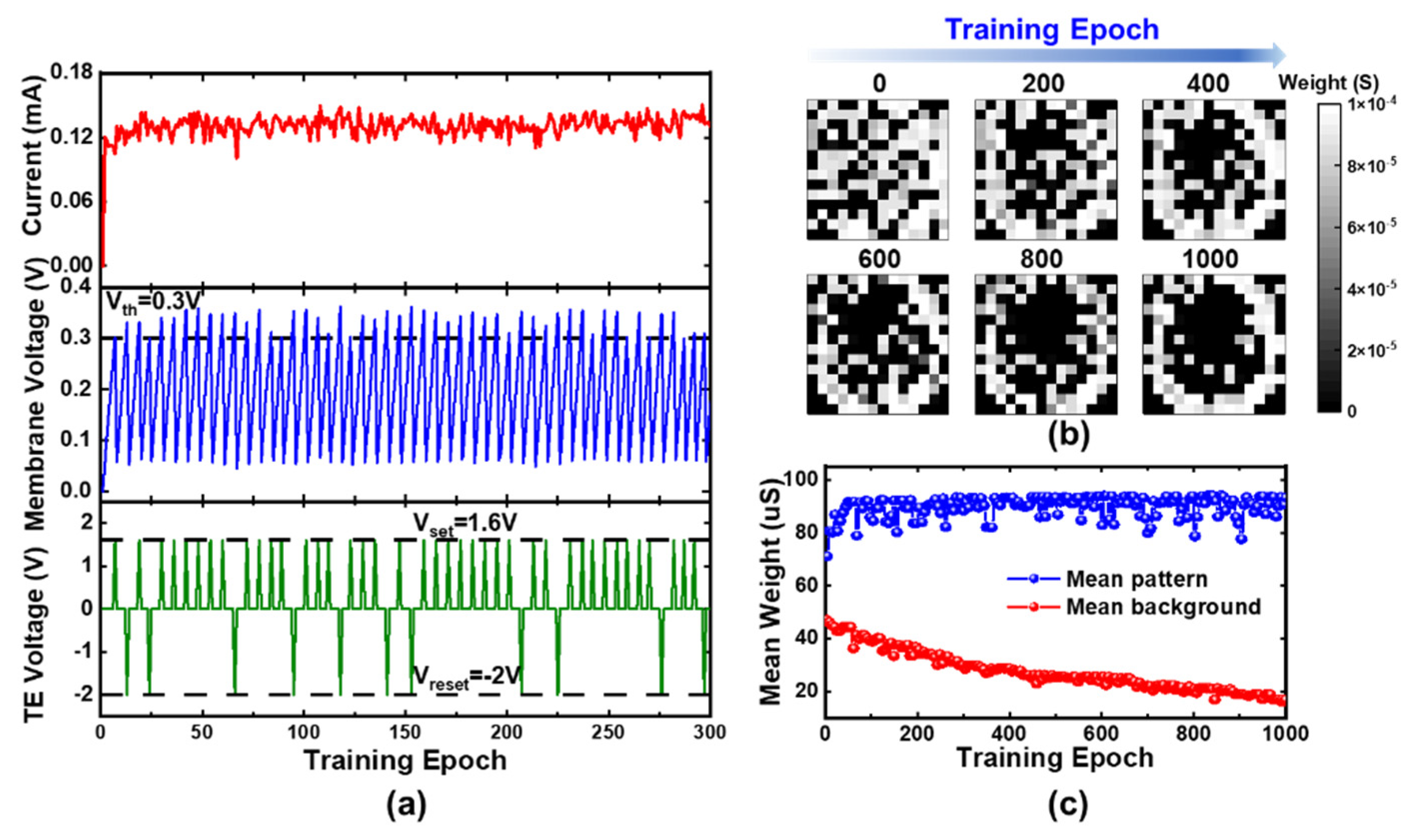
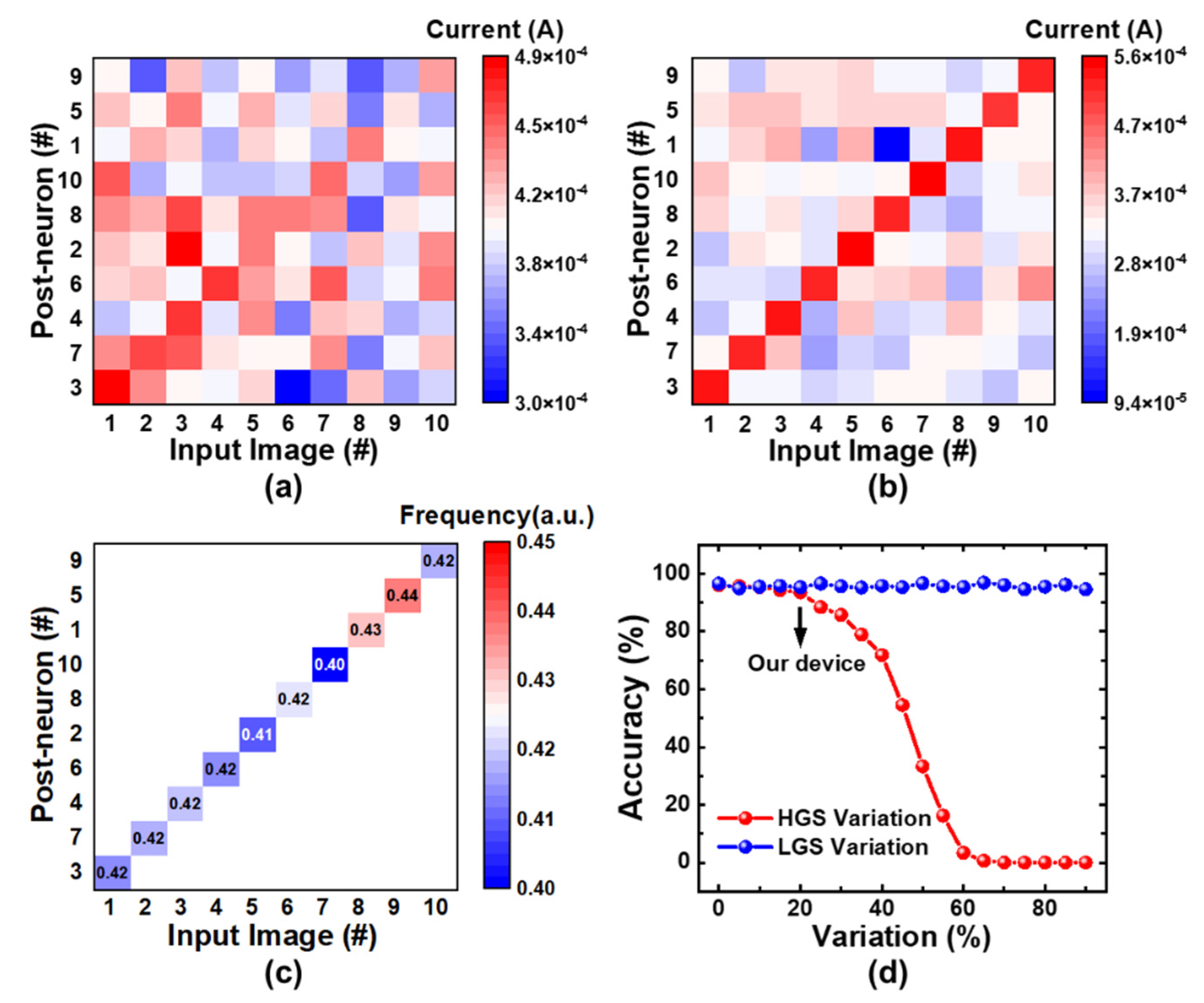
4. Online Unsupervised Learning of SRDP Network
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lennie, P. The Cost of Cortical Computation. Curr. Biol. 2003, 13, 493–497. [Google Scholar] [CrossRef] [Green Version]
- Yu, S. Introduction to Neuro-Inspired Computing Using Resistive Synaptic Devices. In Neuro-Inspired Computing Using Resistive Synaptic Devices; Yu, S., Ed.; Springer International Publishing: Tempe, AZ, USA, 2017; pp. 1–15. [Google Scholar]
- Yu, S.; Wu, Y.; Jeyasingh, R.; Kuzum, D.; Wong, H.-P. An Electronic Synapse Device Based on Metal Oxide Resistive Switching Memory for Neuromorphic Computation. IEEE Trans. Electron Devices 2011, 58, 2729–2737. [Google Scholar] [CrossRef]
- Huang, P.; Li, Z.; Dong, Z.; Han, R.; Zhou, Z.; Zhu, D.; Liu, L.; Liu, X.; Kang, J. Binary Resistive-Switching-Device-Based Electronic Synapse with Spike-Rate-Dependent Plasticity for Online Learning. ACS Appl. Electron. Mater. 2019, 1, 845–853. [Google Scholar] [CrossRef]
- Mead, C. Neuromorphic electronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef] [Green Version]
- Furber, S.; Temple, S. Neural systems engineering. J. R. Soc. Interface 2007, 4, 193–206. [Google Scholar] [CrossRef] [Green Version]
- Kuzum, D.; Jeyasingh, R.; Lee, B.; Wong, H.-P. Nanoelectronic Programmable Synapses Based on Phase Change Materials for Brain-Inspired Computing. Nano Lett. 2012, 12, 2179–2186. [Google Scholar] [CrossRef]
- Boybat, I.; Le Gallo, M.; Nandakumar, S.R.; Moraitis, T.; Parnell, T.; Tuma, T.; Rajendran, B.; Leblebici, Y.; Sebastian, A.; Eleftheriou, E. Neuromorphic computing with multi-memristive synapses. Nat. Commun. 2018, 9, 2514. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-H.; Krishna, T.; Emer, J.; Sze, V. Eyeriss: An energy-efficient reconfigurable accelerator for deep convolutional neural networks. IEEE Int. Solid-State Circuits Conf. (ISSCC) 2016, 52, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Sim, J.; Park, J.-S.; Kim, M.; Bae, D.; Choi, Y.; Kim, L.-S. A 1.42TOPS/W deep convolutional neural network recognition processor for intelligent IoE systems. IEEE Int. Solid-State Circuits Conf. (ISSCC) 2016, 14, 264–265. [Google Scholar]
- Furber, S.B.; Galluppi, F.; Temple, S.; Plana, L.A. The SpiNNaker Project. Proc. IEEE 2014, 102, 652–665. [Google Scholar] [CrossRef]
- Likharev, K.K. CrossNets: Neuromorphic hybrid CMOS/nanoelectronic networks. Sci. Adv. Mater. 2011, 3, 322–331. [Google Scholar] [CrossRef] [Green Version]
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.A.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Gao, B.; Fang, Z.; Yu, H.; Kang, J.; Wong, H.-P. A low energy oxide-based electronic synaptic device for neuromorphic visual systems with tolerance to device variation. Adv. Mater. 2013, 25, 1774–1779. [Google Scholar] [CrossRef]
- Jo, S.; Chang, T.; Ebond, I.; Bhadviya, B.; Mazumder, P.; Lu, W. Nanoscale Memristor Device as Synapse in Neuromorphic Systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef]
- Wong, H.-P.; Lee, H.; Yu, S.; Chen, Y.; Wu, Y.; Chen, P.; Lee, B.; Chen, F.T.; Tsai, M. Metal–oxide RRAM. Proc. IEEE 2012, 100, 1951–1970. [Google Scholar] [CrossRef]
- Yang, J.J.; Strukov, D.B.; Stewart, D.R. Memristive devices for computing. Nat. Nanotechnol. 2013, 8, 13–24. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Burr, G.W.; Narayanan, P.; Shelby, R.M.; Sidler, S.; Boybat, I.; di Nolfo, C.; Leblebici, Y. Large-scale neural networks implemented with non-volatile memory as the synaptic weight element: Comparative performance analysis (accuracy, speed, and power). In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 4.4.1–4.4.4. [Google Scholar]
- Sze, V.V.; Chen, Y.-H.; Yang, T.-J.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef] [Green Version]
- Lillicrap, T.P.; Cownden, D.; Tweed, D.B.; Akerman, C.J. Random synaptic feedback weights support error backpropagation for deep learning. Nat. Commun. 2016, 7, 13276. [Google Scholar] [CrossRef]
- Alibart, F.; Zamanidoost, E.; Strukov, D.B. Pattern classification by memristive crossbar circuits using ex situ and in situ training. Nat. Commun. 2013, 4, 3072. [Google Scholar] [CrossRef] [Green Version]
- Yao, P.; Wu, H.; Gao, B.; Eryilmaz, S.B.; Huang, X.; Zhang, W.; Zhang, Q.; Deng, N.; Shi, L.; Wong, H.-S.P.; et al. Face classification using electronic synapses. Nat. Commun. 2017, 8, 15199. [Google Scholar] [CrossRef] [PubMed]
- Sheridan, P.M.; Cai, F.; Du, C.; Ma, W.; Zhang, Z.; Lu, W.D. Sparse coding with memristor networks. Nat. Nanotechnol. 2017, 12, 784–789. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Ishii, M.; Lewis, S.; Perri, T.; BrightSky, M.; Kim, W.; Jordan, R.; Burr, G.W.; Sosa, N.; Ray, A.; et al. NVM neuromorphic core with 64k-cell (256-by-256) phase change memory synaptic array with on-chip neuron circuits for continuous in-situ learning. In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 17.1.1–17.1.4. [Google Scholar]
- Milo, V.; Pedretti, G.; Carboni, R.; Calderoni, A.; Ramaswamy, N.; Ambrogio, S.; Ielmini, D. A 4-Transistors/1-Resistor Hybrid Synapse Based on Resistive Switching Memory (RRAM) Capable of Spike-Rate-Dependent Plasticity (SRDP). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 2806–2815. [Google Scholar] [CrossRef]
- Serb, A.; Bill, J.; Khiat, A.; Berdan, R.; Legenstein, R.; Prodromakis, T. Unsupervised learning in probabilistic neural networks with multi-state metal-oxide memristive synapses. Nat. Commun. 2016, 7, 12611. [Google Scholar] [CrossRef] [PubMed]
- Milo, V.; Pedretti, G.; Carboni, R.; Calderoni, A.; Ramaswamy, N.; Ambrogio, S.; Ielmini, D. Demonstration of hybrid CMOS/RRAM neural networks with spike time/rate-dependent plasticity. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 16.8.1–16.8.4. [Google Scholar]
- Ambrogio, S.; Balatti, S.; Milo, V.; Carboni, R.; Wang, Z.; Calderoni, A.; Ramaswamy, N.; Ielmini, D. Novel RRAM-enabled 1T1R synapse capable of low-power STDP via burst-mode communication and real-time unsupervised machine learning. In Proceedings of the 2016 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 14–16 June 2016. [Google Scholar]
- Ambrogio, S.; Balatti, S.; Milo, V.; Carboni, R.; Wang, Z.; Calderoni, A.; Ramaswamy, N.; Ielmini, D. Neuromorphic Learning and Recognition With One-Transistor-One-Resistor Synapses and Bistable Metal Oxide RRAM. IEEE Trans. Electron Devices 2016, 63, 1508–1515. [Google Scholar] [CrossRef] [Green Version]
- Masquelier, T.; Thorpe, S.J. Unsupervised Learning of Visual Features through Spike Timing Dependent Plasticity. PLoS. Comput. Biol. 2007, 3, 0247–0257. [Google Scholar] [CrossRef]
- Suri, M.; Bichler, O.; Querlioz, D.; Palma, G.; Vianello, E.; Vuillaume, D.; Gamrat, C.; DeSalvo, B. CBRAM devices as binary synapses for low-power stochastic neuromorphic systems: Auditory (Cochlea) and visual (Retina) cognitive processing applications. In Proceedings of the 2012 International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2012; pp. 10.3.1–10.3.4. [Google Scholar]
- Diehl, P.U.; Cook, M. Unsupervised learning of digit recognition using spike-timing-dependent plasticity. Front. Comput. Neurosci. 2015, 9, 99. [Google Scholar] [CrossRef] [Green Version]
- Bi, G.Q.; Poo, M.M. Synaptic modifications in cultured hippocampal neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 1998, 18, 10464–10472. [Google Scholar] [CrossRef]
- Abbott, L.F.; Nelson, S.B. Synaptic plasticity: Taming the beast. Nat. Neurosci. 2000, 3, 1178–1183. [Google Scholar] [CrossRef]
- Bear, M.F. A synaptic basis for memory storage in the cerebral cortex. Proc. Natl. Acad. Sci. USA 1996, 93, 13453–13459. [Google Scholar] [CrossRef] [Green Version]
- Kempter, R.; Gerstner, W.; Van Hemmen, J.L. Hebbian learning and spiking neurons. Phys. Rev. E 1999, 59, 4498–4514. [Google Scholar] [CrossRef] [Green Version]
- Tan, Z.; Yang, R.; Terabe, K.; Yin, X.; Zhang, X.; Guo, X. Synaptic Metaplasticity Realized in Oxide Memristive Devices. Adv. Mater. 2016, 28, 377–384. [Google Scholar] [CrossRef] [PubMed]
- Rachmuth, G.; Shouval, H.Z.; Bear, M.F.; Poon, C.S. A biophysically-based neuromorphic model of spike rate- and timing-dependent plasticity. Proc. Natl. Acad. Sci. USA 2011, 108, E1266–E1274. [Google Scholar] [CrossRef] [Green Version]
- Bear, M.F.; Cooper, L.N.; Ebner, F.F. A physiological basis for a theory of synapse modification. Science 1987, 237, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Dudek, S.M.; Bear, M.F. Homosynaptic long-term depression in area CA1 of hippocampus and effects of N-methyl-D-aspartate receptor blockade. Proc. Natl. Acad. Sci. USA 1992, 89, 4363–4367. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.-H.; Lim, S.; Woo, S.Y.; Kang, W.-M.; Seo, Y.-T.; Lee, S.-T.; Lee, S.; Kwon, D.; Oh, S.; Noh, Y.; et al. Emerging memory technologies for neuromorphic computing. Nanotechnology 2018, 30, 032001. [Google Scholar] [CrossRef]
- Wang, Z.; Joshi, S.; Savel’ev, S.E.; Jiang, H.; Midya, R.; Lin, P.; Hu, M.; Ge, N.; Strachan, J.P.; Li, Z.; et al. Memristors with diffusive dynamics as synaptic emulators for neuromorphic computing. Nat. Mater. 2017, 16, 101–108. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Zeng, F.; Wan, W.; Li, F.; Sun, Y.; Hu, Y.; Liu, J.; Li, G.; Pan, F. Adaptive Crystallite Kinetics in Homogenous Bilayer Oxide Memristor for Emulating Diverse Synaptic Plasticity. Adv. Funct. Mater. 2018, 28, 1706927.1–1706927.10. [Google Scholar] [CrossRef]
- Ziegler, M.; Riggert, C.; Hansen, M.; Bartsch, T.; Kohlstedt, H. Memristive Hebbian plasticity model: Device requirements for the emulation of Hebbian plasticity based on memristive devices. IEEE Trans. Biomed. Circuits Syst. 2015, 9, 197–206. [Google Scholar] [CrossRef]
- Li, Y.; Zhong, Y.; Zhang, J.; Xu, L.; Wang, Q.; Sun, H.; Tong, H.; Cheng, X.; Miao, X. Activity-dependent synaptic plasticity of a chalcogenide electronic synapse for neuromorphic systems. Sci. Rep. 2014, 4, 4906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ohno, T.; Hasegawa, T.; Tsuruoka, T.; Terabe, K.; Gimzewski, J.K.; Aono, M. Short-term plasticity and long-term potentiation mimicked in single inorganic synapses. Nat. Mater. 2011, 10, 591–595. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Z.; Huang, J. Energy-Efficient Hybrid Perovskite Memristors and Synaptic Devices. Adv. Electron. Mater. 2016, 2, 1600100. [Google Scholar] [CrossRef]
- Kim, B.-Y.; Hwang, H.-G.; Woo, J.-U.; Lee, W.-H.; Lee, T.-H.; Kang, C.-Y.; Nahm, S. Nanogenerator-induced synaptic plasticity and metaplasticity of bio-realistic artificial synapses. Npg Asia. Mater. 2017, 9, e381. [Google Scholar] [CrossRef] [Green Version]
- Covi, E.; Brivio, S.; Serb, A.; Prodromakis, T.; Fanciulli, M.; Spiga, S. Analog memristive synapse in spiking networks implementing unsupervised learning. Front. Neurosci. 2016, 10, 482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boyn, S.; Grollier, J.; Lecerf, G.; Xu, B.; Locatelli, N.; Fusil, S.; Girod, S.; Carrétéro, C.; Garcia, K.; Xavier, S.; et al. Learning through ferroelectric domain dynamics in solid-state synapses. Nat. Commun. 2017, 8, 14736. [Google Scholar] [CrossRef]
- He, W.; Huang, K.; Ning, N.; Ramanathan, K.; Li, G.; Jiang, Y.; Sze, J.; Shi, L.; Zhao, R.; Pei, J. Enabling an Integrated Rate-temporal Learning Scheme on Memristor. Sci. Rep. 2014, 4, 04755. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]



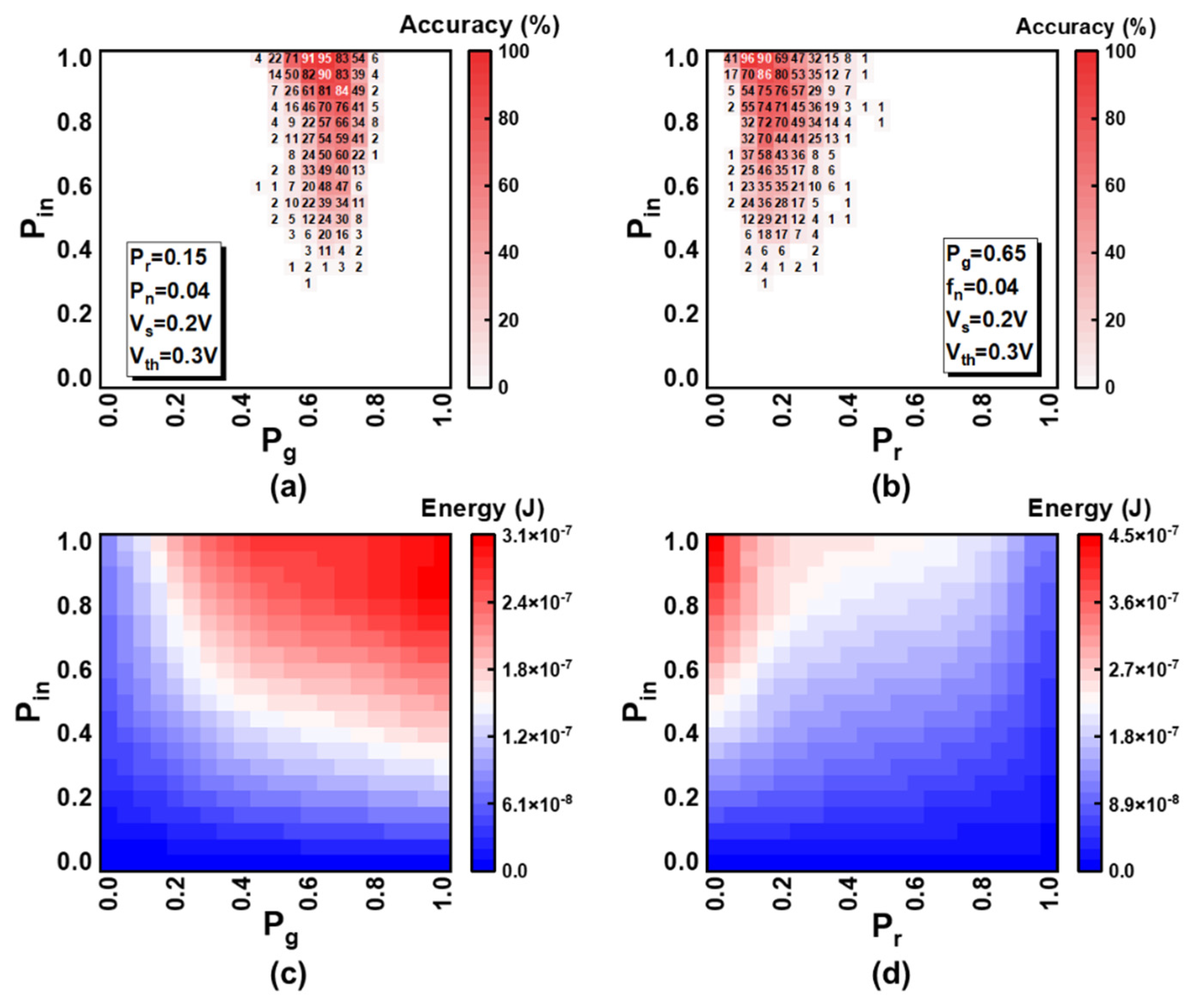
| Parameter | Definition | Value | Unit |
|---|---|---|---|
| Vs | Constant voltage to the top electrode | 0.2 | V |
| Vth | Threshold of the membrane voltage | 0.3 | V |
| Pg | Probability to be in HGS of synaptic weights in the initial state | 0.65 | a.u. |
| Pr | Frequency of the reference random signal | 0.15 | a.u. |
| Pn | Frequency of the noise signal | 0.04 | a.u. |
| Pin | Frequency of the input signal in the pattern pixels | 1 | a.u. |
| Pb | Frequency of the input signal in the background pixels | 0 | a.u. |
| tn | Training epoch of each image | 600 | # |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Huang, P.; Feng, Y.; Zhou, Z.; Zhang, Y.; Ding, X.; Liu, L.; Kang, J. Hardware Demonstration of SRDP Neuromorphic Computing with Online Unsupervised Learning Based on Memristor Synapses. Micromachines 2022, 13, 433. https://doi.org/10.3390/mi13030433
Li R, Huang P, Feng Y, Zhou Z, Zhang Y, Ding X, Liu L, Kang J. Hardware Demonstration of SRDP Neuromorphic Computing with Online Unsupervised Learning Based on Memristor Synapses. Micromachines. 2022; 13(3):433. https://doi.org/10.3390/mi13030433
Chicago/Turabian StyleLi, Ruiyi, Peng Huang, Yulin Feng, Zheng Zhou, Yizhou Zhang, Xiangxiang Ding, Lifeng Liu, and Jinfeng Kang. 2022. "Hardware Demonstration of SRDP Neuromorphic Computing with Online Unsupervised Learning Based on Memristor Synapses" Micromachines 13, no. 3: 433. https://doi.org/10.3390/mi13030433
APA StyleLi, R., Huang, P., Feng, Y., Zhou, Z., Zhang, Y., Ding, X., Liu, L., & Kang, J. (2022). Hardware Demonstration of SRDP Neuromorphic Computing with Online Unsupervised Learning Based on Memristor Synapses. Micromachines, 13(3), 433. https://doi.org/10.3390/mi13030433






