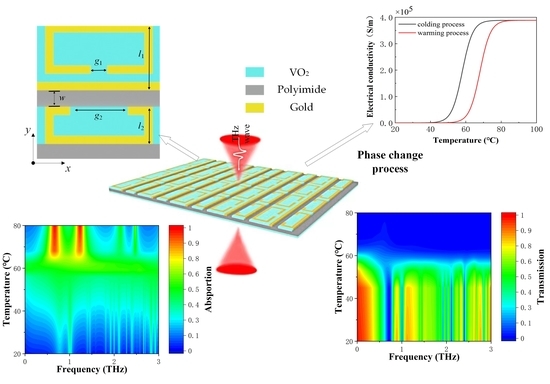
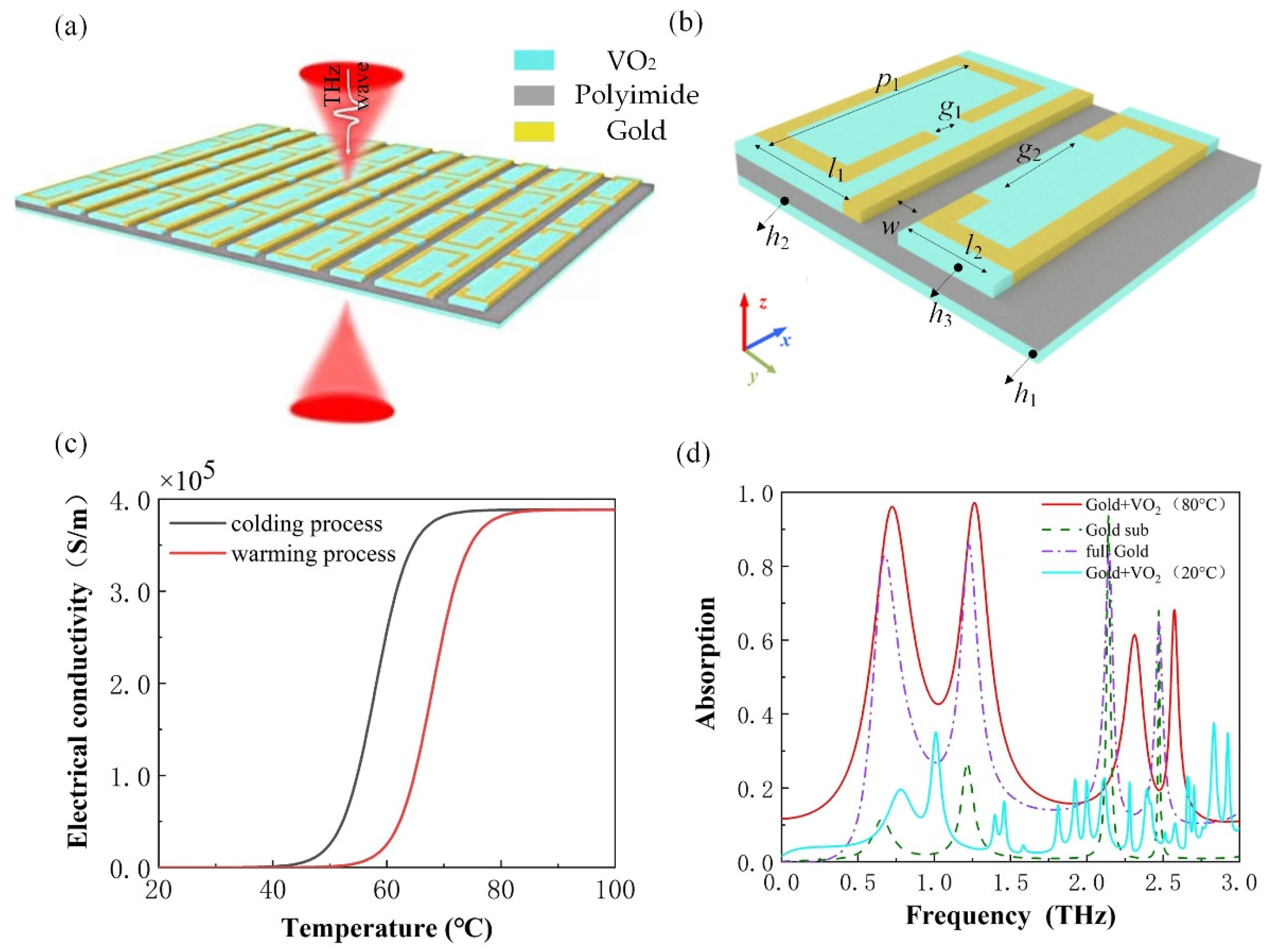
Vanadium Dioxide-Based Terahertz Metamaterial Devices Switchable between Transmission and Absorption
Abstract
:1. Introduction
2. Materials and Methods
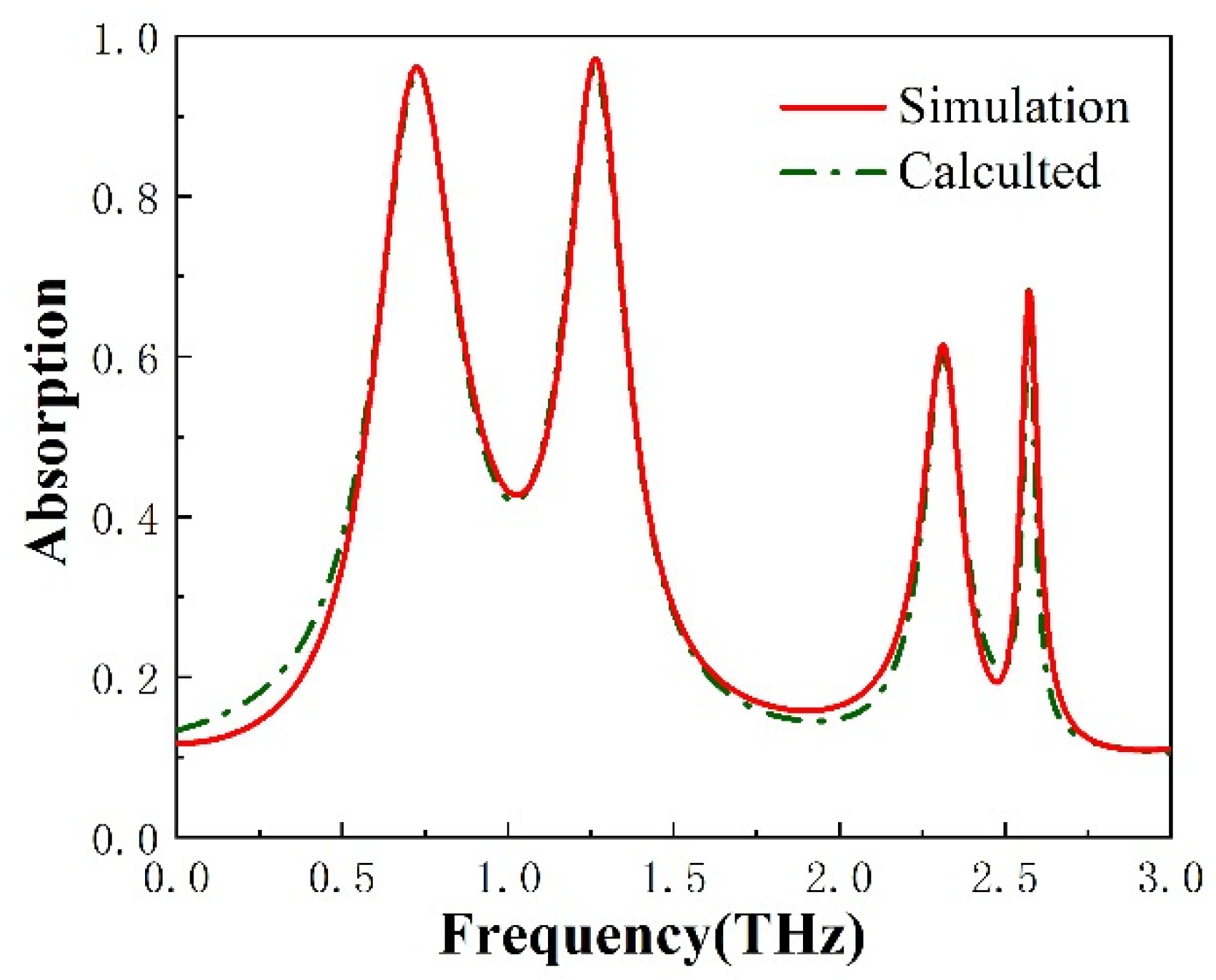
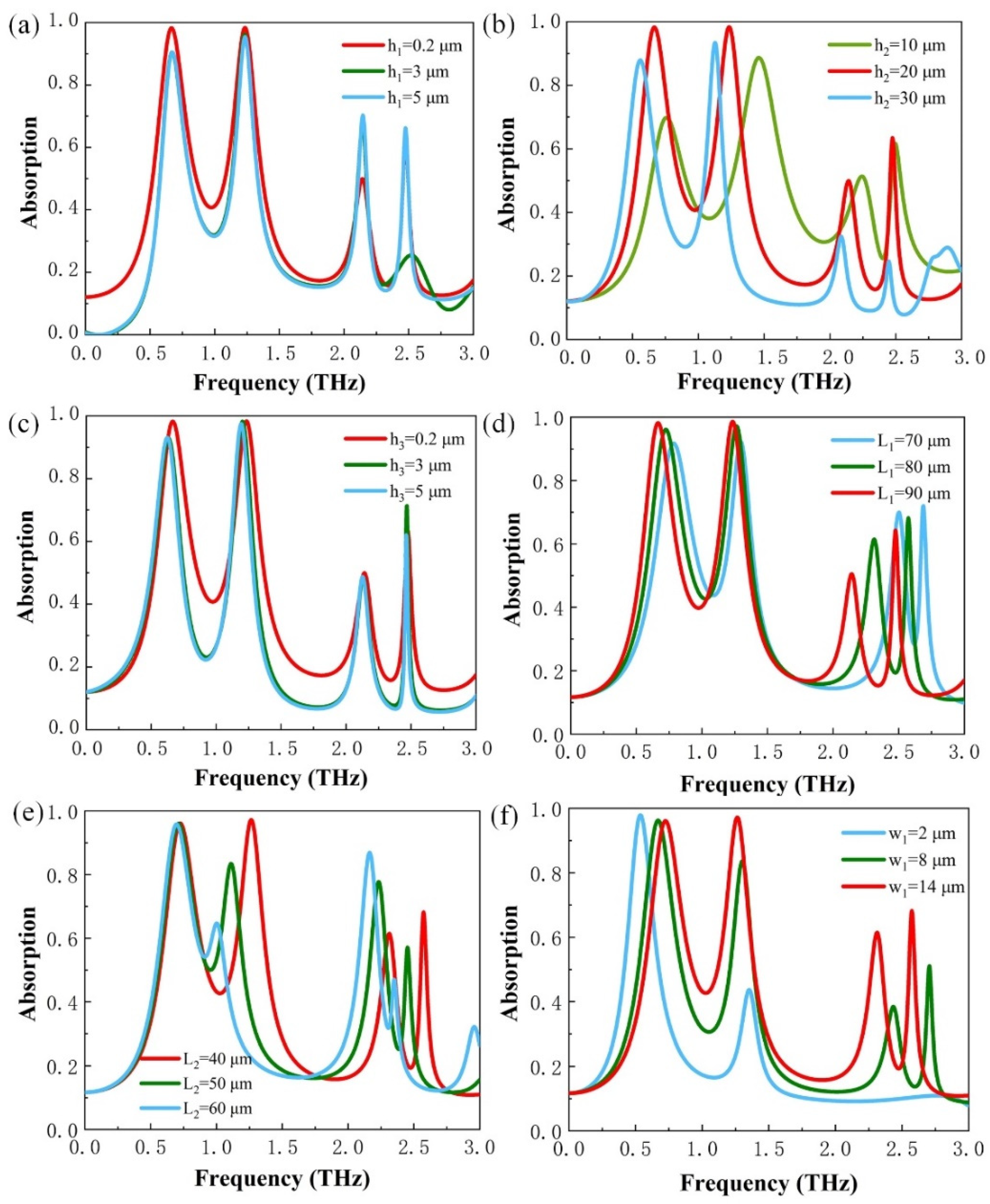
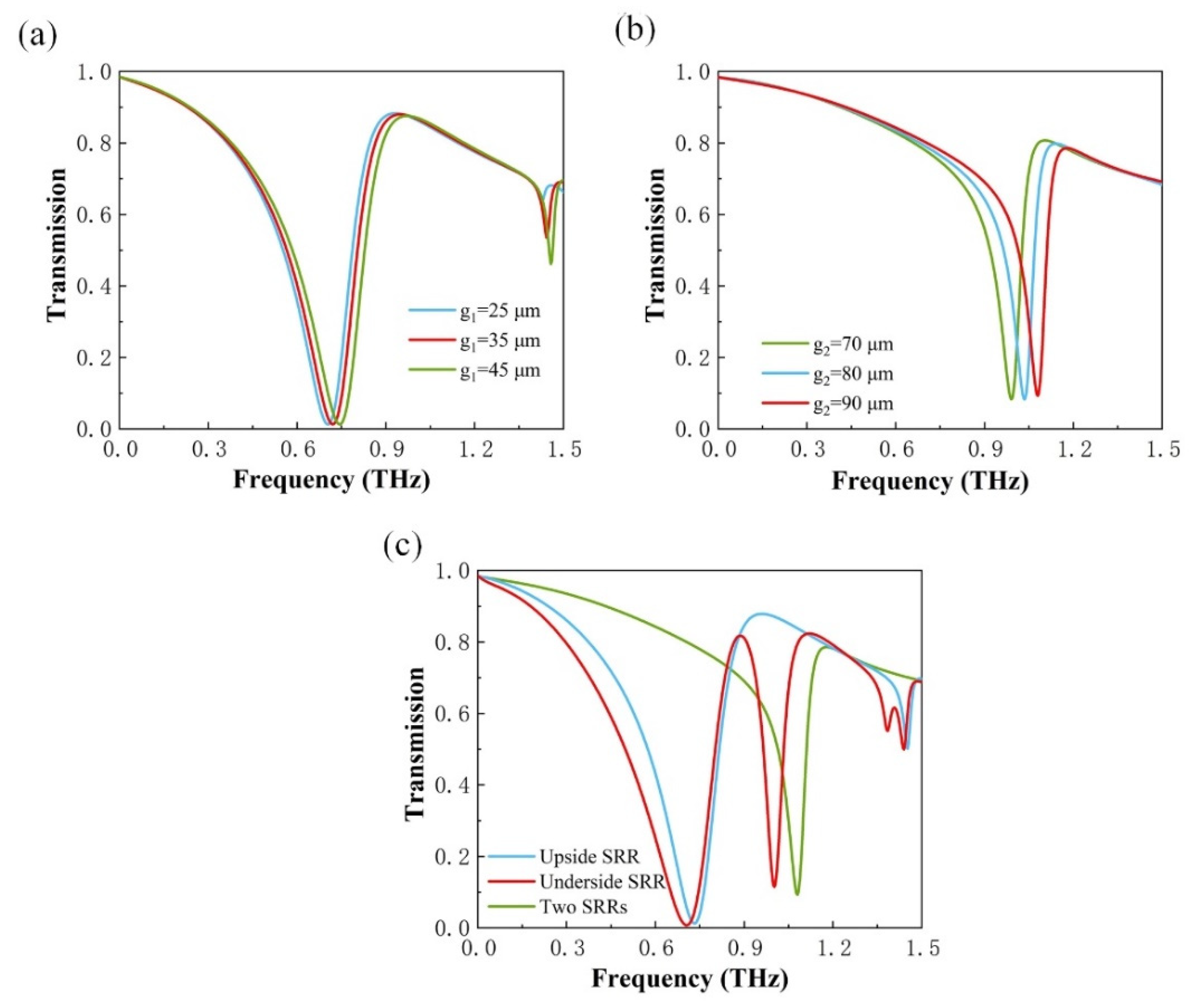
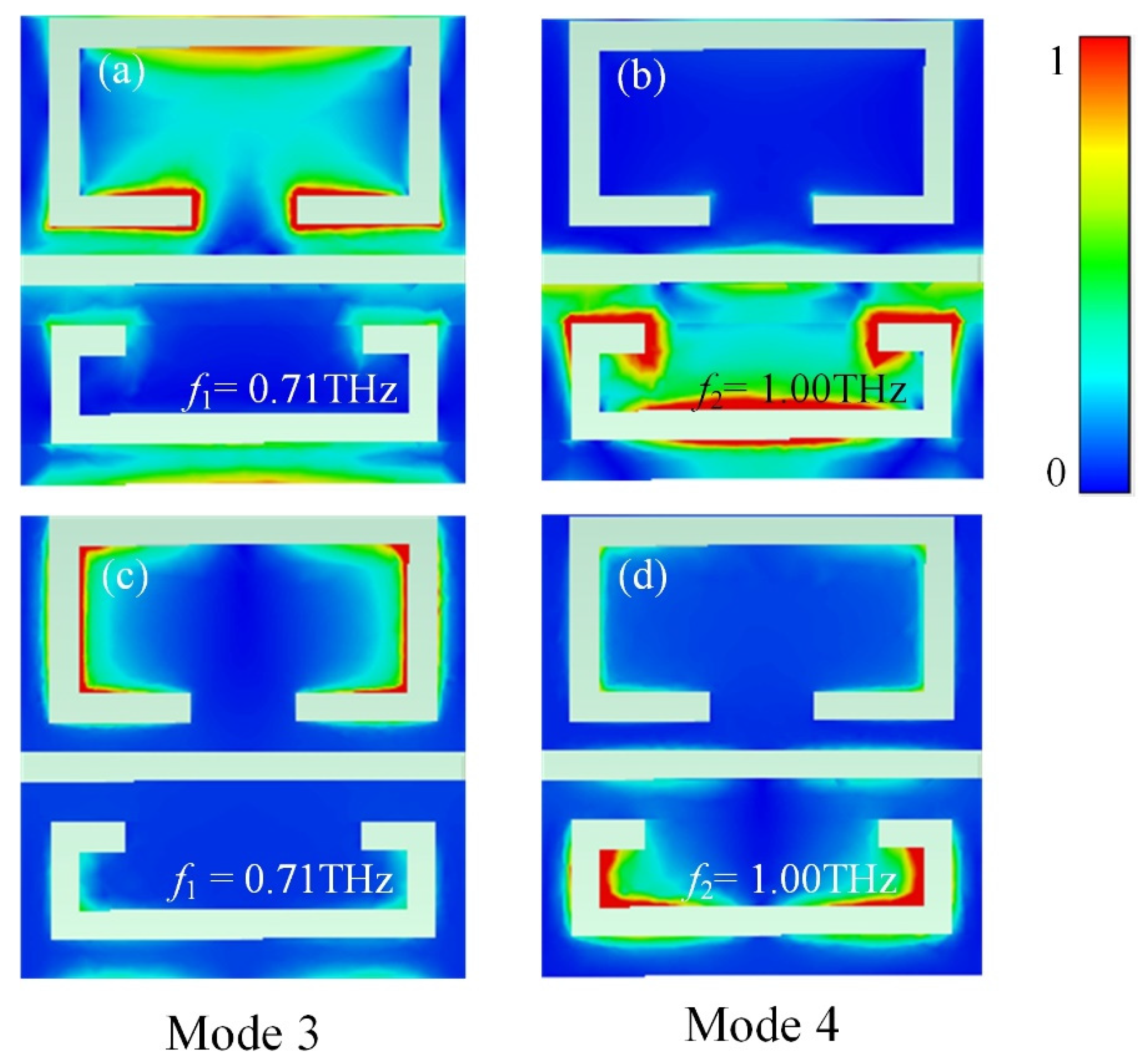
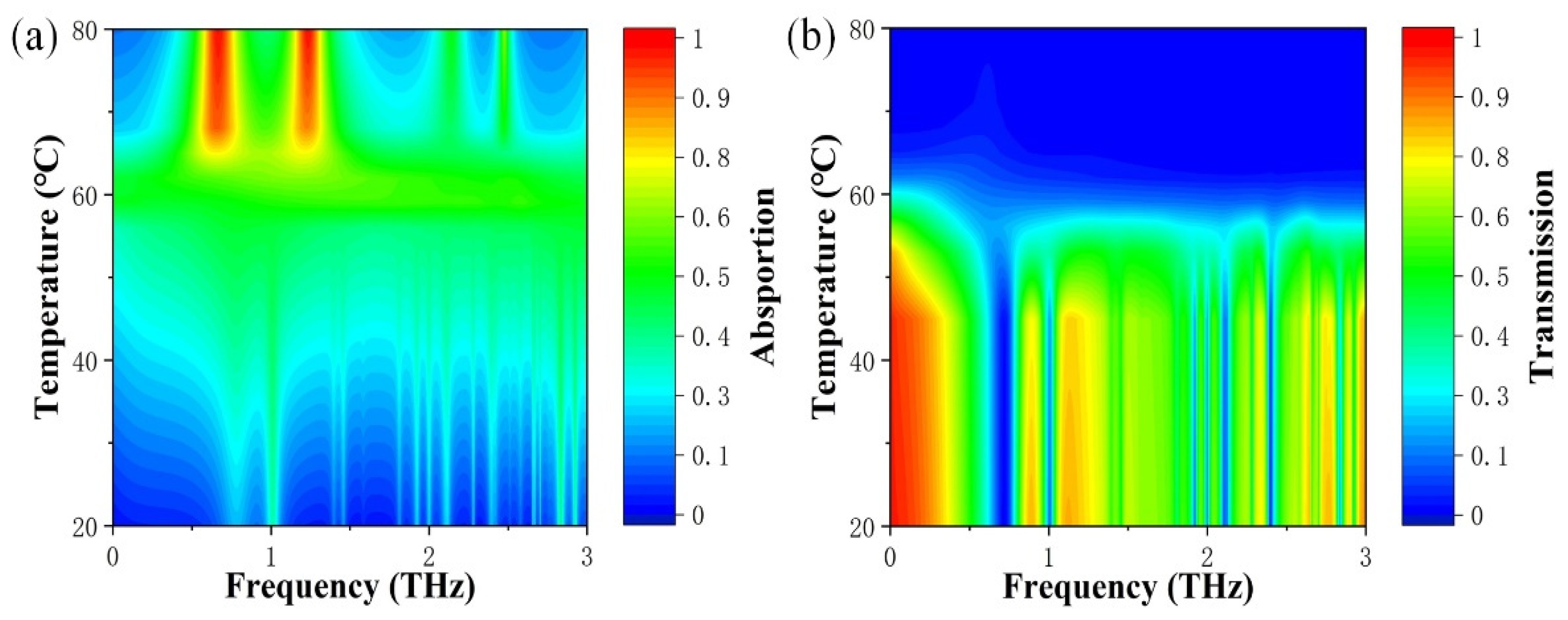
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nagatsuma, T.; Ducournau, G.; Renaud, C.C. Advances in terahertz communications accelerated by photonics. Nat. Photonics 2016, 10, 371–379. [Google Scholar] [CrossRef]
- Serita, K.; Matsuda, E.; Okada, K.; Murakami, H.; Kawayama, I.; Tonouchi, M. Terahertz microfluidic chips sensitivity-enhanced with a few arrays of meta-atoms. APL Phontonics 2018, 3, 10. [Google Scholar]
- Williams, G.P. Filling the THz gap—High power sources and applications. Rep. Prog. Phys. 2006, 69, 301–326. [Google Scholar] [CrossRef]
- Shalaev, V.M. Optical negative-index metamaterials. Nat. Photonics 2007, 1, 41–48. [Google Scholar] [CrossRef]
- Savo, S.; Shrekenhamer, D.; Padilla, W.J. Liquid crystal metamaterial absorber spatial light modulator for THz applications. Adv. Opt. Mater. 2014, 2, 275–279. [Google Scholar] [CrossRef]
- Iwaszczuk, K.; Strikwerda, A.C.; Fan, K.B.; Zhang, X.; Averitt, R.D.; Jepsen, P.U. Flexible metamaterial absorbers for stealth applications at terahertz frequencies. Opt. Express 2012, 20, 635–643. [Google Scholar] [CrossRef] [Green Version]
- Fu, X.M.; Wang, J.F.; Fan, Y.; Feng, M.D.; Yan, M.B.; Li, Y.F.; Chen, H.Y.; Zhang, J.Q.; Qu, S.B. Merging bands of polarization convertors by suppressing Fano resonance. Appl. Phys. Lett. 2018, 113, 4. [Google Scholar] [CrossRef]
- Wang, B.X. Quad-band terahertz metamaterial absorber based on the combining of the dipole and quadrupole resonances of two SRRs. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–7. [Google Scholar] [CrossRef]
- Ferraro, A.; Zografopoulos, D.C.; Caputo, R.; Beccherelli, R. Periodical Elements as low-cost building blocks for tunable terahertz filters. IEEE Photon.Technol. Lett. 2016, 28, 2459–2462. [Google Scholar] [CrossRef]
- Qi, L.M.; Liu, C.; Shah, S.M.A. A broad dual-band switchable graphene-based terahertz metamaterial absorber. Carbon 2019, 153, 179–188. [Google Scholar] [CrossRef]
- Bang, S.; Kim, J.; Yoon, G.; Tanaka, T.; Rho, J. Recent advances in tunable and reconfigurable metamaterials. Micromachines 2018, 9, 560. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hashemi, M.R.M.; Yang, S.H.; Wang, T.; Sepúlveda, N.; Jarrahi, M. Electronically-controlled beam-steering through vanadium dioxide metasurfaces. Sci. Rep. 2016, 6, 35439. [Google Scholar] [CrossRef] [PubMed]
- Kowerdziej, R.; Jaroszewicz, L. Active control of terahertz radiation using a metamaterial loaded with a nematic liquid crystal. Liq. Cryst. 2016, 43, 1120–1125. [Google Scholar] [CrossRef]
- He, X.Y.; Zhao, Z.Y.; Shi, W.Z. Graphene-supported tunable near-IR metamaterials. Opt. Lett. 2015, 40, 178–181. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, S.; Sun, L.; Shi, Q.W.; Huang, W.; Li, L.; Yang, Z. Photoinduced active terahertz metamaterials with nanostructured vanadium dioxide film deposited by sol-gel method. Opt Express 2014, 22, 11070–11078. [Google Scholar] [CrossRef]
- Jeong, Y.G.; Bernien, H.; Kyoung, J.S.; Park, H.R.; Kim, H.S.; Choi, J.W.; Kim, B.J.; Kim, H.T.; Ahn, K.J.; Kim, D.S. Electrical control of terahertz nano antennas on VO2 thin film. Opt. Express 2011, 19, 21211–21215. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Vegesna, S.; Zhao, Y.; Kuryatkov, V.; Holtz, M.; Fan, Z.Y.; Saed, M.; Bernussi, A.A. Tunable dual-band terahertz metamaterial bandpass filters. Opt. Lett. 2013, 38, 2382–2384. [Google Scholar] [CrossRef]
- Wen, Q.Y.; Zhang, H.W.; Yang, Q.H.; Xie, Y.S.; Chen, K.; Liu, Y.L. Terahertz metamaterials with VO2 cut-wires for thermal tunability. Appl. Phys. Lett. 2010, 97, 021111. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, G.; Wu, J.; Tang, Y.; Wen, Q.; Li, S.; Han, J.; Jin, B.; Chen, J.; Wu, P. Active control of terahertz waves using vanadium-dioxide-embedded metamaterials. Phys. Rev. A 2019, 11, 054016. [Google Scholar] [CrossRef]
- Liu, H.; Lu, J.; Wang, X.R. Metamaterials based on the phase transition of VO2. Nanotechnology 2017, 29, 024002. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, T.; Paudel, T.; Zhang, Y.; Ren, Z.; Kempa, K. Metamaterial-plasmonic absorber structure for high efficiency amorphous silicon solar cells. Nano Lett. 2012, 12, 440–445. [Google Scholar] [CrossRef] [PubMed]
- Yi, Z.; Liang, C.P.; Chen, X.F.; Zhou, Z.G.; Tang, Y.J.; Ye, X.; Yi, Y.G.; Wang, J.Q.; Wu, P.H. Dual-band plasmonic perfect absorber based on graphene metamaterials for refractive index sensing application. Micromachines 2019, 10, 443. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zou, H.; Cheng, Y. Design of a six-band terahertz metamaterial absorber for temperature sensing application. Opt. Mater. 2019, 88, 674–679. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Zhang, H.; Cao, M. Dual-controlled switchable broadband terahertz absorber based on a graphene-vanadium dioxide metamaterial. Opt. Mater. Express 2020, 10, 369–386. [Google Scholar] [CrossRef]
- Hu, F.; Rong, Q.; Zhou, Y.; Li, T.; Zhang, W.; Yin, S.; Chen, Y.; Han, J.; Jiang, G.; Zhu, P.; et al. Terahertz intensity modulator based on low current controlled vanadium dioxide composite metamaterial. Opt. Commun. 2019, 440, 184–189. [Google Scholar] [CrossRef]
- Zhao, S.; Hu, F.; Xu, X.; Jiang, M.; Zhang, W.; Yin, S.; Jiang, W. Electrically triggered dual-band tunable terahertz metamaterial band-pass filter based on Si3N4–VO2–Si3N4 sandwich. Chin. Phys. B 2019, 28, 054203. [Google Scholar] [CrossRef]
- Vikhnin, V.S.; Lysenko, S.; Rua, A.; Fernandez, F.; Liu, H. The model of metal–insulator phase transition in vanadium oxide. Phys. Lett. A 2005, 343, 446–453. [Google Scholar] [CrossRef]
- Hendry, E.; Koeberg, M.; O’Regan, B.; Bonn, M. Local field effects on electron transport in nanostructured TiO2 revealed by terahertz spectroscopy. Nano Lett. 2006, 6, 755–759. [Google Scholar] [CrossRef]
- Liu, M.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.; Eiser, G.R.; Ternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.; et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 2012, 487, 345–348. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, Z.M.M. Strong plasmonic coupling between graphene ribbon array and metal gratings. ACS Photonics 2015, 2, 1611–1618. [Google Scholar] [CrossRef]
- Yong, Z.D.; Zhang, S.L.; Gong, C.S.; He, S.L. Narrow band perfect absorber for maximum localized magnetic and electric field enhancement and sensing applications. Sci. Rep. 2016, 6, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yue, L.; Wang, Y.; Cui, Z.; Zhang, X.; Zhu, Y.; Zhang, X.; Chen, S.; Wang, X.; Zhang, K. Multi-band terahertz resonant absorption based on an all-dielectric grating metasurface for chlorpyrifos sensing. Opt. Express 2021, 29, 13563–13575. [Google Scholar] [CrossRef] [PubMed]
- Chau, Y.F.C.; Chou Chao, C.T.; Lim, C.M.; Huang, H.J.; Chiang, H.P. Deploying tunable metal-shell/dielectric core nanorod arrays as the virtually perfect absorber in the near-infrared regime. ACS Omega 2018, 3, 7508–7516. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.G.; Gramotnev, D.K.; Pors, A.; Albrektsen, O.; Bozhevolnyi, S.I. Continuous layer gap plasmon resonators. Opt. Express 2011, 19, 19310–19322. [Google Scholar] [CrossRef] [PubMed]
- Haus, H.A. Waves and Fields in Optoelectronics~Prentice Hall; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984; pp. 197–2350. [Google Scholar]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.T. Interference theory of metamaterial perfect absorbers. Opt. Express 2012, 20, 7165–7172. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cen, C.; Chen, Z.; Xu, D.; Jiang, L.; Chen, X.; Yi, Z.; Wu, P.; Li, G.; Yi, Y. High quality factor, high sensitivity metamaterial graphene—perfect absorber based on critical coupling theory and impedance matching. Nanomaterials 2020, 10, 95. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.; Charipar, N.; Breckenfeld, E.; Rosenberg, A.; Piqué, A. Active terahertz metamaterials based on the phase transition of VO2 thin films. Thin Solid Film. 2015, 596, 45–50. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.V.; Tatarenko, A.Y.; Gorodetsky, A.A.; Makarevich, O.N.; Navarro-Cía, M.; Makarevich, A.M.; Kaul, A.R.; Eliseev, A.A.; Boytsova, O.V. Fabrication of epitaxial W-doped VO2 nanostructured films for terahertz modulation using the solvothermal process. ACS Appl. Nano Mater. 2021, 4, 10592–10600. [Google Scholar] [CrossRef]
- Zheng, Z.P.; Zheng, Y.; Luo, Y.; Yi, Z.; Zhang, J.G.; Liu, Z.M.; Yang, W.X.; Yu, Y.; Wu, X.W.; Wu, P.H. Thermal tuning of terahertz metamaterial absorber properties based on VO2. Phys. Chem. Chem. Phys. 2022, in press. [CrossRef]
- Lai, W.E.; Shi, R.; Yuan, H.; Liu, G.; Amini, A.; Cheng, C. Fully optically tunable and flexible composite films for enhanced terahertz control and multifunctional terahertz devices. ACS Appl. Electron. Mater. 2021, 3, 3044–3051. [Google Scholar] [CrossRef]
- Zheng, Z.P.; Zheng, Y.; Luo, Y.; Yi, Z.; Zhang, J.G.; Liu, Z.M.; Yang, W.X.; Yu, Y.; Wu, X.W.; Wu, P.H. A switchable terahertz device combining ultra-wideband absorption and ultra-wideband complete reflection. Phys. Chem. Chem. Phys. 2022, 24, 2527–2533. [Google Scholar] [CrossRef]
- Arezoomandan, S.; Gopalan, P.; Tian, K.; Chanana, A.; Nahata, A.; Tiwari, A.; Sensale-Rodriguez, B. Tunable terahertz metamaterials employing layered 2-D materials beyond graphene. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 188–194. [Google Scholar] [CrossRef]
- Ozbey, B.; Aktas, O. Continuously tunable terahertz metamaterial employing magnetically actuated cantilevers. Opt. Express 2011, 19, 5741–5752. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| Material | Electric Conductivity | Thermal Conductivity | Epsilon | Tangent Delta |
|---|---|---|---|---|
| Gold | 4.56 × 107 S/m | 314 W/K/m | / | / |
| Polyimide | / | 0.2 W/K/m | 3.5 + 0.00945i F/m | 0.0027% |
| Sample Type | Number of Layers | Frequency (THz) | Modulation Type | Modulation Depth | Practical Implementation | Multifunction | Ref |
|---|---|---|---|---|---|---|---|
| VO2 | 2 | 0.1–1.0 | Transmission | 50% | device | no | [39] |
| W-doped VO2 | 2 | 0.3–2.3 | Transmission | 60% | device | no | [40] |
| VO2 | 3 | 3.7–9.7 | Absorption | 99.9% | model | no | [41] |
| VO2 nanowires | 3 | 0.3–0.5 | Polarization & Transmission | 65% | device | yes | [42] |
| VO2 | 3 | 3.4–6.7 | Reflection & Absorption | 99.8% | model | yes | [43] |
| MoS2 | 3 | 0.6–1.2 | Transmission | 20% | device | no | [44] |
| Si3N4 | 4 | 0.2–0.7 | transmission | 25% | device | no | [45] |
| VO2 | 3 | 0.1–3.0 | Transmission & Absorption | 94.2% | model | yes | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Wang, Y.; Cui, Z.; Zhang, X.; Zhu, Y.; Zhang, K. Vanadium Dioxide-Based Terahertz Metamaterial Devices Switchable between Transmission and Absorption. Micromachines 2022, 13, 715. https://doi.org/10.3390/mi13050715
Jiang H, Wang Y, Cui Z, Zhang X, Zhu Y, Zhang K. Vanadium Dioxide-Based Terahertz Metamaterial Devices Switchable between Transmission and Absorption. Micromachines. 2022; 13(5):715. https://doi.org/10.3390/mi13050715
Chicago/Turabian StyleJiang, Haoqing, Yue Wang, Zijian Cui, Xiaoju Zhang, Yongqiang Zhu, and Kuang Zhang. 2022. "Vanadium Dioxide-Based Terahertz Metamaterial Devices Switchable between Transmission and Absorption" Micromachines 13, no. 5: 715. https://doi.org/10.3390/mi13050715
APA StyleJiang, H., Wang, Y., Cui, Z., Zhang, X., Zhu, Y., & Zhang, K. (2022). Vanadium Dioxide-Based Terahertz Metamaterial Devices Switchable between Transmission and Absorption. Micromachines, 13(5), 715. https://doi.org/10.3390/mi13050715