Numerical Study of Heat Transfer Enhancement within Confined Shell and Tube Latent Heat Thermal Storage Microsystem Using Hexagonal PCMs
Abstract
:1. Introduction
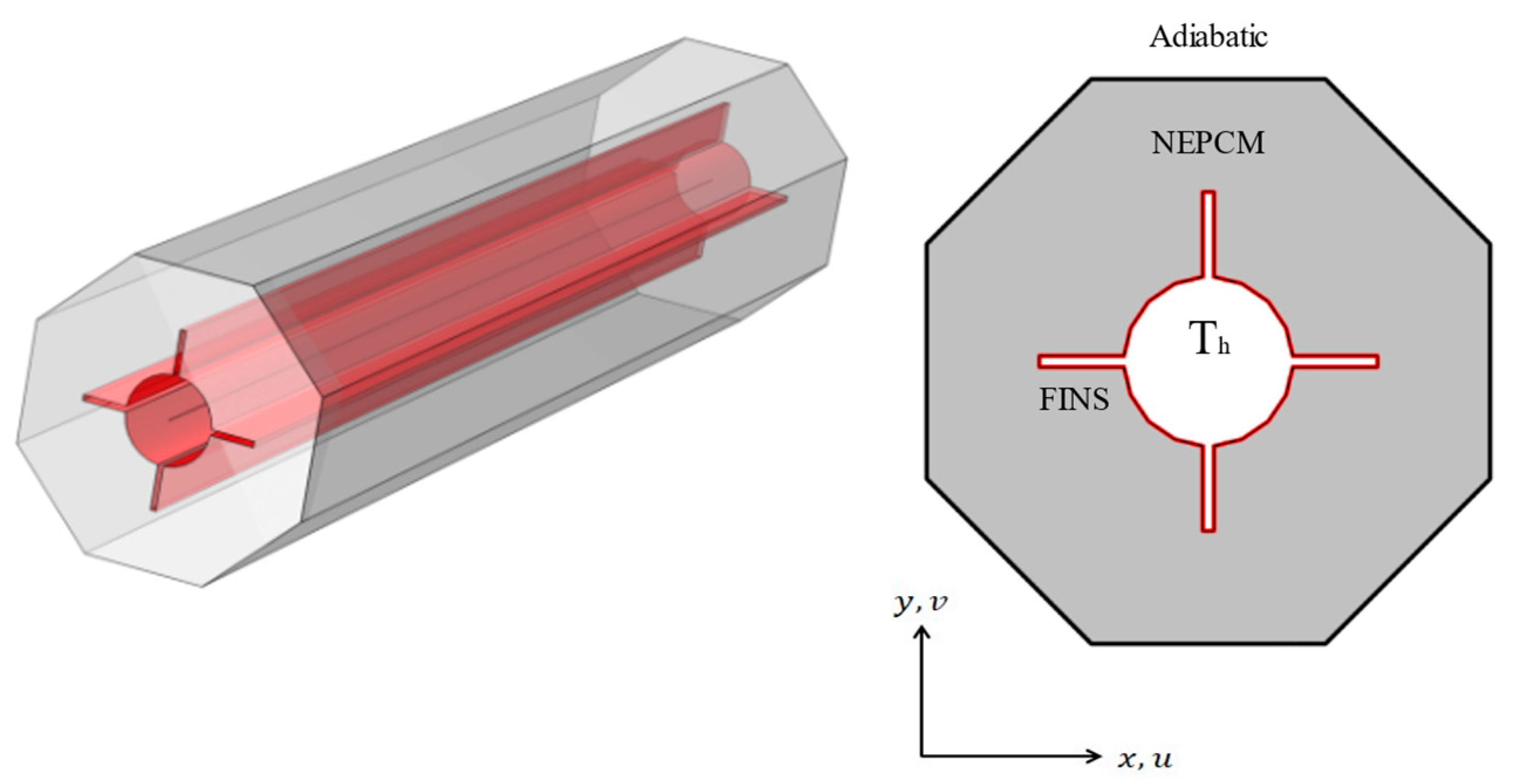
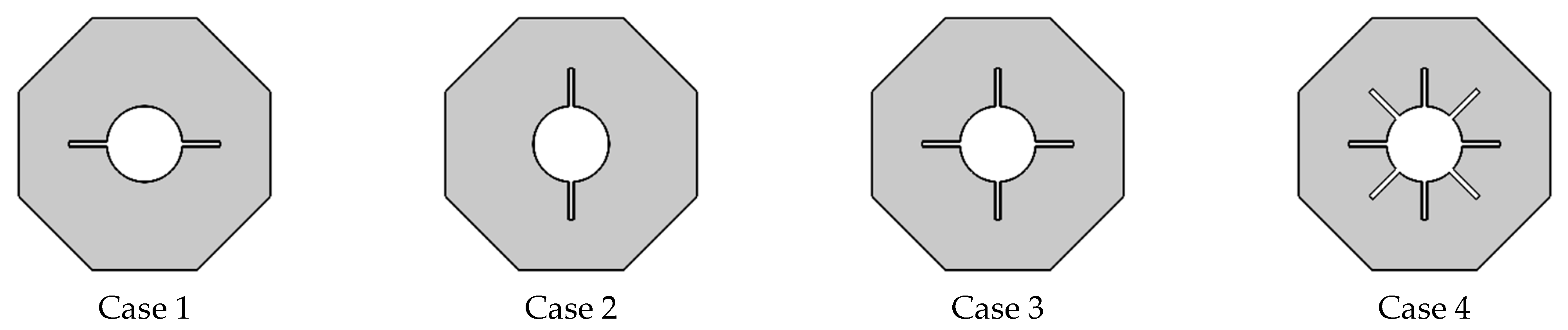
2. Methodology and Problem Definition
2.1. Problem Formulation
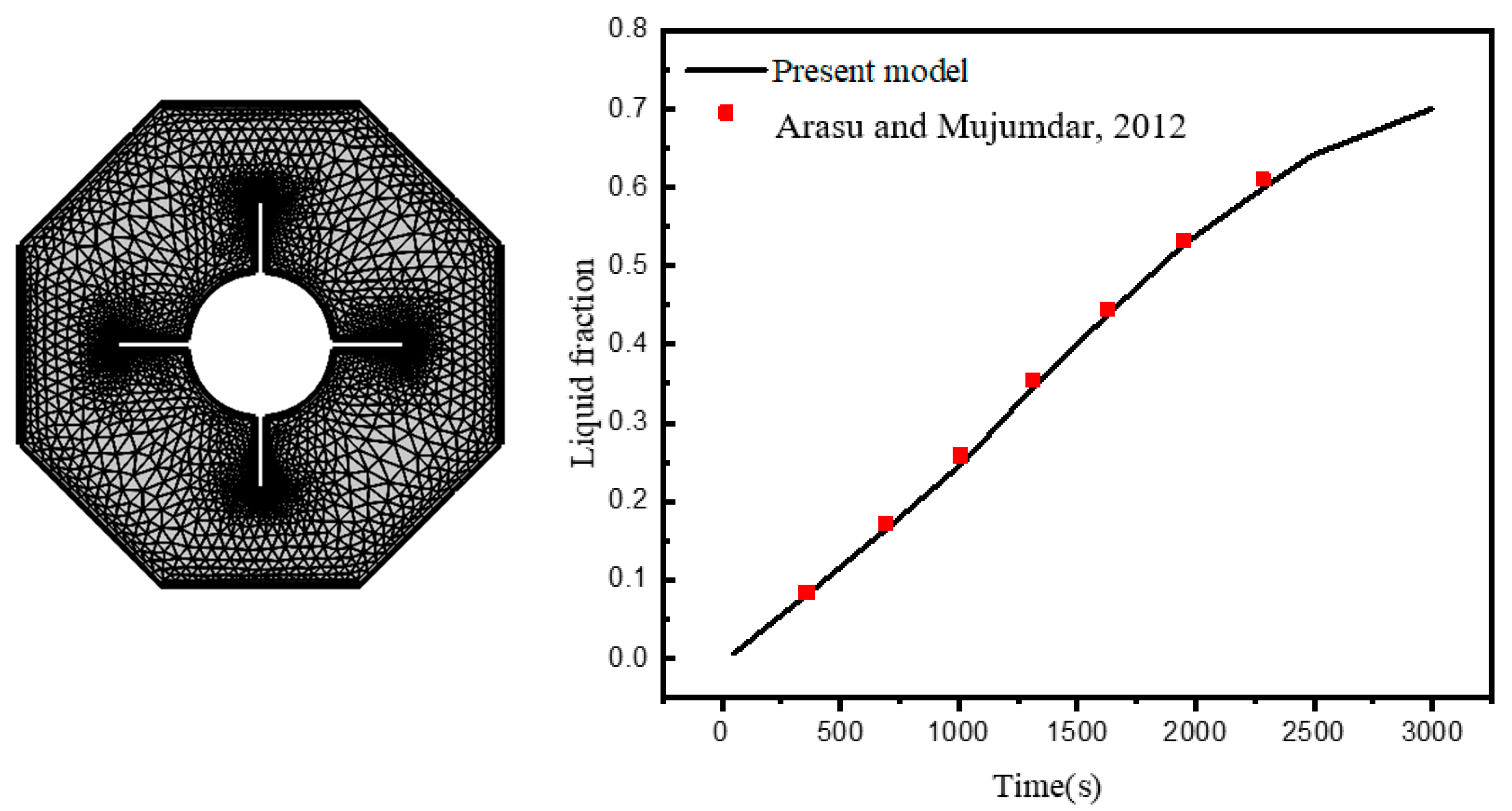
2.2. GFEM Treatments
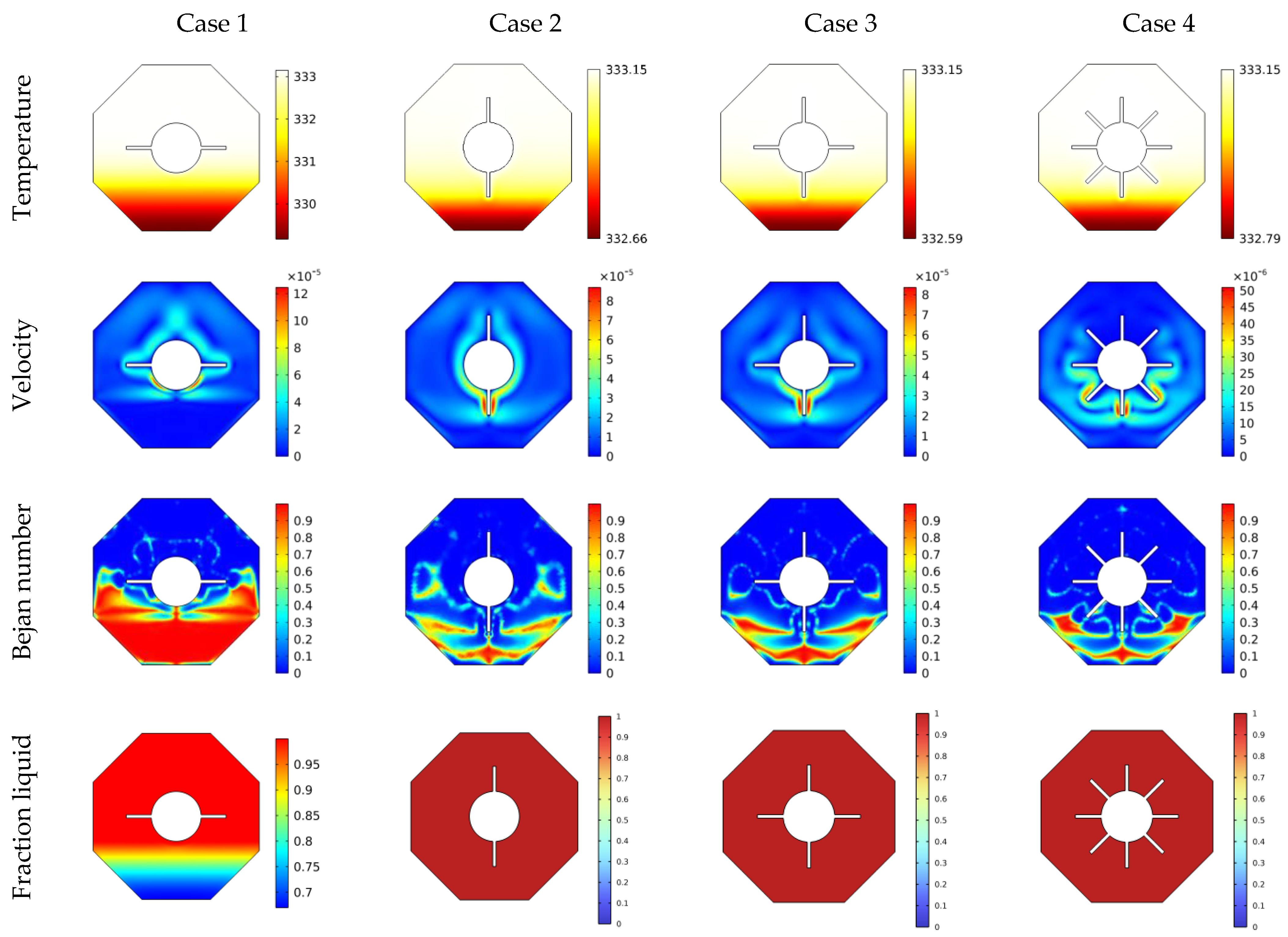
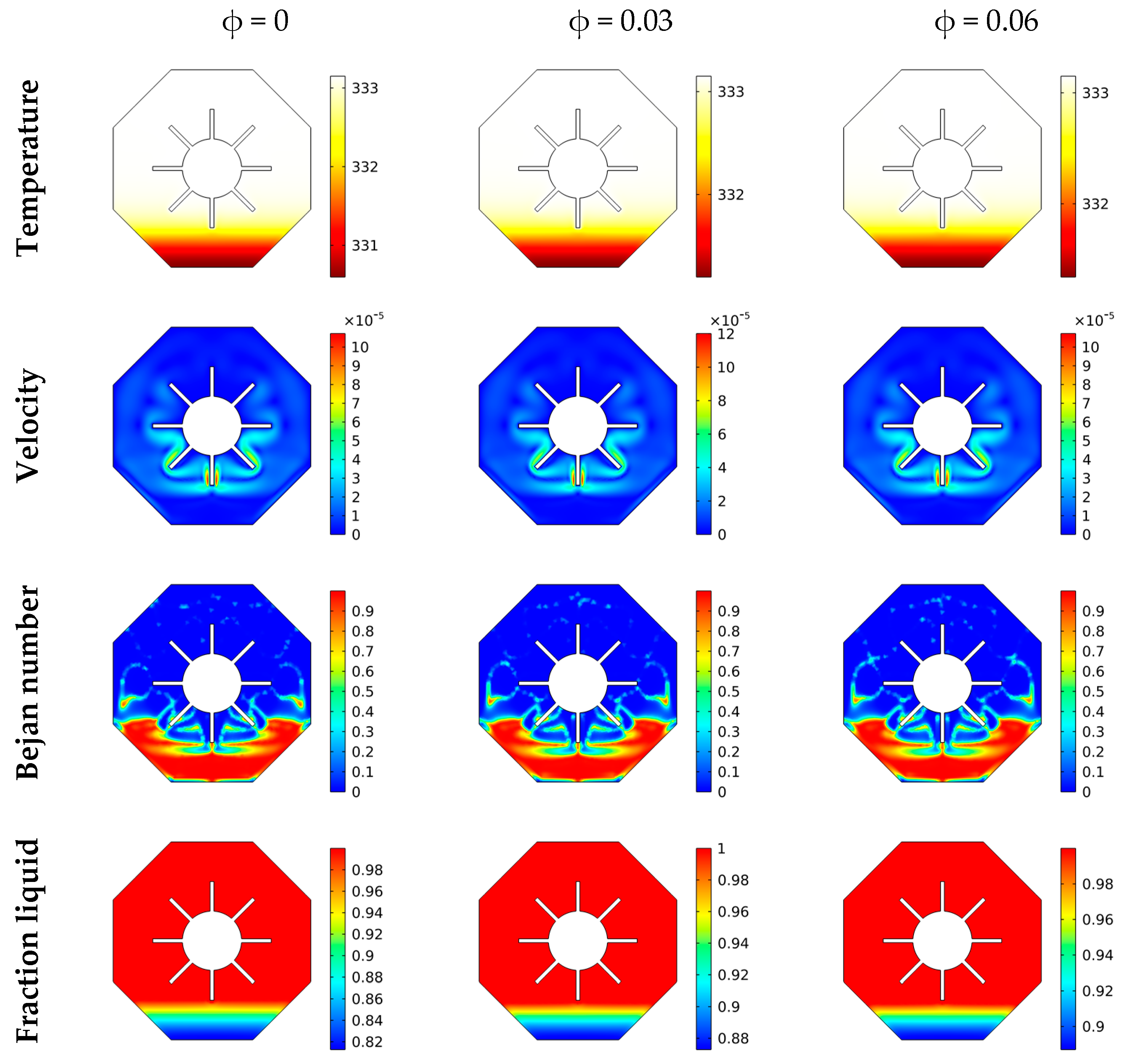
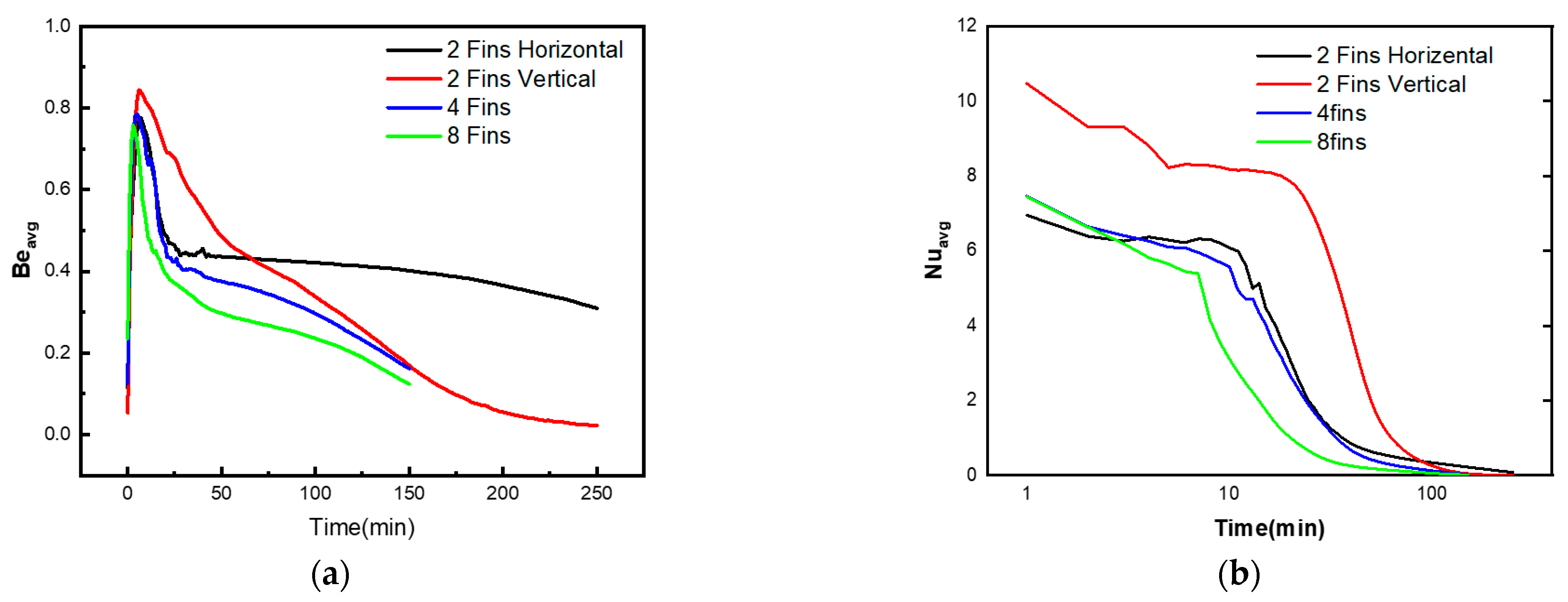
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Mushy zone morphology constant | ||
| Heat capacity | ||
| g | Gravity acceleration ) | |
| Reference sensible enthalpy | ||
| Thermal conductivity | ||
| Latent heat coefficient | ||
| Pressure () | ||
| Total system entropy | ||
| Heat tranfer entropy | ||
| Fluid friction entropy | ||
| Time ( | ||
| Temperature ( | ||
| PCM’s solid temperature | ||
| PCM’s liquid temperature | ||
| Velocity components () | ||
| PCM | Phase change material | |
| 2D | Two-dimensional | |
| 3D | Three-dimensional | |
| LHTES | Latent heat thermal energy storage | |
| HTF | Heat transfer fluid | |
| NEPCM | Nanoparticles-enhanced PCM | |
| Finite Element Method | ||
| Density | ||
| Dynamic viscosity | ||
| Thermal diffusivity | ||
| Thermal expansion coefficient () | ||
| Volume fraction | ||
| Reference case | ||
| Nanofluid | ||
| Solid | ||
| Fluid |
References
- Saeed, A.M.; Abderrahmane, A.; Qasem, N.A.A.; Mourad, A.; Alhazmi, M.; Ahmed, S.E.; Guedri, K. A numerical investigation of a heat transfer augmentation finned pear-shaped thermal energy storage system with nano-enhanced phase change materials. J. Energy Storage 2022, 53, 105172. [Google Scholar] [CrossRef]
- Zandalinas, S.I.; Fritschi, F.B.; Mittler, R. Global Warming, Climate Change, and Environmental Pollution: Recipe for a Multifactorial Stress Combination Disaster. Trends Plant Sci. 2021, 26, 588–599. [Google Scholar] [CrossRef] [PubMed]
- Qasem, N.A.; Abderrahmane, A.; Younis, O.; Guedri, K.; Said, Z.; Mourad, A. Effect of a rotating cylinder on convective flow, heat and entropy production of a 3D wavy enclosure filled by a phase change material. Appl. Therm. Eng. 2022, 214, 118818. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Aissa, A.; Devi, S.S.U.; Prakash, M.; Kolsi, L.; Moria, H.; Jamshed, W.; Younis, O. Effect of a rotating cylinder on the 3D MHD mixed convection in a phase change material filled cubic enclosure. Sustain. Energy Technol. Assess. 2022, 51, 101879. [Google Scholar] [CrossRef]
- Abderrahmane, A.; Hatami, M.; Younis, O.; Mourad, A. Effect of double rotating cylinders on the MHD mixed convection and entropy generation of a 3D cubic enclosure filled by nano-PCM. Eur. Phys. J. Spec. Top. 2022, 1–13. [Google Scholar] [CrossRef]
- Yang, T.; King, W.P.; Miljkovic, N. Phase change material-based thermal energy storage. Cell Rep. Phys. Sci. 2021, 2, 100540. [Google Scholar] [CrossRef]
- Jesumathy, S.P.; Udayakumar, M.; Suresh, S.; Jegadheeswaran, S. An experimental study on heat transfer characteristics of paraffin wax in horizontal double pipe heat latent heat storage unit. J. Taiwan Inst. Chem. Eng. 2014, 45, 1298–1306. [Google Scholar] [CrossRef]
- Zivkovic, B.; Fujii, I. An analysis of isothermal phase change of phase change material within rectangular and cylindrical containers. Sol. Energy 2001, 70, 51–61. [Google Scholar] [CrossRef]
- Saeed, R.M.; Schlegel, J.P.; Sawafta, R.; Kalra, V. Plate type heat exchanger for thermal energy storage and load shifting using phase change material. Energy Convers. Manag. 2019, 181, 120–132. [Google Scholar] [CrossRef]
- Tabassum, T.; Hasan, M.; Begum, L. 2-D numerical investigation of melting of an impure PCM in the arbitrary-shaped annuli. Int. J. Therm. Sci. 2017, 114, 296–319. [Google Scholar] [CrossRef]
- Pahamli, Y.; Hosseini, M.J.; Ranjbar, A.A.; Bahrampoury, R. Inner pipe downward movement effect on melting of PCM in a double pipe heat exchanger. Appl. Math. Comput. 2018, 316, 30–42. [Google Scholar] [CrossRef]
- Vyshak, N.R.; Jilani, G. Numerical analysis of latent heat thermal energy storage system. Energy Convers. Manag. 2007, 48, 2161–2168. [Google Scholar] [CrossRef]
- Pourakabar, A.; Darzi, A.A.R. Enhancement of phase change rate of PCM in cylindrical thermal energy storage. Appl. Therm. Eng. 2019, 150, 132–142. [Google Scholar] [CrossRef]
- Senapati, J.R.; Dash, S.K.; Roy, S. 3D numerical study of the effect of eccentricity on heat transfer characteristics over horizontal cylinder fitted with annular fins. Int. J. Therm. Sci. 2016, 108, 28–39. [Google Scholar] [CrossRef]
- Sadeghi, H.M.; Babayan, M.; Chamkha, A. Investigation of using multi-layer PCMs in the tubular heat exchanger with periodic heat transfer boundary condition. Int. J. Heat Mass Transf. 2020, 147, 118970. [Google Scholar] [CrossRef]
- Ardahaie, S.S.; Hosseini, M.J.; Ranjbar, A.A.; Rahimi, M. Energy storage in latent heat storage of a solar thermal system using a novel flat spiral tube heat exchanger. Appl. Therm. Eng. 2019, 159, 113900. [Google Scholar] [CrossRef]
- Sodhi, G.S.; Jaiswal, A.K.; Vigneshwaran, K.; Muthukumar, P. Investigation of charging and discharging char-acteristics of a horizontal conical shell and tube latent thermal energy storage device. Energy Convers. Manag. 2019, 188, 381–397. [Google Scholar] [CrossRef]
- Shahsavar, A.; Al-Rashed, A.A.A.A.; Entezari, S.; Sardari, P.T. Melting and solidification characteristics of a double-pipe latent heat storage system with sinusoidal wavy channels embedded in a porous medium. Energy 2019, 171, 751–769. [Google Scholar] [CrossRef]
- Rostami, S.; Afrand, M.; Shahsavar, A.; Sheikholeslami, M.; Kalbasi, R.; Aghakhani, S.; Shadloo, M.S.; Oztop, H.F. A review of melting and freezing processes of PCM/nano-PCM and their application in energy storage. Energy 2020, 211, 118698. [Google Scholar] [CrossRef]
- Magendran, S.S.; Khan, F.S.A.; Mubarak, N.; Vaka, M.; Walvekar, R.; Khalid, M.; Abdullah, E.; Nizamuddin, S.; Karri, R.R. Synthesis of organic phase change materials (PCM) for energy storage applications: A review. Nano Struct. Nano Objects 2019, 20, 100399. [Google Scholar] [CrossRef]
- Waqas, A.; Ji, J.; Xu, L.; Ali, M.; Zeashan; Alvi, J. Thermal and electrical management of photovoltaic panels using phase change materials—A review. Renew. Sustain. Energy Rev. 2018, 92, 254–271. [Google Scholar] [CrossRef]
- Gholamibozanjani, G.; Farid, M. A Critical Review on the Control Strategies Applied to PCM-Enhanced Buildings. Energies 2021, 14, 1929. [Google Scholar] [CrossRef]
- Wu, S.; Yan, T.; Kuai, Z.; Pan, W. Thermal conductivity enhancement on phase change materials for thermal energy storage: A review. Energy Storage Mater. 2020, 25, 251–295. [Google Scholar] [CrossRef]
- Leong, K.Y.; Abdul Rahman, M.R.; Gurunathan, B.A. Nano-enhanced phase change materials: A review of thermo-physical properties, applications and challenges. J. Energy Storage 2019, 21, 18–31. [Google Scholar] [CrossRef]
- Alharbi, K.A.M.; Ahmed, A.E.-S.; Sidi, M.O.; Ahammad, N.A.; Mohamed, A.; El-Shorbagy, M.A.; Bilal, M.; Marzouki, R. Computational Valuation of Darcy Ternary-Hybrid Nanofluid Flow across an Extending Cylinder with Induction Effects. Micromachines 2022, 13, 588. [Google Scholar] [CrossRef]
- Rasool, G.; Saeed, A.M.; Lare, A.I.; Abderrahmane, A.; Guedri, K.; Vaidya, H.; Marzouki, R. Darcy-Forchheimer Flow of Water Conveying Multi-Walled Carbon Nanoparticles through a Vertical Cleveland Z-Staggered Cavity Subject to Entropy Generation. Micromachines 2022, 13, 744. [Google Scholar] [CrossRef]
- Chabani, I.; Mebarek-Oudina, F.; Ismail, A.A.I. MHD Flow of a Hybrid Nano-Fluid in a Triangular Enclosure with Zigzags and an Elliptic Obstacle. Micromachines 2022, 13, 224. [Google Scholar] [CrossRef]
- Khetib, Y.; Abo-Dief, H.M.; Alanazi, A.K.; Sajadi, S.M.; Sharifpur, M.; Meyer, J.P. A Computational Fluid Dynamic Study on Efficiency of a Wavy Microchannel/Heat Sink Containing Various Nanoparticles. Micromachines 2021, 12, 1192. [Google Scholar] [CrossRef]
- Yang, L.; Huang, J.N.; Zhou, F. Thermophysical properties and applications of nano-enhanced PCMs: An update review. Energy Convers. Manag. 2020, 214, 112876. [Google Scholar] [CrossRef]
- Ebadi, S.; Tasnim, S.H.; Aliabadi, A.A.; Mahmud, S. Geometry and nanoparticle loading effects on the bio-based nano-PCM filled cylindrical thermal energy storage system. Appl. Therm. Eng. 2018, 141, 724–740. [Google Scholar] [CrossRef]
- Sarrafha, H.; Kasaeian, A.; Jahangir, M.H.; Taylor, R.A. Transient thermal response of multi-walled carbon nanotube phase change materials in building walls. Energy 2021, 224, 120120. [Google Scholar] [CrossRef]
- Kashani, S.; Ranjbar, A.A.; Abdollahzadeh, M.; Sebti, S. Solidification of nano-enhanced phase change material (NEPCM) in a wavy cavity. Heat Mass Transf. 2012, 48, 1155–1166. [Google Scholar] [CrossRef]
- Li, Z.; Hu, N.; Tu, J.; Fan, L. Experimental Investigation of Heat Storage and Heat Transfer Rates during Melting of Nano-Enhanced Phase Change Materials (NePCM) in a Differentially-Heated Rectangular Cavity. J. Therm. Sci. 2020, 29, 503–511. [Google Scholar] [CrossRef]
- Jesumathy, S.; Udayakumar, M.; Suresh, S. Experimental study of enhanced heat transfer by addition of CuO nanoparticle. Heat Mass Transf. Stoffuebertragung 2012, 48, 965–978. [Google Scholar] [CrossRef]
- Mousavi, S.; Rismanchi, B.; Brey, S.; Aye, L. PCM embedded radiant chilled ceiling: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 151, 111601. [Google Scholar] [CrossRef]
- Naghavi, M.S.; Metselaar, H.S.C.; Ang, B.C.; Zamiri, G.; Esmailzadeh, A.; Nasiri-Tabrizi, B. A critical assessment on synergistic improvement in PCM based thermal batteries. Renew. Sustain. Energy Rev. 2021, 135, 110259. [Google Scholar] [CrossRef]
- Mourad, A.; Aissa, A.; Said, Z.; Younis, O.; Iqbal, M.; Alazzam, A. Recent advances on the applications of phase change materials for solar collectors, practical limitations, and challenges: A critical review. J. Energy Storage 2022, 49, 104186. [Google Scholar] [CrossRef]
- Ahmed, S.E.; Abderrahmane, A.; Alotaibi, S.; Younis, O.; Almasri, R.A.; Hussam, W.K. Enhanced Heat Transfer for NePCM-Melting-Based Thermal Energy of Finned Heat Pipe. Nanomaterials 2021, 12, 129. [Google Scholar] [CrossRef]
- Ashouri, M.; Hakkaki-Fard, A. Improving the performance of the finned absorber inclined rooftop solar chimney combined with composite PCM and PV module. Sol. Energy 2021, 228, 562–574. [Google Scholar] [CrossRef]
- Abdulateef, A.M.; Mat, S.; Abdulateef, J.; Sopian, K.; Al-Abidi, A.A. Geometric and design parameters of fins employed for enhancing thermal energy storage systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 1620–1635. [Google Scholar] [CrossRef]
- Duan, J.; Xiong, Y.; Yang, D. Study on the effect of multiple spiral fins for improved phase change process. Appl. Therm. Eng. 2020, 169, 114966. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Gagliardi, F.; Verda, V. Maximization of performance of a PCM latent heat storage system with innovative fins. Appl. Energy 2015, 137, 707–715. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammad, A.T. Internal and external fin heat transfer enhancement technique for latent heat thermal energy storage in triplex tube heat exchangers. Appl. Therm. Eng. 2013, 53, 147–156. [Google Scholar] [CrossRef]
- Mazhar, A.R.; Shukla, A.; Liu, S. Numerical analysis of rectangular fins in a PCM for low-grade heat harnessing. Int. J. Therm. Sci. 2020, 152, 106306. [Google Scholar] [CrossRef]
- Fan, L.W.; Xiao, Y.Q.; Zeng, Y.; Fang, X.; Wang, X.; Xu, X.; Yu, Z.T.; Hong, R.H.; Hu, Y.C.; Cen, K.F. Effects of melting temperature and the presence of internal fins on the performance of a phase change material (PCM)-based heat sink. Int. J. Therm. Sci. 2013, 70, 114–126. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Solidification of NEPCM under the effect of magnetic field in a porous thermal energy storage enclosure using CuO nanoparticles. J. Mol. Liq. 2018, 263, 303–315. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Bendrer, B.A.I.; Aissa, A.; Almuhtady, A.; Jamshed, W.; Nisar, K.S.; Mourad, A.; Alshehri, N.A.; Zakarya, M. Galerkin finite element analysis of magneto two-phase nanofluid flowing in double wavy enclosure comprehending an adiabatic rotating cylinder. Sci. Rep. 2021, 11, 16494. [Google Scholar] [CrossRef]
- Arasu, A.V.; Mujumdar, A.S. Numerical study on melting of paraffin wax with Al2O3 in a square enclosure. Int. Commun. Heat Mass Transf. 2012, 39, 8–16. [Google Scholar] [CrossRef]



| Property | Cu | Paraffin Wax (Liquid/Solid) | |
|---|---|---|---|
| 8954 | 775 | 833.6 | |
| 1.67 | 714 | ||
| 400 | 0.15 | 0.15 | |
| - | 184.48 | ||
| Melting temperature (K) | - | 54.32 | |
| [Pa.s] | - | 6.3 | |
| 383 | 2440 | 2384 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maneengam, A.; Ahmed, S.E.; Saeed, A.M.; Abderrahmane, A.; Younis, O.; Guedri, K.; Alhazmi, M.; Weera, W. Numerical Study of Heat Transfer Enhancement within Confined Shell and Tube Latent Heat Thermal Storage Microsystem Using Hexagonal PCMs. Micromachines 2022, 13, 1062. https://doi.org/10.3390/mi13071062
Maneengam A, Ahmed SE, Saeed AM, Abderrahmane A, Younis O, Guedri K, Alhazmi M, Weera W. Numerical Study of Heat Transfer Enhancement within Confined Shell and Tube Latent Heat Thermal Storage Microsystem Using Hexagonal PCMs. Micromachines. 2022; 13(7):1062. https://doi.org/10.3390/mi13071062
Chicago/Turabian StyleManeengam, Apichit, Sameh E. Ahmed, Abdulkafi Mohammed Saeed, Aissa Abderrahmane, Obai Younis, Kamel Guedri, Muflih Alhazmi, and Wajaree Weera. 2022. "Numerical Study of Heat Transfer Enhancement within Confined Shell and Tube Latent Heat Thermal Storage Microsystem Using Hexagonal PCMs" Micromachines 13, no. 7: 1062. https://doi.org/10.3390/mi13071062
APA StyleManeengam, A., Ahmed, S. E., Saeed, A. M., Abderrahmane, A., Younis, O., Guedri, K., Alhazmi, M., & Weera, W. (2022). Numerical Study of Heat Transfer Enhancement within Confined Shell and Tube Latent Heat Thermal Storage Microsystem Using Hexagonal PCMs. Micromachines, 13(7), 1062. https://doi.org/10.3390/mi13071062










