CFD-DEM Coupling Model for Deposition Process Analysis of Ultrafine Particles in a Micro Impinging Flow Field
Abstract
:1. Introduction
2. Model Formulation
2.1. The Governing Equations of the Fluid Phase
2.2. The Motion Equation of Particles in the Flow
2.2.1. Particle–Particle Interactions
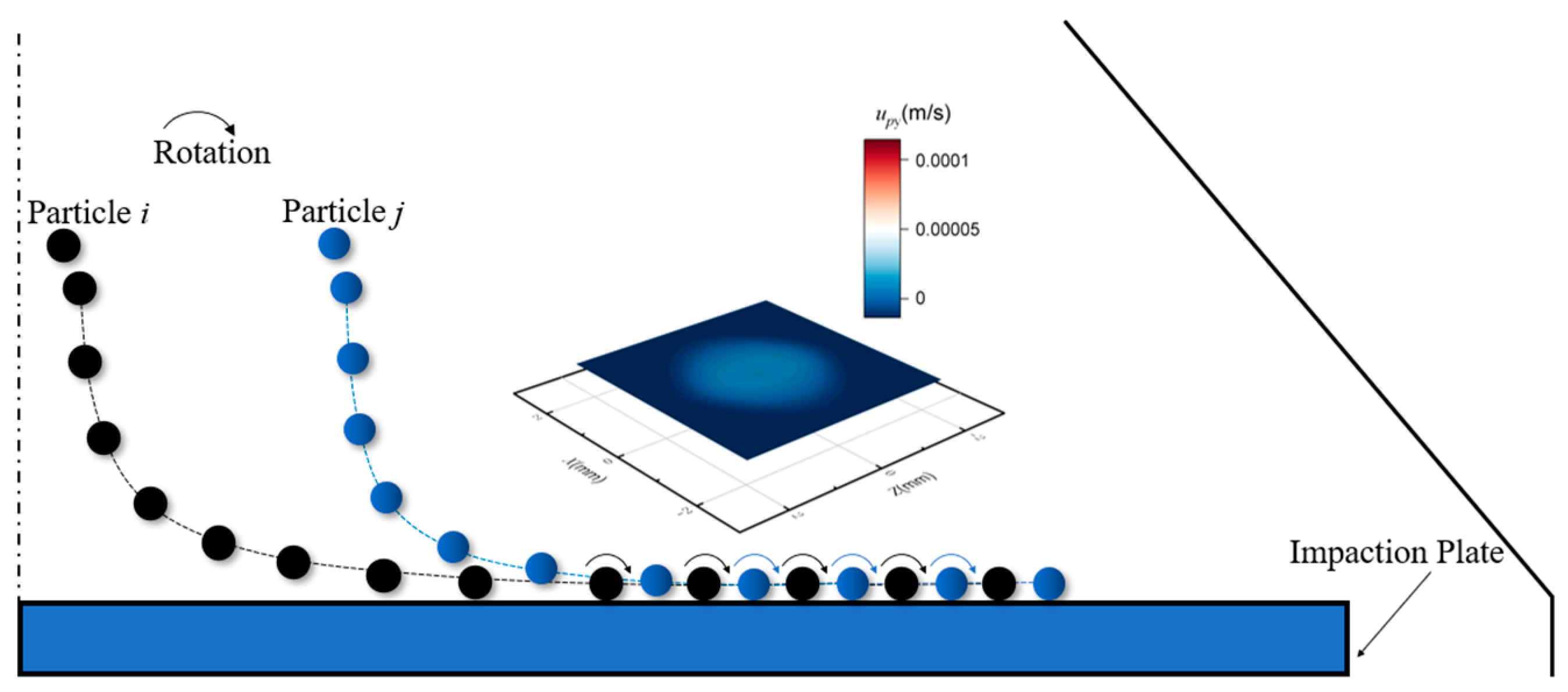
2.2.2. Particle–Wall Interactions
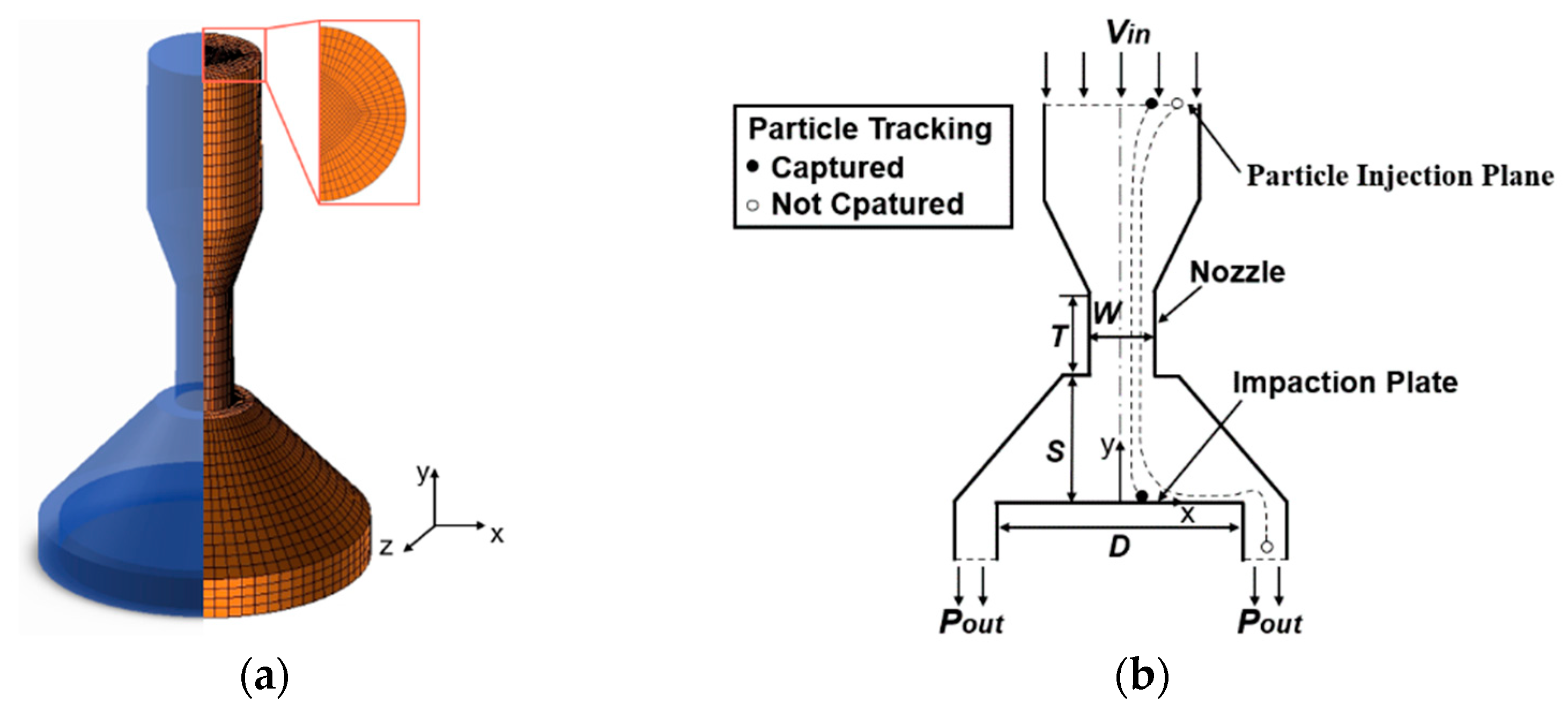
3. Numerical Procedure
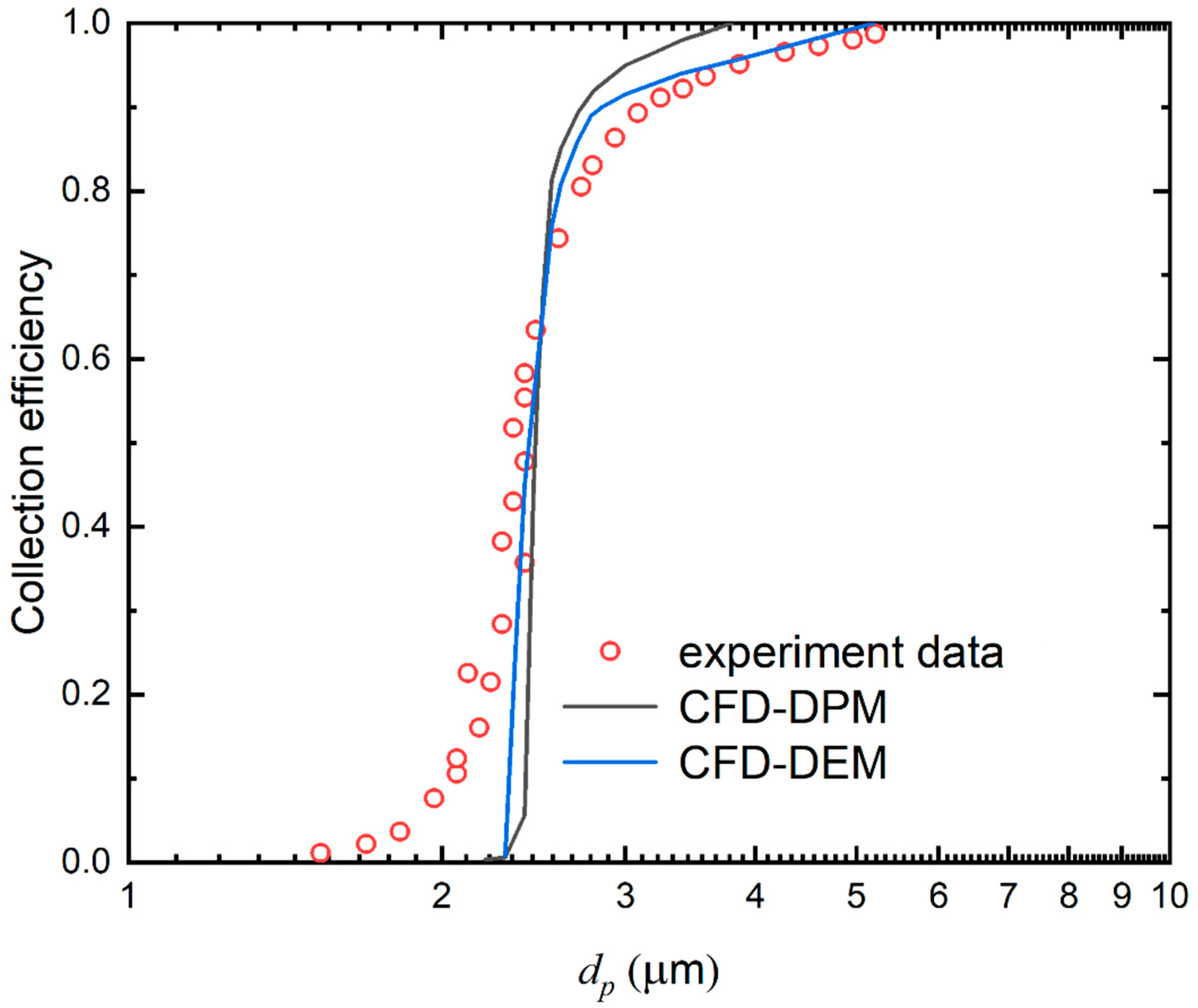
4. Validation of Solvers
5. Results and Discussions
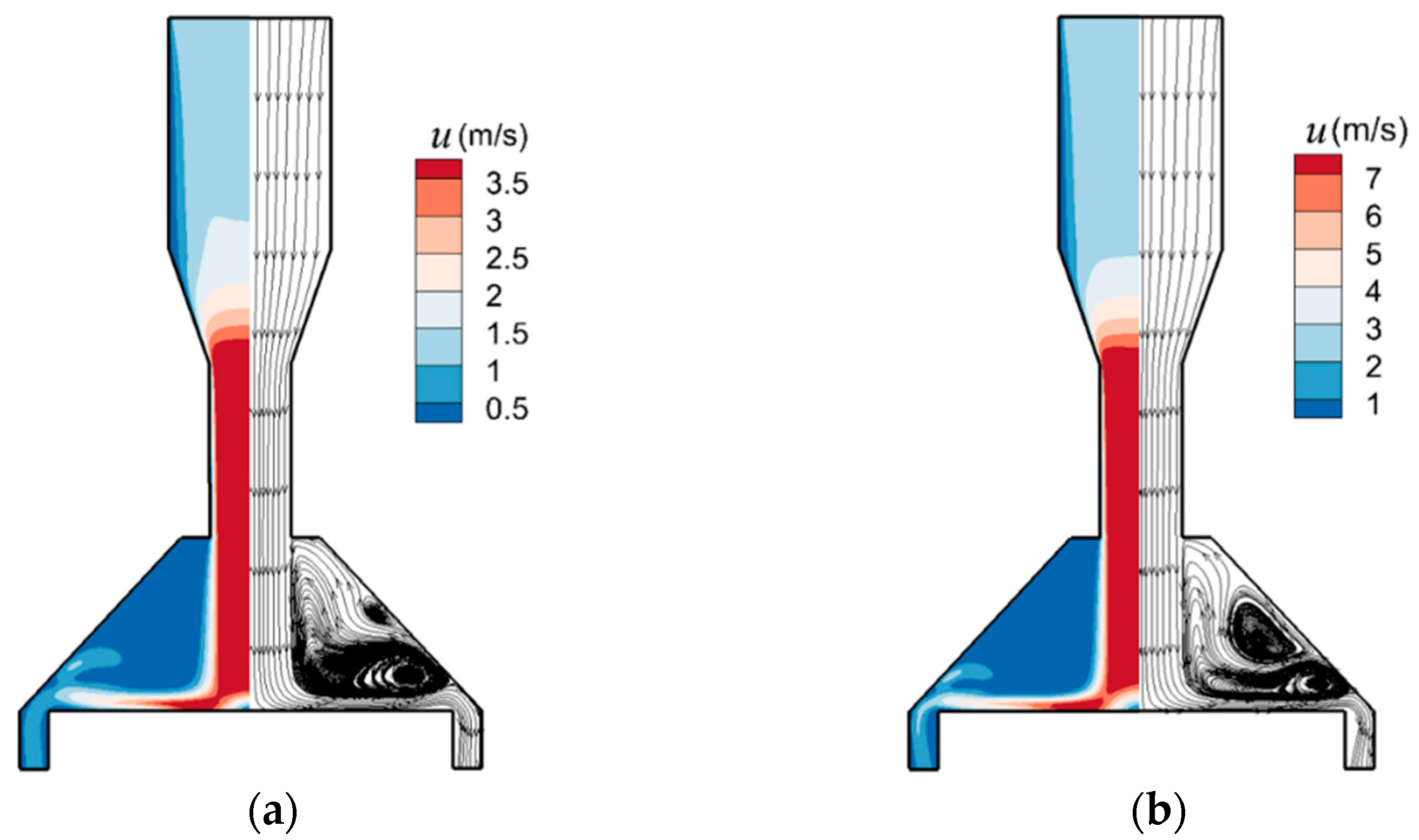
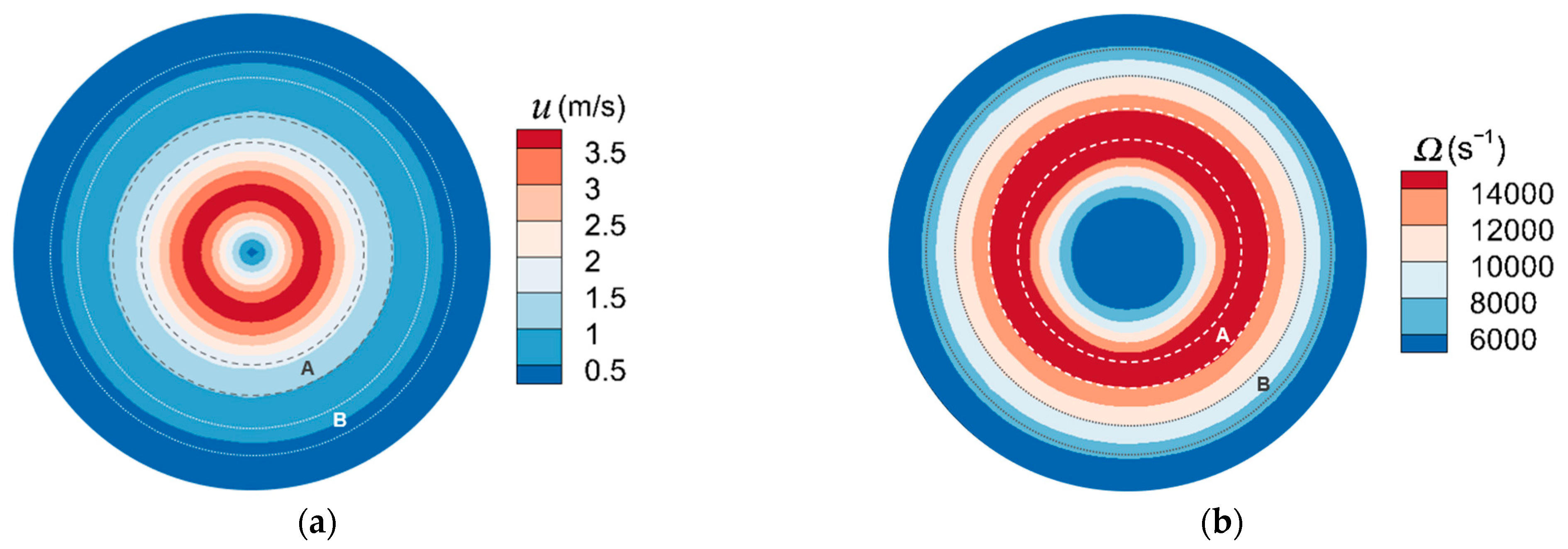
5.1. Particles Deposit Characteristics and Fluid Flow Structure
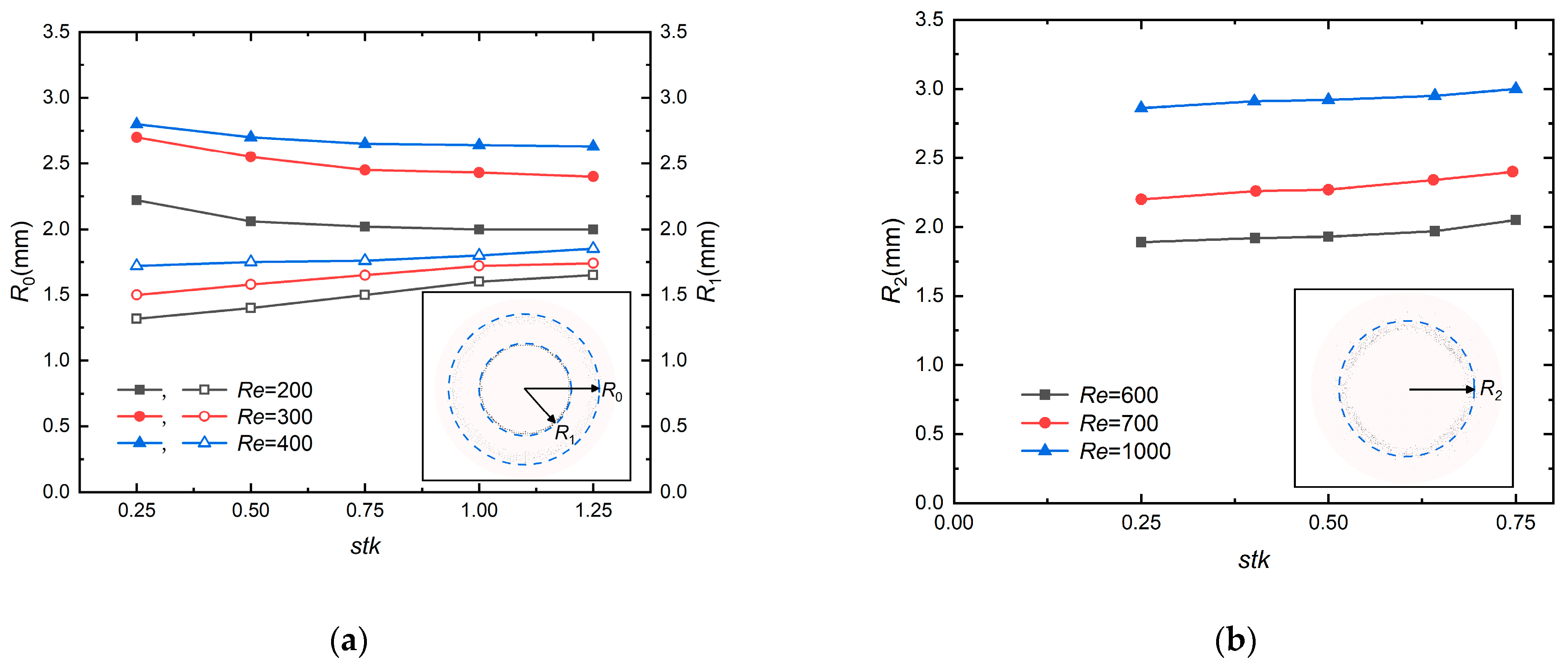
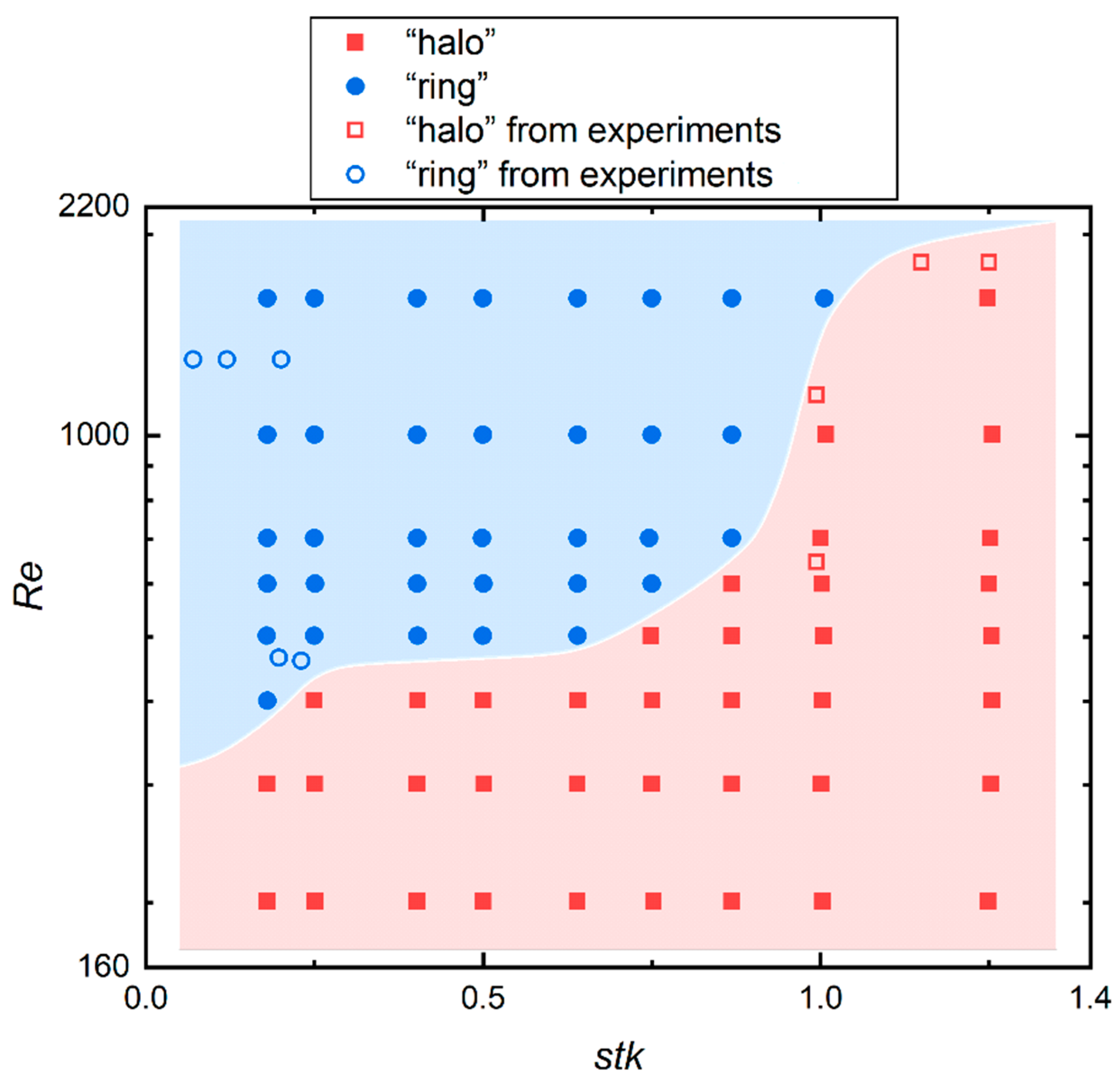
5.2. The Effect of Flow Reynolds Number and Stokes Number on Deposits
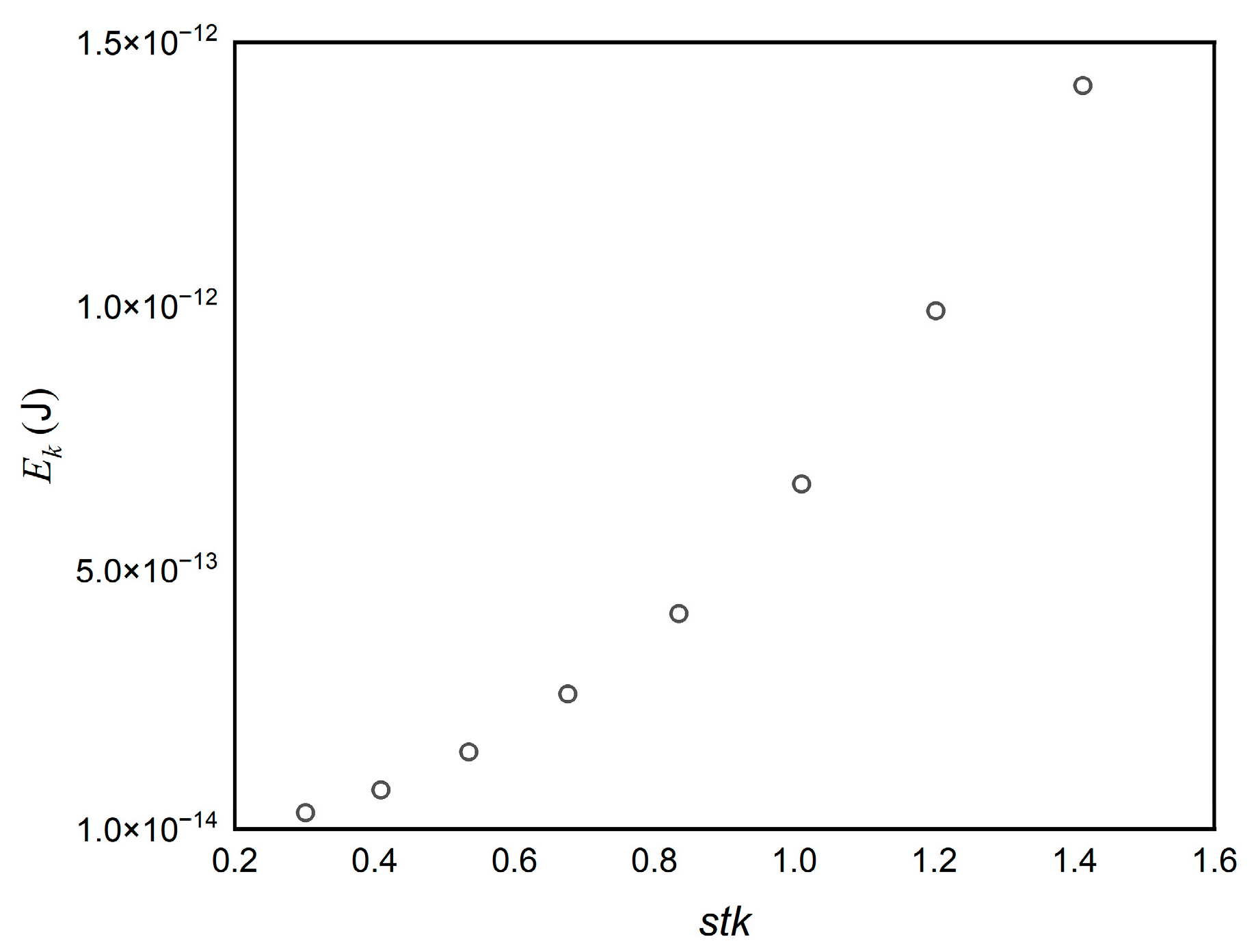
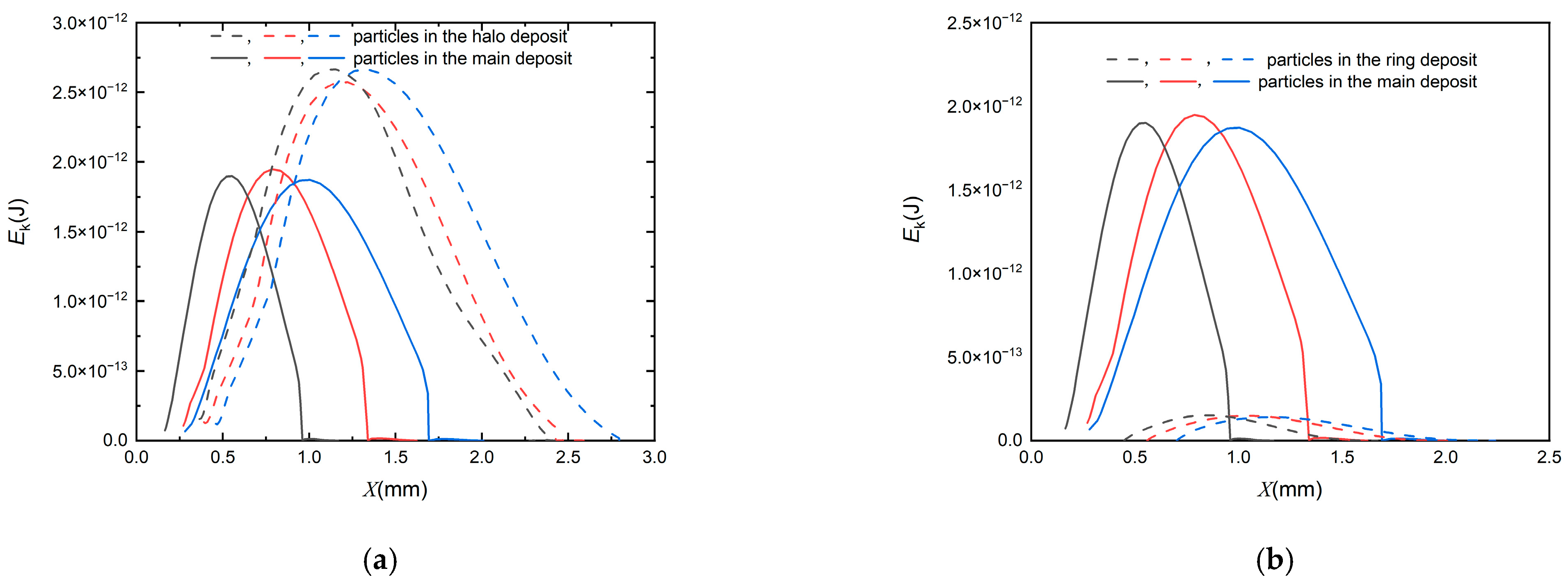
5.3. Energy Variation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ρ | The gas density |
| u | The gas velocity |
| p | The gas pressure |
| τ | The viscous stress tensor of gas |
| g | The gravitational acceleration |
| Sai | The momentum transfer term between the fluid and the ith particle phase |
| Fa,i | The total force exerted on the ith particle |
| Vcell | The volume of cell |
| Re | The flow Reynolds number |
| mp | The particle mass |
| up | The particle velocity |
| upy | The velocity magnitude of particles in the y direction |
| FD | The drag force |
| Ip | The rotational inertia of the particle |
| ωp | The angular velocity of the particle |
| rc | The distance from the contact point to particle center |
| µ | The fluid dynamic viscosity |
| ρp | The particle density |
| dp | The particle size |
| Rep | The particle Reynolds number |
| CD | The drag coefficient |
| stk | The Stokes number |
| Cc | The slip correction factor |
| Ek | The kinetic energy of a particle |
| Ep-w | The particle–wall collision |
| Ed | The friction force and adhesion force |
| Fc | The contact force acted on the particle |
| Fct | The tangential component of the contact force |
| Fcn | The normal component of the contact force |
| Fet | The tangential elastic force |
| Fdt | The tangential damping force |
| Fen | The normal elastic force |
| Fdn | The normal damping force |
| FJKR | The adhesion force |
| γ | The surface energy |
| The equivalent Young’s modulus | |
| The equivalent radius of the particle | |
| a | The contact half-width |
| R | The particle radius |
| E | The Young’s modulus |
| ν | The Poisson’s ratio |
| δn | The normal overlap |
| W | The round–nozzle diameter |
| T | The length of the nozzle throat |
| S | The distance from the nozzle to the impaction plate |
| D | The diameter of the impaction plate |
| R0 | The radius of the halo deposit |
| R1 | The radius of the primary deposit |
| R2 | The radius of the ring deposit |
| X | The x coordinate of the particle deposition |
References
- Saadabadi, S.; Abouali, O.; Emdad, H.; Ahmadi, G. Investigation of the effect of nozzle shape on supersonic/hypersonic impactors designed for size discrimination of nanoparticles. Particuology 2014, 16, 60–68. [Google Scholar] [CrossRef]
- Lee, S.J.; Demokritou, P.; Koutrakis, P. Performance evaluation of commonly used impaction substrates under various loading conditions. J. Aerosol Sci. 2005, 36, 881–895. [Google Scholar] [CrossRef]
- Arffman, A.; Marjamäki, M.; Keskinen, J. Simulation of low pressure impactor collection efficiency curves. J. Aerosol Sci. 2011, 42, 329–340. [Google Scholar] [CrossRef]
- Sethi, V.; John, W. Particle impaction patterns from a circular jet. Aerosol Sci. Technol. 1993, 18, 1–10. [Google Scholar] [CrossRef]
- Kala, S.; Saylor, J. Factors affecting the diameter of ring-shaped deposition patterns in inertial impactors having small S/W ratios. Aerosol Sci. Technol. 2022, 56, 234–246. [Google Scholar] [CrossRef]
- Soysal, U.; Géhin, E.; Marty, F.; Algré, E.; Robine, E.; Motzkus, C. Exploring deposition pattern characteristics of aerosols and bioaerosols by inertial impaction for the development of real-time silicon MEMS mass detection systems. Aerosol Sci. Technol. 2021, 55, 414–422. [Google Scholar] [CrossRef]
- García-Ruiz, E.; Romay, F.J.; García, J.A.; Iza, J.M.; Cambra, J.F.; Gangoiti, G.; Legarreta, J.A. Effect of nozzle spacing in the formation of primary and secondary deposits in multi-nozzle inertial impactors part II: Numerical study. J. Aerosol Sci. 2019, 136, 106–127. [Google Scholar] [CrossRef]
- Rocklage, J.M.; Marple, V.A.; Olson, B.A. Study of secondary deposits in multiple round nozzle impactors. Aerosol Sci. Technol. 2013, 47, 1144–1151. [Google Scholar] [CrossRef] [Green Version]
- May, K. Aerosol impaction jets. J. Aerosol Sci. 1975, 6, 403–411. [Google Scholar] [CrossRef]
- Fredericks, S.; Saylor, J. Ring-shaped deposition patterns in small nozzle-to-plate distance impactors. Aerosol Sci. Technol. 2018, 52, 30–37. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Novosselov, I.V. Design and evaluation of an aerodynamic focusing micro-well aerosol collector. Aerosol Sci. Technol. 2017, 51, 1016–1026. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mottaghi, P.; Abbasalizadeh, M.; Ahmady-Birgani, H. Depositional arrangement of non-spherical atmospheric particles on impaction plate of a multi-nozzle impactor. Aerosol Sci. Technol. 2019, 53, 1381–1392. [Google Scholar] [CrossRef]
- Wu, J.; Xu, J.; Wang, H. Numerical simulation of aerosol dynamics in an impinging jet with microdroplet coalescence. Aerosol Sci. Technol. 2020, 54, 1–22. [Google Scholar] [CrossRef]
- Trofa, M.; D’Avino, G.; Sicignano, L.; Tomaiuolo, G.; Greco, F.; Maffettone, P.L.; Guido, S. CFD-DEM simulations of particulate fouling in microchannels. Chem. Eng. J. 2019, 358, 91–100. [Google Scholar] [CrossRef]
- Chaumeil, F.; Crapper, M. Using the DEM-CFD method to predict Brownian particle deposition in a constricted tube. Particuology 2014, 15, 94–106. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S.; Cleary, P.; Tavares, L.M.; Evertsson, M.; Morrison, R.; Quist, J.; Carvalho, R. The contribution of DEM to the science of comminution. Powder Technol. 2013, 248, 3–24. [Google Scholar] [CrossRef]
- Mitani, R.; Ohsaki, S.; Nakamura, H.; Watano, S. Numerical study on particle adhesion in dry powder inhaler device. Chem. Pharm. Bull. 2020, 68, 726–736. [Google Scholar] [CrossRef]
- Ohsaki, S.; Mitani, R.; Fujiwara, S.; Nakamura, H.; Watano, S. Effect of Particle–Wall Interaction and Particle Shape on Particle Deposition Behavior in Human Respiratory System. Chem. Pharm. Bull. 2019, 67, 1328–1336. [Google Scholar] [CrossRef] [Green Version]
- Johnson, K.L.; Kendall, K.; Roberts, A. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 324, 301–313. [Google Scholar]
- Flynn, S.; Tong, Z.; Yang, R.; Kamiya, H.; Yu, A.; Chan, H. Computational fluid dynamics (CFD) investigation of the gas–solid flow and performance of Andersen cascade impactor. Powder Technol. 2015, 285, 128–137. [Google Scholar] [CrossRef]
- Ponzini, R.; Da Vià, R.; Bnà, S.; Cottini, C.; Benassi, A. Coupled CFD-DEM model for dry powder inhalers simulation: Validation and sensitivity analysis for the main model parameters. Powder Technol. 2021, 385, 199–226. [Google Scholar] [CrossRef]
- Jami, H.; Jabbarzadeh, A. Unravelling ultrafast deformation mechanisms in surface deposition of titanium nanoparticles. Appl. Surf. Sci. 2019, 489, 446–461. [Google Scholar] [CrossRef]
- Jami, H.; Jabbarzadeh, A. Molecular simulation of high-velocity deposition of Titanium dioxide nanoparticles on titanium. Appl. Surf. Sci. 2020, 542, 148567. [Google Scholar] [CrossRef]
- Jami, H.; Jabbarzadeh, A. Ultrafast thermomechanical effects in aerosol deposition of hydroxyapatite nanoparticles on a titanium substrate. Surf. Coat. Technol. 2019, 382, 125173. [Google Scholar] [CrossRef]
- Jami, H.; Jabbarzadeh, A. Effect of particle shape on mechanics of impact in the deposition of titanium nanoparticles on a titanium substrate. Surf. Coat. Technol. 2020, 394, 125880. [Google Scholar] [CrossRef]
- Park, C.W.; Kim, G.; Yook, S.J.; Ahn, K.H. Investigation of collection efficiency of round-nozzle impactors at different atmospheric pressures and temperatures. Adv. Powder Technol. 2015, 26, 868–873. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Morsi, S.; Alexander, A. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Zhao, S.; Evans, T.M.; Zhou, X. Effects of curvature-related DEM contact model on the macro-and micro-mechanical behaviours of granular soils. Géotechnique 2018, 68, 1085–1098. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Soysal, U.; Géhin, E.; Algré, E.; Berthelot, B.; Da, G.; Robine, E. Aerosol mass concentration measurements: Recent advancements of real-time nano/micro systems. J. Aerosol Sci. 2017, 114, 42–54. [Google Scholar] [CrossRef]
- Rennecke, S.; Weber, A.P. The critical velocity for nanoparticle rebound measured in a low pressure impactor. J. Aerosol Sci. 2013, 58, 135–147. [Google Scholar] [CrossRef]
- Liu, C.N.; Awasthi, A.; Hung, Y.H.; Tsai, C.J. Collection efficiency and interstage loss of nanoparticles in micro-orifice-based cascade impactors. Atmos. Environ. 2013, 69, 325–333. [Google Scholar] [CrossRef]
- Marjamäki, M.; Keskinen, J.; Chen, D.R.; Pui, D.Y. Performance evaluation of the electrical low-pressure impactor (ELPI). J. Aerosol Sci. 2000, 31, 249–261. [Google Scholar] [CrossRef]
- Marple, V.A.; Olson, B.A. Aerosol Measurement: Principles, Techniques, and Applications, 3rd ed.; John Wiley and Sons, Inc.: Cincinnati, OH, USA, 2011; pp. 129–151. [Google Scholar]
- Chen, X.; Zhong, W.; Zhou, X.; Jin, B.; Sun, B. CFD–DEM simulation of particle transport and deposition in pulmonary airway. Powder Technol. 2012, 228, 309–318. [Google Scholar] [CrossRef]
- Derakhshani, S.M.; Schott, D.L.; Lodewijks, G. Micro–macro properties of quartz sand: Experimental investigation and DEM simulation. Powder Technol. 2015, 269, 127–138. [Google Scholar] [CrossRef]
- Yao, L.; Xiao, Z.; Liu, J.; Zhang, Q.; Wang, M. An optimized CFD-DEM method for fluid-particle coupling dynamics analysis. Int. J. Mech. Sci. 2020, 174, 105503. [Google Scholar] [CrossRef]
- Olaleye, A.K.; Shardt, O.; Walker, G.M.; Van den Akker, H.E. Pneumatic conveying of cohesive dairy powder: Experiments and CFD-DEM simulations. Powder Technol. 2019, 357, 193–213. [Google Scholar] [CrossRef]
- HadiIabdi, M.; Hanjali, K. Vortical structures and heat transfer in a round impinging jet. J. Fluid Mech. 2008, 596, 221–260. [Google Scholar] [CrossRef]
- Rennecke, S.; Weber, A.P. A novel model for the determination of nanoparticle impact velocity in low pressure impactors. J. Aerosol Sci. 2013, 55, 89–103. [Google Scholar] [CrossRef]



| Parameter Setting | Value | Unit | |
|---|---|---|---|
| Fluid density | 1.225 | kg/m3 | |
| Particle density | 1000 | kg/m3 | |
| Wall density | 7800 | kg/m3 | |
| Particle size | 2–13 | µm | |
| Coefficient of restitution | Particle–Particle | 0.45 | |
| Particle–Wall | 0.45 | ||
| Coefficient of static friction | Particle–Particle | 0.5 | |
| Particle–Wall | 0.8 | ||
| Coefficient of rolling friction | Particle–Particle | 0.01 | |
| Particle–Wall | 0.8 | ||
| Poisson’s ratio of particle | 0.3 | ||
| Poisson’s ratio of wall | 0.3 | ||
| Shear modulus of particle | 1 × 107 | Pa | |
| Shear modulus of wall | 1 × 1010 | Pa | |
| Surface energy (Particle–Wall) | 0.1 | J/m2 | |
| Case | Number of Grids | u (m/s) | Deviation from Experiment [34] (%) |
|---|---|---|---|
| Case 1 | 450,000 | 7.40 | 2.63 |
| Case 2 | 550,000 | 7.48 | 1.58 |
| Case 3 | 650,000 | 7.55 | 0.66 |
| Case 4 | 750,000 | 7.58 | 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yin, Z.; Bao, F.; Shen, J. CFD-DEM Coupling Model for Deposition Process Analysis of Ultrafine Particles in a Micro Impinging Flow Field. Micromachines 2022, 13, 1110. https://doi.org/10.3390/mi13071110
Wang Y, Yin Z, Bao F, Shen J. CFD-DEM Coupling Model for Deposition Process Analysis of Ultrafine Particles in a Micro Impinging Flow Field. Micromachines. 2022; 13(7):1110. https://doi.org/10.3390/mi13071110
Chicago/Turabian StyleWang, Yanru, Zhaoqin Yin, Fubing Bao, and Jiaxin Shen. 2022. "CFD-DEM Coupling Model for Deposition Process Analysis of Ultrafine Particles in a Micro Impinging Flow Field" Micromachines 13, no. 7: 1110. https://doi.org/10.3390/mi13071110
APA StyleWang, Y., Yin, Z., Bao, F., & Shen, J. (2022). CFD-DEM Coupling Model for Deposition Process Analysis of Ultrafine Particles in a Micro Impinging Flow Field. Micromachines, 13(7), 1110. https://doi.org/10.3390/mi13071110






