Design and Measurement of a Novel Overmoded TE01 Mode Converter for a Rectangular Gyro-TWT
Abstract
:1. Introduction
2. Overmoded TE01 Excitation
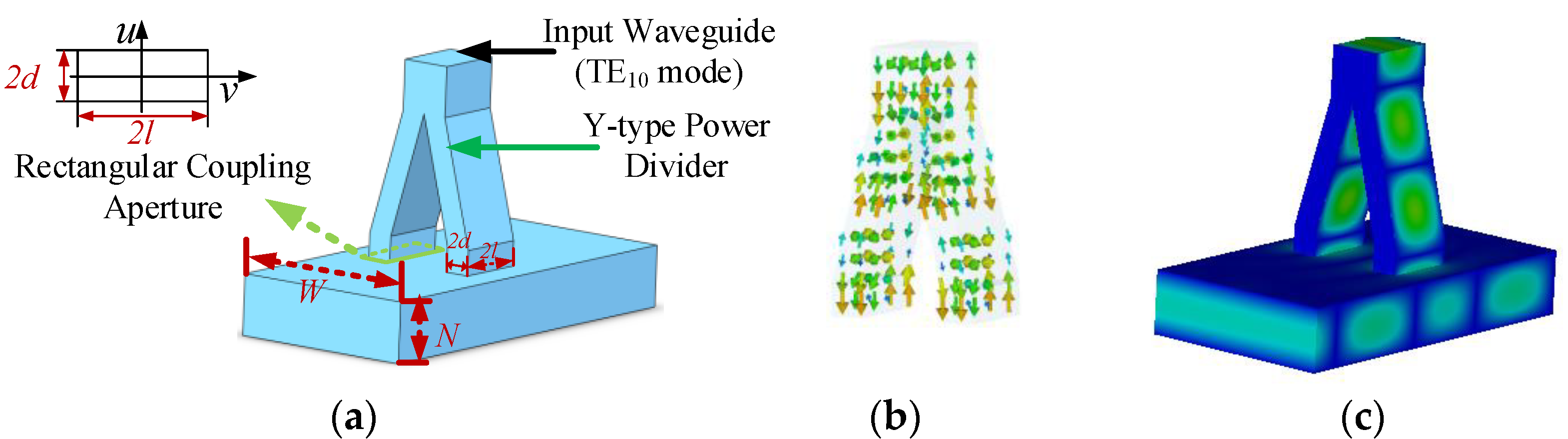
2.1. Design Principle
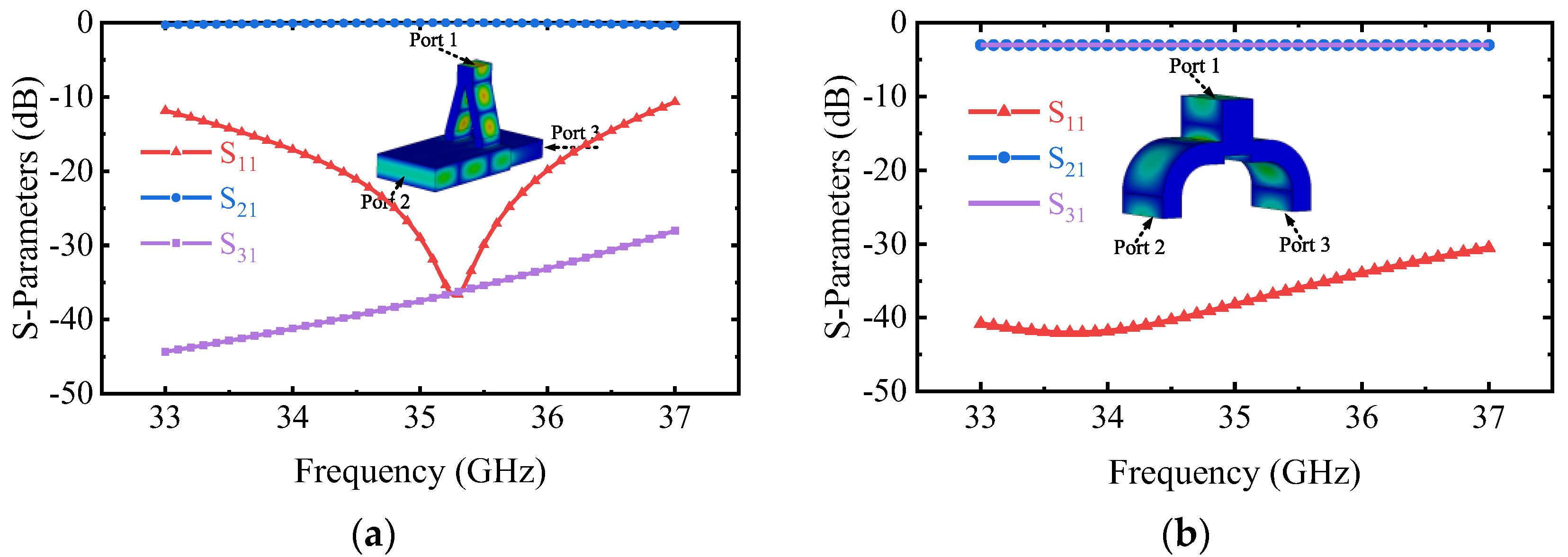
2.2. Simulation and Analysis
3. Manufacture and Microwave Measurement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nguyen, K.; Calame, J.; Pershing, D.; Danly, B.; Garven, M.; Levush, B.; Antonsen, T. Design of a Ka-band gyro-TWT for radar applications. IEEE Trans. Electron Devices 2001, 48, 108–115. [Google Scholar] [CrossRef]
- Nusinovich, G.S.; Thumm, M.K.A.; Petelin, M.I. The Gyrotron at 50: Historical Overview. J. Infrared Millim. Terahertz Waves 2014, 35, 325–381. [Google Scholar] [CrossRef]
- Thumm, M. State-of-the-Art of High-Power Gyro-Devices and Free Electron Masers. J. Infrared Millim. Terahertz Waves 2020, 41, 1–140. [Google Scholar] [CrossRef] [Green Version]
- Sabchevski, S.; Glyavin, M.; Mitsudo, S.; Tatematsu, Y.; Idehara, T. Novel and Emerging Applications of the Gyrotrons Worldwide: Current Status and Prospects. J. Infrared Millim. Terahertz Waves 2021, 42, 715–741. [Google Scholar] [CrossRef]
- Thumm, M. State-of-the-Art of High-Power Gyro-Devices. Update of Experimental Results 2021; KIT Scientific Reports 7761; Karlsruhe Institute of Technology: Karlsruhe, Germany, 2021. [Google Scholar]
- Samsonov, S.V.; Levitan, B.A.; Murzin, V.N.; Gachev, I.G.; Denisov, G.G.; Bogdashov, A.A.; Mishakin, S.V.; Fiks, A.S.; Soluyanova, E.A.; Tai, E.M.; et al. Ka-Band Gyrotron Traveling-Wave Tubes with the Highest Continuous-Wave and Average Power. IEEE Trans. Electron Devices 2014, 61, 4264–4267. [Google Scholar] [CrossRef]
- Joye, C.D.; Shapiro, M.A.; Sirigiri, J.R.; Temkin, R.J. Demonstration of a 140-GHz 1-kW Confocal Gyro-Traveling-Wave Amplifier. IEEE Trans. Electron Devices 2009, 56, 818–827. [Google Scholar] [CrossRef] [Green Version]
- Nanni, E.A.; Lewis, S.M.; Shapiro, M.A.; Griffin, R.G.; Temkin, R.J. Photonic-band-gap traveling-wave gyrotron ampli-fier. Phys. Rev. Lett. 2013, 111, 235101. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; McDermott, D.; Luhmann, N. Operation of a sTable 200-kW second-harmonic gyro-TWT amplifier. IEEE Trans. Plasma Sci. 1996, 24, 700–706. [Google Scholar] [CrossRef]
- Barnett, L.R.; Luhmann, N.C.; Chiu, C.C.; Chu, K.R.; Yan, Y.C. Advances in W-Band TE01 Gyro-TWT Amplifier Design. In Proceedings of the 2007 IEEE International Vacuum Electronics Conference, Kitakyushu, Japan, 15–17 May 2007; pp. 233–234. [Google Scholar] [CrossRef]
- Chu, K.R.; Chen, H.-Y.; Hung, C.-L.; Chang, T.-H.; Barnett, L.; Chen, S.-H.; Yang, T.-T.; Dialetis, D. Theory and experiment of ultrahigh-gain gyrotron traveling wave amplifier. IEEE Trans. Plasma Sci. 1999, 27, 391–404. [Google Scholar] [CrossRef] [Green Version]
- Garven, M.; Calame, J.; Danly, B.; Nguyen, K.; Levush, B.; Wood, F.; Pershing, D. A gyrotron-traveling-wave tube amplifier experiment with a ceramic loaded interaction region. IEEE Trans. Plasma Sci. 2002, 30, 885–893. [Google Scholar] [CrossRef]
- Blank, M.; Borchard, P.; Cauffman, S.; Felch, K. Design and demonstration of W-band gyrotron amplifiers for radar ap-plications. In Proceedings of the 2007 Joint 32nd International Conference on Infrared and Millimeter Waves and the 15th International Conference on Terahertz Electronics, Cardiff, UK, 2–9 September 2007; pp. 364–366. [Google Scholar]
- Liu, B.; Feng, J.; Wang, E.; Li, Z.; Zeng, X.; Qian, L.; Wang, H. Design and Experimental Study of a Ka-band Gyro-TWT With Periodic Dielectric Loaded Circuits. IEEE Trans. Plasma Sci. 2011, 39, 1665–1672. [Google Scholar] [CrossRef]
- Wang, J.; Tian, Q.; Li, X.; Shu, G.; Xu, Y.; Luo, Y. Theory and Experiment Investigate of a 400-kW Ku-Band Gyro-TWT With Mode Selective Loss Loading Structure. IEEE Trans. Electron Devices 2017, 64, 550–555. [Google Scholar] [CrossRef]
- Yan, R.; Li, H.; Wang, D.; Wang, J.; Wang, L.; Pu, Y.; Xu, Y.; Jiang, W.; Liu, G.; Luo, Y. Investigation on High Average Power Operations of Gyro-TWTs With Dielectric-Loaded Waveguide Circuits. IEEE Trans. Electron Devices 2018, 65, 3012–3018. [Google Scholar] [CrossRef]
- Yan, R.; Luo, Y.; Liu, G.; Pu, Y. Design and Experiment of a Q-band Gyro-TWT Loaded with Lossy Dielectric. IEEE Trans. Electron Devices 2012, 59, 3612–3617. [Google Scholar] [CrossRef]
- Liu, G.; Jiang, W.; Yao, Y.; Wang, Y.; Wang, W.; Cao, Y.; Wang, J.; Luo, Y. High Average Power Test of a W-Band Broadband Gyrotron Traveling Wave Tube. IEEE Electron Device Lett. 2022, 43, 950–953. [Google Scholar] [CrossRef]
- Choi, E.M.; Cerfon, A.; Mastovsky, I.; Shapiro, M.A.; Sirigiri, J.R.; Temkin, R. Efficiency Enhancement of a 1.5-MW, 110-GHz Gyrotron with a Single-Stage Depressed Collector. Fusion Sci. Technol. 2007, 52, 334–339. [Google Scholar] [CrossRef]
- Jelonnek, J.; Albajar, F.; Alberti, S.; Avramidis, K.; Benin, P.; Bonicelli, T.; Cismondi, F.; Erckmann, V.; Gantenbein, G.; Hesch, K.; et al. From Series Production of Gyrotrons for W7-X Toward EU-1 MW Gyrotrons for ITER. IEEE Trans. Plasma Sci. 2014, 42, 1135–1144. [Google Scholar] [CrossRef] [Green Version]
- Tsai, W.C.; Chang, T.H.; Chen, N.C.; Chu, K.R.; Song, H.H.; Luhmann, J.N.C. Absolute instabilities in a high-order-mode gyrotron traveling-wave amplifier. Phys. Rev. E 2004, 70, 056402. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.; Dai, B.; Lu, C.; Liu, G.; Wang, J.; Pu, Y.; Luo, Y. High Average Power Investigation of Dielectric Dissipation in the W-Band Gyro-TWT. IEEE Trans. Electron Devices 2022, 69, 3926–3932. [Google Scholar] [CrossRef]
- Zhang, L.; He, W.; Donaldson, C.R.; Garner, J.R.; McElhinney, P.; Cross, A.W. Design and Measurement of a Broadband Sidewall Coupler for a W-Band Gyro-TWA. IEEE Trans. Microw. Theory Tech. 2015, 63, 3183–3190. [Google Scholar] [CrossRef] [Green Version]
- Garner, J.R.; Zhang, L.; Donaldson, C.R.; Cross, A.W.; He, W. Design Study of a Fundamental Mode Input Coupler for a 372-GHz Gyro-TWA I: Rectangular-to-Circular Coupling Methods. IEEE Trans. Electron Devices 2015, 63, 497–503. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.-F.; Chang, T.-H. High-performance circular TE01-mode converter. IEEE Trans. Microw. Theory Tech. 2005, 53, 3794–3798. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Yan, R.; Luo, Y.; Wang, S. A TE13 Mode Converter for High-Order Mode Gyrotron-Traveling-Wave Tubes. IEEE Trans. Electron Devices 2015, 63, 486–490. [Google Scholar] [CrossRef]
- Wu, Z.; Liao, X.; Wang, K.; Wang, M.; Pu, Y.; Luo, Y. A Circular TE02 Mode Generator with High Purity for Gyro-TWT Study. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 137–140. [Google Scholar] [CrossRef]
- Chang, T.-H.; Li, C.-H.; Wu, C.-N.; Yu, C.-F. Generating Pure Circular TEmn Modes Using Y-Type Power Dividers. IEEE Trans. Microw. Theory Tech. 2010, 58, 1543–1550. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Y.; Pu, Y.; Luo, Y. Design and Microwave Measurement of a Novel Compact TE0n/TE1n’-Mode Converter. IEEE Trans. Microw. Theory Tech. 2016, 64, 4108–4116. [Google Scholar] [CrossRef]
- Wang, M.; Wu, Z.; Liao, X.; Yuan, H.; Pu, Y.; Wang, J.; Luo, Y. Exciting Circular TM11 Mode Using Symmetric Probes Based on Ridge Gap Waveguide. IEEE Trans. Microw. Theory Tech. 2021, 70, 334–342. [Google Scholar] [CrossRef]
- Haas, D.; Thumm, M. Design Procedure for a Broadband TE11/HE11 Mode Converter for High-Power Radar Applications. J. Infrared Millim. Terahertz Waves 2021, 42, 380–390. [Google Scholar] [CrossRef]
- Cohn, S.B. The Electric Polarizability of Apertures of Arbitrary Shape. Proc. IRE 1952, 40, 1069–1071. [Google Scholar] [CrossRef]
- McDonald, N. Electric and Magnetic Coupling through Small Apertures in Shield Walls of Any Thickness. IEEE Trans. Microw. Theory Tech. 1972, 20, 689–695. [Google Scholar] [CrossRef]
- Bethe, H.A. Theory of Diffraction by Small Holes. Phys. Rev. 1944, 66, 163–182. [Google Scholar] [CrossRef]
- CST-Computer Simulation Technology. Available online: http://www.cst.com/products/cstmws (accessed on 1 June 2020).
- Kirley, M.P.; Booske, J.H. Terahertz Conductivity of Copper Surfaces. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 1012–1020. [Google Scholar] [CrossRef]





| Structure Type | Mode Conversion | Frequency Band | Relative Bandwidth |
|---|---|---|---|
| T-junction | W-band | 10.5% [23] | |
| Y-type | Q-band | 4.4% [26] | |
| Multiple-hole | Y-band | 28% [24] | |
| Coupling aperture | Q-band | 11.3% [29] | |
| This work | Ka-band | 11.4% |
| Parameter | W | N | s | l | d | H |
|---|---|---|---|---|---|---|
| Design (mm) | 30 | 4.85 | 5.48 | 2.9 | 1.005 | 11.5 |
| Actual (mm) | 29.97 | 4.86 | 5.48 | 2.91 | 1.015 | 12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Jiang, W.; Wu, Z.; Liu, G.; Wang, J.; Pu, Y.; Luo, Y. Design and Measurement of a Novel Overmoded TE01 Mode Converter for a Rectangular Gyro-TWT. Micromachines 2022, 13, 1111. https://doi.org/10.3390/mi13071111
Lu C, Jiang W, Wu Z, Liu G, Wang J, Pu Y, Luo Y. Design and Measurement of a Novel Overmoded TE01 Mode Converter for a Rectangular Gyro-TWT. Micromachines. 2022; 13(7):1111. https://doi.org/10.3390/mi13071111
Chicago/Turabian StyleLu, Chaoxuan, Wei Jiang, Zewei Wu, Guo Liu, Jianxun Wang, Youlei Pu, and Yong Luo. 2022. "Design and Measurement of a Novel Overmoded TE01 Mode Converter for a Rectangular Gyro-TWT" Micromachines 13, no. 7: 1111. https://doi.org/10.3390/mi13071111






