Demonstration of Ultra-High-Q Silicon Microring Resonators for Nonlinear Integrated Photonics
Abstract
:1. Introduction
2. Structure and Fabrication
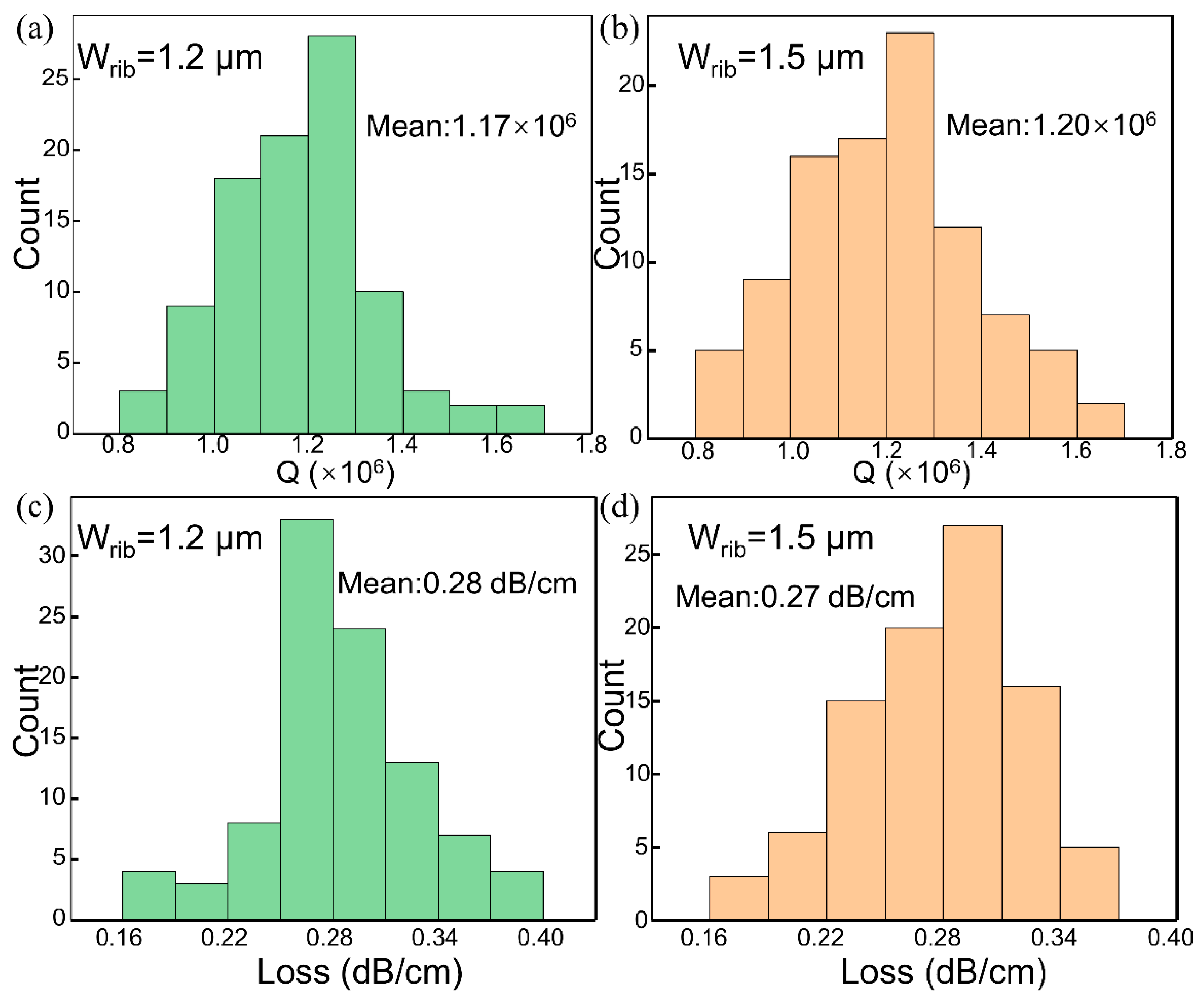
3. Measurement and Analysis of Q
4. Measurement of FWM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Dong, P.; Chen, Y.-K.; Duan, G.-H.; Neilson, D.T. Silicon photonic devices and integrated circuits. Nanophotonics 2014, 3, 215–228. [Google Scholar] [CrossRef]
- Chrostowski, L.; Hochberg, M. Silicon Photonics Design: From Devices to Systems; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Bogaerts, W.; Chrostowski, L. Silicon Photonics Circuit Design: Methods, Tools and Challenges. Laser Photonics Rev. 2018, 12, 4374–4389. [Google Scholar] [CrossRef]
- Zhang, B.; Al Qubaisi, K.; Cherchi, M.; Harjanne, M.; Ehrlichman, Y.; Khilo, A.N.; Popovic, M.A. Compact multi-million Q resonators and 100 MHz passband filter bank in a thick-SOI photonics platform. Opt. Lett. 2020, 45, 3005–3008. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Yu, J. Coherent interaction between two orthogonal travelling-wave modes in a microdonut resonator for filtering and buffering applications. Opt. Express 2014, 22, 25171–25182. [Google Scholar] [CrossRef] [Green Version]
- Naweed, A. Photonic coherence effects from dual-waveguide coupled pair of co-resonant microring resonators. Opt. Express 2015, 23, 12573–12581. [Google Scholar] [CrossRef]
- Chang, L.; Xie, W.; Shu, H.; Yang, Q.F.; Shen, B.; Boes, A.; Peters, J.D.; Jin, W.; Xiang, C.; Liu, S.; et al. Ultra-efficient frequency comb generation in AlGaAs-on-insulator microresonators. Nat. Commun. 2020, 11, 1331. [Google Scholar] [CrossRef]
- Huang, G.; Fu, M.; Qi, J.; Pan, J.; Yi, W.; Li, X. Design of broadband flat optical frequency comb based on cascaded sign-alternated dispersion tellurite microstructure fiber. Micromachines 2021, 12, 1252. [Google Scholar] [CrossRef]
- Buscaino, B.; Zhang, M.; Lončar, M.; Kahn, J.M. Design of efficient resonator-enhanced electro-optic frequency comb generators. J. Lightwave Technol. 2020, 38, 1400–1413. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Q.; Mei, C.; Zeng, D.; Huang, Q.; Zhang, X. Proposal and demonstration of a controllable Q factor in directly coupled microring resonators for optical buffering applications. Photonics Res. 2021, 9, 2006–2015. [Google Scholar] [CrossRef]
- Elshaari, A.W.; Aboketaf, A.; Preble, S.F. Controlled storage of light in silicon cavities. Opt. Express 2010, 18, 3014–3022. [Google Scholar] [CrossRef] [PubMed]
- Vlasov, Y.; Green, W.M.J.; Xia, F. High-throughput silicon nanophotonic wavelength-insensitive switch for on-chip optical networks. Nat. Photonics 2008, 2, 242–246. [Google Scholar] [CrossRef]
- Qavi, A.J.; Washburn, A.L.; Byeon, J.-Y.; Bailey, R.C. Label-free technologies for quantitative multiparameter biological analysis. Anal. Bioanal. Chem. 2009, 394, 121–135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, P.; Qian, W.; Liao, S.R.; Liang, H.; Kung, C.; Feng, N.N.; Shafiiha, R.; Fong, J.; Feng, D.Z.; Krishnamoorthy, A.V.; et al. Low loss shallow-ridge silicon waveguides. Opt. Express 2010, 18, 14474–14479. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.C.; Barbosa, F.A.S.; Roberts, S.P.; Dutt, A.; Cardenas, J.; Okawachi, Y.; Bryant, A.; Gaeta, A.L.; Lipson, M. Ultra-low-loss on-chip resonators with sub-milliwatt parametric oscillation threshold. Optica 2017, 4, 492–495. [Google Scholar] [CrossRef] [Green Version]
- Puckett, M.W.; Liu, K.; Chauhan, N.; Zhao, Q.; Jin, N.; Cheng, H.; Wu, J.; Behunin, R.O.; Rakich, P.T.; Nelson, K.D.; et al. 422 Million intrinsic quality factor planar integrated all-waveguide resonator with sub-MHz linewidth. Nat. Commun. 2021, 12, 934. [Google Scholar] [CrossRef]
- Qiu, H.Q.; Zhang, X.L.; Zhou, F.; Qie, J.R.; Yao, Y.H.; Hu, X.; Zhang, Y.; Xiao, X.; Yu, Y.; Dong, J. A continuously tunable sub-gigahertz microwave photonic bandpass filter based on an ultra-high-Q silicon microring resonator. J. Lightwave Technol. 2018, 36, 4312–4318. [Google Scholar] [CrossRef]
- Guillen-Torres, M.A.; Caverley, M.; Cretu, E.; Jaeger, N.A.F.; Chrostowski, L. Large-area, high-Q SOI ring resonators. In Proceedings of the 2014 IEEE Photonics Conference, San Diego, CA, USA, 12–16 October 2014; pp. 336–337. [Google Scholar]
- Zhang, L.; Jie, L.L.; Zhang, M.; Wang, Y.; Xie, Y.W.; Shi, Y.C.; Dai, D.X. Ultrahigh-Q silicon racetrack resonators. Photonics Res. 2020, 8, 684–689. [Google Scholar] [CrossRef]
- Lee, K.K.; Lim, D.R.; Kimerling, L.C.; Shin, J.; Cerrina, F. Fabrication of ultralow-loss Si/SiO2 waveguides by roughness reduction. Opt. Lett. 2001, 26, 1888–1890. [Google Scholar] [CrossRef]
- Biberman, A.; Shaw, M.J.; Timurdogan, E.; Wright, J.B.; Watts, M.R. Ultralow-loss silicon ring resonators. Opt. Lett. 2012, 37, 4236–4238. [Google Scholar] [CrossRef]
- Takahashi, J.; Tsuchizawa, T.; Watanabe, T.; Itabashi, S. Oxidation-induced improvement in the sidewall morphology and cross-sectional profile of silicon wire waveguides. J. Vac. Sci. Technol. B 2004, 22, 2522–2525. [Google Scholar] [CrossRef]
- Xie, W.; Chang, L.; Shu, H.; Norman, J.C.; Peters, J.D.; Wang, X.; Bowers, J.E. Ultrahigh-Q AlGaAs-on-insulator microresonators for integrated nonlinear photonics. Opt. Express 2020, 28, 32894–32906. [Google Scholar] [CrossRef] [PubMed]
- Hung, S.C.; Liang, E.Z.; Lin, C.F. Silicon waveguide sidewall smoothing by KrF excimer laser reformation. J. Lightwave Technol. 2009, 27, 887–892. [Google Scholar] [CrossRef]
- Ong, J.R.; Kumar, R.; Aguinaldo, R.; Mookherjea, S. Efficient CW four-wave mixing in silicon-on-insulator micro-rings with active carrier Removal. IEEE Photonics Technol. Lett. 2013, 25, 1699–1702. [Google Scholar] [CrossRef]
- Huang, Q.Z.; Shu, Z.; Song, G.; Chen, J.; Xia, J.S.; Yu, J. Electromagnetically induced transparency-like effect in a two-bus waveguides coupled microdisk resonator. Opt. Express 2014, 22, 3219–3227. [Google Scholar] [CrossRef]
- Huang, Q.Z.; Song, G.; Chen, J.G.; Shu, Z.; Yu, J.Z. Proposal and fabrication of an electrooptically controlled multimode microresonator for continuous fast-to-Slow light tuning. IEEE Photonics J. 2014, 6, 1–11. [Google Scholar] [CrossRef]
- Weng, H.; Liu, J.; Afridi, A.A.; Li, J.; Dai, J.; Ma, X.; Zhang, Y.; Lu, Q.; Donegan, J.F.; Guo, W. Directly accessing octave-spanning dissipative Kerr soliton frequency combs in an AlN microresonator. Photonics Res. 2021, 9, 1351–1357. [Google Scholar] [CrossRef]
- Lacava, C.; Strain, M.J.; Minzioni, P.; Cristiani, I.; Sorel, M. Integrated nonlinear Mach Zehnder for 40 Gbit/s all-optical switching. Opt. Express 2013, 21, 21587–21595. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biberman, A.; Lee, B.G.; Turner-Foster, A.C.; Foster, M.A.; Lipson, M.; Gaeta, A.L.; Bergman, K. Wavelength multicasting in silicon photonic nanowires. Opt. Express 2010, 18, 18047–18055. [Google Scholar] [CrossRef] [Green Version]
- Azzini, S.; Grassani, D.; Strain, M.J.; Sorel, M.; Helt, L.G.; Sipe, J.E.; Liscidini, M.; Galli, M.; Bajoni, D. Ultra-low power generation of twin photons in a compact silicon ring resonator. Opt. Express 2012, 20, 23100–23107. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.C.; Li, K.; Gai, X.; Nolan, D.A.; Dainese, P. Ultra-low-power four-wave mixing wavelength conversion in high-Q chalcogenide microring resonators. Opt. Lett. 2021, 46, 2912–2915. [Google Scholar] [CrossRef] [PubMed]
- Absil, P.P.; Hryniewicz, J.V.; Little, B.E.; Cho, P.S.; Wilson, R.A.; Joneckis, L.G.; Ho, P.T. Wavelength conversion in GaAs micro-ring resonators. Opt. Lett. 2000, 25, 554–556. [Google Scholar] [CrossRef]
- Almeida, V.R.; Barrios, C.A.; Panepucci, R.R.; Lipson, M. All-optical control of light on a silicon chip. Nature 2004, 431, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Bristow, A.D.; Rotenberg, N.; van Driel, H.M. Two-photon absorption and Kerr coefficients of silicon for 850-2200 nm. Appl. Phys. Lett. 2007, 90, 191104. [Google Scholar] [CrossRef]
- Tsang, H.K.; Wong, C.S.; Liang, T.K.; Day, I.E.; Roberts, S.W.; Harpin, A.; Drake, J.; Asghari, M. Optical dispersion, two-photon absorption and self-phase modulation in silicon waveguides at 1.5 μm wavelength. Appl. Phys. Lett. 2002, 80, 416–418. [Google Scholar] [CrossRef]
- Kultavewuti, P.; Pusino, V.; Sorel, M.; Stewart Aitchison, J. Low-power continuous-wave four-wave mixing wavelength conversion in AlGaAs-nanowaveguide microresonators. Opt. Lett. 2015, 40, 3029–3032. [Google Scholar] [CrossRef] [Green Version]
- Ferrera, M.; Duchesne, D.; Razzari, L.; Peccianti, M.; Morandotti, R.; Cheben, P.; Janz, S.; Xu, D.X.; Little, B.E.; Chu, S.; et al. Low power four wave mixing in an integrated, micro-ring resonator with Q = 1.2 million. Opt. Express 2009, 17, 14098–14103. [Google Scholar] [CrossRef] [Green Version]
- Xing, P.; Ma, D.h.; Kimerling, L.C.; Agarwal, A.M.; Tan, D.T.H. High efficiency four wave mixing and optical bistability in amorphous silicon carbide ring resonators. APL Photonics 2020, 5, 076110. [Google Scholar] [CrossRef]
- Long, Y.; Wang, Y.; Hu, X.; Ji, M.; Shen, L.; Wang, A.; Wang, J. Channel-selective wavelength conversion of quadrature amplitude modulation signal using a graphene-assisted silicon microring resonator. Opt. Lett. 2017, 42, 799–802. [Google Scholar] [CrossRef]
- Turner, A.C.; Foster, M.A.; Gaeta, A.L.; Lipson, M. Ultra-low power parametric frequency conversion in a silicon microring resonator. Opt. Express 2008, 16, 4881–4887. [Google Scholar] [CrossRef] [Green Version]
- Cantarella, G.; Klitis, C.; Sorel, M.; Strain, M.J. Silicon photonic filters with high rejection of both TE and TM modes for on-chip four wave mixing applications. Opt. Express 2017, 25, 19711–19720. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Hu, X.; Chen, D.; Wang, L.; Li, M.; Feng, P.; Xiao, X.; Yu, S. Design and demonstration of ultra-high-Q silicon microring resonator based on a multi-mode ridge waveguide. Opt. Lett. 2018, 43, 1586–1589. [Google Scholar] [CrossRef] [PubMed]





| Device | Waveguide | Q-Factor | Pump Power (dBm) | CE (dB) | Reference |
|---|---|---|---|---|---|
| AlGaAs racetrack microring | Single mode | 7.5 × 103 | 13.80 | −43 | [38] |
| doped SiO2 add-drop microring | Single mode | 1.2 × 106 | 9.4 | −26 | [39] |
| amorphous SiC all-pass microring | Multimode | 7 × 104 | 11.76 | −21 | [40] |
| SOI all-pass microring | Single mode | 9.15 × 103 | 12 | −29.4 | [41] |
| SOI all-pass microring | Single mode | 1.9 × 104 | 10.5 | −25.4 | [42] |
| SOI cascaded microring | Multimode | 3.0 × 104 | 3 | −22 | [43] |
| SOI racetrack add-drop | Multimode | 1.1 × 106 | 10 | −15.5 | [44] |
| SOI all-pass microring | Multimode | 1.51 × 106 | 6.50 | −17.0 | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, D.; Liu, Q.; Mei, C.; Li, H.; Huang, Q.; Zhang, X. Demonstration of Ultra-High-Q Silicon Microring Resonators for Nonlinear Integrated Photonics. Micromachines 2022, 13, 1155. https://doi.org/10.3390/mi13071155
Zeng D, Liu Q, Mei C, Li H, Huang Q, Zhang X. Demonstration of Ultra-High-Q Silicon Microring Resonators for Nonlinear Integrated Photonics. Micromachines. 2022; 13(7):1155. https://doi.org/10.3390/mi13071155
Chicago/Turabian StyleZeng, Desheng, Qiang Liu, Chenyang Mei, Hongwei Li, Qingzhong Huang, and Xinliang Zhang. 2022. "Demonstration of Ultra-High-Q Silicon Microring Resonators for Nonlinear Integrated Photonics" Micromachines 13, no. 7: 1155. https://doi.org/10.3390/mi13071155
APA StyleZeng, D., Liu, Q., Mei, C., Li, H., Huang, Q., & Zhang, X. (2022). Demonstration of Ultra-High-Q Silicon Microring Resonators for Nonlinear Integrated Photonics. Micromachines, 13(7), 1155. https://doi.org/10.3390/mi13071155





