The Physics and Manipulation of Dean Vortices in Single- and Two-Phase Flow in Curved Microchannels: A Review
Abstract
:1. Introduction
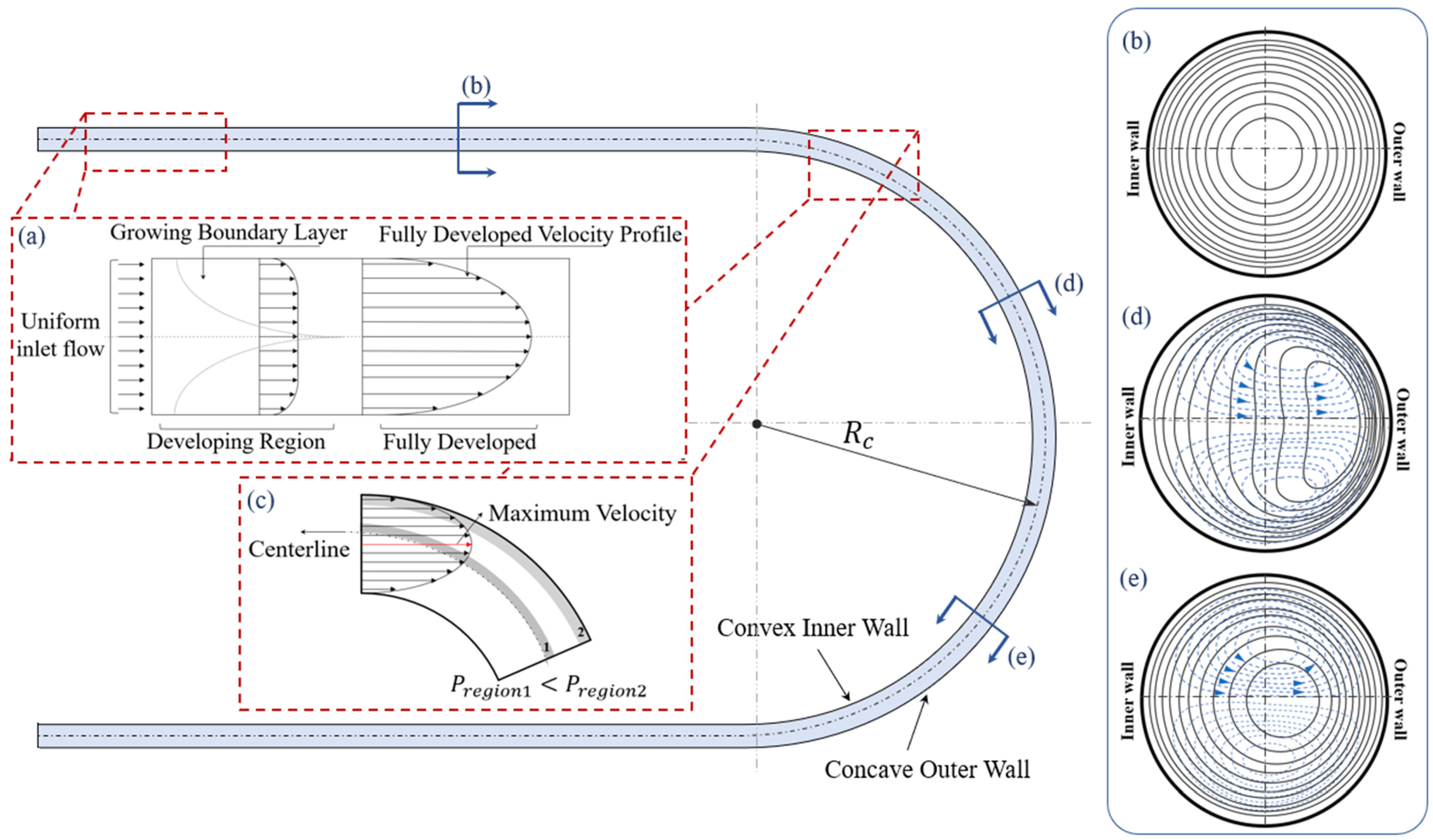
2. The Physics of Flows in a Curved Channel
2.1. The Dean Number
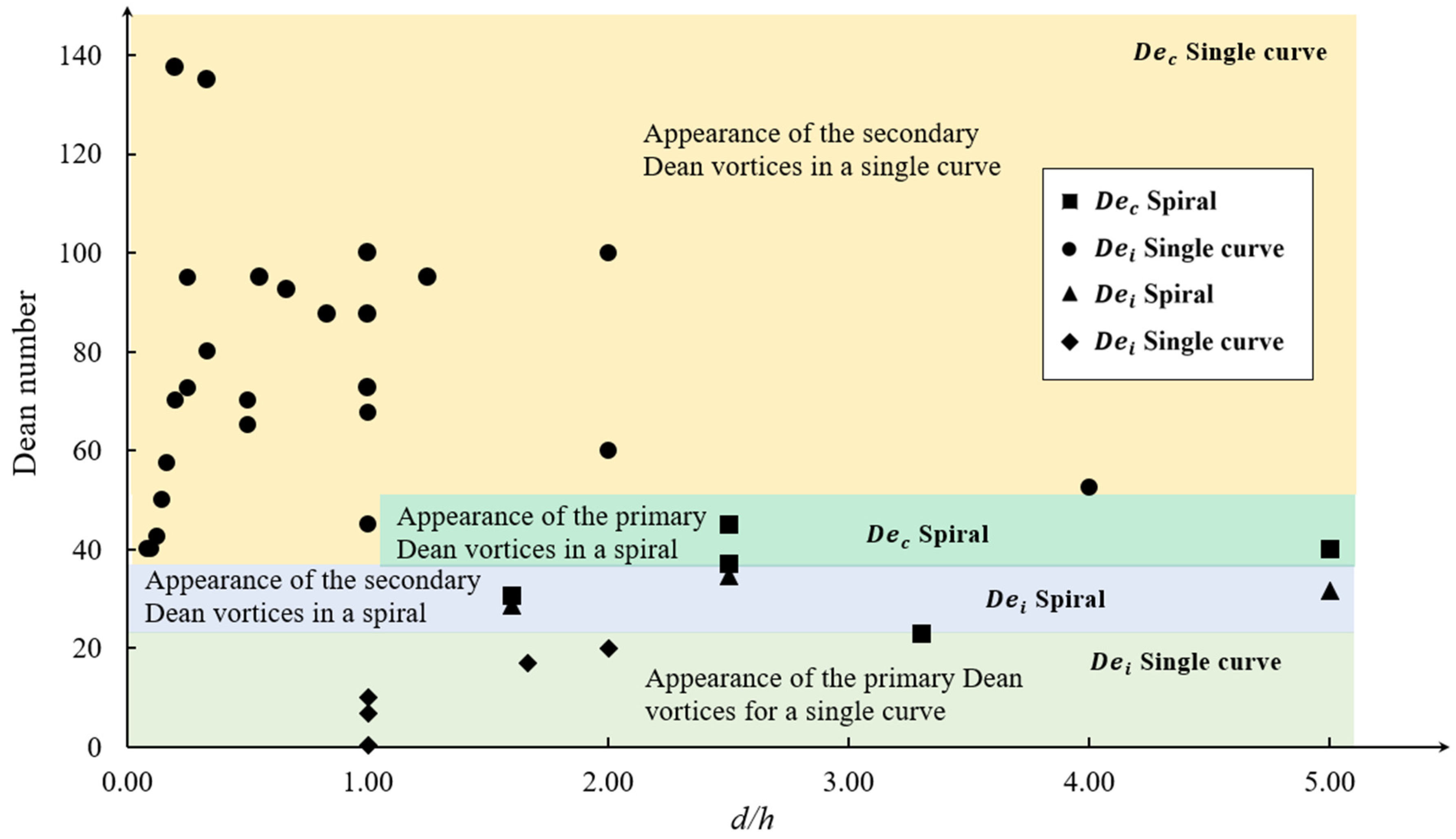
2.2. Dean Number Thresholds
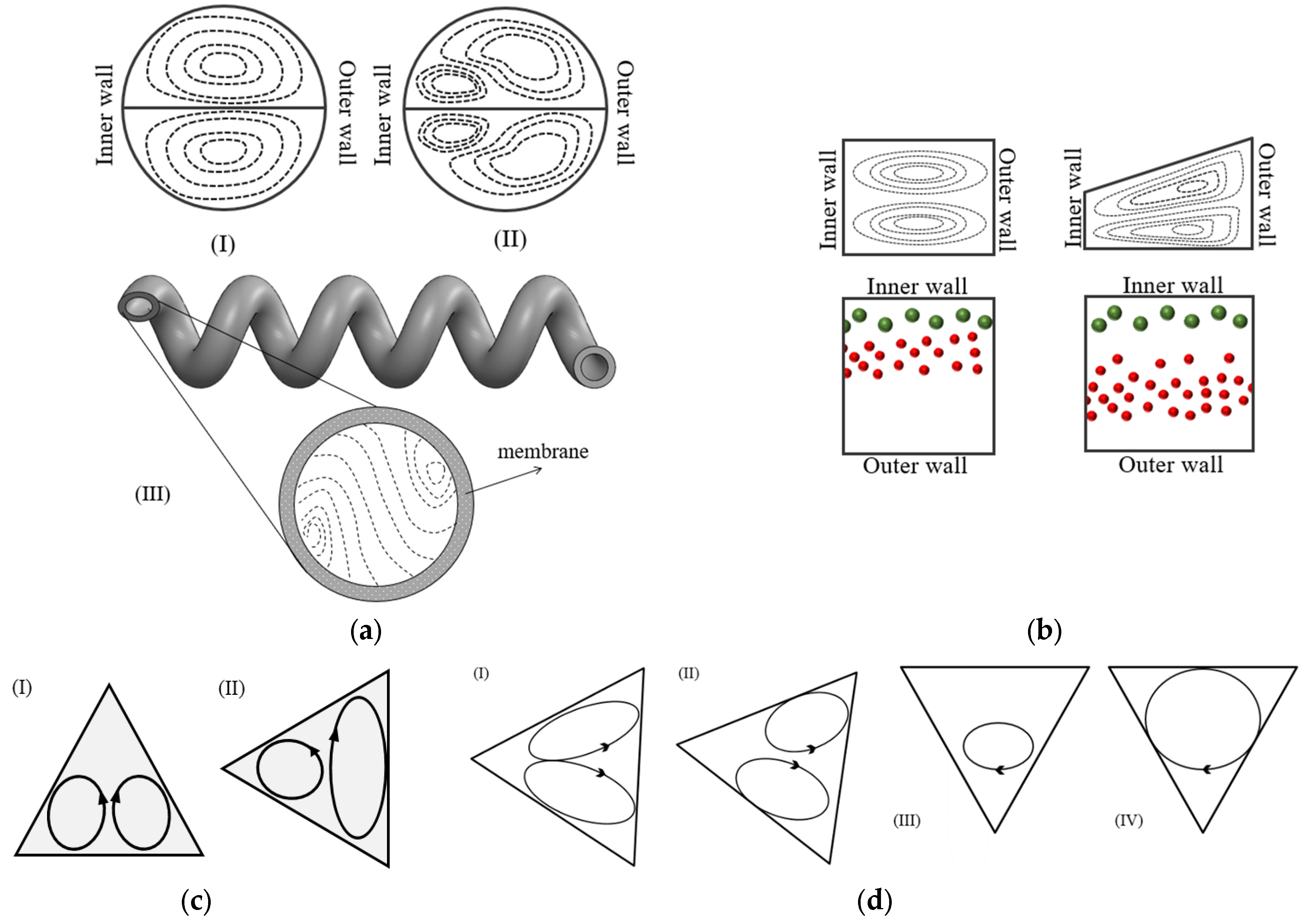
3. The Effect of Geometry on the Structure of the Dean Flow
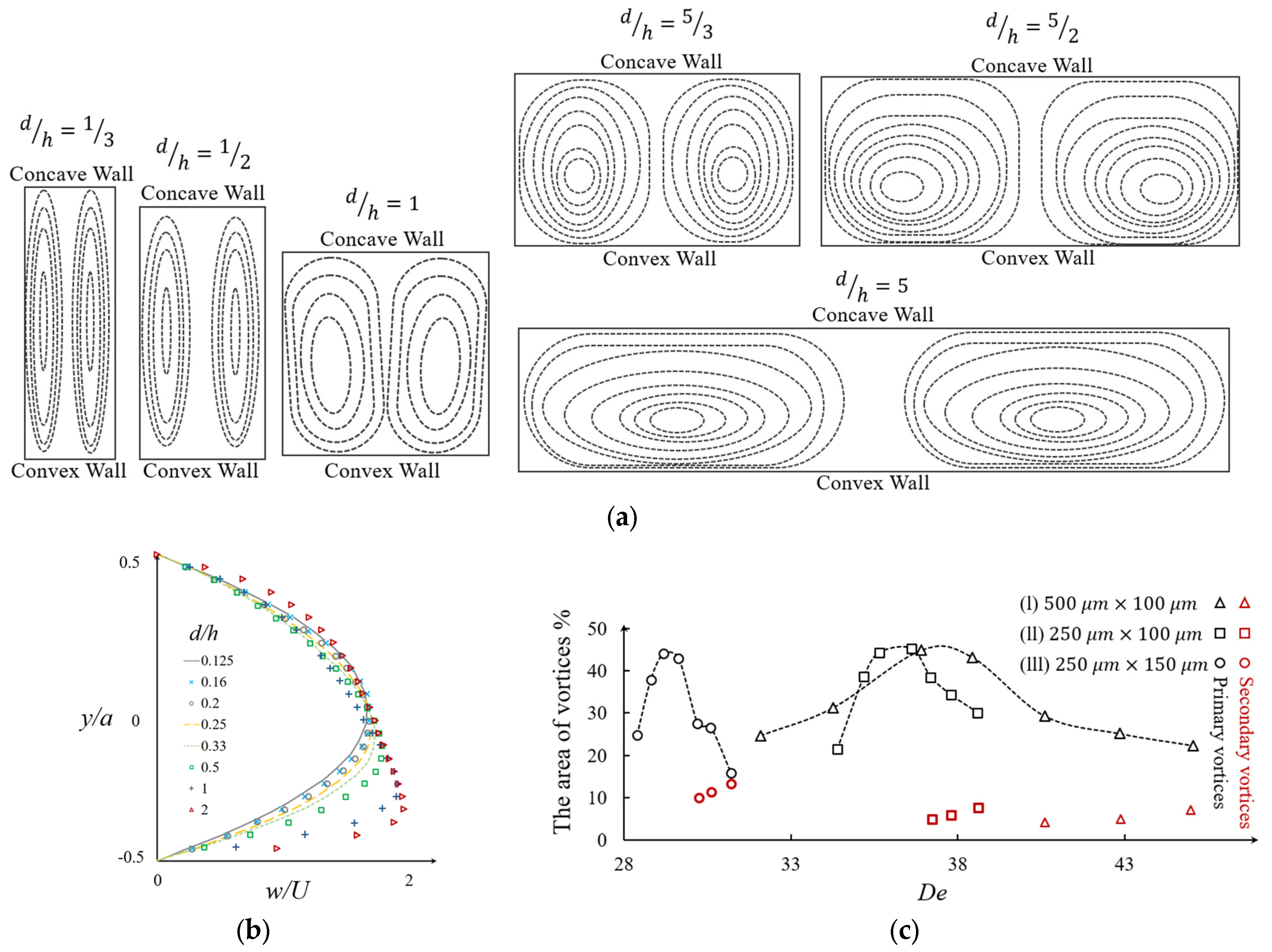
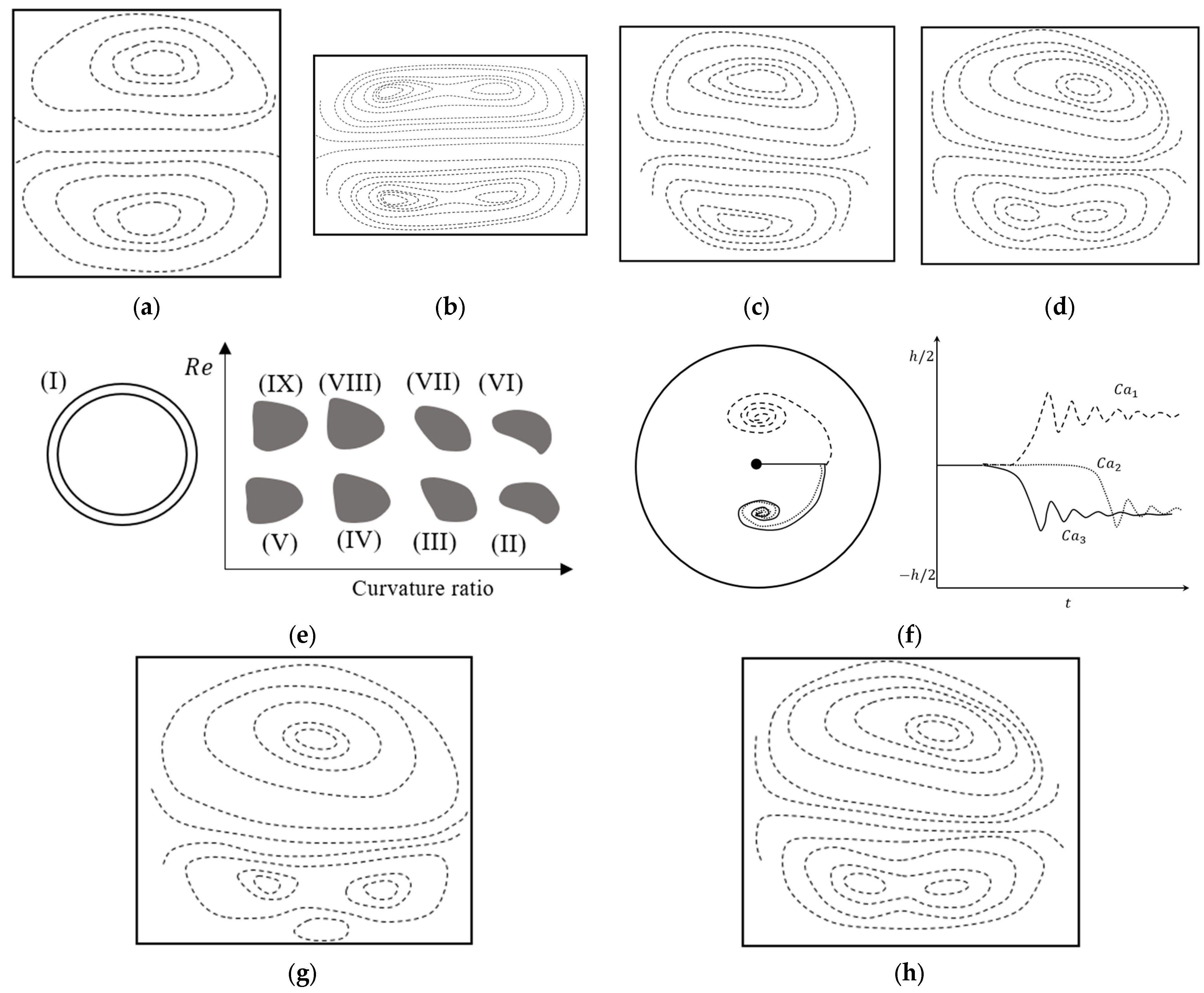
3.1. Effect of the Chanel Aspect Ratio
3.2. The Effect of the Cross-Section Shape
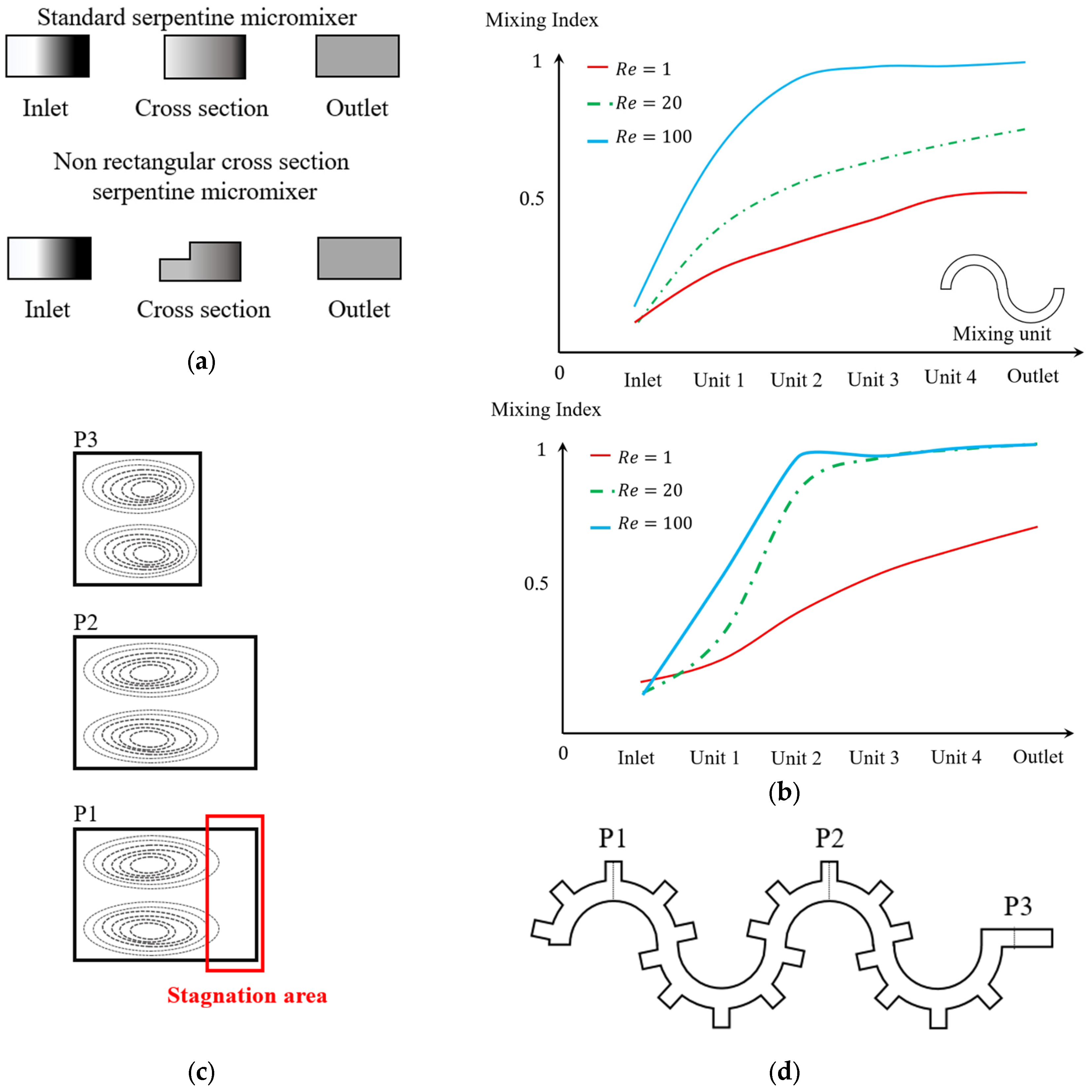
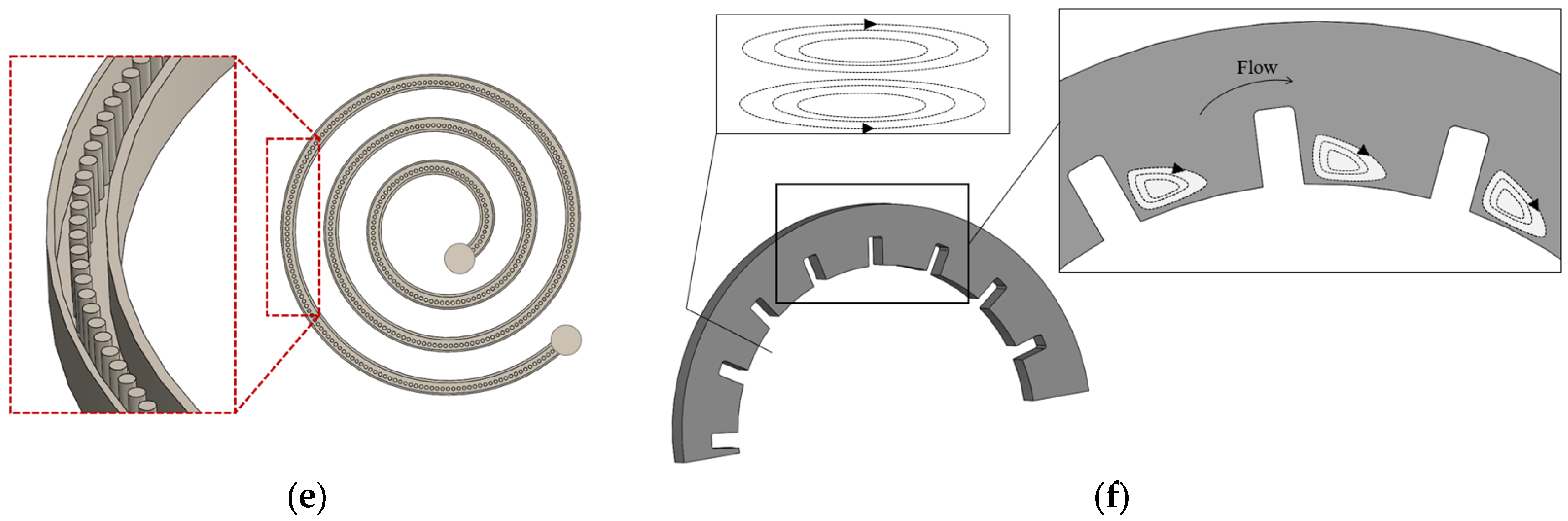
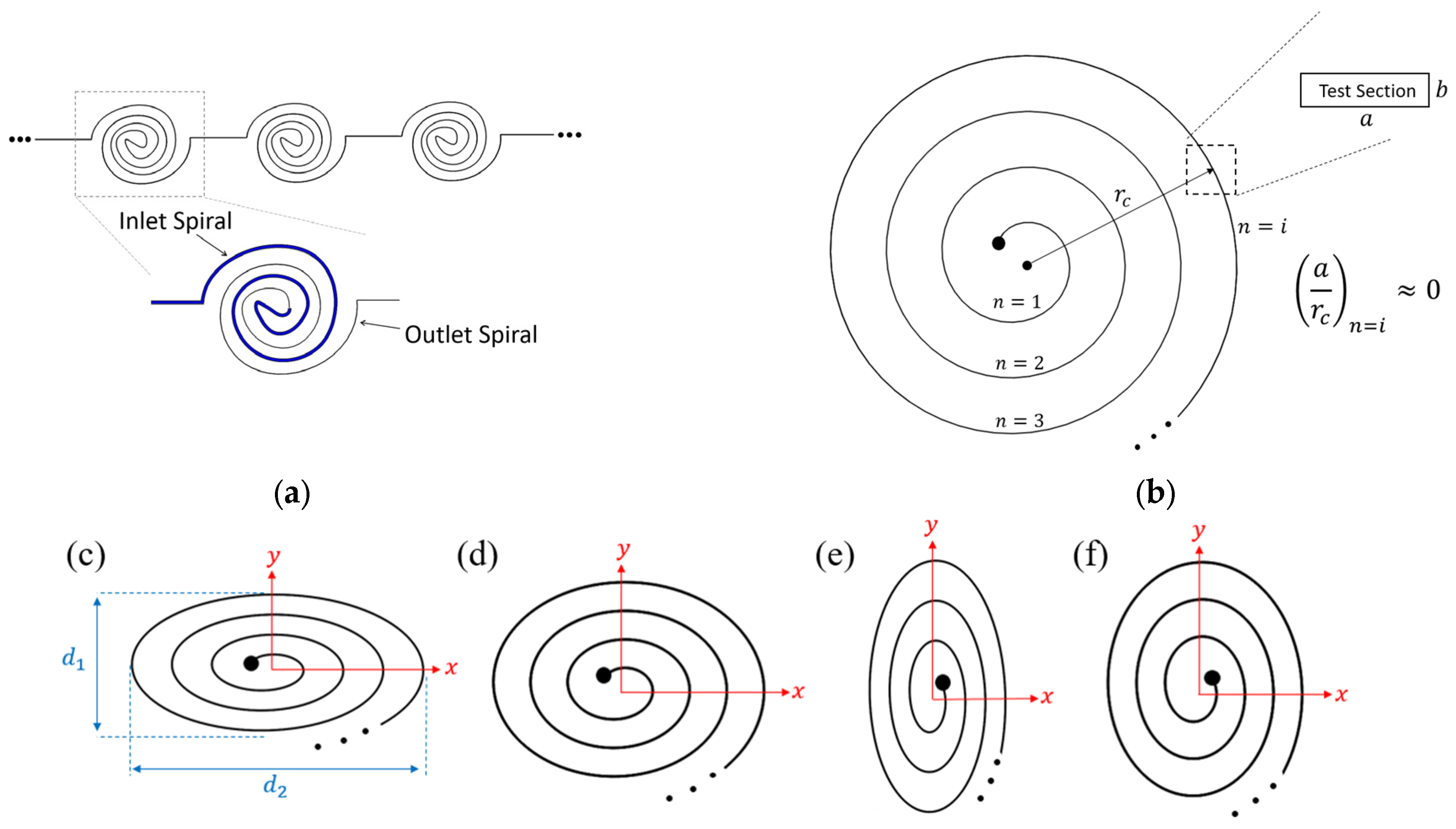
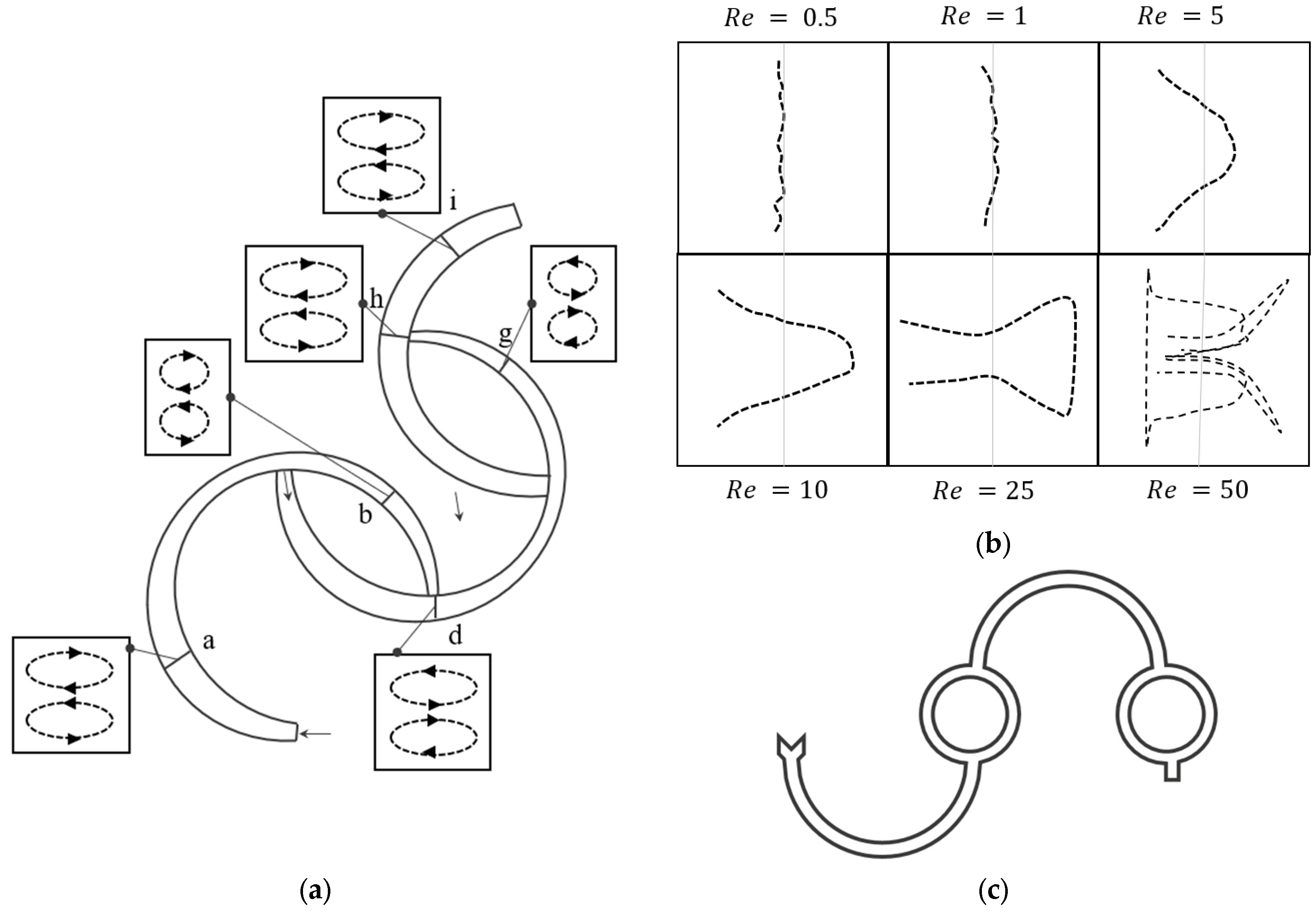
3.3. The Effect of the Curvature Path
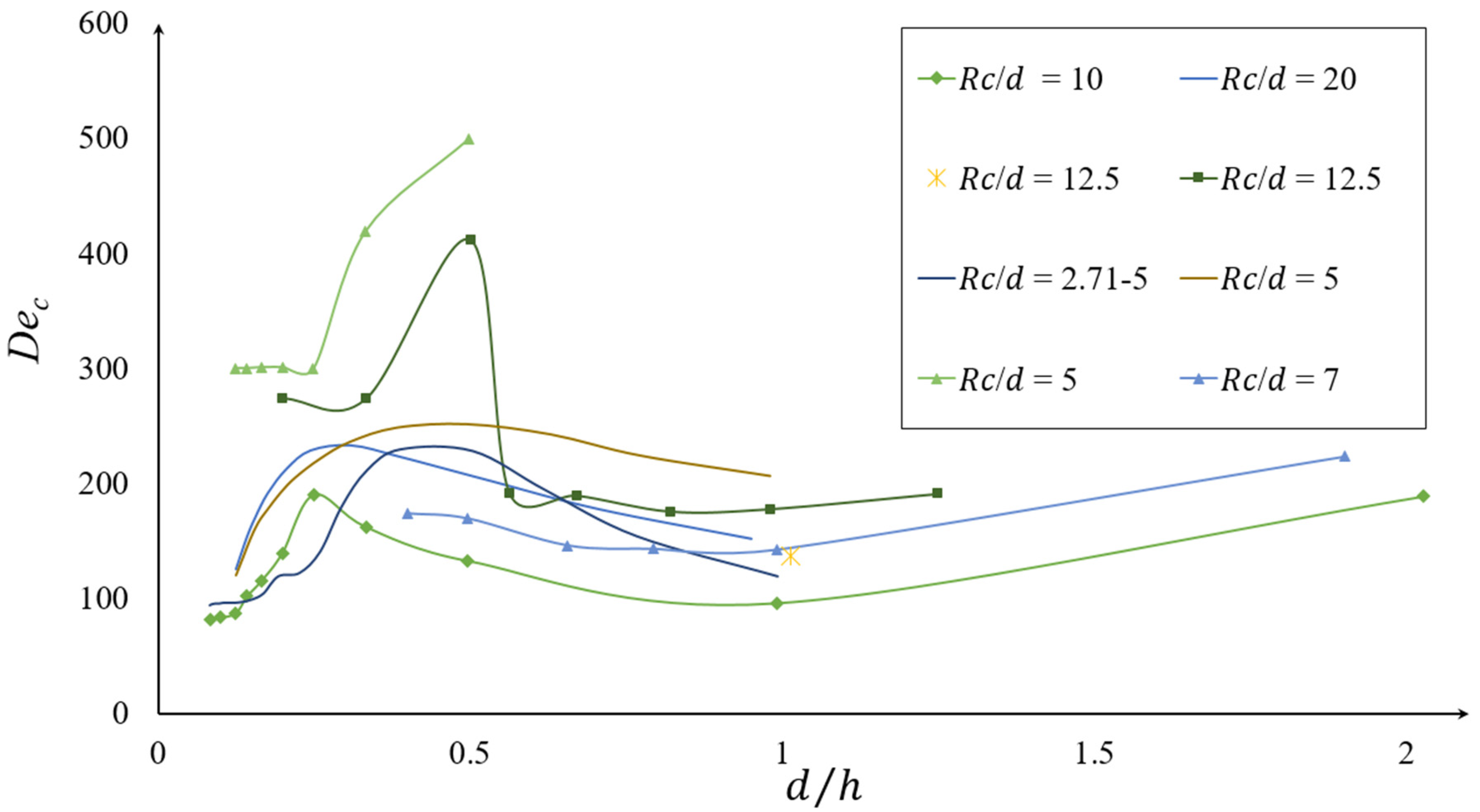
3.3.1. The Variation of the Radius of Curvature
3.3.2. Variation of the Direction of Curvature
3.3.3. Unconventional Paths
4. The Liquid–Liquid Two Phased Flow in Curved Channels
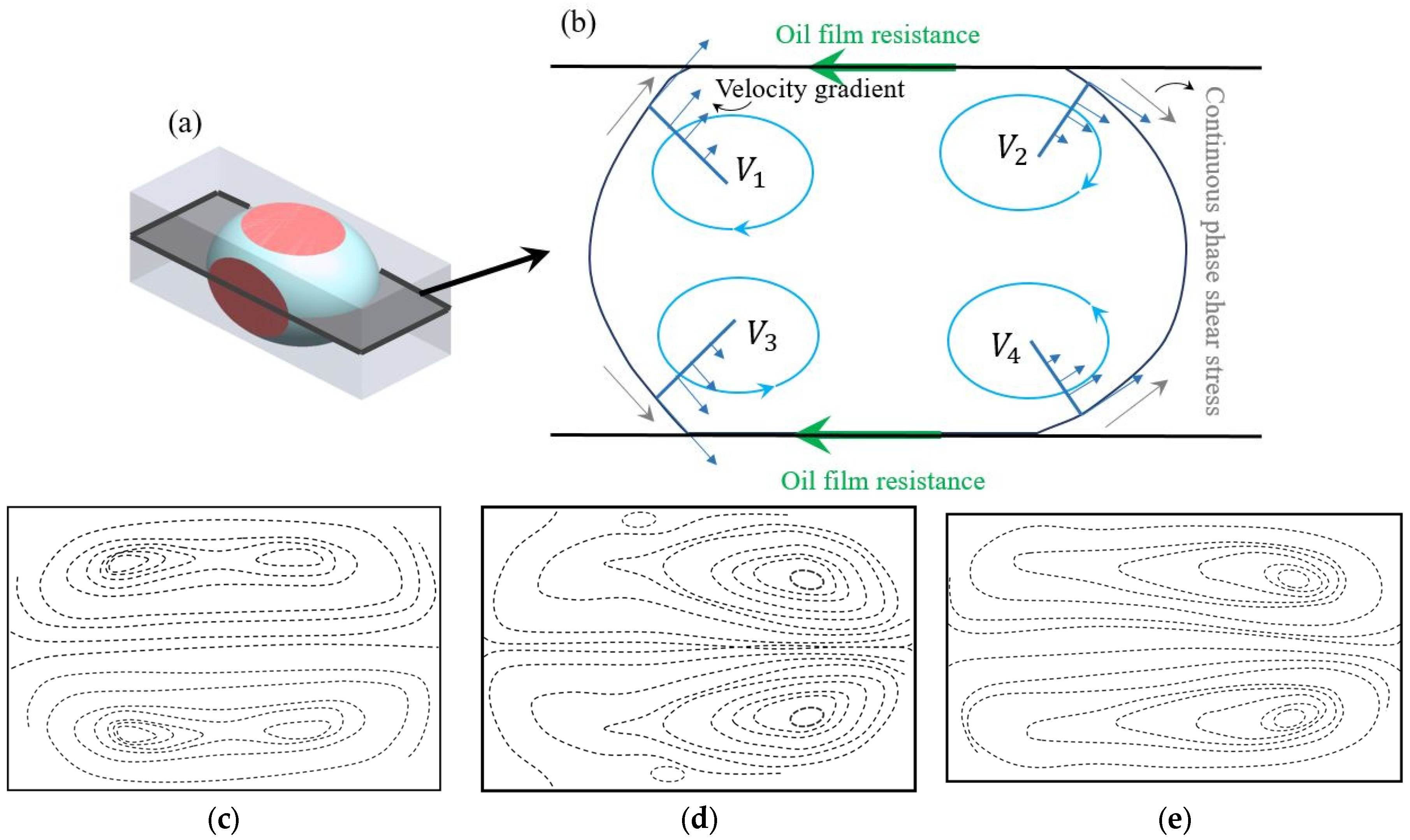
4.1. Physics of the Flow Inside a Droplet in Straight Microchannels
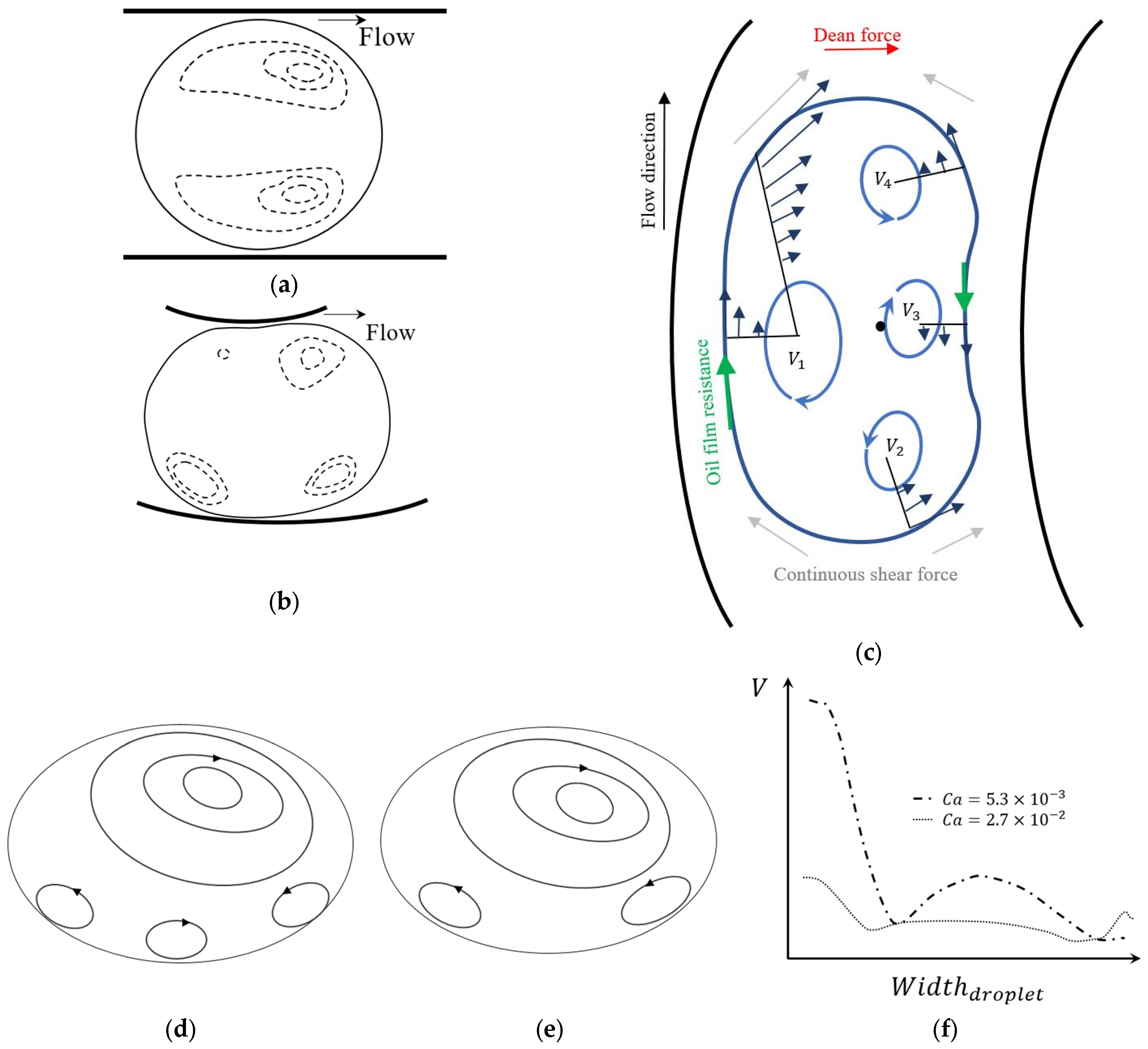
4.2. Physics of the Flow Inside a Droplet in Curved Microchannels
4.3. Effect of Microchannel Geometry on Droplet Topology
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whitesides, G.M. What Comes Next? Lab Chip 2011, 11, 191–193. [Google Scholar] [CrossRef] [PubMed]
- Angell, J.B.; Terry, S.C.; Barth, P.W. Silicon Micromechanical Devices. In Micromechanics and MEMS: Classic and Seminal Papers to 1990; IEEE: Piscataway, NJ, USA, 1997; Volume 248, pp. 38–49. [Google Scholar] [CrossRef]
- Luo, T.; Fan, L.; Zhu, R.; Sun, D. Microfluidic Single-Cell Manipulation and Analysis: Methods and Applications. Micromachines 2019, 10, 104. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.; Sun, J.; Jiang, X. Microfluidics-Mediated Assembly of Functional Nanoparticles for Cancer-Related Pharmaceutical Applications. Nanoscale 2016, 8, 12430–12443. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Du, L.; Wang, Y.; Wang, K. Recent Developments in Microfluidic Device-Based Preparation, Functionalization, and Manipulation of Nano- and Micro-Materials. Particuology 2019, 45, 1–19. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Onck, P.; den Toonder, J. A Concise Review of Microfluidic Particle Manipulation Methods. Microfluid. Nanofluidics 2020, 24, 24. [Google Scholar] [CrossRef]
- Bhagat, A.A.S.; Bow, H.; Hou, H.W.; Tan, S.J.; Han, J.; Lim, C.T. Microfluidics for Cell Separation. Med. Biol. Eng. Comput. 2010, 48, 999–1014. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.D.; Linder, V.; Sia, S.K. Lab-on-a-Chip Devices for Global Health: Past Studies and Future Opportunities. Lab Chip 2007, 7, 41–57. [Google Scholar] [CrossRef]
- Soper, S.A.; Brown, K.; Ellington, A.; Frazier, B.; Garcia-Manero, G.; Gau, V.; Gutman, S.I.; Hayes, D.F.; Korte, B.; Landers, J.L.; et al. Point-of-Care Biosensor Systems for Cancer Diagnostics/Prognostics. Biosens. Bioelectron. 2006, 21, 1932–1942. [Google Scholar] [CrossRef]
- Tüdos, A.J.; Besselink, G.A.J.; Schasfoort, R.B.M. Trends in Miniaturized Total Analysis Systems for Point-of-Care Testing in Clinical Chemistry. Lab Chip 2001, 1, 83–95. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, S.; Yuan, D.; Alici, G.; Nguyen, N.T.; Ebrahimi Warkiani, M.; Li, W. Fundamentals and Applications of Inertial Microfluidics: A Review. Lab Chip 2016, 16, 10–34. [Google Scholar] [CrossRef]
- Bow, H.; Pivkin, I.V.; Diez-Silva, M.; Goldfless, S.J.; Dao, M. A Microfabricated Deformability-Based Flow Cytometer with Application to Malaria. Lab Chip 2011, 11, 1065–1073. [Google Scholar] [CrossRef] [PubMed]
- Al-Halhouli, A.; Al-Faqheri, W.; Alhamarneh, B.; Hecht, L.; Dietzel, A. Spiral Microchannels with Trapezoidal Cross Section Fabricated by Femtosecond Laser Ablation in Glass for the Inertial Separation of Microparticles. Micromachines 2018, 9, 171. [Google Scholar] [CrossRef]
- Srinivasan, V.; Pamula, V.K.; Fair, R.B. An Integrated Digital Microfluidic Lab-on-a-Chip for Clinical Diagnostics on Human Physiological Fluids. Lab Chip 2004, 4, 310–315. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, V.; Pamula, V.K.; Fair, R.B. Droplet-Based Microfluidic Lab-on-a-Chip for Glucose Detection. Anal. Chim. Acta 2004, 507, 145–150. [Google Scholar] [CrossRef]
- Mao, Z.; Yang, C. Micro-Mixing in Chemical Reactors: A Perspective. Chin. J. Chem. Eng. 2017, 25, 381–390. [Google Scholar] [CrossRef]
- Huebner, A.; Srisa-Art, M.; Holt, D.; Abell, C.; Hollfelder, F.; DeMello, A.J.; Edel, J.B. Quantitative Detection of Protein Expression in Single Cells Using Droplet Microfluidics. Chem. Commun. 2007, 2, 1218–1220. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Andreo, J.; Walden, M.; del Campo, J.F.; Basabe-Desmonts, L.; Benito-Lopez, F.; Burg, T.P.; Wuttke, S. The Importance of Dean Flow in Microfluidic Nanoparticle Synthesis: A ZIF-8 Case Study. Small Methods 2023, 1, 2300603. [Google Scholar] [CrossRef]
- Ratner, D.M.; Murphy, E.R.; Jhunjhunwala, M.; Snyder, D.A.; Jensen, K.F.; Seeberger, P.H. Microreactor-Based Reaction Optimization in Organic Chemistry-Glycosylation as a Challenge. Chem. Commun. 2005, 5, 578–580. [Google Scholar] [CrossRef]
- Chen, S.; Liu, W.; Wan, J.; Cheng, X.; Gu, C.; Zhou, H.; Chen, S.; Zhao, X.; Tang, Y.; Yang, X. Preparation of Coenzyme Q10 Nanostructured Lipid Carriers for Epidermal Targeting with High-Pressure Microfluidics Technique. Drug Dev. Ind. Pharm. 2013, 39, 20–28. [Google Scholar] [CrossRef]
- Lo, C.T.; Jahn, A.; Locascio, L.E.; Vreeland, W.N. Controlled Self-Assembly of Monodisperse Niosomes by Microfluidic Hydrodynamic Focusing. Langmuir 2010, 26, 8559–8566. [Google Scholar] [CrossRef]
- Sutterby, E.; Thurgood, P.; Baratchi, S.; Khoshmanesh, K.; Pirogova, E. Microfluidic Skin-on-a-Chip Models: Toward Biomimetic Artificial Skin. Small 2020, 16, 2002515. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.-H.; Jin, S.H.; Lee, B.J.; Kim, T.; Lee, C.-S. Microfluidic Static Droplet Array for Analyzing Microbial Communication on a Population Gradient. Lab Chip 2015, 15, 889–899. [Google Scholar] [CrossRef] [PubMed]
- Neethirajan, S.; Kobayashi, I.; Nakajima, M.; Wu, D.; Nandagopal, S.; Lin, F. Microfluidics for Food, Agriculture and Biosystems Industries. Lab Chip 2011, 11, 1574–1586. [Google Scholar] [CrossRef]
- Deng, B.; Ruiter, J.; Schroën, K. Application of Microfluidics in the Production and Analysis of Food Foams. Foods 2019, 8, 476. [Google Scholar] [CrossRef] [PubMed]
- Schroen, K.; Berton-Carabin, C.; Renard, D.; Marquis, M.; Boire, A.; Cochereau, R.; Amine, C.; Marze, S. Droplet Microfluidics for Food and Nutrition Applications. Micromachines 2021, 12, 863. [Google Scholar] [CrossRef] [PubMed]
- Pudake, R.N.; Chauhan, N.; Kole, C. Nanoscience for Sustainable Agriculture; Springer International Publishing: Cham, Switzerland, 2019; ISBN 9783319978529. [Google Scholar]
- Luecha, J.; Hsiao, A.; Brodsky, S.; Liu, G.L.; Kokini, J.L. Green Microfluidic Devices Made of Corn Proteins. Lab Chip 2011, 11, 3419–3425. [Google Scholar] [CrossRef] [PubMed]
- Juang, Y.J.; Chang, J.S. Applications of Microfluidics in Microalgae Biotechnology: A Review. Biotechnol. J. 2016, 11, 327–335. [Google Scholar] [CrossRef]
- Maeki, M. Microfluidics for Pharmaceutical Applications; Elsevier Inc.: Amsterdam, The Netherlands, 2018; ISBN 9780128126592. [Google Scholar]
- Ran, R.; Sun, Q.; Baby, T.; Wibowo, D.; Middelberg, A.P.J.; Zhao, C.X. Multiphase Microfluidic Synthesis of Micro- and Nanostructures for Pharmaceutical Applications. Chem. Eng. Sci. 2017, 169, 78–96. [Google Scholar] [CrossRef]
- Hamdallah, S.I.; Zoqlam, R.; Erfle, P.; Blyth, M.; Alkilany, A.M.; Dietzel, A.; Qi, S. Microfluidics for Pharmaceutical Nanoparticle Fabrication: The Truth and the Myth. Int. J. Pharm. 2020, 584, 119408. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, Y.; Wang, J.; Zhu, P.; Tian, Y.; Xu, M.; Wang, L.; Huang, X. Passive Mixing inside Microdroplets. Micromachines 2018, 9, 160. [Google Scholar] [CrossRef]
- Sajeesh, P.; Sen, A.K. Particle Separation and Sorting in Microfluidic Devices: A Review. Microfluid. Nanofluidics 2014, 17, 1–52. [Google Scholar] [CrossRef]
- Hatch, A.C.; Patel, A.; Beer, N.R.; Lee, A.P. Passive Droplet Sorting Using Viscoelastic Flow Focusing. Lab Chip 2013, 13, 1308–1315. [Google Scholar] [CrossRef] [PubMed]
- Bayareh, M. An Updated Review on Particle Separation in Passive Microfluidic Devices. Chem. Eng. Process.-Process Intensif. 2020, 153, 107984. [Google Scholar] [CrossRef]
- Narayanamurthy, V.; Jeroish, Z.E.; Bhuvaneshwari, K.S.; Bayat, P.; Premkumar, R.; Samsuri, F.; Yusoff, M.M. Advances in Passively Driven Microfluidics and Lab-on-Chip Devices: A Comprehensive Literature Review and Patent Analysis. RSC Adv. 2020, 10, 11652–11680. [Google Scholar] [CrossRef] [PubMed]
- Yasutaka, H.; Shinichiro, Y.; Shinichi, M.; Shigeru, O.; Takeshi, G.; Kazunori, N.; Kyoji, Y. A Micromixer Using the Chaos of Secondary Flow: Rotation Effect of Channel on the Chaos of Secondary Flow. Open J. Fluid Dyn. 2012, 2012, 195–201. [Google Scholar] [CrossRef]
- Mouza, A.A.; Patsa, C.M.; Schönfeld, F. Mixing Performance of a Chaotic Micro-Mixer. Chem. Eng. Res. Des. 2008, 86, 1128–1134. [Google Scholar] [CrossRef]
- Bothe, D.; Stemich, C.; Warnecke, H.J. Fluid Mixing in a T-Shaped Micro-Mixer. Chem. Eng. Sci. 2006, 61, 2950–2958. [Google Scholar] [CrossRef]
- Suh, Y.K.; Kang, S. A Review on Mixing in Microfluidics. Micromachines 2010, 1, 82–111. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, Z. Hydrodynamics of a Droplet Passing through a Microfluidic T-Junction. J. Fluid Mech. 2017, 819, 401–434. [Google Scholar] [CrossRef]
- Lee, S.J.S.; Kim, S.; Huerre, A.; Theodoly, O.; Leshansky, A.M.; Valignat, M.P.; Cantat, I.; Jullien, M.C.; Raben, J.S.; Klein, S.A.; et al. Hydrodynamics of a Droplet Passing through a Microfluidic T-Junction. Lab Chip 2009, 9, 44072. [Google Scholar]
- Russom, A.; Gupta, A.K.; Nagrath, S.; Di Carlo, D.; Edd, J.F.; Toner, M. Differential Inertial Focusing of Particles in Curved Low-Aspect-Ratio Microchannels. New J. Phys. 2009, 11, 075025. [Google Scholar] [CrossRef] [PubMed]
- Volpe, A.; Gaudiuso, C.; Ancona, A. Sorting of Particles Using Inertial Focusing and Laminar Vortex Technology: A Review. Micromachines 2019, 10, 594. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Aggarwal, M.; Nigam, K.D.P. Mixing in Curved Tubes. Chem. Eng. Sci. 2006, 61, 5742–5753. [Google Scholar] [CrossRef]
- Dean, W.R. Fluid motion in a curved channel. Proc. R. Soc. Lond. 1928, 121, 402–420. [Google Scholar]
- Amini, H.; Lee, W.; Di Carlo, D. Inertial Microfluidic Physics. Lab Chip 2014, 14, 2739–2761. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D. Inertial Microfluidics. Lab Chip 2009, 9, 3038–3046. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Niu, J.; Jin, H.; Lin, S.; Cui, D. Geometric Structure Design of Passive Label-Free Microfluidic Systems for Biological Micro-Object Separation. Microsyst. Nanoeng. 2022, 8, 62. [Google Scholar] [CrossRef]
- Zhao, Q.; Yuan, D.; Zhang, J.; Li, W. A Review of Secondary Flow in Inertial Microfluidics. Micromachines 2020, 11, 461. [Google Scholar] [CrossRef]
- Afsaneh, H.; Mohammadi, R. Microfluidic Platforms for the Manipulation of Cells and Particles. Talanta Open 2022, 5, 100092. [Google Scholar] [CrossRef]
- Mishra, S.; Mukherjee, J.; Chaturvedi, D.; Jain, R.; Dandekar, P. The Mechanisms and Properties of Inertial Microfluidics: From Fundamental Models to Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2023; Volume 27, ISBN 0123456789. [Google Scholar]
- Jiang, D.; Liu, S.; Tang, W. Fabrication and Manipulation of Non-Spherical Particles in Microfluidic Channels: A Review. Micromachines 2022, 13, 1659. [Google Scholar] [CrossRef]
- Cheng, K.C.; Lin, R.C. Fully Developed Laminar Flow in Curved Rectangular Channels. J. Fluids Eng. 1976, 98, 41–48. [Google Scholar] [CrossRef]
- Cheng, K.C.; Akiyama, M. Laminar Forced Convection Heat Transfer in Curved Rectangular Channels. Int. J. Heat Mass Transf. 1970, 13, 471–490. [Google Scholar] [CrossRef]
- Churchill, S.W. Comprehensive Correlating Equations for Heat, Mass and Momentum Transfer in Fully Developed Flow in Smooth Tubes. Ind. Eng. Chem. Fundam. 1977, 16, 109–116. [Google Scholar] [CrossRef]
- Corcos, G.M.; Sellars, J.R. On the Stability of Fully Developed Flow in a Pipe. J. Fluid Mech. 1968, 5, 97–112. [Google Scholar] [CrossRef]
- Berger, S.A.; Talbot, L.; Yao, L.-S. Flow in Curved Pipes. Annu. Rev. Fluid Mech. 1983, 15, 461–512. [Google Scholar] [CrossRef]
- Williams, G.S.; Hubbell, C.W.; Fenkell, G.H. Experiments at Detroit, Mich., on the Effect of Curvature upon the Flow of Water in Pipes. Trans. Am. Soc. Civ. Eng. 1902, 1, 1–196. [Google Scholar] [CrossRef]
- Eustice, J. Flow of Water in Curved Pipes. Proc. R. Soc. London. Ser. A 1910, 84, 107–118. [Google Scholar]
- Eustice, J. Experiments on Stream-Line Motion in Curved Pipes. Proc. R. Soc. London. Ser. A Contain. Pap. A Math. Phys. Character 1911, 85, 119–131. [Google Scholar] [CrossRef]
- Dean, W.R. The Stream-Line Motion of Fluid in a Curved Pipe (Second Paper). Lond. Edinb. Dublin Philos. Mag. J. Sci. 1928, 5, 673–695. [Google Scholar] [CrossRef]
- Siggers, J.H.; Waters, S.L. Steady Flows in Pipes with Finite Curvature. Phys. Fluids 2005, 17, 077102. [Google Scholar] [CrossRef]
- Nivedita, N.; Ligrani, P.; Papautsky, I. Dean Flow Dynamics in Low-Aspect Ratio Spiral Microchannels. Sci. Rep. 2017, 7, 44072. [Google Scholar] [CrossRef] [PubMed]
- Bara, B.; Masliyah, J.H. An Experimental and Numerical Study of the Dean Problem: Flow Development towards Two-Dimensional Multiple Solutions. J. Fluid Mech. 1992, 244, 339–376. [Google Scholar] [CrossRef]
- Mojola, O.O. On Secondary Flow in Streamwise Corners. J. Mec. Appl. 1980, 4, 177–196. [Google Scholar]
- Soh, W.Y.; Berger, S.A. Laminar Entrance Flow in a Curved Pipe. J. Fluid Mech. 1984, 148, 109–135. [Google Scholar] [CrossRef]
- Srivastava, R.S.; McConalogue, D.J. Motion of a Fluid in a Curved Tube. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1968, 307, 37–53. [Google Scholar] [CrossRef]
- Harirchian, T.; Garimella, S.V. A Systematic Investigation of the Effects of Microchannel Width, Depth, and Aspect Ratio on Convective Boiling Heat Transfer and Flow Regimes in Parallel Microchannels. Heat Transf. Summer Conf. 2009, 43567, 907–916. [Google Scholar]
- Lee, P.S.; Garimella, S.V.; Liu, D. Investigation of Heat Transfer in Rectangular Microchannels. Int. J. Heat Mass Transf. 2005, 48, 1688–1704. [Google Scholar] [CrossRef]
- Zheng, L.; Fang, M.; Chen, W.; Huo, D.; Li, H. Enhancement Mechanism of Fish-Scale Surface Texture on Flow Switching and Mixing Efficiency in Microfluidic Chips. Langmuir 2023, 39, 7396–7407. [Google Scholar] [CrossRef]
- Dyke, M. Van Extended Stokes Series: Laminar Flow through a Loosely Coiled Pipe. J. Fluid Mech. 1978, 86, 129–145. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Niver, R.D. Flow Visualization of Dean Vortices in a Curved Channel with 40 to 1 Aspect Ratio. Phys. Fluids 1988, 31, 3605–3617. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.J. Measurement of Dean Flow in a Curved Micro-Tube Using Micro Digital Holographic Particle Tracking Velocimetry. Exp. Fluids 2009, 46, 255–264. [Google Scholar] [CrossRef]
- Seo, K.W.; Choi, Y.S.; Lee, S.J. Dean-Coupled Inertial Migration and Transient Focusing of Particles in a Curved Microscale Pipe Flow. Exp. Fluids 2012, 53, 1867–1877. [Google Scholar] [CrossRef]
- Norouzi, M.; Biglari, N. An Analytical Solution for Dean Flow in Curved Ducts with Rectangular Cross Section. Phys. Fluids 2013, 25, 053602. [Google Scholar] [CrossRef]
- Howell, P.B.; Mott, D.R.; Golden, J.P.; Ligler, F.S. Design and Evaluation of a Dean Vortex-Based Micromixer. Lab Chip 2004, 4, 663–669. [Google Scholar] [CrossRef] [PubMed]
- Fellouah, H.; Castelain, C.; Ould El Moctar, A.; Peerhossaini, H. A Criterion for Detection of the Onset of Dean Instability in Newtonian Fluids. Eur. J. Mech. B/Fluids 2006, 25, 505–531. [Google Scholar] [CrossRef]
- Duryodhan, V.S.; Chatterjee, R.; Govind Singh, S.; Agrawal, A. Mixing in Planar Spiral Microchannel. Exp. Therm. Fluid Sci. 2017, 89, 119–127. [Google Scholar] [CrossRef]
- Baheri Islami, S.; Khezerloo, M. Enhancement of Mixing Performance of Non-Newtonian Fluids Using Curving and Grooving of Microchannels. J. Appl. Fluid Mech. 2017, 10, 127–141. [Google Scholar] [CrossRef]
- Kim, S.; Lee, S.J. Micro Holographic PTV Measurements of Dean Flows in a Curved Micro-Tube. In Proceedings of the The 12th Asian Congress of Fluid Mechanics, Daejeon, Korea, 18–21 August 2008; pp. 689–690. [Google Scholar]
- Ma, D.; Zhang, Y.; Chen, Y. Effects of Microchannel Cross-Section Shape on Particle Focusing. In Proceedings of the 2019 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Zhenjiang, China, 4–8 August 2019; pp. 237–240. [Google Scholar] [CrossRef]
- Altay, R.; Yetisgin, A.A.; Erdem, K.; Koşar, A. The Effect of Varying Radius of Curvature on Mixing in Elliptical Spiral Microchannels. Chem. Eng. Process.-Process Intensif. 2021, 164, 108401. [Google Scholar] [CrossRef]
- Ookawara, S.; Street, D.; Ogawa, K. Numerical Study on Development of Particle Concentration Profiles in a Curved Microchannel. Chem. Eng. Sci. 2006, 61, 3714–3724. [Google Scholar] [CrossRef]
- Johnston, I.D.; McDonnell, M.B.; Tan, C.K.L.; McCluskey, D.K.; Davies, M.J.; Tracey, M.C. Dean Flow Focusing and Separation of Small Microspheres within a Narrow Size Range. Microfluid. Nanofluidics 2014, 17, 509–518. [Google Scholar] [CrossRef]
- Chung, K.Y.; Brewster, M.E.; Belfort, G. Dean Vortices with Wall Flux in a Curved Channel Membrane System: 2. The Velocity Field. AIChE J. 1996, 42, 347–358. [Google Scholar] [CrossRef]
- Schönfeld, F.; Hardt, S. Simulation of Helical Flows in Microchannels. AIChE J. 2004, 50, 771–778. [Google Scholar] [CrossRef]
- Jiang, F.; Drese, K.S.; Hardt, S.; Küpper, M.; Schönfeld, F. Helical Flows and Chaotic Mixing in Curved Micro Channels. AIChE J. 2004, 50, 2297–2305. [Google Scholar] [CrossRef]
- Jarrahi, M.; Castelain, C.; Peerhossaini, H. Secondary Flow Patterns and Mixing in Laminar Pulsating Flow through a Curved Pipe. Exp. Fluids 2011, 50, 1539–1558. [Google Scholar] [CrossRef]
- Sudarsan, A.P.; Ugaz, V.M. Fluid Mixing in Planar Spiral Microchannels. Lab Chip 2006, 6, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wu, P.; Luo, Z. Dean Flow Assisted Single Cell and Bead Encapsulation for High Performance Single Cell Expression Profiling. ACS Sens. 2019, 4, 1299–1305. [Google Scholar] [CrossRef]
- Chandratilleke, T.T.; Nursubyakto, A. Numerical Prediction of Secondary Flow and Convective Heat Transfer in Externally Heated Curved Rectangular Ducts. Int. J. Therm. Sci. 2003, 42, 187–198. [Google Scholar] [CrossRef]
- Thangam, S.; Hur, N. Laminar Secondary Flows in Curved Rectangular Ducts. J. Fluid Mech. 1990, 217, 421–440. [Google Scholar] [CrossRef]
- Komiyama, Y.; Mikami, F.; Okui, K.; Hori, T. Laminar Faced Convection Heat Transfer in Curved Channels of Rectangular Cross Section. Heat Transf. Jpn. Res. 1984, 13, 68–91. [Google Scholar]
- Chen, J.K.; Luo, W.J.; Yang, R.J. Electroosmotic Flow Driven by DC and AC Electric Fields in Curved Microchannels. Jpn. J. Appl. Phys. 2006, 45, 7983–7990. [Google Scholar] [CrossRef]
- Sheu, T.S.; Chen, S.J.; Chen, J.J. Mixing of a Split and Recombine Micromixer with Tapered Curved Microchannels. Chem. Eng. Sci. 2012, 71, 321–332. [Google Scholar] [CrossRef]
- Chu, J.C.; Teng, J.T.; Greif, R. Experimental and Numerical Study on the Flow Characteristics in Curved Rectangular Microchannels. Appl. Therm. Eng. 2010, 30, 1558–1566. [Google Scholar] [CrossRef]
- Alam, A.; Kim, K.Y. Analysis of Mixing in a Curved Microchannel with Rectangular Grooves. Chem. Eng. J. 2012, 181–182, 708–716. [Google Scholar] [CrossRef]
- Dore, V.; Tsaoulidis, D.; Angeli, P. Mixing Patterns in Water Plugs during Water/Ionic Liquid Segmented Flow in Microchannels. Chem. Eng. Sci. 2012, 80, 334–341. [Google Scholar] [CrossRef]
- Xiang, N.; Dai, Q.; Han, Y.; Ni, Z. Circular-Channel Particle Focuser Utilizing Viscoelastic Focusing. Microfluid. Nanofluidics 2019, 23, 16. [Google Scholar] [CrossRef]
- Agrawal, Y.; Talbot, L.; Gong, K. Laser Anemometer Study of Flow Development in Curved Circular Pipes. J. Fluid Mech. 1978, 85, 497–518. [Google Scholar] [CrossRef]
- Filimonov, R.; Sorvari, J. Numerical Study on the Effect of Cross-Section Orientation on Fluid Flow and Heat Transfer in a Periodic Serpentine Triangular Microchannel. Appl. Therm. Eng. 2017, 125, 366–376. [Google Scholar] [CrossRef]
- Raoufi, M.A.; Bazaz, S.R.; Niazmand, H.; Rouhi, O.; Asadian, M.; Razmjou, A.; Ebrahimi Warkiani, M. Fabrication of Unconventional Inertial Microfluidic Channels Using Wax 3D Printing. Soft Matter 2020, 16, 2448–2459. [Google Scholar] [CrossRef]
- Wu, L.; Guan, G.; Hou, H.W.; Bhagat, A.A.S.; Han, J. Separation of Leukocytes from Blood Using Spiral Channel with Trapezoid Cross-Section. Anal. Chem. 2012, 84, 9324–9331. [Google Scholar] [CrossRef]
- Kuntaegowdanahalli, S.S.; Bhagat, A.A.S.; Kumar, G.; Papautsky, I. Inertial Microfluidics for Continuous Particle Separation in Spiral Microchannels. Lab Chip 2009, 9, 2973–2980. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, M.; Liu, Z.; Shi, L.; Li, T.; Zhou, T. Microalgae Separation Using Spiral Inertial Microchannel. Microfluid. Nanofluidics 2023, 27, 1–13. [Google Scholar] [CrossRef]
- Lee, S.W.; Lee, S.S. Rotation Effect in Split and Recombination Micromixing. Sens. Actuators B Chem. 2008, 129, 364–371. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, C.; Xie, B.; Zhang, J. Simulation of the Enhancement of Dean Flow on the Liquid–Liquid Extraction in Membrane Contactors. Sep. Purif. Technol. 2022, 285, 120384. [Google Scholar] [CrossRef]
- Rafeie, M.; Hosseinzadeh, S.; Taylor, R.A.; Warkiani, M.E. New Insights into the Physics of Inertial Microfluidics in Curved Microchannels. I. Relaxing the Fixed Inflection Point Assumption. Biomicrofluidics 2019, 13, 034117. [Google Scholar] [CrossRef]
- Clark, J.; Kaufman, M.; Fodor, P.S. Mixing Enhancement in Serpentine Micromixers with a Non-Rectangular Cross-Section. Micromachines 2018, 9, 107. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.H.; Stremler, M.A.; Sharp, K.V.; Olsen, M.G.; Santiago, J.G.; Adrian, R.J.; Aref, H.; Beebe, D.J. Passive Mixing in a Three-Dimensional Serpentine Microchannel. J. Microelectromechanical Syst. 2000, 9, 190–197. [Google Scholar] [CrossRef]
- Stroock, A.D.; Dertinger, S.K.W.; Ajdari, A.; Mezić, I.; Howard, A.; Whitesides, G.M.; Ajdari, A.; Mezic, I.; Stone, H.A. Chaotic Mixer for Microchannels. Am. Assoc. Adv. Sci. 2016, 295, 647–651. [Google Scholar] [CrossRef]
- Geng, Z.; Ju, Y.; Wang, W.; Li, Z. Continuous Blood Separation Utilizing Spiral Filtration Microchannel with Gradually Varied Width and Micro-Pillar Array. Sens. Actuators B Chem. 2013, 180, 122–129. [Google Scholar] [CrossRef]
- Geng, Z.; Ju, Y.; Wang, Q.; Wang, W.; Li, Z. Multi-Component Continuous Separation Chip Composed of Micropillar Arrays in a Split-Level Spiral Channel. RSC Adv. 2013, 3, 14798–14806. [Google Scholar] [CrossRef]
- Shen, S.; Wang, X.; Niu, Y. Multi-Vortex Regulation for Efficient Fluid and Particle Manipulation in Ultra-Low Aspect Ratio Curved Microchannels. Micromachines 2021, 12, 758. [Google Scholar] [CrossRef]
- Shamloo, A.; Vatankhah, P.; Akbari, A. Analyzing Mixing Quality in a Curved Centrifugal Micromixer through Numerical Simulation. Chem. Eng. Process.-Process Intensif. 2017, 116, 9–16. [Google Scholar] [CrossRef]
- Madadelahi, M.; Shamloo, A. Droplet-Based Flows in Serpentine Microchannels: Chemical Reactions and Secondary Flows. Int. J. Multiph. Flow 2017, 97, 186–196. [Google Scholar] [CrossRef]
- Bhagat, A.A.S.; Kuntaegowdanahalli, S.S.; Papautsky, I. Continuous Particle Separation in Spiral Microchannels Using Dean Flows and Differential Migration. Lab Chip 2008, 8, 1906–1914. [Google Scholar] [CrossRef] [PubMed]
- Erdem, K.; Ahmadi, V.E.; Kosar, A.; Kuddusi, L. Differential Sorting of Microparticles Using Spiral Microchannels with Elliptic Configurations. Micromachines 2020, 11, 412. [Google Scholar] [CrossRef] [PubMed]
- Shen, S.; Zhang, F.; Zhang, Y.; Li, Y.; Niu, Y.; Pang, L.; Wang, J. Construction of Multiple Concentration Gradients for Single-Cell Level Drug Screening. Microsyst. Nanoeng. 2023, 9, 46. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Li, M.; Alici, G.; Nguyen, N.T. Particle Inertial Focusing and Its Mechanism in a Serpentine Microchannel. Microfluid. Nanofluidics 2014, 17, 305–316. [Google Scholar] [CrossRef]
- Nicodemus, G.D.; Bryant, S.J. Cell Encapsulation in Biodegradable Hydrogels for Tissue Engineering Applications. Tissue Eng.-Part B Rev. 2008, 14, 149–165. [Google Scholar] [CrossRef]
- Kantak, C.; Zhu, Q.; Beyer, S.; Bansal, T.; Trau, D. Utilizing Microfluidics to Synthesize Polyethylene Glycol Microbeads for Forster Resonance Enery Transfer Based Glucose Sensing. Biomicrofluidics 2012, 6, 22006–220069. [Google Scholar] [CrossRef]
- Boruah, M.P.; Sarker, A.; Randive, P.R.; Pati, S.; Sahu, K.C. Tuning of Regimes during Two-Phase Flow through a Cross-Junction. Phys. Fluids 2021, 33, 122101. [Google Scholar] [CrossRef]
- Teh, S.Y.; Lin, R.; Hung, L.H.; Lee, A.P. Droplet Microfluidics. Lab Chip 2008, 8, 198–220. [Google Scholar] [CrossRef]
- Casadevall i Solvas, X.; De Mello, A. Droplet Microfluidics: Recent Developments and Future Applications. Chem. Commun. 2011, 47, 1936–1942. [Google Scholar] [CrossRef] [PubMed]
- Seemann, R.; Brinkmann, M.; Pfohl, T.; Herminghaus, S. Droplet Based Microfluidics. Rep. Prog. Phys. 2012, 75, 016601. [Google Scholar] [CrossRef] [PubMed]
- Azadi, R.; Wong, J.; Nobes, D.S. Determination of Fluid Flow Adjacent to a Gas/Liquid Interface Using Particle Tracking Velocimetry (PTV) and a High-Quality Tessellation Approach. Exp. Fluids 2021, 62, 48. [Google Scholar] [CrossRef]
- Ansari, S.; Yusuf, Y.; Sabbagh, R.; Nobes, D.S. Determining the Pressure Distribution of a Multi-Phase Flow through a Pore Space Using Velocity Measurement and Shape Analysis. Meas. Sci. Technol. 2019, 30, 054004. [Google Scholar] [CrossRef]
- Azadi, R.; Nobes, D.S. Local Flow Dynamics in the Motion of Slug Bubbles in a Flowing Mini Square Channel. Int. J. Heat Mass Transf. 2021, 178, 121588. [Google Scholar] [CrossRef]
- Azadi, R.; Wong, J.; Nobes, D.S. Experimental and Analytical Investigation of Meso-Scale Slug Bubble Dynamics in a Square Capillary Channel. Phys. Fluids 2020, 32, 083304. [Google Scholar] [CrossRef]
- Azadi, R.; Nobes, D.S. On the Three-Dimensional Features of a Confined Slug Bubble in a Flowing Square Capillary. Phys. Fluids 2021, 33, 033327. [Google Scholar] [CrossRef]
- Raffel, J.; Ansari, S.; Nobes, D.S. An Experimental Investigation of Flow Phenomena in a Multi-Stage Micro Tesla Valve. J. Fluids Eng. 2021, 143, 111205. [Google Scholar] [CrossRef]
- Ansari, S.; Bayans, M.; Rasimarzabadi, F.; Nobes, D.S. Flow Visualization of the Newtonian and Non- Newtonian Behavior of Fluids in a Tesla-Diode Valve. In Proceedings of the 5th International Conference on Experimental. Fluid Mechanics (ICEFM 2018), Munich, Germany, 2–4 July 2018. [Google Scholar]
- Saffar, Y.; Nobes, D.S.; Sabbagh, R. Experimental Investigation of the Motion and Deformation of Droplets in Curved Microchannel. Ind. Eng. Chem. Res. 2023, 62, 17275–17286. [Google Scholar] [CrossRef]
- Yan, C. Flow Topology and Its Transformation inside Droplets Traveling in Rectangular Microchannels. Phys. Fluids 2020, 32, 052009. [Google Scholar] [CrossRef]
- Hodges, S.R.; Jensen, O.E.; Rallison, J.M. The Motion of a Viscous Drop through a Cylindrical Tube. J. Fluid Mech. 2004, 501, 279–301. [Google Scholar] [CrossRef]
- Oishi, M.; Kinoshita, H.; Fujii, T.; Oshima, M. Simultaneous Measurement of Internal and Surrounding Flows of a Moving Droplet Using Multicolour Confocal Micro-Particle Image Velocimetry (Micro-PIV). Meas. Sci. Technol. 2011, 22, 105401. [Google Scholar] [CrossRef]
- Kinoshita, H.; Kaneda, S.; Fujii, T.; Oshima, M. Three-Dimensional Measurement and Visualization of Internal Flow of a Moving Droplet Using Confocal Micro-PIV. Lab Chip 2007, 7, 338–346. [Google Scholar] [CrossRef] [PubMed]
- Malsch, D.; Kielpinski, M.; Merthan, R.; Albert, J.; Mayer, G.; Köhler, J.M.; Süße, H.; Stahl, M.; Henkel, T. ΜPIV-Analysis of Taylor Flow in Micro Channels. Chem. Eng. J. 2008, 135, 166–172. [Google Scholar] [CrossRef]
- Liu, Z.; Li, M.; Pang, Y.; Zhang, L.; Ren, Y.; Wang, J. Flow Characteristics inside Droplets Moving in a Curved Microchannel with Rectangular Section. Phys. Fluids 2019, 31, 022004. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L.; Pang, Y.; Wang, X.; Li, M.-P. Investigation of the internal flow transitions inside droplets traveling in a rectangular microchannel Micro-PIV Investigation of the Internal Flow Transitions inside Droplets Traveling in a Rectangular Microchannel. Microfluid. Nanofluidics 2017, 21, 180. [Google Scholar] [CrossRef]
- Zhu, L.; Brandt, L. The Motion of a Deforming Capsule through a Corner. J. Fluid Mech. 2015, 770, 374–397. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Balogh, P.; Bagchi, P. Motion of a Capsule in a Curved Tube. J. Fluid Mech. 2020, 908, A28. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Bagchi, P. Inertial and Non-Inertial Focusing of a Deformable Capsule in a Curved Microchannel. J. Fluid Mech. 2021, 929, 1–38. [Google Scholar] [CrossRef]
- Chen, X.; Xue, C.; Zhang, L.; Hu, G.; Jiang, X.; Sun, J. Inertial Migration of Deformable Droplets in a Microchannel. Phys. Fluids 2014, 26, 112003. [Google Scholar] [CrossRef]
- Ye, T.; Phan-Thien, N.; Lim, C.T.; Li, Y. Red Blood Cell Motion and Deformation in a Curved Microvessel. J. Biomech. 2017, 65, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.D.; Chen, X.D.; Liu, C.; Hu, G.Q. Lateral Migration of Dual Droplet Trains in a Double Spiral Microchannel. Sci. China Phys. Mech. Astron. 2016, 59, 674711. [Google Scholar] [CrossRef]
- Wen, N.; Zhao, Z.; Fan, B.; Chen, D.; Men, D.; Wang, J.; Chen, J. Development of Droplet Microfluidics Enabling High-Throughput Single-Cell Analysis. Molecules 2016, 21, 881. [Google Scholar] [CrossRef] [PubMed]





| Equations | Author(s) | Description | ||
|---|---|---|---|---|
| Velocity-based | (2) | Dean (1928) | Study the relationship between mass flux and geometry [47]. | |
| (3) | Dyke (1978) | Dean’s series for steady fully developed laminar flow through a toroidal pipe with a small curvature ratio [73]. | ||
| (4) | Bara et al. (1992) | Laminar Newtonian flow inside a square duct with non-symmetrical geometries [66]. | ||
| (5) | Berger and Talbot (1988) | Study the characteristics of the flow in the curved channel [59]. | ||
| (6) | Ligrani and Niver (1988) | Curved channels with a high radius of curvature, [74]. | ||
| (7) | Kim and Lee (2009) | 3D velocity field inside a circular microtube; is the inner diameter of the microtube [75]. | ||
| (8) | Berger et al. (1983) Nivedita et al. (2017), Seo et al. (2012) | Investigate Dean vortices inside a low-aspect-ratio spiral [59,65,76]. | ||
| Equation | Author(s) | Description | ||
|---|---|---|---|---|
| Pressure-based | (9) | McConalogue and Srivastava (1968) | Study the motion of the flow in curved tubes assuming that [69]. | |
| (10) | Burger and Talbot (1988) | Study the flow characteristics in a curved channel with a constant fully developed flow [59]. | ||
| (11) | Burger and Talbot (1988) | Study characteristics of the flow in a curved channel [59]. | ||
| (12) | Norouzi and Biglari (2003) | Analytical solution for the flow in a curved channel for low Dean numbers [77]. | ||
| (13) | Howell et al. (2004) | Experimental study of the Dean vortices in a micromixer. is the pressure gradient on the channel centerline [78]. | ||
| Case | AR | d | h | Rc | Dei | Dec | Cross-Section | Channel | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.60 | 250 | 150 | various | 28.5 | 30.5 | rectangle | spiral | [52] |
| 2 | 2.5 | 250 | 100 | various | 34.5 | 37 | rectangle | spiral | [52] |
| 3 | 5 | 500 | 100 | various | 31.5 | 40 | rectangle | spiral | [63] |
| 4 | 2.5 | 250 | 100 | various | NA | 45 | rectangle | spiral | [59] |
| 5 | 3.3 | 200 | 60 | 2000 | 23 | rectangle | spiral | [75] | |
| 6 | 0.25 | NA | NA | NA | NA | 72.5 | rectangle | curved | [77] |
| 7 | 0.5 | NA | NA | NA | NA | 70 | rectangle | curved | [78] |
| 8 | 1 | NA | NA | NA | NA | 67.5 | rectangle | curved | [79] |
| 9 | 2 | NA | NA | NA | NA | 60 | rectangle | curved | [80] |
| 10 | 4 | NA | NA | NA | NA | 52.5 | rectangle | curved | [81] |
| 11 | 2 | NA | NA | NA | NA | 100 | rectangle | curved | [82] |
| 12 | 1 | NA | NA | NA | NA | 45 | rectangle | curved | [52] |
| 13 | 0.5 | NA | NA | NA | NA | 65 | rectangle | curved | [52] |
| 14 | 0.3 | NA | NA | NA | NA | 80 | rectangle | curved | [63] |
| 15 | 0.25 | NA | NA | NA | NA | 95 | rectangle | curved | [59] |
| 16 | 0.2 | NA | NA | NA | NA | 70 | rectangle | curved | [75] |
| 17 | 0.17 | NA | NA | NA | NA | 57.5 | rectangle | curved | [77] |
| 18 | 0.14 | NA | NA | NA | NA | 50 | rectangle | curved | [78] |
| 19 | 0.125 | NA | NA | NA | NA | 42.5 | rectangle | curved | [79] |
| 20 | 0.1 | NA | NA | NA | NA | 40 | rectangle | curved | [80] |
| 21 | 0.08 | NA | NA | NA | NA | 40 | rectangle | curved | [81] |
| 22 | 1 | NA | NA | NA | NA | 72.5 | rectangle | curved | [82] |
| 23 | 1.25 | NA | NA | NA | NA | 95 | rectangle | curved | [52] |
| 24 | 1 | NA | NA | NA | NA | 87.5 | rectangle | curved | [52] |
| 25 | 0.8 | NA | NA | NA | NA | 87.5 | rectangle | curved | [63] |
| 26 | 0.7 | NA | NA | NA | NA | 92.5 | rectangle | curved | [59] |
| 27 | 0.55 | NA | NA | NA | NA | 95 | rectangle | curved | [75] |
| 28 | 0.5 | NA | NA | NA | NA | 204 | rectangle | curved | [77] |
| 29 | 0.3 | NA | NA | NA | NA | 135 | rectangle | curved | [78] |
| 30 | 0.2 | NA | NA | NA | NA | 137.5 | rectangle | curved | [79] |
| 31 | 1.7 | 250 | 150 | 2000 | 17 | 206 | rectangle | curved | [80] |
| 32 | 2 | 30 | 15 | 400 | 20 | NA | rectangle | curved | [81] |
| 33 | 1 | 150 | 150 | 4000 | 6.8 | 100 | rectangle | curved | [82] |
| 34 | 1 | 200 | 200 | 5000 | 10 | NA | rectangle | curved | [82] |
| 35 | 1 | 200 | 200 | 2500 | 0.316 | NA | rectangle | curved | [82] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saffar, Y.; Kashanj, S.; Nobes, D.S.; Sabbagh, R. The Physics and Manipulation of Dean Vortices in Single- and Two-Phase Flow in Curved Microchannels: A Review. Micromachines 2023, 14, 2202. https://doi.org/10.3390/mi14122202
Saffar Y, Kashanj S, Nobes DS, Sabbagh R. The Physics and Manipulation of Dean Vortices in Single- and Two-Phase Flow in Curved Microchannels: A Review. Micromachines. 2023; 14(12):2202. https://doi.org/10.3390/mi14122202
Chicago/Turabian StyleSaffar, Yeganeh, Sina Kashanj, David S. Nobes, and Reza Sabbagh. 2023. "The Physics and Manipulation of Dean Vortices in Single- and Two-Phase Flow in Curved Microchannels: A Review" Micromachines 14, no. 12: 2202. https://doi.org/10.3390/mi14122202
APA StyleSaffar, Y., Kashanj, S., Nobes, D. S., & Sabbagh, R. (2023). The Physics and Manipulation of Dean Vortices in Single- and Two-Phase Flow in Curved Microchannels: A Review. Micromachines, 14(12), 2202. https://doi.org/10.3390/mi14122202