Precise Position Control of Holonomic Inchworm Robot Using Four Optical Encoders
Abstract
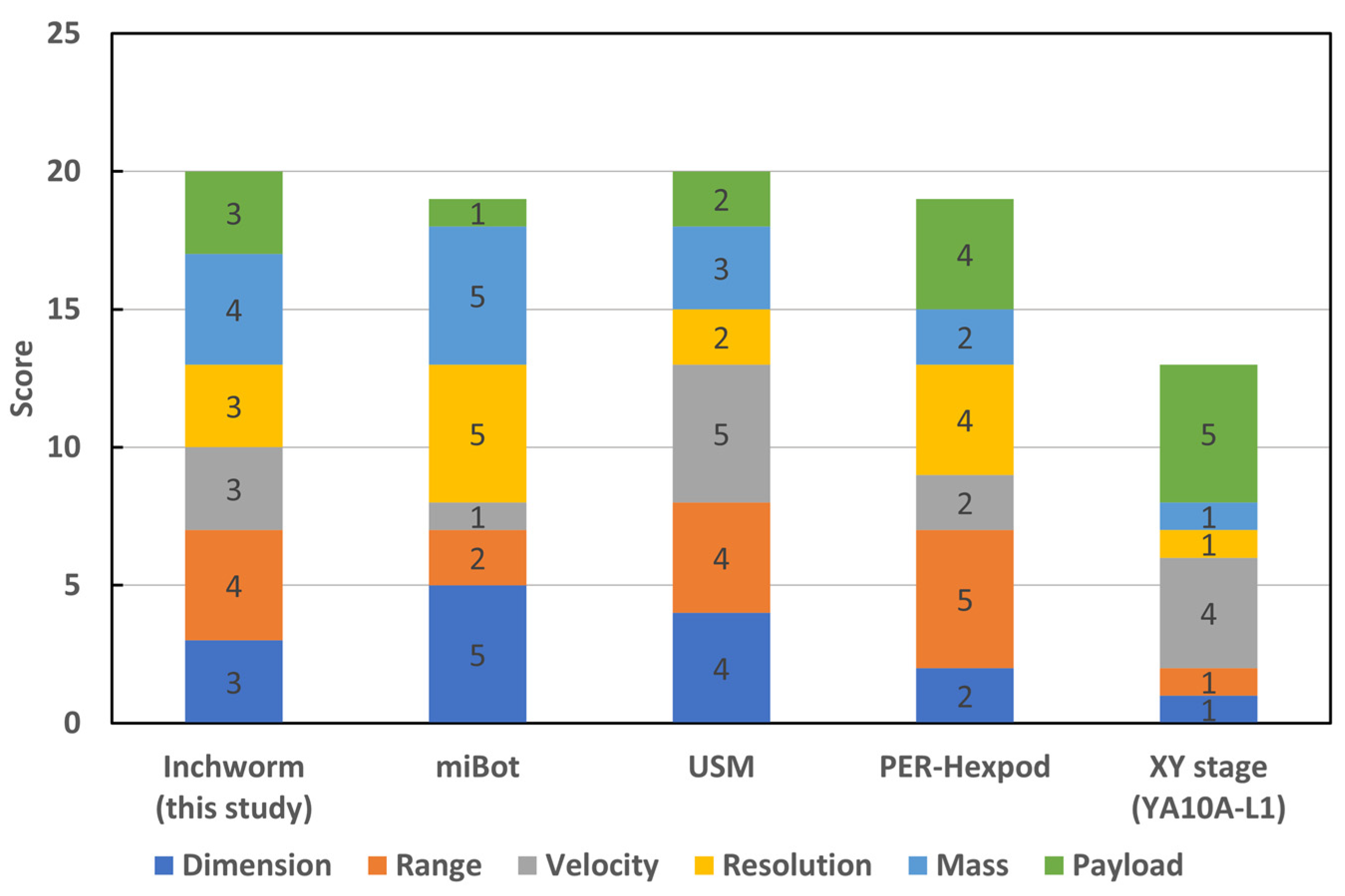
:1. Introduction
2. Holonomic Inchworm Robot
2.1. Structure
2.2. Principle
2.3. Dynamic Model
2.4. Input Voltages
3. XYθ Position Sensor
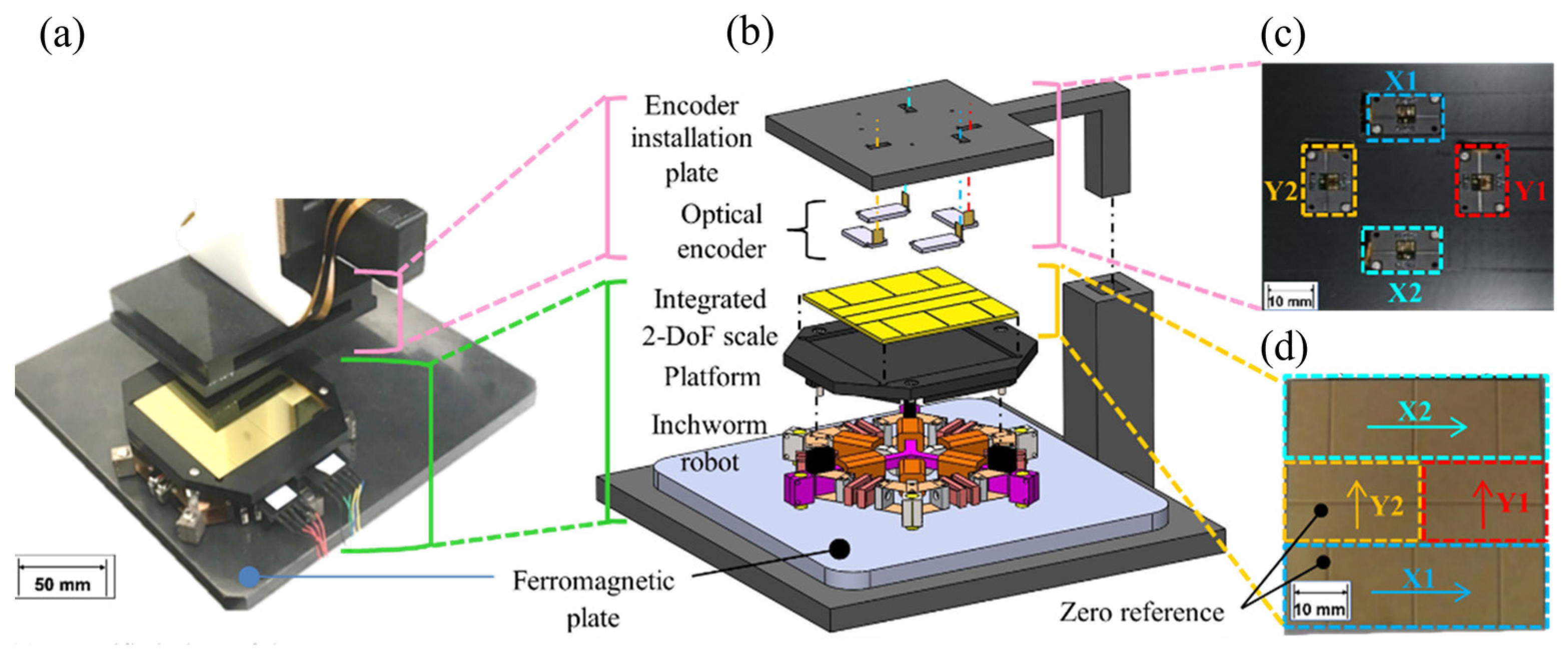
3.1. Structure
3.2. Signal Processing
3.3. Measurement Principle
3.4. Experimental Results
4. Sequence Control of Multiple Step Motions
4.1. Control Sequence
4.2. Experimental Results
5. 3-Axis PID Control of One-Step Motion
5.1. Transfer Function
5.2. Experimental Results
6. Conclusions and Future Prospects
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shin, G.; Gomez, A.M.; Al-Hasani, R.; Jeong, Y.R.; Kim, J.; Xie, Z.; Banks, A.; Lee, S.M.; Han, S.Y.; Yoo, C.J.; et al. Miniaturized flexible electronic systems with wireless power and near-field communication capabilities. Adv. Funct. Mater. 2015, 25, 4761–4767. [Google Scholar]
- Templier, F. GaN-based emissive microdisplays: A very promising technology for compact, ultra-high brightness display systems. J. Soc. Inf. Disp. 2016, 24, 669–675. [Google Scholar] [CrossRef]
- Henley, F.J. 52-3: Invited Paper: Combining Engineered EPI Growth Substrate Materials with Novel Test and Mass-Transfer Equipment to Enable MicroLED Mass-Production. In SID Symposium Digest of Technical Papers; John Wiley & Sons, Inc.: New York, NY, USA, 2018. [Google Scholar]
- Boudaoud, M.; Regnier, S. An overview on gripping force measurement at the micro and nano-scales using two-fingered microrobotic systems. Int. J. Adv. Robot. Syst. 2014, 11, 45. [Google Scholar] [CrossRef]
- Itaki, T.; Taira, Y.; Kuwamori, N.; Maebayashi, T.; Takeshima, S.; Toya, K. Automated collection of single species of microfossils using a deep learning–micromanipulator system. Prog. Earth Planet Sci. 2020, 7, 19. [Google Scholar] [CrossRef]
- Ishimoto, K. Bacterial spinning top. J. Fluid Mech. 2019, 880, 620–652. [Google Scholar] [CrossRef]
- Yamada, T.; Iima, M. Hydrodynamic turning mechanism of microorganism by solitary loop propagation on a single flagellum. J. Phys. Soc. Jpn. 2018, 88, 114401. [Google Scholar] [CrossRef]
- Rong, W.; Fan, Z.; Wang, L.; Xie, H.; Sun, L. A vacuum microgripping tool with integrated vibration releasing capability. Rev. Sci. Instrum. 2014, 85, 085002. [Google Scholar] [CrossRef]
- Tiwari, B.; Billot, M.; Clévy, C.; Agnus, J.; Piat, E.; Lutz, P. A two-axis piezoresistive force sensing tool for microgripping. Sensors 2021, 21, 6059. [Google Scholar] [CrossRef]
- Tanaka, K.; Ito, T.; Nishiyama, Y.; Fukuchi, R.; Fuchiwaki, O. Double-nozzle capillary force gripper for cubical, triangular prismatic, and helical 1-mm-sized-objects. IEEE Robot Autom. Lett. 2022, 7, 1324–1331. [Google Scholar] [CrossRef]
- Overton, J.K.; Kinnell, P.K.; Lawes, S.D.A.; Ratchev, S. High precision self-alignment using liquid surface tension for additively manufactured micro components. Prec. Eng. 2015, 40, 230–240. [Google Scholar] [CrossRef]
- Maeda, G.; Sato, K. Practical control method for ultra-precision positioning using a ballscrew mechanism. Prec. Eng. 2008, 32, 309–318. [Google Scholar] [CrossRef]
- Chen, S.; Chiang, H. Precision motion control of permanent magnet linear synchronous motors using adaptive fuzzy fractional-order sliding-mode control. IEEE/ASME Trans. Mechatron. 2019, 24, 741–752. [Google Scholar] [CrossRef]
- Fuchiwaki, O.; Tanaka, Y.; Notsu, H.; Hyakutake, T. Multi-axial non-contact in situ micromanipulation by steady streaming around two oscillating cylinders on holonomic miniature robots. Microfluid. Nanofluidics 2018, 22, 80. [Google Scholar] [CrossRef]
- Tamadazte, B.; Piat, N.L.F.; Dembélé, S. Robotic micromanipulation and microassembly using monoview and multiscale visual servoing. IEEE/ASME Trans. Mechatron. 2011, 16, 277–287. [Google Scholar] [CrossRef]
- Fuchiwaki, O.; Ito, A.; Misaki, D.; Aoyama, H. Multi-axial micromanipulation organized by versatile micro robots and micro tweezers. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 893–898. [Google Scholar]
- Fatikow, S.; Wich, T.; Hulsen, H.; Sievers, T.; Jahnisch, M. Microrobot system for automatic nanohandling inside a scanning electron microscope. IEEE/ASME Trans. Mechatron. 2007, 12, 244–252. [Google Scholar] [CrossRef]
- Brufau, J.; Puig-Vidal, M.; Lopez-Sanchez, J.; Samitier, J.; Snis, N.; Simu, U.; Johansson, S.; Driesen, W.; Breguet, J.M.; Gao, J.; et al. MICRON: Small autonomous robot for cell manipulation applications. In Proceedings of the IEEE International Conference On Robotics and Automation (ICRA 2015), Barcelona, Spain, 18–22 April 2005; pp. 844–849. [Google Scholar]
- Saadabad, N.A.; Moradi, H.; Vossoughi, G. Dynamic modeling, optimized design, and fabrication of a 2DOF piezo-actuated stick-slip mobile microrobot. Mech. Mach. Theory 2019, 133, 514–530. [Google Scholar] [CrossRef]
- Ji, X.; Liu, X.; Cacucciolo, V.; Imboden, M.; Civet, Y.; El Haitami, A.; Cantin, S.; Perriard, Y.; Shea, H. An autonomous untethered fast soft robotic insect driven by low-voltage dielectric elastomer actuators. Sci. Robot. 2019, 4, eaaz6451. [Google Scholar] [CrossRef]
- Zhong, B.; Zhu, J.; Jin, Z.; He, H.; Wang, Z.; Sun, L. A large thrust trans-scale precision positioning stage based on the inertial stick–slip driving. Microsyst. Technol. 2019, 25, 3713–3721. [Google Scholar] [CrossRef]
- Imina. Available online: https://imina.ch/en/products/nano-robotics-solutions-electron-microscopes (accessed on 21 December 2022).
- Vartholomeos, P.; Vlachos, K.; Papadopoulos, E. Analysis and motion control of a centrifugal-force microrobotic platform. IEEE Trans. Autom. Sci. Eng. 2013, 10, 545–553. [Google Scholar] [CrossRef]
- Zhou, J.; Suzuki, M.; Takahashi, R.; Tanabe, K.; Nishiyama, Y.; Sugiuchi, H.; Maeda, Y.; Fuchiwaki, O. Development of a Δ-type mobile robot driven by thee standing-wave-type piezoelectric ultrasonic motors. IEEE Robot. Autom. Lett. 2020, 5, 6717–6723. [Google Scholar] [CrossRef]
- Jia, B.; Wang, L.; Wang, R.; Jin, J.; Zhao, Z.; Wu, D. A novel traveling wave piezoelectric actuated wheeled robot: Design, theoretical analysis, and experimental investigation. Smart Mater. Struct. 2021, 30, 035016. [Google Scholar] [CrossRef]
- Fuchiwaki, O.; Yatsurugi, M.; Sato, T. The basic performance of a miniature omnidirectional 6-legged inchworm robot from cm- to μm-scale precise positioning. Trans. Mater. Res. Soc. Jpn. 2014, 39, 211–215. [Google Scholar] [CrossRef]
- Yu, H.; Liu, Y.; Deng, J.; Li, J.; Zhang, S.; Chen, W.; Zhao, J. Bioinspired Multilegged piezoelectric robot: The design philosophy aiming at high-performance micromanipulation. Adv. Intell. Syst. 2021, 4, 2100142. [Google Scholar] [CrossRef]
- Tanabe, K.; Masato, S.; Eiji, K.; Fuchiwaki, O. Precise trajectory measurement of self-propelled mechanism by XYθ 3-axis displacement sensor consisting of multiple optical encoders. In Proceedings of the 2021 60th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Tokyo, Japan, 8–10 September 2021; pp. 998–1003. [Google Scholar]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.L.; Lu, X.D.; Knapp, W.; Weckenmann, A.; Estler, W.T.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann.—Manuf. Technol. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Estana, R.; Woern, H. Moire-based positioning system for microrobots. In Optical Measurement Systems for Industrial Inspection III; SPIE: Bellingham, WA, USA, 2003; Available online: https://ui.adsabs.harvard.edu/link_gateway/2003SPIE.5144 (accessed on 21 December 2022).
- Fuchiwaki, O.; Yamagiwa, T.; Omura, S.; Hara, Y. In-situ repetitive calibration of microscopic probes maneuvered by holonomic inchworm robot for flexible microscopic operations. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS 2015), Hamburg, Germany, 28 September–2 October 2015; pp. 1467–1472. [Google Scholar] [CrossRef]
- Peng, Y.; Ito, S.; Shimizu, Y.; Azuma, T.; Gao, W.; Niwa, E. A Cr-N thin film displacement sensor for precision positioning of a micro-stage. Sens. Actuator A Phys. 2014, 211, 89–97. [Google Scholar] [CrossRef]
- Jang, Y.; Kim, S.W. Compensation of the refractive index of air in laser interferometer for distance measurement: A review. Int. J. Precis. Eng. Manuf. 2017, 18, 1881–1890. [Google Scholar] [CrossRef]
- Li, X. A six-degree-of-freedom surface encoder for precision positioning of a planar motion stage. Precis. Eng. 2013, 37, 771–781. [Google Scholar] [CrossRef]
- Dejima, S.; Gao, W.; Shimizu, H.; Kiyono, S.; Tomita, Y. Precision positioning of a five degree-of-freedom planar motion stage. Mechatronics 2005, 15, 969–987. [Google Scholar] [CrossRef]
- Fuchiwaki, O.; Yatsurugi, M.; Ogawa, A. Design of an integrated 3DoF inner position sensor and 2DoF feedforward control for a 3DoF precision inchworm mechanism. In Proceedings of the IEEE International Conference Robotics and Automation (ICRA 2013), Karlsruhe, Germany, 6–10 May 2013; pp. 5475–5481. [Google Scholar] [CrossRef]









| Characteristic Value | Quantity |
|---|---|
| Step length (120 V) | ~65 μm |
| Resolution (15–25 °C, less than 50% rH) | Less than 10 nm |
| DoF | X, Y, θ |
| Natural Frequency (blocked free) | X: 413, Y: 418, θ: 476 Hz |
| Maximum Velocity [frequency] | ~6.5 mm/s [100 Hz] |
| Repeatability (CV; ratio of SD of final points to a path length with 10 mm path) [frequency] | ~3% [100 Hz] |
| Maximum payload | <1000 g |
| Dimension | 86 × 86 × 15 mm |
| Weight | 100 g |
| Characteristic Value | Quantity |
|---|---|
| Displacement (100 V) | 95.5 ± 5 μm |
| Generative Force (100 V) | 18.0 N |
| Spring constant | 115,000 N/m |
| Capacitance | 1.04 μF |
| Resolution (15–25 °C, less than 50% rH) | 1.52 nm |
| Natural Frequency (blocked free) | 1.45 kHz |
| Dimension | 12.9 × 6.4 × 9.2 mm |
| Weight | 4 g |
| Characteristic Value | Quantity |
|---|---|
| Resolution [μm/count] | 0.1 |
| Maximum measurement speed [mm/s] | 800 |
| Dimension [mm] | 15 × 10 × 1.5 |
| Characteristic Value | Quantity |
|---|---|
| Measurement range X × Y [mm], θ [°] | 16 × 16, ±25 |
| Measurement resolution in X (Y) [μm], θ [millidegrees] | 0.1, 0.3 |
| Uncertainty in static state in X (Y) [μm], θ [millidegrees] | ±0.2, ±0.6 |
| Measurement frequency [MHz] | 2.86 |
| Maximum measurable speed [mm/s] | 800 |
| Principle of measurement | Incremental |
| Measurement accuracy in X and Y (−8~8mm) [%] | 0.08–0.18 |
| Measurement accuracy in θ (−25~25°) [%] | 0.06–0.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanabe, K.; Shiota, M.; Kusui, E.; Iida, Y.; Kusama, H.; Kinoshita, R.; Tsukui, Y.; Minegishi, R.; Sunohara, Y.; Fuchiwaki, O. Precise Position Control of Holonomic Inchworm Robot Using Four Optical Encoders. Micromachines 2023, 14, 375. https://doi.org/10.3390/mi14020375
Tanabe K, Shiota M, Kusui E, Iida Y, Kusama H, Kinoshita R, Tsukui Y, Minegishi R, Sunohara Y, Fuchiwaki O. Precise Position Control of Holonomic Inchworm Robot Using Four Optical Encoders. Micromachines. 2023; 14(2):375. https://doi.org/10.3390/mi14020375
Chicago/Turabian StyleTanabe, Kengo, Masato Shiota, Eiji Kusui, Yohei Iida, Hazumu Kusama, Ryosuke Kinoshita, Yohei Tsukui, Rintaro Minegishi, Yuta Sunohara, and Ohmi Fuchiwaki. 2023. "Precise Position Control of Holonomic Inchworm Robot Using Four Optical Encoders" Micromachines 14, no. 2: 375. https://doi.org/10.3390/mi14020375
APA StyleTanabe, K., Shiota, M., Kusui, E., Iida, Y., Kusama, H., Kinoshita, R., Tsukui, Y., Minegishi, R., Sunohara, Y., & Fuchiwaki, O. (2023). Precise Position Control of Holonomic Inchworm Robot Using Four Optical Encoders. Micromachines, 14(2), 375. https://doi.org/10.3390/mi14020375






