Effect of Strain Rate on Nano-Scale Mechanical Behavior of A-Plane (
Abstract
:1. Introduction
2. Experimental
2.1. Experimental Procedure
2.2. Basic Principle
3. Results and Discussion
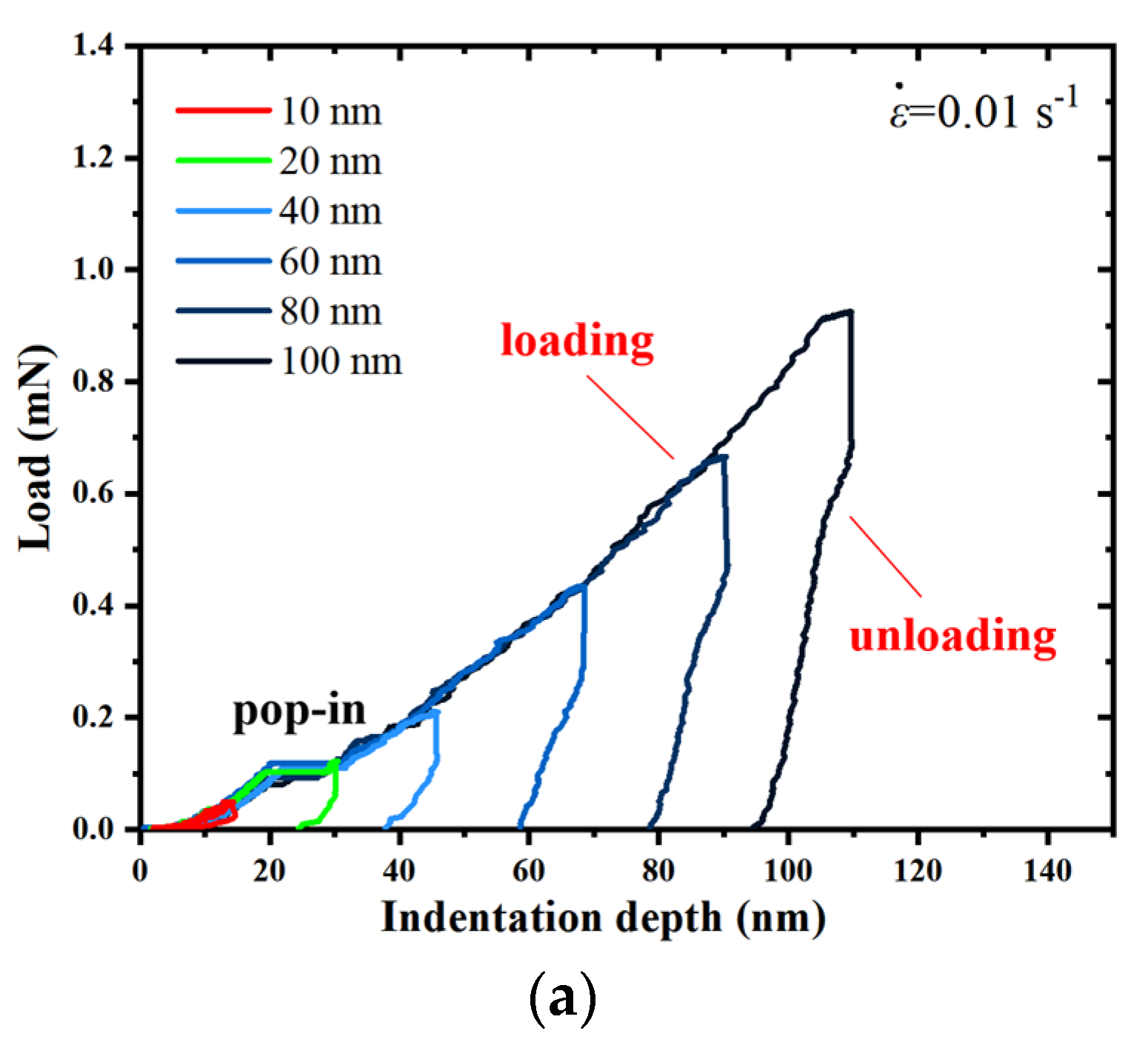
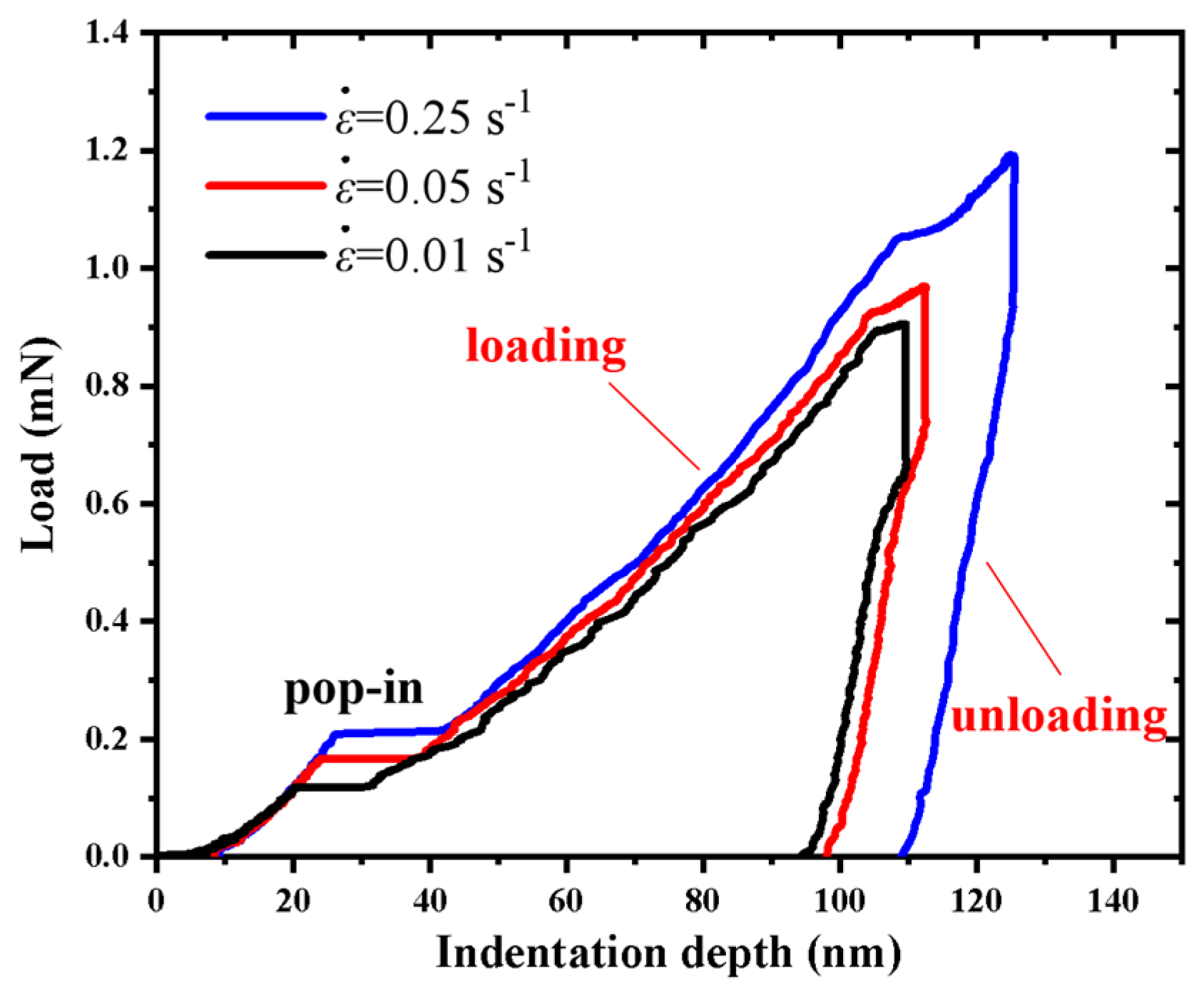
3.1. Load-Indentation Depth Curves
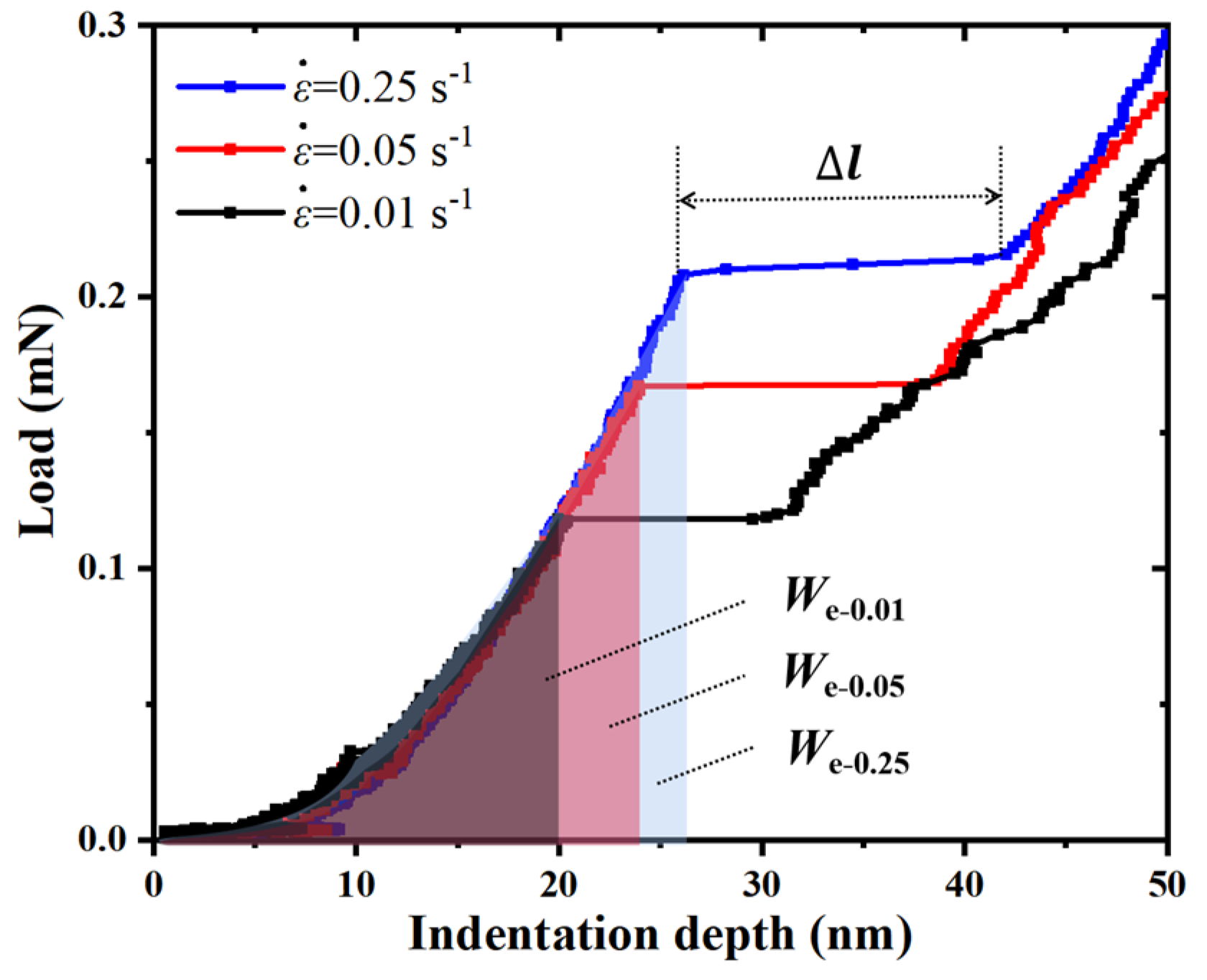
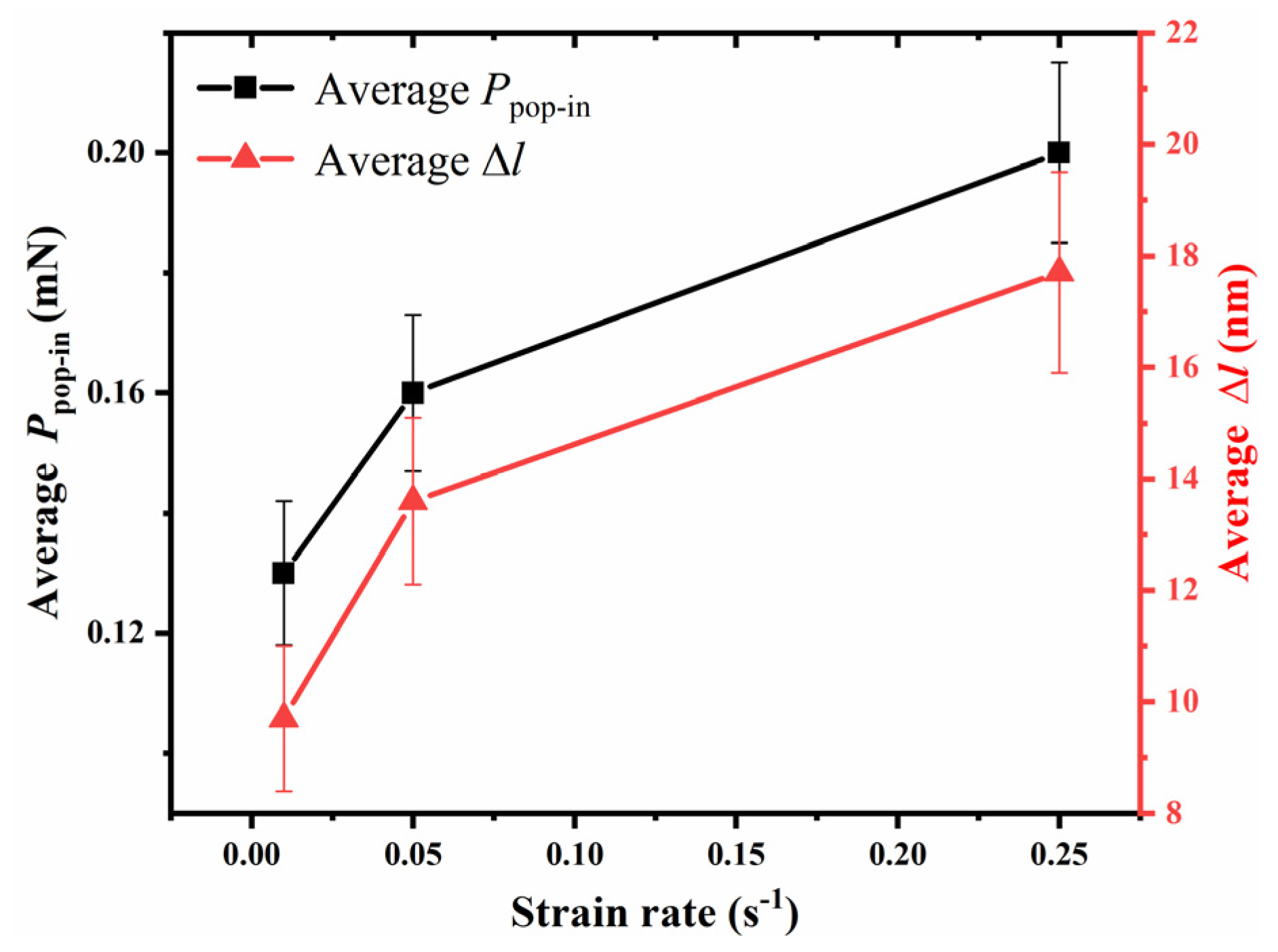
3.2. Pop-In
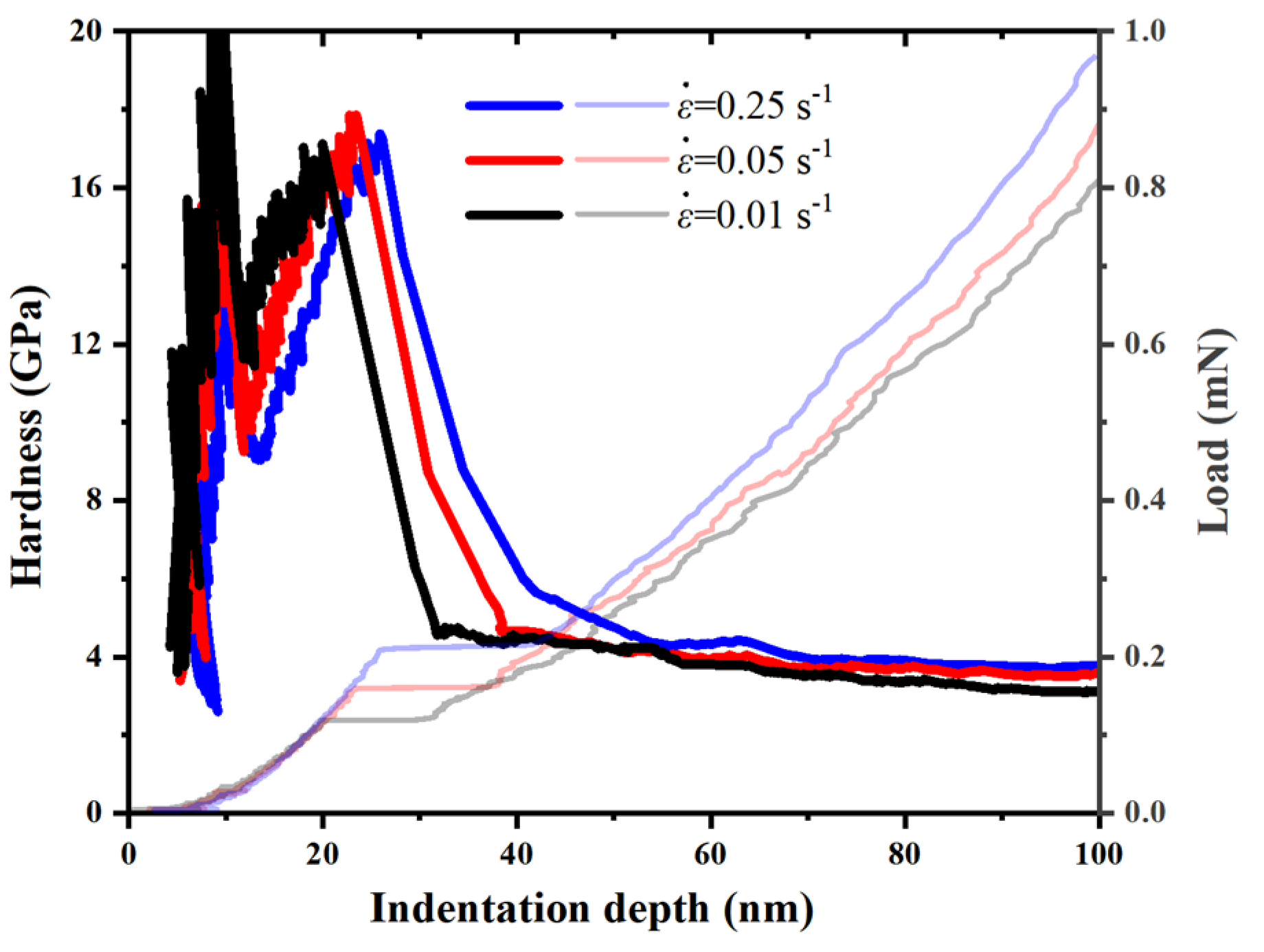
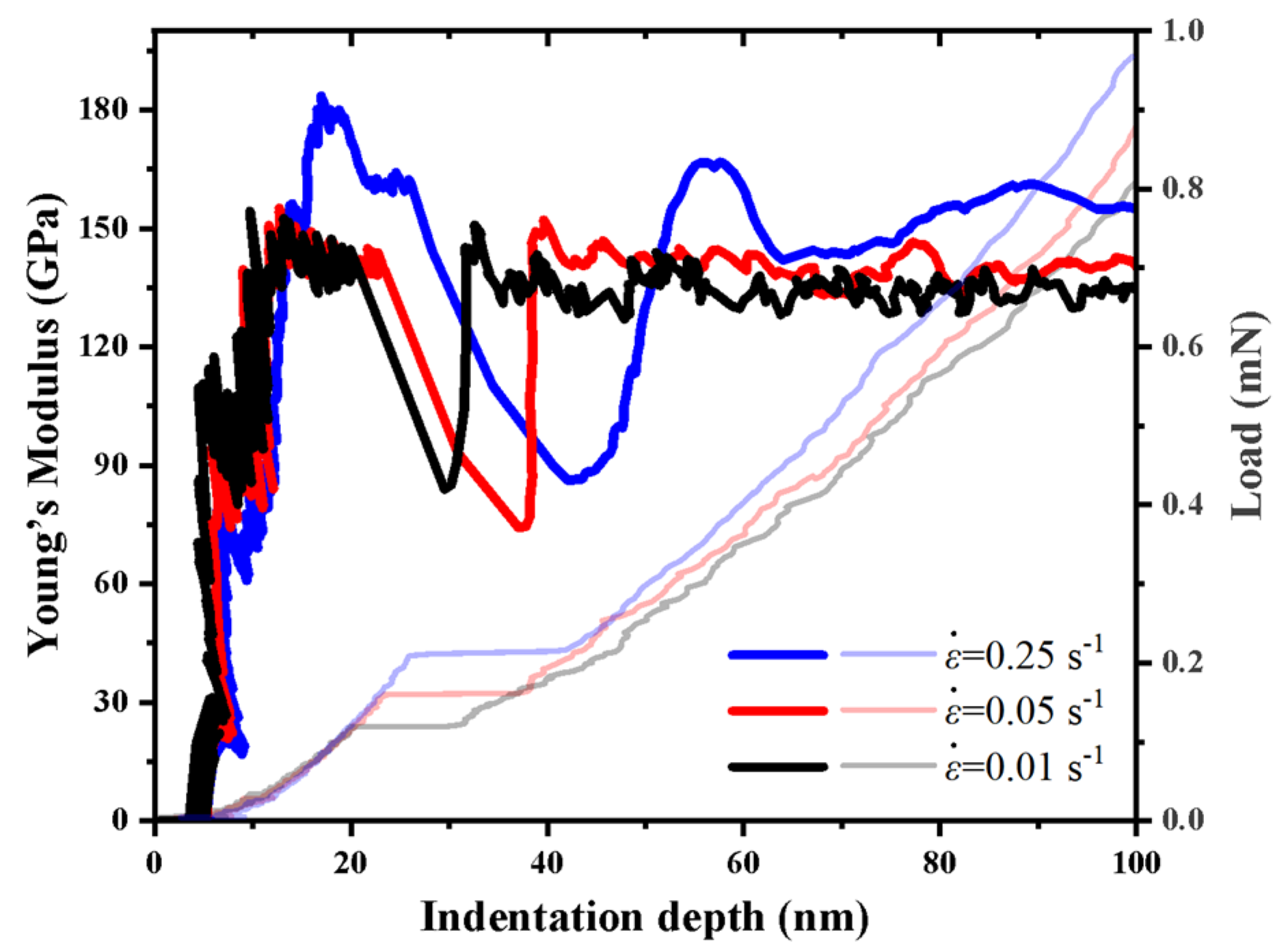
3.3. Hardness and Young’s Modulus
4. Conclusions
- With the indentation depth increasing, the load increased gradually at each maximum indentation depth, hmax, during the loading process of the a-plane () ZnO single crystal. A distinct pop-in event occurred on each loading curve, except that corresponding to the hmax of 10 nm. Only the elastic deformation occurred in the a-plane () ZnO single crystal at the hmax of 10 nm, while at other hmax, the irreversible plastic deformation emerged.
- The applied load at the same indentation depth increased with the increasing strain rate, showing the positive strain-rate sensitivity during the nanoindentation of the a-plane () ZnO single crystal. Due to the creep deformation increasing with strain rate during the holding stage, the actual maximum indentation depth at higher strain rate was greater.
- The lower strain rate made it easier to induce the pop-in event of the a-plane () ZnO single crystal, while the higher strain rate deferred the pop-in event to higher load and deeper indentation depth, and made the pop-in extension width larger. Therefore, the pop-in load, pop-in depth and pop-in extension width all showed positive strain-rate sensitivities during the nanoindentation of the a-plane () ZnO single crystal.
- The hardness of the a-plane () ZnO single crystal showed reverse indentation size effect (ISE) before the pop-in, and exhibited normal ISE after the pop-in. Except during the pop-in, the Young’ modulus of the a-plane () ZnO single crystal at each strain rate showed no apparent dependency on the indentation depth. Both the hardness and Young’s modulus of the a-plane () ZnO single crystal increased with the increasing strain rate, exhibiting the positive strain-rate sensitivity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Byun, J.; Lee, S.; Seo, J.; Park, B.; Kim, J.C.; Jeong, H.U.; Bang, J.; Lee, J.; Oh, S.H. Vacancy driven surface disorder catalyzes anisotropic evaporation of ZnO (0001) polar surface. Nat. Commun. 2022, 13, 5616. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Li, W.; Qin, G.; Ruan, H.; Ye, L.; Kong, C.; Wu, F.; Fang, L. Understanding the thermal evolution of defects in carbon-implanted ZnO single crystal. Ceram. Int. 2020, 46, 672–677. [Google Scholar] [CrossRef]
- Massabuau, F.; Calahorra, Y. Piezoelectric III-V and II-VI semiconductors. Encycl. Smart Mater. 2022, 4, 35–49. [Google Scholar]
- Cheng, L.; Zhu, S.; Zheng, W.; Huang, F. Ultra-wide spectral range (0.4–8 μm) transparent conductive ZnO bulk single crystals: A leading runner for mid-infrared optoelectronics. Mater. Today Phys. 2020, 14, 100244. [Google Scholar]
- Gierster, L.; Vempati, S.; Stähler, J. Ultrafast generation and decay of a surface metal. Nat. Commun. 2021, 12, 978. [Google Scholar]
- Huang, F.; Lin, Z.; Lin, W.; Zhang, J.; Ding, K.; Wang, Y.; Zheng, Q.; Zhan, Z.; Yan, F.; Chen, D.; et al. Research progress in ZnO single-crystal: Growth, scientific understanding, and device applications. Chin. Sci. Bull. 2014, 59, 1235–1250. [Google Scholar]
- Polman, A.; Knight, M.; Garnett, E.C.; Ehrler, B.; Sinke, W.C. Photovoltaic materials: Present efficiencies and future challenges. Science 2016, 352, aad4424. [Google Scholar] [CrossRef]
- Keil, P.; Gehringer, M.; Frömling, T.; Novak, N.; Rödel, J. ZnO-based single crystal-polycrystal structures for piezotronic applications. J. Am. Ceram. Soc. 2019, 102, 2640–2647. [Google Scholar]
- Park, J.; Rim, Y.S.; Senanayake, P.; Wu, J.; Streit, D. Electrical defect state distribution in single crystal ZnO Schottky barrier diodes. Coatings 2020, 10, 206. [Google Scholar]
- Suzuki, T.T.; Ohgaki, T.; Adachi, Y.; Sakaguchi, I.; Nakamura, M.; Ohashi, H.; Aimi, A.; Fujimoto, K. Ethanol gas sensing by a Zn-terminated ZnO (0001) bulk single-crystalline substrate. ACS Omega 2020, 5, 21104–21112. [Google Scholar]
- Gurylev, V.; Perng, T.P. Defect engineering of ZnO: Review on oxygen and zinc vacancies. J. Eur. Ceram. Soc. 2021, 41, 4977–4996. [Google Scholar] [CrossRef]
- Ye, H.; Su, Z.; Tang, F.; Wang, M.; Chen, G.; Wang, J.; Xu, S. Excitation dependent phosphorous property and new model of the structured green luminescence in ZnO. Sci. Rep. 2017, 7, 41460. [Google Scholar] [PubMed]
- Bai, X.; Sun, B.; Wang, X.; Zhang, T.; Hao, Q.; Ni, B.J.; Zong, R.; Zhang, Z.; Zhang, X.; Li, H. Defective crystal plane-oriented induced lattice polarization for the photocatalytic enhancement of ZnO. CrystEngComm 2020, 22, 2709–2717. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, Y.; Peng, L.; Wang, X.; Li, J.; Liu, Z.; Wu, W. Crystal growth, finite element analysis and oxygen annealing of ZnO bulk crystal grown by low-temperature-gradient chemical vapor transport. Ceram. Int. 2020, 46, 23107–23115. [Google Scholar]
- Coleman, V.A.; Bradby, J.E.; Jagadish, C.; Phillips, M.R. A comparison of the mechanical properties and the impact of contact induced damage in a-and c-axis ZnO single crystals. Mater. Res. Soc. Symp. Proc. 2007, 957, 717. [Google Scholar]
- Yamanoi, K.; Empizo, M.J.F.; Mori, K.; Iwano, K.; Minami, Y.; Arita, R.; Iwasa, Y.; Fukuda, K.; Kato, K.; Takano, K.; et al. ZnO crystal as a potential damage-recoverable window material for fusion reactors. Opt. Mater. 2016, 62, 646–650. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Jian, S.R.; Lee, J.W.; Juang, J.Y. The indentation-induced pop-in phenomenon and fracture behaviors of GaP (100) single-crystal. Micromachines 2019, 10, 752. [Google Scholar]
- Tao, P.; Ye, F.; Gong, J.; Barrett, R.A.; Leen, S.B. A dislocation-based yield strength model for nano-indentation size effect. Proc. Inst. Mech. Eng. Part L- J. Mater. Des. Appl. 2021, 235, 1238–1247. [Google Scholar]
- Wang, J.W.; Yu, K.; Li, M.; Wu, J.; Wang, J.; Wan, C.W.; Xiao, C.L.; Xia, B.; Huang, J. Application of nanoindentation technology in testing the mechanical properties of skull materials. Sci. Rep. 2022, 12, 8717. [Google Scholar]
- Yang, R.; Zhang, Q.; Xiao, P.; Wang, J.; Bai, Y. Two opposite size effects of hardness at real nano-scale and their distinct origins. Sci. Rep. 2017, 7, 16053. [Google Scholar]
- Chai, P.; Li, S.; Li, Y.; Liang, L.; Yin, X. Mechanical behavior investigation of 4H-SiC single crystal at the micro–nano scale. Micromachines 2020, 11, 102. [Google Scholar] [PubMed]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Si, B.; Li, Z.; Yang, X.; Shu, X.; Xiao, G. Characterizations of specific mechanical behaviors for metallic materials with representative crystal structures using nanoindentation. Vacuum 2023, 207, 111661. [Google Scholar] [CrossRef]
- Li, H.; Gao, K.; Gao, C.; Ding, Y.; Xiong, X.; Wu, X.; Huang, H.; Wen, S.; Nie, Z.; Zhang, Q. Hardness and Young’s modulus of Al3Yb single crystal studied by nano indentation. Intermetallics 2020, 127, 106980. [Google Scholar]
- Filippov, P.; Koch, U. Nanoindentation of aluminum single crystals: Experimental study on influencing factors. Materials 2019, 12, 3688. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chen, L.; Cheng, Y.; Yu, L.; Yi, X.; Gao, H.; Duan, H. Model of nanoindentation size effect incorporating the role of elastic deformation. J. Mech. Phys. Solids 2019, 126, 245–255. [Google Scholar]
- Jian, S.R. Pop-in effects and dislocation nucleation of c-plane single-crystal ZnO by Berkovich nanoindentation. J. Alloys Compd. 2015, 644, 54–58. [Google Scholar] [CrossRef]
- Juday, R.; Silva, E.M.; Huang, J.Y.; Caldas, P.G.; Prioli, R.; Ponce, F.A. Strain-related optical properties of ZnO crystals due to nanoindentation on various surface orientations. J. Appl. Phys. 2013, 113, 183511. [Google Scholar]
- Sung, T.H.; Huang, J.C.; Chen, H.C. Mechanical response of polar/non-polar ZnO under low dimensional stress. Appl. Phys. Lett. 2013, 102, 241901. [Google Scholar] [CrossRef]
- Hirakata, H.; Sano, K.; Shimada, T. Electron-beam irradiation alters bond strength in zinc oxide single crystal. Appl. Phys. Lett. 2020, 116, 111902. [Google Scholar]
- Mao, J.; Liu, W.; Li, D.; Zhang, C.; Ma, Y. The strain rate sensitivity and creep behavior for the tripler plane of potassium dihydrogen phosphate crystal by nanoindentation. Micromachines 2021, 12, 369. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Huang, X.; Hang, W.; Liu, M.; Song, Y.; Yuan, J.; Zhang, T. Nanoindentation size effect on stochastic behavior of incipient plasticity in a LiTaO3 single crystal. Eng. Fract. Mech. 2020, 226, 106877. [Google Scholar]
- Nguyen, N.V.; Kim, S.E. Experimental study to investigate microstructure and continuous strain rate sensitivity of structural steel weld zone using nanoindentation. Int. J. Mech. Sci. 2020, 174, 105482. [Google Scholar]
- Jarząbek, D.M.; Milczarek, M.; Nosewicz, S.; Bazarnik, P.; Schift, H. Size effects of hardness and strain rate sensitivity in amorphous silicon measured by nanoindentation. Metall. Mater. Trans. A 2020, 51, 1625–1633. [Google Scholar]
- Kucheyev, S.O.; Bradby, J.E.; Williams, J.S.; Jagadish, C.; Swain, M.V. Mechanical deformation of single-crystal ZnO. Appl. Phys. Lett. 2002, 80, 956–958. [Google Scholar]
- Lin, P.H.; Du, X.H.; Chen, Y.H.; Chen, H.C.; Huang, J.C. Nano-scaled diffusional or dislocation creep analysis of single-crystal ZnO. AIP Adv. 2016, 6, 095125. [Google Scholar]
- Fang, T.H.; Chang, W.J.; Lin, C.M. Nanoindentation characterization of ZnO thin films. Mat. Sci. Eng. A Struct. 2007, 452–453, 715–720. [Google Scholar]
- Alsayed, Z.; Awad, R.; Badawi, M.S. Thermo-mechanical properties of high density polyethylene with zinc oxide as a filler. Iran. Polym. J. 2020, 29, 309–320. [Google Scholar] [CrossRef]
- Lucas, B.N.; Oliver, W.C. Indentation power-law creep of high-purity indium. Metall. Mater. Trans. A 1999, 30, 601–610. [Google Scholar] [CrossRef]
- Bhushan, B. Depth-sensing nanoindentation measurement techniques and applications. Microsyst. Technol. 2017, 23, 1595–1649. [Google Scholar]
- Hao, X.; Xiao, G.; Jin, T.; Su, B.; Liu, E.; Shu, X. Effect of indentation size on strain rate sensitivity of zirconia ceramics by nanoindentation. J. Aust. Ceram. Soc. 2021, 57, 1471–1478. [Google Scholar] [CrossRef]
- Xiao, G.; Yuan, G.; Jia, C.; Yang, X.; Li, Z.; Shu, X. Strain rate sensitivity of Sn–3.0 Ag–0.5 Cu solder investigated by nanoindentation. Mat. Sci. Eng. A Struct. 2014, 613, 336–339. [Google Scholar] [CrossRef]
- Fang, X.; Bishara, H.; Ding, K.; Tsybenko, H.; Porz, L.; Höfling, M.; Bruder, E.; Li, Y.; Dehm, G.; Durst, K. Nanoindentation pop-in in oxides at room temperature: Dislocation activation or crack formation? J. Am. Ceram. Soc. 2021, 104, 4728–4741. [Google Scholar]
- Sato, Y.; Shinzato, S.; Ohmura, T.; Hatano, T.; Ogata, S. Unique universal scaling in nanoindentation pop-ins. Nat. Commun. 2020, 11, 4177. [Google Scholar]
- Basu, S.; Barsoum, M.W. Deformation micromechanisms of ZnO single crystals as determined from spherical nanoindentation stress–strain curves. J. Mater. Res. 2007, 22, 2470–2477. [Google Scholar] [CrossRef]
- Yonenaga, I. Atomic structures and dynamic properties of dislocations in semiconductors: Current progress and stagnation. Semicond. Sci. Technol. 2020, 35, 043001. [Google Scholar]
- Yonenaga, I.; Ohno, Y.; Taishi, T.; Tokumoto, Y. Recent knowledge of strength and dislocation mobility in wide band-gap semiconductors. Phys. B Condens. Matter 2009, 404, 4999–5001. [Google Scholar]
- Schuh, C.A.; Mason, J.K.; Lund, A.C. Quantitative insight into dislocation nucleation from high-temperature nanoindentation experiments. Nat. Mater. 2005, 4, 617–621. [Google Scholar] [CrossRef]
- Wang, D.; Lu, X.; Lin, M.; Wan, D.; Li, Z.; He, J.; Johnsen, R. Understanding the hydrogen effect on pop-in behavior of an equiatomic high-entropy alloy during in-situ nanoindentation. J. Mater. Sci. Technol. 2022, 98, 118–122. [Google Scholar]
- Zhang, W.; Li, J.; Xing, Y.; Lang, F.; Zhao, C.; Hou, X.; Yang, S.; Xu, G. Determination of the mechanical properties of PIN–PMN–PT bulk single crystals by nanoindentation. Crystals 2020, 10, 28. [Google Scholar]
- Dub, N.; Brazhkin, V.V.; Belous, V.A.; Tolmacheva, G.N.; Konevskii, P.V. Comparative nanoindentation of single crystals of hard and superhard oxidess. J. Superhard Mater. 2014, 36, 217–230. [Google Scholar] [CrossRef]
- Petrík, J.; Blaško, P.; Mihaliková, M.; Vasilňáková, A.; Mikloš, V. The relationship between the deformation and the indentation size effect (ISE). Metall. Res. Technol. 2019, 116, 622. [Google Scholar] [CrossRef]
- Sung, T.H.; Huang, J.C.; Hsu, J.H.; Jian, S.R.; Nieh, T.G. Yielding and plastic slip in ZnO. Appl. Phys. Lett. 2012, 100, 211903. [Google Scholar] [CrossRef]
- Man, G.; Jiang, Y.; Wang, X.; He, H. Phase transformation and anelastic behaviors of PMN-0.33 PT single crystals via nanoindentation with different strain rates. Ceram. Int. 2020, 46, 21604–21609. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Dey, A.; Mukhopadhyay, A.K. Influence of loading rate on nanohardness of sapphire. Ceram. Int. 2016, 42, 13378–13386. [Google Scholar]
- Ma, Y.; Cao, L.; Hang, W.; Zhang, T.; Yuan, J. Crystallographic orientation effect on the incipient plasticity and its stochastic behavior of a sapphire single crystal by spherical nanoindentation. Ceram. Int. 2020, 46, 15554–15564. [Google Scholar]
- Jian, S.R. Mechanical responses of single-crystal ZnO. J. Alloys Compd. 2010, 494, 214–218. [Google Scholar]
- Jin, T.; Zhou, Z.; Liu, Z.; Xiao, G.; Yuan, G.; Shu, X. Sensitivity of PMMA nanoindentation measurements to strain rate. J. Appl. Polym. Sci. 2015, 132, 41896. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Li, J.; Zhang, L.; Lang, F.; Hou, X.; Zhao, X.; Zhang, W.; Zhao, C.; Yang, Z.
Effect of Strain Rate on Nano-Scale Mechanical Behavior of A-Plane (
Zhu X, Li J, Zhang L, Lang F, Hou X, Zhao X, Zhang W, Zhao C, Yang Z.
Effect of Strain Rate on Nano-Scale Mechanical Behavior of A-Plane (
Zhu, Xiaolin, Jijun Li, Lihua Zhang, Fengchao Lang, Xiaohu Hou, Xueping Zhao, Weiguang Zhang, Chunwang Zhao, and Zijian Yang.
2023. "Effect of Strain Rate on Nano-Scale Mechanical Behavior of A-Plane (
Zhu, X., Li, J., Zhang, L., Lang, F., Hou, X., Zhao, X., Zhang, W., Zhao, C., & Yang, Z.
(2023). Effect of Strain Rate on Nano-Scale Mechanical Behavior of A-Plane (




