Design of a Low-Reflection Flat Lens Antenna Based on Conformal Transformation Optics
Abstract
1. Introduction
2. Design Method
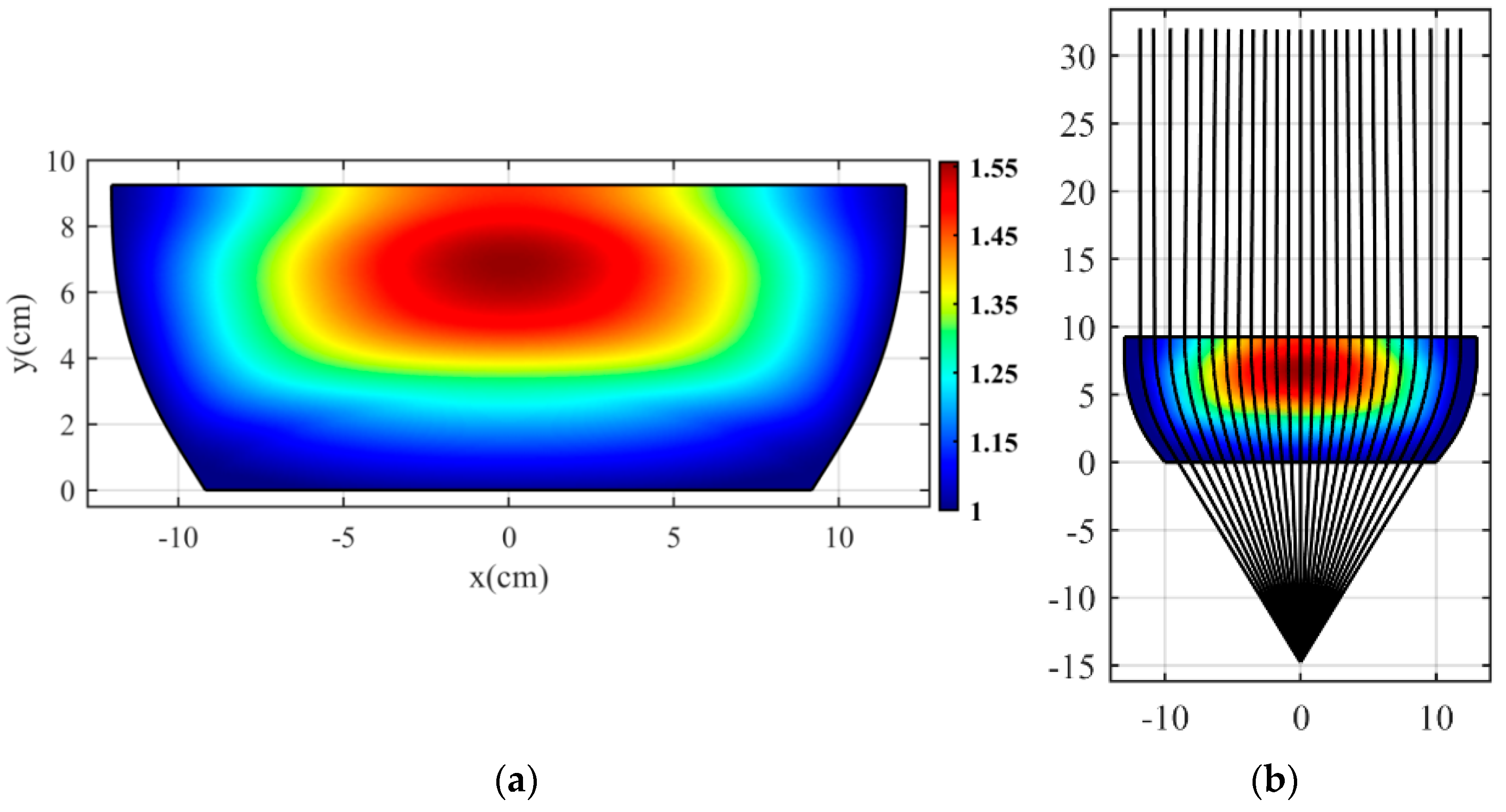
2.1. Design of Flat Lens Based on CTO
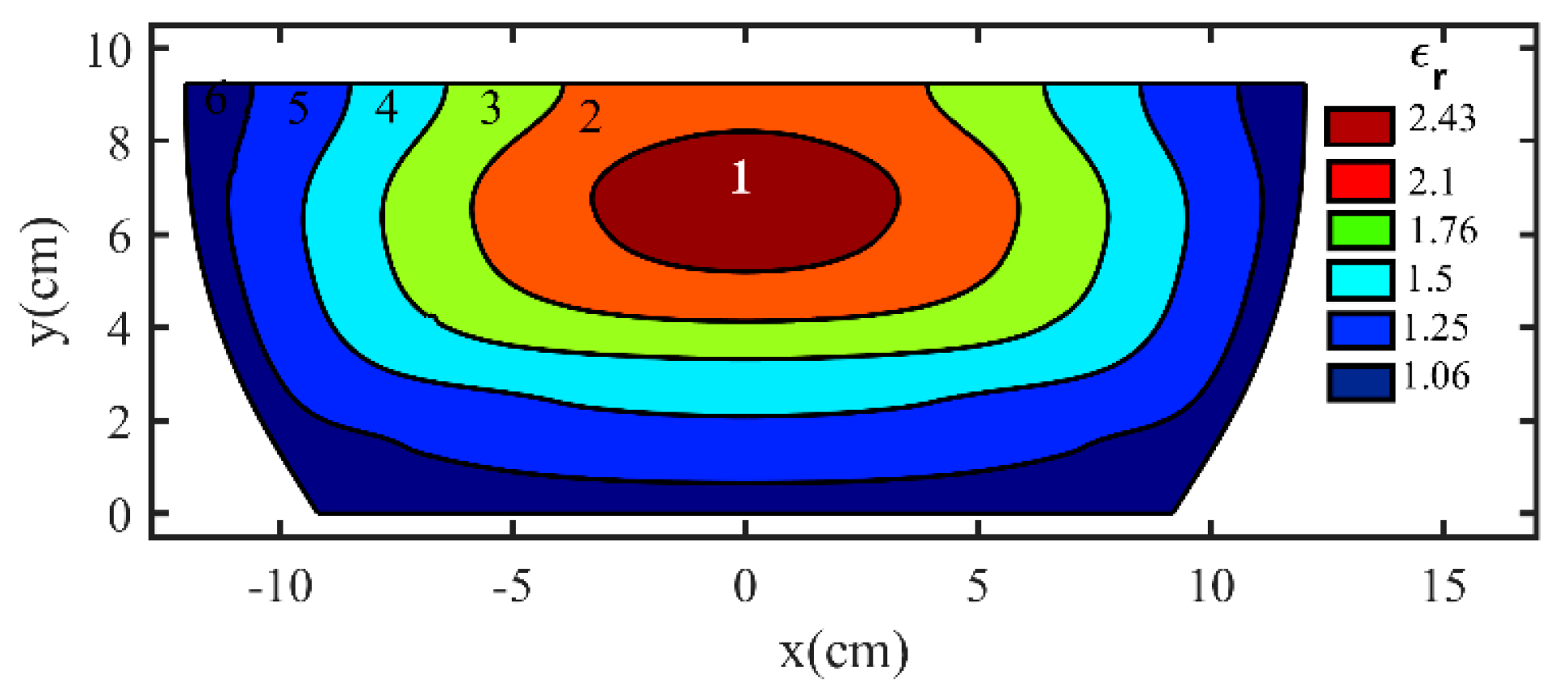
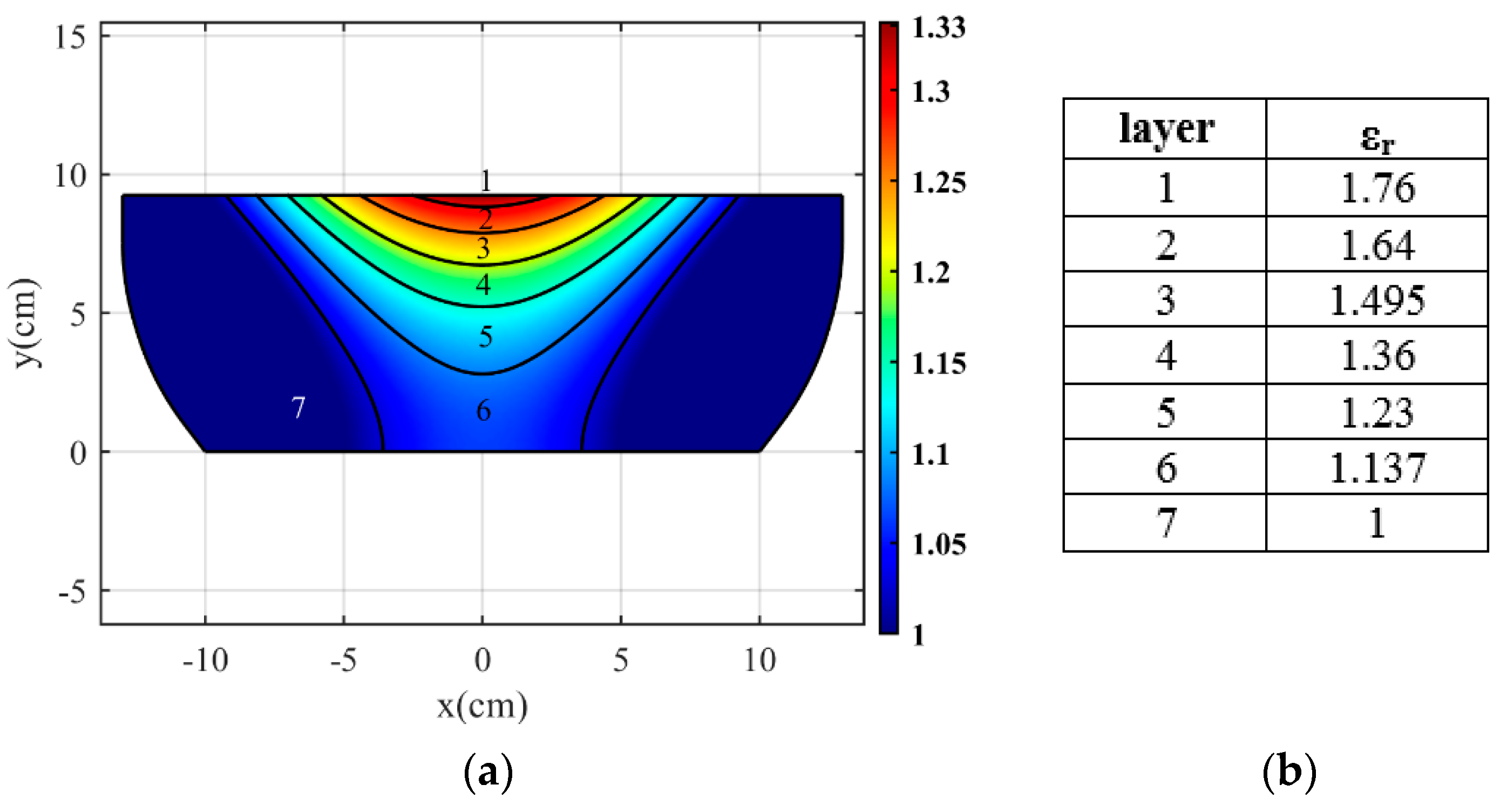
2.2. Refractive Index Control
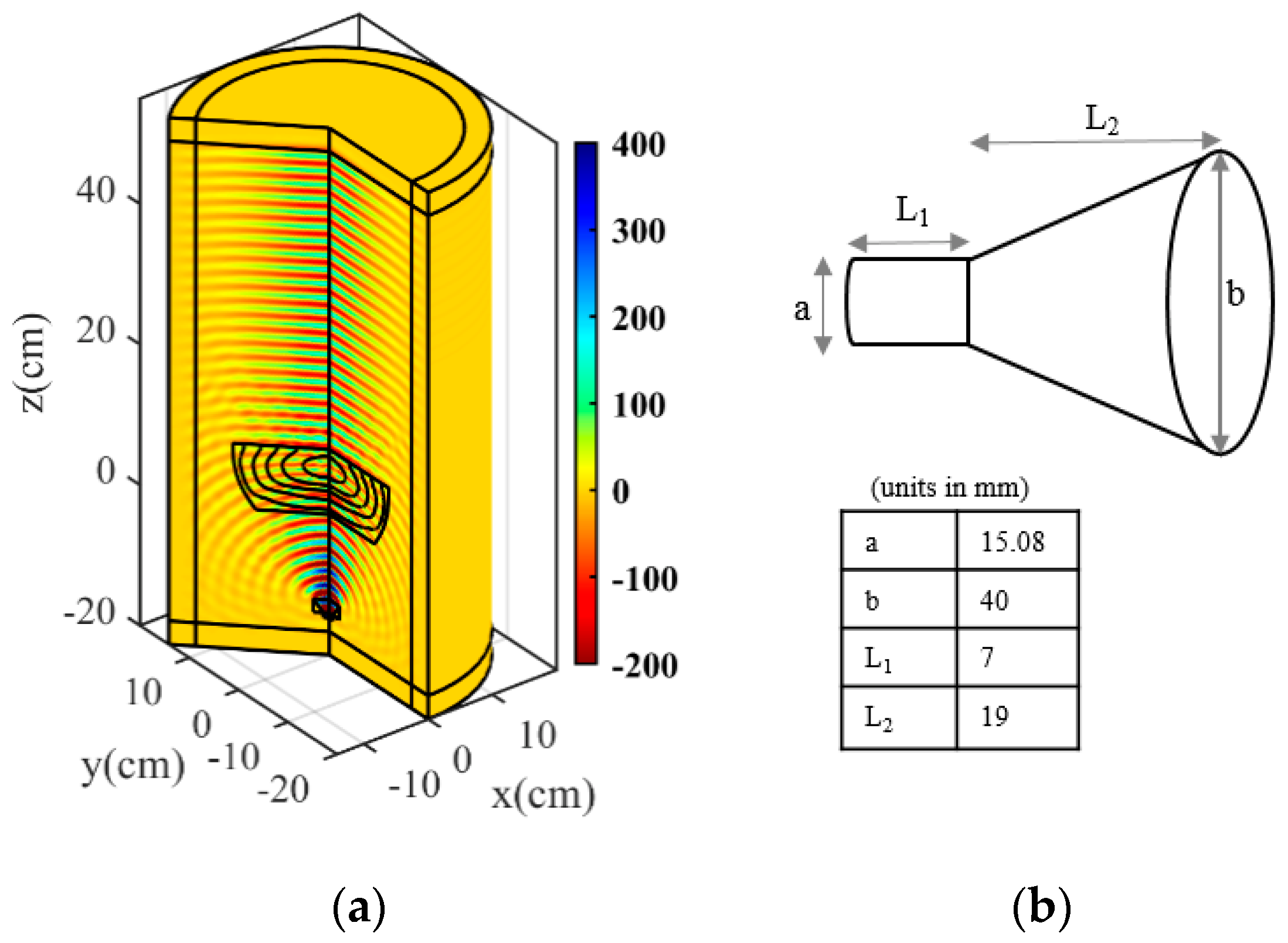
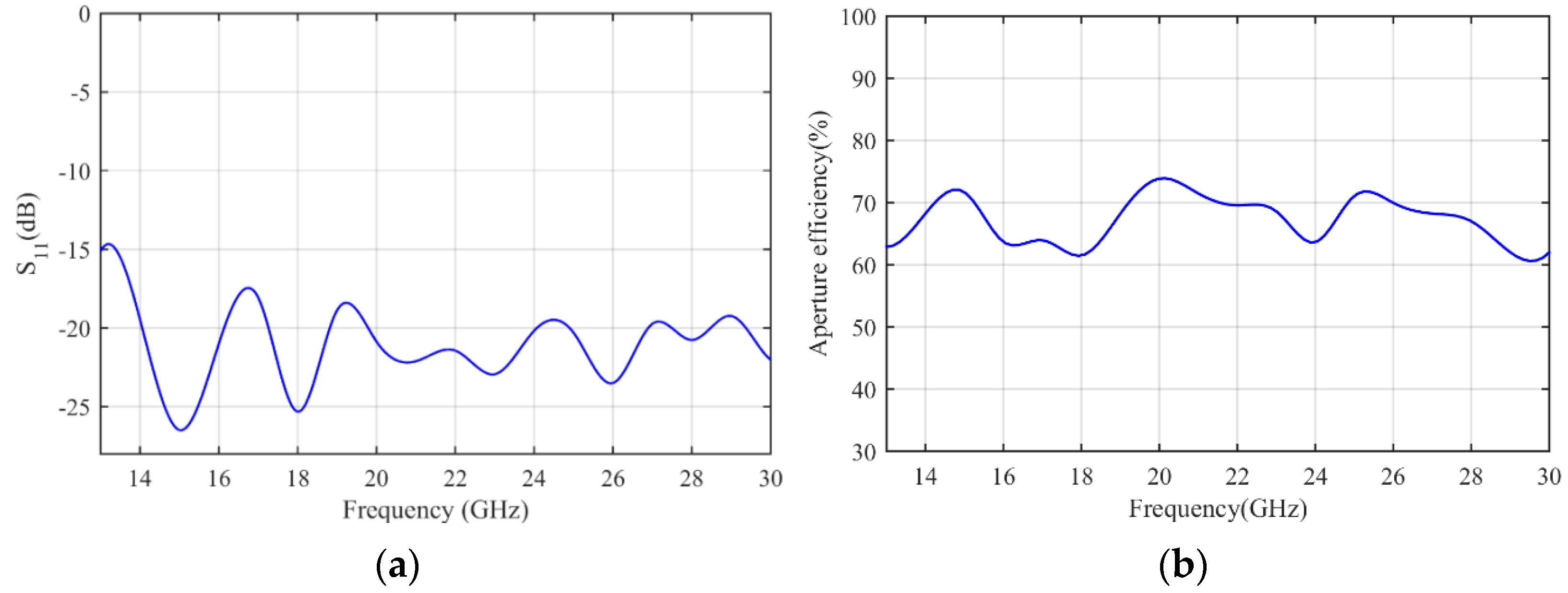
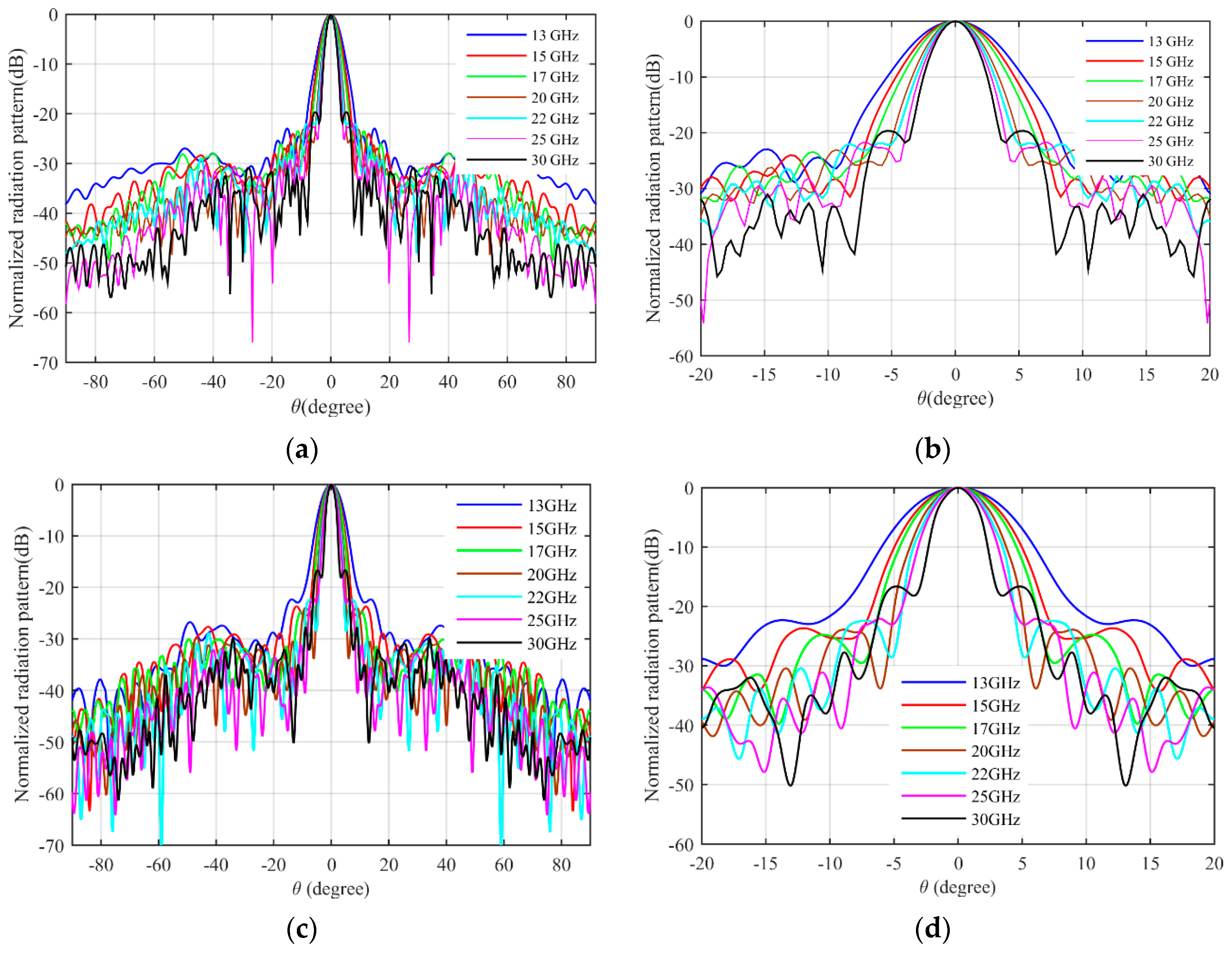
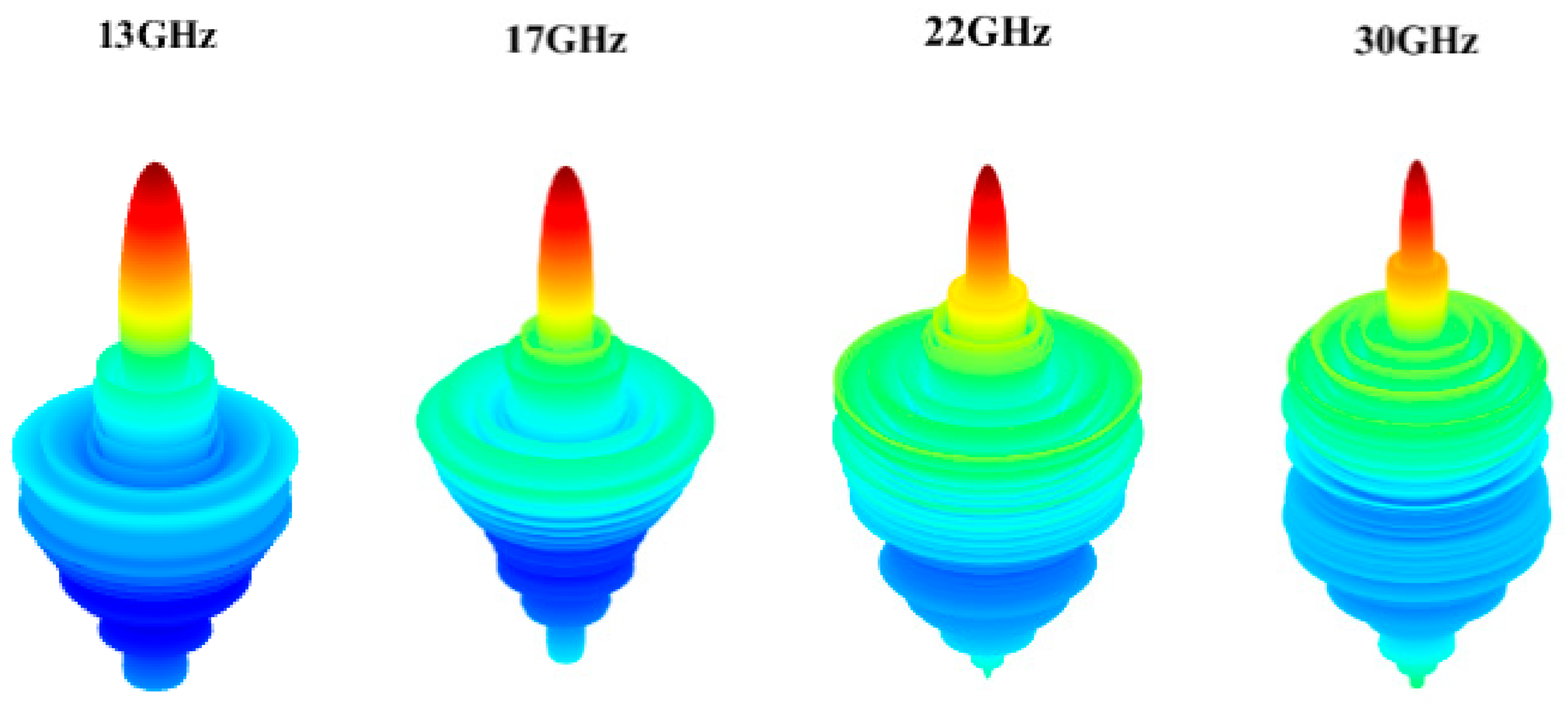
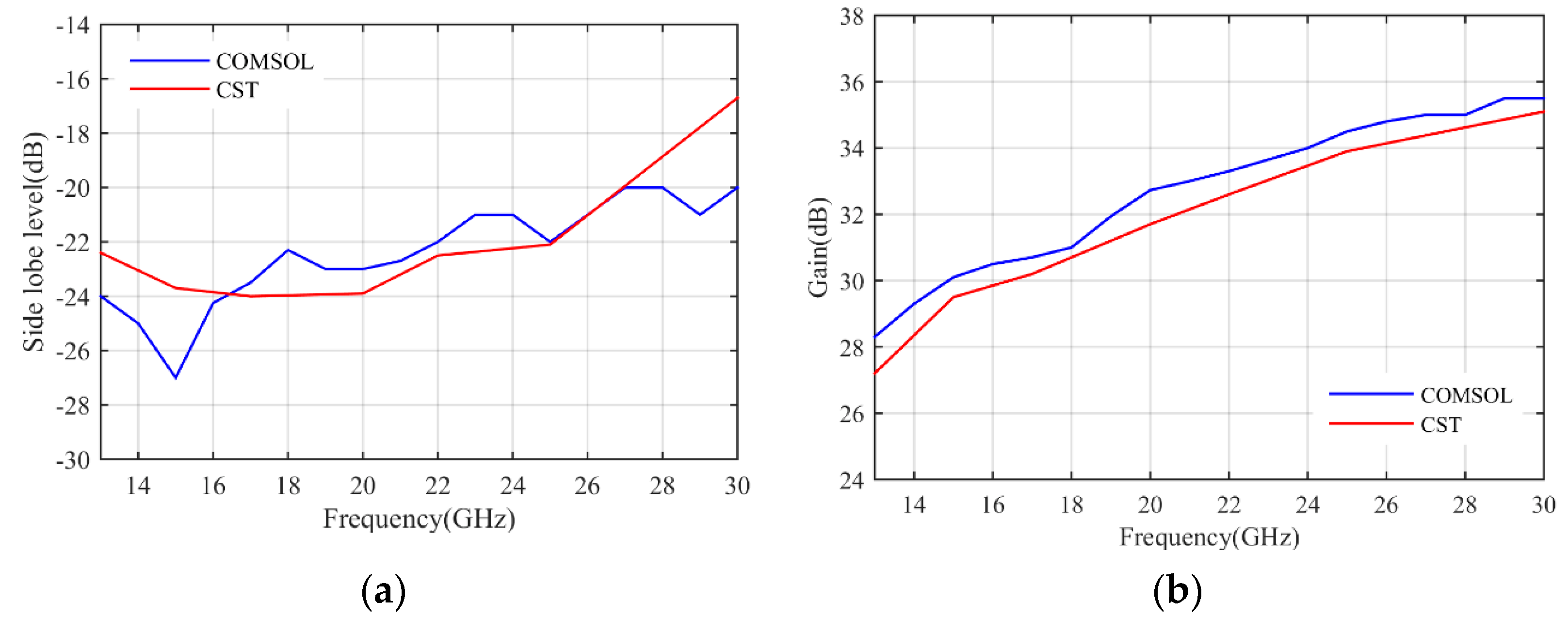
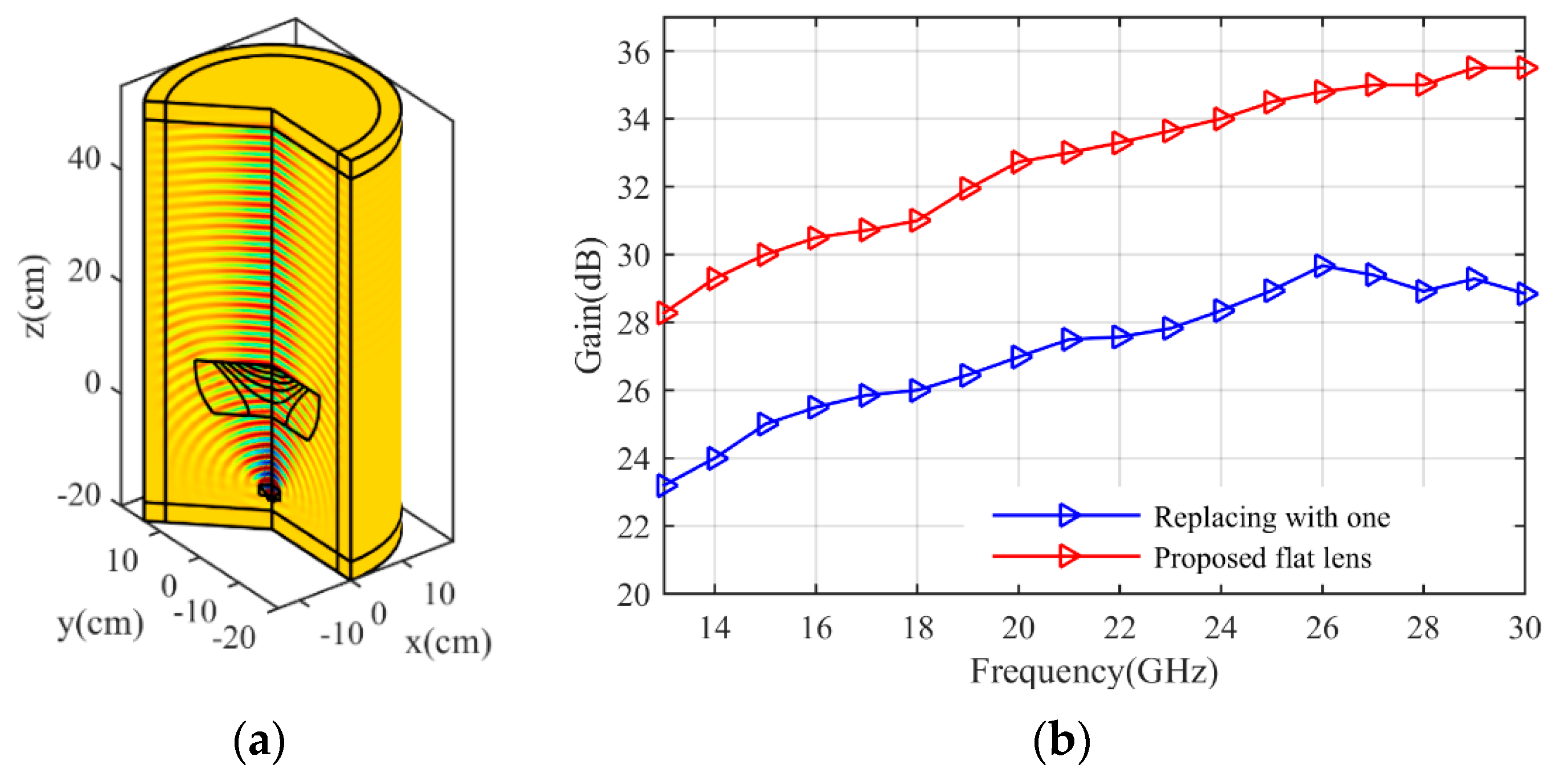
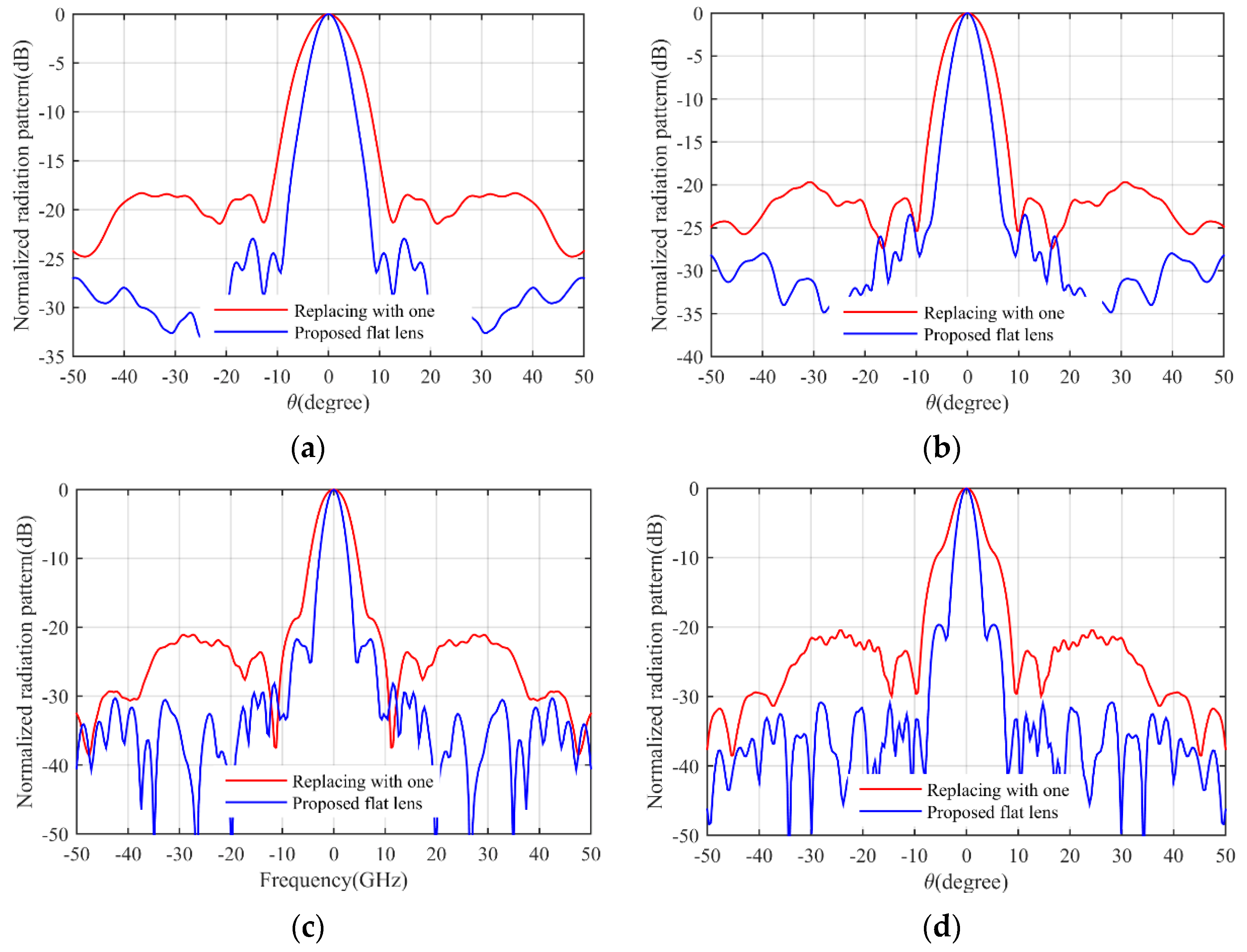
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Werner, D.H.; Kwon, D.-H. Transformation Electromagnetics and Metamaterials; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chen, H.; Yu, F.; Li, E.; Chen, H. A full-parameter, broadband, homogeneous, and compact waveguide coupler designed with transformation optics. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 634–637. [Google Scholar] [CrossRef]
- Eskandari, H.; Attari, A.R.; Majedi, M.S. Reflectionless compact nonmagnetic optical waveguide coupler designed based on transformation optics. Appl. Opt. 2017, 56, 5599–5606. [Google Scholar] [CrossRef] [PubMed]
- Eskandari, H.; Attari, A.R.; Majedi, M.S. Reflectionless design of a nonmagnetic homogeneous optical waveguide coupler based on transformation optics. J. Opt. Soc. Am. B 2018, 35, 54–60. [Google Scholar] [CrossRef]
- Tang, W.; Argyropoulos, C.; Kallos, E.; Song, W.; Hao, Y. Discrete coordinate transformation for designing all-dielectric flat antennas. IEEE Trans. Antennas Propag. 2010, 58, 3795–3804. [Google Scholar] [CrossRef]
- Liang, L.; Hum, S.V. Wide-angle scannable reflector design using conformal transformation optics. Opt. Express 2013, 21, 2133. [Google Scholar] [CrossRef]
- Yang, R.; Tang, W.; Hao, Y. Wideband beam-steerable flat reflectors via transformation optics. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 1290–1294. [Google Scholar] [CrossRef]
- Nazarzadeh, F.; Heidari, A.A. Wideband flat reflector antenna based on conformal transformation optics. Optik 2022, 264, 169429. [Google Scholar] [CrossRef]
- Zhou, J.; Li, M.; Xie, L.; Liu, D. Design of a new kind of polarization splitter based on transformation optics. Optik 2011, 122, 1672–1675. [Google Scholar] [CrossRef]
- Zhai, T.; Zhou, Y.; Zhou, J.; Liu, D. Polarization controller based on embedded optical transformation. Opt. Express 2009, 17, 17206. [Google Scholar] [CrossRef]
- Kwon, D.-H.; Werner, D.H. Polarization splitter and polarization rotator designs based on transformation optics. Opt. Express 2008, 16, 18731. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.X.; Cui, T.J.; Cheng, Q.; Chin, J.Y.; Yang, X.M.; Liu, R.; Smith, D.R. Design of arbitrarily shaped concentrators based on conformally optical transformation of nonuniform rational B-spline surfaces. Appl. Phys. Lett. 2008, 92, 29–32. [Google Scholar] [CrossRef]
- Rahm, M.; Schurig, D.; Roberts, D.A.; Cummer, S.A.; Smith, D.R.; Pendry, J.B. Design of electromagnetic cloaks and concentrators using form-invariant coordinate transformations of Maxwell’s equations. Photonics Nanostruct.–Fundam. Appl. 2008, 6, 87–95. [Google Scholar] [CrossRef]
- Rahm, M.; Roberts, D.A.; Pendry, J.B.; Smith, D.R. Transformation-optical design of adaptive beam bends and beam expanders. Opt. Express 2008, 16, 11555–11567. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.X.; Cui, T.J.; Zhou, X.Y.; Yang, X.M.; Cheng, Q. Arbitrary bending of electromagnetic waves using realizable inhomogeneous and anisotropic materials. Phys. Rev. E–Stat. Nonlinear Soft Matter Phys. 2008, 78, 066607. [Google Scholar] [CrossRef]
- Su, Y.; Chen, Z. A radial transformation-optics mapping for flat ultra-wide-angle dual-polarized stacked GRIN MTM Luneburg lens antenna. IEEE Trans. Antennas Propag. 2019, 67, 2961–2970. [Google Scholar] [CrossRef]
- Aghanejad, I.; Abiri, H.; Yahaghi, A. Design of high-gain lens antenna by gradient-index metamaterials using transformation optics. IEEE Trans. Antennas Propag. 2012, 60, 4074–4081. [Google Scholar] [CrossRef]
- Xu, L.; Chen, H. Conformal transformation optics. Nat. Photonics 2014, 9, 15–23. [Google Scholar] [CrossRef]
- Chang, Z.; Zhou, X.; Hu, J.; Hu, G. Design method for quasi-isotropic transformation materials based on inverse Laplace’s equation with sliding boundaries. Opt. Express 2010, 18, 6089. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Z.; Wang, J.; He, X. Design of conformal lens by drilling holes materials using quasi-conformal transformation optics. Opt. Express 2014, 22, 25455. [Google Scholar] [CrossRef]
- Falco, A.; Kehr, S.; Leonhardt, U. Luneburg lens in silicon photonics. Opt. Express 2011, 19, 5156–5162. [Google Scholar] [CrossRef]
- Gilarlue, M.M.; Badri, S.H.; Rasooli Saghai, H.; Nourinia, J.; Ghobadi, C. Photonic crystal waveguide intersection design based on Maxwell’s fish-eye lens. Photonics Nanostruct.–Fundam. Appl. 2018, 31, 154–159. [Google Scholar] [CrossRef]
- Moshiri, M.; Ghafoorzadeh-Yazdi, A.; Heidari, A.A. A wideband quad-layer transmitarray antenna with double cross slot rings elements. AEU–Int. J. Electron. Commun. 2020, 115, 153031. [Google Scholar] [CrossRef]
- Nazarzadeh, F.; Heidari, A.A. Design of a new cylindrical to plane wave transformer based on transformation optics. In Proceedings of the 2020 28th The International Council on Electrical Engineering, Takamatsu, Japan, 28 June–2 July 2020; pp. 1–4. [Google Scholar]
- Kwon, D.-H.; Werner, D.H. Transformation optical designs for wave collimators, flat lenses and right-angle bends. New J. Phys. 2008, 10, 115023. [Google Scholar] [CrossRef]
- Wu, Q.; Jiang, Z.H.; Quevedo-Teruel, O.; Turpin, J.P.; Tang, W.X.; Hao, Y.; Werner, D.H. Transformation optics inspired multibeam lens antennas for broadband directive radiation. IEEE Trans. Antennas Propag. 2013, 61, 5910–5922. [Google Scholar] [CrossRef]
- Kundtz, N.; Smith, D.R. Extreme-angle broadband metamaterial lens. Nat. Mater. 2010, 9, 129–132. [Google Scholar] [CrossRef]
- Yi, J.; Burokur, S.N.; Piau, G.P.; De Lustrac, A. Coherent beam control with an all-dielectric transformation optics based lens. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef]
- Ma, H.F.; Cui, T.J. Three-dimensional broadband and broad-angle transformation-optics lens. Nat. Commun. 2010, 1, 124. [Google Scholar] [CrossRef]
- Mateo-Segura, C.; Dyke, A.; Dyke, H.; Haq, S.; Hao, Y. Flat Luneburg lens via transformation optics for directive antenna applications. IEEE Trans. Antennas Propag. 2014, 62, 1945–1953. [Google Scholar] [CrossRef]
- DIng, T.; Yi, J.; Li, H.; Zhang, H.; Burokur, S.N. 3D field-shaping lens using all-dielectric gradient refractive index materials. Sci. Rep. 2017, 7, 782. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimpouri, M.; Zetterstrom, O.; Quevedo-Teruel, O. Experimental Validation of a Bespoke Lens for a Slot Log-Spiral Feed. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 557–560. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Quevedo-Teruel, O. Bespoke lenses based on Quasi-conformal Transformation optics Technique. IEEE Trans. Antennas Propag. 2017, 65, 2256–2264. [Google Scholar] [CrossRef]
- Poyanco, J.M.; Pizarro, F.; Rajo-Iglesias, E. Wideband hyperbolic flat lens in the Ka-band based on 3D-printing and transformation optics. Appl. Phys. Lett. 2021, 118, 123503. [Google Scholar] [CrossRef]
- Papamichael, N.; Stylianopoulos, N. Numerical Conformal Mapping: Domain Decomposition and the Mapping of Quadrilaterals; World Scientific: Singapore, 2010; pp. 51–63. [Google Scholar]




| Reference | [19] | [33] | [35] | [36] | This Work |
|---|---|---|---|---|---|
| Simulation software | COMSOL | COMSOL | CST | CST | COMSOL and CST |
| Method | CTO | QCTO | QCTO | QCTO | CTO |
| Implementation method | Graded photonic crystal | 8 layers with εr between 1–2.8 | 22 layers with εr between 1–3.2 | 9 layers with εr between 3–12 | 6 layers with εr between 1.06–2.43 |
| Frequency range | 14–22 GHz | 7–13 GHz | 8–12 GHz | 27–40 GHz | 13–30 GHz |
| Size (Diameter, Height) | D = 22.7 cm, h = 32 cm | D = 14.8 cm, h = 4 cm | D = 2.6 cm, h = 8.5 cm | D = 7.6 cm, h = 1.2 cm | D = 24 cm, h = 9.25 cm |
| Gain | 33–35 dB | Not stated | 17.5–22.5 dB (directivity) | 23.4–25.5 dB | 28.3–35.5 dB |
| Side lobe level | −24 dB | −11.5 dB | −14 dB | −10 dB | −20 dB |
| HPBW | 12°–10° | Not stated | Not stated | 6°–4° | 5.6°–2.7° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazarzadeh, F.; Heidari, A.A. Design of a Low-Reflection Flat Lens Antenna Based on Conformal Transformation Optics. Micromachines 2023, 14, 558. https://doi.org/10.3390/mi14030558
Nazarzadeh F, Heidari AA. Design of a Low-Reflection Flat Lens Antenna Based on Conformal Transformation Optics. Micromachines. 2023; 14(3):558. https://doi.org/10.3390/mi14030558
Chicago/Turabian StyleNazarzadeh, Fateme, and Abbas Ali Heidari. 2023. "Design of a Low-Reflection Flat Lens Antenna Based on Conformal Transformation Optics" Micromachines 14, no. 3: 558. https://doi.org/10.3390/mi14030558
APA StyleNazarzadeh, F., & Heidari, A. A. (2023). Design of a Low-Reflection Flat Lens Antenna Based on Conformal Transformation Optics. Micromachines, 14(3), 558. https://doi.org/10.3390/mi14030558







