Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes
Abstract
:1. Introduction
2. Equations of Momentum and Energy
3. Full and Perturbation Solutions
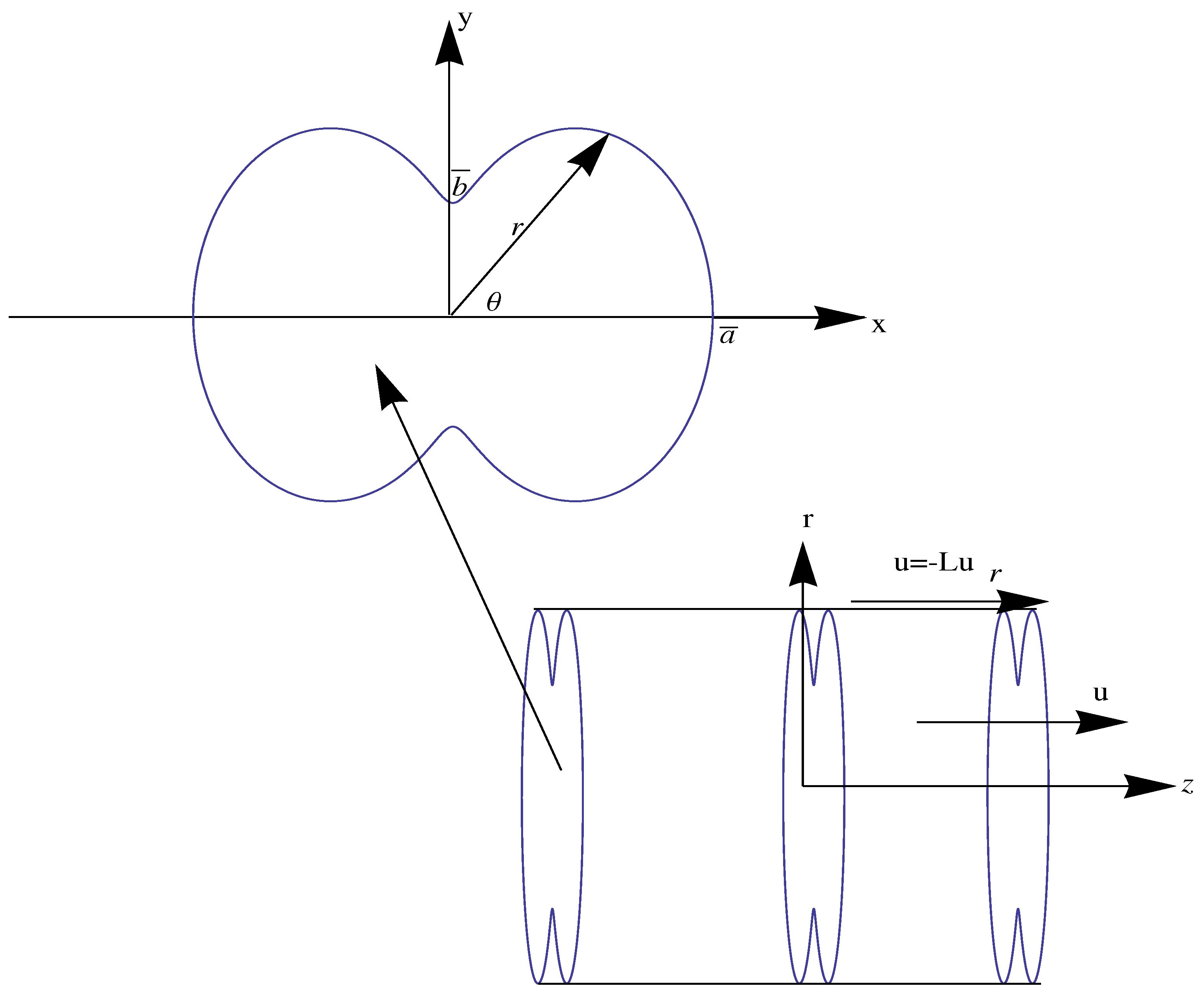
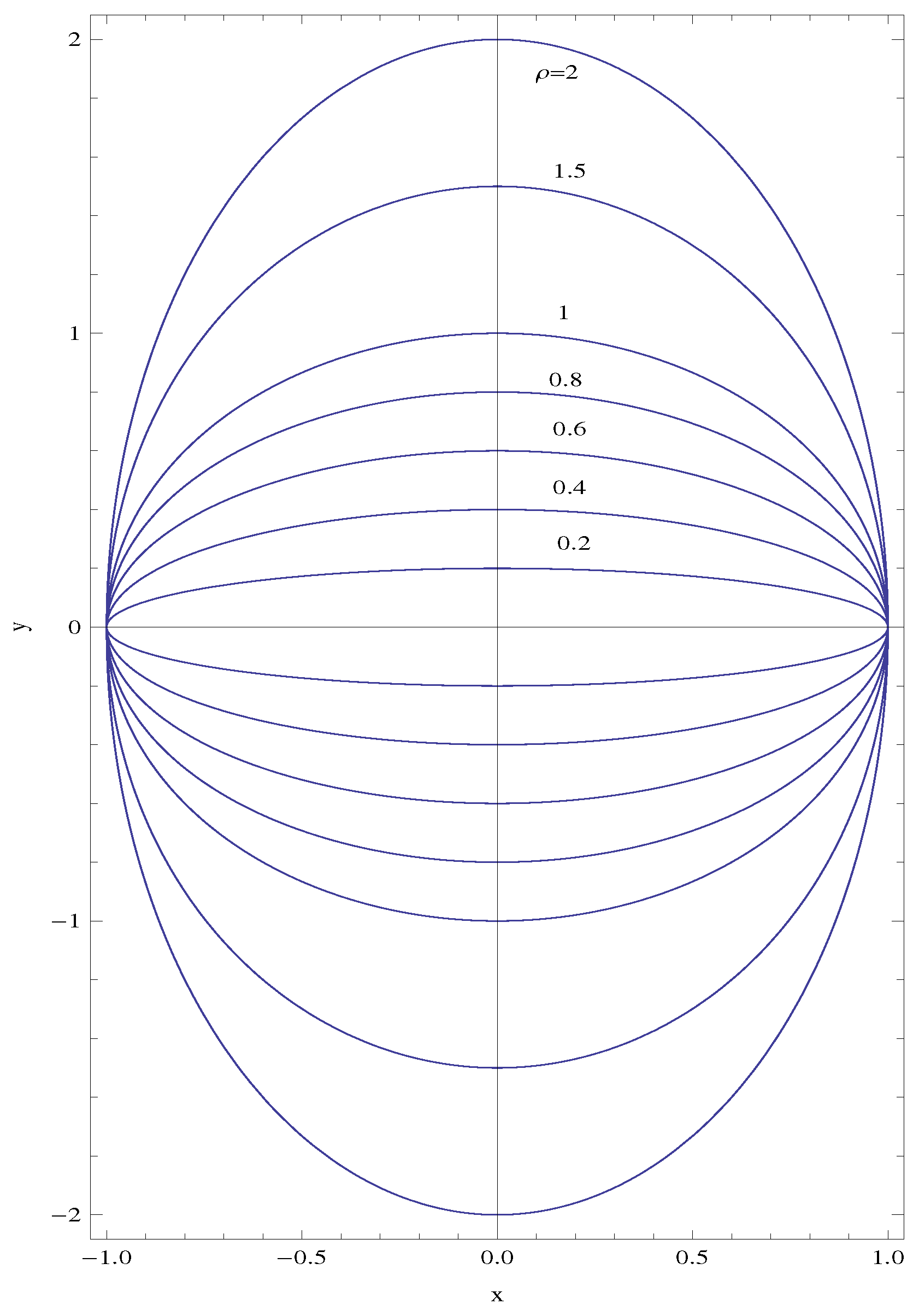
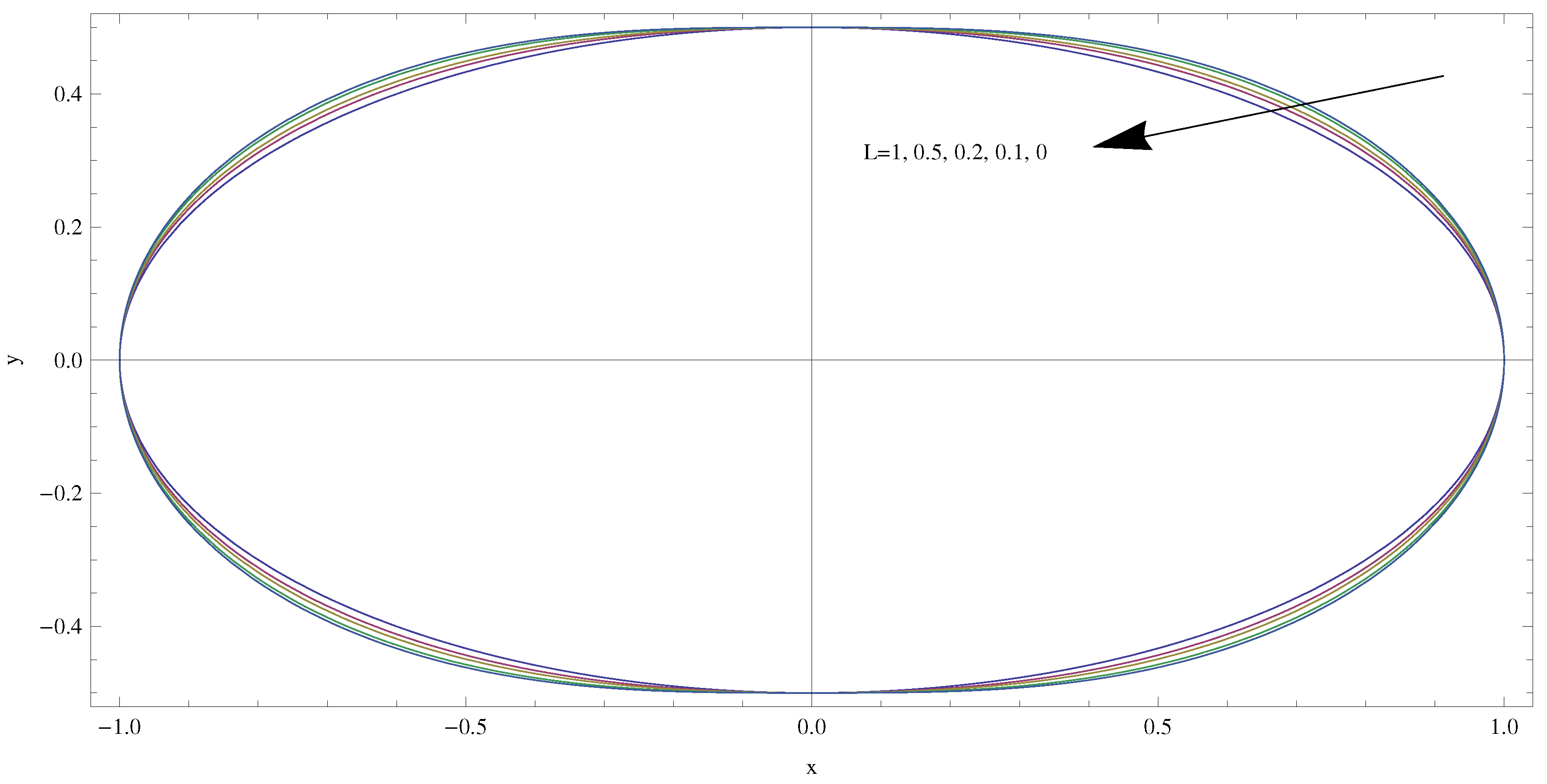
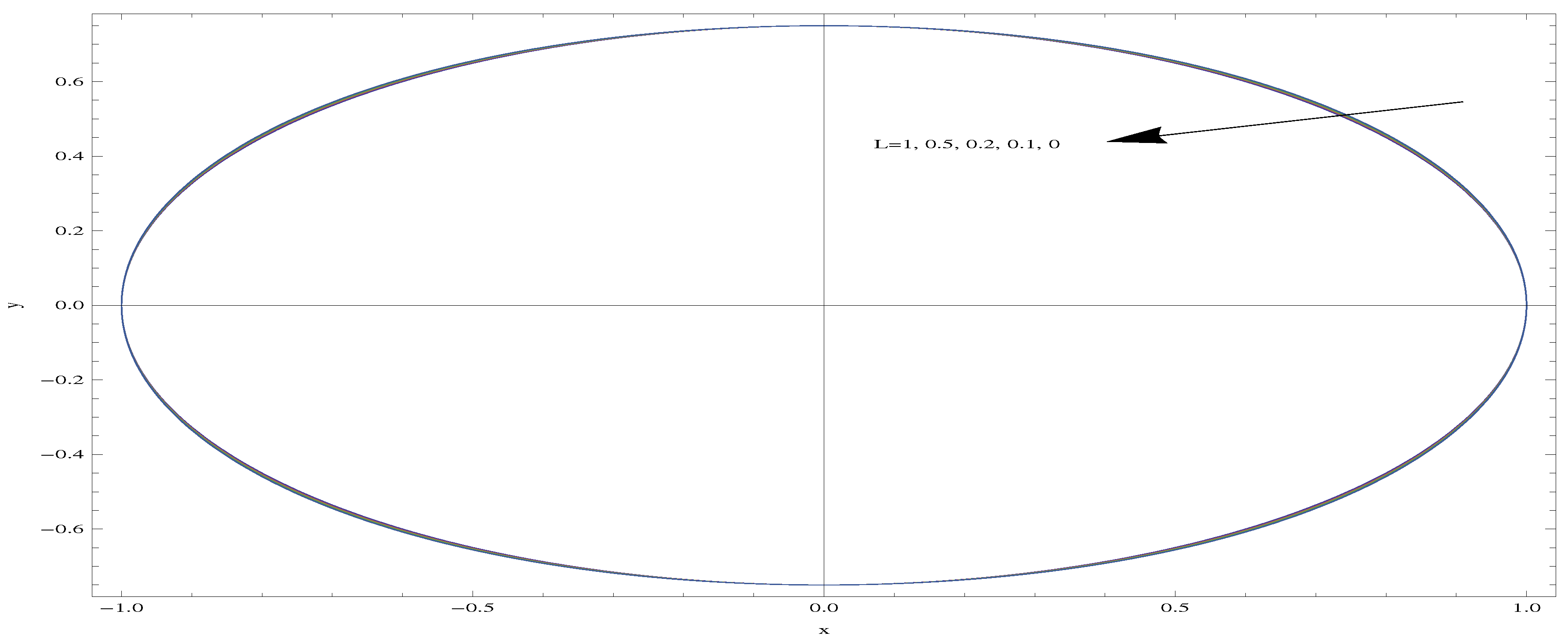
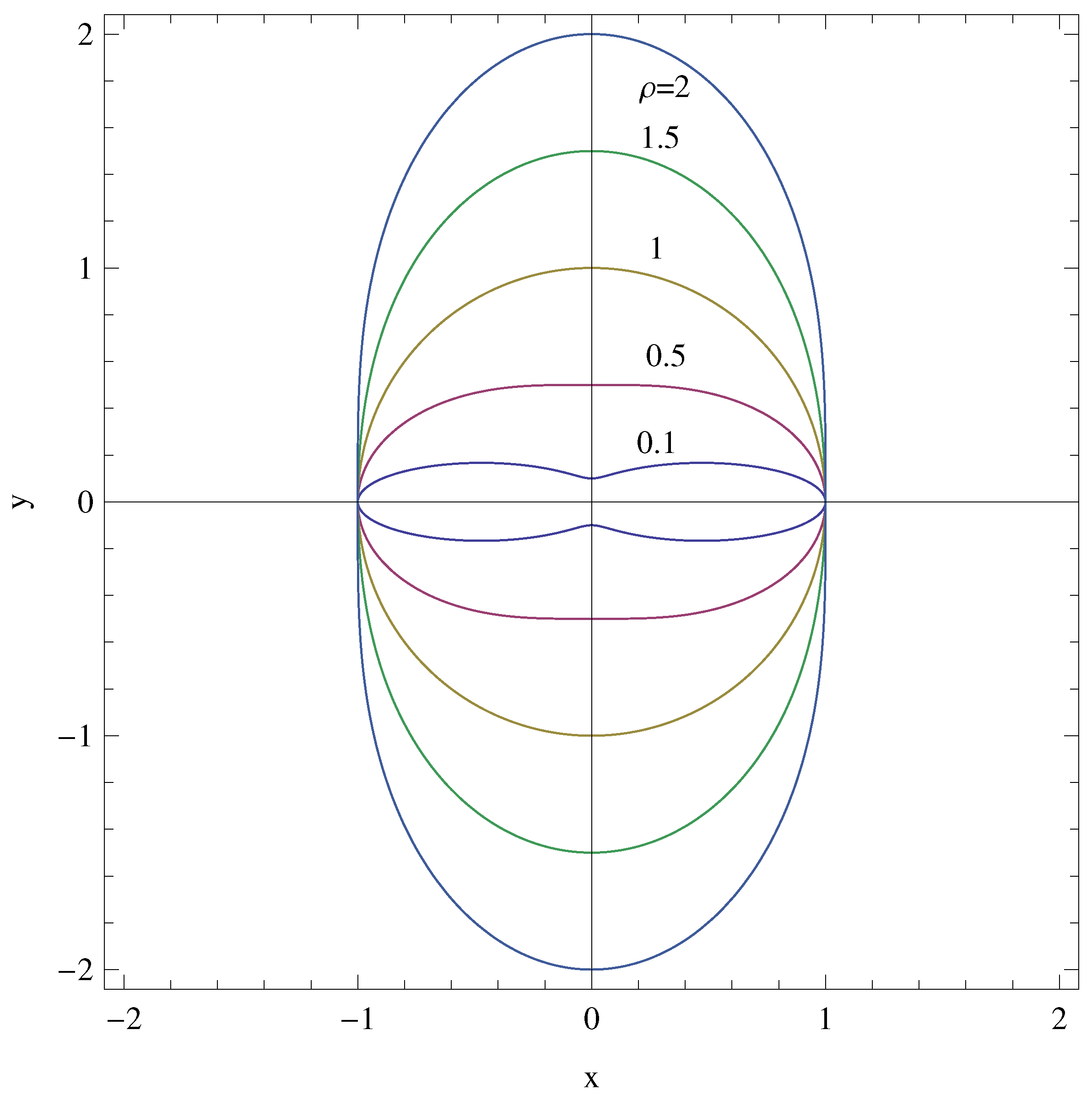
3.1. Full Velocity Solution and Pipe Surface Formation
3.2. Perturbative Temperature Solution
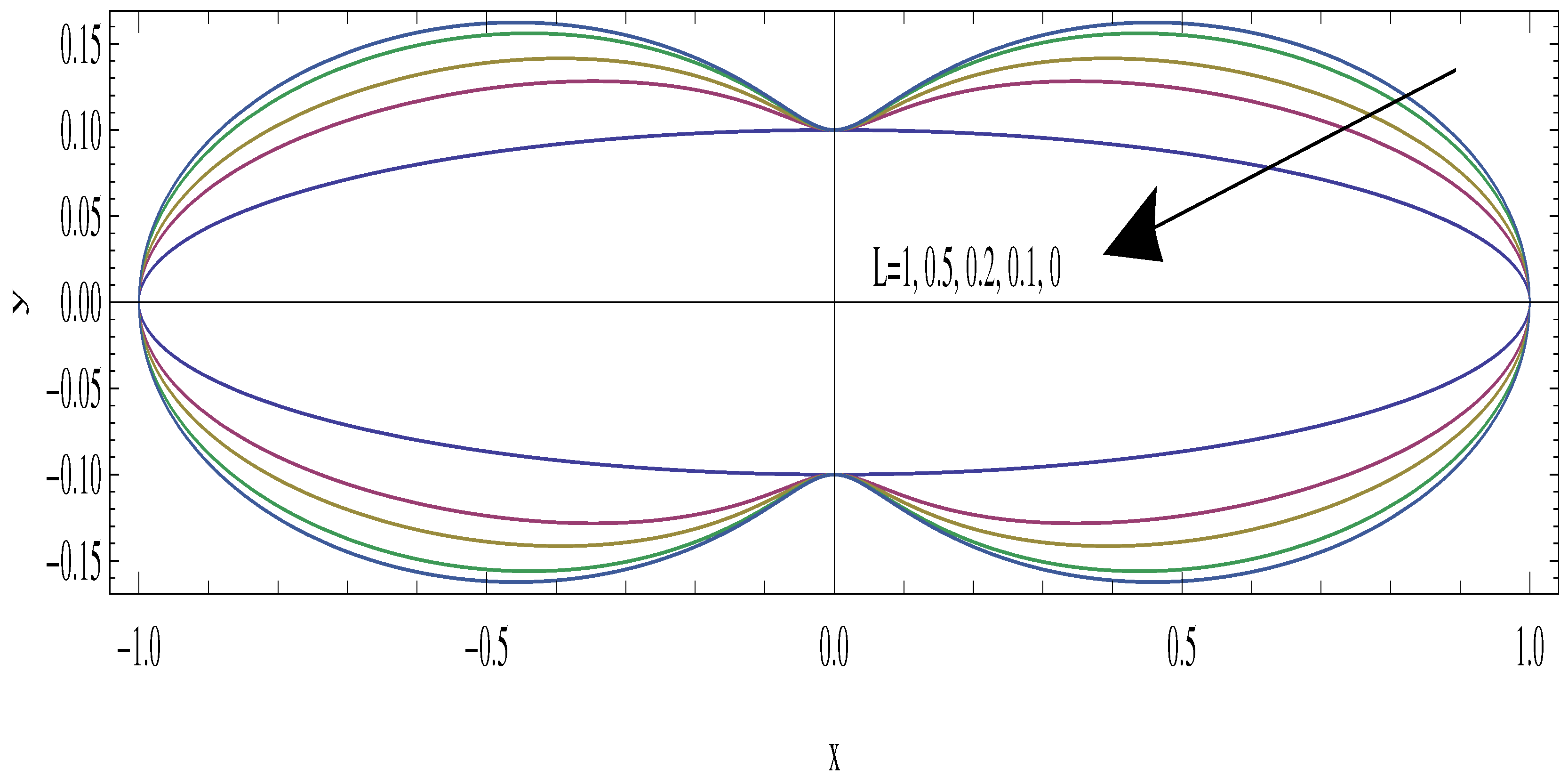
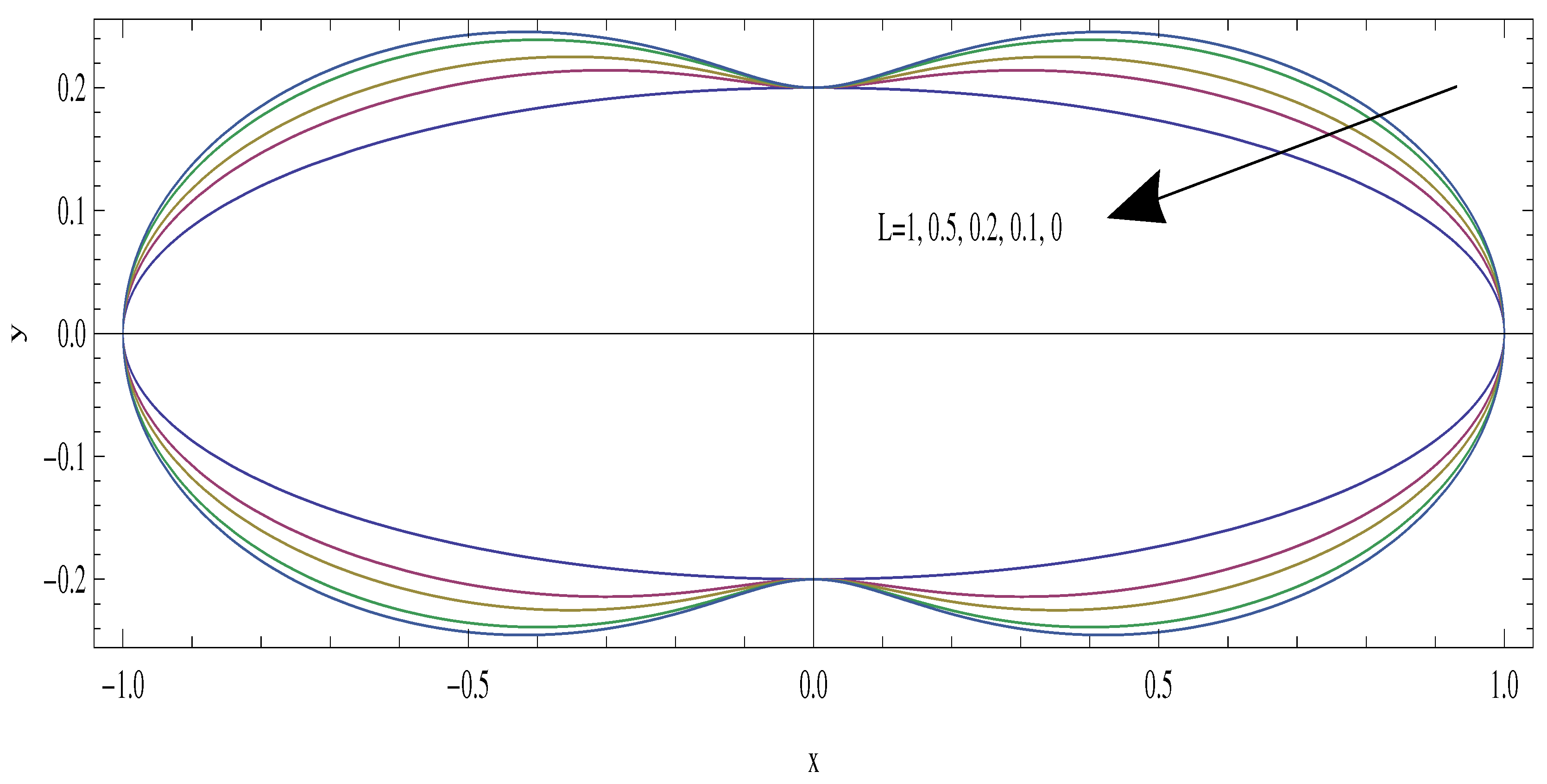
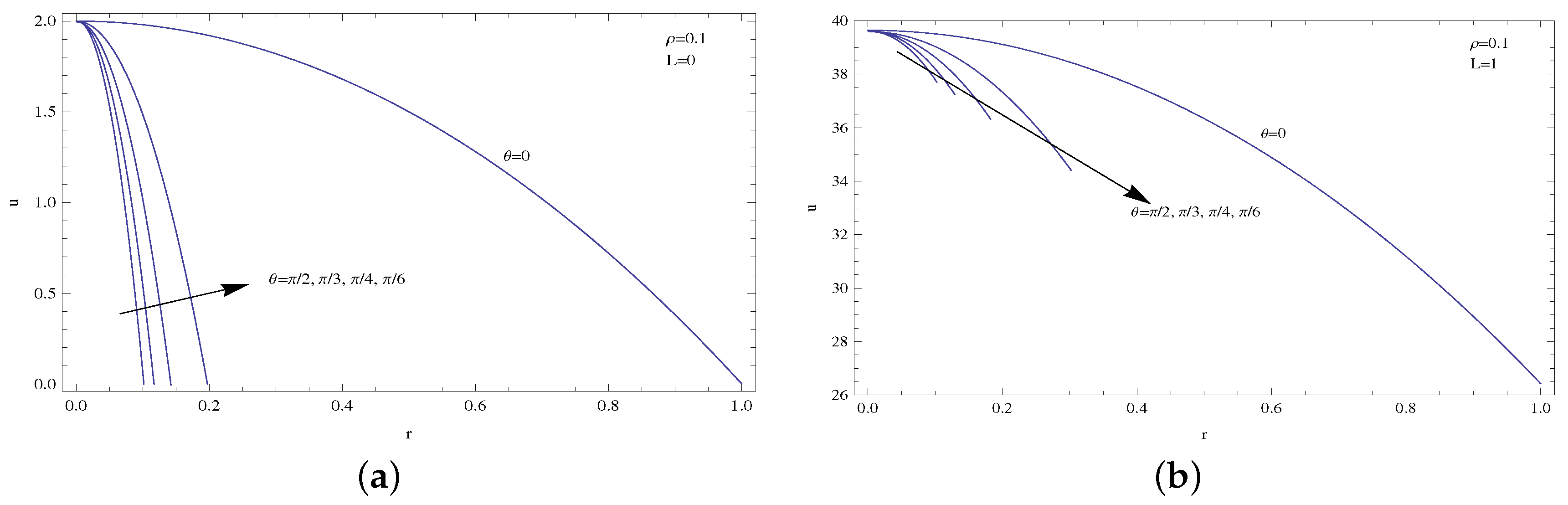
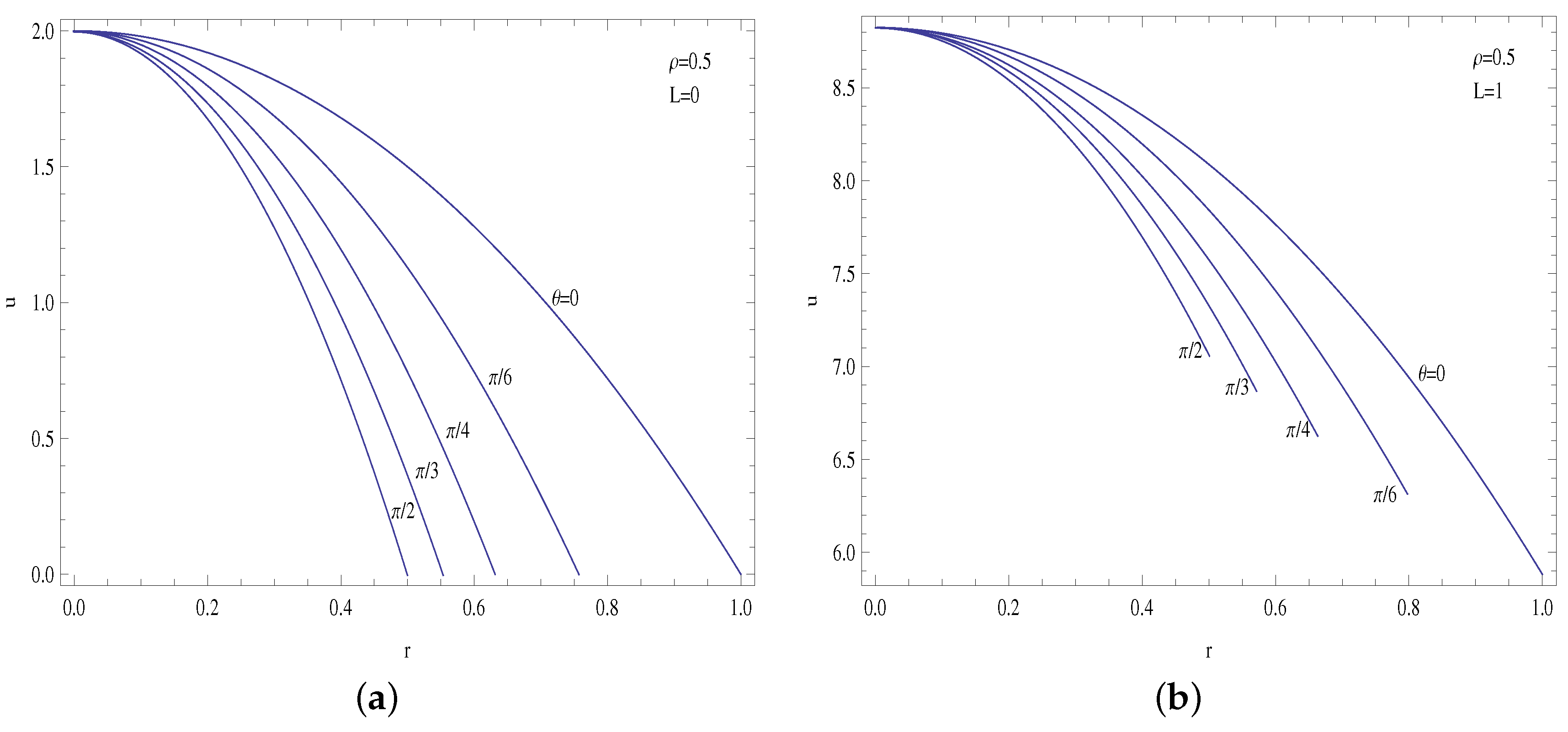
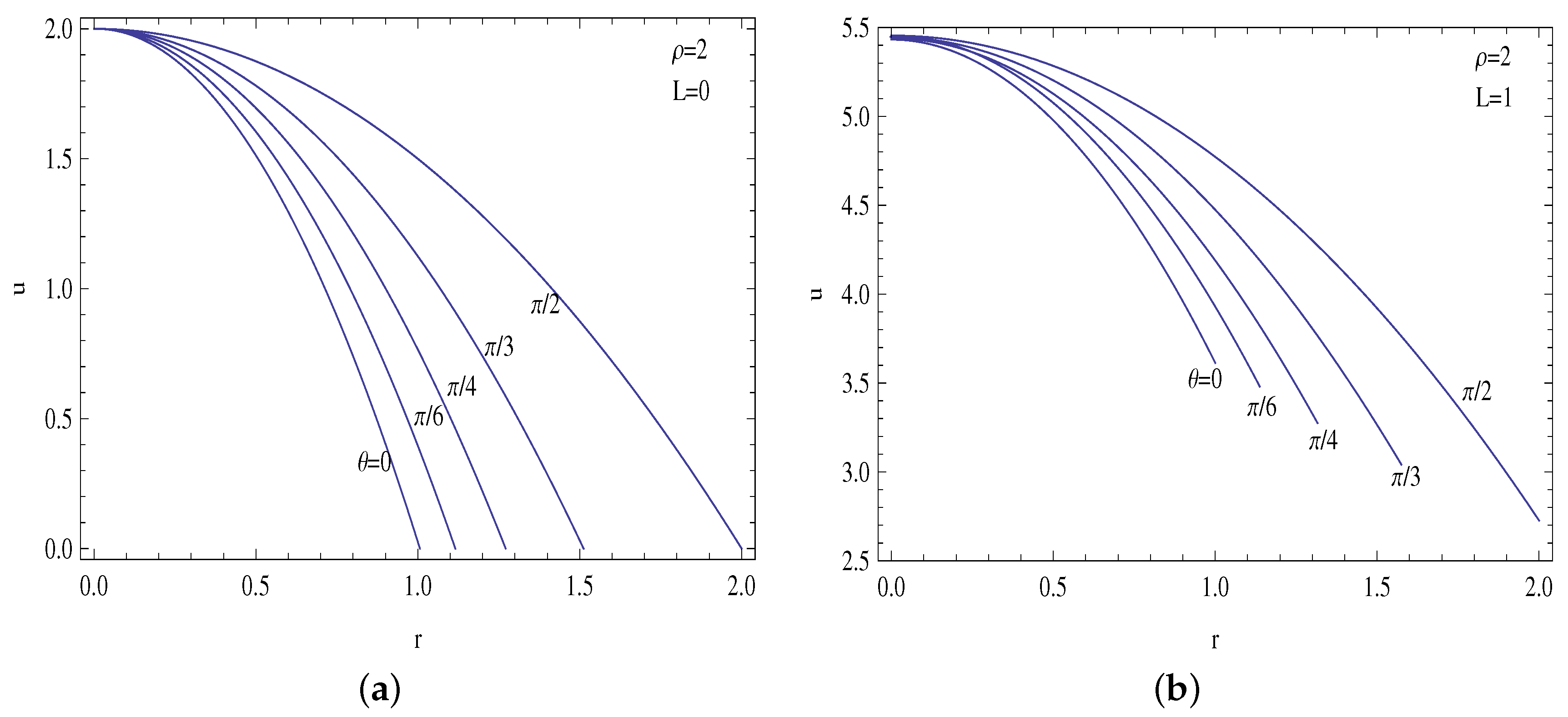
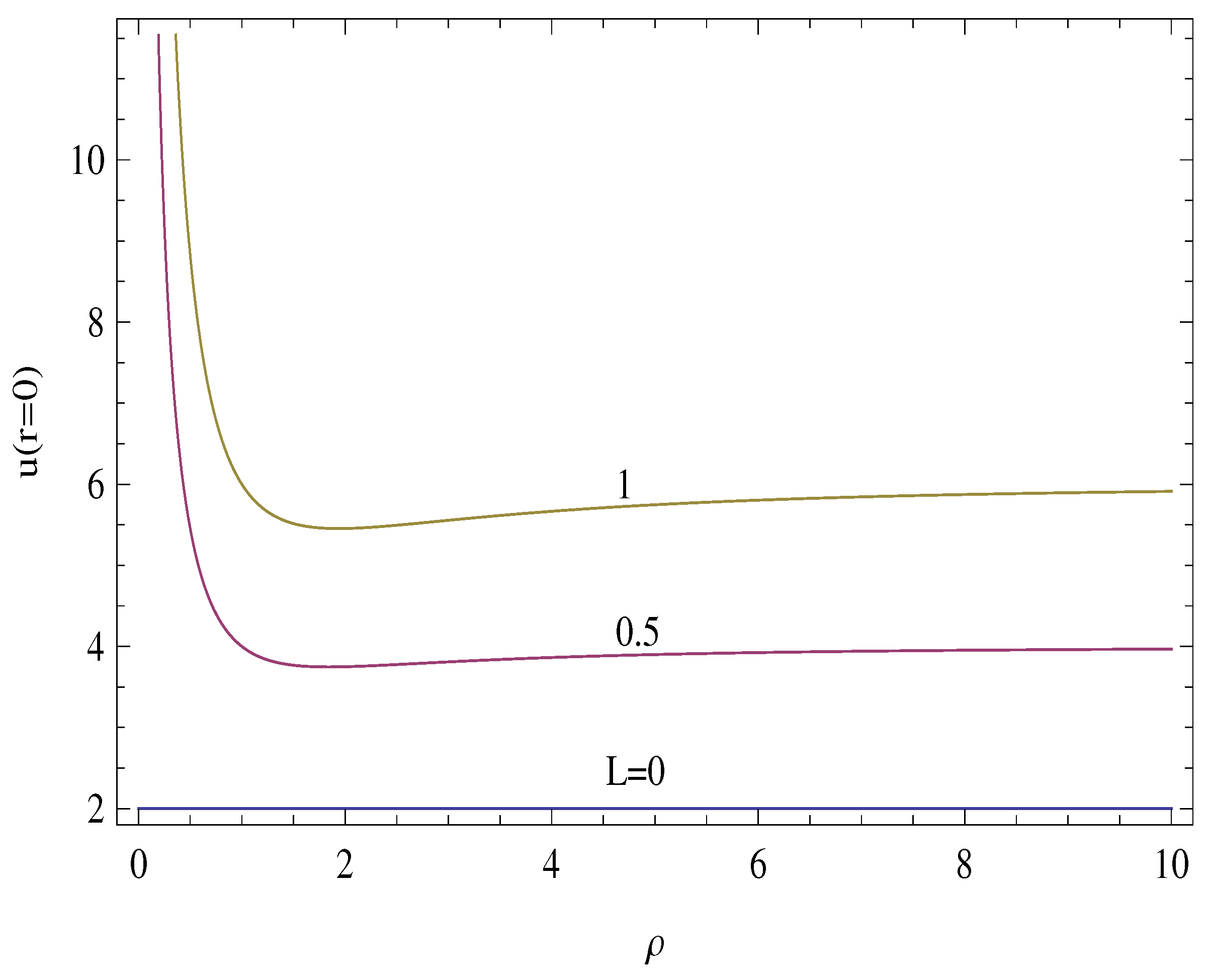
4. Results and Discussions
5. Conclusions
- For small aspect ratios, the slip increases the volumetric flow rate continuously and it decreases the skin friction factor, leading to a reduction in the Poiseuille number.
- For large aspect ratios, the Poiseuille number increases with slip.
- For aspect ratios less than unity, the slip velocity becomes larger on the minor axis, with a maximum on the major axis for larger aspect ratios.
- The total shear stress helps the surface to achieve a lower drag force under the influence of the slip mechanism.
- In the presence of a stronger slip, the maximum/minimum shear is off the minor axis.
- The centerline temperature is reduced by the presence of slip, which results in lower heat transfer rates compared to no slip profiles.
Author Contributions
Funding
Conflicts of Interest
References
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Harley, J.; Huang, Y.; Bau, H.; Zemel, J.N. Gas flows in microchannels. J. Fluid Mech. 1995, 284, 257–274. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Beskok, A.; Aluru, N. Microflows and Nanoflows: Fundamentals and Simulation; Springer: New York, NY, USA, 2005. [Google Scholar]
- Lienhard, J.H. A Heat Transfer Textbook, 3rd ed.; Phlogiston Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Kakac, S.; Yener, Y.; Pramuanjaroenkij, A. Convective Heat Transfer, 3rd ed.; CRC Press, Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Higgins, T.J. A comprehensive review of Saint-Venant’s torsion problem. Am. J. Phys. 1942, 10, 248–259. [Google Scholar] [CrossRef]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Zhang, H.; Ebadian, M.; Campo, A. An analytical/numerical solution of convective heat transfer in the thermal entrance region of irregular ducts. Int. Heat Mass Transf. 1991, 18, 273–291. [Google Scholar] [CrossRef]
- Sakalis, V.; Hatzikonstantinou, P.; Kafousias, N. Thermally developing flow in elliptic ducts with axially variable wall temperature distribution. Int. J. Heat Mass Transfer. 2002, 45, 25–35. [Google Scholar] [CrossRef]
- Tunc, G.; Bayazitoglu, Y. Heat transfer in rectangular microchannels. Int. J. Heat Mass Transfer. 2002, 45, 765–773. [Google Scholar] [CrossRef]
- Duan, Z.; Muzychka, Y.S. Slip flow in elliptic microchannels. Int. J. Therm. Sci. 2007, 46, 1104–1111. [Google Scholar] [CrossRef]
- Lekner, J. Viscous flow through pipes of various cross-sections. Eur. J. Phys. 2007, 28, 521–527. [Google Scholar] [CrossRef]
- Muzychka, Y.S.; Yovanovich, M.M. Pressure drop in laminar developing flow in noncircular ducts: A scaling and modeling approach. J. Fluids Eng. 2009, 131, 111105. [Google Scholar] [CrossRef]
- Akbari, M.; Sinton, D.; Bahrami, M. Viscous flow in variable cross-section microchannels of arbitrary shapes. J. Heat Mass Transf. 2011, 54, 3970–3978. [Google Scholar] [CrossRef]
- Shahmardan, M.M.; Norouzi, M.; Kayhani, M.H.; Delouei, A.A. An exact analytical solution for convective heat transfer in rectangular ducts. J. Zhejiang Univ. Sci. A 2012, 13, 768–781. [Google Scholar] [CrossRef]
- Shahmardan, M.; Sedaghat, M.; Norouzi, M. An analytical solution for fully developed forced convection in triangular ducts. Heat Transf. Res. 2015, 44, 489–498. [Google Scholar] [CrossRef]
- Kozlovsky, P.; Zaretsky, U.; Jaffa, A.J.; Elad, D. General tube law for collapsible thin and thick wall tubes. J. Biomech. 2014, 47, 2378–2384. [Google Scholar] [CrossRef] [PubMed]
- Tahmouresi, F.; Das, S.K. Analytical modeling of gaseous slip flow in parabolic microchannels. ASME J. Fluids Eng. 2014, 136, 071201. [Google Scholar] [CrossRef]
- Weigand, B.; Eisenschmidt, K. The extended Graetz problem with piecewise constant wall temperature for laminar and turbulent flows through a concentric annulus. Int. J. Therm. Sci. 2012, 54, 89–97. [Google Scholar] [CrossRef]
- Ryzhkov, I.I. The extended Graetz problem with specified heat flux for multicomponent fluids with Soret and Dufour effects. Int. J. Heat Mass Transf. 2013, 66, 461–471. [Google Scholar] [CrossRef]
- Cetin, B.; Zeinali, S. Analysis of heat transfer and entropy generation for a low-Peclet-number microtube flow using a second-order slip model: An extended-Graetz problem. J. Eng. Math. 2014, 89, 13–25. [Google Scholar] [CrossRef]
- Barrera, C.; Letelier, M.; Siginer, D.; Stockle, J. The Graetz problem in tubes of arbitrary cross section. Acta Mech. 2016, 227, 3239–3246. [Google Scholar] [CrossRef]
- Letelier, M.F.; Hinojosa, C.B.; Siginer, D.A. Analytical solution of the Graetz problem for non-linear viscoelastic fluids in tubes of arbitrary cross-section. Int. J. Therm. Sci. 2017, 111, 369–378. [Google Scholar] [CrossRef]
- Ali, N.; Khan, M.W.S. The Graetz problem for the Ellis fluid model. Z. Naturforsch. 2019, 74, 15–24. [Google Scholar] [CrossRef]
- Navardi, S.; Bhattacharya, S. Dispersion in channels of arbitrary cross-sections in presence of active surfaces. Chem. Eng. Sci. 2015, 130, 197–206. [Google Scholar] [CrossRef]
- Rana, S.K.; Jena, A. A BEM formulation of two dimensional steady state heat conduction in exchanger tubes of arbitrary cross sections. Int. J. Heat Mass Transf. 2017, 106, 195–211. [Google Scholar] [CrossRef]
- Gay-Balmaz, F.; Georgievskii, D.; Putkaradze, V. Stability of helical tubes conveying fluid. J. Fluids Struct. 2018, 78, 146–174. [Google Scholar] [CrossRef]
- Zhang, Z. Modeling and simulation for cross-sectional ovalization of thin-walled tubes in continuous rotary straightening process. Int. J. Mech. Sci. 2019, 153–154, 83–102. [Google Scholar] [CrossRef]
- Bilston, D.; Ruan, D.; Candido, A.; Durandet, Y. Parametric study of the cross-section shape of aluminium tubes in dynamic three-point bending. Thin-Walled Struct. 2019, 136, 315–322. [Google Scholar] [CrossRef]
- Minko, K.B.; Yankov, G.G.; Artemov, V.I.; Milman, O.O. A mathematical model of forced convection condensation of steam on smooth horizontal tubes and tube bundles in the presence of noncondensables. Int. J. Heat Mass Transfer. 2019, 140, 41–50. [Google Scholar] [CrossRef]
- Qian-bei, Y.; Liu, G.R.; Ju-bao, L.; Liu, G.Z.; Ri-zhi, D. Analyses of fluid-solid coupling dynamics of elastic tubes vibrating in cross flows. Eur. Mech. A Solids 2019, 73, 248–259. [Google Scholar] [CrossRef]
- Mirjavadi, S.S.; Forsat, M.; Badnava, S. Nonlinear modeling and dynamic analysis of bioengineering hyper-elastic tubes based on different material models. Biomech. Model. Mechanobiol. 2020, 19, 971–983. [Google Scholar] [CrossRef]
- Rostamzadeh, A.; Razavi, S.E.; Mirsajedi, S.M. Towards Multidimensional Artificially Characteristic-Based Scheme for Incompressible Thermo-Fluid Problems. Mechanika 2017, 23, 826–834. [Google Scholar] [CrossRef]
- Rahbarshahlan, S.; Esmaeilzadeh, E.; Khosroshahi, A.R.; Bakhshayesh, A.G. Numerical simulation of fluid flow and heat transfer in microchannels with patterns of hydrophobic/hydrophilic walls. Eur. Phys. J. Plus 2020, 135, 157. [Google Scholar] [CrossRef]
- Arciniegas, A.; Amaya, L.E.; Puccini, M. Mathematical model of geometry of the eye. Ann. Ophthalmol. 1985, 17, 502–505. [Google Scholar]
- Aletti, M.C.M. Mathematical Modelling and Simulations of the Hemodynamics in the Eye. Ph.D. Thesis, Universite Pierre et Marie Curie, Paris, France, 2017. [Google Scholar]
- Kays, W.; Crawford, M.; Weigand, B. Convective Heat and Mass Transfer, 4th ed.; Mc Graw-Hill Publishing Co., Ltd.: New York, NY, USA, 2005. [Google Scholar]
- Fernandez, E.D. Analysis of Newtonian Viscous Flows through Tubes of Arbitrary Varying Cross Sections. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 2017. [Google Scholar]
- Turkyilmazoglu, M. Laminar slip wall jet of Glauert type and heat transfer. Int. J. Heat Mass Transf. 2019, 134, 1153–1158. [Google Scholar] [CrossRef]
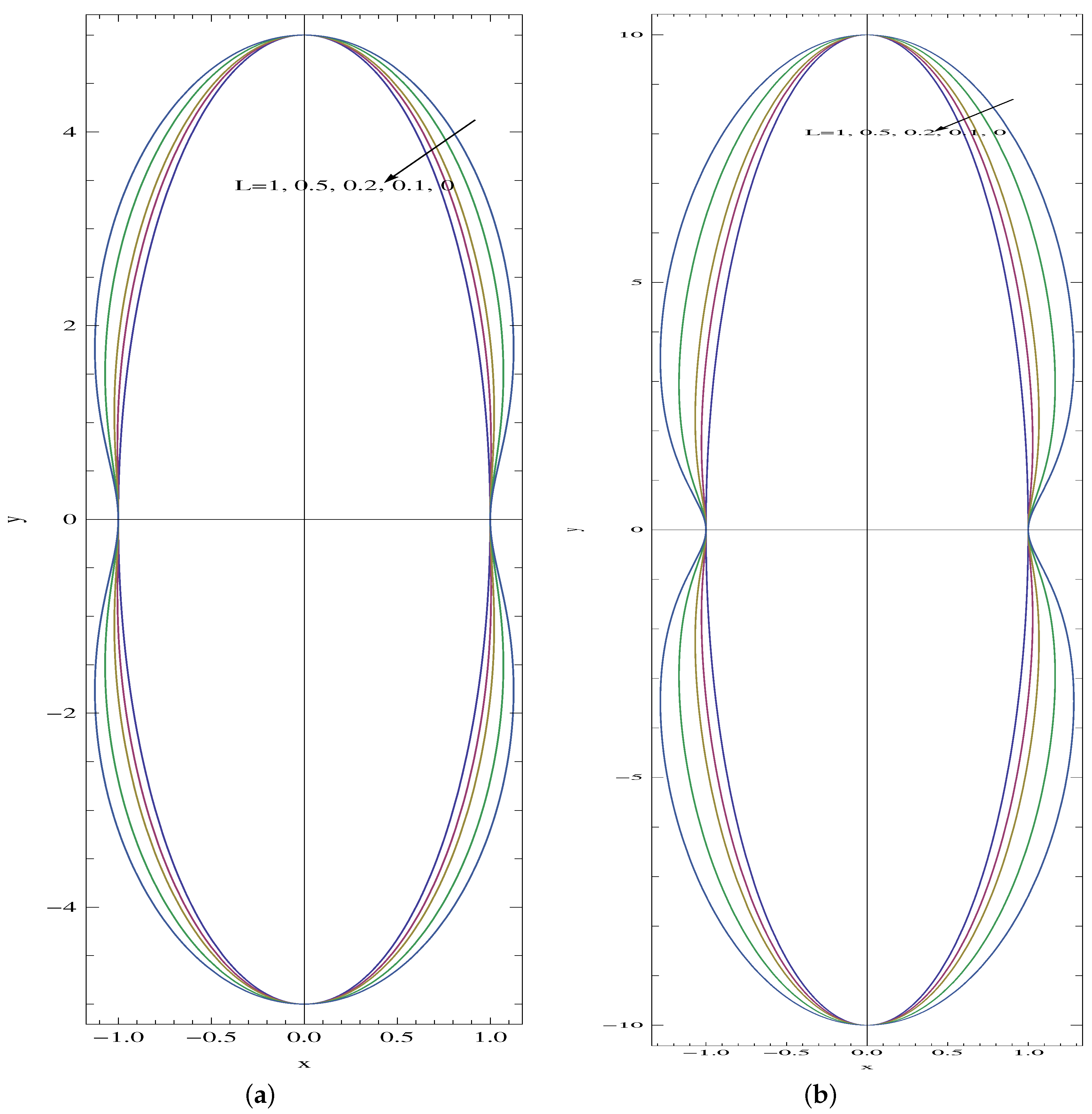
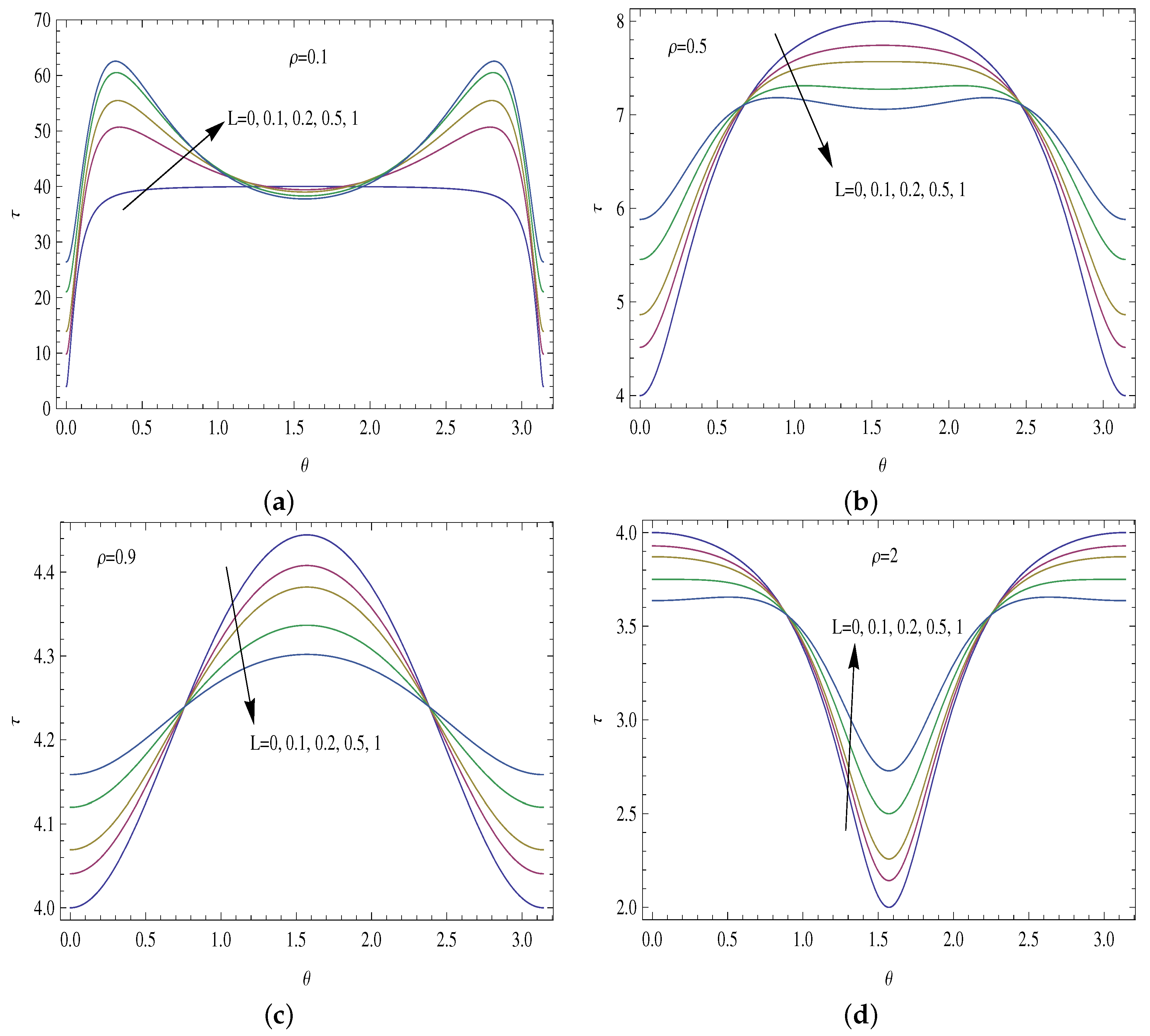

| A | P | Q | ||
|---|---|---|---|---|
| 0.31416 | 4.06397 | 0.00078 | 19.3139 | |
| 0.53260 | 4.23009 | 0.04548 | 1.48516 | |
| 1.57080 | 4.84422 | 0.07854 | 16.8233 | |
| 1.65528 | 4.94139 | 0.62797 | 2.36630 | |
| 3.14159 | 6.28319 | 0.39270 | 16.0000 | |
| 3.14159 | 6.28319 | 1.96350 | 3.20000 | |
| 15.7080 | 21.0100 | 3.77595 | 18.6024 | |
| 18.9085 | 21.5626 | 18.1058 | 6.42452 | |
| 31.4159 | 40.6397 | 7.77622 | 19.3139 | |
| 42.2733 | 41.2846 | 38.9915 | 9.09372 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turkyilmazoglu, M.; Duraihem, F.Z. Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes. Micromachines 2023, 14, 894. https://doi.org/10.3390/mi14040894
Turkyilmazoglu M, Duraihem FZ. Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes. Micromachines. 2023; 14(4):894. https://doi.org/10.3390/mi14040894
Chicago/Turabian StyleTurkyilmazoglu, Mustafa, and Faisal Z. Duraihem. 2023. "Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes" Micromachines 14, no. 4: 894. https://doi.org/10.3390/mi14040894
APA StyleTurkyilmazoglu, M., & Duraihem, F. Z. (2023). Full Solutions to Flow and Heat Transfer from Slip-Induced Microtube Shapes. Micromachines, 14(4), 894. https://doi.org/10.3390/mi14040894





