Polymer Ring–Flexure–Membrane Suspended Gate FET Gas Sensor: Design, Modelling and Simulation
Abstract
:1. Introduction
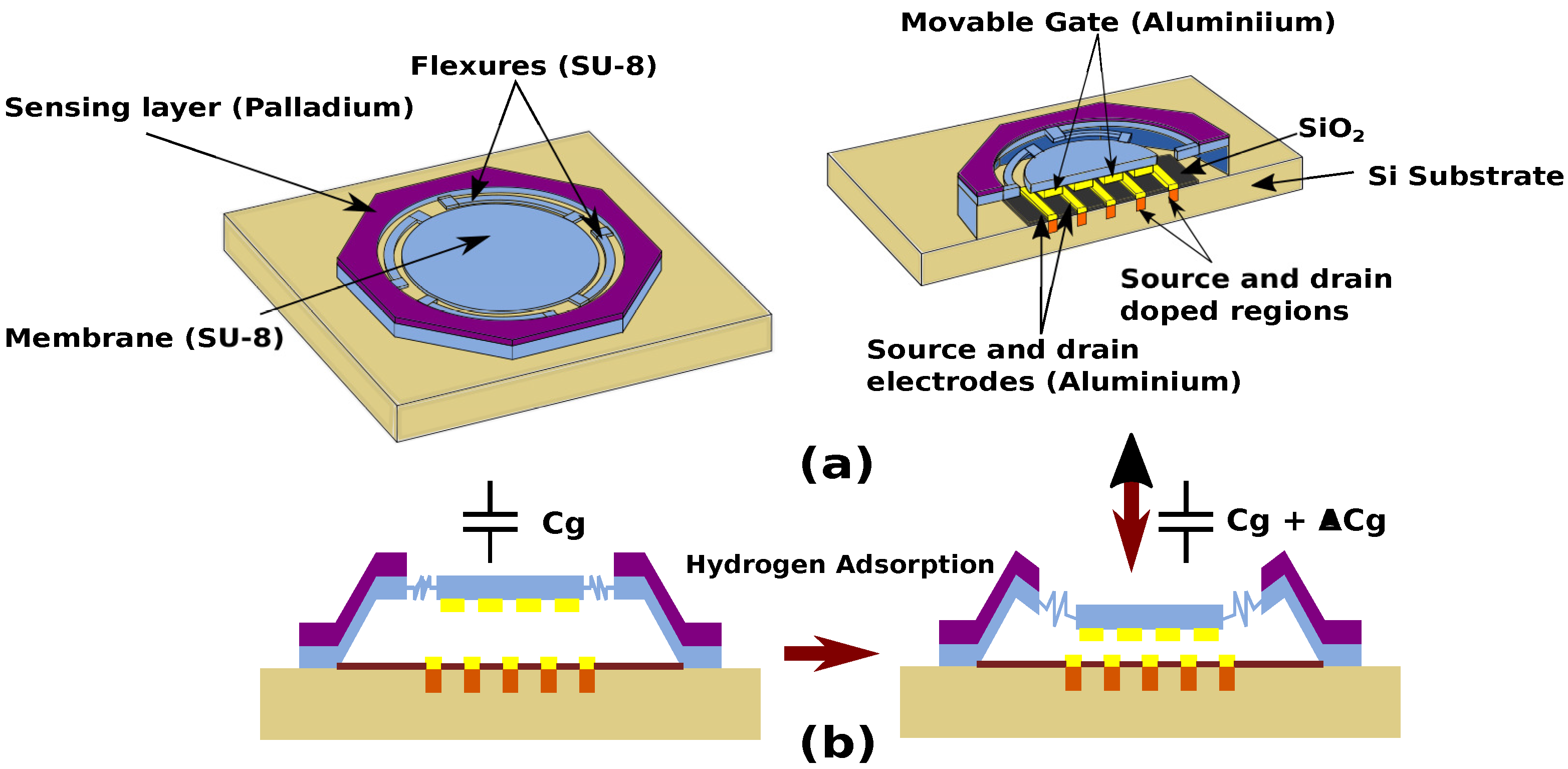
2. RFM-SGFET Sensor Design and Operation
3. Simulation and Modelling
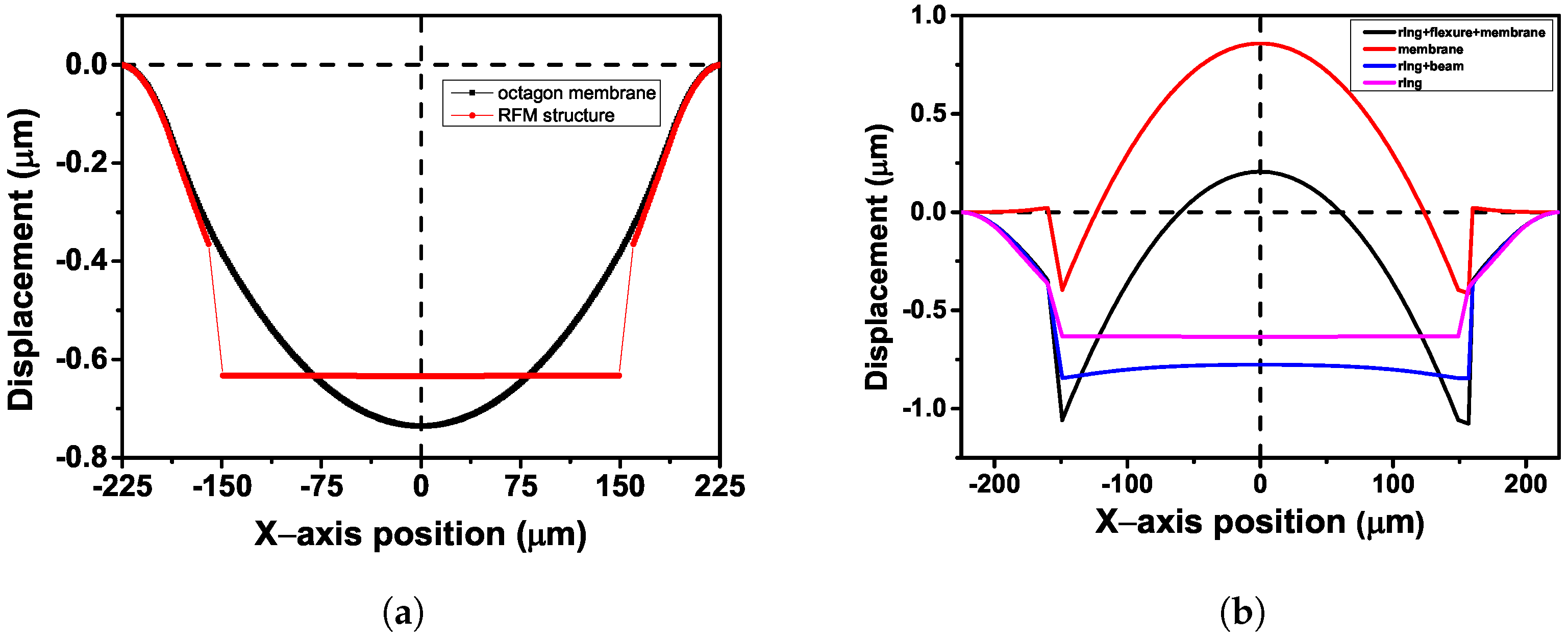
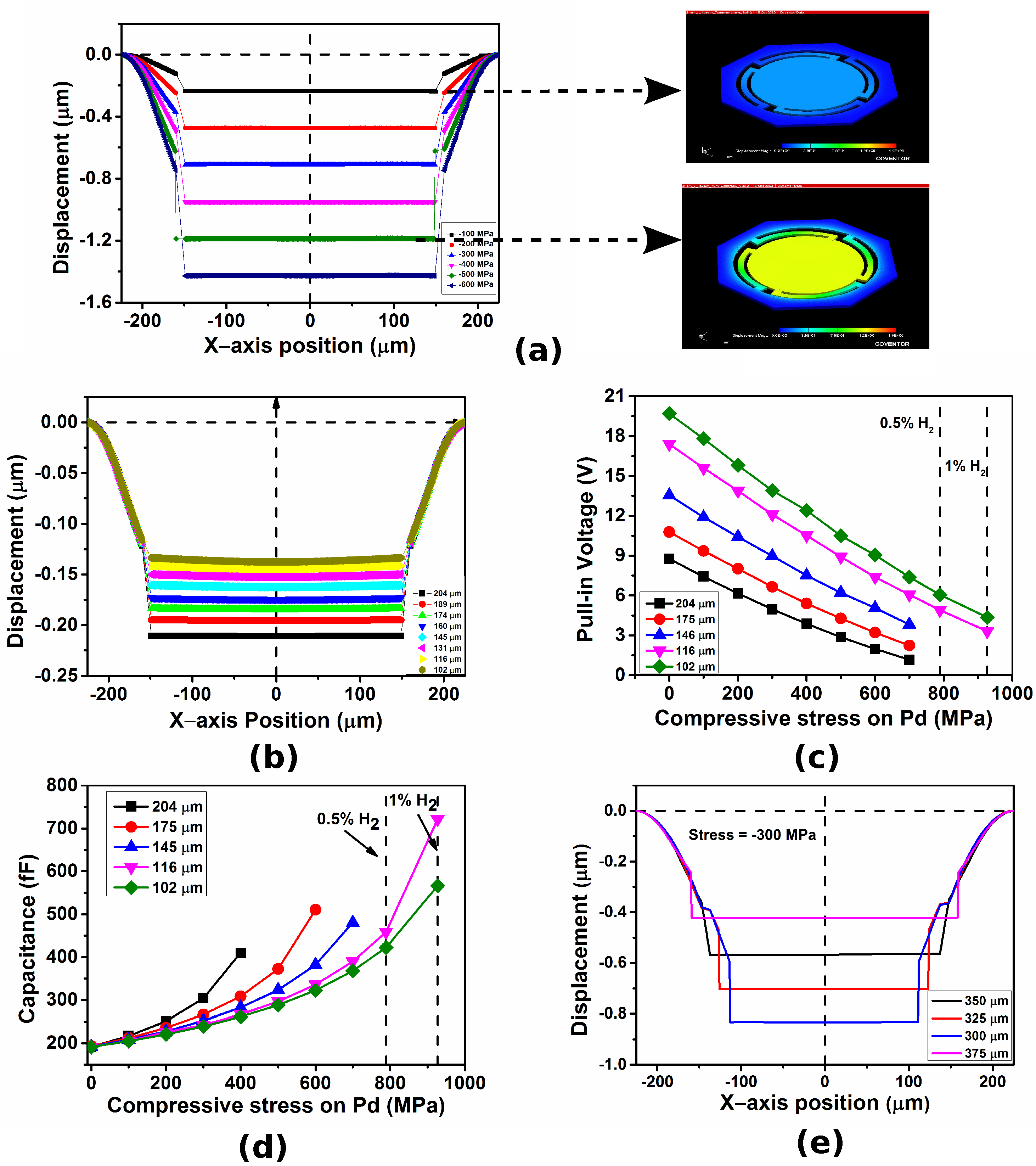
3.1. MEMS Ring–Flexure–Membrane Design, Simulation, and Electromechanical Analysis
3.2. Analytical Model of the Fingered SGFET
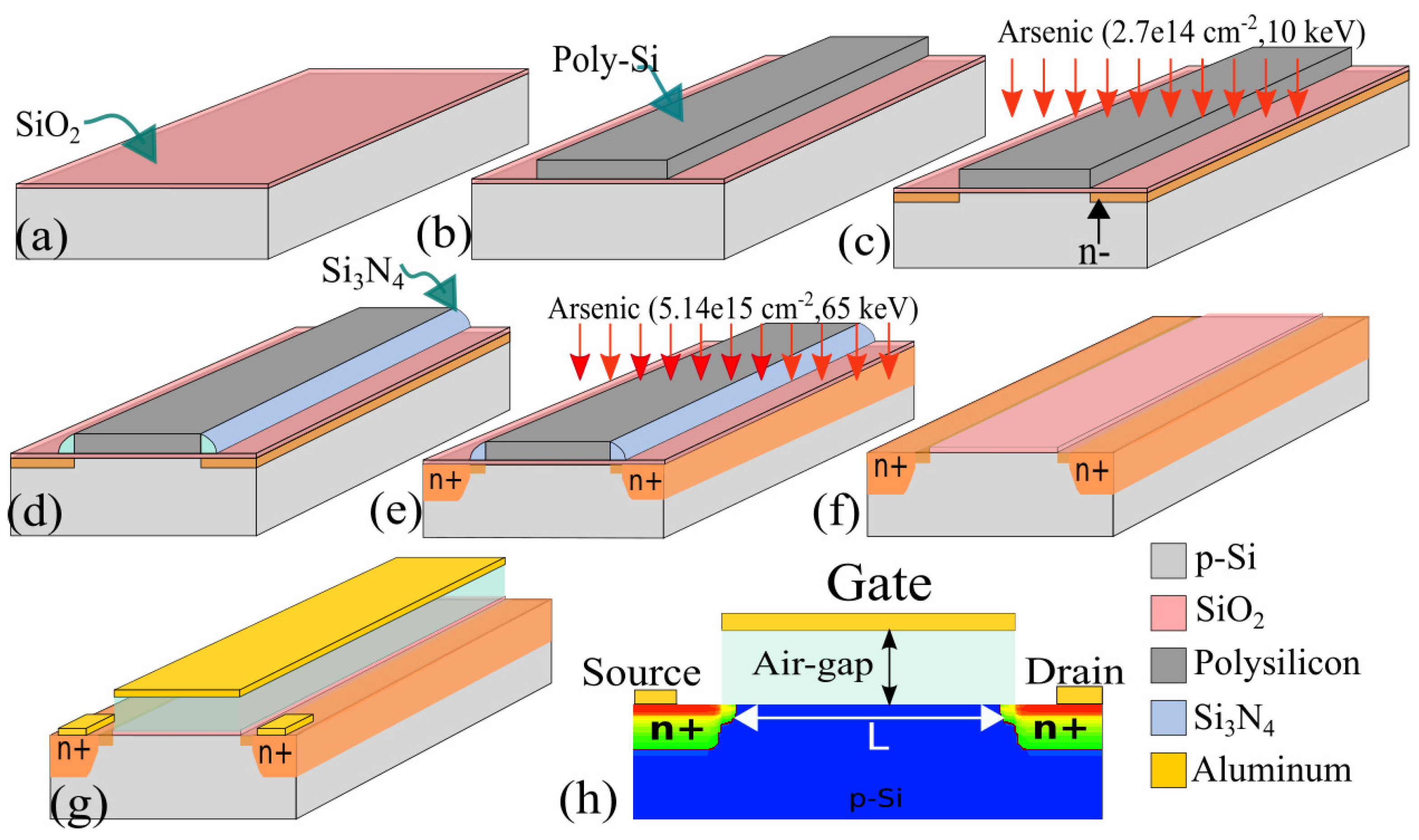
3.3. TCAD Design and Simulation of the Fingered SGFET Array
- The gate dielectric is formed by thermal oxidation;
- The 200 nm thick polysilicon is deposited and patterned to define the gate area;
- Lightly doped source and drain are obtained by ion implantation (arsenic (As), 2.7 × 1014 cm−2, 10 keV);
- Deposition and patterning of nitride spacer (Si3N4);
- Deep n+ source and drain are obtained by ion implantation (As, 5.14 × 1015 cm−2, 65 keV);
- The spacer nitride and polysilicon are removed from the substrate;
- The second part of the gate dielectric is the air gap, which, in TCAD, is defined by a user-defined material ’air gap’ with all the properties of air included in the material database;
- Aluminum (Al) metal is deposited and patterned to define gate and contact for source and drain.
3.4. RFM-SGFET Differential Amplifier
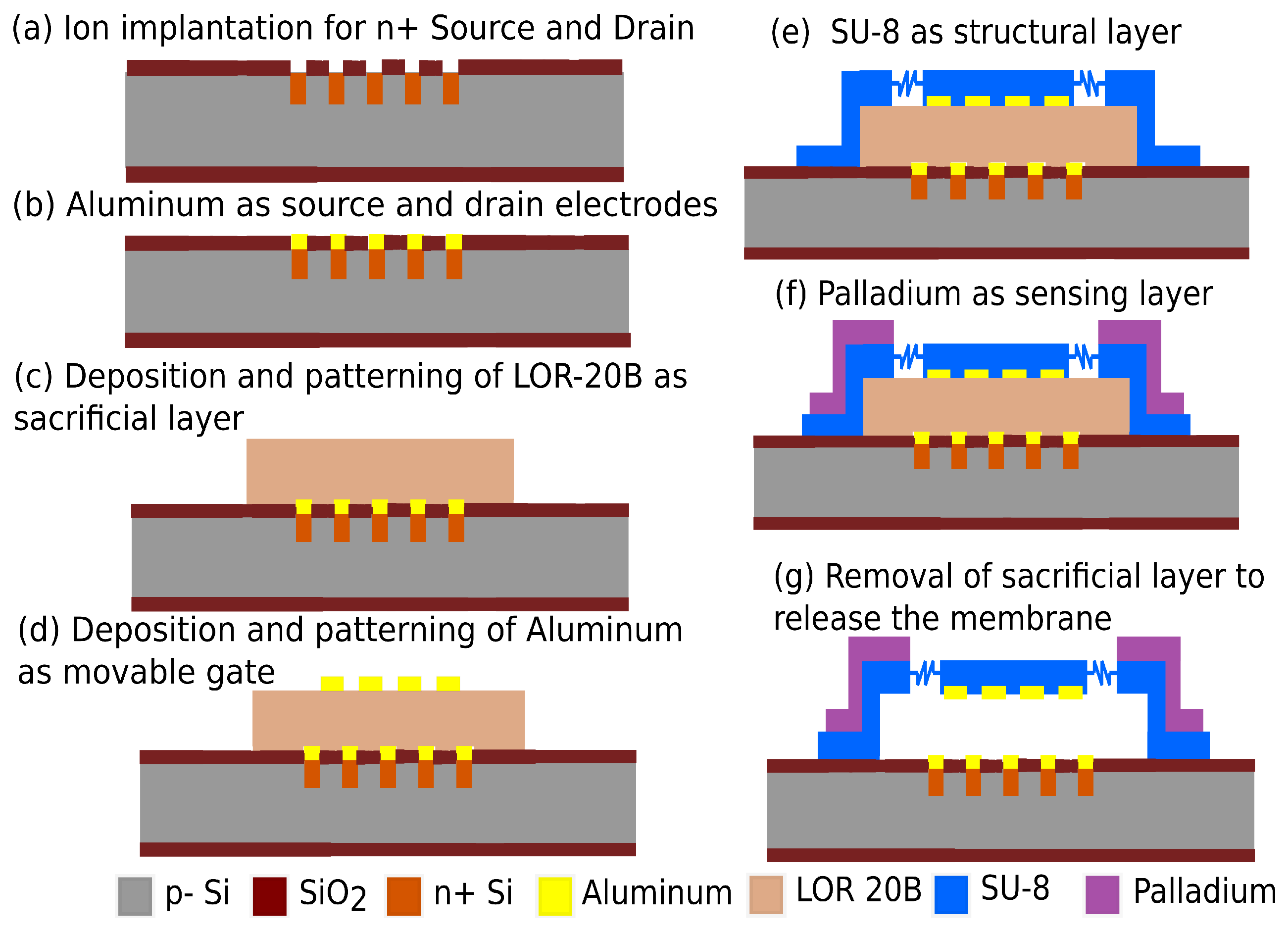
4. Fabrication Integration Plan
- The sensor fabrication process begins with the fabrication of the n-channel SGFET using a self-aligned CMOS fabrication method. The fabrication process of the fingered n-channel SGFET is similar to the fabrication process shown in Figure 5a–f.
- Aluminum is then sputtered to a thickness of 50 nm and patterned to form the source and drain electrode.
- LOR-20B of 2 m thickness is spin-coated on the substrate and patterned by wet etching. This will act as the sacrificial layer for the RFM structure.
- The suspended gate is then deposited by sputtering 250 nm of aluminum, and then it is patterned by wet etching.
- The SU-8 based RFM layer of 7 m thickness is then spin-coated and patterned by wet etching.
- The sensing layer can be deposited onto the SU-8 membrane by lift-off deposition of palladium using sputtering.
- The RFM structure is then released by the removal of the sacrificial layer by wet etching. This is followed by drying the substrate in a critical point dryer to avoid stiction.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nazemi, H.; Joseph, A.; Park, J.; Emadi, A. Advanced Micro- and Nano-Gas Sensor Technology: A Review. Sensors 2019, 19, 1285. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, J.; Chen, D.; Jin, L.; Li, Y.; Zhang, Y.; Xu, L.; Guo, Y.; Lin, F.; Wu, F. Gas Detection Microsystem With MEMS Gas Sensor and Integrated Circuit. IEEE Sens. J. 2018, 18, 6765–6773. [Google Scholar] [CrossRef]
- Shekhawat, G.; Tark, S.H.; Dravid, V.P. MOSFET-Embedded Microcantilevers for Measuring Deflection in Biomolecular Sensors. Science 2006, 311, 1592–1595. [Google Scholar] [CrossRef]
- Adams, J.D.; Parrott, G.; Bauer, C.; Sant, T.; Manning, L.; Jones, M.; Rogers, B.; McCorkle, D.; Ferrell, T.L. Nanowatt chemical vapor detection with a self-sensing, piezoelectric microcantilever array. Appl. Phys. Lett. 2003, 83, 3428–3430. [Google Scholar] [CrossRef]
- Okuyama, S.; Mitobe, Y.; Okuyama, K.; Matsushita, K. Hydrogen Gas Sensing Using a Pd-Coated Cantilever. Jpn. J. Appl. Phys. 2000, 39, 3584–3590. [Google Scholar] [CrossRef]
- Britton, C.; Jones, R.; Oden, P.; Hu, Z.; Warmack, R.; Smith, S.; Bryan, W.; Rochelle, J. Multiple-input microcantilever sensors. Ultramicroscopy 2000, 82, 17–21. [Google Scholar] [CrossRef] [PubMed]
- Lang, H.P.; Hegner, M.; Gerber, C. Cantilever array sensors. Mater. Today 2005, 8, 30–36. [Google Scholar] [CrossRef]
- Arntz, Y.; Seelig, J.D.; Lang, H.P.; Zhang, J.; Hunziker, P.; Ramseyer, J.P.; Meyer, E.; Hegner, M.; Gerber, C. Label-free protein assay based on a nanomechanical cantilever array. Nanotechnology 2002, 14, 86–90. [Google Scholar] [CrossRef]
- Ziegler, C. Cantilever-based biosensors. Anal. Bioanal. Chem. 2004, 379, 946–959. [Google Scholar] [CrossRef]
- Boisen, A.; Thaysen, J.; Jensenius, H.; Hansen, O. Environmental sensors based on micromachined cantilevers with integrated read-out. Ultramicroscopy 2000, 82, 11–16. [Google Scholar] [CrossRef]
- Ndieyira, J.W.; Watari, M.; Barrera, A.D.; Zhou, D.; Vögtli, M.; Batchelor, M.; Cooper, M.A.; Strunz, T.; Horton, M.A.; Abell, C.; et al. Nanomechanical detection of antibiotic–mucopeptide binding in a model for superbug drug resistance. Nat. Nanotechnol. 2008, 3, 691–696. [Google Scholar] [CrossRef] [PubMed]
- Voiculescu, I.R.; Zaghloul, M.E.; McGill, R.A.; Vignola, J.F. Modelling and measurements of a composite microcantilever beam for chemical sensing applications. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 1601–1608. [Google Scholar] [CrossRef]
- Dutta, P.; Senesac, L.; Lavrik, N.; Datskos, P.; Sepaniak, M. Response signatures for nanostructured, optically-probed, functionalized microcantilever sensing arrays. Sens. Lett. 2004, 2, 238–245. [Google Scholar] [CrossRef]
- Long, Z.; Storey, J.; Lewis, S.; Sepaniak, M.J. Landfill Siloxane Gas Sensing Using Differentiating, Responsive Phase Coated Microcantilever Arrays. Anal. Chem. 2009, 81, 2575–2580. [Google Scholar] [CrossRef] [PubMed]
- Senesac, L.R.; Dutta, P.; Datskos, P.G.; Sepaniak, M.J. Analyte species and concentration identification using differentially functionalized microcantilever arrays and artificial neural networks. Anal. Chim. Acta 2006, 558, 94–101. [Google Scholar] [CrossRef]
- Liu, C. Recent Developments in Polymer MEMS. Adv. Mater. 2007, 19, 3783–3790. [Google Scholar] [CrossRef]
- Long, Z.; Kou, L.; Sepaniak, M.J.; Hou, X. Recent advances in gas phase microcantilever-based sensing. Rev. Anal. Chem. 2013, 32, 135–158. [Google Scholar] [CrossRef]
- Tina, B.S.; Anjana, C.; Kumar, N.; Seena, V. Polymer/Ceramic MEMS: A Nanomechanical Sensor Platform With Low Temperature High Gauge Factor ITO for Electromechanical Transduction. J. Microelectromech. Syst. 2021, 30, 116–125. [Google Scholar] [CrossRef]
- Seena, V.; Rajorya, A.; Pant, P.; Mukherji, S.; Rao, V.R. Polymer microcantilever biochemical sensors with integrated polymer composites for electrical detection. Solid State Sci. 2009, 11, 1606–1611. [Google Scholar] [CrossRef]
- Thuau, D.; Ayela, C.; Poulin, P.; Dufour, I. Highly piezoresistive hybrid MEMS sensors. Sens.Actuators A Phys. 2014, 209, 161–168. [Google Scholar] [CrossRef]
- Loui, A.; Goericke, F.; Ratto, T.; Lee, J.; Hart, B.; King, W. The effect of piezoresistive microcantilever geometry on cantilever sensitivity during surface stress chemical sensing. Sens. Actuators A Phys. 2008, 147, 516–521. [Google Scholar] [CrossRef]
- Yoshikawa, G.; Akiyama, T.; Gautsch, S.; Vettiger, P.; Rohrer, H. Nanomechanical Membrane-type Surface Stress Sensor. Nano Lett. 2011, 11, 1044–1048. [Google Scholar] [CrossRef] [PubMed]
- Loizeau, F.; Akiyama, T.; Gautsch, S.; Vettiger, P.; Yoshikawa, G.; de Rooij, N.F. Comparing membrane- and cantilever-based surface stress sensors for reproducibility. Sens. Actuators A Phys. 2015, 228, 9–15. [Google Scholar] [CrossRef]
- Tina, B.S.; Joel, Z.; Rao, R.S.S.; Seena, V. Silicon MEMS Nanomechanical Membrane Flexure Sensor With Integrated High Gauge Factor ITO. J. Microelectromech. Syst. 2021, 30, 939–949. [Google Scholar] [CrossRef]
- Vamshi, G.P.; Tina, B.; Seena, V. Polymer Based Hybrid Membrane-Flexure Nanomechanical Piezoresistive Sensor. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Amírola, J.; Rodríguez, A.; Castañer, L.; Santos, J.; Gutiérrez, J.; Horrillo, M. Micromachined silicon microcantilevers for gas sensing applications with capacitive read-out. Sens. Actuators B Chem. 2005, 111–112, 247–253. [Google Scholar] [CrossRef]
- Walewyns, T.; Emmerechts, C.; Gérard, P.; André, N.; Francis, L.A. A highly selective MEMS transducer for hydrogen sensing based on stress modification in palladium thin films. In Proceedings of the 2015 IEEE SENSORS, Busan, Republic of Korea, 1–4 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Yamazaki, H.; Hayashi, Y.; Masunishi, K.; Ono, D.; Ikehashi, T. A review of capacitive MEMS hydrogen sensor using Pd-based metallic glass with fast response and low power consumption. Electron. Commun. Jpn. 2019, 102, 70–77. [Google Scholar] [CrossRef]
- Yamazaki, H.; Hayashi, Y.; Masunishi, K.; Ono, D.; Ikehashi, T. High sensitivity MEMS capacitive hydrogen sensor with inverted T-shaped electrode and ring-shaped palladium alloy for fast response and low power consumption. J. Micromech. Microeng. 2018, 28, 094001. [Google Scholar] [CrossRef]
- Zacharias, J.; Nikhita, K.H.; Seena, V. Novel Polymer MEMS Capacitive Hydrogen sensor with Palladium Ring on Membrane-Mass Architecture. In Proceedings of the 2020 5th IEEE International Conference on Emerging Electronics (ICEE), New Delhi, India, 26–28 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Seena, V.; Nigam, A.; Pant, P.; Mukherji, S.; Rao, V.R. “Organic CantiFET”: A Nanomechanical Polymer Cantilever Sensor With Integrated OFET. J. Microelectromech. Syst. 2012, 21, 294–301. [Google Scholar] [CrossRef]
- Martha, P.; Kadayinti, N.; Seena, V. CMOS-MEMS Accelerometer With Stepped Suspended Gate FET Array: Design & Analysis. IEEE Trans. Electron Devices 2021, 68, 5133–5141. [Google Scholar] [CrossRef]
- Martha, P.; Kadayinti, N.; Seena, V. A CMOS-MEMS Accelerometer With U-Channel Suspended Gate SOI FET. IEEE Sens. J. 2021, 21, 10465–10472. [Google Scholar] [CrossRef]
- Jang, J.; Kim, H.; Ji, S.; Kim, H.J.; Kang, M.S.; Kim, T.S.; Won, J.e.; Lee, J.H.; Cheon, J.; Kang, K.; et al. Mechanoluminescent, Air-Dielectric MoS2 Transistors as Active-Matrix Pressure Sensors for Wide Detection Ranges from Footsteps to Cellular Motions. Nano Lett. 2020, 20, 66–74. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.H.; Ji, S.; Choi, S.; Pyo, K.H.; An, B.; Park, J.; Kim, J.; Kim, J.Y.; Lee, K.S.; Kwon, S.Y.; et al. Integrated arrays of air-dielectric graphene transistors as transparent active-matrix pressure sensors for wide pressure ranges. Nat. Commun. 2017, 8, 14950. [Google Scholar] [CrossRef] [PubMed]
- Paryavi, M.; Montazeri, A.; Tekieh, T.; Sasanpour, P. Nanoscale deflection detection of a cantilever-based biosensor using MOSFET structure: A theoretical analysis. Superlattices Microstruct. 2016, 98, 116–120. [Google Scholar] [CrossRef]
- Martha, P.; Sebastian, A.; Seena, V.; Kadayinti, N. A Technique for Modeling and Simulating Transistor Based MEMS Sensors. In Proceedings of the 2021 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 22–25 March 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Martha, P.; Ganga, K.M.; Sebastian, A.; Seena, V.; Kadayinti, N. A Closed Loop In-Plane Movable Suspended Gate FET (CLIP-SGFET) Sensor with a Dynamically Reconfigurable Charge pump. IEEE Sens. J. 2022, 22, 21550–21560. [Google Scholar] [CrossRef]
- Hayashi, Y.; Yamazaki, H.; Ono, D.; Masunishi, K.; Ikehashi, T. Investigation of PdCuSi metallic glass film for hysteresis-free and fast response capacitive MEMS hydrogen sensors. Int. J. Hydrogen Energy 2018, 43, 9438–9445. [Google Scholar] [CrossRef]

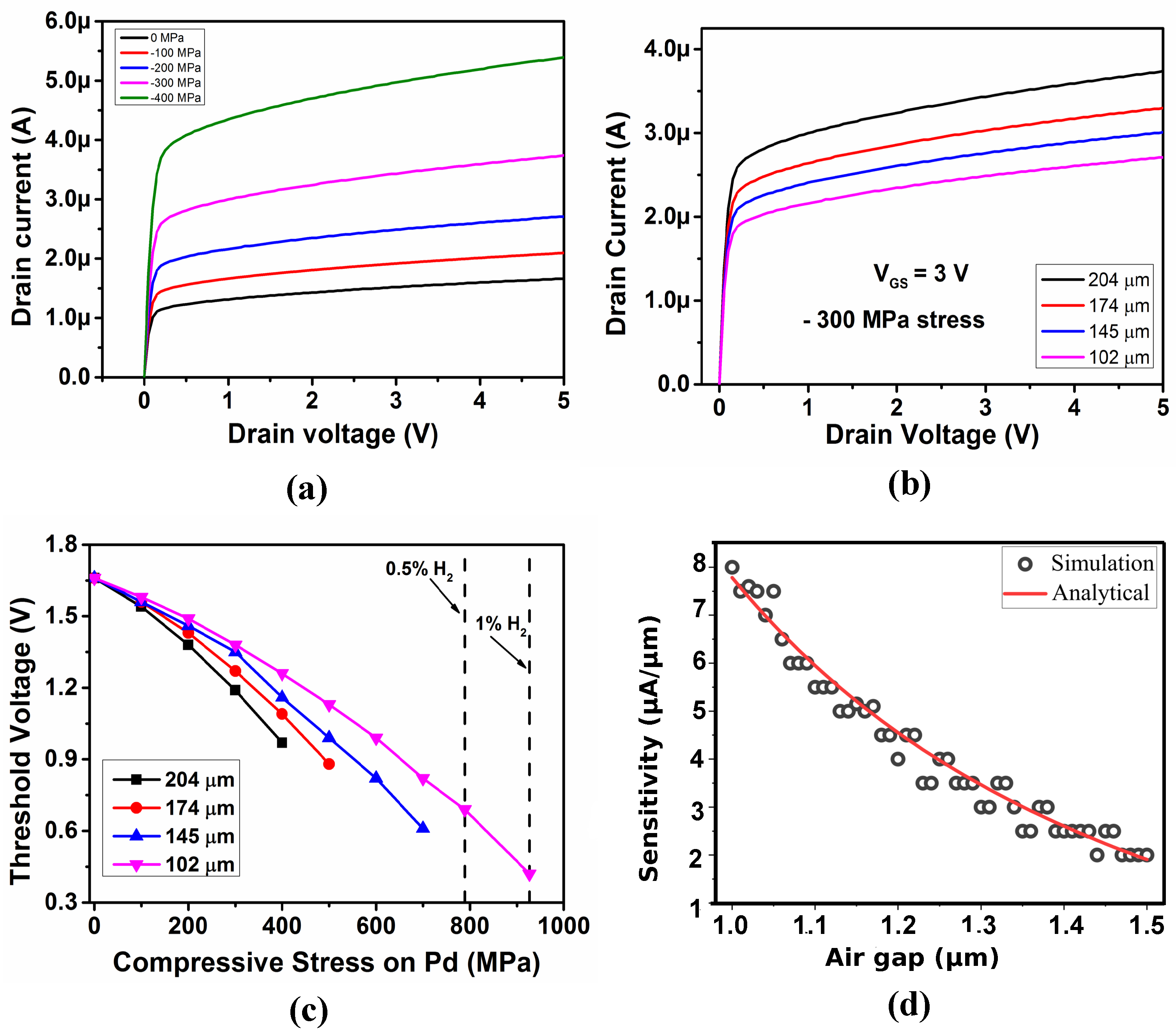

| PARAMETERS | VALUES |
|---|---|
| Substrate doping () | 1 × 10cm |
| Arsenic ion-implantation dose | 5 × 10 cm |
| Ion implantation energy | 40 keV |
| Gate oxide thickness () | 3 nm |
| Gate length (L) | 10 m |
| Gate width (W) | 210 m |
| Junction depth () | 0.35 m |
| Air gap () | 2 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zacharias, J.; Martha, P.; Seena, V. Polymer Ring–Flexure–Membrane Suspended Gate FET Gas Sensor: Design, Modelling and Simulation. Micromachines 2023, 14, 944. https://doi.org/10.3390/mi14050944
Zacharias J, Martha P, Seena V. Polymer Ring–Flexure–Membrane Suspended Gate FET Gas Sensor: Design, Modelling and Simulation. Micromachines. 2023; 14(5):944. https://doi.org/10.3390/mi14050944
Chicago/Turabian StyleZacharias, Joel, Pramod Martha, and V. Seena. 2023. "Polymer Ring–Flexure–Membrane Suspended Gate FET Gas Sensor: Design, Modelling and Simulation" Micromachines 14, no. 5: 944. https://doi.org/10.3390/mi14050944
APA StyleZacharias, J., Martha, P., & Seena, V. (2023). Polymer Ring–Flexure–Membrane Suspended Gate FET Gas Sensor: Design, Modelling and Simulation. Micromachines, 14(5), 944. https://doi.org/10.3390/mi14050944






