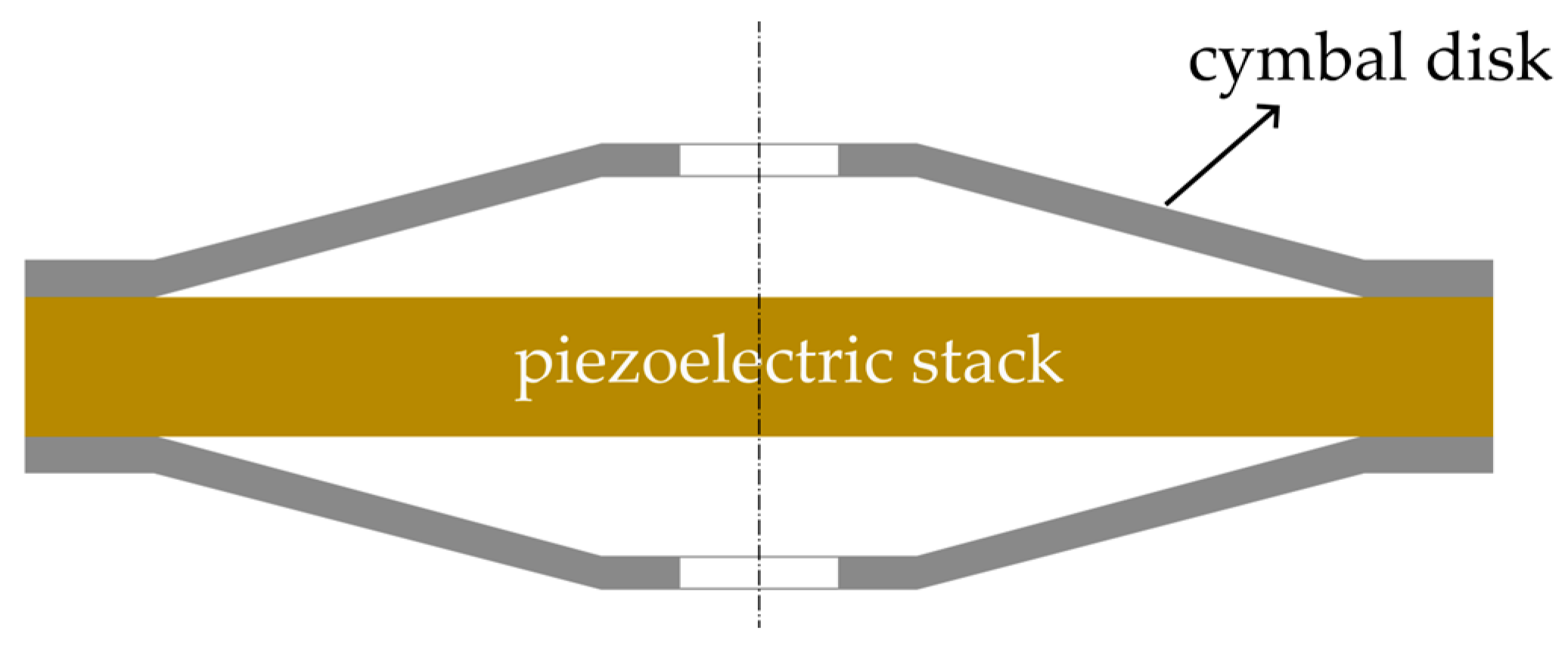
Equivalent Circuit of a Stacked Piezoelectric Cymbal Vibrator
Abstract
1. Introduction
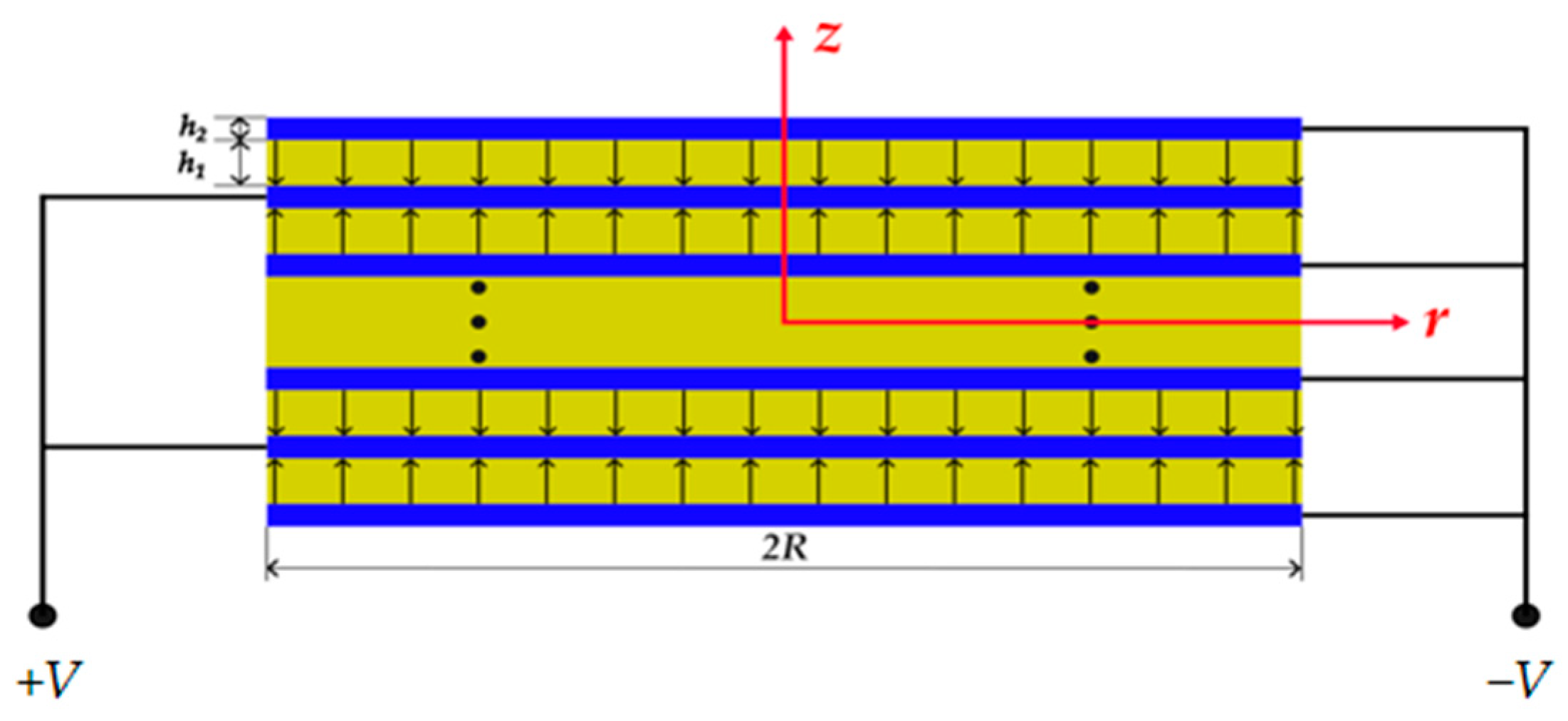
2. Equivalent Circuit and Analysis of Piezoelectric Stack
2.1. Equivalent Circuit Models of Piezoelectric Ceramic Disk and Electrode
2.1.1. Piezoelectric Ceramic Disk
2.1.2. Electrodes
2.2. Comparison between Equivalent Circuit and Finite Element Method of Piezoelectric Stack
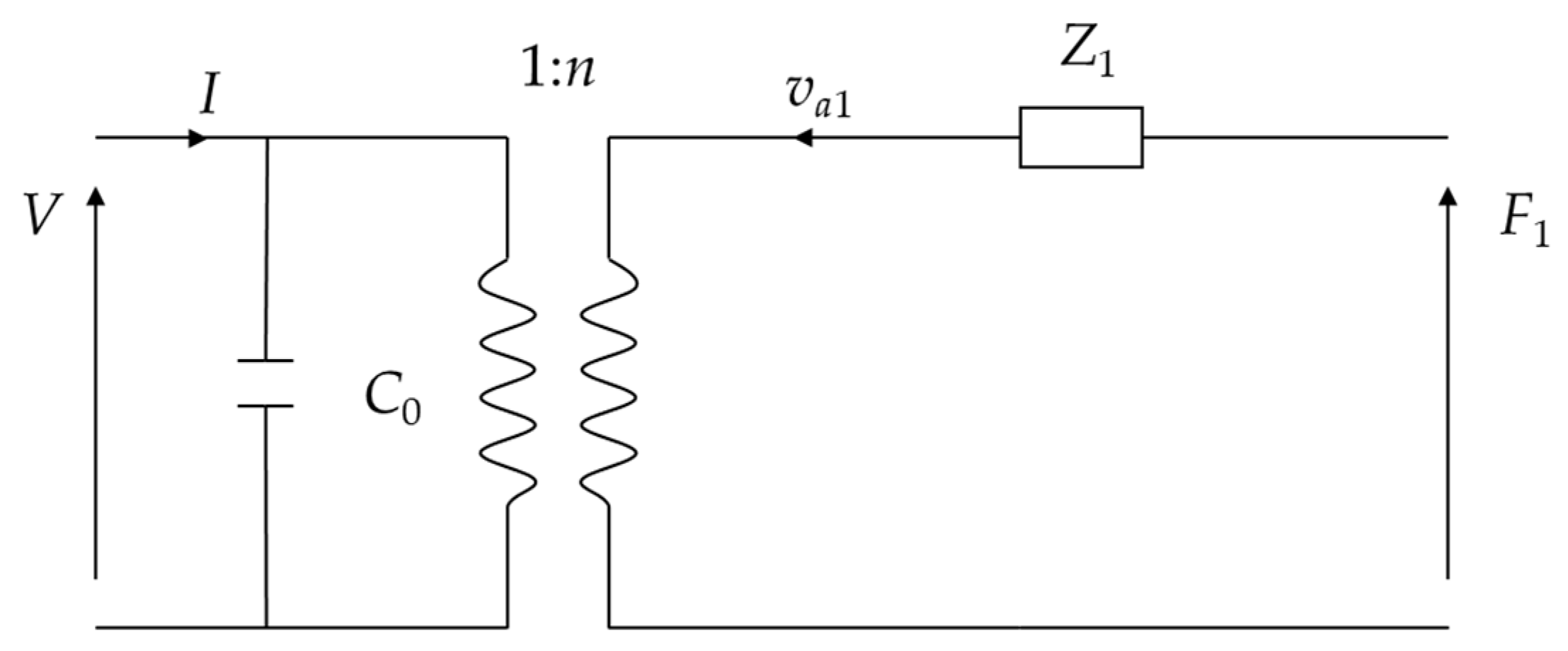
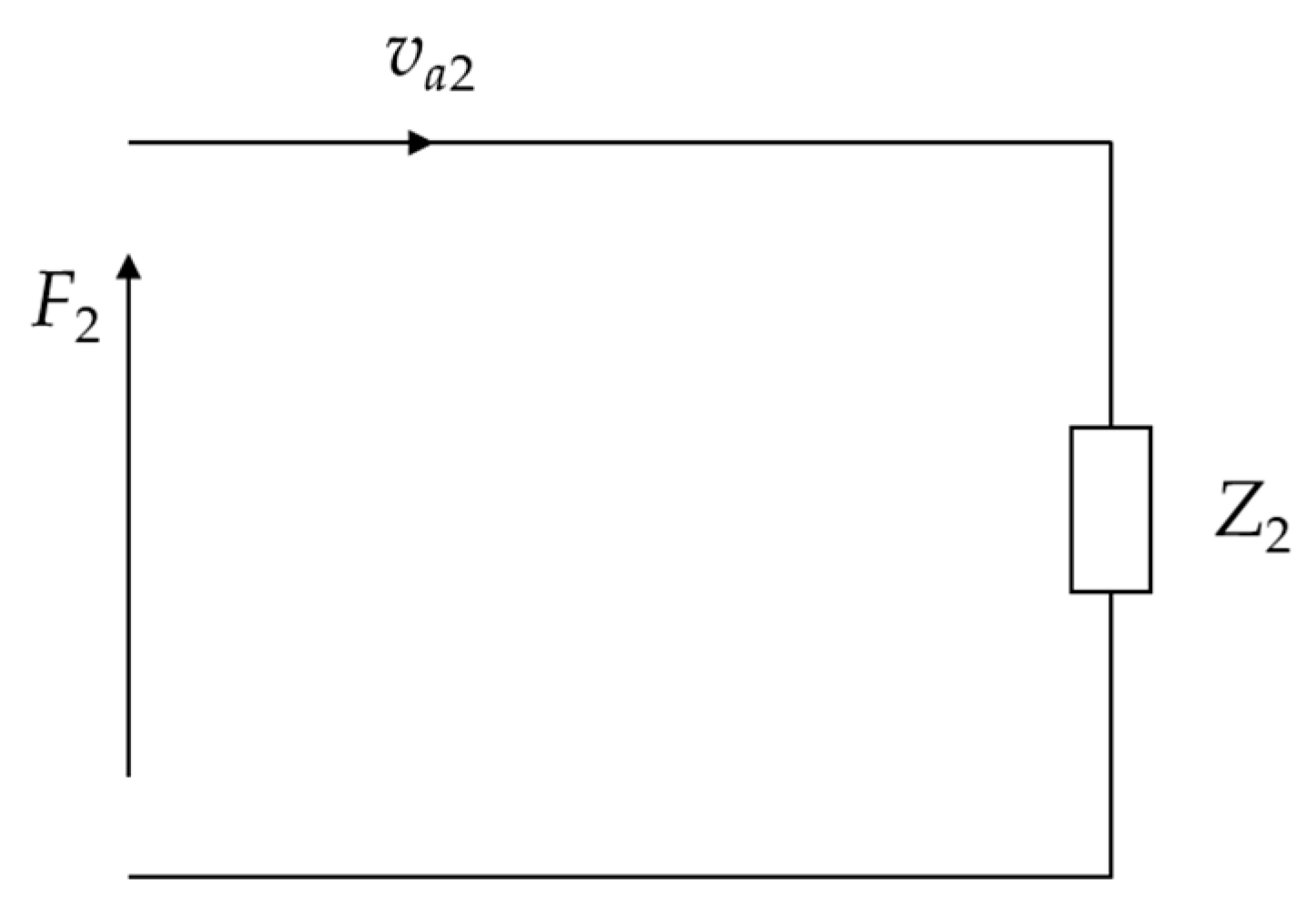
2.2.1. Equivalent Circuit of Piezoelectric Stack
2.2.2. Comparing Results of Two Methods
3. Equivalent Circuit Model of Cymbal Disk and Comparison between Two Methods
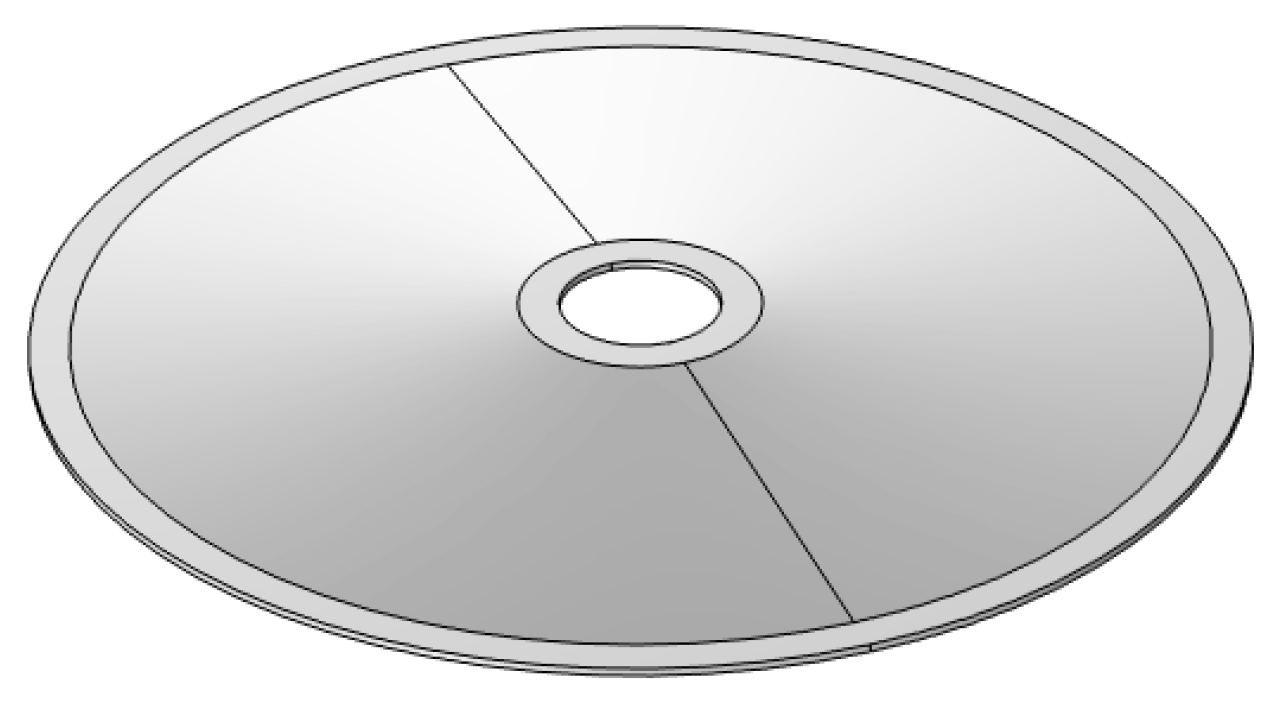
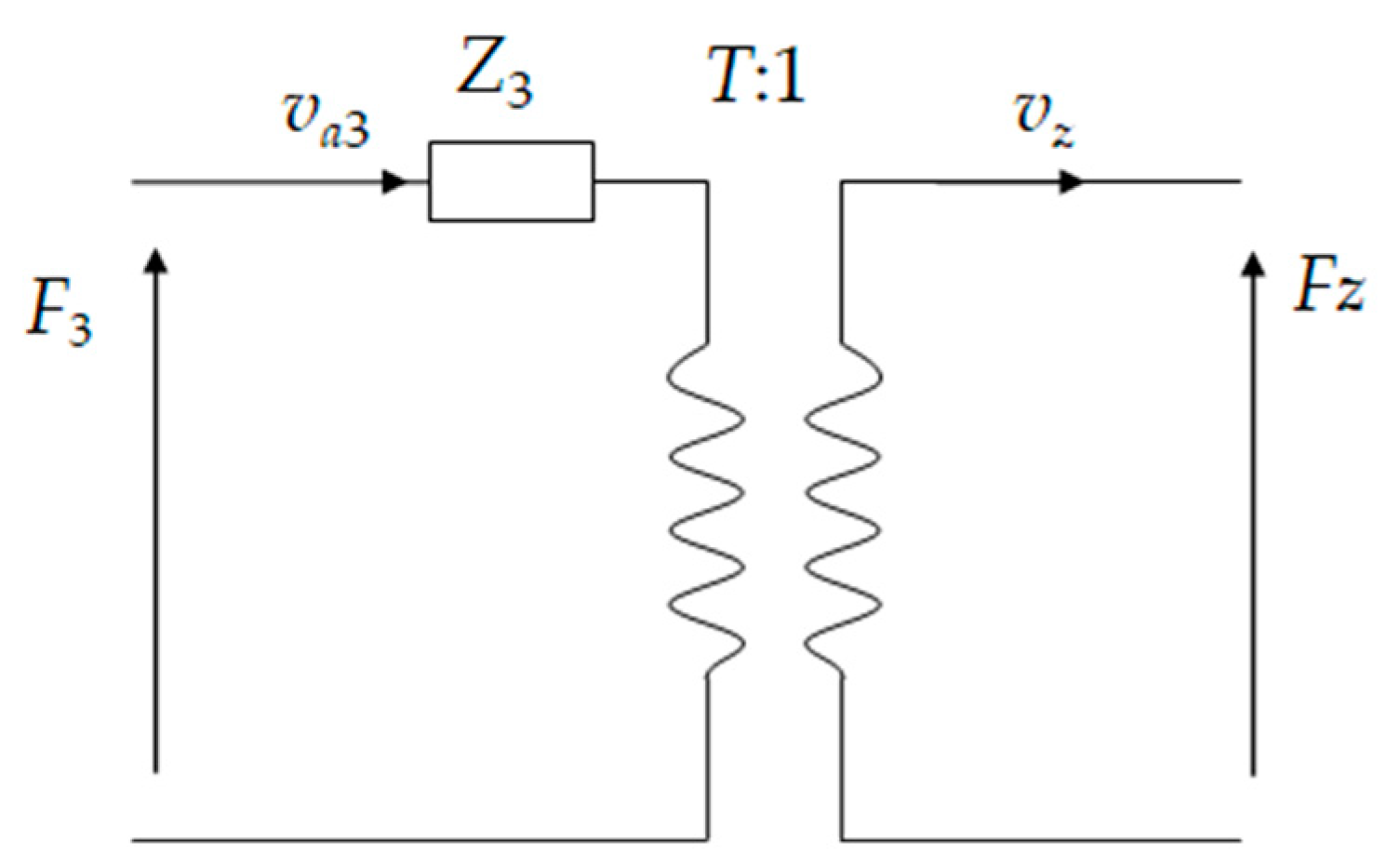
3.1. Equivalent Circuit Model of Cymbal Disk
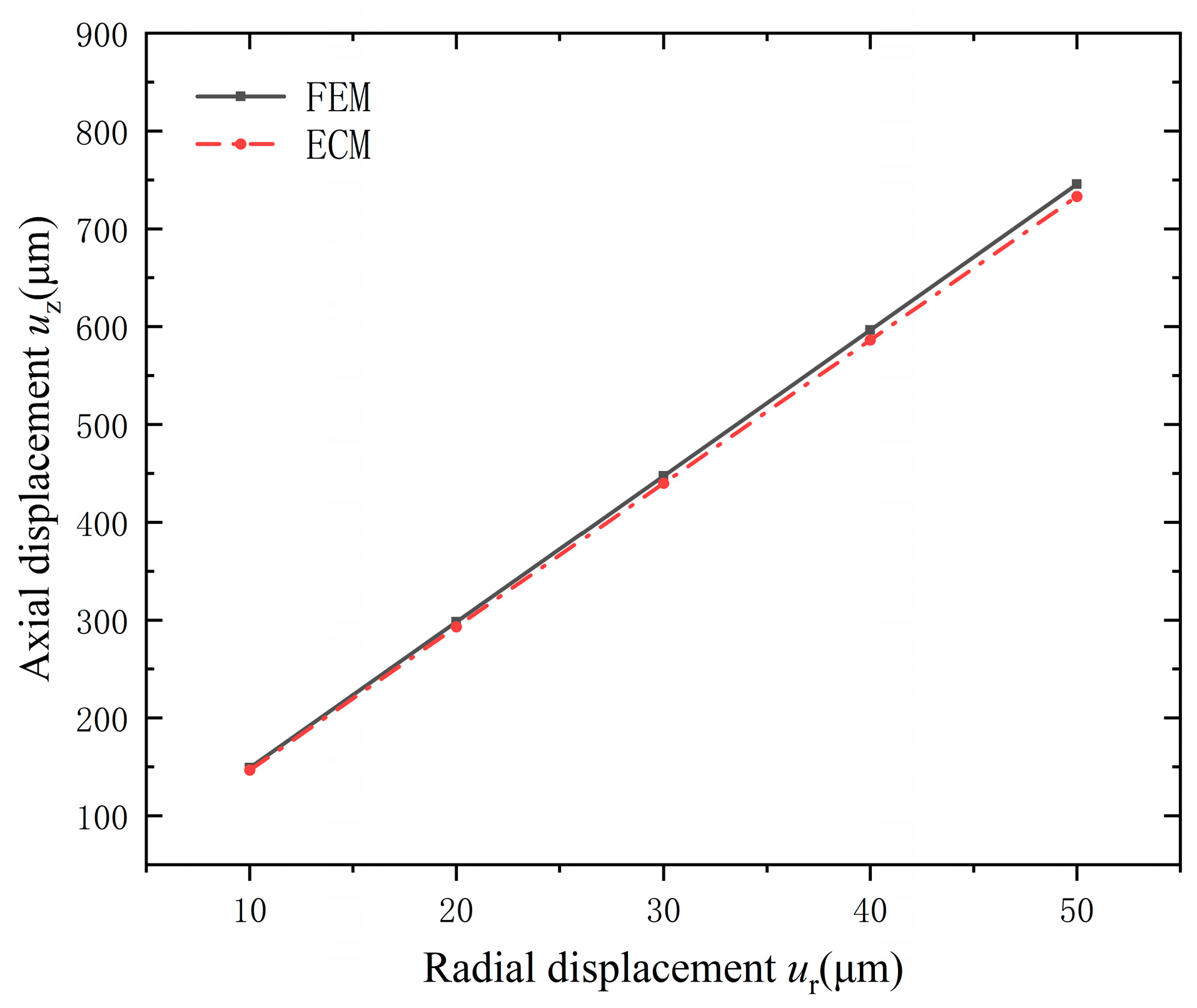
3.2. Comparison Results of Cymbal between Equivalent Circuit and Finite Element Methods
4. Overall Analysis of Stacked Cymbal Vibrator
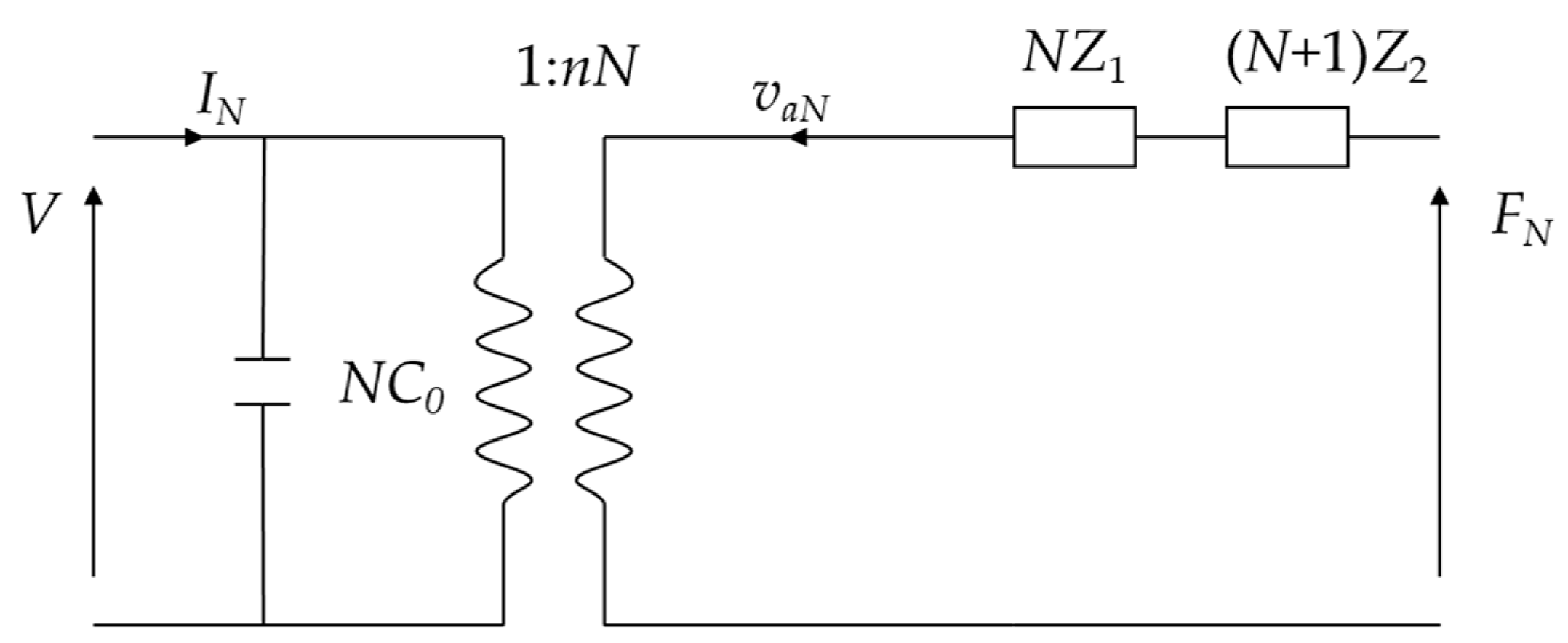
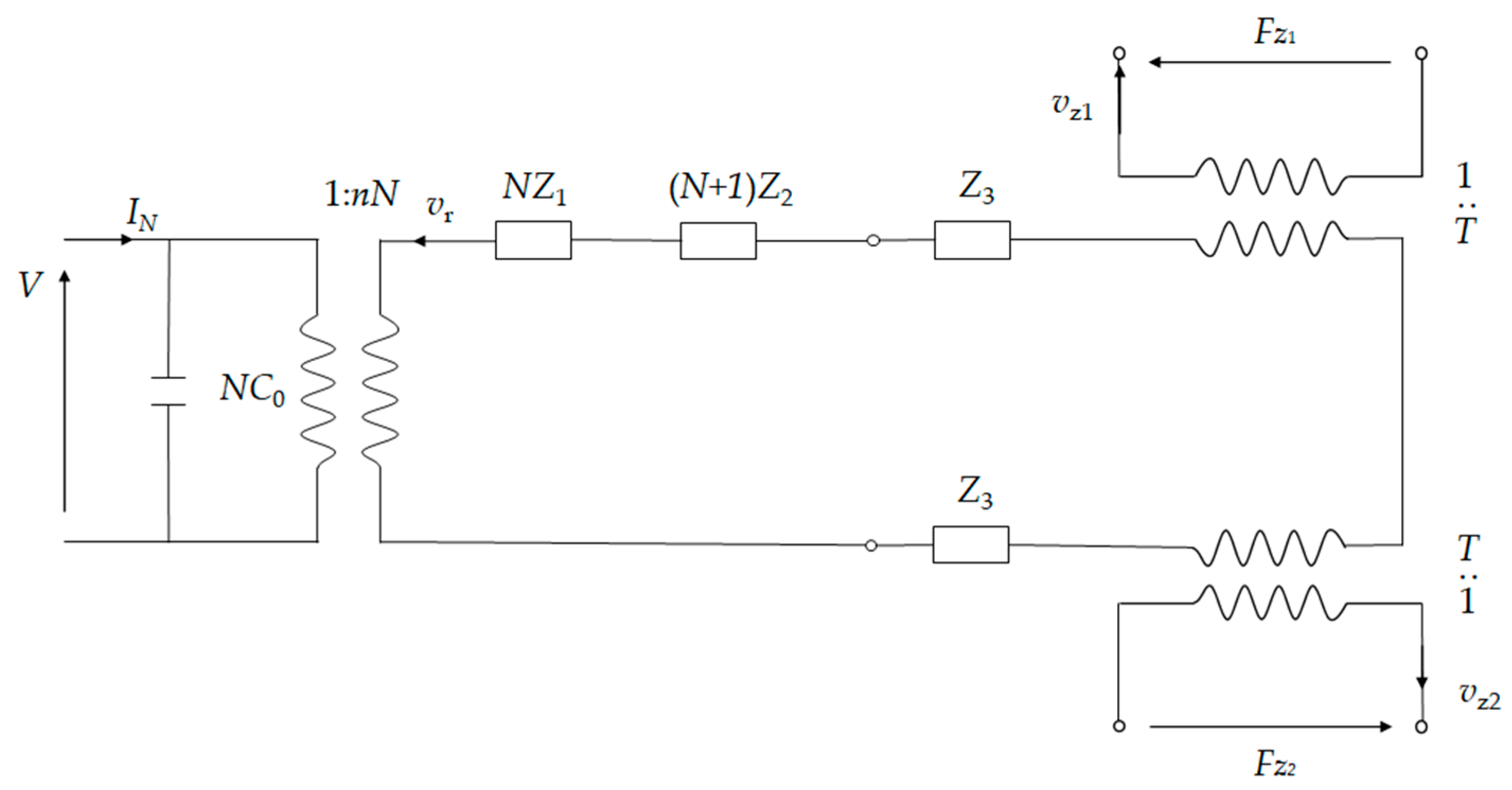
4.1. Equivalent Circuit Model of Stacked Cymbal Vibrator
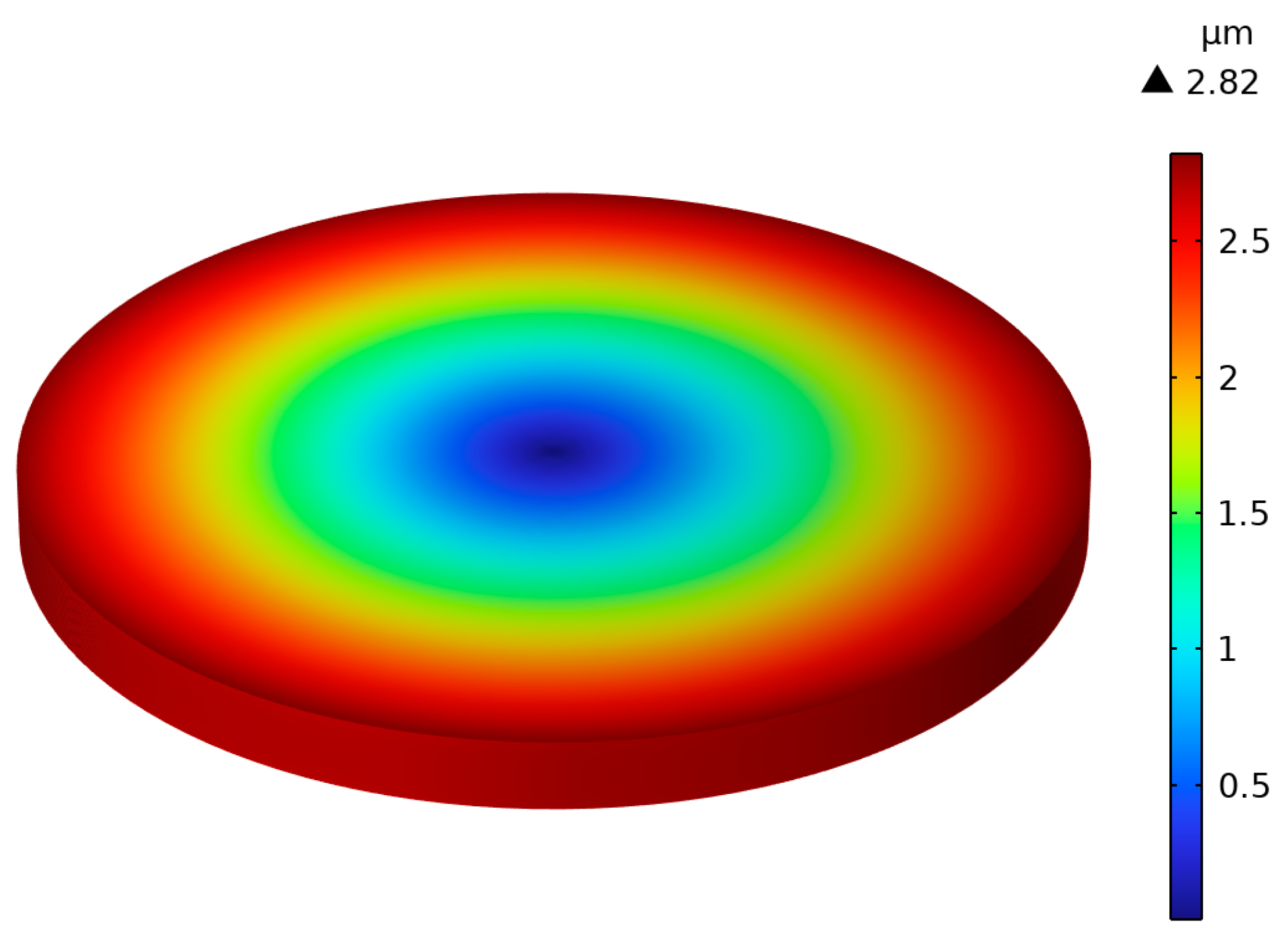
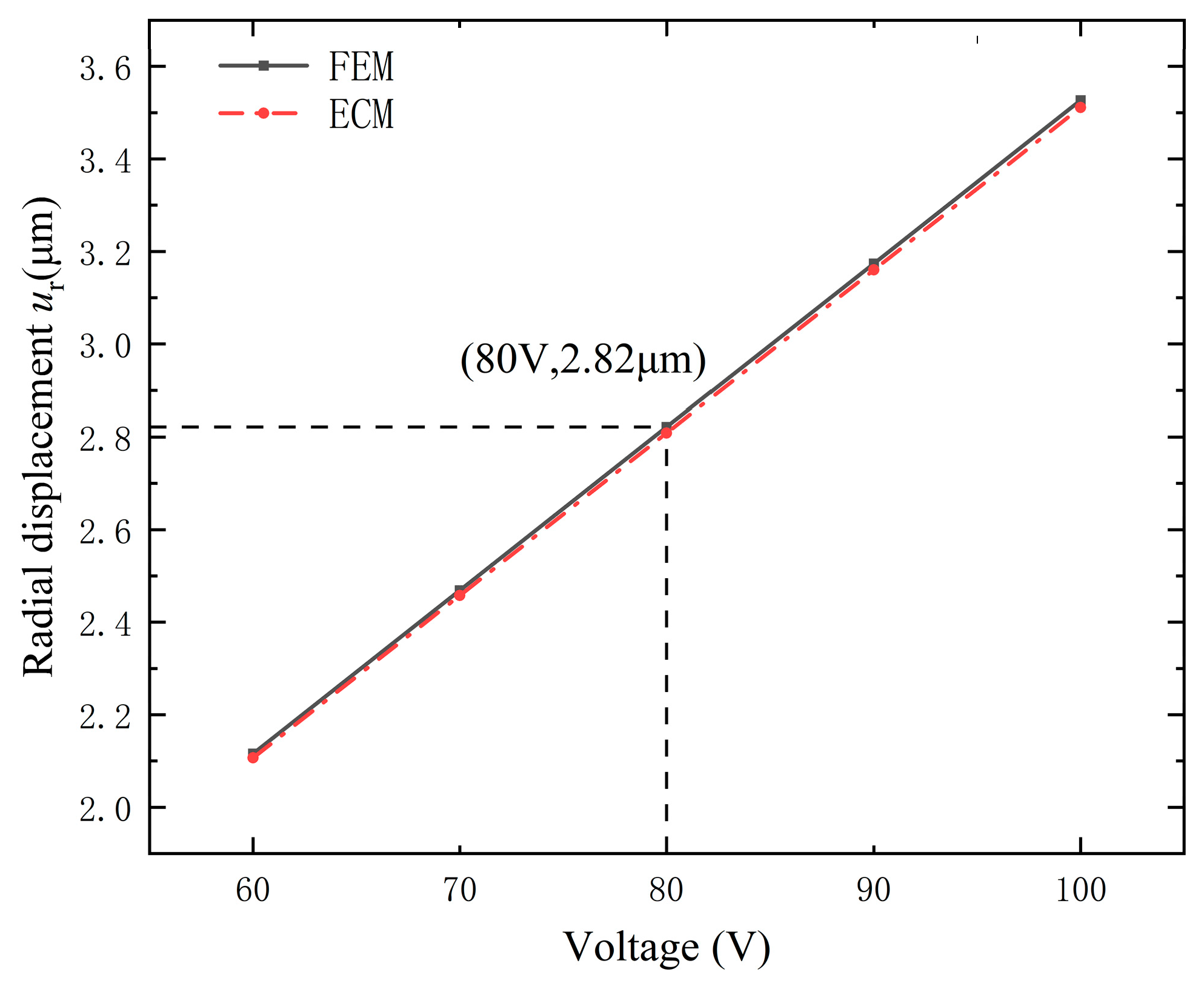
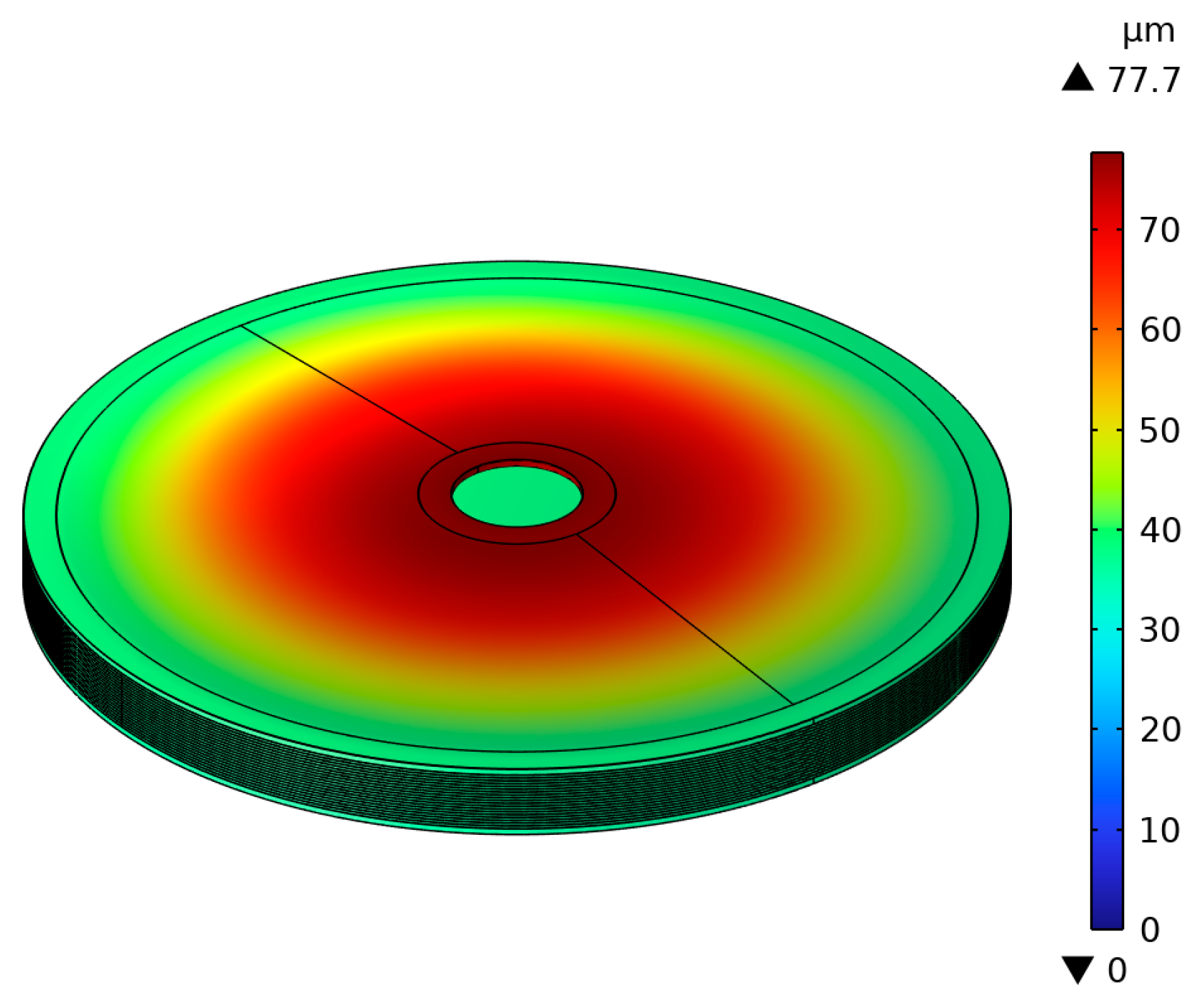
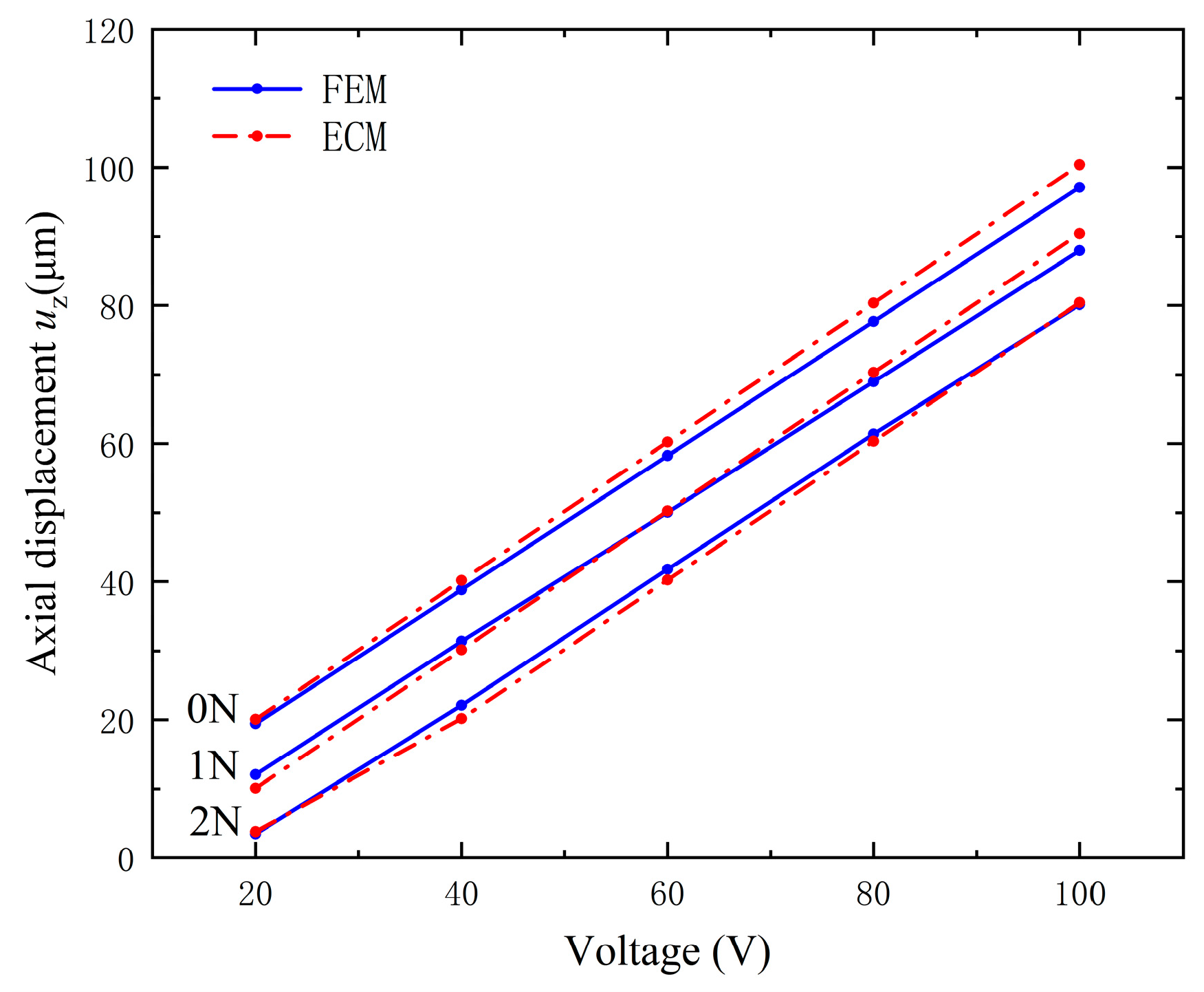
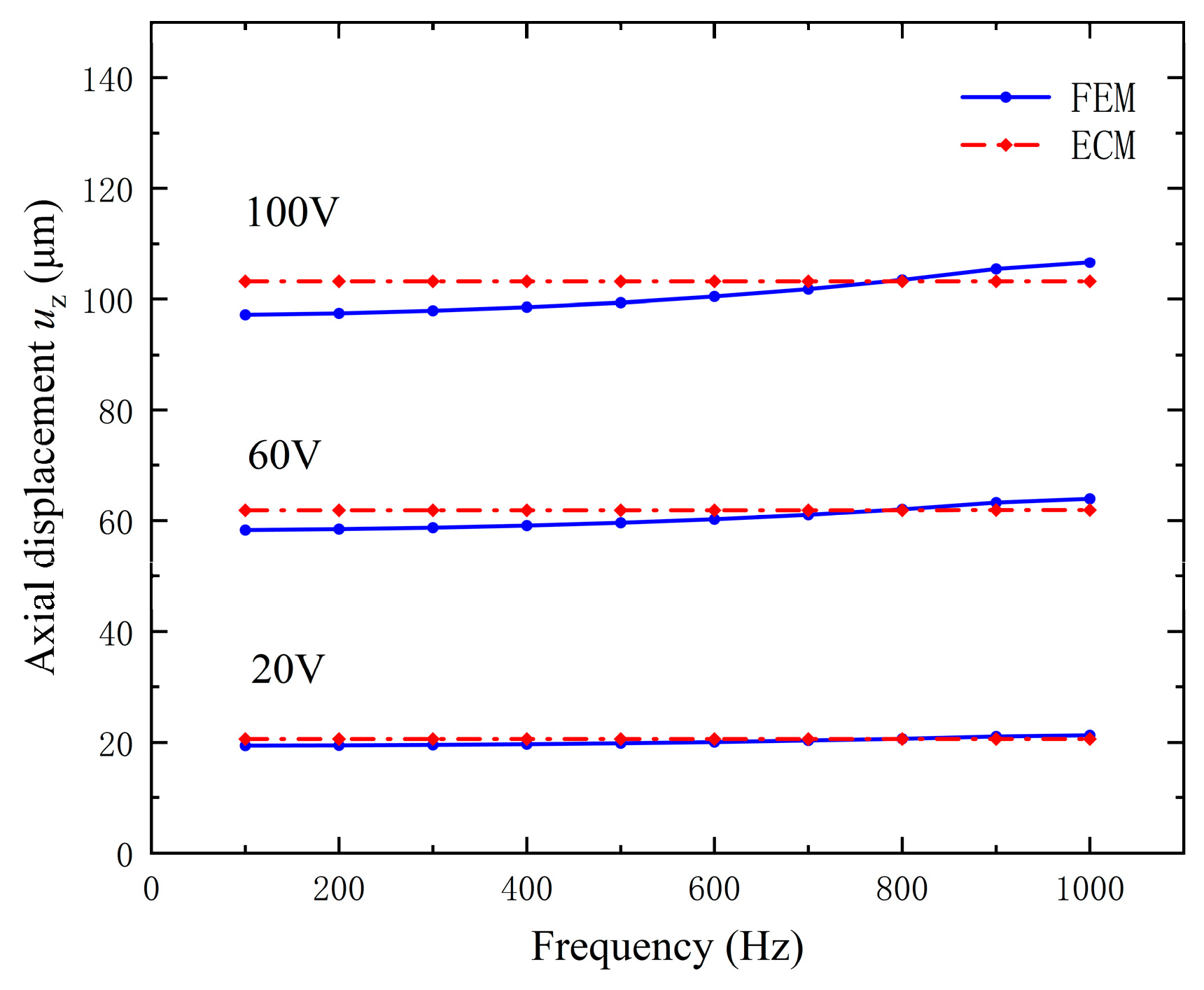
4.2. Comparison between Results of Finite Element and Equivalent Circuit
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Lin, S. Optimization design of Cymbal transducer. J. Appl. Acoust. 2018, 37, 765–771. [Google Scholar]
- Shim, H.; Roh, Y. Design and Fabrication of a Wideband Cymbal Transducer for Underwater Sensor Networks. Sensors 2019, 19, 4659. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Pan, C.; Jiang, J.; Wang, G.; Xu, H. The Modeling Design and Analysis of Spherical-Cymbal Piezoelectric Transducer. IEEE Sens. J. 2023, 23, 6537–6544. [Google Scholar] [CrossRef]
- Mudiyala, J.; Shim, H.; Kim, D.; Roh, Y. Development of a Dual-Layer Structure for Cymbal Transducer Arrays to Achieve a Wider Bandwidth. Sensors 2022, 22, 6614. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Shim, H.; Roh, Y. Comparative analysis of the acoustic characteristics of different types of cymbal transducers. J. Acoust. Soc. Korea 2019, 38, 256–265. [Google Scholar]
- Bejarano, F.; Lucas, M.; Wallace, R.; Spadaccino, A.M.; Simpson, H. Ultrasonic cutting device for bone surgery based on a cymbal transducer. In Proceedings of the 43rd Annual Symposium of the Ultrasonic-Industry-Association (UIA Symposium), Madrid, Spain, 23–25 April 2014. [Google Scholar]
- Bejarano, F.; Feeney, A.; Lucas, M. A cymbal transducer for power ultrasonics applications. Sens. Actuators A Phys. 2014, 210, 182–189. [Google Scholar] [CrossRef]
- Tressler, J.F.; Newnham, R.E.; Hughes, W.J. Capped ceramic underwater sound projector: The “cymbal” transducer. J. Acoust. Soc. Am. 1999, 105, 591–600. [Google Scholar] [CrossRef]
- Wang, G.; Yu, L.; Li, G.; Luan, G.; Zhang, F. Research on Structure Parameters and Electromechanical Characteristics of Cymbal Transducer. Piezoelectrics Acoustooptics 2005, 27, 320–323. [Google Scholar]
- Kim, D.; Oh, C.; Shim, H.; Kang, S.; Roh, Y. Design of the broadband pattern of a cymbal transducer array. J. Acoust. Soc. Korea 2021, 40, 10–17. [Google Scholar]
- Li, D.; Xia, S.; Huang, X. Finite element analysis on cymbal piezocomposite transducer. J. Funct. Mater. Devices 2002, 8, 155–160. [Google Scholar]
- Lu, Y.; Yan, Z. Finite element analysis on energy harvesting with cymbal transducer. J. Vib. Shock 2013, 32, 157–162. [Google Scholar]
- Wu, S.; Zhang, Q.; Huang, Z.; Pan, Z. Finite Element Analysis on Displacement Performance of Spherical-Cymbal Transducers. Chin. J. Sens. Actuators 2009, 22, 131–136. [Google Scholar]
- He, G.; Wang, H.; Ming, T.; Wang, X. Modelling and simulation of equivalent circuit for ultrasonic liquid level transducer. J. Huazhong Univ. Sci. Technol.-Nat. Sci. 2012, 40, 54–58. [Google Scholar]
- Zhou, H.; Han, L. Experimental Studies of Equivalent Circuit for Operating-mode Piezoelectric Transducer. Piezoelectrics Acoustooptics 2006, 28, 543–544, 548. [Google Scholar]
- Liu, Z.; Huang, J.; Yan, S.; Zhang, B. Research on Nonlinear Equivalent Circuit of High Power Piezoelectric Transducer. In Proceedings of the 14th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Shijiazhuang, China, 1–4 November 2019. [Google Scholar]
- Wang, S.; Shan, J.; Lin, S. Radial vibration analysis for functionally graded ring piezoelectric transducers based on electromechanical equivalent circuit method. Ultrasonics 2022, 120, 106640. [Google Scholar] [CrossRef]
- Yu, J.; Xu, L. Nonlinear Equivalent Circuit of High-Power Sandwich Piezoelectric Ultrasonic Transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3126–3136. [Google Scholar] [CrossRef]
- Kubo, K.; Yagi, K.; Kanda, T.; Yasuda, K.; Yamaguchi, D.; Wakimoto, S. Evaluation of transducer for cryogenic actuators by equivalent circuit model. Jpn. J. Appl. Phys. 2024, 63, 03SP03. [Google Scholar] [CrossRef]
- Pyo, S.; Roh, Y. Equivalent circuit for analyzing the transmitting characteristics of multimode Tonpilz transducer. J. Acoust. Soc. Am. 2022, 151, 3594–3602. [Google Scholar] [CrossRef]
- Dong, X.X.; Majzoubi, M.; Choi, M.; Ma, Y.T.; Hu, M.Q.; Jin, L.; Xu, Z.K.; Uchino, K. A new equivalent circuit for piezoelectrics with three losses and external loads. Sens. Actuators A Phys. 2017, 256, 77–83. [Google Scholar] [CrossRef]
- Koc, B.; Delibas, B. Impact Force Analysis in Inertia-Type Piezoelectric Motors. Actuators 2023, 12, 52. [Google Scholar] [CrossRef]
- Shim, H.; Kim, K.; Seo, H.; Roh, Y. Equivalent Circuit to Analyze the Transmitting Characteristics of a Cymbal Array. Sensors 2022, 22, 8743. [Google Scholar] [CrossRef] [PubMed]
- Shim, H.; Kim, K.; Seo, H.; Roh, Y. New Equivalent Circuit of a Cymbal Transducer Incorporating the Third Harmonic Mode of Vibration. IEEE Sens. J. 2022, 22, 15750–15758. [Google Scholar] [CrossRef]
- Shim, H.; Mudiyala, J.; Roh, Y. Optimal Design of Cymbal Array Patterns to Achieve Broadband Characteristics Using an Equivalent Circuit. IEEE Sens. J. 2023, 23, 22285–22294. [Google Scholar] [CrossRef]
- Shim, H.; Roh, Y. Development of an Equivalent Circuit of a Cymbal Transducer. IEEE Sens. J. 2021, 21, 13146–13155. [Google Scholar] [CrossRef]
- Hu, Y.; Hu, H.; Yang, J. A low frequency piezoelectric power harvester using a spiral-shaped bimorph. Sci. China Ser. G Phys. Mech. Astron. 2006, 49, 649–659. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lian, Z.Y.; Wang, J.; Hu, H.P. Analysis of a piezoelectric power harvester with adjustable frequency by precise electric field method. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 2154–2161. [Google Scholar] [CrossRef] [PubMed]
- Rajapurkar, A.; Puchleitner, R.; Neuwirth, D.; Prall, M. Device that Conveys Haptic Feedback, and Component Comprising the Device. US Patent 11,640,205, 2 May 2023. [Google Scholar]
- Liu, X.; Zheng, Y.; Guo, Y.; Hu, N.; Hu, H. Research on Stacked Piezoelectric Cymbal Vibrator. Micromachines 2023, 14, 2039. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.S. An Introduction to the Theory of Piezoelectricity; Springer: Boston, MA, USA, 2005. [Google Scholar]
- Piao, C.; Kim, J.O. Vibration characteristics of a piezoelectric disk laminated with an elastic disk. J. Mech. Sci. Technol. 2016, 30, 5351–5362. [Google Scholar] [CrossRef]
- Lin, S. Analysis on the resonance frequency of a thin piezoelectric ceramic disk in radial vibration. J. Shaanxi Norm. Univ. Nat. Sci. Ed. 2006, 34, 27–31. [Google Scholar]
- Lin, S. Radial vibration of isotropic elastic thin disk and its equivalent circuit. J. Shaanxi Norm. Univ. Nat. Sci. Ed. 2001, 29, 31. [Google Scholar]
- Peng, H.; Jia, S.; Yang, J.; Cai, H. Study on Equivalent Circuit Model of Cymbal Transducer. Chin. J. Sens. Actuators 2014, 27, 747–751. [Google Scholar]
- Bagheri, H.; Kiani, Y.; Eslami, M. Free vibration of joined conical-conical shells. Thin-Walled Struct. 2017, 120, 446–457. [Google Scholar] [CrossRef]
- Pang, F.; Wu, C.; Song, H.; Li, H.J.C.; Structures, L. The free vibration characteristics of isotropic coupled conical-cylindrical shells based on the precise integration transfer matrix method. Curved Layer. Struct. 2017, 4, 272–287. [Google Scholar] [CrossRef][Green Version]
- Wu, C.; Pang, F. Free vibration characteristics of the conical shells based on precise integration transfer matrix method. Lat. Am. J. Solids Struct. 2018, 15, e03. [Google Scholar] [CrossRef]
- Bagheri, H.; Kiani, Y.; Eslami, M. Free vibration of joined conical–cylindrical–conical shells. Acta Mech. 2018, 229, 2751–2764. [Google Scholar] [CrossRef]



| Materials | i | Density ρi (kg/m3) | Young’s Modulus Ei (GPa) | Poisson’s Ratio μi | Piezoelectric Constants (C/m2) | Thickness (μm) | ||
|---|---|---|---|---|---|---|---|---|
| e31 | e33 | e15 | ||||||
| PZT-5H | 1 | 7500 | \ | \ | −6.5 | 23.3 | 17 | 45 |
| silver | 2 | 10,490 | 73 | 0.38 | \ | \ | \ | 5 |
| Material | Density ρ (kg/m3) | Young’s Modulus E (GPa) | Poisson’s Ratio μ | α (°) | r0 (mm) | r1 (mm) | h (mm) | Thickness (h0) (mm) |
|---|---|---|---|---|---|---|---|---|
| 304SS | 7750 | 193 | 0.31 | 86 | 1.5 | 7 | 0.48 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Z.; Zheng, Y.; Yao, S.; Liu, X.; Hu, N.; Hu, H. Equivalent Circuit of a Stacked Piezoelectric Cymbal Vibrator. Micromachines 2024, 15, 1205. https://doi.org/10.3390/mi15101205
Gong Z, Zheng Y, Yao S, Liu X, Hu N, Hu H. Equivalent Circuit of a Stacked Piezoelectric Cymbal Vibrator. Micromachines. 2024; 15(10):1205. https://doi.org/10.3390/mi15101205
Chicago/Turabian StyleGong, Zhaohan, Yajun Zheng, Shuhan Yao, Xinhu Liu, Ningdong Hu, and Hongping Hu. 2024. "Equivalent Circuit of a Stacked Piezoelectric Cymbal Vibrator" Micromachines 15, no. 10: 1205. https://doi.org/10.3390/mi15101205
APA StyleGong, Z., Zheng, Y., Yao, S., Liu, X., Hu, N., & Hu, H. (2024). Equivalent Circuit of a Stacked Piezoelectric Cymbal Vibrator. Micromachines, 15(10), 1205. https://doi.org/10.3390/mi15101205







