Characterization of Sensitivity of Time Domain MEMS Accelerometer
Abstract
1. Introduction
2. Characterization of Sensitivity
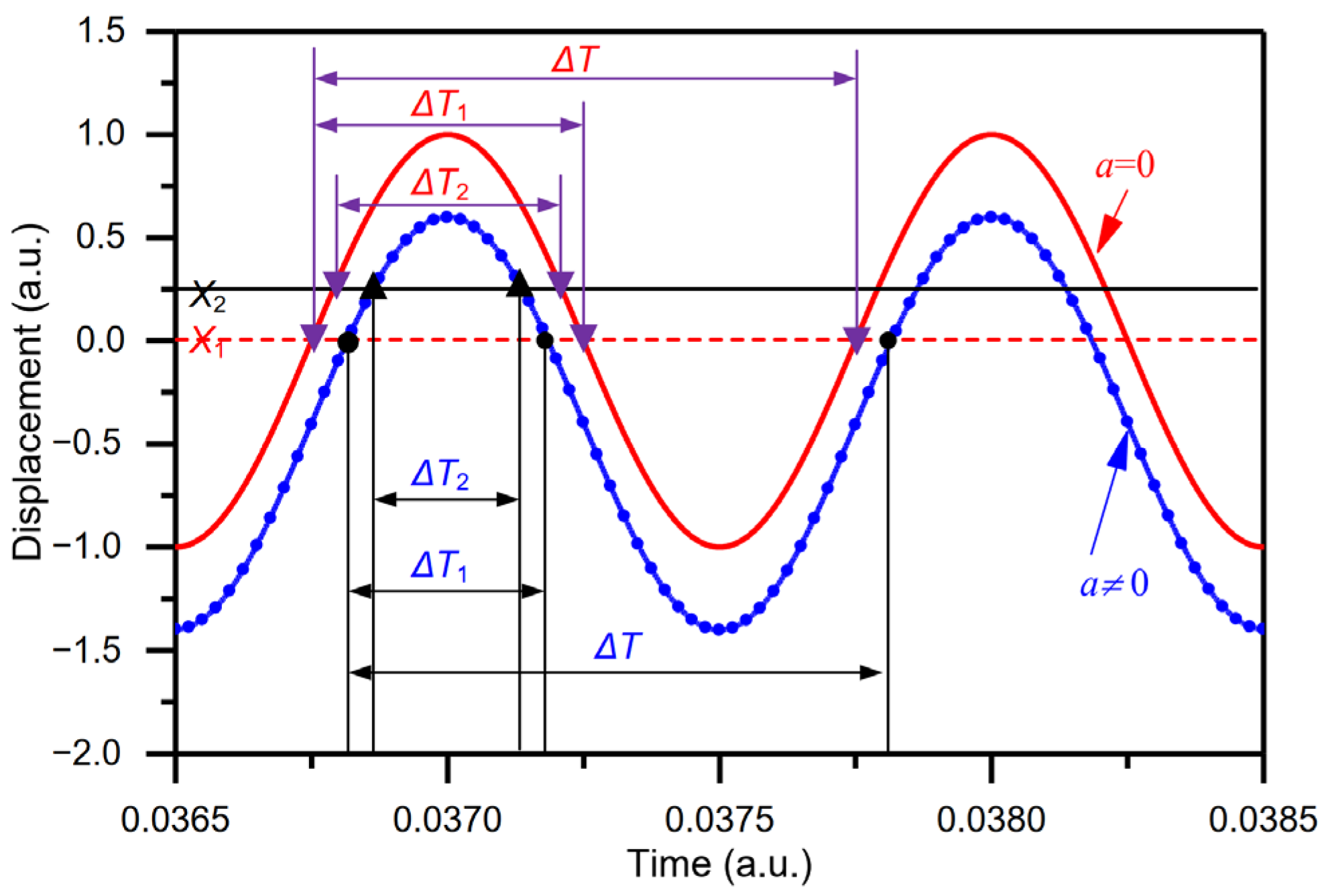
2.1. Definition and Deducing of Sensitivity Formulas
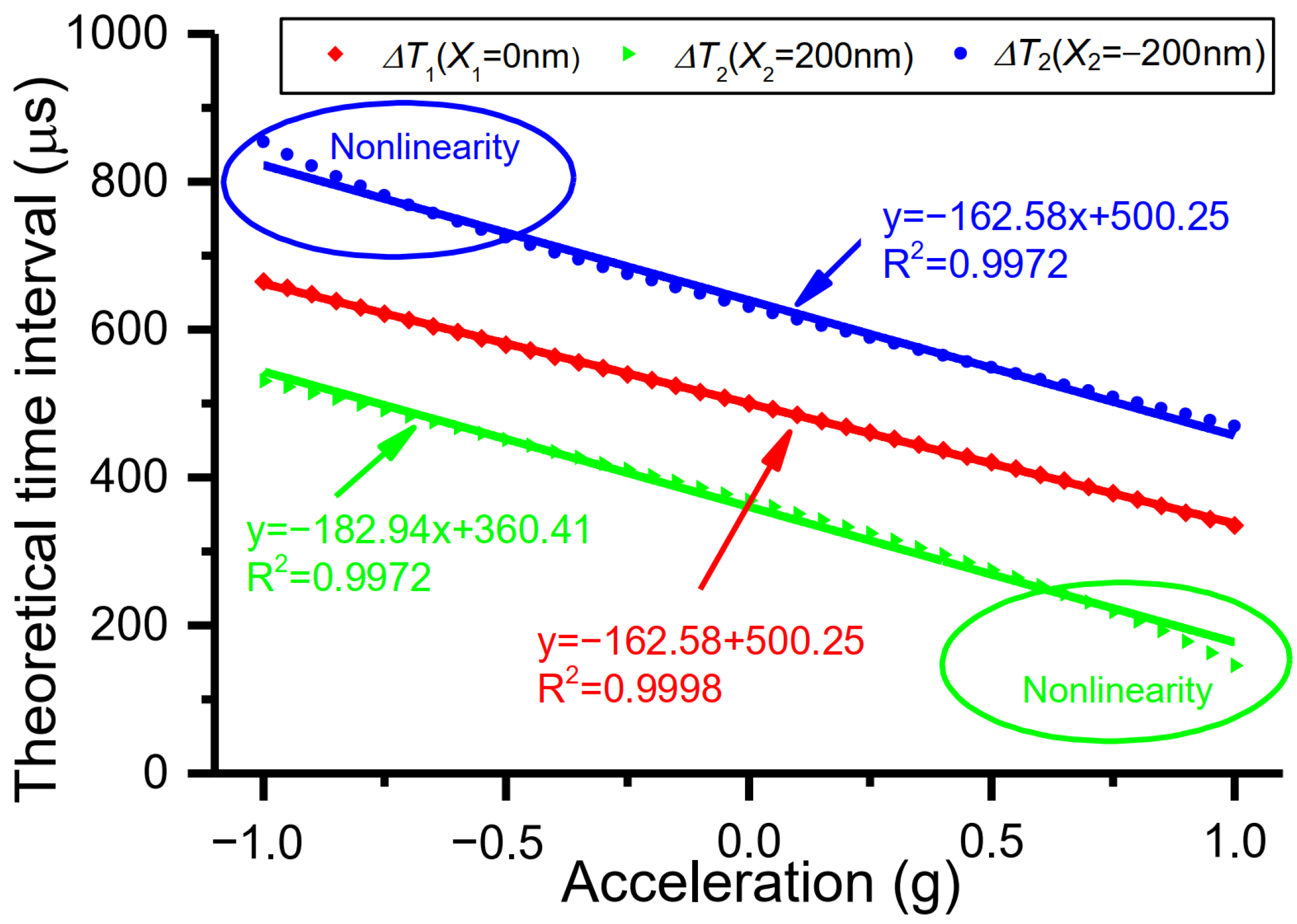
2.2. Making a Better Choice between Sensitivities S1 and S2 Based on Nonlinearity for Evaluating Time Domain Sensor
2.3. Adjustment Principle of Sensitivity
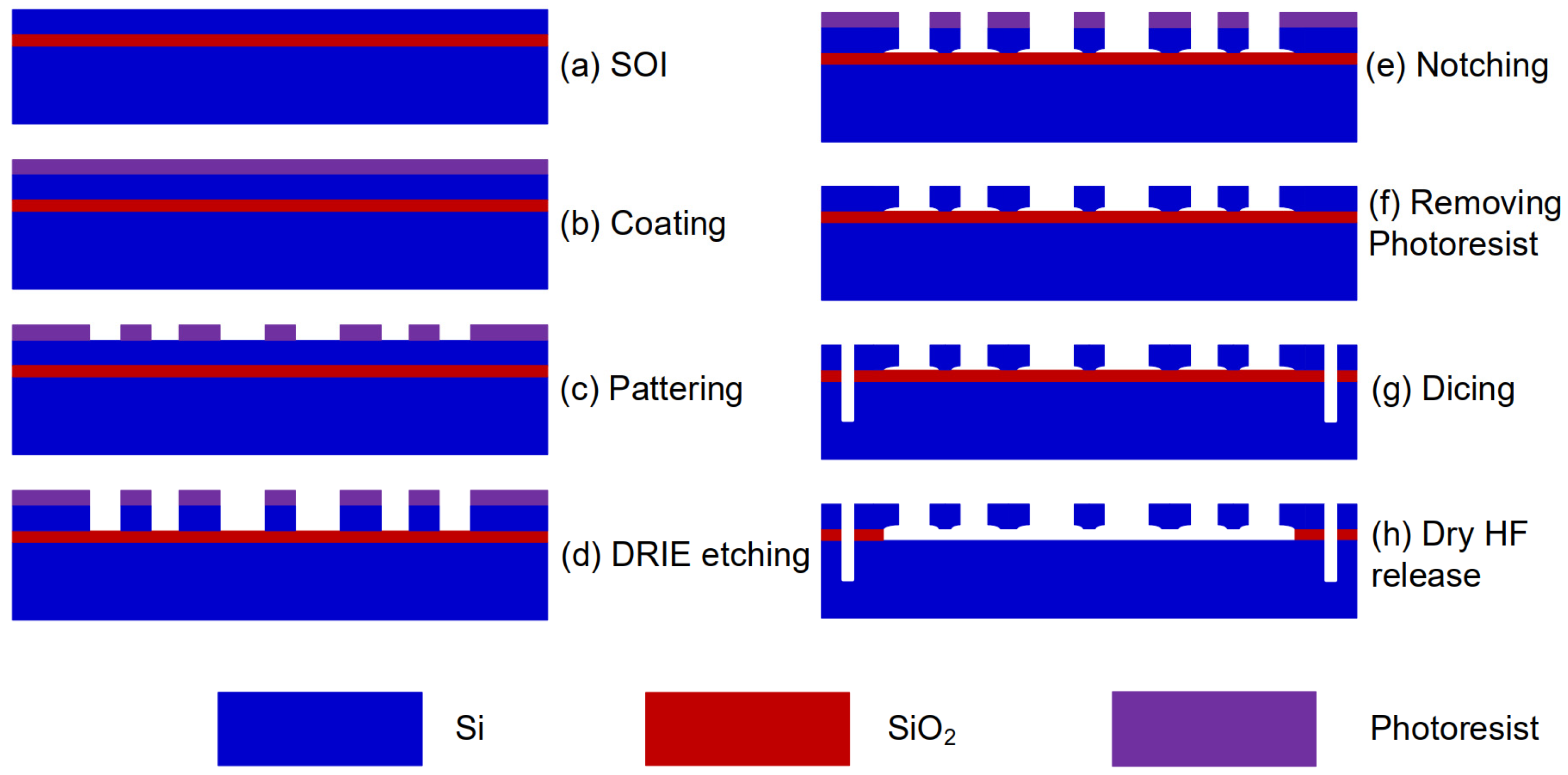
3. Device Implementation and Experimental Method
4. Results and Discussion
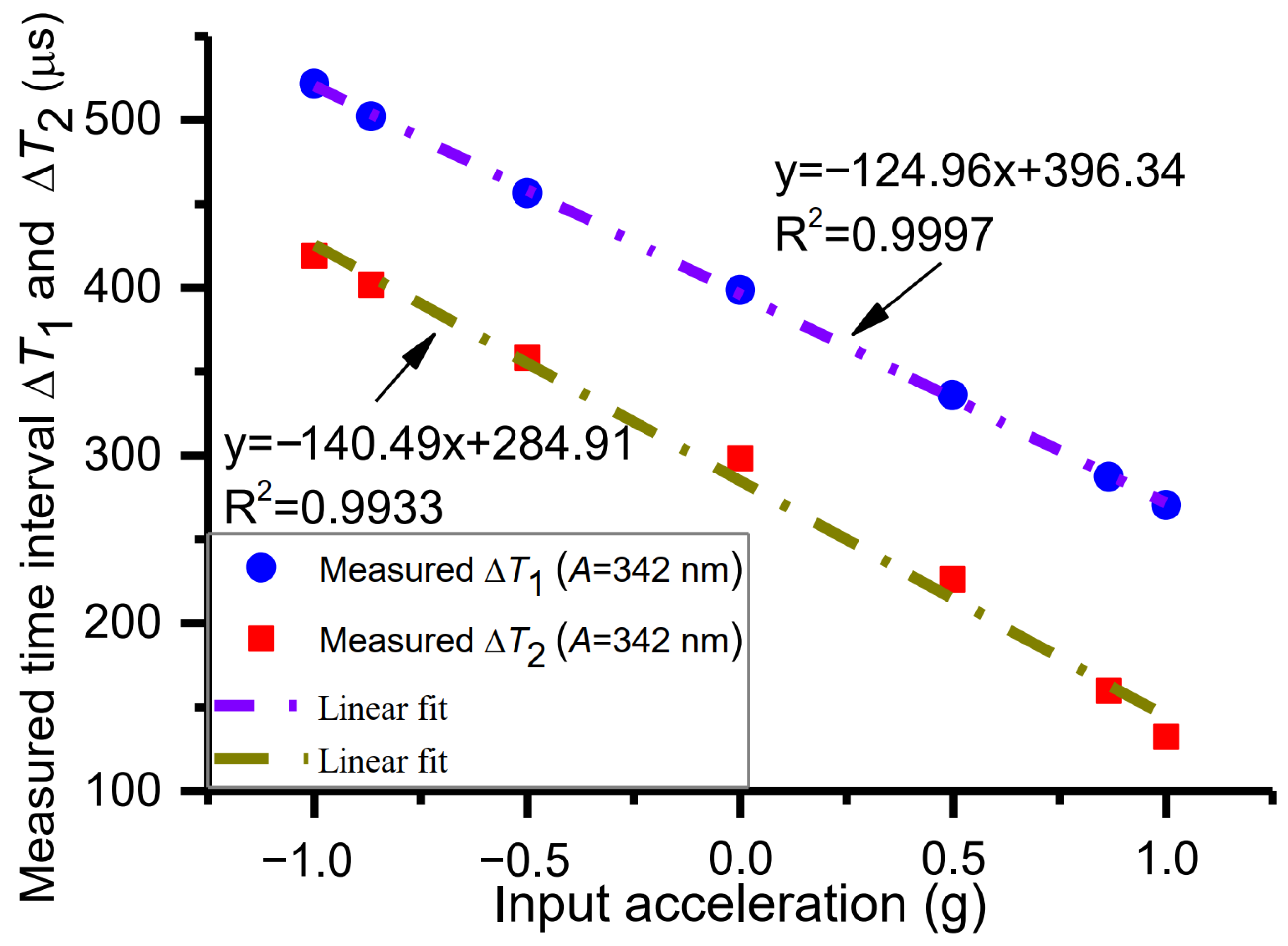
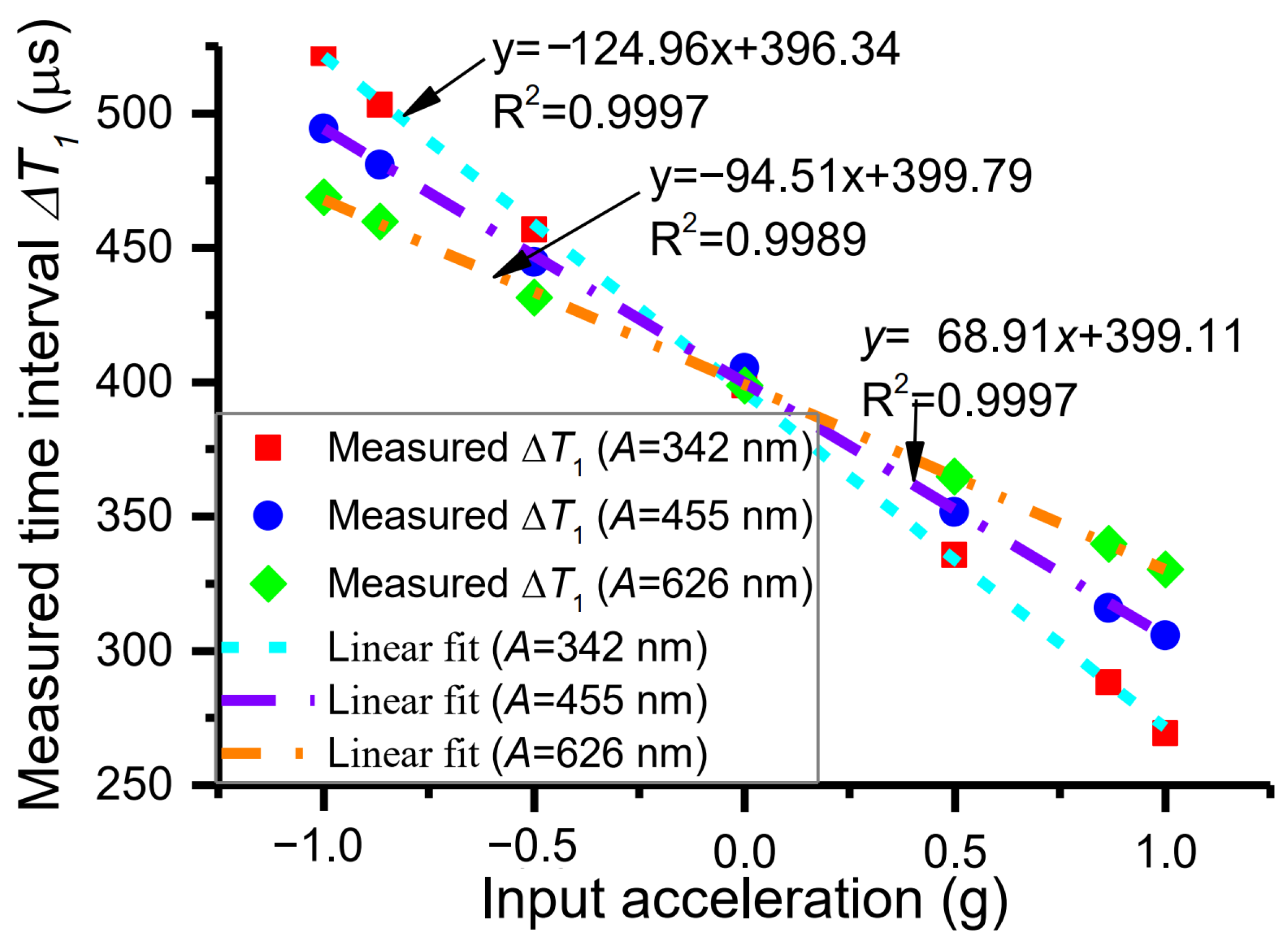
4.1. Sensitivity Measurement and Comparison of Measured Nonlinearity
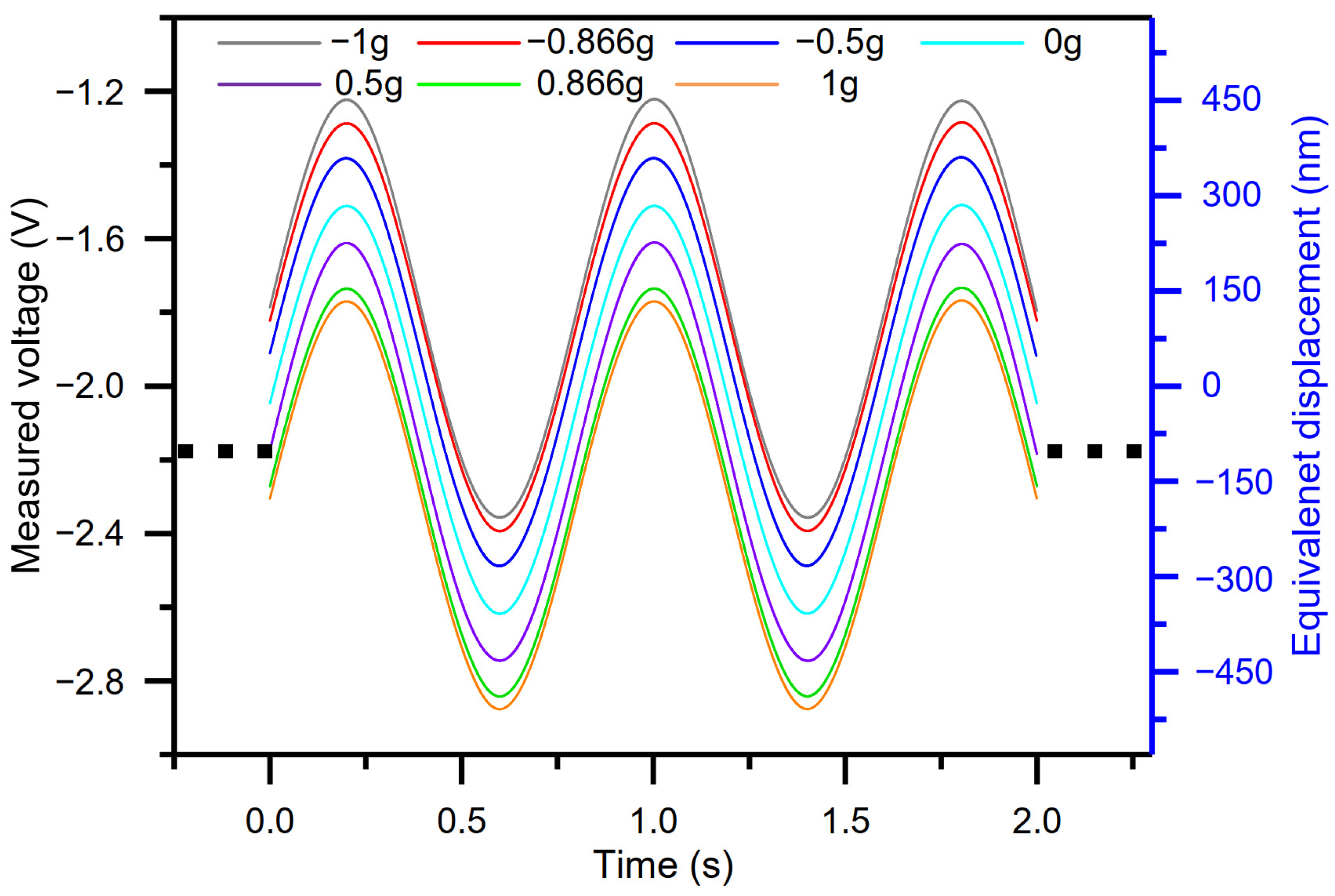
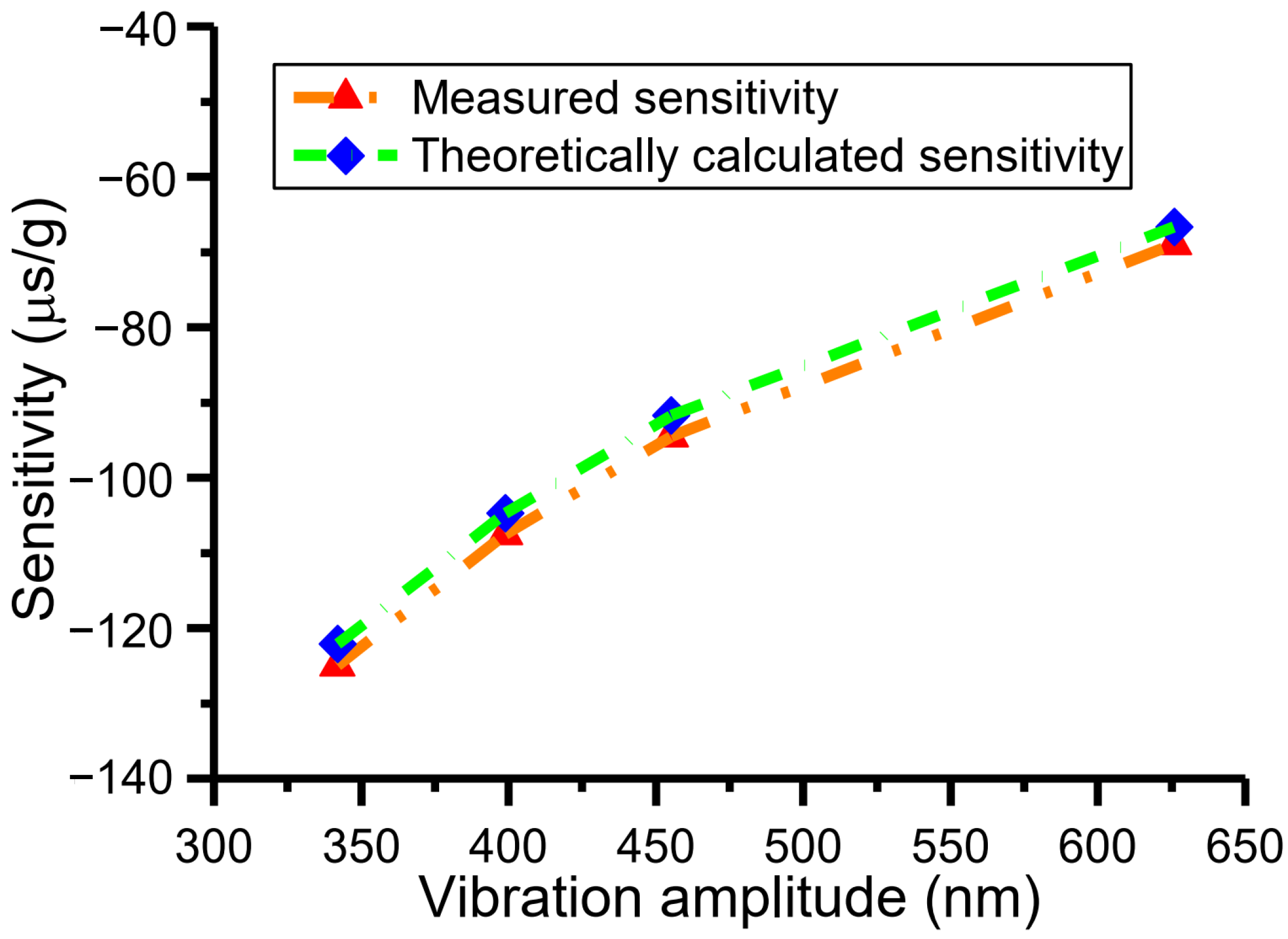
4.2. Measurement and Discussion of Adjustable Sensitivity Resulting from Varying Vibration Amplitude
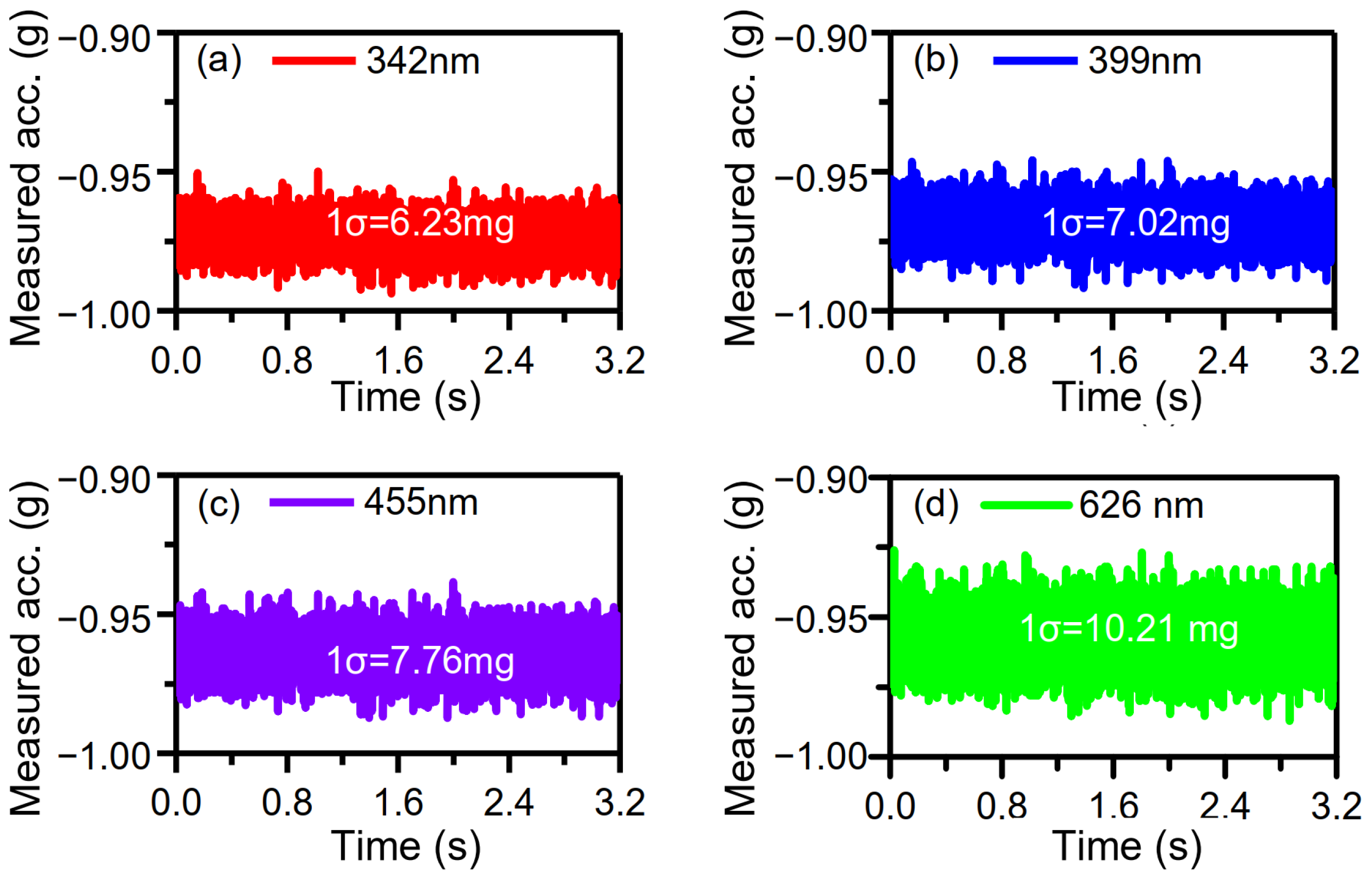
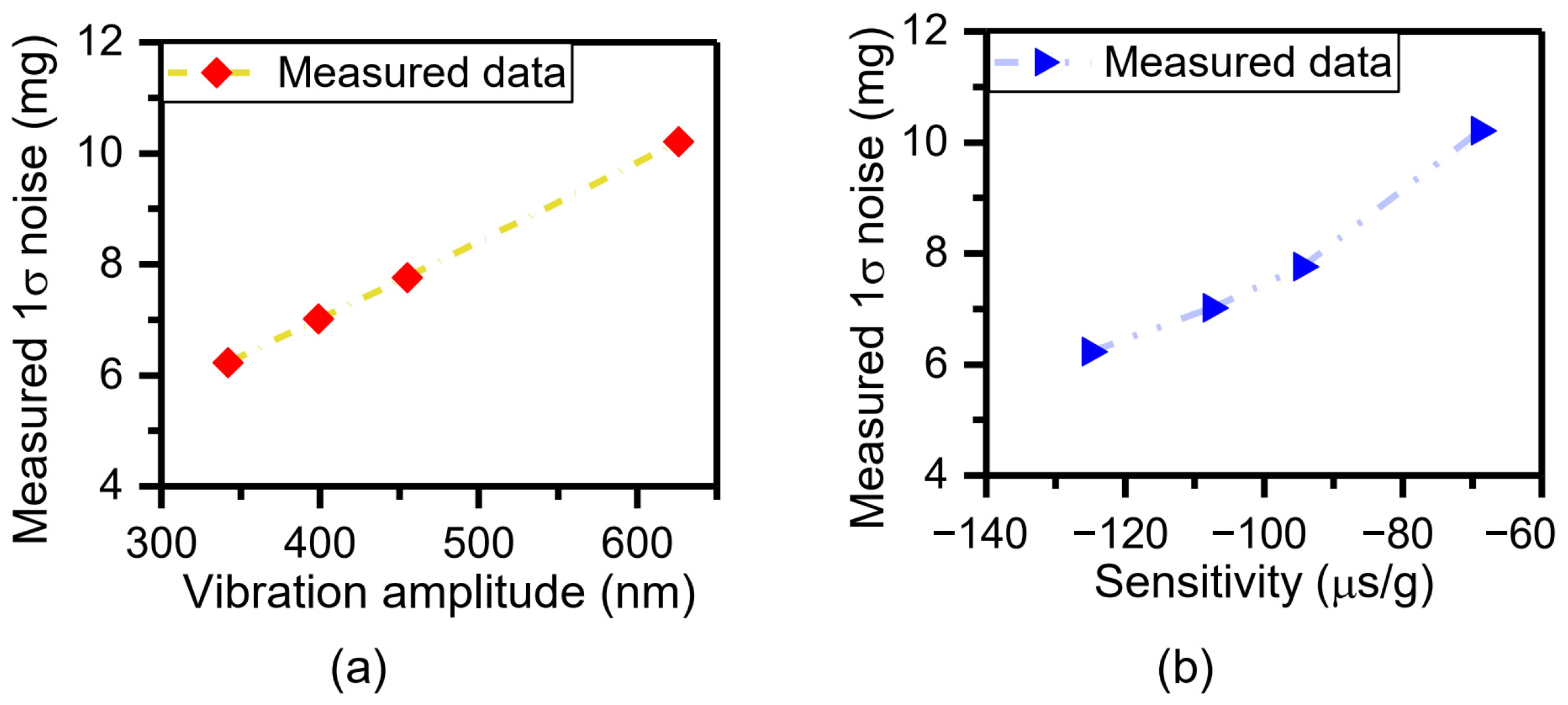
4.3. Measurement and Analysis of Tunable Sensor Performance Based on Adjustable Vibration Parameters or Sensitivities
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bijjahalli, S.; Sabatini, R.; Gardi, A. Advances in intelligent and autonomous navigation systems for small UAS. Prog. Aerosp. Sci. 2020, 115, 100617. [Google Scholar] [CrossRef]
- Furubayashi, Y.; Oshima, T.; Yamawaki, T.; Watanabe, K.; Mori, K.; Mori, N.; Matsumoto, A.; Kamada, Y.; Isobe, A.; Sekiguchi, T. A 22-ng/√ Hz 17-mW Capacitive MEMS Accelerometer with Electrically Separated Mass Structure and Digital Noise- Reduction Techniques. IEEE J. Solid-State Circuits 2020, 55, 2539–2552. [Google Scholar] [CrossRef]
- Wang, C.; Hao, Y.; Sun, Z.; Zu, L.; Yuan, W.; Chang, H. Design of a capacitive MEMS accelerometer with softened beams. Micromachines 2022, 13, 459. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Kwon, H.-K.; Vukasin, G.D.; Kenny, T.W.; Ayazi, F. A temperature compensated biaxial eFM accelerometer in Epi-seal process. Sens. Actuators A Phys. 2021, 330, 112860. [Google Scholar] [CrossRef]
- Zu, L.; Hao, Y.; Wang, M.; Chang, H. A Novel Mode-Localized Accelerometer Employing a Tunable Annular Coupler. IEEE Sens. J. 2022, 22, 6426–6434. [Google Scholar] [CrossRef]
- Zhao, C.; Zhou, X.; Pandit, M.; Sobreviela, G.; Du, S.; Zou, X.; Seshia, A. Toward High-Resolution Inertial Sensors Employing Parametric Modulation in Coupled Micromechanical Resonators. Phys. Rev. Appl. 2019, 12, 1. [Google Scholar] [CrossRef]
- Li, E.; Zhang, L.; Guan, X.; Hao, Y.; Shen, Q.; Chang, H. Novel acceleration measurement method during attenuation vibration of inertial sensor based on time domain sensing mechanism. Measurement 2023, 218, 113077. [Google Scholar] [CrossRef]
- Li, E.; Li, P.; Shen, Q.; Chang, H. High-accuracy silicon-on-insulator accelerometer with an increased yield rate. Micro Nano Lett. 2015, 10, 477–482. [Google Scholar] [CrossRef]
- Barbin, E.; Nesterenko, T.; Koleda, A.; Shesterikov, E.; Kulinich, I.; Kokolov, A. An Optical Measuring Transducer for a Micro-Opto-Electro-Mechanical Micro-g Accelerometer Based on the Optical Tunneling Effect. Micromachines 2023, 14, 802. [Google Scholar] [CrossRef]
- Jia, C.; Yu, M.; Luo, G.; Han, X.; Yang, P.; Chen, Y.; Zhao, L.; Wang, L.; Wang, Y.; Wang, J.; et al. Modeling and Characterization of a Novel In-Plane Dual-Axis MEMS Accelerometer Based on Self-Support Piezoresistive Beam. J. Microelectromech. Syst. 2022, 31, 867–876. [Google Scholar] [CrossRef]
- Levinzon, F.A. Ultra-low-noise seismic piezoelectric accelerometer with integral FET amplifier. IEEE Sens. J. 2012, 12, 2262–2268. [Google Scholar] [CrossRef]
- Abdolvand, R.; Amini, B.V.; Ayazi, F. Sub-Micro-Gravity In-Plane Accelerometers With Reduced Capacitive Gaps and Extra Seismic Mass. J. Microelectromech. Syst. 2007, 16, 1036–1043. [Google Scholar] [CrossRef]
- De Laat, M.L.C.; Garza, H.P.; Herder, J.L.; Ghatkesar, M.K. A review on in situ stiffness adjustment methods in MEMS. J. Micromech. Microeng. 2016, 26, 063001. [Google Scholar] [CrossRef]
- Middlemiss, R.P.; Samarelli, A.; Paul, D.J.; Hough, J.; Rowan, S.; Hammond, G.D. Measurement of the Earth tides with a MEMS gravimeter. Nature 2016, 531, 614–617. [Google Scholar] [CrossRef] [PubMed]
- Jeong, D.-H.; Yun, S.-S.; Lee, B.-G.; Lee, M.-L.; Choi, C.-A.; Lee, J.-H. High-Resolution Capacitive Microinclinometer With Oblique Comb Electrodes Using (110) Silicon. J. Microelectromech. Syst. 2011, 20, 1269–1276. [Google Scholar] [CrossRef]
- Bae, K.M.; Lee, J.M.; Kwon, K.B.; Han, K.-H.; Kwon, N.Y.; Han, J.S.; Ko, J.S. High-shock silicon accelerometer with suspended piezoresistive sensing bridges. J. Mech. Sci. Technol. 2014, 28, 1449–1454. [Google Scholar] [CrossRef]
- Tsai, C.C.; Chien, Y.C.; Hong, C.S.; Chu, S.Y.; Wei, C.L.; Liu, Y.H.; Kao, H.Y. Study of Pb(Zr0.52Ti0.48)O3 microelectromechanical system piezoelectric accelerometers for health monitoring of mechanical motors. J. Am. Ceram. Soc. 2019, 102, 4056–4066. [Google Scholar] [CrossRef]
- Jangra, M.; Arya, D.S.; Khosla, R.; Sharma, S.K. Maskless lithography: An approach to SU-8 based sensitive and high-g Z-axis polymer MEMS accelerometer. Microsyst. Technol. 2021, 27, 2925–2934. [Google Scholar] [CrossRef]
- CComi, C.; Corigliano, A.; Langfelder, G.; Longoni, A.; Tocchio, A.; Simoni, B. A Resonant microaccelerometer with high sensitivity operating in an oscillating circuit. J. Microelectromech. Syst. 2010, 19, 1140–1152. [Google Scholar] [CrossRef]
- Pandit, M.; Zhao, C.; Sobreviela, G.; Zou, X.; Seshia, A. A High Resolution Differential Mode-Localized MEMS Accelerometer. J. Microelectromech. Syst. 2019, 28, 782–789. [Google Scholar] [CrossRef]
- Satija, J.; Singh, S.; Zope, A.; Li, S.-S. An Aluminum Nitride-Based Dual-Axis MEMS In-Plane Differential Resonant Accelerometer. IEEE Sens. J. 2023, 23, 16736–16745. [Google Scholar] [CrossRef]
- Ding, H.; Zhao, J.; Ju, B.-F.; Xie, J. A high-sensitivity biaxial resonant accelerometer with two-stage microleverage mechanisms. J. Micromech. Microeng. 2016, 26, 015011. [Google Scholar] [CrossRef]
- Kang, H.; Ruan, B.; Hao, Y.; Chang, H. Mode-localized accelerometer with ultrahigh sensitivity. Sci. China Inf. Sci. 2022, 65, 142402. [Google Scholar] [CrossRef]
- Swanson, P.D.; Tally, C.H.; Waters, R.L. Proposed digital, auto ranging, self calibrating inertial sensor. In Proceedings of the IEEE Sensors 2011, Limerick, Ireland, 28–31 October 2011; pp. 1457–1460. [Google Scholar]
- Hinkley, N.; Sherman, J.A.; Phillips, N.B.; Schioppo, M.; Lemke, N.D.; Beloy, K.; Pizzocaro, M.; Oates, C.W.; Ludlow, A.D. An atomic clock with 10-18 instability. Science 2013, 341, 1215–1218. [Google Scholar] [CrossRef] [PubMed]
- Swanson, P.D.; Waters, R.L. Apparatus and Method for Providing an In-Plane Inertial Device with Integrated Clock. U.S. Patent 8,875,576, 4 November 2014. [Google Scholar]
- Tally, C.H.; Swanson, P.D.; Waters, R.L. Intelligent polynomial curve fitting for time-domain triggered inertial devices. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium 2012, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 1–7. [Google Scholar]
- Swanson, P.D.; Waters, R.L. Time Domain Switched Gyroscope. U.S. Patent 8,650,955, 18 February 2014. [Google Scholar]
- Sabater, A.B.; Swanson, P. Angular Random Walk Estimation of a Time-Domain Switching Micromachined Gyroscope; Technology digest: Rockville, MD, USA, 2016. [Google Scholar]
- Li, E.; Shen, Q.; Hao, Y.; Xun, W.; Chang, H. A Novel Virtual Accelerometer Array Using One Single Device Based on Time Intervals Measurement. In Proceedings of the IEEE SENSORS 2018, New Delhi, India, 28–31 October 2018; pp. 586–589. [Google Scholar]
- Li, E.; Shen, Q.; Hao, Y.; Chang, H. A Virtual Accelerometer Array Using One Device Based on Time Domain Measurement. IEEE Sens. J. 2019, 19, 6067–6075. [Google Scholar] [CrossRef]
- Waters, R.L.; Fralick, M.; Jacobs, D.; Abassi, S.; Dao, R.; Carbonari, D.; Maurer, G. Factors influencing the noise floor and stability of a time domain switched inertial device. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium 2012, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 1099–1105. [Google Scholar]
- Li, E.; Zhong, J.; Chang, H. Tilt sensor based on a dual-axis microaccelerometer with maximum sensitivity and minimum uncertainty in the full measurement range. Micro Nano Lett. 2017, 12, 866–870. [Google Scholar] [CrossRef]
- National Instruments. DAQ S Series User Manuscript. Available online: https://www.ni.com/docs/zh-CN/bundle/ni-611x-612x-613x-6143-features/resource/370781h.pdf (accessed on 1 November 2023).
- Glenn, D.R.; Bucher, D.B.; Lee, J.; Lukin, M.D.; Park, H.; Walsworth, R.L. High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 2018, 555, 351–354. [Google Scholar] [CrossRef] [PubMed]
- Piekarz, I.; Sorocki, J.; Górska, S.; Bartsch, H.; Rydosz, A.; Smolarz, R.; Wincza, K.; Gruszczynski, S. High sensitivity and selectivity microwave biosensor using biofunctionalized differential resonant array implemented in LTCC for Escherichia coli detection. Measurement 2023, 208, 112473. [Google Scholar] [CrossRef]
- Ashakirin, S.N.; Zaid, M.H.M.; Haniff, M.A.S.M.; Masood, A.; Wee, M.M.R. Sensitive electrochemical detection of creatinine based on electrodeposited molecular imprinting polymer modified screen printed carbon electrode. Measurement 2023, 210, 112502. [Google Scholar] [CrossRef]
- Ghaffar, A.; Li, Q.; Haider, S.A.; Sun, A.; Leal-Junior, A.G.; Xu, L.; Chhattal, M.; Mehdi, M. A simple and high-resolution POF displacement sensor based on face-coupling method. Measurement 2022, 187, 110285. [Google Scholar] [CrossRef]

| Capacitive and Similar [3,8,9,10,11] | Resonant [4] | Mode- Localized [5] | Time Domain [24,31] | |
|---|---|---|---|---|
| Proof mass | Quasi-static | Quasi-static | Quasi-static | Resonant |
| Elastic beam | Quasi-static | Resonant | Resonant | Quasi-static |
| Converting acceleration into | Displacement | Frequency | Amplitude ratio | Time intervals |
| Measured quantity for representing acceleration | Voltage or current | Voltage or current | Voltage or current | Time intervals |
| Mechanical sensitivity | m/g | Hz/g or ppm/g | 1/g or ppm/g | s/g |
| Interface circuit gain | V/m or A/m | 1 * | 1 * | 1 * |
| Total sensitivity ** | V/g or A/g | Hz/g | ppm/g | s/g |
| Parameters | Value |
|---|---|
| Resonant frequency | 1245.88 Hz |
| Measurement range | ±1 g |
| Bandwidth | 1.25 Hz |
| Quality factor | ~1000 |
| Input Acceleration (g) | Measured Time Intervals (μs) | Measured Acceleration (g) | ||
|---|---|---|---|---|
| ΔT1 | ΔT2 | ΔT | ||
| −1 | 521.6 | 418.8 | 802.4 | −0.96335 |
| −0.866 | 502.0 | 401.6 | 802.4 | −0.81670 |
| −0.5 | 456.4 | 358.0 | 802.4 | −0.45568 |
| 0 | 398.4 | 298.0 | 802.4 | 0.02333 |
| 0.5 | 336.0 | 226.0 | 802.4 | 0.53922 |
| 0.866 | 287.2 | 159.6 | 802.8 | 0.92645 |
| 1 | 270.4 | 132.4 | 802.8 | 1.05361 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, E.; Jian, J.; Yang, F.; Ma, Z.; Hao, Y.; Chang, H. Characterization of Sensitivity of Time Domain MEMS Accelerometer. Micromachines 2024, 15, 227. https://doi.org/10.3390/mi15020227
Li E, Jian J, Yang F, Ma Z, Hao Y, Chang H. Characterization of Sensitivity of Time Domain MEMS Accelerometer. Micromachines. 2024; 15(2):227. https://doi.org/10.3390/mi15020227
Chicago/Turabian StyleLi, Enfu, Jiaying Jian, Fan Yang, Zhiyong Ma, Yongcun Hao, and Honglong Chang. 2024. "Characterization of Sensitivity of Time Domain MEMS Accelerometer" Micromachines 15, no. 2: 227. https://doi.org/10.3390/mi15020227
APA StyleLi, E., Jian, J., Yang, F., Ma, Z., Hao, Y., & Chang, H. (2024). Characterization of Sensitivity of Time Domain MEMS Accelerometer. Micromachines, 15(2), 227. https://doi.org/10.3390/mi15020227







