Consideration of Power Transmission Characteristics in a Micro-Gear Train
Abstract
:1. Introduction
2. Materials and Methods
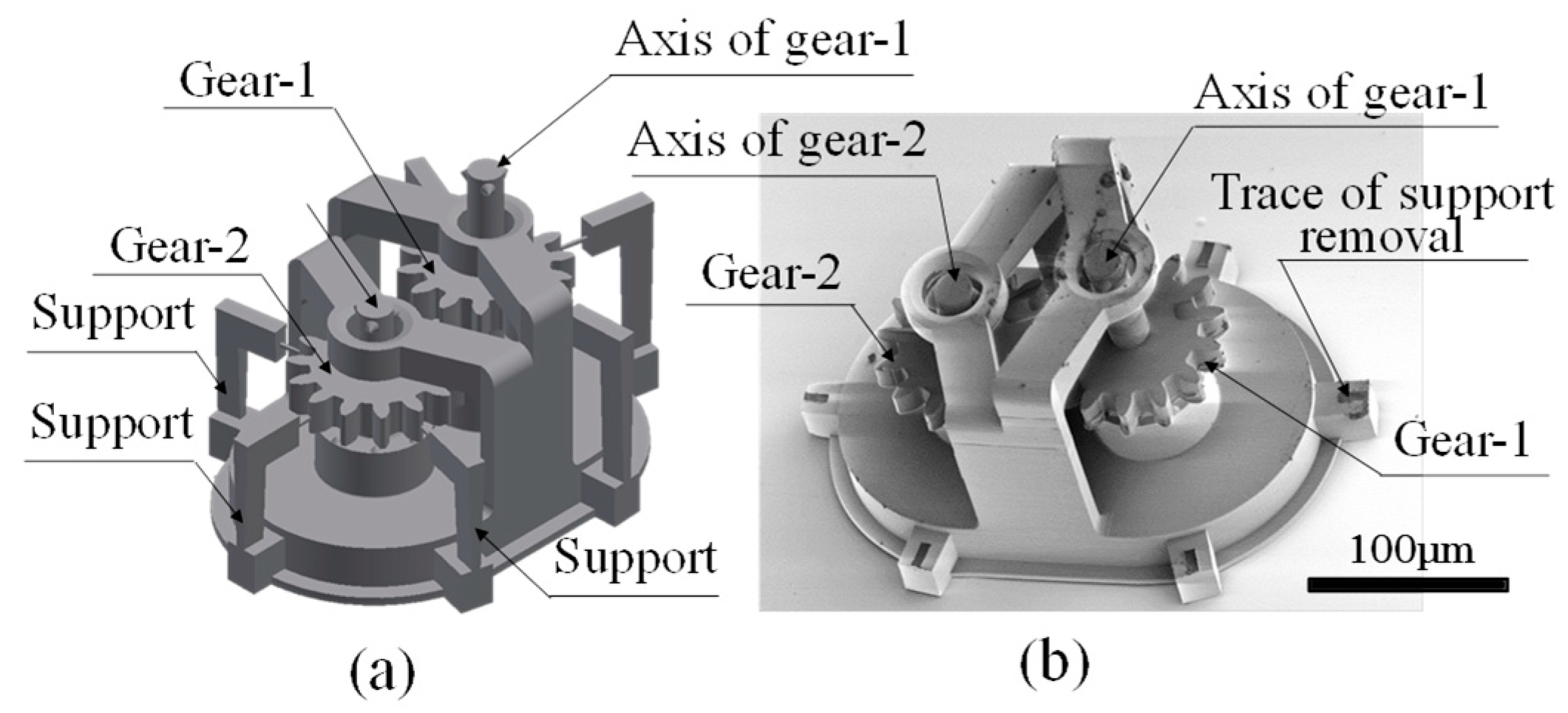
2.1. Fabrication of Micro-Gears Using a 3D Optical Fabrication System
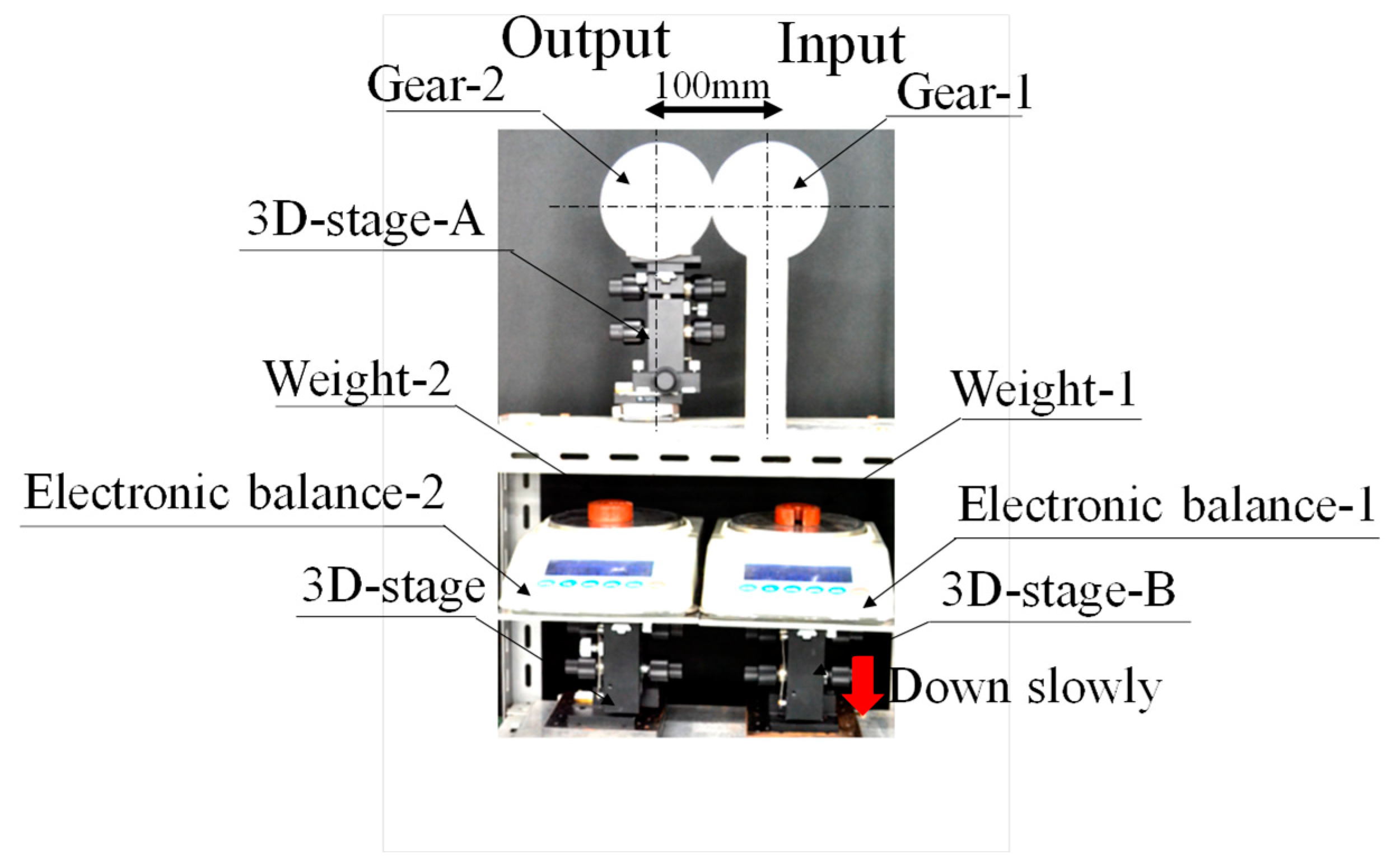
2.2. Measuring Power Transmission Efficiency Using the Moment Balance Method
2.2.1. Moment Balance Method
2.2.2. Detecting the Power Transmission Characteristics of Macro-Gears Using the Moment Balance Method
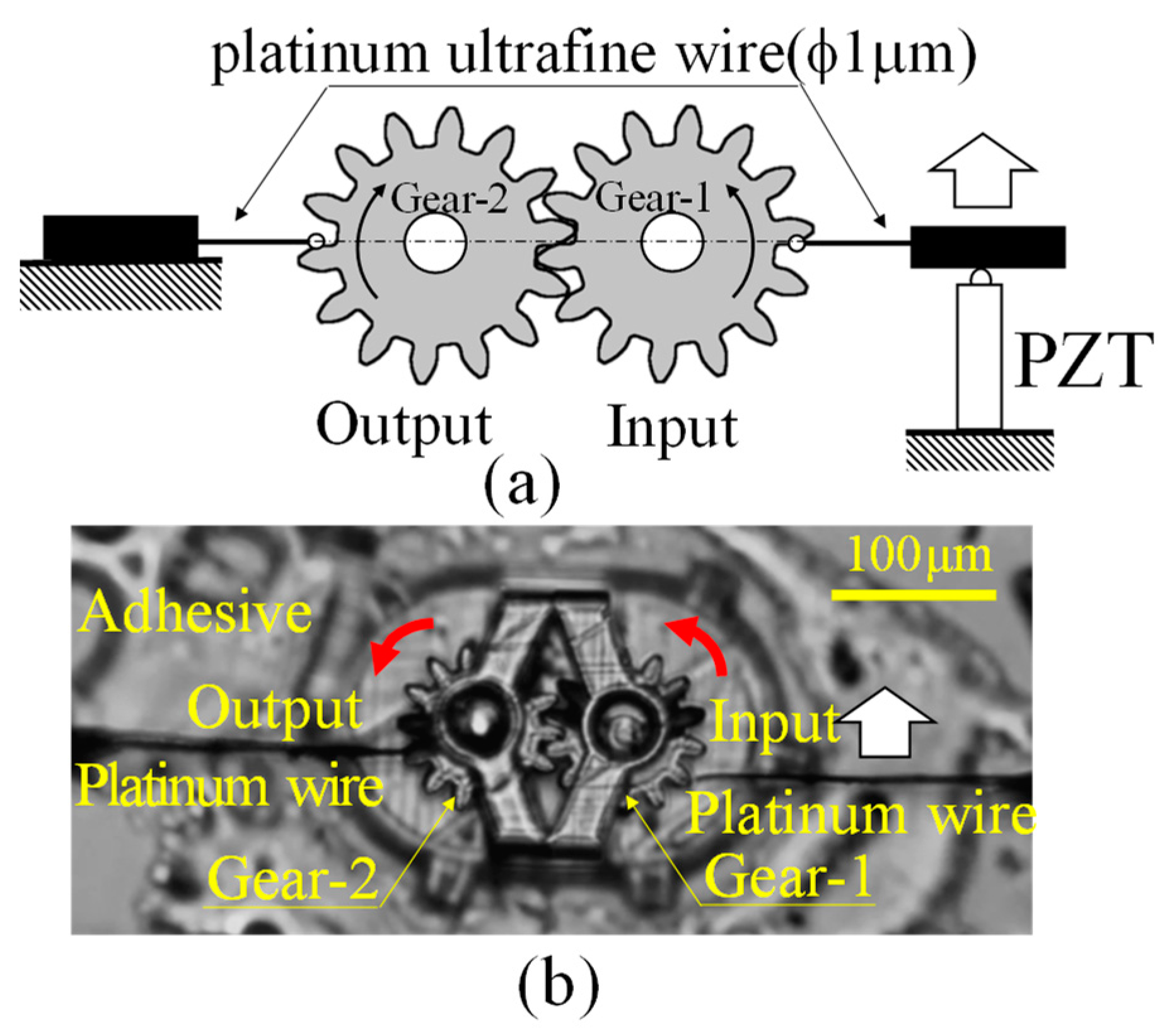
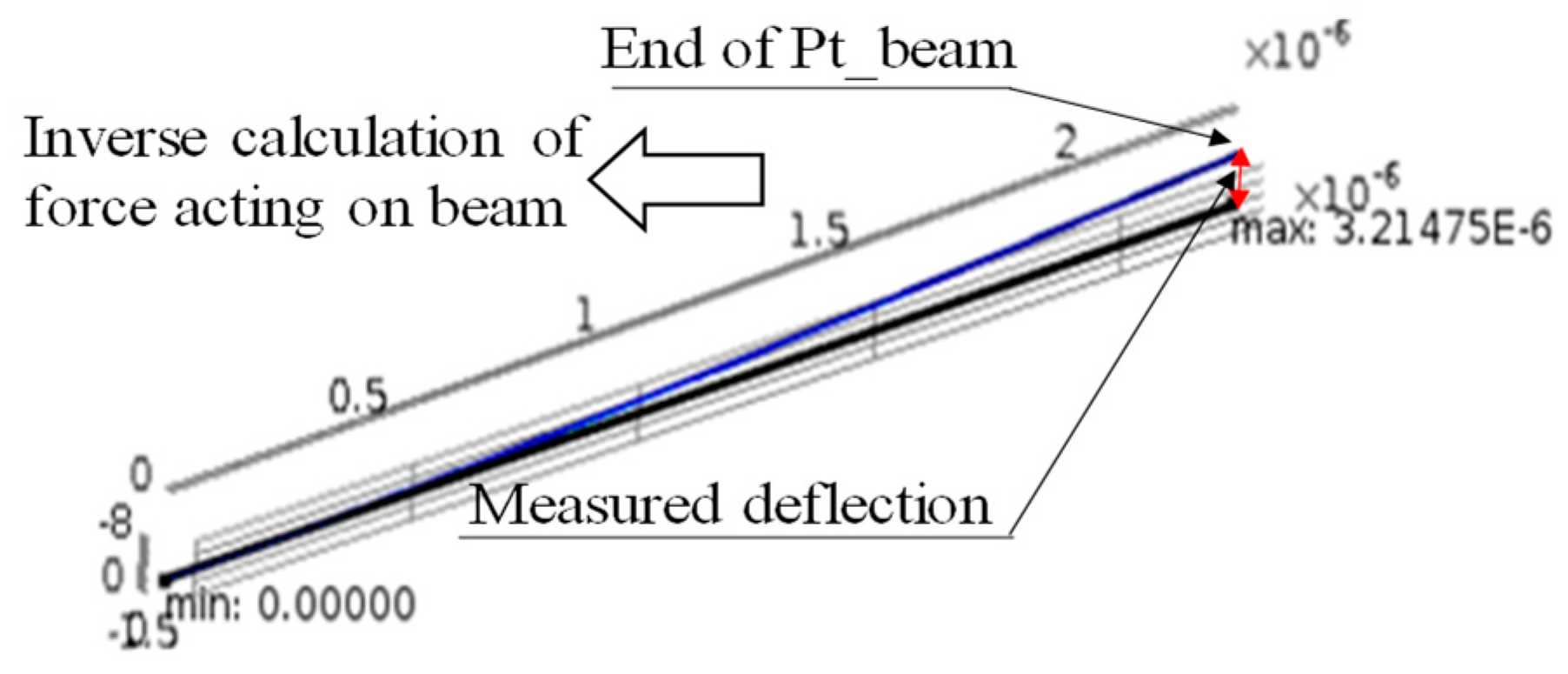
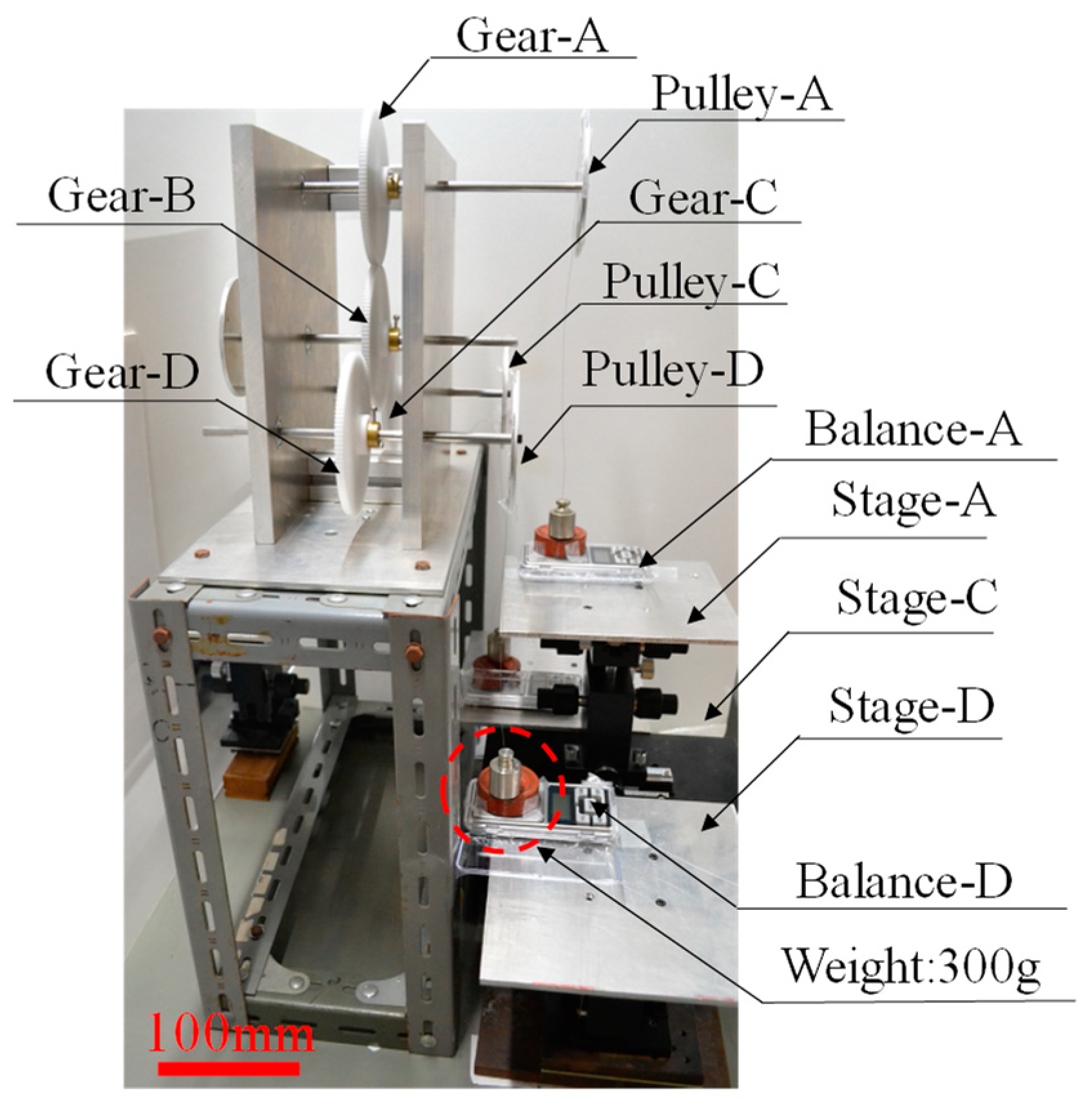
2.2.3. Micro-Domain Measurement of Power Transmission Characteristics Using the Moment Balance Method
3. Results and Discussion
3.1. Investigation of the Power Transmission Characteristics of Two Micro-Spur Gears
3.2. Investigation of the Power Transmission Characteristics of a Gear Train with Four Micro-Spur Gears under Load
3.2.1. Gear Train with Four Micro-Spur Gears Used in the Experiment
3.2.2. Power Transmission Efficiency of a Gear Train with Four Gears Considering the Load
3.2.3. Comparison of the Power Transmission Characteristics of Four Micro-Spur Gears with Those of a Gear Train in the Macro-Domain
- (1)
- First, it is necessary to consider the design of the gear train, taking into account the fact that the transmission loss in the micro-range is greater than that in the macro-range.
- (2)
- When performing activities using power in the micro-range, the mechanism should be designed so that the power source is installed as close as possible to the actual object to be driven, while the installation location of the power source should be considered so that transmission losses do not occur. If a gear train is used, the power transmission mechanism should be designed to use a simple gear train in which power is transmitted through a shaft.
- (3)
- In the micro-range, a gear train, such as a planetary gear train in which multiple gears mesh with a single gear, which may cause mutual loading, is not considered an effective design for reducing transmission losses.
- (4)
- If a power transmission mechanism using a gear train is to be used in the micro-range, it is necessary to consider a solid lubrication mechanism to replace oil lubrication in the macro-range [17].
- (5)
- If a power transmission mechanism using a gear train is to be used in the micro-range, the involute gears that are currently primarily used in the macro-range have convex tooth surfaces that come into contact with each other, resulting in a situation where a large frictional force acts on the gears. Therefore, it is believed that a detailed study of a gear train suitable for use in the micro-range is required, such as a module suitable for the micro-range, pressure angle, solid lubrication (as mentioned above), and increased tooth surface strength.
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frazier, A.B. The miniaturization technologies: Past, present, and future. IEEE Trans. Ind. Electron. 1995, 42, 423–430. [Google Scholar] [CrossRef]
- Nielson, G.N. Dynamic pull-in of parallel-plate and torsional electrostatic MEMS actuators. J. Microelectromech. Syst. 2006, 15, 811–821. [Google Scholar] [CrossRef]
- Rao, R. An Introduction to MEMS (Micro-Electromechanical Systems); Prime Faraday Partnership: Loughborough, UK, 2002; ISBN 1-84402-020-7. [Google Scholar]
- Hajare, R.; Reddy, V.; Srikanth, R. MEMS based sensor—A comprehensive review of commonly used fabrication technique. Mater. Today Proc. 2022, 49, 720–730. [Google Scholar] [CrossRef]
- Pattanaik, P.; Ojha, M. Review on challenges in MEMS technology. Mater. Today Proc. 2023, 81, 224–226. [Google Scholar] [CrossRef]
- Faudzi, A.A.; Sabzehmeidani, M.Y.; Suzumori, K. Application of Micro-Electro-Mechanical Systems (MEMS) as Sensors: A Review. J. Robot. Mechatron. 2020, 32, 281–288. [Google Scholar] [CrossRef]
- Algamili, A.S.; Khir, M.H.M.; Dennis, J.O.; Ahmed, A.Y.; Alabsi, S.S.; Ba Hashwan, S.S.; Junaid, M.M. A review of actuation and sensing mechanisms in MEMS-based sensor devices. Nanoscale Res. Lett. 2021, 16, 16. [Google Scholar] [CrossRef]
- Almuramady, N.; Borodich, F.M.; Goryacheva, I.G.; Torskaya, E.V. Damage of functionalized self-assembly monomolecular layers applied to silicon microgear MEMS. Tribol. Int. 2019, 129, 202–213. [Google Scholar] [CrossRef]
- Zhang, B.; Lee, H.; Byun, D. Direct Fabrication of Metallic Microgear via Electrohydrodynamic Inkjet 3D Printing. Adv. Eng. Mater. 2020, 22, 1901362. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, X.N.; Sun, C. Micro-stereolithography of polymeric and ceramic microstructructures. Sens. Actuators A Phys. 1999, 77, 149–156. [Google Scholar] [CrossRef]
- Arai, Y.; Yane, E.; Koyama, R. Feasibility of Optical Bearing Fabrication Using Radistion Pressure. Micromachiunes 2022, 13, 733. [Google Scholar] [CrossRef] [PubMed]
- Teodorescu, M.; Theodossiades, S.; Rahnejat, H. Impact dynamics of rough and surface protected MEMS gears. Tribol. Int. 2009, 42, 197–205. [Google Scholar] [CrossRef]
- Hegadekatte, V.; Hilgert, J.; Kraft, O.; Huber, N. Multi time scale simulations for wear prediction in micro-gears. Wear 2009, 268, 316–324. [Google Scholar] [CrossRef]
- Saotome, Y.; Iwazaki, H. Superplastic extrusion of microgear shaft of 10 μm inmodule. Microsyst. Technol. 2000, 8, 126–129. [Google Scholar] [CrossRef]
- Inoue, H.; Haga, S.; Maruo, S. Development of Optical Driven Microgears by Using Two-photon Microstereolithgraphy. IEEJ Trans. Sens. Micromach. 2006, 126, 216–221. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, H.; Fu, M.W. Size effect on process performance and product quality in progressive microforming of shafted gears revealed by experiment and numerical modeling. Adv. Manuf. 2023, 11, 1–20. [Google Scholar] [CrossRef]
- Niemann, G. Maschinenelemente; Springer-Verlag: Berlin, Germany, 1965. [Google Scholar] [CrossRef]
- Takeda, H.; Arai, Y. Development of optical actuator—Fabrication of micro rotor. In Proceedings of the International Symposium on Optomechatronics Technology 2016, Itabashi, Japan, 7–9 November 2016; p. 5. [Google Scholar]
- Sonoda, K.; Haraga, T.; Sunagawa, Y. Measurement of Power Transmission Efficiency of Gears. J. JSDE 2014, 49, 415–419. (In Japanese) [Google Scholar]
- (11 page). Available online: https://www.kggear.co.jp/wp-content/uploads/2023/02/KG4002_reference.pdf (accessed on 12 February 2024).
- (3 page). Available online: https://www.khkgears.co.jp/gear_technology/pdf/gijutu.pdf (accessed on 12 February 2024).
- Larson, H.J. Introduction to Probability Theory and Statistical Inference, 3rd ed.; John Wile and Sons: New York, NY, USA, 1982; pp. 411–462. [Google Scholar]
- McCollough, C. Statistical Concepts; McGraw Hill: New York, NY, USA, 1963; pp. 223–244. [Google Scholar]
- Welch, B.L. The significance of the difference between two means when the population variances are unequal. Biometrika 1938, 29, 350–362. [Google Scholar] [CrossRef]
- Doebelin, E.O. Measurement Systems, 4th ed.; McGraw Hill: New York, NY, USA, 1990; pp. 38–58. [Google Scholar]
- Anderson, T.W.; Darling, D.A. Asmptotic theory of certain “Goodness of Fit” criteria based on stochastic processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]

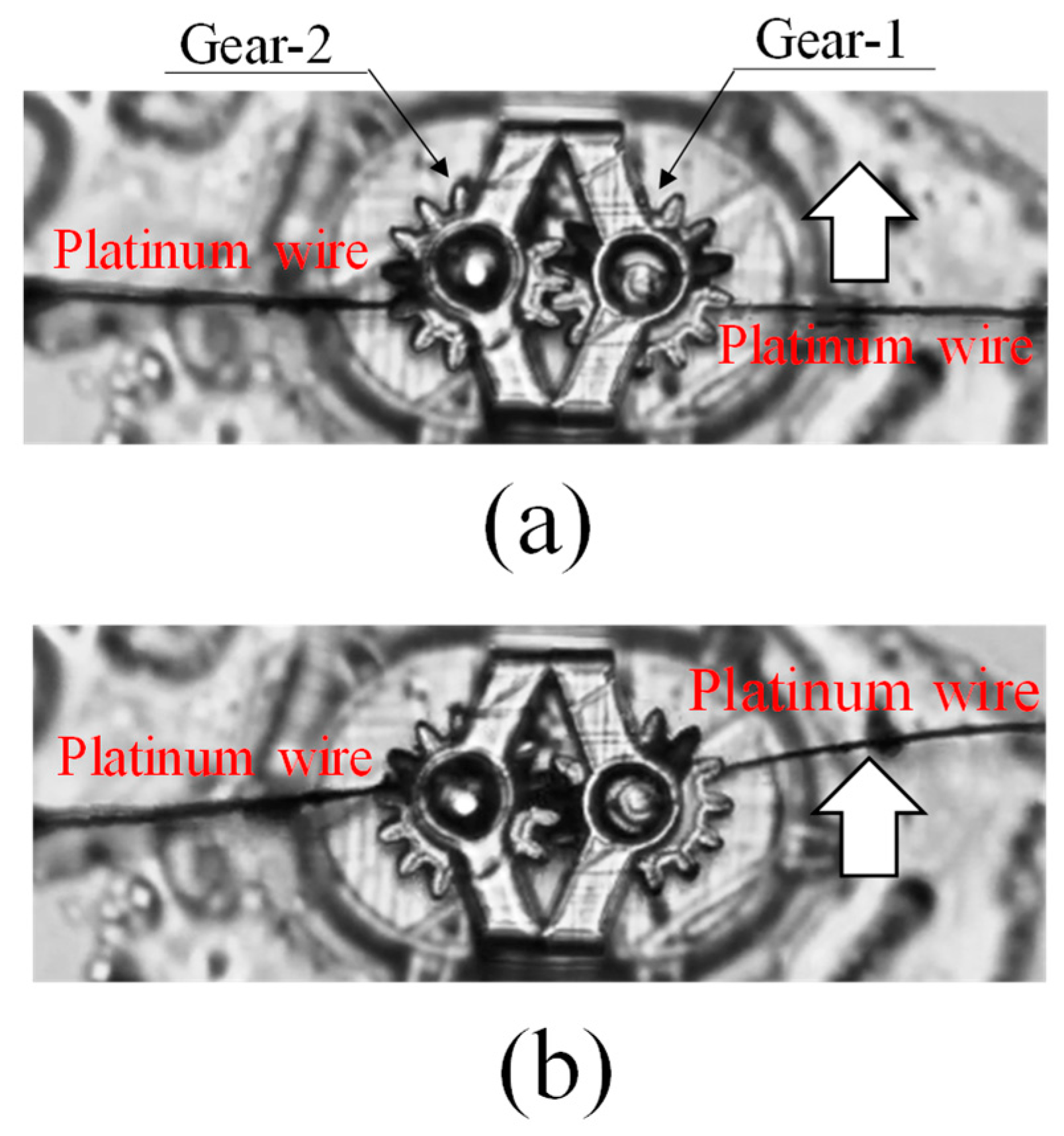

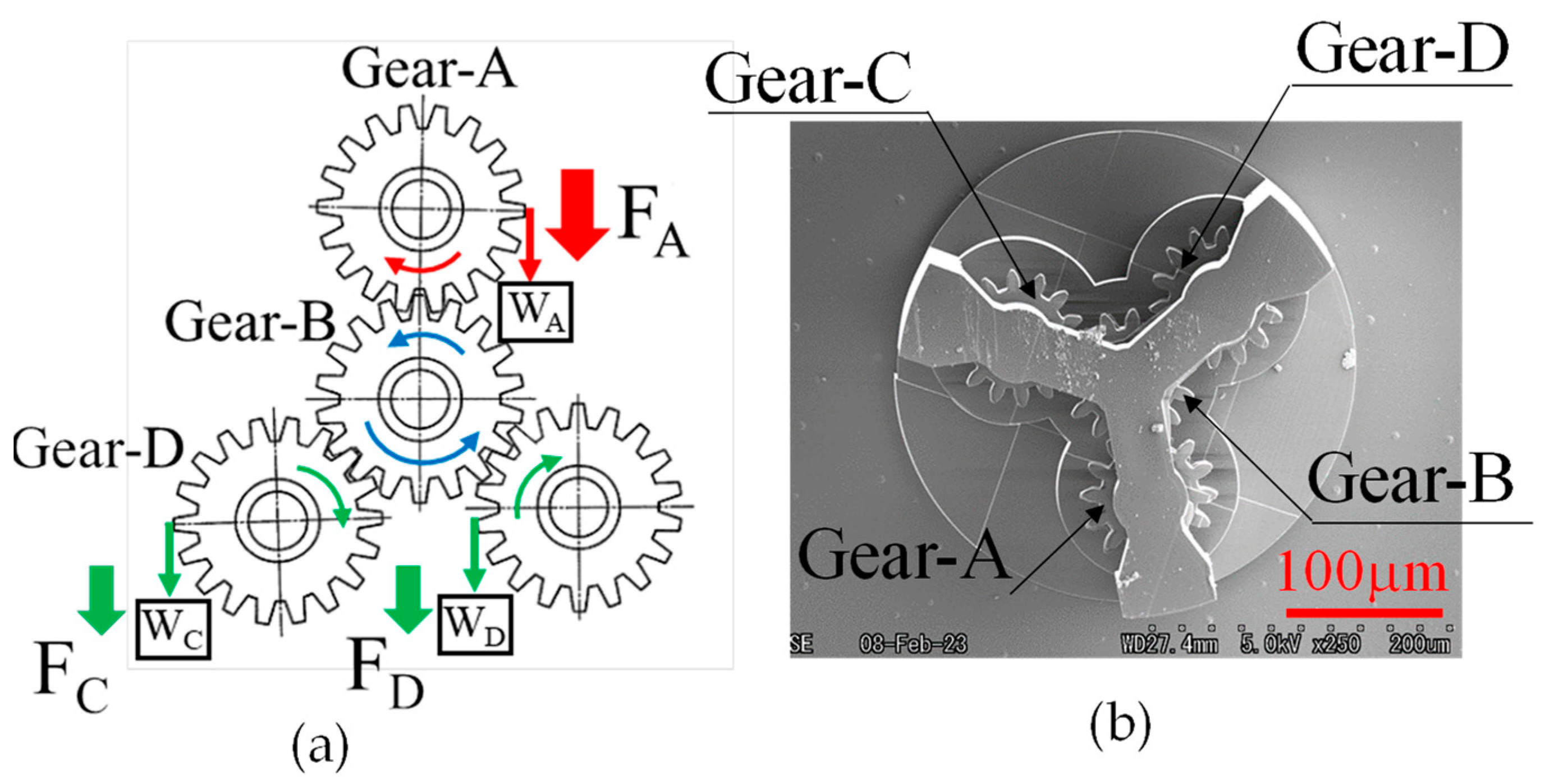
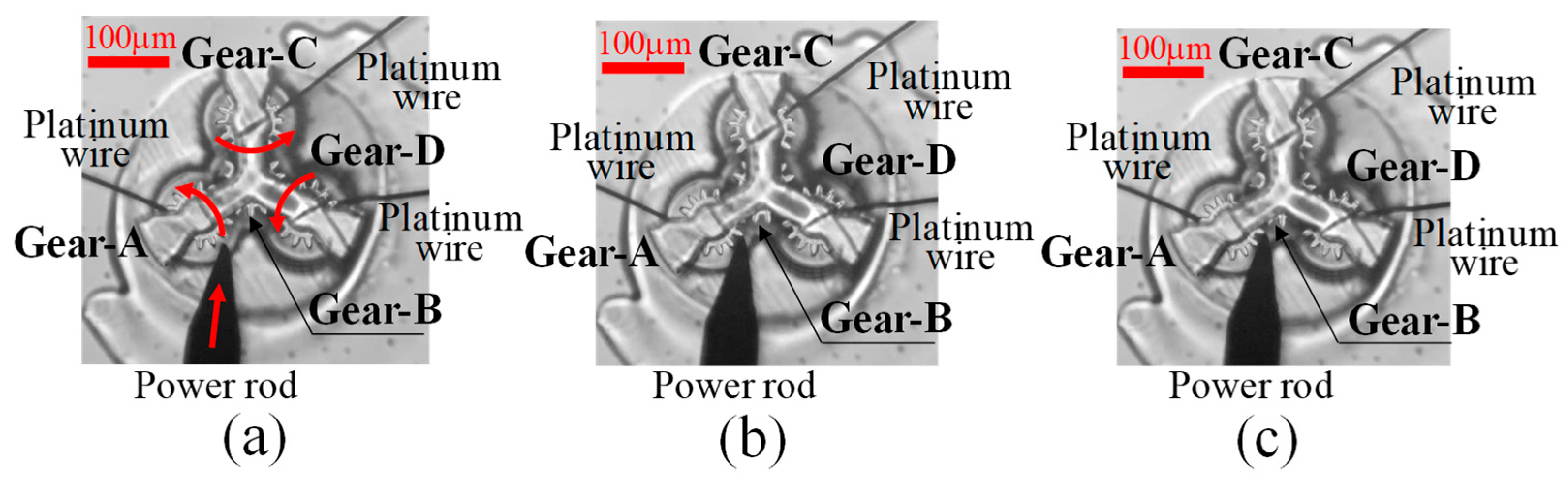

| Deflection of Wire [μm] | Force [μN] | Torque [pNm] | Efficiency | |
|---|---|---|---|---|
| Gear-1 | 11.43 | 3.06 | 0.129 | - |
| Gear-2 | 8.78 | 2.87 | 0.121 | 0.937 |
| Micro-Gear Train | Macro-Gear Train | |
|---|---|---|
| Efficiency [%] | 94.1 | 94.3 |
| Square sum | 82.6 | 68.2 |
| Unbiased dispersion | 9.2 | 3.4 |
| Number of measurements | 10 | 20 |
| p-value (Anderson-Darling test) | p = 0.573 > 0.05 | p = 0.429 > 0.05 |
| F0 = Vmicro/Vmacro | F0 = 2.71 < F(9, 19; 0.025) = 2.89 | |
| t0 | t0 = 0.00223 < t(28, 0.025) = 2.048 | |
| Deflection of Wire [μm] | Force [μN] | Torque [pNm] | Efficiency [%] | ||
|---|---|---|---|---|---|
| (1) Input | Gear-A | 13.60 | 9.58 | 432.0 | - |
| (2) Output | Gear-C | 8.50 | 3.72 | 161.0 | 37.2 |
| Gear-D | 11.20 | 3.56 | 153.0 | 35.5 | |
| (3) | Gear-C + Gear-D | - | - | 314.0 | 72.7 (314.0/432.0) |
| Micro-Gear Train | Macro-Gear Train | |
|---|---|---|
| Efficiency [%] | 69.6 | 75.5 |
| Square sum | 61.5 | 148.7 |
| Unbiased dispersion | 6.83 | 7.82 |
| Number of measurements | 10 | 20 |
| p-value (Anderson-Darling test) | p = 0.548 > 0.05 | p = 0.214 > 0.05 |
| F0 = Vmicro/Vmacro | F0 =1.146 < F(19, 9; 0.025) = 2.88 | |
| t0 | t0 = 5.56 > t(28, 0.025) = 2.048 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arai, Y. Consideration of Power Transmission Characteristics in a Micro-Gear Train. Micromachines 2024, 15, 284. https://doi.org/10.3390/mi15020284
Arai Y. Consideration of Power Transmission Characteristics in a Micro-Gear Train. Micromachines. 2024; 15(2):284. https://doi.org/10.3390/mi15020284
Chicago/Turabian StyleArai, Yasuhiko. 2024. "Consideration of Power Transmission Characteristics in a Micro-Gear Train" Micromachines 15, no. 2: 284. https://doi.org/10.3390/mi15020284
APA StyleArai, Y. (2024). Consideration of Power Transmission Characteristics in a Micro-Gear Train. Micromachines, 15(2), 284. https://doi.org/10.3390/mi15020284






