Numerical Simulations of Combined Dielectrophoresis and Alternating Current Electrothermal Flow for High-Efficient Separation of (Bio)Microparticles
Abstract
:1. Introduction
2. Separator Design and Numerical Simulation
2.1. Design Principle
2.2. Separator Layout
2.3. Governing Equations and Boundary Conditions
2.3.1. Dielectrophoresis and ACET
2.3.2. Governing Equations and Boundary Conditions
2.3.3. Model and Mesh-Independence Study
3. Results and Discussion
3.1. Physical Field Distribution
3.2. Combined Effect of DEP and ACET on the Separation of PS Microparticles
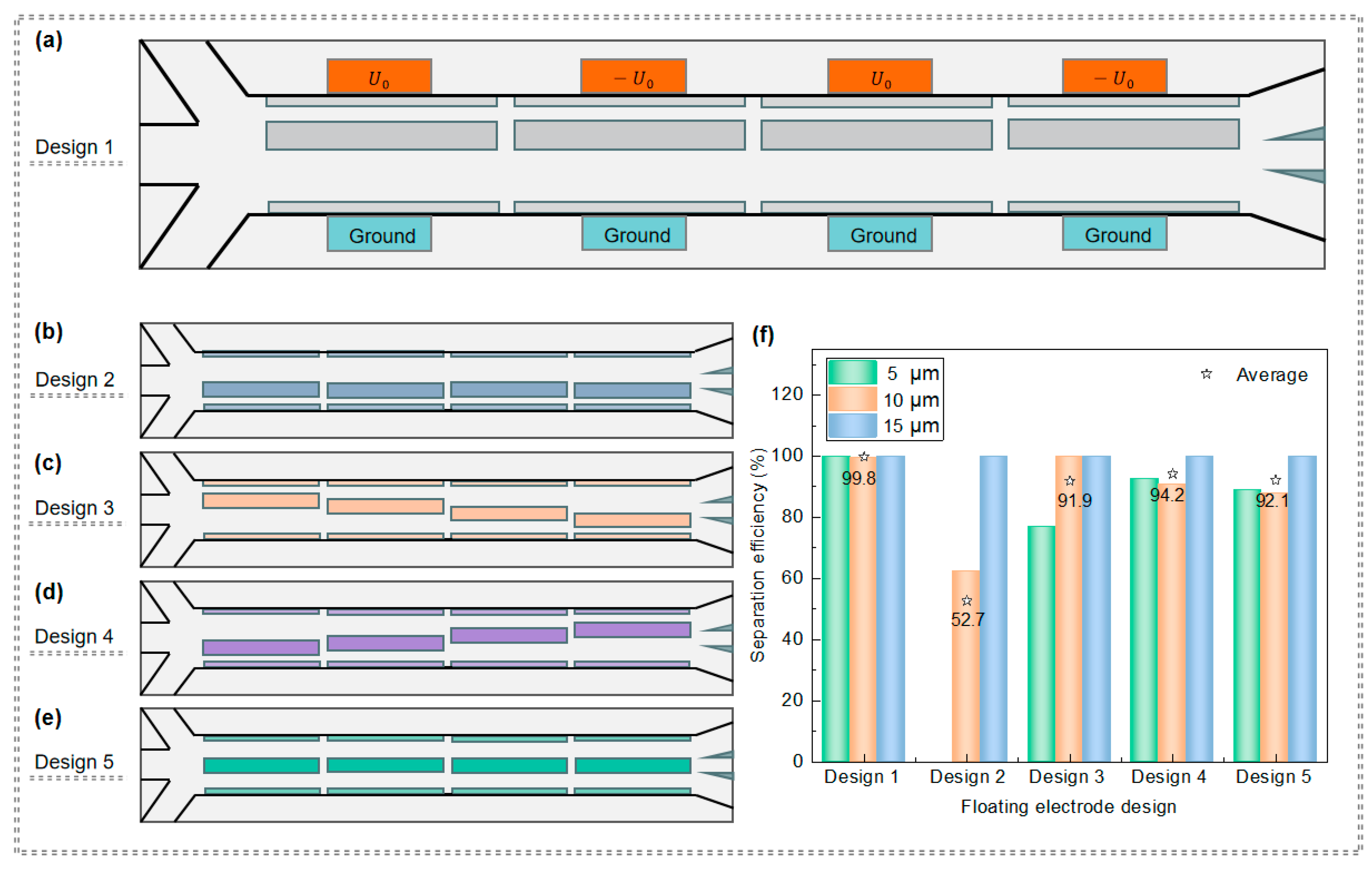
3.2.1. Impact of the Floating Electrode Arrangement on PS Particle Separation
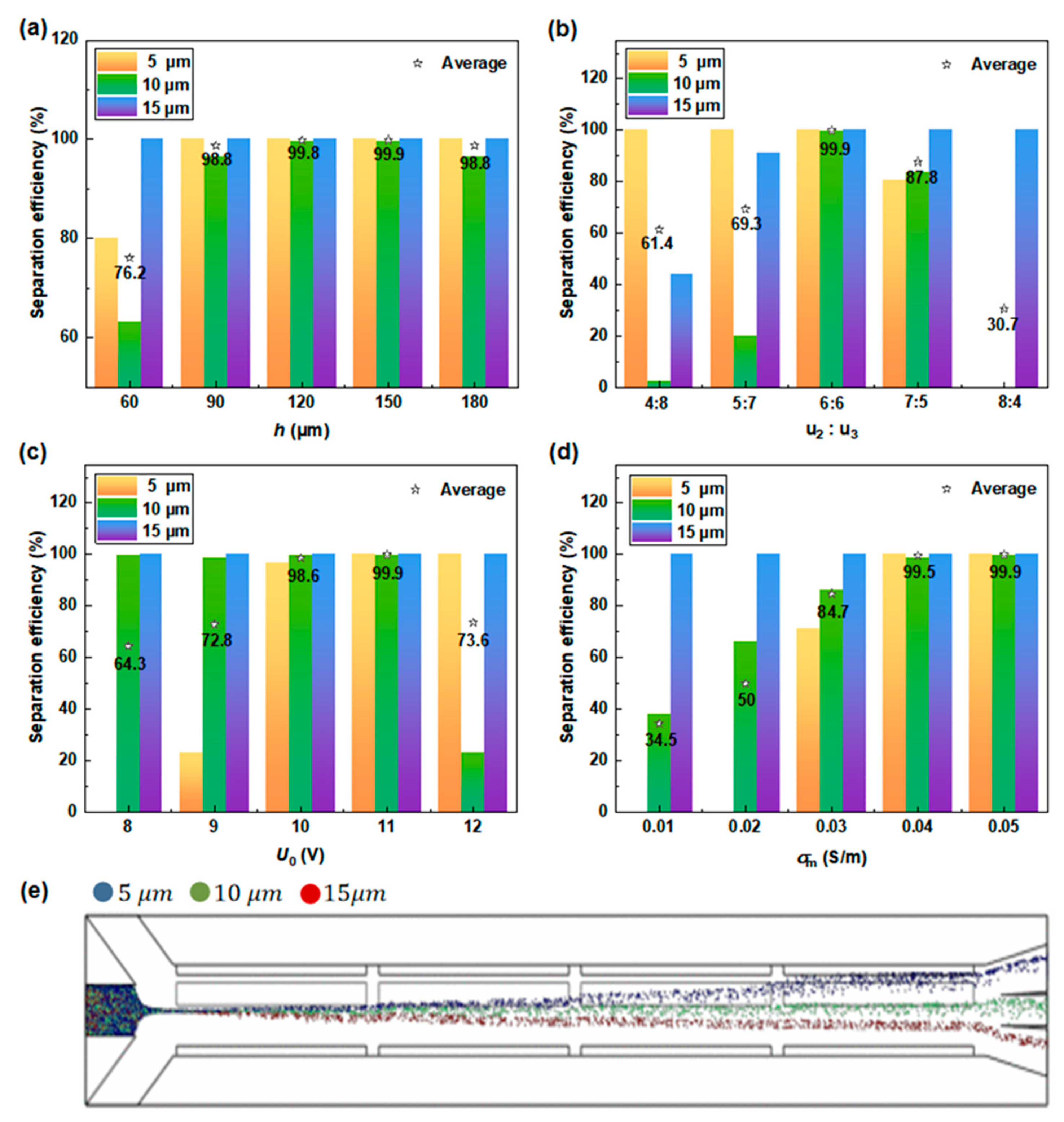
3.2.2. Impact of Operating Parameters on PS Particle Separation
3.3. Separation of Biological Cells
3.3.1. Isolation of CTCs from Normal Blood Cells
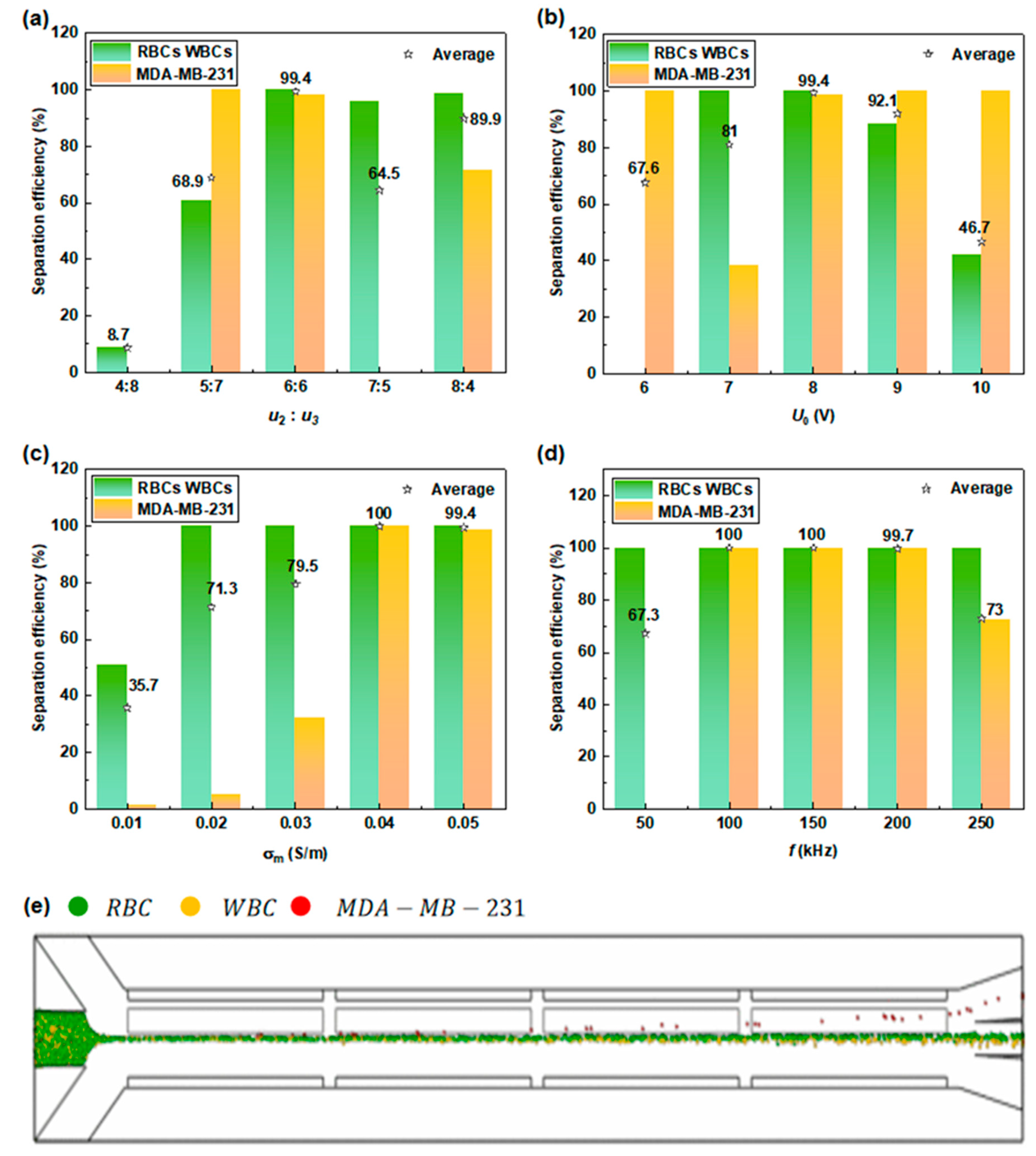
3.3.2. Separation of Red and White Blood Cells
3.3.3. Separation of Viable and Nonviable Yeast Cells
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hata, M.; Suzuki, M.; Yasukawa, T. Selective retrieval of antibody-secreting hybridomas in cell arrays based on the dielectrophoresis. Biosens. Bioelectron. 2022, 209, 114250. [Google Scholar] [CrossRef]
- Zhao, Y.; Gu, Y.; Gao, G. Piezoelectricity induced by pulsed hydraulic pressure enables in situ membrane demulsification and oil/water separation. Water Res. 2022, 215, 118245. [Google Scholar] [CrossRef]
- Oshiro, K.; Wakizaka, Y.; Takano, M.; Itoi, T.; Ohge, H.; Koba, K.; Yarimizu, K.; Fujiyoshi, S.; Maruyama, F. Fabrication of a new all-in-one microfluidic dielectrophoresis integrated chip and living cell separation. Iscience 2022, 25, 103776. [Google Scholar] [CrossRef]
- Muhsin, S.A.; Al-Amidie, M.; Shen, Z.; Mlaji, Z.; Liu, J.; Abdullah, A.; El-Dweik, M.; Zhang, S.; Almasri, M. A microfluidic biosensor for rapid simultaneous detection of waterborne pathogens. Biosens. Bioelectron. 2022, 203, 113993. [Google Scholar] [CrossRef]
- Russo, G.I.; Musso, N.; Romano, A.; Caruso, G.; Petralia, S.; Lanzano, L.; Broggi, G.; Camarda, M. The Role of Dielectrophoresis for Cancer Diagnosis and Prognosis. Cancers 2022, 14, 198. [Google Scholar] [CrossRef]
- Vaghef-Koodehi, A.; Dillis, C.; Lapizco-Encinas, B.H. High-Resolution Charge-Based Electrokinetic Separation of Almost Identical Microparticles. Anal. Chem. 2022, 94, 6451–6456. [Google Scholar] [CrossRef]
- Torres-Castro, K.; Honrado, C.; Varhue, W.B.; Farmehini, V.; Swami, N.S. High-throughput dynamical analysis of dielectrophoretic frequency dispersion of single cells based on deflected flow streamlines. Anal. Bioanal. Chem. 2020, 412, 3847–3857. [Google Scholar] [CrossRef]
- Giesler, J.; Weirauch, L.; Pesch, G.R.; Baune, M.; Thöming, J. Semi-continuous dielectrophoretic separation at high throughput using printed circuit boards. Sci. Rep. 2023, 13, 20696. [Google Scholar] [CrossRef]
- Khan, M.; Chen, X.L. Numerical study of dielectrophoresis-modified inertial migration for overlapping sized cell separation. Electrophoresis 2022, 43, 879–891. [Google Scholar] [CrossRef]
- Jiang, A.Y.L.; Yale, A.R.; Aghaamoo, M.; Lee, D.H.; Lee, A.P.; Adams, T.N.G.; Flanagan, L.A. High-throughput continuous dielectrophoretic separation of neural stem cells. Biomicrofluidics 2019, 13, 064111. [Google Scholar] [CrossRef]
- Zellner, P.; Agah, M. Silicon insulator-based dielectrophoresis devices for minimized heating effects. Electrophoresis 2012, 33, 2498–2507. [Google Scholar] [CrossRef]
- Yan, Y.; Guo, D.; Wen, S.Z. Joule Heating Effects on Two-phase Flows in Dielectrophoresis Microchips. Biochip J. 2017, 11, 196–205. [Google Scholar] [CrossRef]
- Tian, L.; Ye, Z.; Gui, L. A Study of Dielectrophoresis-Based Liquid Metal Droplet Control Microfluidic Device. Micromachines 2021, 12, 340. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Du, F.; Pesch, G.R.; Köser, J.; Baune, M.; Thöming, J. Microparticle trajectories in a high-throughput channel for contact-free fractionation by dielectrophoresis. Chem. Eng. Sci. 2016, 153, 34–44. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Pesch, G.R.; Baune, M.; Du, F.; Liu, X. Rational Design and Numerical Analysis of a Hybrid Floating cIDE Separator for Continuous Dielectrophoretic Separation of Microparticles at High Throughput. Micromachines 2022, 13, 582. [Google Scholar] [CrossRef] [PubMed]
- Kwizera, E.A.; Sun, M.; White, A.M.; Li, J.; He, X. Methods of Generating Dielectrophoretic Force for Microfluidic Manipulation of Bioparticles. ACS Biomater. Sci. Eng. 2021, 7, 2043–2063. [Google Scholar] [CrossRef]
- MacQueen, L.A.; Buschmann, M.D.; Wertheimer, M.R. Gene delivery by electroporation after dielectrophoretic positioning of cells in a non-uniform electric field. Bioelectrochemistry 2008, 72, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Derakhshan, R.; Ramiar, A.; Ghasemi, A. Numerical investigation into continuous separation of particles and cells in a two-component fluid flow using dielectrophoresis. J. Mol. Liq. 2020, 310, 113211. [Google Scholar] [CrossRef]
- Sun, H.Z.; Ren, Y.K.; Hou, L.K.; Tao, Y.; Liu, W.Y.; Jiang, T.Y.; Jiang, H.Y. Continuous Particle Trapping, Switching, and Sorting Utilizing a Combination of Dielectrophoresis and Alternating Current Electrothermal Flow. Anal. Chem. 2019, 91, 5729–5738. [Google Scholar] [CrossRef]
- Green, N.G.; Ramos, A.; Gonzalez, A.; Castellanos, A.; Morgan, H. Electrothermally induced fluid flow on microelectrodes. J. Electrostat. 2001, 53, 71–87. [Google Scholar] [CrossRef]
- Hawkins, B.G.; Kirby, B.J. Electrothermal flow effects in insulating (electrodeless) dielectrophoresis systems. Electrophoresis 2010, 31, 3622–3633. [Google Scholar] [CrossRef] [PubMed]
- Sridharan, S.; Zhu, J.; Hu, G.; Xuan, X. Joule heating effects on electroosmotic flow in insulator-based dielectrophoresis. Electrophoresis 2011, 32, 2274–2281. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X.; Ren, Y.; Yan, Y.; Wu, A. Numerical simulation of circulating tumor cell separation in a dielectrophoresis based Y-Y shaped microfluidic device. Sep. Purif. Technol. 2021, 255, 117343. [Google Scholar] [CrossRef]
- Lian, M.; Islam, N.; Wu, J. AC electrothermal manipulation of conductive fluids and particles for lab-chip applications. Iet Nanobiotechnol. 2007, 1, 36–43. [Google Scholar] [CrossRef]
- Sun, H.; Ren, Y.; Tao, Y.; Liu, W.; Jiang, T.; Jiang, H. Combined alternating current electrothermal and dielectrophoresis-induced tunable patterning to actuate on-chip microreactions and switching at a floating electrode. Sens. Actuators B Chem. 2020, 304, 127397. [Google Scholar] [CrossRef]
- Loire, S.; Kauffmann, P.; Mezić, I.; Meinhart, C.D. A theoretical and experimental study of ac electrothermal flows. J. Phys. D Appl. Phys. 2012, 45, 185301. [Google Scholar] [CrossRef]
- Riahi, R.; Gogoi, P.; Sepehri, S.; Zhou, Y.; Handique, K.; Godsey, J.; Wang, Y. A novel microchannel-based device to capture and analyze circulating tumor cells (CTCs) of breast cancer. Int. J. Oncol. 2014, 44, 1870–1878. [Google Scholar] [CrossRef] [PubMed]
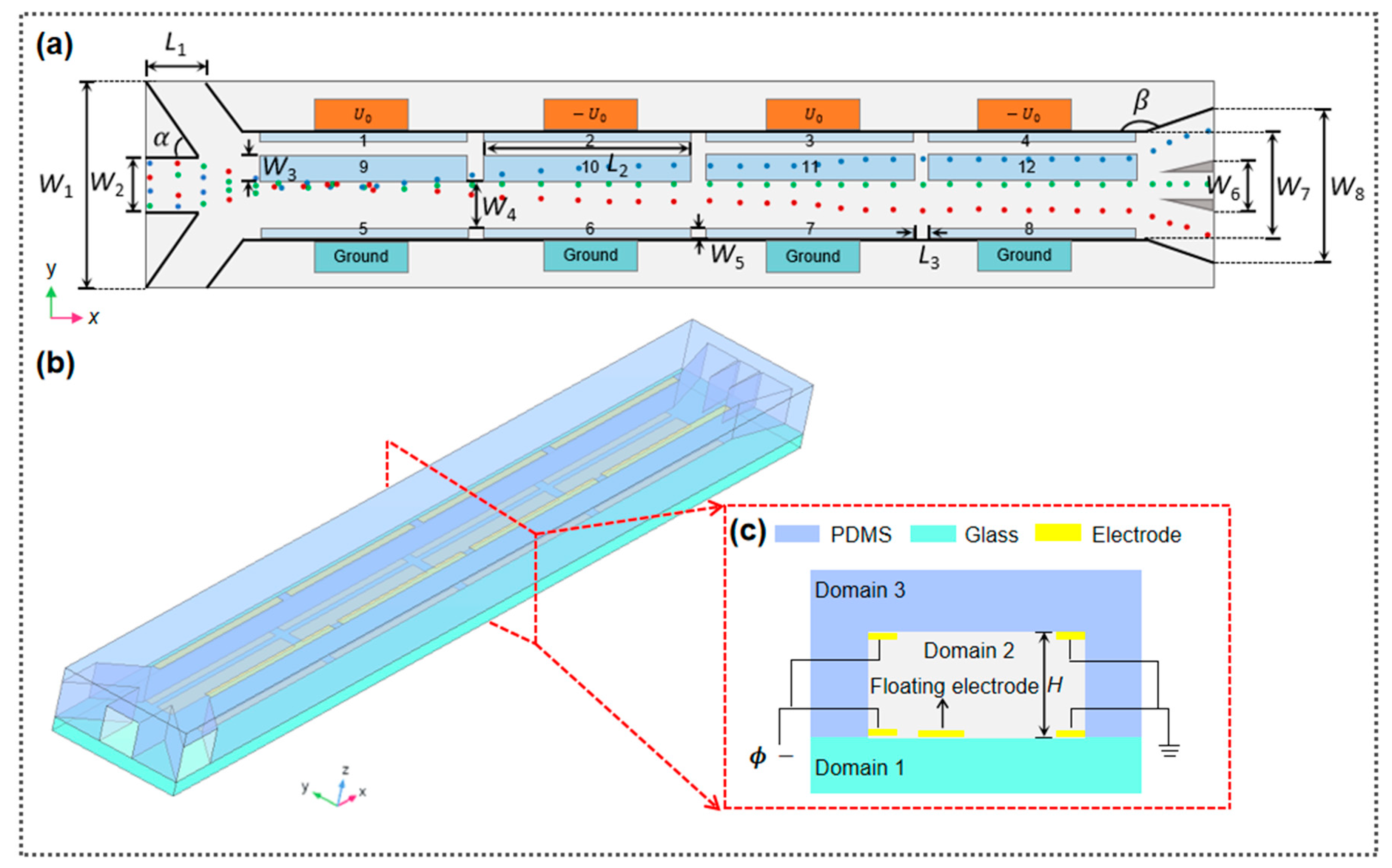
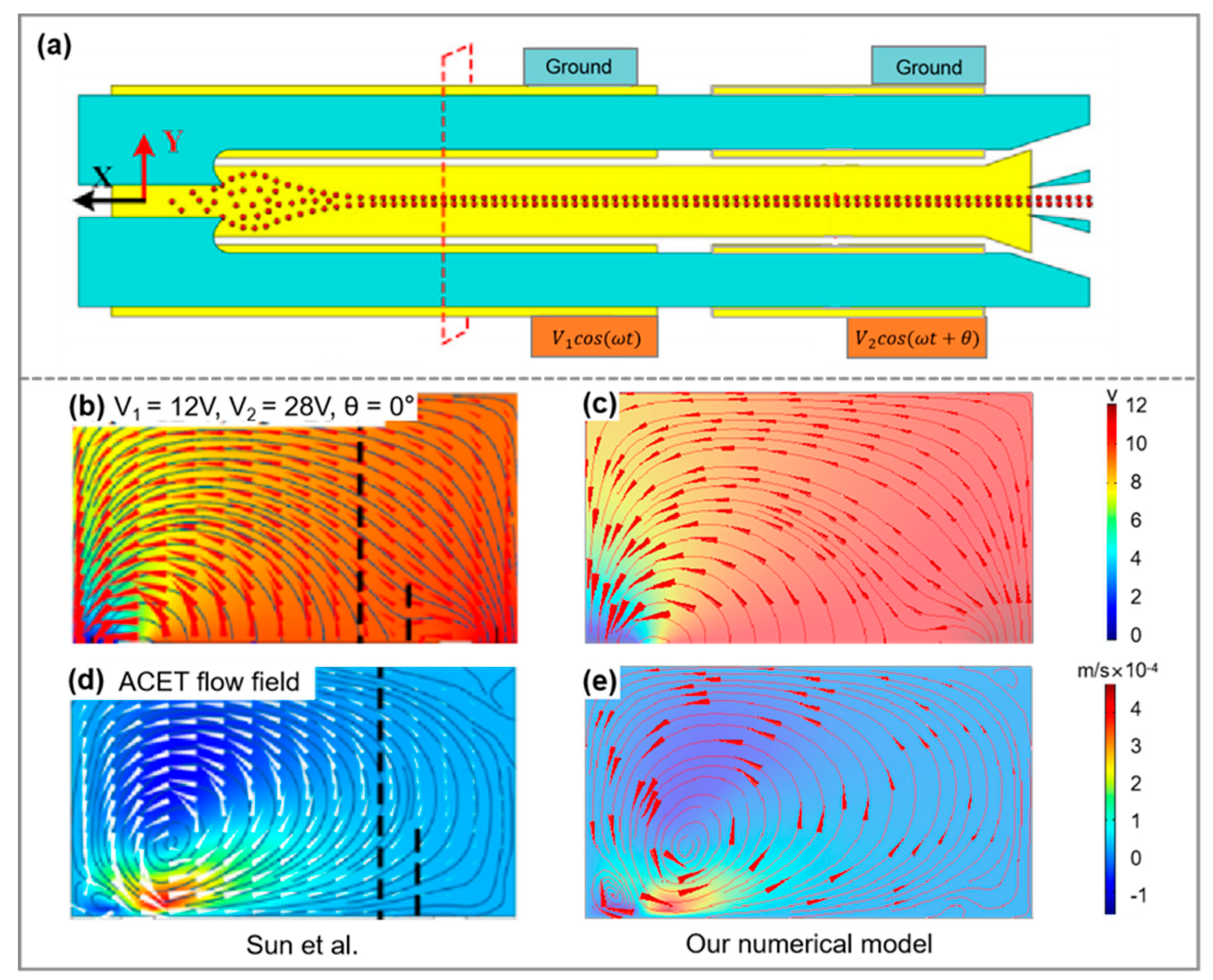
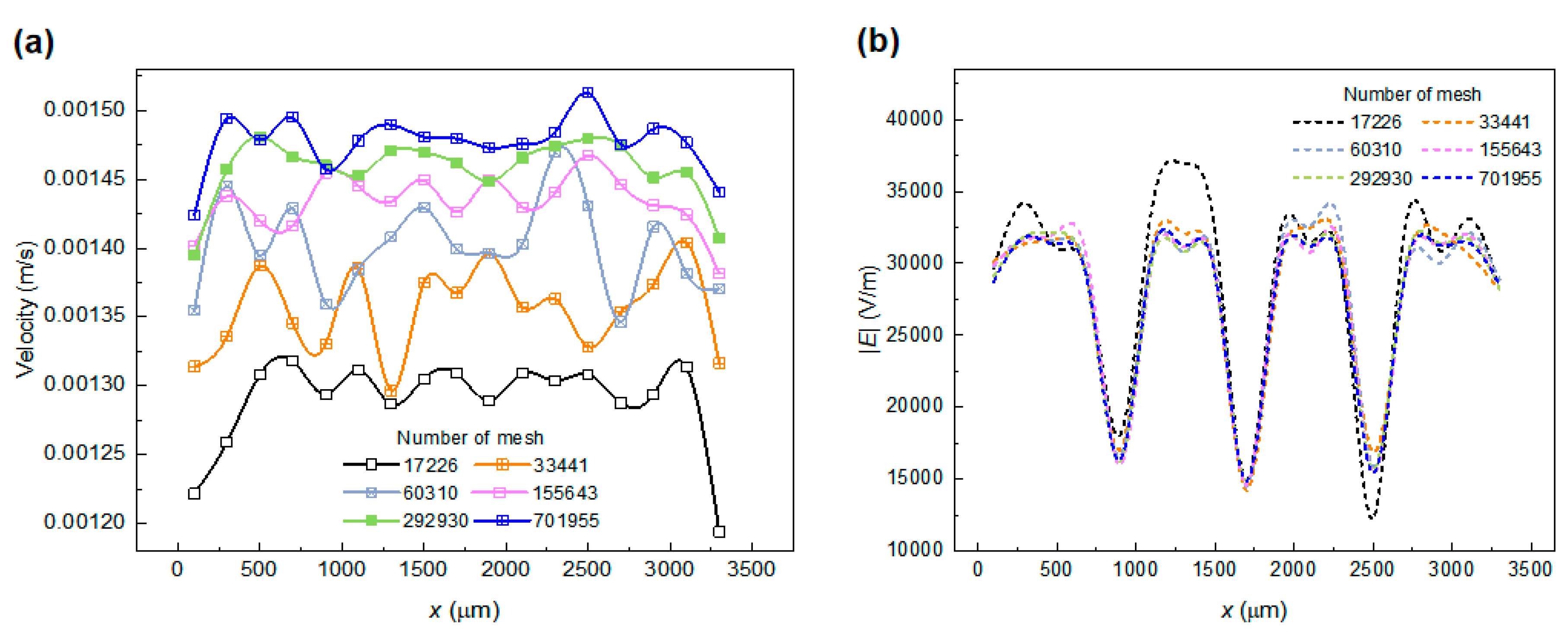
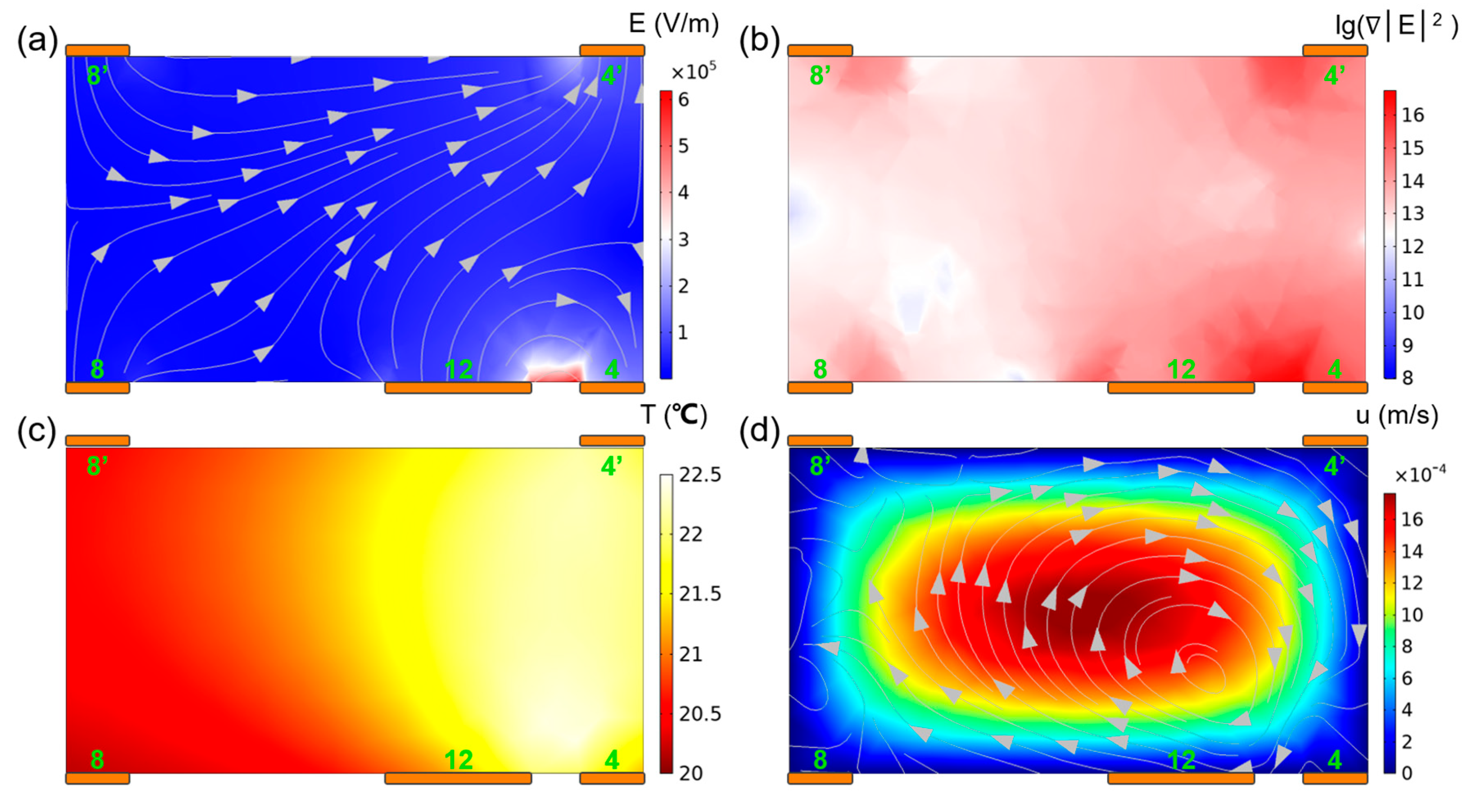


| Parameters | L1 | L2 | L3 | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | H | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Value (μm) | 210 | 775 | 50 | 560 | 150 | 68 | 120 | 30 | 110 | 270 | 390 | 152 | 45° | 166.5° |
| PS | RBSs | Granulocytes | MDA-MB-231 | Medium | |
|---|---|---|---|---|---|
| Diameter (µm) | 5, 10, 15 | 5 | 9.42 0.46 | 12.4 1.16 | |
| Density (kg/m3) | 1050 | 1050 | 1050 | 1050 | 1000 |
| Dynamic viscosity () | 0.001 | ||||
| Conductivity (S/m) | 8, 2, 1.14( | 0.31 | 0.6 | 0.62 | 0.001~0.055 |
| Dielectric constant | 2.55 | 59 | 151 | 52 | 80 |
| Membrane conductivity (S/m) | |||||
| Dielectric constant of membrane | 4.44 | 5 | 11.75 | ||
| Membrane thickness (nm) | 9 | 4 | 4 |
| Current Module | Domain/Boundary Conditions (Scope of Application) | Governing Conditions/Equations |
|---|---|---|
| Conservation of current (domains 1 and 2) | ||
| Initial values (fields 1 and 2) | ||
| Electrical insulation (wall) | ||
| Potential 1 (electrodes 1, 1’, 3, and 3’) | ||
| Potential 2 (electrodes 2, 2’, 4, and 4’) | ||
| Ground (electrodes 5, 5’–8, and 8’) | ||
| Suspension potential (electrodes 9–12) | ||
| Laminar flow module | ||
| Entrance (entrances 1, 2, and 3) | ||
| Export (exports 1, 2, and 3) | ||
| No slip (wall, electrode) | ||
| Volume Force (domain 3) | ||
| Heat-transfer fluid | ||
| Entrance (entrances 1, 2, and 3) | ||
| Export (exports 1, 2, and 3) | ||
| Temperature (wall) | ||
| Particle tracking | ||
| Entrance (entrance 2) | ||
| Export (exports 1, 2, and 3) | ||
| Gravity (domain 3) | ||
| Drag (domain 3) | ||
| DEP force (domain 3) |
| Dielectric Properties | Viable Yeast Cell | Nonviable Yeast Cell |
|---|---|---|
| Internal radius (μm) | 3.772 | 3.242 |
| Membrane radius (μm) | 3.78 | 3.25 |
| Wall radius (μm) | 4 | 3.5 |
| Intracellular dielectric constant | 50 | 50 |
| Membrane permittivity | 6 | 6 |
| Cell wall permittivity | 60 | 60 |
| Intracellular electrical conductivity (S/m) | 0.2 | 7 × 10−3 |
| Cell membrane conductivity (S/m) | 2.5 × 10−7 | 1.6 × 10−4 |
| Cell wall conductivity (S/m) | 1.4 × 10−2 | 1.5 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Li, Y.; Du, F.; Nie, Z.; Wei, G.; Wang, Y.; Liu, X. Numerical Simulations of Combined Dielectrophoresis and Alternating Current Electrothermal Flow for High-Efficient Separation of (Bio)Microparticles. Micromachines 2024, 15, 345. https://doi.org/10.3390/mi15030345
Jiang H, Li Y, Du F, Nie Z, Wei G, Wang Y, Liu X. Numerical Simulations of Combined Dielectrophoresis and Alternating Current Electrothermal Flow for High-Efficient Separation of (Bio)Microparticles. Micromachines. 2024; 15(3):345. https://doi.org/10.3390/mi15030345
Chicago/Turabian StyleJiang, Hao, Yalin Li, Fei Du, Zhaoguang Nie, Gang Wei, Yan Wang, and Xiaomin Liu. 2024. "Numerical Simulations of Combined Dielectrophoresis and Alternating Current Electrothermal Flow for High-Efficient Separation of (Bio)Microparticles" Micromachines 15, no. 3: 345. https://doi.org/10.3390/mi15030345
APA StyleJiang, H., Li, Y., Du, F., Nie, Z., Wei, G., Wang, Y., & Liu, X. (2024). Numerical Simulations of Combined Dielectrophoresis and Alternating Current Electrothermal Flow for High-Efficient Separation of (Bio)Microparticles. Micromachines, 15(3), 345. https://doi.org/10.3390/mi15030345








