Design and Optimization of MEMS Resonant Pressure Sensors with Wide Range and High Sensitivity Based on BP and NSGA-II
Abstract
:1. Introduction
2. Principle and Design of High-Sensitivity and Wide Range Resonator Structure
3. Mathematical Modeling and Parametric Analysis of Resonators
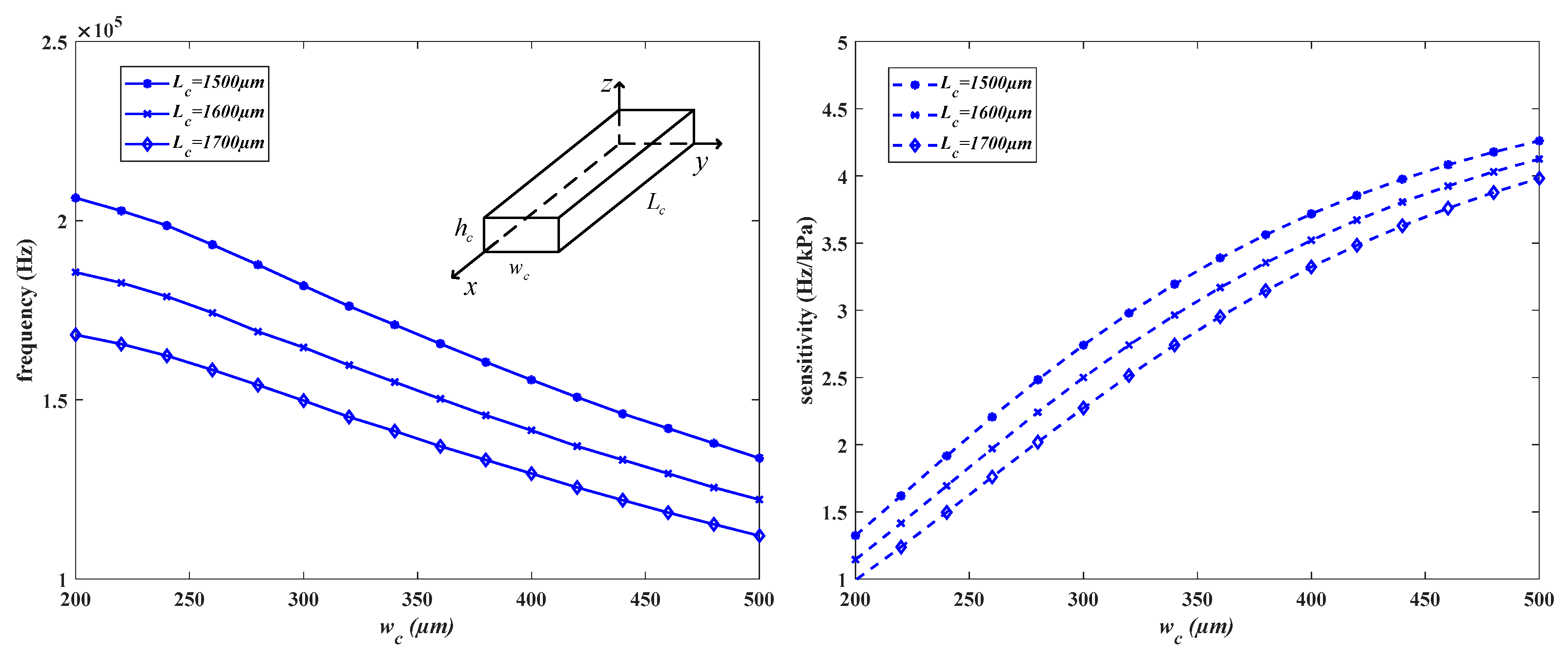
3.1. Analysis of the Connecting Beam
3.2. Analysis of the Diaphragm
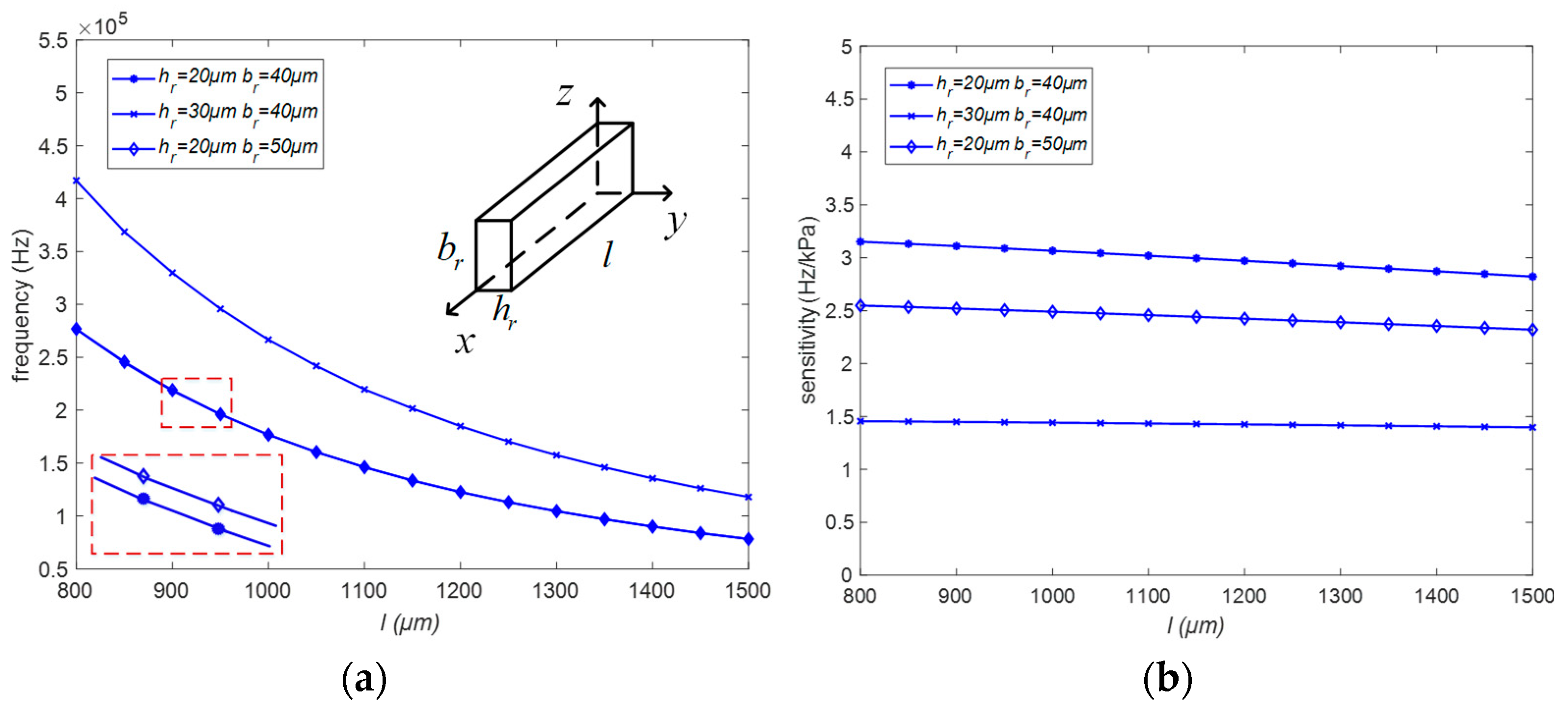
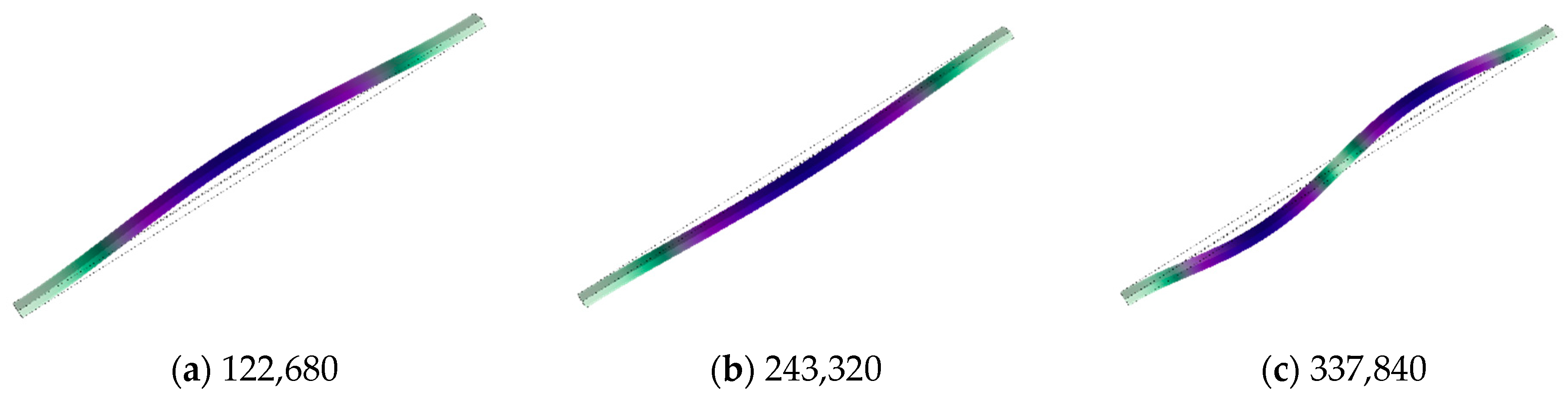
3.3. Resonant Beam Analysis
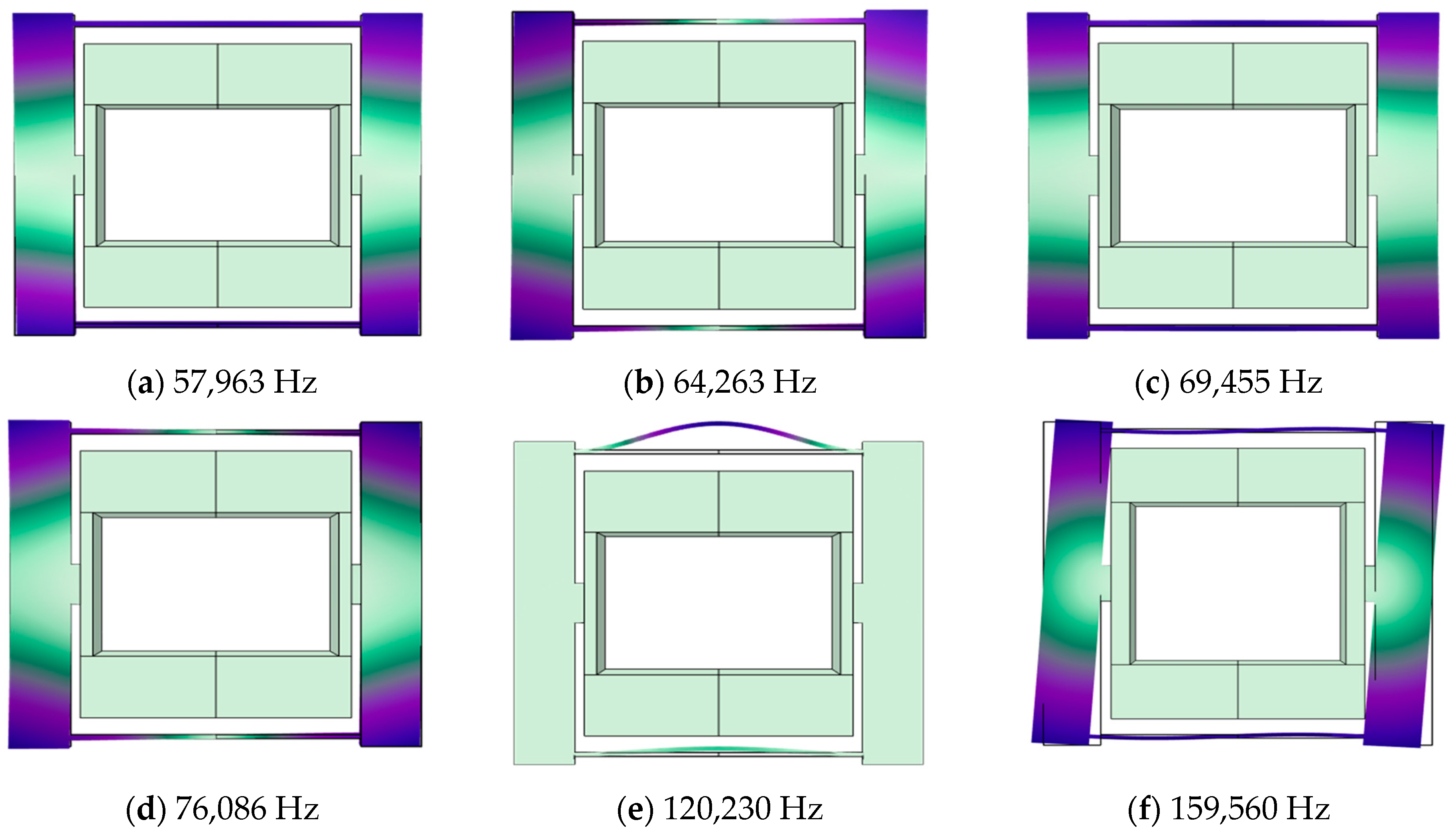
3.4. Overall Structural Analysis
4. Pressure Sensor Design and Optimization
4.1. Resonant Beam Structural Analysis and Design
4.2. Connecting Beam Structure Analysis and Design
4.3. Sensitive Diaphragm Structural Analysis and Design
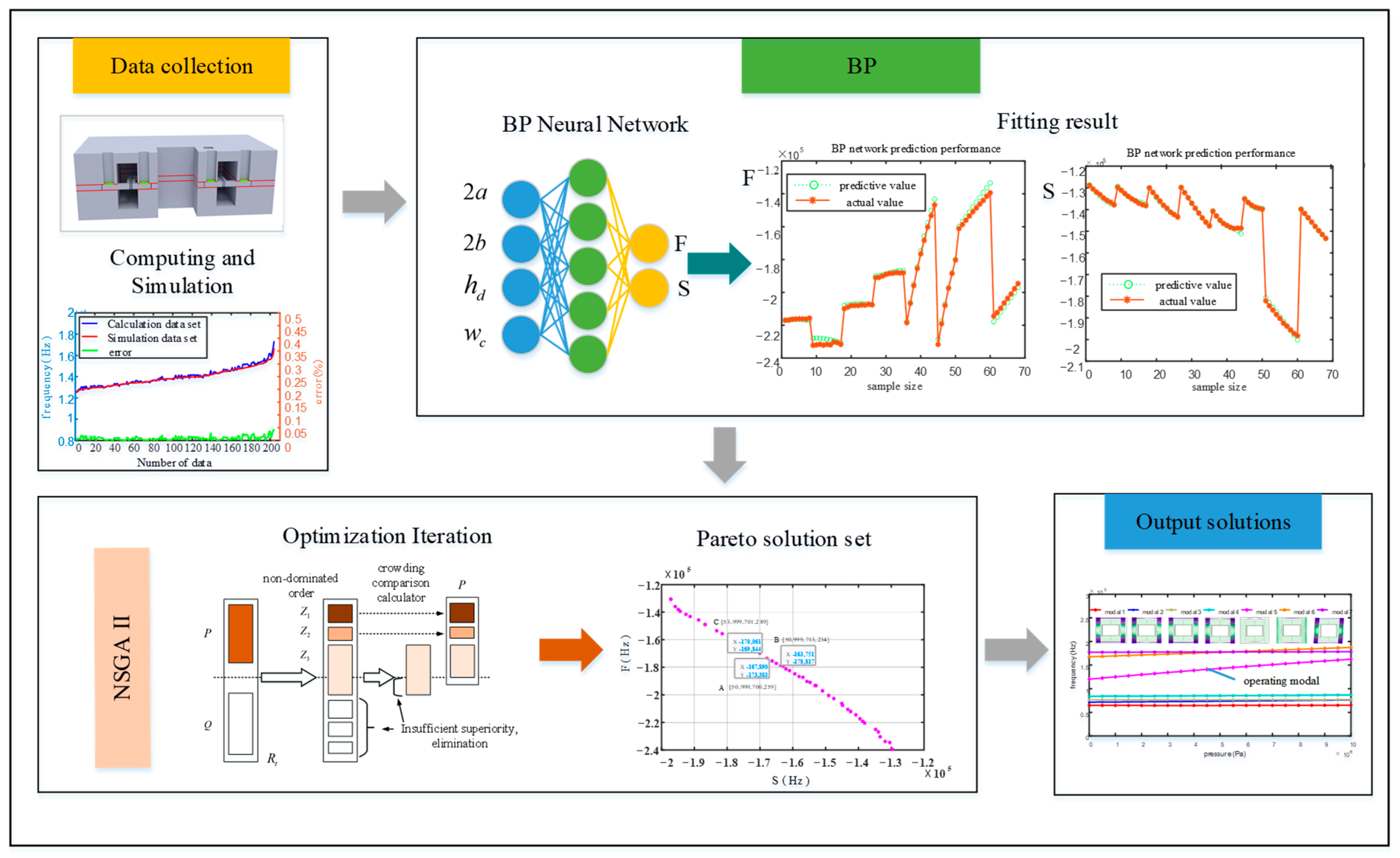
4.4. Resonator Structure Optimization
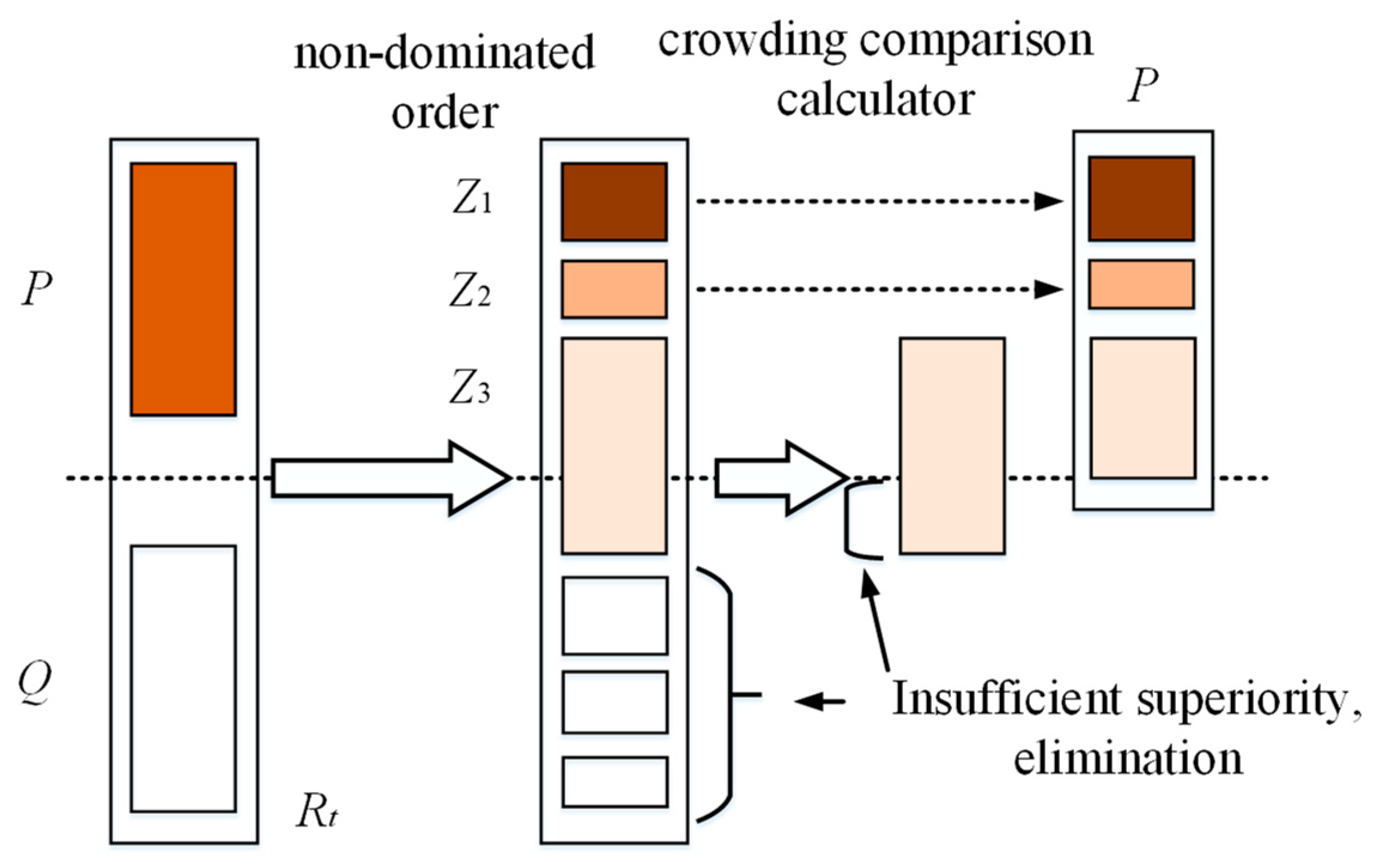
4.4.1. BP- and NSGA II-Optimized Structures
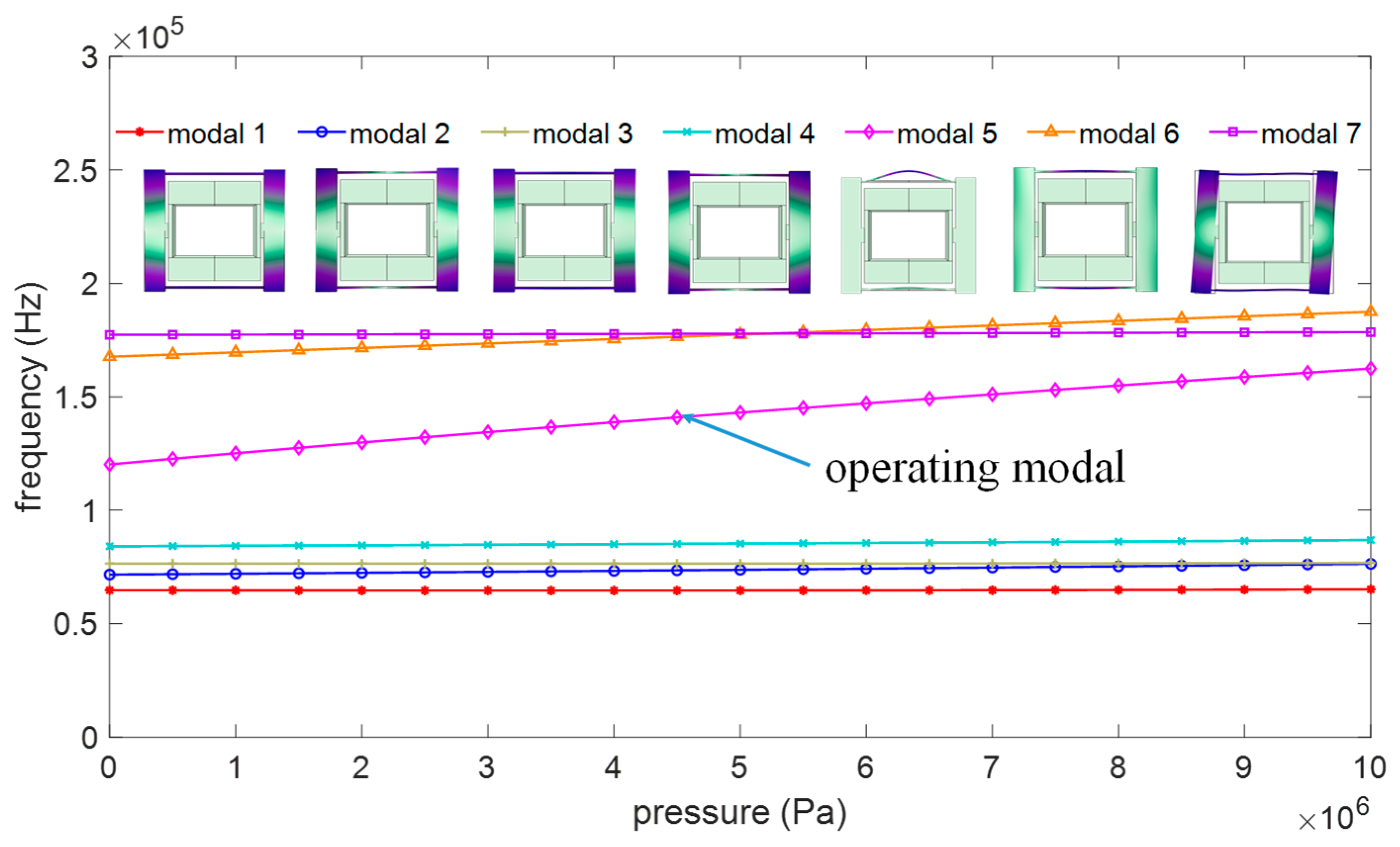
4.4.2. Optimization Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, X.; Mao, Q.; Zhao, L.; Li, X.; Wang, L.; Yang, P.; Lu, D.; Wang, Y.; Yan, X.; Wang, S.; et al. Novel resonant pressure sensor based on piezoresistive detection and symmetrical in-plane mode vibration. Microsyst. Nanoeng. 2020, 6, 95. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, S.; Chen, D.; Wang, J.; Chen, J. A Micromachined Resonant Low-Pressure Sensor With High Quality Factor. IEEE Sens. J. 2021, 21, 19840–19846. [Google Scholar] [CrossRef]
- Shi, X.; Lu, Y.; Xie, B.; Li, Y.; Wang, J.; Chen, D.; Chen, J. A Resonant Pressure Microsensor Based on Double-Ended Tuning Fork and Electrostatic Excitation/Piezoresistive Detection. Sensors 2018, 18, 2494. [Google Scholar] [CrossRef]
- Xiang, C.; Lu, Y.; Cheng, C.; Wang, J.; Chen, D.; Chen, J. A resonant pressure microsensor with a wide pressure measurement range. Micromachines 2021, 12, 382. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Lu, Y.; Chen, D.; Wang, J.; Chen, J.; Xie, B. A resonant high-pressure sensor based on integrated resonator-diaphragm structure. IEEE Sens. J. 2021, 22, 3920–3927. [Google Scholar] [CrossRef]
- Yu, J.; Lu, Y.; Xie, B.; Meng, Q.; Yu, Z.; Qin, J.; Chen, J.; Wang, J.; Chen, D. An Electrostatic Comb Excitation Resonant Pressure Sensor for High Pressure Applications. IEEE Sens. J. 2022, 22, 15759–15768. [Google Scholar] [CrossRef]
- Yan, P.; Lu, Y.; Xiang, C.; Wang, J.; Chen, D.; Chen, J. A Temperature-Insensitive Resonant Pressure Micro Sensor Based on Silicon-on-Glass Vacuμm Packaging. Sensors 2019, 19, 3866. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Yan, P.; Xiang, C.; Chen, D.; Wang, J.; Xie, B.; Chen, J. A resonant pressure microsensor with the measurement range of 1 MPa based on sensitivities balanced dual resonators. Sensors 2019, 19, 2272. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Zhao, L.; Wang, J.; Wang, L.; Huang, M.; Chen, C.; Yang, P.; Li, Z.; Zhu, N.; Wang, S.; et al. High-accuracy differential resonant pressure sensor with linear fitting method. J. Micromech. Microeng. 2021, 31, 045006. [Google Scholar] [CrossRef]
- Li, Y.; Cheng, C.; Lu, Y.; Xie, B.; Chen, J.; Wang, J.; Chen, D. A High-Sensitivity Resonant Differential Pressure Microsensor Based on Bulk Micromachining. IEEE Sens. J. 2021, 21, 8927–8934. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, S.; Chen, D.; Wang, J.; Chen, J.; Xie, B.; Lu, Y.; Li, Y. A Resonant Pressure Sensor Based upon Electrostatically Comb Driven and Piezoresistively Sensed Lateral Resonators. Micromachines 2019, 10, 460. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Yu, Z.; Xie, B.; Chen, D.; Wang, J. A pressure-temperature microsensor based on synergistical sensing of dual resonators. Measurement 2024, 224, 113946. [Google Scholar] [CrossRef]
- Du, X.; Liu, Y.; Li, A.; Zhou, Z.; Sun, D.; Wang, L. Laterally Driven Resonant Pressure Sensor with Etched Silicon Dual Diaphragms and Combined Beams. Sensors 2016, 16, 158. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, S.; Yan, P.; Li, Y.; Yu, J.; Chen, D.; Wang, J.; Xie, B.; Chen, J. Resonant Pressure Micro Sensors Based on Dual Double Ended Tuning Fork Resonators. Micromachines 2019, 10, 560. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Zhuang, X.; Sheng, Y.; Qiao, Q.; Lv, M.; Gao, Z.; Liao, J. Design and Optimization of Hemispherical Resonators Based on PSO-BP and NSGA-II. Micromachines 2023, 14, 1054. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ren, S.; Yuan, W.; Qiao, D.; Deng, J.; Sun, X. A Micromachined Pressure Sensor with Integrated Resonator Operating at Atmospheric Pressure. Sensors 2013, 13, 17006–17024. [Google Scholar] [CrossRef]
- Zhang, F.; Li, A.; Bu, Z.; Wang, L.; Sun, D.; Du, X.; Gu, D. Vibration modes interference in the MEMS resonant pressure sensor. Int. J. Mod. Phys. B 2017, 31, 1750223. [Google Scholar] [CrossRef]
- Xiang, C.; Lu, Y.; Yan, P.; Chen, J.; Wang, J.; Chen, D. A resonant pressure microsensor with temperature compensation method based on differential outputs and a temperature sensor. Micromachines 2020, 11, 1022. [Google Scholar] [CrossRef]

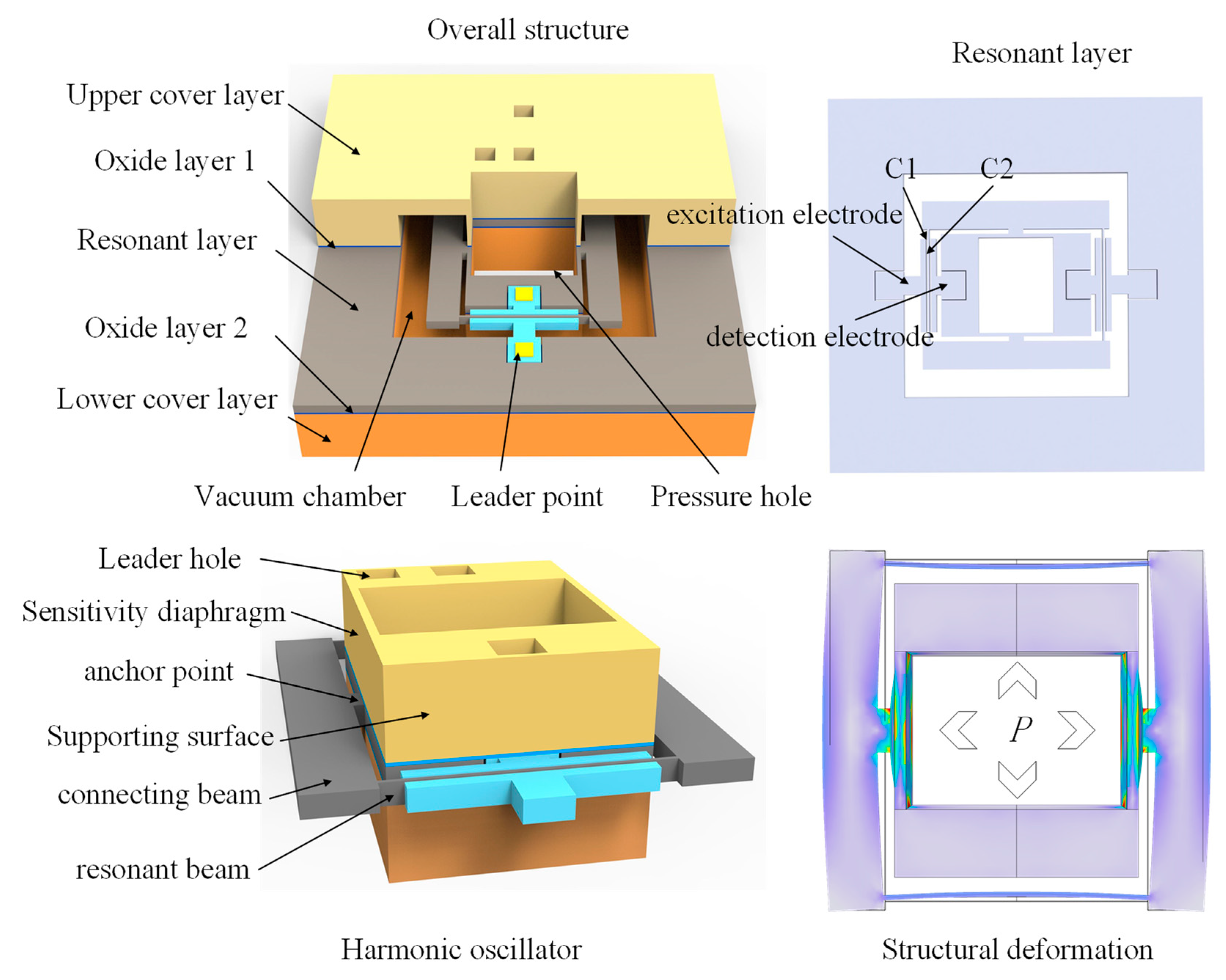





| hd/μm | 2b/μm | 2a/μm | wc/μm | S/Hz | F/Hz |
|---|---|---|---|---|---|
| 50 | 800 | 600 | 230 | −145,745.2954 | −206,431.3251 |
| 50 | 800 | 600 | 240 | −147,728.3998 | −203,625.0286 |
| 60 | 800 | 700 | 250 | −144,926.1623 | −195,884.3529 |
| 65 | 800 | 700 | 250 | −140,845.8125 | −202,368.2791 |
| 70 | 800 | 700 | 250 | −137,959.511 | −207,989.4299 |
| 75 | 800 | 700 | 250 | −135,335.4896 | −213,111.4485 |
| 70 | 750 | 700 | 250 | −136,039.2568 | −207,997.5868 |
| 70 | 800 | 700 | 250 | −137,959.511 | −207,989.4299 |
| 70 | 850 | 700 | 250 | −139,393.7201 | −207,660.0328 |
| 60 | 800 | 650 | 250 | −142,946.4384 | −206,745.8811 |
| 60 | 800 | 700 | 250 | −144,926.1623 | −195,884.3529 |
| 60 | 800 | 750 | 250 | −146,436.1059 | −185,449.8793 |
| 60 | 800 | 800 | 250 | −147,310.5528 | −176,572.7048 |
| 60 | 800 | 850 | 250 | −148,220.33 | −168,312.7138 |
| … | … | … | … | … | … |
| Name | Definition of Parameters | Range (μm) |
|---|---|---|
| 2a | Width of diaphragm | 713 |
| 2b | Height of diaphragm | 999 |
| hd | Thickness of diaphragm | 50 |
| wc | Width of connect beam | 234 |
| Lc | Length of connect beam | 1626 |
| hc | Height of connect beam | 40 |
| l | Length of resonant beam | 1200 |
| br | Height of resonant beam | 40 |
| hr | Width of resonant beam | 20 |
| S | Resonant frequency | 162,479 Hz |
| F | Interference frequency | 178,493 Hz |
| Time | Author | Range (MPa) | Sensitivity (Hz/kPa) | Linear Influence Factor | Linearity |
|---|---|---|---|---|---|
| 2019 | Lu Y [8] | 0.02–1 | 13.1 | 12.838 | 0.9999 |
| 2019 | Yan P [7] | 0.01–1 | 11.89 | 11.6522 | 0.9999 |
| 2020 | Xiang C [19] | 0.02–2 | 3.15 | 6.237 | 0.9999 |
| 2021 | Xiang C [3] | 0.02–7 | 2.26 | 18.0348 | 0.9998 |
| 2021 | X Han [9] | 0–0.2 | 35.5 | 7.01 | 0.9999 |
| 2022 | Yu J [5] | 0.11–30 | 0.428 | 12.84 | 0.9999 |
| 2022 | Yu J [6] | 0.11–50 | 0.066 | 3.3 | 0.9999 |
| This structure | 1–10 | 4.23 | 38.07 | 0.9984 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, M.; Li, P.; Miao, J.; Qiao, Q.; Liang, R.; Li, G.; Zhuang, X. Design and Optimization of MEMS Resonant Pressure Sensors with Wide Range and High Sensitivity Based on BP and NSGA-II. Micromachines 2024, 15, 509. https://doi.org/10.3390/mi15040509
Lv M, Li P, Miao J, Qiao Q, Liang R, Li G, Zhuang X. Design and Optimization of MEMS Resonant Pressure Sensors with Wide Range and High Sensitivity Based on BP and NSGA-II. Micromachines. 2024; 15(4):509. https://doi.org/10.3390/mi15040509
Chicago/Turabian StyleLv, Mingchen, Pinghua Li, Jiaqi Miao, Qi Qiao, Ruimei Liang, Gaolin Li, and Xuye Zhuang. 2024. "Design and Optimization of MEMS Resonant Pressure Sensors with Wide Range and High Sensitivity Based on BP and NSGA-II" Micromachines 15, no. 4: 509. https://doi.org/10.3390/mi15040509





